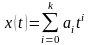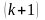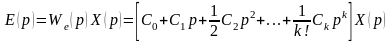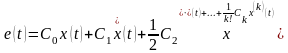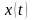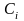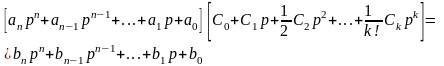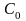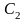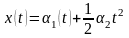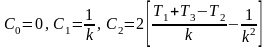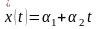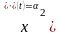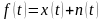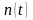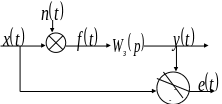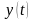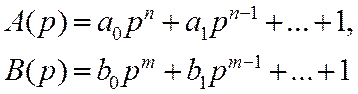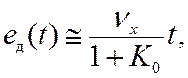Динамическая ошибка радиоавтоматика

1. Динамическая ошибка сау. Нахождение коэффициентов ошибок.

Помимо статистических
ошибок точность работы систем
радиоавтоматики характеризуется
динамическими и переходными ошибками.

Динамическая
ошибка – ошибка в установившемся режиме
работы системы при действии на неё
нестационарного сигнала.

Переходная ошибка
– ошибка при работе системы в переходном
процессе, который возникает при отработке
начального рассогласования.

Динамическая
точность работы систем радиоавтоматики
определяется при медленно изменяющихся
входных сигналах (воздействия, число
производных от которых ограничено).

Cигнал

относится
к медленно изменяющемуся воздействию,
так как число производных от этого
сигнала неравных нулю, равно
,
а

-я
производная равна нулю. Гармонический
сигнал не является медленно изменяющимся,
так как число производных от него равно

.

Переходные процессы
в системах радиоавтоматики затухают
значительно быстрее по сравнению с
изменением медленно изменяющегося
сигнала, поэтому и достигается
установившейся динамический режим
работы системы.

По определению
передаточной функции рассогласования
преобразование Лапласа для ошибки
системы:

(6.1)

или
в области действительного переменного

(6.2)

Число слагаемых
в последнем выражении ограничено, так
как сигнал

является медленно изменяющимся
воздействием. Для нахождения неизвестных
коэффициентов

,
которые называются коэффициентами
ошибки, известны три способа.

1)

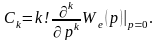
2) Вторым способом
коэффициенты ошибок находятся путём
деления числителя передаточной функции
ошибки на её знаменатель.

3) Для реализации
третьего способа представим передаточную
функцию ошибки в виде:

.

Перемножив полином
знаменателя на (6.1), получим:

(6.3)

Приравняв
коэффициенты при одинаковых степенях

слева и справа в выражении (6.3), определим
формулы для последовательного вычисления
коэффициентов ошибок:

2 Влияние на ошибку системы коэффициента усиления системы и введение форсирующего звена

В
инженерных расчётах коэффициенты ошибок
удобнее рассчитывать через коэффициенты
передаточной функции разомкнутой
системы:

,
(6.4)

где

—
порядок астатизма системы.

Первое
слагаемое в выражении (6.2) называют
ошибкой по положению, а коэффициент

-коэффициентом
ошибки по положению, второе слагаемое
– ошибкой по скорости, а коэффициент

—
коэффициентом ошибки по скорости.
Аналогично, третье слагаемое в (6.2)
называют ошибкой по ускорению, а
коэффициент

— коэффициентом ошибки по ускорению.

В
астатических системах

первых коэффициентов ошибок равны нулю,
где

—
порядок астатизма системы радиоавтоматики.

При
анализе качества работы систем
радиоавтоматики помимо вычисления
ошибок при медленно изменяющихся
сигналах приходится оценивать точность
и при гармонических воздействиях. В
этом случае нельзя применять метод
коэффициентов ошибок, так как число
производных от гармонического сигнала
не ограничено. При этом для расчёта
ошибок необходимо использовать частотные
характеристики. По амплитудно-частотной
характеристике ошибки вычисляется
амплитуда колебаний ошибки, по
фазочастотной характеристике – сдвиг
колебаний ошибки относительно входного
сигнала.

Пример
6.1. Найти динамическую ошибку при входном
сигнале

следящей системы, передаточная функция
которой в разомкнутом состоянии

.

Преобразуем

.

Коэффициент
астатизма

.Тогда

,

,

.

Подставим
данные в выражение (2), получим:

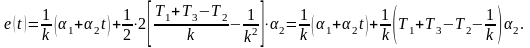
Вывод.
При увеличении коэффициента усиления
системы и введении форсирующего звена
ошибка уменьшается, увеличение же
постоянных времени инерционных звеньев
ухудшает динамическую ошибку системы.

3
Средняя
квадратическая ошибка системы.

В
большинстве случаев закон распределения
ошибки системы можно считать гауссовским,
поэтому для расчёта составляющих
суммарной средней квадратической ошибки
достаточно учесть математическое
ожидание и корреляционную функцию
ошибки или её спектральную плотность.

На
вход системы подаётся воздействие вида:

,

где

—
случайный сигнал;

— случайная помеха.

—
cуммарная
ошибка системы, где

— выходной сигнал системы.

Рис.
7.1. К определению суммарной ошибки

На
приведённом рисунке круг означает
сумматор, а сектор круга со знаком минус
означает операцию вычитания.

Преобразование
Лапласа для суммарной ошибки:

(7.1)

Вывод.
Суммарная ошибка состоит из двух
составляющих, одна из которых, определяющая
точность воспроизведения сигнала,
зависит от передаточной функции ошибки,
вторая, обусловленная действием помехи,
— от передаточной функции замкнутой
системы.

Предположим,
что сигнал и помеха являются стационарными
случайными функциями. Тогда математическое
ожидание помехи

,
а случайный сигнал представим в виде:

,

где

—
математическое ожидание сигнала;

— случайная составляющая сигнала.

Математическое
ожидание суммарной ошибки рассчитывают
по теореме о конечном значении функции:

.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Определение динамических ошибок (по
скорости, по ускорению) для статической и астатических систем.

Точность АС
характеризуется величиной ошибки в установившемся режиме и зависит от характера
воздействия, а также структуры и параметров системы.

Реальные воздействия
в радиотехнических следящих системах описывается сложными (случайными)
функциями времени. Однако при анализе точности управления часто используют
простые детерминированные воздействия: постоянное ступенчатое, линейное,
квадратичное и другие. Это позволяет упростить анализ и в то же время сохранить
в модели задающего воздействия наиболее существенные признаки (начальное
значение, скорость изменения, ускорение). Большинство систем радиоавтоматики
описываются передаточными функциями вида

,                                                 (11.1)

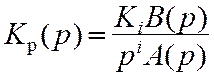
где K_i — общее усиление
разомкнутой системы, i – число интегрирующих
звеньев, определяющее порядок астатизма системы;

– полиномы, порядок которых определяется числом типовых
звеньев (n и m соответственно инерционных и форсирующих), а
коэффициенты полиномов – постоянными времени типовых звеньев.

11.1. Статические ошибки

Ошибка системы при постоянном
(ступенчатом) воздействии x(t)=x₀=const при t³0
называется статическойe_ст.

Для установившейся
ошибки, учитывая, что изображение X(p)=x₀/p,
запишем:

.  (11.2)

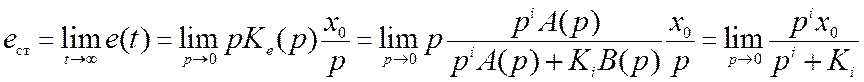
Для статической
системы (не содержащей интегрирующих звеньев) статическая ошибка равна

.                                                                      (11.3)

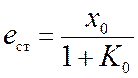
Таким образом, в
статических системах установившееся значение управляемой переменной не равно
заданному: меньше на величину ошибки, значение которой обратно пропорционально
усилению К₀ по постоянному току (обычно К₀>>1).

Для астатических
систем (i ³ 1) ошибка при постоянном воздействии

,

так как числитель в (11.2) равен нулю, а знаменатель равен
К_i.

Отсутствие
статической ошибки обусловило название таких систем – астатические.

11.2. Динамические ошибки

Ошибка,
характеризующая точность замкнутой системы при меняющемся воздействии,
называется динамической e_д(t).

Любое детерминированное
воздействие (при условии существования его производных d^(k)/dt^(k),
k=1, 2, …) можно представить в виде ряда

,                                  (11.4)

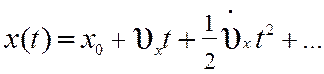
где x₀ — начальное значение,  — скорость изменения, — ускорение и т. д.

Для вычисления
динамических ошибок при типовых воздействиях (линейном и квадратическом)
представим выражение для ошибки в операторной форме:

                                   (11.5)

Используя разложение
передаточной функции K_e(p) в ряд Маклорена по степеням
переменной р, перепишем (11.5) в виде

                           (11.6)

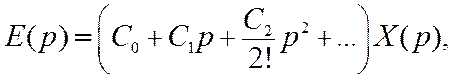
где C₀, C₁, C₂,
… — коэффициенты ошибок, определяемые
как

                                        (11.7)

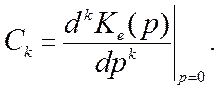
Установившееся
значение ошибки при произвольном воздействии x(t)
на основании (11.6) определяется временным рядом

                                       (11.8)

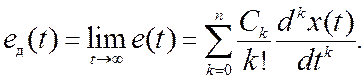
Чем меньше
коэффициенты ошибок, тем выше точность системы при произвольном
детерминированном воздействии. При вычислении коэффициентов C_k
обычно ограничиваются только первыми тремя (для систем с астатизмом не выше
второго порядка).

Коэффициент C₀
в соответствии с (11.7) равен

.

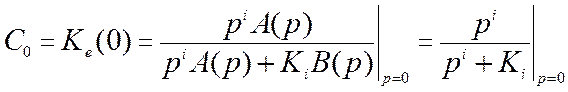
Для статических
систем (i=0) C₀=1/(1+K₀), а для
астатических систем C₀=0.

Определим динамические
ошибки типовых систем при линейном воздействии (изменение с постоянной
скоростью) x(t)=n_xt.

В соответствии с
формулой (11.8) динамическая ошибка (ошибка по скорости) определяется как

.

Для статической
системы она равна

так как вклад составляющей C₁n_x
значительно меньше, чем C₀ x(t), которая растет
линейно со временем. Таким образом, скоростная ошибка в статических системах
накапливается со временем со скоростью n_x/(1+K₀), что делает неприемлемым использование
таких систем при меняющемся воздействии. Для астатических систем C₀=0 и скоростная ошибка

.

Нахождение
коэффициента ошибки C₁ с использованием формулы (11.7)
затруднительно. Более простой способ его вычисления основан на сравнении
точного выражения для передаточной функции K_e(p) и
аппроксимирующего ее ряда:

                (11.9)

Уравнение (11.9)
можно представить в виде

              (11.10)

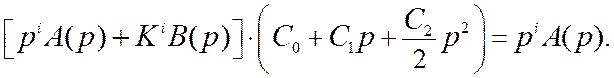
Полагая i= 1 (астатическая система первого порядка) и приравнивая
коэффициенты при переменной p в левой и правой частях уравнения, находим

или C₁=1/K₁, так как C₀=0.

Таким образом,
скоростная ошибка системы первого порядка астатизма e_д=n_x/K₁
определяется усилением разомкнутой системы K₁ и не зависит от
времени. Параметр K₁, имеющий размерность c ^–1,
называется добротностью системы по скорости (чем выше добротность, тем
точнее система).

Для астатической
системы второго порядка скоростная ошибка равна нулю, так как оба коэффициента C₀=C₁=0.
Равенство C₁=0 вытекает из уравнения (11.10), так как в
правой части уравнения не содержится слагаемого, в которое входит переменная p
(есть только с p² и выше).

Оценим динамические
ошибки типовых систем при квадратичном воздействии (изменение с постоянным
ускорением).

В соответствии с (11.8)
для динамической ошибки (ошибки по ускорению) запишем

.                                        (11.11)

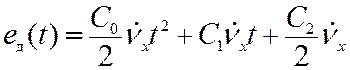
Для статической
системы ошибка по ускорению равна

                                    (11.12)

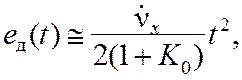
так как составляющие ошибки с коэффициентами C₁ и C₂
вносят пренебрежимо малый вклад в результирующую ошибку. Накопление ошибки по
квадратичному закону исключает применение статических систем при наличии
ускорения.

Для системы первого
порядка астатизма ошибка по ускорению равна

                                      (11.13)

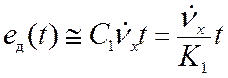
(вкладом составляющей  можно
пренебречь). Накопление ошибки со временем (со скоростью ) не позволяет применять такие
системы при наличии ускорения. Для астатической системы второго порядка ошибка
по ускорению равна

.                                      (11.14)

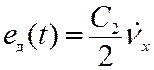
Определение
коэффициента ошибки C₂ с использованием уравнения (11.7)
сводится к приравниванию коэффициентов при p² в обеих частях
уравнения:

.                           (11.15)

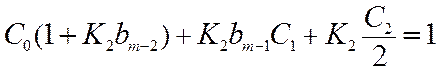
Откуда
C₂/2=1/K₂, так как C₀=C₁=0.