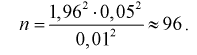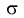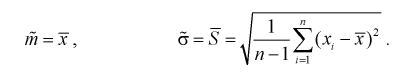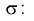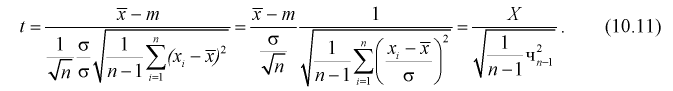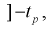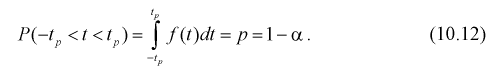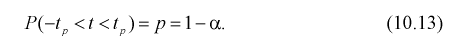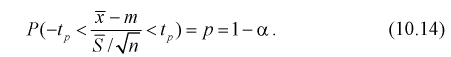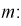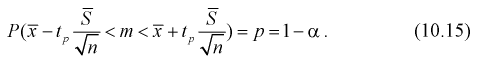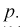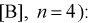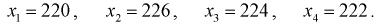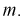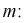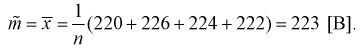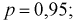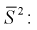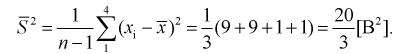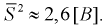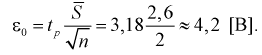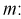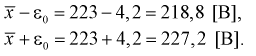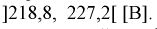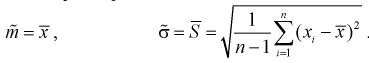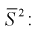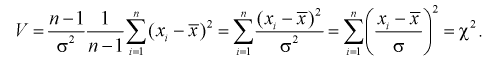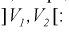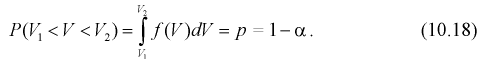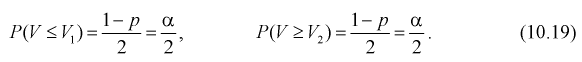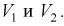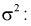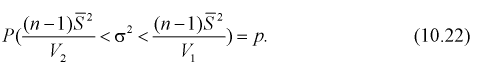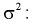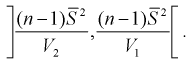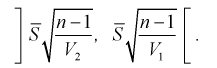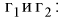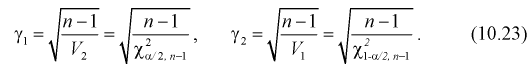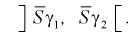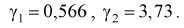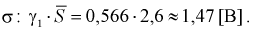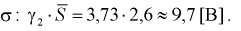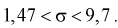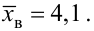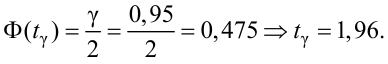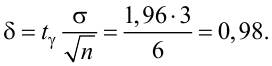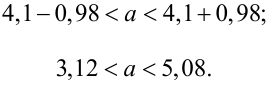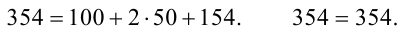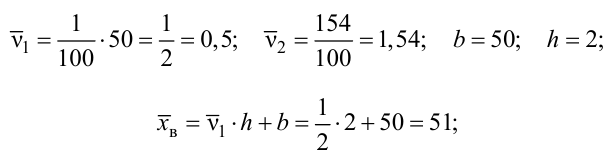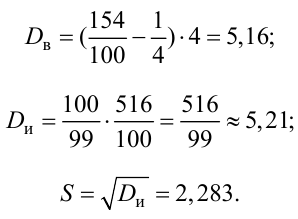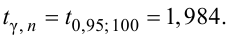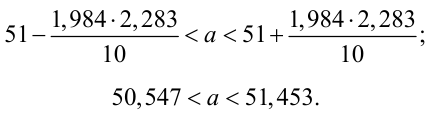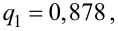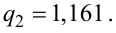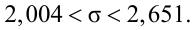Методы исследований в менеджменте.
Статистические выводы. Оценки и проверка
гипотез
Лекция № 3.
Статистические выводы: оценки и проверка
гипотез
3.1 Точечные оценки
и их свойства
3.2 Свойства
выборочных оценок
3.3 Интервальные
оценки
3.4
Проверка гипотез: основные понятия
3.5
Критерии проверки. Критическая область
Статистические
выводы – это
заключения о генеральной совокупности
(т. е. о законе распределения исследуемой
СВ и его параметрах либо о наличии и
силе связи между исследуемыми переменными)
на основе выборки, случайно отобранной
из генеральной совокупности.
При
исследовании различных параметров
генеральной совокупности на основе
выборки возможно лишь получение оценок
этих параметров. Эти оценки строятся
на основе ограниченного набора
данных, что влечет за собой вероятность
погрешности. Заметим, что значения
оценок могут изменяться от выборки к
выборке. Процесс нахождения оценок по
определенному правилу (формуле) будем
называть оцениванием. Цель любого
оценивания – получение наиболее точного
значения оцениваемой характеристики.
Можно
выделить два типа оценивания: оценивание
вида распределения и оценивание
параметров распределения. В качестве
оценки вида распределения (в силу закона
больших чисел) можно взять выборочное
распределение, подсчитав частоты
попадания рассматриваемой СВ в заданные
подынтервалы интервального статистического
ряда. Процедура оценивания всегда
однотипна. На основе выборки с помощью
соответствующей формулы рассчитывается
оценка исследуемой характеристики.
В качестве оценок параметров распределения
генеральной совокупности берутся
их выборочные оценки. При этом различают
два вида оценок — точечные и интервальные.
После
определения оценок обычно встает вопрос
об их качестве и статистической
значимости. С другой стороны, часто до
определения оценок выдвигаются
предположения о значениях исследуемых
параметров. Анализ соответствия
результатов выборки выдвигаемым
предположениям и определение статистической
значимости полученных выводов обычно
осуществляются по схеме статистической
проверки гипотез, что также требует
рассмотрения.
Пусть
оценивается некоторый параметр
наблюдаемой СВ Х
генеральной
совокупности. Пусть из генеральной
совокупности извлечена выборка объема
п:
х1,
х2,
хn,
по
которой может быть найдена оценка
параметра
.
Например, для нормального закона
распределения с плотностью вероятности

параметрами
являются математическое ожидание т
и
среднее квадратическое отклонение σ.
Точечной
оценкой
параметра называется числовое значение
этого параметра, полученное по выборке
объема п.
Оценка
является функцией от выборки, т. е.
=
(х1,
х2,
хn).
Так как выборка носит случайный характер,
то оценка
является СВ, принимающей различные
значения для различных выборок. Любую
оценку
(х1,
х2,
хn)
называют статистикой
или
статистической
оценкой параметра
.
Число
ε такое, что
называется точностью оценки
Естественно стремление получить по
возможности наиболее точную оценку при
данном объеме выборки.
Приведем свойства,
выполнимость которых желательна для
того, чтобы оценка была признана
удовлетворительной.
В силу
случайности точечной оценки
она может рассматриваться как СВ со
своими числовыми характеристиками —
математическим ожиданием
и
дисперсией
.
Чем ближе
к
истинному значению
и чем меньше
,
тем лучше будет оценка (при прочих
равных условиях). Таким образом,
качество оценок характеризуется
следующими основными свойствами:
несмещенность, эффективность и
состоятельность.
Оценка
называется несмещенной
оценкой параметра
,
если ее математическое ожидание равно
оцениваемому параметру:
=
.
Хотя
каждая отдельная оценка лишь в редких
случаях совпадает с соответствующей
характеристикой генеральной совокупности,
при «аккуратном» оценивании многократное
осуществление выборок одного объема
п
обеспечивает
совпадение среднего значения оценки
по всем выборкам с истинным значением
оцениваемого параметра.
Разность
—
называется смещением
или
систематической
ошибкой оценивания.
Для несмещенных оценок систематическая
ошибка равна нулю.
Свойство
несмещенности оценки является важнейшим,
но не единственным. Зачастую существует
несколько возможных оценок одного и
того же параметра. Какая из них лучше?
Очевидно, выбор будет сделан в пользу
той из них, вероятность совпадения
которой с истинным значением оцениваемого
параметра выше. Оценка должна иметь
такую плотность вероятности, которая
наиболее «сжата» вокруг истинного
значения оцениваемого параметра.
Нетрудно заметить, что в этом случае
она будет иметь наименьшую среди других
оценок дисперсию.
Оценка
называется эффективной
оценкой параметра
,
если ее дисперсия
меньше
дисперсии любой другой альтернативной
оценки при фиксированном объеме выборки
п,
т.е.
=
.
На рисунке 3.1 приведена схема, наглядно
демонстрирующая преимущество эффективной
оценки
по сравнению с неэффективной оценкой
параметра
.
Каждая
отдельная эффективная оценка не
гарантирует того, что она дает более
точное значение исследуемого параметра,
чем менее эффективная. Однако вероятность
такого исхода превышает 0,5.
Оценка
называется асимптотически
эффективной, если
с увеличением объема выборки ее дисперсия
стремится к нулю, т.е.
при
(индекс
n
в оценке
применяется
для подчеркивания объема выборки).

Рисунок 3.1
Рисунок 3.2
Оценка
называется состоятельной
оценкой параметра
,
если
сходится по вероятности к
при
,
т. е. для любого
при
.
Другими словами, состоятельной называется
такая оценка, которая дает истинное
значение при достаточно большом объеме
выборки вне зависимости от значений
входящих в нее конкретных наблюдений.
Схема
возможного улучшения точности
(несмещенности) состоятельной оценки
приведена на рисунке 3.2.
В
большинстве случаев несмещенная оценка
является и состоятельной. С другой
стороны, состоятельные оценки (возможно,
не являющиеся несмещенными при малых
объемах выборок) с увеличением объема
выборки будут приближаться и лежать
все «плотнее» к истинному значению
(рисунок 3.2). Это указывает на асимптотическую
несмещенность состоятельной оценки.
Поэтому при невозможности получения
несмещенной оценки целесообразно найти
хотя бы состоятельную оценку.
Справедливо
следующее утверждение: если
и
при
,
то
—
состоятельная
оценка параметра
.
Оценки,
являющиеся линейными функциями от
выборочных наблюдений, называются
линейными.
Очень
важную роль в эконометрике играют так
называемые наилучшие
линейные несмещенные оценки, или
коротко BLUE-оценки
(Best
Linear
Unbiased
Estimators).
Такие оценки, являясь линейными и
несмещенными, имеют наименьшую дисперсию
среди всех возможных оценок данного
класса.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
План:
1. Задачи математической статистики.
2. Виды выборок.
3. Способы отбора.
4. Статистическое распределение выборки.
5. Эмпирическая функция распределения.
6. Полигон и гистограмма.
7. Числовые характеристики вариационного ряда.
8. Статистические оценки параметров
распределения.
9. Интервальные оценки параметров распределения.
1.
Задачи и методы математической статистики
Математическая статистика— это раздел математики, посвященный методам
сбора, анализа и обработки результатов статистических данных наблюдений для
научных и практических целей.
Пусть требуется
изучить совокупность однородных объектов относительно некоторого качественного
или количественного признака, характеризующего эти объекты. Например, если
имеется партия деталей, то качественным признаком может служить стандартность детали,
а количественным- контролируемый размер детали.
Иногда проводят
сплошное исследование, т.е. обследуют каждый объект относительно нужного
признака. На практике сплошное обследование применяется редко. Например, если
совокупность содержит очень большое число объектов, то провести сплошное
обследование физически невозможно. Если обследование объекта связано с его
уничтожением или требует больших материальных затрат, то проводить сплошное
обследование не имеет смысла. В таких случаях случайно отбирают из всей
совокупности ограниченное число объектов (выборочную совокупность) и подвергают
их изучению.
Основная задача
математической статистики заключается в исследовании всей совокупности по
выборочным данным в зависимости от поставленной цели, т.е. изучение
вероятностных свойств совокупности: закона распределения, числовых
характеристик и т.д. для принятия управленческих решений в условиях
неопределенности.
2.
Виды выборок
Генеральная совокупность – это совокупность объектов, из которой производится выборка.
Выборочная совокупность (выборка) – это совокупность случайно отобранных
объектов.
Объем совокупности –
это число объектов этой совокупности. Объем генеральной совокупности
обозначается N,
выборочной – n.
Пример:
Если из 1000
деталей отобрано для обследования 100 деталей, то объем генеральной
совокупности N =
1000, а объем выборки n =
100.
При составлении выборки можно поступить двумя
способами: после того, как объект отобран и над ним произведено наблюдение, он
может быть возвращен либо не возвращен в генеральную совокупность. Т.о. выборки
делятся на повторные и бесповторные.
Повторной называют выборку, при которой
отобранный объект (перед отбором следующего) возвращается в генеральную
совокупность.
Бесповторной называют выборку, при которой отобранный
объект в генеральную совокупность не возвращается.
На практике обычно
пользуются бесповторным случайным отбором.
Для того, чтобы по
данным выборки можно было достаточно уверенно судить об интересующем признаке
генеральной совокупности, необходимо, чтобы объекты выборки правильно его
представляли. Выборка должна правильно представлять пропорции генеральной
совокупности. Выборка должна быть репрезентативной (представительной).
В силу закона больших чисел можно утверждать,
что выборка будет репрезентативной, если ее осуществлять случайно.
Если объем
генеральной совокупности достаточно велик, а выборка составляет лишь
незначительную часть этой совокупности, то различие между повторной и
бесповторной выборками стирается; в предельном случае, когда рассматривается
бесконечная генеральная совокупность, а выборка имеет конечный объем, это
различие исчезает.
Пример:
В американском журнале
«Литературное обозрение» с помощью статистических методов было проведено исследование прогнозов
относительно исхода предстоящих выборов президента США в 1936 году.
Претендентами на этот пост были Ф.Д. Рузвельт и А. М. Ландон. В качестве
источника для генеральной совокупности исследуемых американцев были взяты
справочники телефонных абонентов. Из них случайным образом были выбраны 4
миллиона адресов., по которым редакция журнала разослала открытки с просьбой
высказать свое отношение к кандидатам на пост президента. Обработав результаты
опроса, журнал опубликовал социологический прогноз о том, что на предстоящих
выборах с большим перевесом победит Ландон. И … ошибся: победу одержал
Рузвельт.
Этот пример можно рассматривать, как пример нерепрезентативной выборки. Дело в
том, что в США в первой половине двадцатого века телефоны имела лишь зажиточная
часть населения, которые поддерживали взгляды Ландона.
3.
Способы отбора
На практике
применяются различные способы отбора, которые можно разделить на 2 вида:
1. Отбор не требует
расчленения генеральной совокупности на части (а) простой случайный
бесповторный; б) простой случайный повторный).
2. Отбор, при
котором генеральная совокупность разбивается на части. (а) типичный отбор;
б) механический отбор; в) серийный отбор).
Простым случайным
называют такой отбор, при котором объекты извлекаются по одному из всей
генеральной совокупности (случайно).
Типичным называют отбор, при котором объекты
отбираются не из всей генеральной совокупности, а из каждой ее «типичной»
части. Например, если деталь изготавливают на нескольких станках, то отбор
производят не из всей совокупности деталей, произведенных всеми станками, а из
продукции каждого станка в отдельности. Таким отбором пользуются тогда, когда
обследуемый признак заметно колеблется в различных «типичных» частях
генеральной совокупности.
Механическим называют отбор, при котором
генеральную совокупность «механически» делят на столько групп, сколько объектов
должно войти в выборку, а из каждой группы отбирают один объект. Например, если
нужно отобрать 20 % изготовленных станком деталей, то отбирают каждую 5-ую
деталь; если требуется отобрать 5 % деталей- каждую 20-ую и т.д. Иногда такой
отбор может не обеспечивать репрезентативность выборки (если отбирают каждый
20-ый обтачиваемый валик, причем сразу же после отбора производится замена
резца, то отобранными окажутся все валики, обточенные затупленными резцами).
Серийным называют отбор, при котором объекты
отбирают из генеральной совокупности не по одному, а «сериями», которые
подвергают сплошному обследованию. Например, если изделия изготавливаются
большой группой станков-автоматов, то подвергают сплошному обследованию
продукцию только нескольких станков.
На практике часто
применяют комбинированный отбор, при котором сочетаются указанные выше способы.
4.
Статистическое распределение выборки
Пусть из генеральной совокупности извлечена выборка, причем значение x1–наблюдалось
раз,
x2-n2
раз,… xk — nk
раз. n =
n1+n2+…+nk– объем
выборки. Наблюдаемые значения
называются вариантами, а
последовательность вариант, записанных в возрастающем порядке- вариационным
рядом. Числа наблюдений
называются
частотами (абсолютными частотами), а их отношения к объему выборки
— относительными частотами или статистическими вероятностями.
Если количество
вариант велико или выборка производится из непрерывной генеральной
совокупности, то вариационный ряд составляется не по отдельным точечным
значениям, а по интервалам значений генеральной совокупности. Такой
вариационный ряд называется интервальным.
Длины интервалов при этом должны быть равны.
Статистическим
распределением выборки
называется перечень вариант и соответствующих им частот или относительных
частот.
Статистическое
распределение можно задать также в виде последовательности интервалов и
соответствующих им частот (суммы частот, попавших в этот интервал значений)
Точечный
вариационный ряд частот может быть представлен таблицей:
|
xi |
x1 |
x2 |
… |
xk |
|
ni |
n1 |
n2 |
… |
nk |
Аналогично можно
представить точечный вариационный ряд относительных частот.
Причем:
Пример:
Число букв в
некотором тексте Х оказалось равным 1000. Первой встретилась буква «я», второй- буква «и», третьей- буква
«а», четвертой- «ю». Затем шли буквы
«о», «е», «у», «э», «ы».
Выпишем места,
которые они занимают в алфавите, соответственно имеем: 33, 10, 1, 32, 16, 6,
21, 31, 29.
После упорядочения
этих чисел по возрастанию получаем вариационный ряд: 1, 6, 10, 16, 21, 29, 31,
32, 33.
Частоты появления
букв в тексте: «а» — 75, «е» -87, «и»- 75, «о»- 110, «у»- 25, «ы»- 8, «э»- 3,
«ю»- 7, «я»- 22.
Составим точечный
вариационный ряд частот:
Пример:
Задано
распределение частот выборки объема n
= 20.
Составьте точечный
вариационный ряд относительных частот.
Решение:
Найдем
относительные частоты:
|
xi |
2 |
6 |
12 |
|
wi |
0,15 |
0,5 |
0,35 |
При построении интервального
распределения существуют правила выбора
числа интервалов или величины каждого интервала. Критерием здесь служит
оптимальное соотношение: при увеличении числа интервалов улучшается репрезентативность,
но увеличивается объем данных и время на их обработку. Разность
xmax — xmin между наибольшим и наименьшим значениями
вариант называют размахом выборки.
Для подсчета числа
интервалов k
обычно применяют эмпирическую формулу Стреджесса (подразумевая округление до
ближайшего удобного целого): k
= 1 + 3.322 lg n.
Соответственно,
величину каждого интервала h
можно вычислить по формуле
:
5.
Эмпирическая
функция распределения
Рассмотрим некоторую
выборку из генеральной совокупности. Пусть известно статистическое
распределение частот количественного признака Х. Введем обозначения: nx
– число наблюдений, при которых
наблюдалось значение признака, меньшее х; n – общее число наблюдений (объем
выборки). Относительная частота события Х<х равна
nx/n. Если х изменяется, то изменяется и относительная частота, т.е.
относительная частота nx/n—
есть функция от х. Т.к. она находится эмпирическим путем, то она называется
эмпирической.
Эмпирической функцией распределения
(функцией распределения выборки) называют функцию
,
определяющую для каждого х относительную частоту события Х<х.
где
число вариант, меньших х,
n— объем выборки.
В отличие от эмпирической функции
распределения выборки, функцию распределения F(x)
генеральной совокупности называют теоретической функцией распределения.
Различие между эмпирической и
теоретической функциями распределения состоит в том, что теоретическая функция F(x) определяет вероятность события Х<x , а эмпирическая
функция
F*(x) -относительную
частоту этого же события. Из теоремы Бернулли следует, что относительная
частота события Х<х , т.е
F*(x) стремится
по вероятности к вероятности F(x) этого события. Т.е.при
большом n F*(x)
и
F(x) мало отличаются друг от друга.
Т.о. целесообразно использовать
эмпирическую функцию распределения выборки для приближенного представления
теоретической (интегральной) функции распределения генеральной совокупности.
F*(x) обладает всеми свойствами F(x).
1. Значения
F*(x)
принадлежат
интервалу [0; 1].
2.
F*(x)
— неубывающая
функция.
3. Если
– наименьшая варианта, то
F*(x)= 0, при х
< x1
; если xk
– наибольшая варианта, то
F*(x)= 1, при х
> xk
.
Т.е.
F*(x) служит для
оценки F(x).
Если выборка задана вариационным рядом, то эмпирическая
функция имеет вид:
График эмпирической функции называется кумулятой.
Пример:
Постройте эмпирическую функцию по данному распределению
выборки.
Решение:
Объем выборки n = 12 + 18 +30 = 60. Наименьшая
варианта 2, т.е.
при х <
2. Событие X<6,
( x1= 2) наблюдалось 12 раз, т.е.
F*(x)=12/60=0,2 при 2 < x <
6. Событие Х<10, (
x1=2,
x2= 6) наблюдалось 12 + 18 = 30 раз, т.е. F*(x)=30/60=0,5
при 6 < x <
10. Т.к. х=10 наибольшая варианта, то F*(x) = 1
при х>10. Искомая эмпирическая функция имеет вид:
Кумулята:
Кумулята дает возможность
понимать графически представленную информацию, например, ответить на вопросы:
«Определите число наблюдений, при которых значение признака было меньше 6 или
не меньше 6. F*(6)=0,2
» Тогда число наблюдений, при которых
значение наблюдаемого признака было меньше 6 равно 0,2*n = 0,2*60 = 12. Число наблюдений, при
которых значение наблюдаемого признака было не меньше 6 равно (1-0,2)*n = 0,8*60 = 48.
Если задан интервальный вариационный
ряд, то для составления эмпирической функции распределения находят середины
интервалов и по ним получают эмпирическую функцию распределения аналогично
точечному вариационному ряду.
6. Полигон и гистограмма
Для наглядности строят различные графики
статистического распределения: полином и гистограммы
Полигон
частот- это ломаная, отрезки которой соединяют точки (
x1
;n1
), (
x2
;n2
),…, (
xk
; nk
), где
– варианты,
–
соответствующие им частоты.
Полигон
относительных частот- это ломаная, отрезки которой соединяют точки (
x1
;w1
), (x2
;w2
),…, (
xk
;wk
), где
xi–варианты,
wi –
соответствующие им относительные частоты.
Пример:
Постройте полином относительных
частот по данному распределению выборки:
Решение:
В случае
непрерывного признака целесообразно строить гистограмму, для чего интервал, в
котором заключены все наблюдаемые значения признака, разбивают на несколько
частичных интервалов длиной h
и находят для каждого частичного интервала ni – сумму частот вариант,
попавших в i-ый
интервал. (Например, при измерении роста человека или веса, мы имеем дело с
непрерывным признаком).
Гистограмма
частот- это ступенчатая фигура, состоящая из прямоугольников, основаниями
которых служат частичные интервалы длиною h, а высоты равны отношению
(плотность
частот).
Площадь i-го частичного
прямоугольника равна— сумме частот вариант i— го интервала, т.е. площадь
гистограммы частот равна сумме всех частот, т.е. объему выборки.
Пример:
Даны результаты изменения напряжения
(в вольтах) в электросети. Составьте вариационный ряд, постройте полигон и
гистограмму частот, если значения напряжения следующие: 227, 215, 230, 232,
223, 220, 228, 222, 221, 226, 226, 215, 218, 220, 216, 220, 225, 212, 217, 220.
Решение:
Составим вариационный ряд. Имеем n = 20, xmin=212
, xmax=232
.
Применим формулу
Стреджесса для подсчета числа интервалов.
.
Интервальный вариационный ряд
частот имеет вид:
|
|
|
Плотность частот |
|
212-216 |
3 |
0,75 |
|
216-220 |
3 |
0,75 |
|
220-224 |
7 |
1,75 |
|
224-228 |
4 |
1 |
|
228-232 |
3 |
0,75 |
Построим гистограмму частот:
Построим полигон частот, найдя предварительно середины
интервалов:
Гистограммой относительных
частот называют ступенчатую фигуру, состоящую из прямоугольников ,
основаниями которых служат частичные
интервалы длиною h, а
высоты равны отношению wi/h
(плотность
относительной частоты).
Площадь i-го частичного прямоугольника равна
— относительной частоте вариант, попавших в i— ый интервал. Т.е. площадь
гистограммы относительных частот равна сумме всех относительных частот, т.е.
единице.
7.
Числовые
характеристики вариационного ряда
Рассмотрим основные характеристики генеральной и выборочной
совокупностей.
Генеральным средним
называется среднее
арифметическое значений признака генеральной совокупности.
Для различных значений x1, x2
, x3
, …, xn.
признака
генеральной совокупности объема N
имеем:
Если
значения признака имеют соответствующие частоты N1
+N2
+…+Nk
=N,
то
Выборочным средним называется среднее арифметическое значений
признака выборочной совокупности.
Для различных значений x1, x2
, x3, …, xn
признака выборочной
совокупности объема n
имеем:
Если
значения признака имеют соответствующие частоты n1+n2+…+nk
= n,
то
Пример:
Вычислите выборочное среднее для выборки :
x1= 51,12;
x2= 51,07;
x3= 52,95; x4
=52,93;
x5= 51,1;x6
= 52,98; x7
= 52,29; x8
= 51,23; x9
= 51,07; x10
= 51,04.
Решение:
Генеральной дисперсией называется среднее арифметическое квадратов отклонений
значений признака Х генеральной совокупности от генерального среднего .
Для различных значений x1, x2, x3, …, xN
признака
генеральной совокупности объема N
имеем:
Если
значения признака имеют соответствующие частоты
N1+N2+…+Nk
=N,
то
Генеральным среднеквадратическим отклонением (стандартом)
называют квадратный корень из генеральной дисперсии
Выборочной дисперсией называется среднее
арифметическое квадратов отклонений наблюдаемых значений признака от среднего
значения.
Для различных значений
x1, x2, x3, …, xn
признака выборочной
совокупности объема n
имеем:
Если
значения признака имеют соответствующие частоты n1+n2+…+nk
= n,
то
Выборочным среднеквадратическим
отклонением (стандартом) называется квадратный корень из выборочной
дисперсии.
Пример:
Выборочная совокупность задана таблицей распределения. Найдите
выборочную дисперсию.
Решение:
Теорема: Дисперсия
равна разности среднего квадратов значений признака и квадрата общего среднего.
Пример:
Найдите дисперсию по данному распределению.
Решение:
8. Статистические оценки параметров распределения
Пусть генеральная совокупность исследуется по некоторой
выборке. При этом можно получить лишь приближенное значение неизвестного
параметра Q, который
служит его оценкой. Очевидно, что оценки могут изменяться от одной выборки к
другой.
Статистической
оценкой Q* неизвестного параметра
теоретического распределения называется функция f, зависящая от наблюдаемых значений
выборки. Задачей статистического оценивания неизвестных параметров по выборке
заключается в построении такой функции от имеющихся данных статистических
наблюдений, которая давала бы наиболее точные приближенные значения реальных,
не известных исследователю, значений этих параметров.
Статистические оценки делятся на
точечные и интервальные, в зависимости от способа их предоставления (числом или
интервалом).
Точечной
называют статистическую оценку параметра Q теоретического распределения определяемую одним значением
параметра Q*=f(x1, x2, …, xn), где x1, x2, …, xn — результаты эмпирических наблюдений над
количественным признаком Х некоторой выборки.
Такие оценки параметров, полученные по
разным выборкам, чаще всего отличаются друг от друга. Абсолютная разность /Q*-Q/ называют ошибкой выборки (оценивания).
Для того, чтобы статистические оценки
давали достоверные результаты об оцениваемых параметрах, необходимо, чтобы они
были несмещенными, эффективными и состоятельными.
Точечная
оценка, математическое ожидание которой равно (не равно) оцениваемому
параметру, называется несмещенной
(смещенной). М(Q*)=Q.
Разность М(Q*)-Q называют смещением или
систематической ошибкой. Для несмещенных оценок систематическая ошибка
равна 0.
Эффективной
называют такую статистическую оценку
Q*, которая при
заданном объеме выборки n
имеет наименьшую возможную дисперсию: D[Q*]min
(n=const). Эффективная оценка
имеет наименьший разброс по сравнению с другими несмещенными и состоятельными
оценками.
Состоятельной
называют такую статистическую оценку
Q*,
которая при n стремится по вероятности к оцениваемому
параметру Q,
т.е. при увеличении объема выборки n
оценка стремится по вероятности к истинному значению параметра Q.
Требование состоятельности
согласуется с законом больших числе: чем больше исходной информации об
исследуемом объекте, тем точнее результат. Если объем выборки мал, то точечная
оценка параметра может привести к серьезным ошибкам.
Любую выборку (объема n) можно рассматривать
как упорядоченный набор
x1, x2, …, xn независимых
одинаково распределенных случайных величин.
Выборочные средние для
различных выборок объема n из одной и той же генеральной
совокупности будут различны. Т. е. выборочное среднее можно рассматривать как
случайную величину, а значит, можно говорить о распределении выборочного
среднего и его числовых характеристиках.
Выборочное среднее
удовлетворяет всем накладываемым к статистическим оценкам требованиям, т.е.
дает несмещенную, эффективную и состоятельную оценку генерального среднего.
Можно доказать, что. Таким образом, выборочная дисперсия
является смещенной оценкой генеральной дисперсии, давая ее заниженное значение.
Т. е. при небольшом объеме выборки она будет давать систематическую ошибку. Для
несмещенной, состоятельной оценки достаточно взять величину
, которую называют исправленной
дисперсией. Т. е.
На практике для оценки генеральной дисперсии применяют исправленную
дисперсию при n
< 30. В остальных случаях (n>30) отклонение
от
малозаметно. Поэтому при больших значениях n
ошибкой смещения можно пренебречь.
Можно
так же доказать, что относительная
частота
ni / n является
несмещенной и состоятельной оценкой вероятности P(X=xi). Эмпирическая функция распределения F*(x) является несмещенной
и состоятельной оценкой теоретической функции распределения F(x)=P(X<x).
Пример:
Найдите
несмещенные оценки математического ожидания
и дисперсии по таблице выборки.
Решение:
Объем выборки n=20.
Несмещенной оценкой математического
ожидания является выборочное среднее.
Для вычисления несмещенной оценки
дисперсии сначала найдем выборочную дисперсию:
Теперь найдем
несмещенную оценку:
9.
Интервальные
оценки параметров распределения
Интервальной называется статистическая
оценка, определяемая двумя числовыми значениями- концами исследуемого
интервала.
Число> 0, при котором |Q—Q*|<
, характеризует точность интервальной
оценки.
Доверительным
называется интервал
, который с заданной вероятностью
покрывает неизвестное значение параметра Q. Дополнение
доверительного интервала до множества всех возможных значений параметра Q называется критической областью. Если критическая
область расположена только с одной стороны от доверительного интервала, то
доверительный интервал называется односторонним:
левосторонним, если критическая область существует только слева, и правосторонним- если только справа. В
противном случае, доверительный интервал называется двусторонним.
Надежностью,
или доверительной вероятностью, оценки Q (с помощью Q*) называют вероятность,
с которой выполняется следующее неравенство: |Q—Q*|<
.
Чаще всего доверительную вероятность
задают заранее (0,95; 0,99; 0,999) и на нее накладывают требование быть близкой
к единице.
Вероятность
называют вероятностью
ошибки, или уровнем значимости.
Пусть |Q—Q*|<
, тогда
. Это означает, что с вероятностью
можно утверждать, что истинное значение
параметра Q
принадлежит интервалу. Чем меньше величина отклонения
, тем точнее оценка.
Границы (концы) доверительного интервала
называют доверительными границами, или
критическими границами.
Значения границ доверительного интервала
зависят от закона распределения параметра Q*.
Величину отклонения
равную половине ширины доверительного
интервала, называют точностью оценки.
Методы построения доверительных
интервалов впервые были разработаны американским статистом Ю. Нейманом.
Точность оценки
, доверительная вероятность
и
объем выборки n связаны между собой. Поэтому, зная
конкретные значения двух величин, всегда можно вычислить третью.
Нахождение
доверительного интервала для оценки математического ожидания нормального
распределения, если известно среднеквадратическое отклонение.
Пусть произведена выборка из генеральной
совокупности, подчиненной закону нормального распределения. Пусть известно
генеральное среднеквадратическое отклонение
, но неизвестно математическое ожидание
теоретического распределения a
().
Справедлива следующая формула:
Т.е.
по заданному значению отклонения
можно найти, с какой вероятностью неизвестное
генеральное среднее принадлежит интервалу. И наоборот. Из формулы видно, что при
возрастании объема выборки и фиксированной величине доверительной вероятности
величина
—
уменьшается, т.е. точность оценки увеличивается. С увеличением надежности
(доверительной вероятности), величина
-увеличивается,
т.е. точность оценки уменьшается.
Пример:
В результате испытаний
были получены следующие значения -25, 34, -20, 10, 21. Известно, что они
подчиняются закону нормального распределения с среднеквадратическим отклонением
2. Найдите оценку а* для математического ожидания а. Постройте для него 90%-ый
доверительный интервал.
Решение:
Найдем несмещенную
оценку
Тогда
Доверительный интервал
для а имеет вид: 4 – 1,47< a
< 4+ 1,47 или 2,53 < a
< 5, 47
Нахождение
доверительного интервала для оценки математического ожидания нормального
распределения, если неизвестно среднеквадратическое отклонение.
Пусть известно, что генеральная
совокупность подчинена закону нормального распределения, где неизвестны а и
. Точность доверительного интервала,
покрывающего с надежностью
истинное значение параметра а, в данном случае вычисляется по формуле:
, где n— объем выборки,
,
— коэффициент Стьюдента (его следует
находить по заданным значениям n и
из
таблицы «Критические точки распределения Стьюдента»).
Пример:
В результате испытаний были получены
следующие значения -35, -32, -26, -35, -30, -17. Известно, что они подчиняются
закону нормального распределения. Найдите доверительный интервал для
математического ожидания а генеральной совокупности с доверительной вероятностью
0,9.
Решение:
Найдем несмещенную оценку
.
Найдем
.
Далее найдем
.
Тогда
Доверительный интервал примет вида (-29,2
— 5,62; -29,2 + 5,62) или (-34,82; -23,58).
Нахождение
доверительного интерла для дисперсии и среднеквадратического отклонения
нормального распределения
Пусть из некоторой генеральной
совокупности значений, распределенной по нормальному закону, взята случайная
выборка объема n <
30, для которой вычислены выборочные
дисперсии: смещенная
и
исправленная s2
. Тогда для нахождения интервальных
оценок с заданной надежностью
для генеральной дисперсии D генерального
среднеквадратического отклонения
используются следующие формулы.
или
,
Значения
— находят с помощью таблицы значений
критических точек распределения
Пирсона.
Доверительный интервал для дисперсии
находится из этих неравенств путем возведения всех частей неравенства в
квадрат.
Пример:
Было проверено качество 15 болтов.
Предполагая, что ошибка при их изготовлении подчинена нормальному закону
распределения, причем выборочное среднеквадратическое отклонение
равно 5 мм, определить с надежностью
доверительный интервал для неизвестного
параметра
.
Решение:
Т. к. n = 15 <30, то воспользуемся формулой
.
Найдем пограничные значения вероятности
для .
Тогда:
Границы интервала представим в виде двойного неравенства:
Концы двустороннего доверительного
интервала для дисперсии можно определить и без выполнения арифметических
действий по заданному уровню доверия и объему выборки с помощью соответствующей
таблицы (Границы доверительных интервалов для дисперсии в зависимости от числа
степеней свободы и надежности). Для этого полученные из таблицы концы интервала
умножают на исправленную дисперсию s2
.
Пример:
Решим предыдущую задачу другим способом.
Решение:
Найдем исправленную
дисперсию:
По таблице «Границы
доверительных интервалов для дисперсии в зависимости от числа степеней свободы
и надежности» найдем границы доверительного интервала для дисперсии при k=14 и
: нижняя граница 0,513 и верхняя 2,354.
Умножим полученные
границы на
s2 и
извлечем корень (т.к. нам нужен доверительный интервал не для дисперсии, а для
среднеквадратического отклонения).
Как видно из примеров,
величина доверительного интервала зависит от способа его построения и дает
близкие между собой, но неодинаковые результаты.
При выборках достаточно
большого объема (n>30)
границы доверительного интервала для генерального среднеквадратического
отклонения можно определить по формуле:
Существует и другой
способ определения границы доверительного интервала для дисперсии, в основе
которого лежит выбор интервала, симметричного относительно
:
Причем
—
некоторое число, которое табулировано и приводится в соответствующей справочной
таблице.
Если 1- q<1, то формула имеет
вид:
Пример:
Решим предыдущую задачу третьим способом.
Решение:
Ранее было найдено s
= 5,17. q(0,95;
15) = 0,46 – находим по таблице.
Тогда:
Содержание:
Интервальные оценки параметров распределения. Непрерывное и дискретное распределения признаков:
В материалах сегодняшней лекции мы рассмотрим интервальные оценки параметров распределения, а именно непрерывное и дискретное распределения признаков генеральной и выборочной совокупности.
Статистические ряды и их геометрическое изображение дают представление о распределении наблюдаемой случайной величины X по данным выборки. Во многих задачах вид распределения случайной величины X известен, необходимо получить приближённое значение неизвестных параметров этого распределения: m,
Пусть
Точечной оценкой 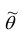
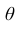
Очевидно, что 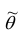
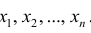
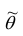
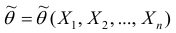
Точечная оценка 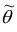
1. Состоятельность. Оценка 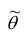
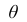
состоятельной, если 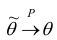
Состоятельность оценки можно установить с помощью теоремы: если 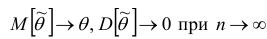
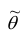
2. Несмещённость. Оценка 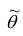
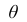
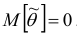
Для оценки параметра 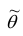
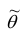
Отсюда вытекает третье свойство.
3. Эффективность. Несмещённая оценка 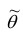
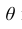
Запишем точечные оценки числовых характеристик случайной величины X.
1. Точечная оценка 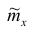
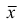
Проверим свойства оценки:
а) состоятельность следует из теоремы Чебышева: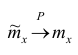
б) несмещённость:
в)эффективность:
так как
2. Точечная оценка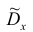
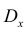
она обладает свойствами: состоятельность, несмещённость,
эффективность.
3. Точечная оценка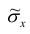
Интервальные оценки
При статистической обработке результатов наблюдений необходимо знать не только точечную оценку 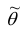
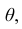
Характеристики вариационного ряда
В материалах сегодняшней лекции мы рассмотрим характеристики вариационного ряда.
Вариационные ряды
Установление закономерностей, которым подчиняются массовые случайные явления, основано на изучении статистических данных — сведений о том, какие значения принял в результате наблюдений интересующий исследователя признак.
Пример:
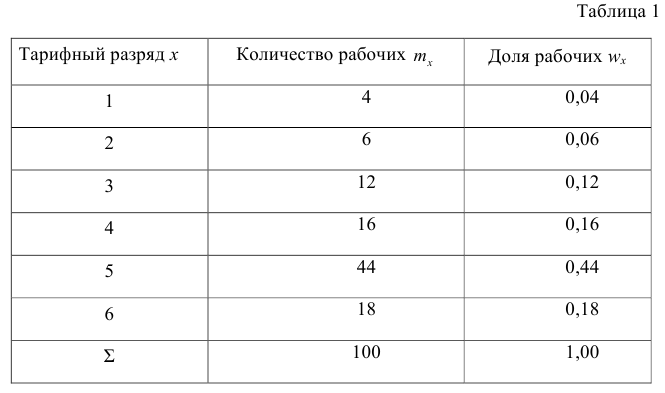
Исследователь, интересующийся тарифным разрядом рабочих механического цеха, в результате опроса 100 рабочих получил следующие сведения:
Здесь признаком является тарифный разряд, а полученные о нём сведения образуют статистические данные. Для изучения данных прежде всего необходимо их сгруппировать. Расположим наблюдавшиеся значения признака в порядке возрастания. Эта операция называется ранжированием статистических данных. В результате получим следующий ряд, который называется ранжированным:
(1, 1, 1, 1) — 4 раза; (2, 2, 2, 2, 2, 2) — 6 раз; (3, 3, …, 3) — 12 раз; (4, 4, …, 4) —
16 раз; (5, 5, …, 5) — 44 раза; (6, 6, …, 6) — 18 раз.
Из ранжированного ряда следует, что признак (тарифный разряд) принял шесть различных значений: первый, второй и т.д. до шестого разряда.
В дальнейшем различные значения признака условимся называть вариантами, а под варьированием — понимать изменение значений признака. Если признак по своей сущности таков, что различные его значения не могут отличаться друг от друга меньше чем на некоторую конечную величину, то говорят, что это дискретно варьирующий признак.
Тарифный разряд — дискретно варьирующий признак: его различные значения не могут отличаться друг от друга меньше, чем на единицу. В примере этот признак принял 6 различных значений — 6 вариантов: вариант 1 повторился 4 раза, вариант 2-6 раз и т.д. Число, показывающее. сколько раз встречается вариант л* в ряде наблюдений, называется частотой варианта 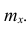
Вместо частоты варианта x можно рассматривать её отношение к общему числу наблюдений n, которое называется частостью варианта х и обозначается 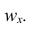
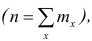
Таблица, позволяющая судить о распределении частот (или частостей) между вариантами, называется дискретным вариационным рядом.
В примере 1 была поставлена задача изучить результаты наблюдений. Если просмотр первичных данных не позволил составить представление о варьировании значений признака, то, рассматривая вариационный, ряд, можно сделать следующие выводы: тарифный разряд колеблется от 1-го до 6-го; наиболее часто встречается 5-й тарифный разряд; с ростом тарифного разряда (до 5-го разряда) растёт число рабочих, имеющих соответствующий разряд.
Наряду с понятием частоты используют понятие накопленной частоты, которую обозначают 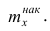
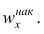
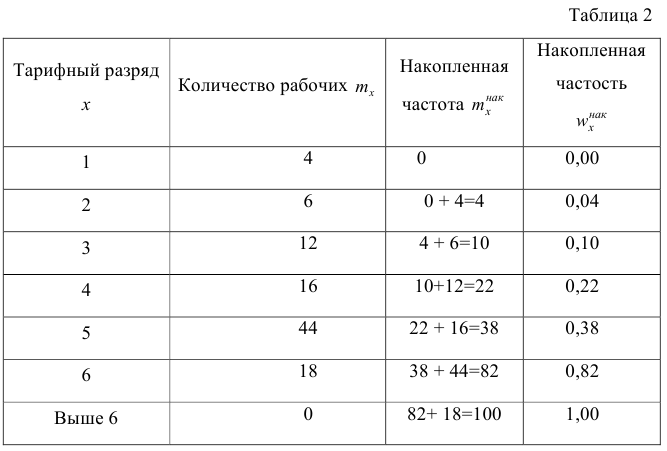
В дискретном вариационном ряду накопленные частоты (частости) вычисляются для каждого варианта и являются результатом последовательного суммирования частот (частостей). Накопленные частоты (частости) для вариационного ряда, заданного в табл. 1, вычислены в табл. 2.
Например, варианту 1 соответствует накопленная частота, равная нулю, так как среди опрошенных рабочих не было таких, у которых тарифный разряд был бы меньше 1-го; варианту 5 соответствует накопленная частота 38, так как было 4+6+12+16 рабочих с тарифным разрядом, меньшим 5-го, накопленная частость для этого варианта равна 0,38 (38: 100); если тарифный разряд выше 6-го, то ему соответствует накопленная частота 100, так как тарифный разряд всех опрошенных рабочих не выше 6-го.
Пример:
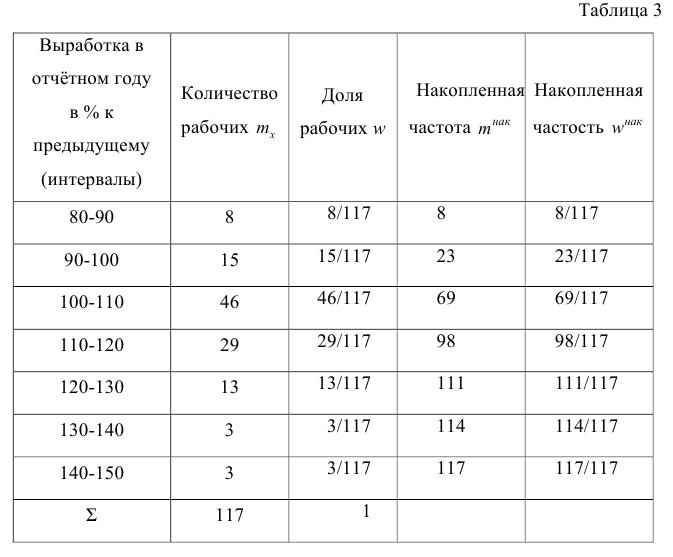
Исследователь, изучающий выработку на одного рабочего-станочника механического цеха в отчётном году в процентах к предыдущему году, получил следующие данные (в целых процентах) по 117 рабочим:
В этом примере признаком является выработка в отчётном году в процентах к предыдущему. Очевидно, что значения, принимаемые этим признаком, могут отличаться одно от другого на сколь угодно малую величину, т. е. признак может принять любое значение в некотором числовом интервале (только для упрощения дальнейших расчетов полученные данные округлены до целых процентов). Такой признак называют непрерывно варьирующим. По приведенным данным трудно выявить характерные черты варьирования значений признака. Построение дискретного вариационного ряда также не даст желаемых результатов (слишком велико число различных наблюдавшихся значений признака). Для получения ясной картины объединим в группы рабочих, у которых величина выработки колеблется, например, в пределах 10%. Сгруппированные данные представим в табл. 3.
В табл. 3 частоты m показывают, во скольких наблюдениях признак принял значения, принадлежащие тому или иному интервалу. Такую частоту называют интервальной, а отношение её к общему числу наблюдений — интервальной частостью w. Таблицу, позволяющую судить о распределении частот (или частостей) между интервалами варьирования значений признака, называют интервальным вариационным рядом.
Интервальный вариационный ряд, представленный в табл. 3, позволяет выявить закономерности распределения рабочих по интервалам выработки. В табл. 3 для верхних границ интервалов приведены накопленные частоты (частости) (они получены последовательным суммированием интервальных частот (частостей), начиная с частоты (частости) первого интервала). Например, для верхней границы третьего интервала, равной 110, накопленная частота равна 69; так как 8+15+46 рабочих имели выработку меньше 110%, накопленная частость равна 69/117.
Интервальный вариационный ряд строят по данным наблюдений за непрерывно варьирующим признаком, а также за дискретно варьирующим, если велико число наблюдавшихся вариантов. Дискретный вариационный ряд строят только для дискретно варьирующего признака.
Иногда интервальный вариационный ряд условно заменяют дискретным. Тогда серединное значение интервала принимают за вариант х, а соответствующую интервальную частоту — за
Построение интервального вариационного ряда
Для построения интервального вариационного ряда необходимо определить величину интервала, установить полную шкалу интервалов, в соответствии с ней сгруппировать результаты наблюдений. В примере 2 при выборе величины интервала учитывались требования наибольшего удобства отсчётов. Интервал был принят равным 10% и оказался удачным. Построенный интервальный ряд позволил выявить закономерности варьирования значений признака. Для определения оптимального интервала h, т.е. такого, при котором построенный интервальный ряд не был бы слишком громоздким и в то же время позволял выявить характерные черты рассматриваемого явления, можно использовать формулу Стэрджеса
где 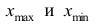
За начало первого интервала рекомендуется принимать величину
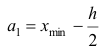
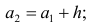
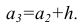
После установления шкалы интервалов следует сгруппировать результаты наблюдений. Границы последовательных интервалов записывают в столбец слева, а затем, просматривая статистические данные в том порядке, в каком они были получены, проставляют чёрточки справа от соответствующего интервала. В интервал включается данные, большие или равные нижней границе интервала и меньшие верхней границы. Целесообразно каждые пятое и шестое наблюдения отмечать диагональными черточками, пересекающими квадрат из четырёх предшествующих. Общее количество чёрточек, проставленных против какого-либо интервала, определяет его частоту.
Графическое изображение вариационных рядов
Графическое изображение вариационного ряда позволяет представить в наглядной форме закономерности варьирования значений признака. Наиболее широко используются следующие виды графического изображения вариационных рядов: полигон, гистограмма, кумулятивная
кривая.
Полигон, как правило, служит для изображения дискретного вариационного ряда. Для его построения в прямоугольной системе координат наносят точки с координатами 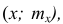
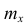
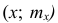
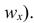
Гистограмма служит для изображения только интервального вариационного ряда. Для её построения в прямоугольной системе координат по оси абсцисс откладывают отрезки, изображающие интервалы варьирования, и на этих отрезках, как на основании, строят прямоугольники с высотами, равными частотам (или частостям) соответствующего интервала. В результате получают ступенчатую фигуру, состоящую из прямоугольников, которую и называют гистограммой.
Если по оси абсцисс выбрать такой масштаб, чтобы ширина интервала была равна единице, и считать, что по оси ординат единица масштаба соответствует одному наблюдению, то площадь гистограммы равна общему числу наблюдений, если по оси ординат откладывались частоты, и эта площадь равна единице, если откладывались частости.
Иногда интервальный ряд изображают с помощью полигона. В этом случае интервалы заменяют их серединными значениями и к ним относят интервальные частоты. Для полученного дискретного ряда строят полигон.
Кумулятивная кривая (кривая накопленных частот или накопленных частостей) строится следующим образом. Если вариационный ряд дискретный, то в прямоугольной системе координат строят точки с координатами 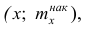
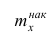
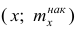
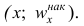
Если вариационный ряд интервальный, то по оси абсцисс откладывают интервалы. Верхним границам интервалов соответствуют накопленные частоты (или накопленные частости); нижней границе первого интервала — накопленная частота, равная нулю. Построив кумулятивную кривую, можно приблизительно установить число наблюдений (или их долю в общем количестве наблюдений), в которых признак принял значения, меньшие заданного.
Построение вариационного ряда — первый шаг к осмысливанию ряда наблюдений. Однако на практике этого недостаточно, особенно когда необходимо сравнить два ряда или более. Сравнению подлежат только так называемые однотипные вариационные ряды, т. е. ряды, которые построены по результатам обработки сходных статистических данных. Например, можно сравнивать распределения рабочих по возрасту на двух заводах или распределения времени простоев станков одного вида. Однотипные вариационные ряды обычно имеют похожую форму при графическом изображении, однако могут отличаться друг от друга, а именно: иметь различные значения признака, вокруг которых концентрируются наблюдения (меры этой качественной особенности называется средними величинами); различаться рассеянием наблюдений вокруг средних величин (меры этой особенности получили название показателей вариации).
Средние величины и показатели вариации позволяют судить о характерных особенностях вариационного ряда и называются статистическими характеристиками. К статистическим характеристикам относятся также показатели, характеризующие различия в скошенности полигонов и различия в их островершинности.
Средние величины
Средние величины являются как бы «представителями» всего ряда наблюдений, поскольку вокруг них концентрируются наблюдавшиеся значения признака. Заметим, что только для качественно однородных наблюдений имеет смысл вычислять средние величины.
Различают несколько видов средних величин: средняя арифметическая, средняя геометрическая, средняя гармоническая, средняя квадратическая, средняя кубическая и т.д. При выборе вида средней величины необходимо прежде всего ответить на вопрос: какое свойство ряда мы хотим представить средней величиной или, иначе говоря, какая цель преследуется при вычислении средней? Это свойство, получившее название определяющего, и определяет вид средней. Понятие определяющего свойства впервые введено советским статистиком А. Я. Боярским.
Наиболее распространенной средней величиной является средняя арифметическая. Пусть 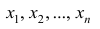
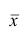
Так как 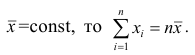
вычисления средней арифметической по данным наблюдений:
Если по наблюдениям построен вариационный ряд, то средняя арифметическая
где x- — вариант, если ряд дискретный, и центр интервала, если ряд интервальный;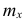
Частоты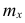
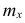
Очевидно, что если по данным наблюдений построен дискретный вариационный ряд, то формулы (3) и (4) дают одинаковые значения средней арифметической. Если же по наблюдениям построен интервальный ряд, то средние арифметические, вычисленные по формулам
(3) и (4), могут не совпадать, так как в формуле (4) значения признака внутри каждого интервала принимаются равными центрам интервалов. Ошибка, возникающая в результате такой замены, вообще говоря, очень мала, если наблюдения, распределены равномерно вдоль каждого интервала, а не скапливаются к одноименным границам интервалов (т.е. либо все к нижним границам, либо все к верхним границам).
Среднюю арифметическую для вариационного ряда можно вычислять по формуле
которая является следствием формулы (4). Действительно,
Свойство, определяющее среднюю арифметическую, сводилось к требованию неизменности суммы наблюдений при замене каждого из них средней арифметической. При решении практических задач может оказаться необходимым вычислить такую среднюю 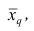
где q — положительное или отрицательное число. Среднюю 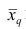
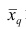
Сравнивая формулы (7) и (3), можно сделать вывод, что степенная средняя первого порядка есть не что иное, как средняя арифметическая, т.е.
При q=-l из формулы (7) получаем выражение для средней гармонической, при q=2 — для среднеквадратической, при q=3 — для средней кубической и т.д.
Средней геометрической 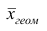
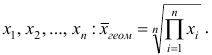
Рассмотрим основные свойства средней арифметической.
1°. Сумма отклонений результатов наблюдений от средней арифметической равна нулю.
Доказательство. Исходя из определяющего свойства (2) средней арифметической, получаем
Если по результатам наблюдений построен вариационный ряд и средняя арифметическая взвешенная, то свойство 1° формулируется так: сумма произведений отклонений вариантов от средней арифметической на соответствующие частоты равна нулю. Действительно, на основании формулы (4) получаем
или
2°. Если все результаты наблюдений уменьшить (увеличить) на одно и то же число, то средняя арифметическая уменьшится (увеличится) на то же число. (Доказательство свойств 2° и 3° проведём в предположении, что по результатам наблюдений построен вариационный ряд и средняя арифметическая — взвешенная).
Доказательство. Очевидно, что при уменьшении вариантов на одно и то же число с соответствующие им частоты останутся прежними. Поэтому взвешенная средняя арифметическая для изменённого вариационного ряда такова:
Аналогично можно показать, что 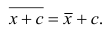
3°. Если все результаты наблюдений уменьшить (увеличить) в одно и то же число раз, то средняя арифметическая уменьшится (увеличится) во столько же раз.
Доказательство. Очевидно, что при уменьшении вариантов в k раз их частоты останутся прежними. Поэтому средняя арифметическая для изменённого ряда
Аналогично можно доказать, что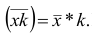
(уменьшить) в k раз, то получим среднюю арифметическую для первоначального вариационного ряда.
4°. Если ряд наблюдений состоит из двух групп наблюдений, то средняя арифметическая всего ряда равна взвешенной средней арифметической групповых средних, причём весами являются объёмы групп.
Пусть 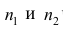
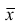
средняя арифметическая для всего ряда 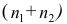
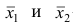
Доказательство. Исходя из определяющего свойству средней арифметической, имеем: произведение 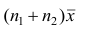
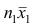
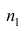
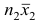
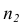
Следовательно,
Следствие. Если ряд наблюдений состоит из k групп наблюдений, то средняя арифметическая всего ряда 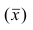
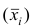
5°. Средняя арифметическая для сумм (разностей) взаимно соответствующих значений признака двух рядов наблюдений с одинаковым числом наблюдений равна сумме (разности) средних арифметических этих рядов.
Пусть 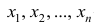
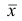
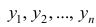
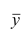
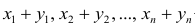
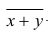
Доказательство. Имеем
Аналогично можно показать, что
Следствие. Средняя арифметическая алгебраической суммы соответствующих значений признака нескольких рядов наблюдений с одинаковым числом наблюдений равна алгебраической сумме средних арифметических этих рядов.
Вычисление средней арифметической вариационного ряда непосредственно по формуле (4) приводит к громоздким расчётам, если числовые значения вариантов и соответствующие им частоты велики. Поэтому часто используют следующий способ, основанный на свойствах 3° и 2° средней арифметической: среднюю вычисляют не по первоначальным вариантам л-, а по уменьшенным на не которое число с, а затем разделённым на некоторое число k т.е. для вариантов 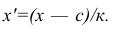
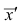
Действительно, принимая во внимание свойства 3° и 2° средней арифметической, получаем
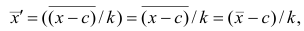
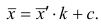
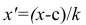
Медиана и мода
Наряду со средними величинами в качестве описательных характеристик вариационного ряда применяют медиану и моду.
Медианой 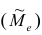
Пусть проведено нечётное число наблюдений, т.е. n=2q—1, и результаты наблюдений проранжированы и выписаны в следующий ряд:
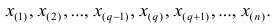
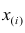
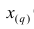
Если проведено чётное число наблюдений, т.е. n=2q, то на середину ранжированного ряда 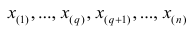
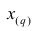
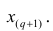
, т.е.
Покажем на примерах на практическом занятии, как определяется медиана дискретного и интервального вариационных рядов.
В общем случае медиана для интервального вариационного ряда определяется по формуле
или по следующей формуле, полученной из формулы (9) в результате деления числителя и знаменателя входящей в неё дроби на n:
где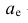
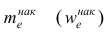
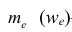
Модой 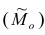
В случае интервального вариационного ряда мода вычисляется по следующей формуле (вывод формулы можно найти в кн.: Венецкий И. Г Кильдишев Г. С. Теория вероятностей и математическая статистика. М., 1975.):
или по тождественной формуле:
где 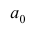
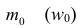
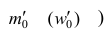
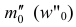
Моду используют в случаях, когда нужно ответить на вопрос, какой товар имеет наибольший спрос, каковы преобладающие в данный момент уровни производительности труда, себестоимости и т. д. Модальная производительность, себестоимость и т.д. помогают вскрыть ресурсы, имеющиеся в экономике.
Показатели вариации
Средние величины, характеризуя вариационный ряд числом, не отражают изменчивости наблюдавшихся значений признака, т.е. вариацию. Простейшим показателем вариации является вариационный размах 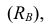
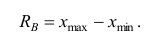
Вариационный размах — приближённый показатель вариации, так как почти не зависит от изменения вариантов, а крайние варианты, которые используются для его вычисления, как правило, ненадёжны.
Более содержательными являются меры рассеяния наблюдений вокруг средних величин. Средняя арифметическая является основным видом средних, поэтому ограничимся рассмотрением мер рассеяния наблюдений вокруг средней арифметической.
Сумма отклонений результатов наблюдений 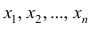
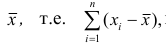
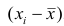
Средним линейным отклонением (d) называют среднюю арифметическую абсолютных величин отклонений результатов наблюдений от их средней ар и ф метической:
Эмпирической дисперсией 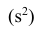
Если по результатам наблюдений построен вариационный ряд, то эмпирическая дисперсия
Вместо эмпирической дисперсии в качестве меры рассеяния наблюдений вокруг средней арифметической часто используют эмпирическое среднеквадратическое отклонение, равное арифметическому значению корня квадратного из дисперсии и имеющее ту же размерность, что и значения признака.
где x — вариант (если ряд дискретный) и центр интервала (если ряд интервальный); 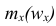
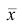
Для краткости величину 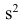
Приведем свойство минимальности эмпирической дисперсии: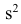
если
Доказательство. Найдём экстремум функции 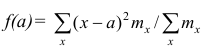
этого решим уравнение 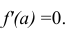
Так как 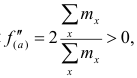
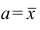
Можно показать, что среднее линейное отклонение не обладает свойством минимальности. Поэтому наиболее употребительными мерами рассеяния
Для вариационного ряда среднеквадратическое отклонение наблюдений вокруг средней арифметической являются эмпирическая дисперсия и эмпирическое среднеквадратическое отклонение.
Итальянский статистик Коррадо Джинни предложил в качестве показателя вариации использовать величину 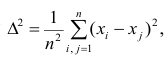
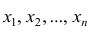
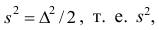
Свойства эмпирической дисперсии
Рассмотрим основные свойства эмпирической дисперсии, знание которых позволит упростить её вычисление.
1 °. Дисперсия постоянной величины равна нулю.
Доказательство этого свойства очевидно вытекает из того, что дисперсия является показателем рассеяния наблюдений вокруг средней арифметической, а средняя арифметическая постоянной равна этой постоянной.
2°. Если все результаты наблюдений уменьшить (увеличить) на одно и то же число с, то дисперсия не изменится.
Доказательство свойств 2° и 3° проведём в предположении, что по результатам наблюдений построен вариационный ряд.
Доказательство. Если все варианты уменьшить на число с, то в соответствии со свойством 2° средней арифметической средняя для измененного вариационного ряда равна 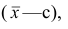
,т.е. совпадает с дисперсией первоначального вариационного ряда. Аналогично можно показать, что
Доказанное свойство позволяет вычислять дисперсию не по данным вариантам, а по уменьшенным, (увеличенным) на одно и то же число с, так как дисперсия, вычисленная для измененного ряда, равна первоначальной.
3°. Если все результаты наблюдений уменьшить (увеличить) в одно и то же число k раз, то дисперсия уменьшится (увеличится) в 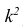
Доказательство. Если все варианты уменьшить в k раз, то, согласно свойству 3 средней арифметической, средняя для измененного вариационного ряда равна 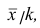
Аналогично можно показать, что
Это свойство позволяет эмпирическую дисперсию вычислять не по данным вариантам, а по уменьшенным (увеличенным) в одно и то же число k раз. Если дисперсию, вычисленную для измененного ряда, увеличить (уменьшить) в 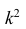
Следствие. Если все варианты уменьшить (увеличить) в k раз, то среднеквадратическое отклонение уменьшится (увеличится) в число раз, равное k.
Следствие очевидно вытекает из определения среднеквадратического
отклонения.
Прежде чем рассматривать следующее свойство дисперсии, докажем теорему.
Теорема. Эмпирическая дисперсия равна разности между средней
арифметической квадратов наблюдений и квадратом средней
арифметической, т.е.
Доказательство проведём для случая взвешенных средних арифметических, т.е.
Доказательство. Тождественно преобразуя выражения для дисперсии, имеем
4°, Если ряд наблюдений состоит из двух групп наблюдений, то дисперсия всего ряда равна сумме средней арифметической групповых дисперсий и средней арифметической квадратов отклонений групповых средних от средней всего ряда, причем ‘ при вычислении средних арифметических весами являются объемы групп.
Пусть 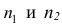
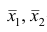
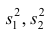
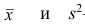
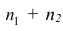
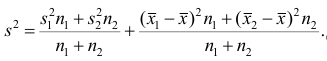
Пусть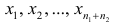
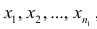
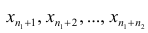
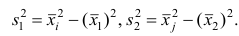
В соответствии со свойством 4° средней арифметической можно записать 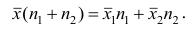
Используя найденные выражения для слагаемых, получаем
Свойство 4° можно обобщить на случай, когда ряд наблюдений состоит из любого количества 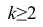
Если ряд наблюдений состоит из k групп наблюдений, то межгрупповой дисперсией 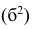
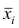
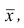
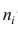
Средней групповых дисперсий или внутригрупповой дисперсией 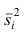
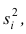
Следствие (свойства 4°). Если ряд наблюдений состоит из k групп наблюдений, то дисперсия всего ряда s2 равна сумме внутригрупповой и межгрупповой дисперсий, т.е.
Вычисление дисперсии вариационного ряда непосредственно по формуле (16) приводит к громоздким расчётам, если числовые значения вариантов и соответствующие им частоты велики. Поэтому часто дисперсию вычисляют не по первоначальным вариантам х, а по вариантам 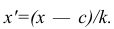
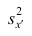
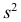
Действительно, принимая во внимание свойства 3° и 2° дисперсии, получаем
откуда следует, что
Требования к с и k предъявляют те же, что и в упрощенном способе вычисления средней арифметической.
Эмпирические центральные и начальные моменты
Средняя арифметическая и дисперсия вариационного ряда являются частными случаями более общего понятия о моментах вариационного ряда.
Эмпирическим начальным моментом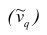
Эмпирический начальный момент нулевого порядка
Эмпирический начальный момент первого порядка
Эмпирический начальный момент второго порядка 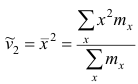
Эмпирическим центральным моментом 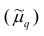
Эмпирический центральный момент нулевого порядка
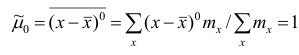
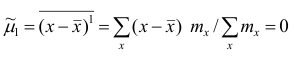
Эмпирический центральный момент второго порядка
В дальнейшем для краткости величину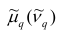
Используя формулу бинома Ньютона, разложим в ряд выражение для центрального момента q-го порядка:
В проведенных тождественных преобразованиях использованы свойства 5° и 3° средней арифметической; 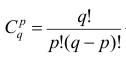
Итак, центральный момент q-го порядка выражается через начальные моменты следующим образом:
Полагая q = 0, 1, 2,…, можно получить выражения центральных моментов различных порядков через начальные моменты:
и т.д.
Заметим, что формула (23) для центрального момента второго порядка, как и следовало ожидать, аналогична формуле (18) для дисперсии.
Рассмотрим свойства центральных моментов, которые позволят значительно упростить их вычисление.
1°. Если все варианты уменьшить (увеличить) на одно и то же число с, то центральный момент q-го порядка не изменится.
Доказательство. Если все варианты уменьшить на число с, то средняя арифметическая для измененного ряда равна 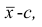
Аналогично можно показать, что
2°. Если все варианты уменьшить (увеличить) в одно и то же число k раз, то центральный момент q-го порядка уменьшится (увеличится) в 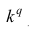
то средняя арифметическая для измененного вариационного ряда равна
поэтому центральный момент q-го порядка
Аналогично можно показать, что
Для облегчения расчётов центральные моменты вычисляют не по первоначальным вариантам х, а по вариантам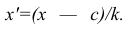
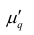
внимание свойства центрального момента, получаем
откуда следует, что
Эмпирические асимметрия и эксцесс
Эмпирическим коэффициентом асимметрии 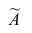
Если полигон вариационного ряда скошен, т.е. одна из его ветвей, начиная от вершины, зримо длиннее другой, то такой ряд называют асимметричным. Из формулы (27) следует, что если в вариационном ряду преобладают варианты, меньшие 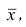
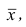
Эмпирическим эксцессом или коэффициентом крутости 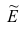
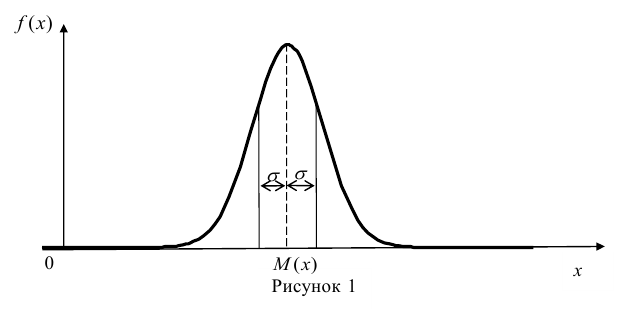
За стандартное значение эксцесса принимают нуль-эксцесс так называемой нормальной кривой (см. рис. 1).
Кривые, у которых эксцесс отрицательный, по сравнению с нормальной менее крутые, имеют, более плоскую вершину и называются «плосковершинными» Кривые с положительным эксцессом более крутые по сравнению с нормальной кривой, имеют более острую вершину и называются «островершинными».
Интервальные оценки параметров распределений
Доверительный интервал, доверительная вероятность:
Точечная оценка неизвестного параметра 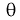
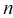
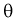
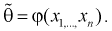
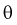
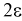
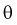
Чем меньше разность 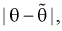
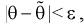
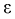
Доверительной вероятностью оценки называется вероятность 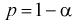
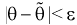
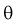
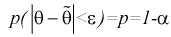
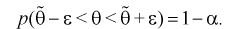
Из (10.1) видно, что неизвестный параметр 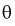
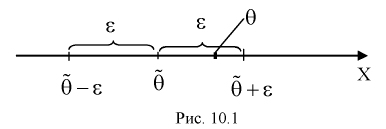
Доверительным интервалом называется интервал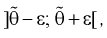
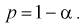
Длина его (см. рис. 10.1) 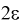
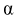
Доверительный интервал для математического ожидания случайной величины X при известной дисперсии
Доверительный интервал для математического ожидания случайной величины X при известной дисперсии (или 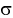
Пусть эксперимент Е описывается нормальной случайной величиной X.
Плотность распределения 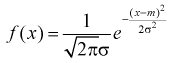
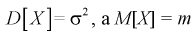
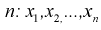
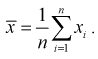
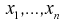
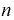
откуда получим
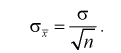
Для определения доверительного интервала рассмотрим разность между оценкой и параметром: 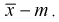
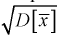
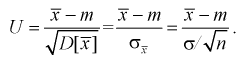
Покажем, что случайная величина U имеет нормированный нормальный закон распределения. Найдем ее числовые характеристики:
Таким образом 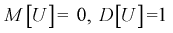
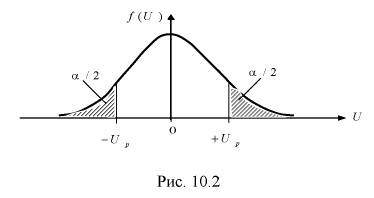
Зная плотность распределения случайной величины U, легко найти вероятность попадания случайной величины U в интервал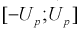
Левая часть этого уравнения представляет собой доверительную вероятность
Тогда из (10.4) и (10.5) следует уравнение
Решая уравнение (10.6), по таблицам функции Лапласа для заданной доверительной вероятности 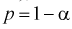
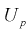
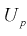
Считая, что 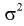
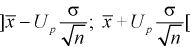
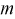
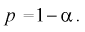
Замечания по формуле (10.8):
- при увеличении объема выборки
из (10.8) видим, что е уменьшается, значит, уменьшается длина доверительного интервала, а точность оценки увеличивается;
- увеличение доверительной вероятности
приводит к увеличению длины доверительного интервала (см. рис. 10.2, где квантили
увеличиваются), т. е. е увеличивается, а точность оценки падает;
- если задать точность е и доверительную вероятность
, то можно найти объем выборки, который обеспечит заданную точность:
Пример №1
Сколько конденсаторов одного номинала надо измерить, чтобы с вероятностью 0,95 можно было утверждать, что мы с точностью 1 % определили их среднее значение — математическое ожидание.
Обозначим 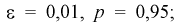
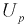
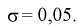
Доверительный интервал для математического ожидания нормальной случайной величины X при НЕизвестной дисперсии
Доверительный интервал для математического ожидания нормальной случайной величины X при неизвестной дисперсии или
Пусть эксперимент описывается случайной величиной X с нормальным распределением с неизвестными параметрами 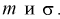
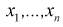
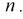
Здесь использовали для оценки дисперсии 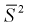
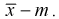
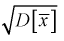
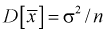
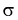
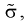
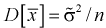
Умножим числитель и знаменатель в (10.10) на
Здесь X — нормированная нормальная случайная величина, знаменатель — распределение 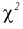
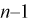
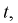
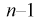
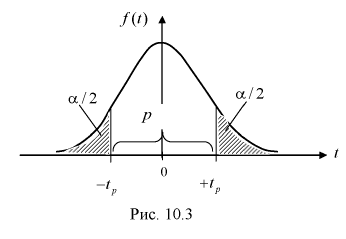
Зная закон распределения случайной величины t и задавая доверительную вероятность 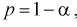
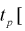
Из таблиц распределений Стьюдента по заданной доверительной вероятности 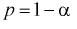
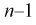
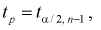
Подставляя в (10.13) вместо t равенство (10.10), получаем
Разрешим неравенство в левой части формулы (10.14) относительно
Отсюда непосредственно следует, что доверительный интервал 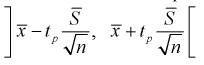
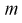
Интервал (10.15) несколько шире интервала (10.7), определенного для той же выборки и той же доверительной вероятности. Зато в (10.15) используется меньшая априорная информация — 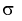
Можно обозначить ширину доверительного интервала или точность через 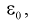
Все замечания, сделанные по формуле (10.8), справедливы и для формулы (10.16).
Пример №2
Даны результаты четырех измерений напряжения сети (значения приведены в
Считаем, что X — напряжение сети — является нормальной случайной величиной. Построить доверительный интервал с вероятностью 0,95 для истинного напряжения сети —
Найдем точечную оценку
Из таблиц распределения Стьюдента для 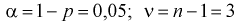
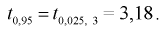
Тогда
Полученные значения подставим в формулу (10.16):
Найдем левую и правую границы доверительного интервала для
Таким образом, истинное напряжение сети с вероятностью 0,95 накрывается доверительным интервалом
Найдем минимальное число измерений, чтобы с вероятностью 0,95 точ ность определения истинного напряжения сети не превышала 0,5 В, т. е. 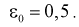
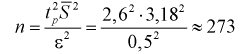
Видим, что число измерений 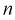
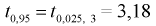
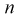
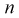
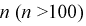
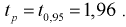
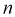
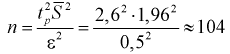
Доверительный интервал для дисперсии или ст нормальной случайной величины X
Рассмотрим вероятностный эксперимент с нормальной моделью, где параметры 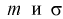
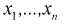
Составим вспомогательную случайную величину
Эта случайная величина имеет распределение 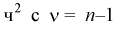
Это и есть распределение хи-квадрат с 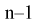
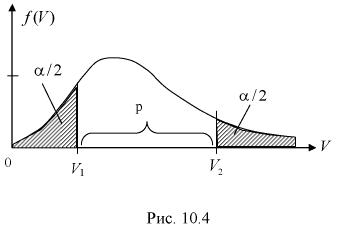
Зная закон распределения случайной величины У, определим вероятность того, что случайная величина 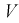
Здесь 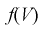
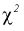
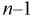
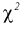
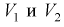
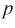
Это означает, что площади заштрихованных фигур равны. Задавая доверительную вероятность 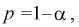
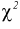
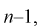
Считая 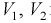
Подставим в (10.20) значение 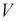
Решаем неравенство в левой части (10.21) относительно
Из (10.22) записываем доверительный интервал для
Для среднего квадратического отклонения 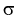
Можно ввести коэффициенты
Тогда доверительный интервал для о определится следующим образом:
Коэффициенты 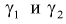
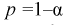
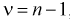

Пример №3
В предыдущем разделе (10.3) приведен пример для измеренных значений напряжения сети. Продолжим и найдем доверительный интервал для среднего квадратического отклонения 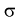
Найдена точечная оценка для 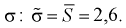
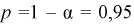
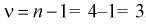
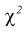
Тогда нижняя граница для
Верхняя граница для
И окончательно:
Пример №4
Случайная величина 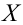
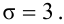
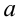
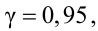
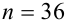
Решение. Определим значение 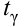
Точность оценки
Подставим в неравенство (4.1):
Смысл полученного результата: если произведено достаточно большое число выборок по 36 в каждой, то 95 % из них определяют такие доверительные
интервалы, в которых 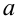
Пример №5
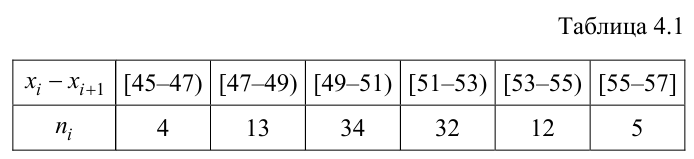
Для исследования нормального распределения 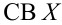
Найти с надежностью 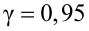
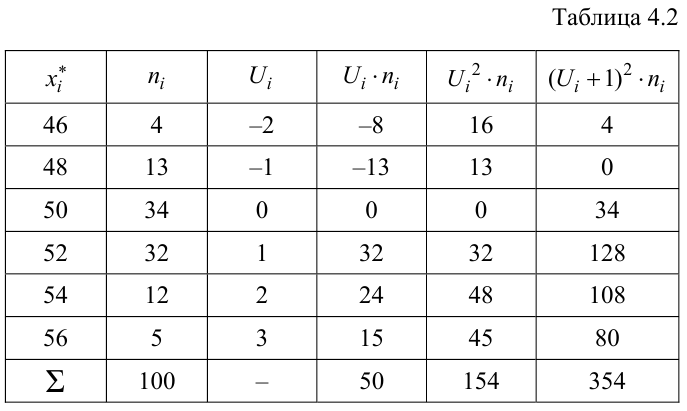
Решение. Найдем несмещенные оценки для математического ожидания и дисперсии, используя метод произведений (табл. 4.2).
Контроль:
По табл. П3 по данным 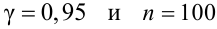
Для определения доверительного интервала для математического ожидания используем неравенство (4.2):
Таким образом, интервал (50, 547; 51, 453) накрывает точку 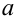
Для определения доверительного интервала для среднего квадратического отклонения используем неравенство (4.3). По табл. П4 по заданным 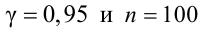
С вероятностью 0,95 неизвестное значение 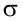
- Алгебра событий — определение и вычисление
- Свойства вероятности
- Многомерные случайные величины
- Случайные события — определение и вычисление
- Основные законы распределения дискретных случайных величин
- Непрерывные случайные величины
- Закон больших чисел
- Генеральная и выборочная совокупности


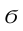
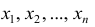
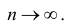
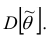
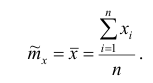
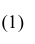
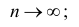
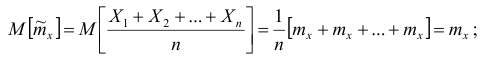
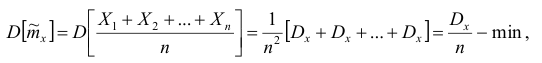
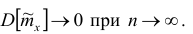



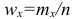
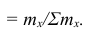
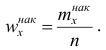

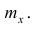
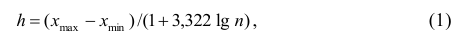
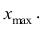




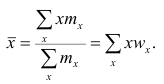


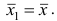
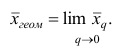
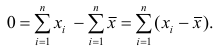
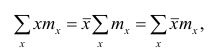
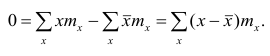
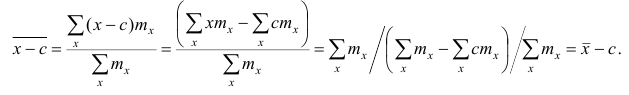
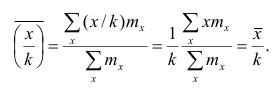
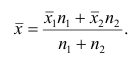
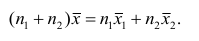
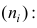
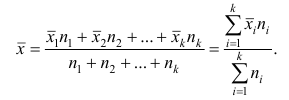
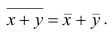
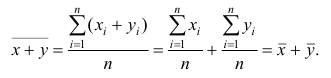
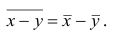

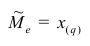
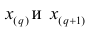
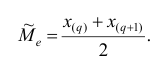
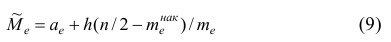
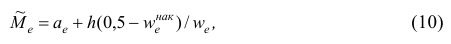
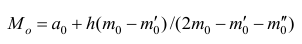
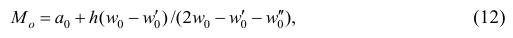


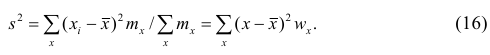
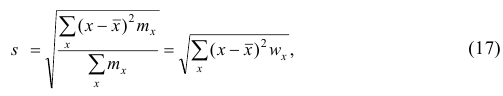
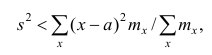
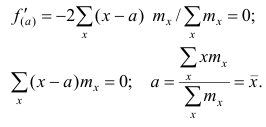
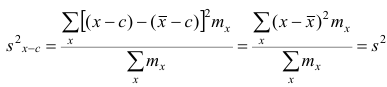
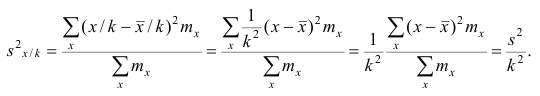

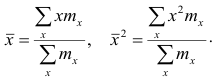
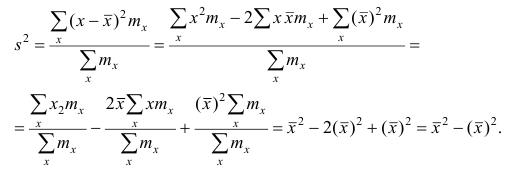
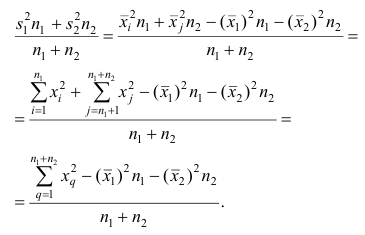
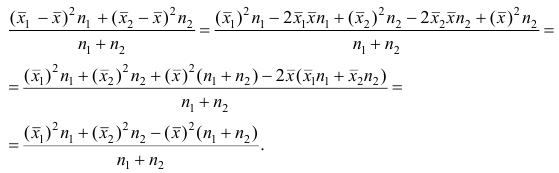
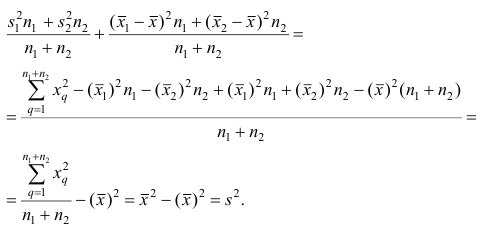
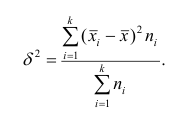
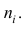
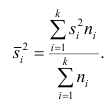
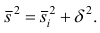

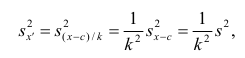

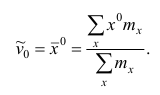
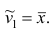
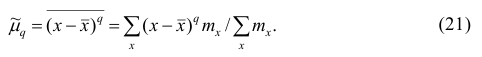
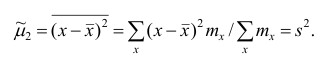
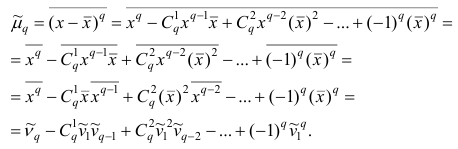

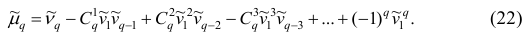
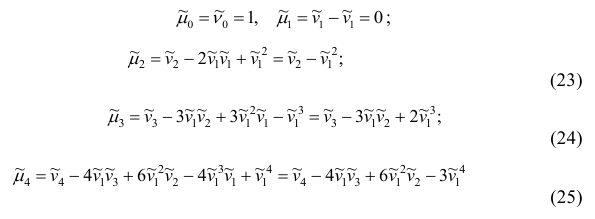
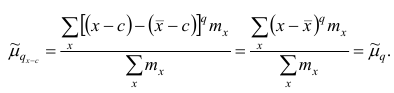
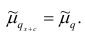
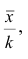
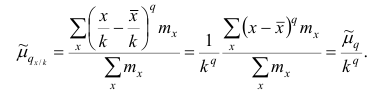

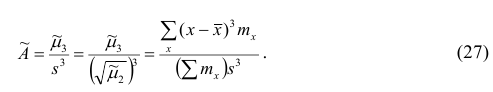

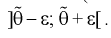
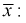
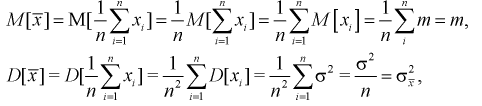
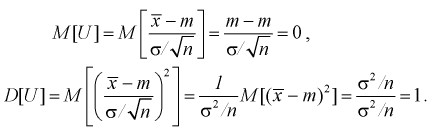
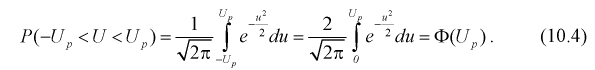
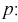
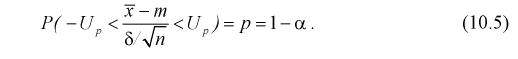

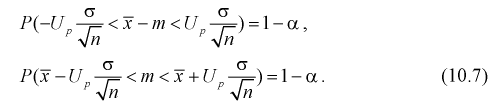

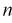 из (10.8) видим, что е уменьшается, значит, уменьшается длина доверительного интервала, а точность оценки увеличивается;
из (10.8) видим, что е уменьшается, значит, уменьшается длина доверительного интервала, а точность оценки увеличивается;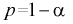 приводит к увеличению длины доверительного интервала (см. рис. 10.2, где квантили
приводит к увеличению длины доверительного интервала (см. рис. 10.2, где квантили 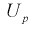 увеличиваются), т. е. е увеличивается, а точность оценки падает;
увеличиваются), т. е. е увеличивается, а точность оценки падает;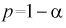 , то можно найти объем выборки, который обеспечит заданную точность:
, то можно найти объем выборки, который обеспечит заданную точность: