Empty stack error python

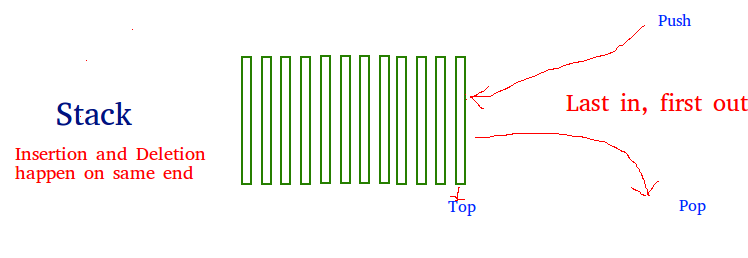
Stack in Python

A stack is a linear data structure that stores items in a Last-In/First-Out (LIFO) or First-In/Last-Out (FILO) manner. In stack, a new element is added at one end and an element is removed from that end only. The insert and delete operations are often called push and pop.

The functions associated with stack are:

• empty() – Returns whether the stack is empty – Time Complexity: O(1)
• size() – Returns the size of the stack – Time Complexity: O(1)
• top() / peek() – Returns a reference to the topmost element of the stack – Time Complexity: O(1)
• push(a) – Inserts the element ‘a’ at the top of the stack – Time Complexity: O(1)
• pop() – Deletes the topmost element of the stack – Time Complexity: O(1)

Implementation:

There are various ways from which a stack can be implemented in Python. This article covers the implementation of a stack using data structures and modules from the Python library.
Stack in Python can be implemented using the following ways:

• list
• Collections.deque
• queue.LifoQueue

Implementation using list:

Python’s built-in data structure list can be used as a stack. Instead of push(), append() is used to add elements to the top of the stack while pop() removes the element in LIFO order.
Unfortunately, the list has a few shortcomings. The biggest issue is that it can run into speed issues as it grows. The items in the list are stored next to each other in memory, if the stack grows bigger than the block of memory that currently holds it, then Python needs to do some memory allocations. This can lead to some append() calls taking much longer than other ones.

Python3

Implementation using collections.deque:

Python stack can be implemented using the deque class from the collections module. Deque is preferred over the list in the cases where we need quicker append and pop operations from both the ends of the container, as deque provides an O(1) time complexity for append and pop operations as compared to list which provides O(n) time complexity.

The same methods on deque as seen in the list are used, append() and pop().

Python3

Implementation using queue module

Queue module also has a LIFO Queue, which is basically a Stack. Data is inserted into Queue using the put() function and get() takes data out from the Queue.

There are various functions available in this module:

• maxsize – Number of items allowed in the queue.
• empty() – Return True if the queue is empty, False otherwise.
• full() – Return True if there are maxsize items in the queue. If the queue was initialized with maxsize=0 (the default), then full() never returns True.
• get() – Remove and return an item from the queue. If the queue is empty, wait until an item is available.
• get_nowait() – Return an item if one is immediately available, else raise QueueEmpty.
• put(item) – Put an item into the queue. If the queue is full, wait until a free slot is available before adding the item.
• put_nowait(item) – Put an item into the queue without blocking. If no free slot is immediately available, raise QueueFull.
• qsize() – Return the number of items in the queue.

Источник

How to Solve Python Coding Questions using Stack

An essential data type for Data Scientists and Soft Engineers in 2021

Python is a versatile script-based programming language with a wide application in Artificial Intelligence, Machine Learning, Deep Learning, and Soft Engineering. Its popularity benefits from the various Data Types that Python stores.

Dictionary is the natural choice if we have to store key and value pairs, as in today’s Question 5. String and list are a pair of twin sisters that come together and solve string manipulation questions. Set holds a unique position as it does not allow duplicates, a unique feature that allows us to identify the repetitive and non-repetitive items. Well, tuple is the least frequently asked data type in technical interviews. Last week, a senior Data Scientist posted a coding question on Twitter, which can be easily solved via tuple. However, a lot of candidates got tripped over. I’ll write another post on the topic soon.

Data Types play an essential part in Python programming! Being able to differentiate one from another is super important for solving interview questions. In today’s post, let’s shift gears to another essential data type called Stack.

In writing this blog post, I have spent countless hours selecting the following questions and rank them in a way that is easily understandable to new programmers. Each question builds up upon the previous ones. If possible, please solve the problems in sequence.

Stack it up

A stack is a linear data structure that keeps elements in a Last-In/First-Out (LIFO) or First-In/Last-Out (FILO) manner (GeeksForGeeks ). It means that elements last added will be popped from the stack first. We can picture a stack of plates: we always use the plate on the top that last added to the pile. Push and pop are the most fundamental operations of a stack, laying the ground for other more advanced adoptions.

In Python, there are three ways of implementing a stack: using a list, collections.deque, and linked list. To prepare for Data Science Interviews, the first approach is sufficiently good enough. In case you are interested in the other two, please check this post (link).

In Python, we can simply use a list to represent a stack. So, it has the same attributes as a list. It has two basic operations: push() and pop(). To push, or add, an element to a stack, we use the append() method. To pop, or delete, the last element, we use the pop() method, as follows.

Question 1: Remove All Adjacent Duplicates In String, by Facebook, Amazon, Bloomberg, Oracle

— Given a string S of lowercase letters, a duplicate removal consists of choosing two adjacent and equal letters, and removing them.
— We repeatedly make duplicate removals on S until we no longer can.
— Return the final string after all such duplicate removals have been made. It is guaranteed the answer is unique.
— https://leetcode.com/problems/remove-all-adjacent-duplicates-in-string/

Walk Through My Thinking

Facebook, Amazon, Bloomberg, and Oracle included this question. While reading the question prompt, I find the following keywords worth noting: duplicate removal, two adjacent and equal, and duplicate removals. Simply put, the question translates into removing the adjacent equal letters. The translation process is crucial to simplify the question, as a lot of times, the prompt contains too much trivial information that distracts us from solving the problem. Also, identifying the key points and speaking them out loud keep the interviewer engaged.

To check if two letters are equal, the first thing that comes to my mind is to adopt brutal force and check for the same element at two consecutive positions. However, this method does not work as the removal process is dynamic.

Let’s say the test case is ‘ abbaca.’ If using the brutal force, we would only be able to remove ‘ bb’ the string but not the new combination ‘ aa’ created after deleting ‘ bb.’

We need a dynamic solution that checks if the newly created consecutive positions have the same element.

Fortunately, the universe offers stack!

We can create an empty stack (list) to store new elements. If the element is equal to the last element in the stack, we pop it out from the stack and don’t add the new element to the list. In other words, the simple pop operation removes two neighboring identical letters. Pretty neat! In the end, we rejoin the list to an empty string, a common transformation tactic.

Solution

As a warm-up, I intentionally choose this question for its simplicity. The following questions may look slightly challenging but totally solvable following the same process.

# Question 2: Make The String Great, by Google

— Given a string s of lower and upper case English letters.
— A good string is a string which doesn’t have two adjacent characters s[i] and s[i + 1] where: 0 Google asked this question. Let’s scan the prompt again and retrieve the key information. Here are the eye-catching keywords: two adjacent characters, one in lower-case and the next is in upper-case (vice-versa), remove two adjacent characters of different cases. Simply, the question wants us to remove two adjacent characters of different cases (one upper and one lower, regardless of positions).

Remember to speak out your mind and let your interviewer know you have captured the key information. If you don’t, your interviewer will ask for justifications why you decide to adopt stack but not other data types.

Following the same logic as Question 1, we create an empty stack to store elements and check if the to-be-added letter is the same but of a different case. In Python, there are different ways of checking cases. If you don’t know any built-in method/function, like me, we can follow the following steps: first make sure these two letters are not the same ( stack[-1] != i) and second they become the same after using the lower method ( stack[-1].lower() ==i.lower()).

Here is a catch. We can’t pop an element from an empty stack. It would generate an index error. Like the following:

To avoid the error message, we have to ensure the stack is not empty using if stack in line 4. This is one of the most common mistakes that Python programmers make while using a stack.

Solution 1

Solution 2

As it turns out, Python has a built-in method, swapcase(), that switches letters from upper case to lower case, vice versa. Also, you may want to check with the interviewer if you can use any built-in method. Keep communicating!

# Question 3: Build an Array With Stack Operations, by Google

— Given an array target and an integer n. In each iteration, you will read a number from list = <1,2,3…, n>.
— Build the target array using the following operations:
— Push: Read a new element from the beginning list, and push it in the array.
— Pop: delete the last element of the array.
— If the target array is already built, stop reading more elements.
— Return the operations to build the target array. You are guaranteed that the answer is unique.
— https://leetcode.com/problems/build-an-array-with-stack-operations/

Walk Through My Thinking

Google asked this question. This question is so user-friendly, and it explicitly tells you to push and pop elements. A stack is in order!

Creating an empty stack and iterate over the list: pushing elements to the new stack and popping the last element. Lastly, check if the constructed array is the same as the target array. If so, stop the iteration.

The only catch is to break the for loop if we have obtained the target array. To do so, keep the indentation block of stack==target (line 16 & 17) in line with the if-else statement. Interviewers may likely ask follow-up questions about why you keep the indentation inside the for loop rather than outside.

Solution

# Question 4: Baseball Game, by Amazon

— You are keeping score for a baseball game with strange rules. The game consists of several rounds, where the scores of past rounds may affect future rounds’ scores.
— At the beginning of the game, you start with an empty record. You are given a list of strings ops, where ops[i] is the ith operation you must apply to the record and is one of the following:
— An integer x — Record a new score of x.
— “+” — Record a new score that is the sum of the previous two scores. It is guaranteed there will always be two previous scores.
— “D” — Record a new score that is double the previous score. It is guaranteed there will always be a previous score.
— “C” — Invalidate the previous score, removing it from the record. It is guaranteed there will always be a previous score.
— Return the sum of all the scores on the record.
— https://leetcode.com/problems/baseball-game/

Walk Through My Thinking

Amazon picked this question. This is another interviewee-friendly question as it tells you to push and pop elements. Also, we need to use a control flow using multiple if statements. The procedure of building a stack and adding/removing elements is the same as the above questions. Here, I focus on the unique attribute of this question that needs special attention.

Usually, we have to check if a stack is empty or not before popping elements, as in Question 2. However, we don’t have to check for this question because the prompt tells us that there will always be a previous score. Without the extra condition, the question becomes slightly messier. In the end, we use a sum() function to return the sum of all the scores.

Solution

# Question 5: Next Greater Element I, by Amazon and Bloomberg

— You are given two integer arrays nums1 and nums2 both of unique elements, where nums1 is a subset of nums2.
— Find all the next greater numbers for nums1’s elements in the corresponding places of nums2.
— The Next Greater Number of a number x in nums1 is the first greater number to its right in nums2. If it does not exist, return -1 for this number.
— https://leetcode.com/problems/next-greater-element-i/

Walk Through My Thinking

Amazon and Blooomberg picked this question. Question 5 requires more than a 2-step solution. But first, the eye-catching keywords include: nums1 is a subset of nums2, find the next greater numbers for nums1 in nums2, and return -1 for none.

In my mind, here is the translation process:

Taken together, we have to find a way of identifying the position and value of an element and use if-else statements to compare values.

To find the position and value of an element, the natural choice is to use the enumerate() function. Also, we want to use a dictionary to keep records of the key-value pairs.

Next, we iterate over the array nums2 and find the next greater item. If there is such an item, we break the for loop; otherwise, return -1. The complete code is in Solution 1.

Solution 1

This approach makes intuitive sense, and it’s easy to follow.

Solution 2

Disclaimer: Solution 2 is not my original code, and special credits go to aditya baurai ’s post .

As it turns out, we can adopt a stack and a dictionary. First, we create an empty stack/dictionary and iterate over nums2:

To clarify, the for loop iterates over all of the elements in nums2, and the while loop is to find the next greater element in nums2 compared to the stack. To better help us understand, we can loop over the first 2 elements of nums2.

In brief, the above code finds all of the greater elements in nums2, and then we find the corresponding value for elements in nums1 in the end.

The complete Python code is available on my Github .

Takeaways

• Stack has two operations: push() and pop().
• Identify the keywords and communicate with your interviewer.
• Stack often teams up with the following keywords: two consecutive identical letters/numbers/words, push and pop an element if it is related somehow to the previous position.
• Check if it is an empty stack before popping.
• Indentation is crucial for loops. Understand the question well and decide its position (inside or outside the loop).
• Complicated coding questions can be disaggregated into multiple smaller pieces.

Medium recently evolved its Writer Partner Program , which supports ordinary writers like myself. If you are not a subscriber yet and sign up via the following link, I’ll receive a portion of the membership fees.

Источник

Array-Based Stack Implementation.

This utilizes the built-in Python list type, and wraps it with a Stack ADT interface.

Class description

Recap: Definition of stack abstract data type (Stack ADT):

A stack is an abstract data type (ADT) such that an instance S supports the following two methods:

• S.push(e): add element e to the top of the stack S
• S.pop: remove and return the top element from the stack S; an error occurs if the stack is empty.

Additionally, accessor methods for convenience:

• S.peek(): get reference to top element without removing it; an error occurs if the stack is empty.
• S.is_empty(): return True if stack S contains no elements
• len(S): implemented via builtin __len__

The ArrayStack class implements the above abstraction using an array-based structure (a list).

Link: https://git.charlesreid1.com/cs/python/src/master/stacks-queues-deques/stacks/ArrayStack.py

Class test

Taking a look first at our test, we should be able to run the following code after implementing the above methods:

if __name__=="__main__":
    a = ArrayStack()
    a.push(5)
    a.push(15)
    a.push(17)
    a.push(28)
    print("Peeking: {0}".format(a.peek()))
    print("Length of stack: {0}".format(len(a)))
    a.pop()
    a.pop()
    a.push(100)
    a.push(200)
    a.push(300)
    a.push(400)
    while(not a.is_empty()):
        a.pop()
        print("Popping... {0}".format(len(a)))
    print("Done testing ArrayStack.")

Exceptions and error handling

The specification of the ADT mentions two cases where errors should be thrown — both occurring if the stack is empty.

Create our own Empty exception:

class Empty(Exception):
    pass

Class implementation

"""
Stack ADT: ArrayStack

This class implements the following methods:
    S.push(e)
    S.pop()
    S.peek()
    S.is_empty()
    len(S)

This class utilizes an array-based data structure,
a list, to store its data under the hood.
It only needs to keep track of that list.

This makes it an adapter class for the list,
since it adheres to the Stack ADT but does not change
the implementation of the underlying list type.
"""

class ArrayStack:
    """
    Implement the Stack ADT using an array-based data structure (list).
    """
    def __init__(self):
        self._data = []

    def __len__(self):
        return len(self._data)

    def __str__(self):
        return str(self._data)

    def is_empty(self):
        """
        Check if empty. Don't bother calling our own __len__.
        Just do what is sensible.
        """
        return (len(self._data)==0)

    def push(self,o):
        """
        Add an element to the top of the stack
        """
        self._data.append(o)

    def pop(self):
        """
        Pop the next item.
        This should handle an empty stack.
        """
        if( self.is_empty() ):
            raise Empty("Stack is empty")
        return self._data.pop()

    def peek(self):
        """
        Peek at the next item.
        This should handle an empty stack.
        """
        if( self.is_empty() ):
            raise Empty("Stack is empty")
        return self._data[-1]

This is an adapter pattern for the list class.

Flags

In this tutorial we will create a stack in Python step-by-step. The stack is a LIFO (Last-in First-out) data structure.

To create a stack in Python you can use a class with a single attribute of type list. The elements of the stack are stored in the list using the push method and are retrieved using the pop method. Additional methods allow to get the size of the stack and the value of the element at the top of the stack.

We will build a custom class that implements the common operations provided by a stack data structure.

Let’s start building it!

How to Start Building the Class For the Stack

The data structure we will use inside our class to create a Python stack is a list.

The class will restrict the type of operations that can be performed against the list considering that a stack doesn’t allow all the operations that are possible with a Python list.

When working with a list you have the freedom to add and remove elements at the beginning in the middle and at the end of the list. The same doesn’t apply to a stack.

When working with a stack you can only add an element to the top of the stack and remove the element from the top of the stack. That’s because by definition a stack is a Last-in First-Out data structure.

Let’s start by creating a class called Stack that has a list attribute called elements.

The constructor of the stack class initialises the attribute elements to an empty list.

class Stack:
    def __init__(self):
        self.elements = []

The first two operations we want to support in our stack are push and pop:

• Push adds an element to the top of the stack.
• Pop removes the last element from the top of the stack.

Add two methods to our class to support the push and pop operations:

def push(self, data):
    self.elements.append(data)

To push data to the top of the stack we use the list append method.

def pop(self):
    return self.elements.pop()

To retrieve the last element from the top of the stack we use the list pop method.

Using the Push and Pop Operations on our Stack

Let’s test the class we have created so far.

class Stack:
    def __init__(self):
        self.elements = []

    def push(self, data):
        self.elements.append(data)

    def pop(self):
        return self.elements.pop()

Create an instance of stack and use __dict__ to view the instance attributes.

stack = Stack()
print(stack.__dict__)

[output]
{'elements': []}

As expected the only instance attribute is the empty list elements.

Then call the push method followed by the pop method.

stack.push(3)
stack.push('test')
print(stack.pop())
print(stack.pop())

[output]
test
3

You can see that after calling the pop method twice we get back the two elements we have pushed to the top of the stack using the push operation.

Note: notice that the first element returned by pop() is the string “test” that is the second element we have pushed to the stack. That’s because of the LIFO nature of the stack.

Handling Errors When Using Pop on an Empty Stack

After calling the pop method twice in the previous section our stack is empty.

I wonder what happens if we call the pop operation again:

print(stack.pop())

We get back the following exception:

Traceback (most recent call last):
   File "/opt/Python/Tutorials/create_stack.py", line 17, in 
     print(stack.pop())
   File "/opt/Python/Tutorials/create_stack.py", line 9, in pop
     return self.elements.pop()
 IndexError: pop from empty list

This exception doesn’t fully make sense…

The reference to pop in the error message is correct but a list is mentioned in the error because our class uses a list as instance attribute.

This could be confusing for a user that would be using our class as a way to work with a stack and not with a list.

Let’s handle this error better…

We will check if the internal list is empty before trying to “pop” an element from it:

def pop(self):
    if self.elements:
        return self.elements.pop()
    else:
        return None

If the list is empty the pop operation performed against the stack object will return None.

stack = Stack()
print(stack.pop())

Confirm that the print statement above returns None.

Retrieve the Number of Elements in a Python Stack

At the moment we are not able to determine the number of elements in the stack. 

Let’s add another method that returns the number of elements in the stack.

def size(self):
    return len(self.elements)

The new method simply returns the length of the internal list elements using the len() function. Let’s test it…

stack = Stack()
stack.push(3)
stack.push('test')
print("Number of elements in the stack: {}".format(stack.size()))

[output]
Number of elements in the stack: 2

Looks good 🙂

I would also like to be able to know if the stack is empty. Here is a new method that does that:

def empty(self):
    return True if self.size() == 0 else False

This is an example of how you can call a class method from another method within the same class.

Notice how the empty() method calls the size() method.

Let’s test the new method:

stack = Stack()
print(stack.empty())
stack.push(3)
print(stack.empty())

[output]
True
False

We are getting back the correct response from the empty() method.

Retrieve the Value of the Element at the Top of the Stack

Before completing this tutorial I would also like to implement a method that retrieves the value of the element at the top of the stack without removing it from the stack.

Considering that the internal attribute of the class is a list we can use an index to retrieve the last element.

The operation of retrieving the element at the top of the stack is called peek.

def peek(self):
    return self.elements[-1]

This method is super simple. We are using a negative index to get the last element in the elements list that is basically the element at the top of our stack.

stack = Stack()
stack.push('cat')
stack.push(3)
stack.push(1.2)
print(stack.peek())

[output]
1.2

The method does exactly what we wanted to do.

Conclusion

In this tutorial we have seen how to implement a stack in Python step-by-step using a custom class.

We have implemented five operations for our custom stack:

• Push: to add an element to the top of the stack.
• Pop: to retrieve the element at the top of the stack.
• Size: to get the size of the stack.
• Empty: to check if the stack is empty.
• Peek: to get the value of the element at the top of the stack.

I hope you found it useful 🙂

A stack is a linear data structure that stores items in a Last-In/First-Out (LIFO) or First-In/Last-Out (FILO) manner. In stack, a new element is added at one end and an element is removed from that end only. The insert and delete operations are often called push and pop.

The functions associated with stack are:

• empty() – Returns whether the stack is empty – Time Complexity: O(1)
• size() – Returns the size of the stack – Time Complexity: O(1)
• top() / peek() – Returns a reference to the topmost element of the stack – Time Complexity: O(1)
• push(a) – Inserts the element ‘a’ at the top of the stack – Time Complexity: O(1)
• pop() – Deletes the topmost element of the stack – Time Complexity: O(1)

Implementation:

There are various ways from which a stack can be implemented in Python. This article covers the implementation of a stack using data structures and modules from the Python library. 
Stack in Python can be implemented using the following ways: 

• list
• Collections.deque
• queue.LifoQueue

Implementation using list:

Python’s built-in data structure list can be used as a stack. Instead of push(), append() is used to add elements to the top of the stack while pop() removes the element in LIFO order. 
Unfortunately, the list has a few shortcomings. The biggest issue is that it can run into speed issues as it grows. The items in the list are stored next to each other in memory, if the stack grows bigger than the block of memory that currently holds it, then Python needs to do some memory allocations. This can lead to some append() calls taking much longer than other ones.

Initial stack
['a', 'b', 'c']

Elements popped from stack:
c
b
a

Stack after elements are popped:
[]

Implementation using collections.deque:

Python stack can be implemented using the deque class from the collections module. Deque is preferred over the list in the cases where we need quicker append and pop operations from both the ends of the container, as deque provides an O(1) time complexity for append and pop operations as compared to list which provides O(n) time complexity. 

The same methods on deque as seen in the list are used, append() and pop().

Initial stack:
deque(['a', 'b', 'c'])

Elements popped from stack:
c
b
a

Stack after elements are popped:
deque([])

Implementation using queue module

Queue module also has a LIFO Queue, which is basically a Stack. Data is inserted into Queue using the put() function and get() takes data out from the Queue. 

There are various functions available in this module: 

• maxsize – Number of items allowed in the queue.
• empty() – Return True if the queue is empty, False otherwise.
• full() – Return True if there are maxsize items in the queue. If the queue was initialized with maxsize=0 (the default), then full() never returns True.
• get() – Remove and return an item from the queue. If the queue is empty, wait until an item is available.
• get_nowait() – Return an item if one is immediately available, else raise QueueEmpty.
• put(item) – Put an item into the queue. If the queue is full, wait until a free slot is available before adding the item.
• put_nowait(item) – Put an item into the queue without blocking. If no free slot is immediately available, raise QueueFull.
• qsize() – Return the number of items in the queue.

0
Full:  True
Size:  3

Elements popped from the stack
c
b
a

Empty:  True

Implementation using a singly linked list:

The linked list has two methods addHead(item) and removeHead() that run in constant time. These two methods are suitable to implement a stack. 

• getSize()– Get the number of items in the stack.
• isEmpty() – Return True if the stack is empty, False otherwise.
• peek() – Return the top item in the stack. If the stack is empty, raise an exception.
• push(value) – Push a value into the head of the stack.
• pop() – Remove and return a value in the head of the stack. If the stack is empty, raise an exception.

Below is the implementation of the above approach:

Stack: 10->9->8->7->6->5->4->3->2->
Pop: 10
Pop: 9
Pop: 8
Pop: 7
Pop: 6
Stack: 5->4->3->2->

Advantages of Stack:

• Stacks are simple data structures with a well-defined set of operations, which makes them easy to understand and use.
• Stacks are efficient for adding and removing elements, as these operations have a time complexity of O(1).
• In order to reverse the order of elements we use the stack data structure.
• Stacks can be used to implement undo/redo functions in applications.

Drawbacks of Stack:

• Restriction of size in Stack is a drawback and if they are full, you cannot add any more elements to the stack.
• Stacks do not provide fast access to elements other than the top element.
• Stacks do not support efficient searching, as you have to pop elements one by one until you find the element you are looking for.