Fatal gradient amplifier error

How to fix MySQL incorrect datetime value error

Posted on Oct 23, 2021

The MySQL Incorrect datetime value error (which is also known as ERROR 1292 ) is triggered when you perform an INSERT statement that contains one or more DATETIME values with the wrong format.

MySQL only accepts DATETIME values in the format of YYYY-MM-DD hh:mm:ss for string type or YYYYMMDDhhmmss for integer type.

To show you an example, suppose you have a table with DATE and DATETIME columns as shown below:

Now suppose you want to INSERT a new value to the last_update column with the following statement:

MySQL will throw an error as shown below:

This is because the DATETIME value in the statement above uses the DD-MM-YYYY HH:MM:SS format, which is unacceptable by MySQL.

The obvious way to fix the error is to change the formatting of your value into the format that MySQL can accept.

But rather than editing the value manually, you can use the STR_TO_DATE() function to help you convert the string value into date value.

Here’s an example of STR_TO_DATE() function in action:

The STR_TO_DATE() function requires two arguments to run:

• The datetime string that you want to convert
• The format of the datetime string you pass to the function

Because there are many valid datetime formats in the world, it’s impossible for MySQL to guess what format the string value you passed to the function.

The STR_TO_DATE() function uses the same specifiers as the DATE_FORMAT() function that you can see here.

With the STR_TO_DATE() function, the previous INSERT statement won’t cause an error:

And that’s how you can fix the error Incorrect datetime value in MySQL.

Keep in mind that the error can also be triggered when you try to insert a DATE value to a DATE type column as follows:

The error will say Incorrect date value instead of Incorrect datetime value , but they are both the same error.

You can use STR_TO_DATE() to format your date value as shown below:

Just remember that you need to pass the right format to the STR_TO_DATE() function, or MySQL won’t be able to process your value.

In another example, if you’re using the forward slash / as the separator for your date value, then you need to use the same separator for the format parameter:

When you have many values that you want to insert to your table, using STR_TO_DATE function will save you from having to edit your values format manually.

But if you only want to insert a single value, then formatting your value manually might be faster.

Now you’ve learned how to fix the invalid datetime value error in MySQL database server. Great job! 👍

Level up your programming skills

I’m sending out an occasional email with the latest programming tutorials. Drop your email in the box below and I’ll send new stuff straight into your inbox!

About

Nathan Sebhastian is a software engineer with a passion for writing tech tutorials.
Learn JavaScript and other web development technology concepts through easy-to-understand explanations written in plain English.

Источник

How to Fix Quickly the Incorrect datetime value: ‘0000-00-00 00:00:00’ for column ‘your_column’ at row … Error in MySQL / MariaDB

In some settings MySQL / MariaDB treats empty or null ‘datetime’ and ‘timestamp’ fields/columns as simply null, in others it writes out zeros (0s) like 0000-00-00 00:00:00. If you designed your own database, you probably know what you’re dealing with, already. But if you are working on someone else’s database, like migrating data to or from, or just doing development for it, for example, you may encounter the error “Incorrect datetime value: ‘0000-00-00 00:00:00’ for column …”.

This error can become a bit of headache if a sync .sql script or dump file you need to run now and then or on a regular basis contains datetime values filled with zeros instead of null, or if you are like me and using a tool like Navicat to transfer or synchronize entire databases between two servers, you are prone to encounter this error – especially if you have no control on the settings of the remote database server such as that of a shared hosting. The root cause of the error is simply the executed SQL command does not conform the “SQL mode” of the server in dealing with empty date, date time or timestamp values.

While the section 5.1.10 Server SQL Modes section of the MySQL reference manual published at https://dev.mysql.com/doc/refman/5.7/en/sql-mode.html#sqlmode_no_zero_date explains what these SQL modes are and how they work, it may at first site look or sound a bit complicated in order to solve simply a date(time) or timestamp value such as ‘0000-00-00 00:00:00’ existing as actual data in one instance of a MySQL / MariaDb can’t simply be put in another instance.

A typical MySQL installation comes with a default mode denoted by MySQL’s ‘@@sqlmode’ notation which is queryable via an SQL command like below:

and when run, it returns a result such as

I have marked the related mode values in bold, above. In such a case as the above setting which has NO_ZERO_DATE and/or NO_ZERO_IN_DATE, a query like the following produces the error (coded 1292) Incorrect datetime value: ‘0000-00-00 00:00:00’ for column ‘blah_blah’ :

Error produced:

ERROR 1292 (22007): Incorrect datetime value: ‘0000-00-00 00:00:00’ for column ‘created’ at row 1

Temporary, Case-basis Solution :

Add or run the SQL command SET sql_mode = ”; before your INSERT or UPDATE QUERY which contains such date or datetime values as ‘0000-00-00 00:00:00’.

If you need the other settings such as ERROR_FOR_DIVISION_BY_ZERO or NO_ENGINE_SUBSTITUTION and only want to allow zero-filled date / datetime values then you can use something like the following:

Permanent Solution :

If this is something you will encounter more often than once or twice, such as regular database synchronizations with another host or a dumped SQL file to be used more than once, then you may want to set the above SQL mode permanently to avoid the incorrect datetime value error.

In that case, simply edit your mysql.cnf options file, find the section starting with “[mysql]” (without quotes), and then after the [mysql] line at add following:

If your MySQL instance is in MAMP Pro,

1. Open the main window of MAMP Pro and via the menu go to File > Edit Templates > MySQL > (your version).
   This opens a text editor with your MySQL configuration.
2. In the configuration file, find the line starting with [mysqld] (be sure to locate the d at the end, and not to confuse with [mysql]).
3. If sql_mode isn’t set, you can add it under the [mysqld] heading: Right after this line, add a new line containing:
4. Save the file, and restart MySQL.

If you don’t have a GUI admin interface or simply just prefer getting things done in a command-line terminal:

If you are not happy with the other modes you can simply set the sql_mode to a blank string like so: sql_mode=”, but again if all we care about is zero-date-time tolerance and to avoid the error 1292, all we need is to take out

• STRICT_TRANS_TABLES
• NO_ZERO_IN_DATE
• NO_ZERO_DATE

from the sql_mode of MySQL / MariaDb.

Источник

MySQL Error 1292 – Solve it now

MySQL error 1292 occurs if the syntax for the date is incorrectly entered.

Here at Bobcares, we have seen several causes for this error while troubleshooting MySQL issues as part of our Server Management Services for web hosts and online service providers.

Today we’ll take a look at the cause for this error and how to fix it.

Why does MySQL Error 1292 occur

Before we get into the solution part, let us first see what causes this error to occur.

This error normally occurs when the date is entered in an incorrect format. The date value like 0000-00-00 00:00:00 is not allowed with MySQL 5.7 version.

Also, this error can occur when trying to compare a number and a string in a WHERE or ON clause.

For instance, the error appears as below.

How we fix MySQL Error 1292

This error is of different types and can occur due to many reasons and also the solution will differ according to the error. Here are the different errors and the solutions that our Engineers provide to our customers.

1. If a field type is a DATE, then we make sure that the date is entered in the format “yyyy-mm-dd”.

2. Error Code: 1292 – Incorrect date value

Many of our customers use MySQL 5.7. But in this version date value like 0000-00-00 00:00:00 is not allowed. Hence, the above error occurs. In case, if our customers want to allow it, then we update their my.cnf like:

In this file, we find

Then after that, we add the below line.

After adding the above line, we restart the MySQL service. For that, we run the below command.

3. #1292 – Truncated incorrect DOUBLE value

Usually, this error message appears when customers try to compare a number and a string in a WHERE or ON clause.

So we make sure that they have similar declarations or convert the number to a string. Also, if we turn off strict mode, the error turns into a warning.

[Need any further assistance in fixing MySQL errors? – We’re available 24*7]

Conclusion

In short, this error can arise with different messages and has its own way to fix it. Today, we saw the resolution to this MySQL error.

PREVENT YOUR SERVER FROM CRASHING!

Never again lose customers to poor server speed! Let us help you.

Our server experts will monitor & maintain your server 24/7 so that it remains lightning fast and secure.

ERROR 1292 (22007): Incorrect date value: ’24-02-2020′ for column ‘date’ at row 1

Hi,
Please contact our support team via live chat(click on the icon at right-bottom).

Источник

mysqlimport Error 1292. Incorrect datetime value

Проблема

Имеется база данных с заранее подготовленной структурой. Сервер БД — mariadb-10.5.8. В результате импорта данных из CSV-дампа mailing_views_details.txt (создан при помощи mysqldump —tab)

где
-d — очистка таблицы mailing_views_details перед ипортированием
-k — отключить проверку foreign key во время импортирования
-v — добавляет немного «болтливости» при импорте

в таблицу mailing_views_details получаю следующую ошибку:

Loading data from SERVER file: mailing_views_details.txt into mailing_views_details
mysqlimport Error 1292, Incorrect datetime value: ‘2018-03-25 03:01:08’ for column `test`.`mailing_views_details`.`created_at` at row 706660, when using table: mailing_views_details

Разбираемся

Смотрим строку 706660 и соседнюю с ней 706659 дампа mailing_views_details.txt

507967 15550 2018-03-25 02:59:22
450087 15559 2018-03-25 03:01:08

Значение третьего поля ‘2018-03-25 03:01:08’ недопустимо из-за перехода на летнее время (Daylight saving time (DST)) между 2 и 3 часами ночи 25 марта. Следовательно все значения времени после 3 часов ночи в любой день введения летнего времени недопустимы. Это утверждение истинно если тип поля таблицы timestamp

Решение

Их есть несколько

1. Сменить системный часовой пояс на тот, который не использует DST
2. Изменить тип поля таблицы с текущего timestamp на datetime
3. Задать другое значение переменной mysql — time_zone

Ясно, что первый вариант вовсе и не вариант для нашего часового пояса. Поэтому рассмотрим варианты два и три

Вариант 2

Меняем тип поля таблицы mailing_views_details на datetime

После чего дамп накатывается без ошибок

Вариант 3

Меняем переменную time_zone с текущего значения SYSTEM на +2:00

И накатываем дамп. Чтобы всякий раз после перезагрузки mysql не изменять значение time_zone на нужное, необходимо в файле my.cnf добавить следующее:

И вишенка на торте!

Такая ошибка импортирования наблюдается только в случае если дамп был сделан с использованием mysqldump —tab в CSV-файл. Если же дампить без опции —tab, то при заливке подобной ошибки не возникает

Источник

Поднимая данный вопрос, мы понимаем, что он достаточно сложный и требует обширного и развернутого объяснения. Вместить все тонкости в рамки данной статьи, скорее всего не получится…Попробуем сделать это в краткой форме.

Одна из основных систем магнинто-резонансного томографа (МРТ) – подсистема градиента магнитного поля.

Что такое градиент?

Градиент (от лат. gradiens, «шагающий, растущий») – вектор, своим направлением указывающий направление наибольшего возрастания некоторой величины, значение которой меняется от одной точки пространства к другой (скалярного поля), а по величине (модулю) равный скорости роста этой величины в этом направлении.
В нашем случае градиент — это изменяющееся магнитное поле, которое позволяет однозначно определить от какой точки пришел эхо сигнал.
Градиентный усилитель в МРТ – генерирует мощное магнитное поле, по заданному закону.
Сам градиентный усилитель – это не усилитель вовсе. Любой усилитель — это генератор мощной копии входного сигнала. За счет энергии источника питания эта копия и формируется.
Для создания градиента магнитного поля, нужно пропустить через градиентные обмотки большой ток, причем импульс должен быть с крутым фронтом, а для некоторых программ и вовсе требуется, чтобы направление тока в градиентной обмотке мгновенно менялось на противоположное для перемагничивания. Этим занимаются градиентные усилители, они занимают целую стойку в аппаратной МРТ.
Чтобы получить высокий КПД градиентного усилителя используют ключевой режим работы силовых элементов (полевых транзисторов, IGBI сборки, комплементарных пар биполярных транзисторов…).
Один из частных случаев ключевого режима работы силовых элементов градиентного усилителя — это широтно импульсная модуляция (ШИМ).
Принцип работы ШИМ можно сравнить с наполнением бочки через тонкую трубу. Но кран открываем не плавно, а рывками на короткие промежутки времени. Причем стараемся, чтобы от полностью закрытого до полностью открытого положения прошло минимальное время. А скорость наполнения регулируем частотой открытия крана и длительностью открытого положения
Основные элементы градиентного усилителя МРТ:

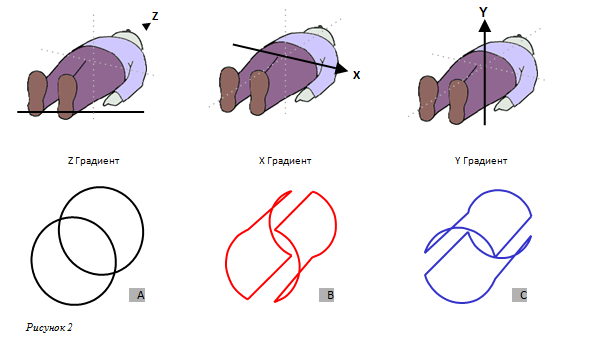
1. Так как мы живем в трехмерном пространстве, то в градиентном усилителе применяются 3 перпендикулярные оси для получения 3-х основных проекций изображений. Изменяя закон управления градиентными усилителями можно получитьпроизвольную проекцию изображения.
2. Как правило, в градиентном усилителе есть основной контроллер, который управляет всей стойкой, самодиагностикой, охлаждением, питанием и т.д.
3. Один из основных элементов – блок питания. Преобразует энергию электрической сети к необходимым параметрам питания оборудования.
4. Сам усилительный модуль (ось – сленговое название) в количестве 3х штук, по количеству проекций.
5. Несмотря на высокий КПД, градиентныйусилитель выделяет очень много тепла и нуждается в системе охлаждения. Система охлаждениябывает, как воздушная, так и водяная, в зависимости от конкретнойконструкцииградиентного усилителя.

И, немного, теории

Если предположить, что магнитное поле однородно на 100 % (что не так), то все протоны в организме вращались бы с Ларморовой частотой (Рисунок1). Это также означает, что все протоны возвращали бы сигнал. Как узнать, от головы или от ног поступает сигнал? В общем, мы этого не знаем. Если оставить все как есть, мы не получим хорошее изображение; или точно не то, которое ожидали. Оно будет содержать только неразборчивые пятна. Решение нашей проблемы может быть найдено в свойствах РЧ волны, а именно: фаза, частота иамплитуда.
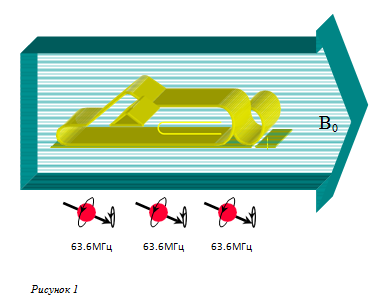
Сначала мы разделим тело на элементы объема, известные как вокселы. Затем закодируем воксел таким образом, что протоны, содержащиеся в нем, будут испускать РЧ волнус известной фазой и частотой. Амплитуда сигнала зависит от количества протонов в вокселе.
Введем новое понятие – градиентные катушки.

Градиентные катушки

Градиентные катушки представляют собой набор проводов в магните, которые позволяют создавать дополнительные магнитные поля, в некотором отношении, накладывающиеся на главное магнитное поле B0. Звучит сложно, но в действительности все проще.

Имеются 3 набора проводов. Каждый набор может создавать магнитное поле в определенном направлении: Z, X или Y. Когда ток поступает в Z градиент, магнитное поле создается в Z направлении (Рисунок 2A). Аналогично происходит в других градиентах (Рисунок 2B и2C).
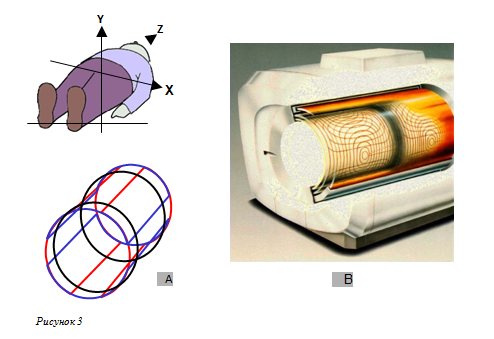
Интересная деталь: Известно, что МРТ может создавать много помех во время сбора данных. Генерируемое магнитное поле очень сильное. Хотя градиентные катушки надежно зафиксированы в смоле, силы ими создаваемые, достаточны для возникновения вибрации катушек, и как следствиепомех.

Рисунок 3A схематически показывает формирование цилиндра из 3 градиентных катушек. Затем этот цилиндр помещается в отверстие магнита (Рисунок 3B).
Далее обсудим использование градиентов при кодировании сигнала.

Кодирование сигнала

• Будем получать аксиальные изображениямозга.
• Используем магнит с полем 1.5Т.
• Магнитное поле однородно и покрывает все тело с ног до головы. (В действительности это не так, однородная область находится в изоцентре магнита и составляет лишь 40 см в диаметре, но это допущение упростит объяснение).
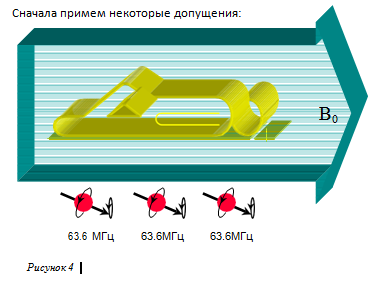
Когда мы помещаем пациента в магнит, все протоны от головы до пальцев ног выравниваются вдоль B0. Они вращаются с Ларморовой частотой 63.6 МГц (Рисунок 4).
При использовании 90º РЧ импульса возбуждения для перевода вектора намагниченности в плоскость X-Y, все протоны реагируют и возвращают сигнал, но откуда поступает сигнал: от головы или ног – мы не знаем.

При включенном Z-градиенте в этом направлении генерируется дополнительное магнитное поле, накладывающееся на B0. Обозначение
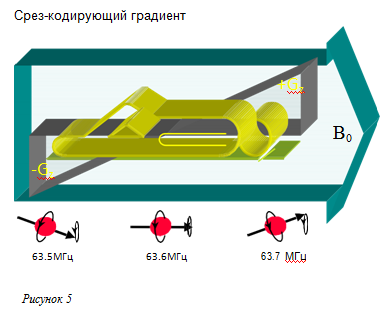
+Gz на Рисунке 5показывает, что поле B0 у головы немного сильнее, чем в изоцентре магнита. Более сильное поле B0 означает более высокую Ларморовую частоту. Вдоль всего наклона градиента поле B0 различно и, следовательно, протоны вращаются с разными частотами. Поэтому, протоны головы будут вращаться немного
быстрее, чем в изоцентре. Для протонов ног – обратная картина. Рисунок 5показывает, что частота вращения протонов ног составляет 63.5 МГц, в изоцентре магнита все еще 63.6 МГц, а протоны головы имеют частоту 63.7 МГц.
(Эти частоты взяты в качестве примера; в действительности разница между частотами гораздо меньше).
Теперь, если мы применим РЧ импульс с частотой 63.7 МГц, прореагируют ТОЛЬКО протоны в тонком срезе головы, потому что они — единственные, вращающиеся с этой же самой частотой (Рисунок 6).

Это называется срез-кодированием или срез-селекцией. В этом примере Gz – срез-кодирующий градиент.
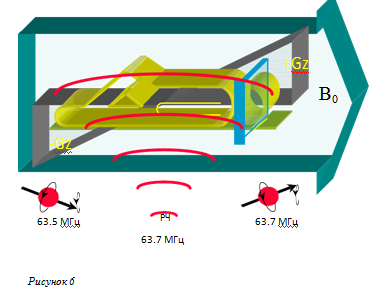
Если на данном этапе принять ответный сигнал, мы сможем определить, что сигнал получен от единственного среза головы.

Теперь для одного направления (Z-направления) мы знаем, откуда поступает сигнал. Это –
большое достижение

Рисунок 7 показывает аксиальный срез, который только что был создан градиентом Gz. Если подробнее рассмотреть протоны 1 и 2 в этом срезе, мы увидим, что они оба вращаются с одной частотой И имеют одинаковуюфазу.
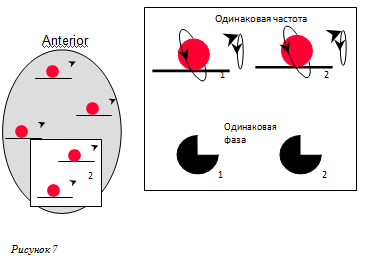
В срезе находится огромное количество протонов, и мы все равно не знаем из какой части среза получен сигнал: передней, задней, левой или правой сторон. Поэтому для точного определения непосредственного источника сигнала требуется дальнейшее кодирование.

Фазо-кодирующий градиент

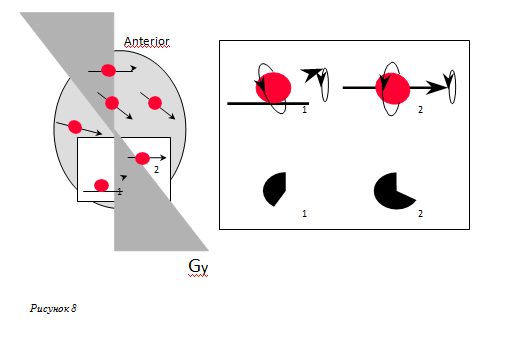
Для дальнейшего кодирования протонов на очень короткое время включается градиент Gy. В течение этого времени в anterior-posterior направлении создается дополнительное магнитное поле градиента.

В этом случае передние протоны будут вращаться немного быстрее, чем задние протоны. Из-за этого различия протоны больше не вращаются в фазе. Взглянув на протоны 1 и 2, мы увидим, что протон 1 накопил большую фазу по сравнению с протоном 2 (Рисунок 8).

Когда градиент Gy выключен, каждый протон в срезе вращается с одинаковой частотой, НО каждый имеет различную фазу (Рисунок 9).
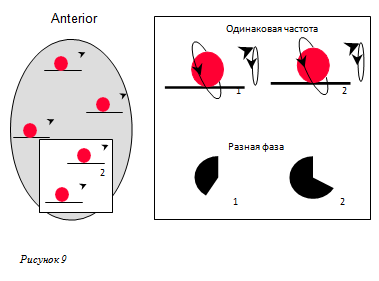
Это называется кодированием фазы.

После второго процесса кодирования необходимо сделать следующий шаг в поиске точного определения непосредственного источника сигнала.

Мы можем определить две вещи:

1.Сигнал поступает из среза головы. (Кодированиесреза)
2.Сигнал содержит ряд РЧ волн, имеющих одинаковую частоту, но разные фазы. Можно отличить, поступает ли сигнал с передней или задней сторон.(Кодирование фазы)
Все, что нам нужно сделать, – выполнить еще одно кодирование для определения стороны поступления сигнала: левая, центральная или правая часть головы.

Частотно-кодирующий градиент

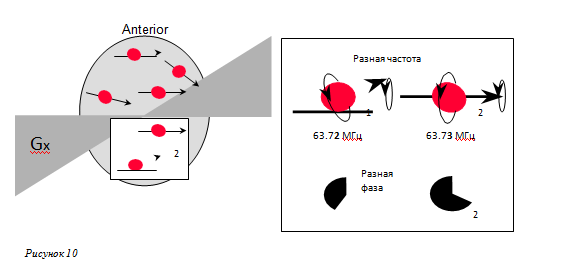
Для кодирования левого-правого направления включается третий и последний градиент Gx, создающий дополнительное магнитное поле в этом направлении.
Протоны с левой стороны вращаются с более низкой частотой, чем с правой. (Рисунок 10).

Они накапливают дополнительный сдвиг фазы из-за различий в частотах, но — что крайне важно — уже приобретенная разность фаз, полученная при кодировании фазы градиента на предыдущем шаге, сохраняется.
Теперь возможно определить, поступает ли сигнал с левой, центральной или правой стороны среза.
Задача выполнена!
Мы можем точно определять непосредственное происхождение сигналов, которые принимаются катушкой.
Давайте подведем итог и взглянем, чего мы достигли в течение всего процесса.

Рисунок 11 показывает конечный результат:

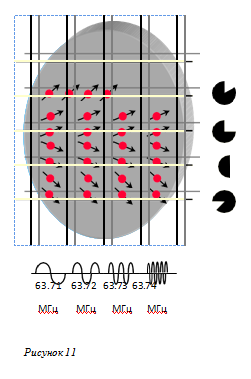
1.Gz градиент выбрал аксиальныйсрез.
2.Gy градиент создал строкисразными фазами.
3.Gx градиент сформировал столбцы с разными частотами.

Как видите, были созданы маленькие объемы (вокселы). Каждый воксел имеет уникальную комбинацию частоты и фазы. Количество протонов в каждом вокселе определяет силу (амплитуду) РЧ волны.
Полученный сигнал, поступающий из различных областей (вокселей) мозга, содержит сложное сочетание частот, фаз и амплиту

Компьютер получает это огромное количество информации и затем происходит «чудо».
Приблизительно через 0.25 секунды компьютер проанализирует данные и создаст изображение. «Чудо» – математический процесс, известный как двумерное преобразование Фурье (ДПФ), которое позволяет компьютеру вычислить точное размещение и интенсивность (яркость) каждого воксела. (Объяснение действия преобразования Фурье выходит за границы этой истории. Однако ПФ можно сравнить с призмой, преломляющей «белый» свет (МР сигнал) в цвета радуги (изображение). Мы сами постоянно проделываем ПФ ушами. Мы воспринимаем много различных звуков (МР сигнал) в одно и то же время. Наш мозг выполняет ПФ, чтобы точно определить происхождение и интенсивность отдельных звуков (МР изображение).

Примечание: за один шаг кодирование фазы выполняется только для одной строки. Для сканирования целого среза полный процесс кодирования среза, фазы и частоты должен быть повторен столько раз, сколько определено параметром Матрицакодированияфазы(Mxpe). Это также объясняет потребность в параметре сканирования – время повторения (RepetitionTime -TR). Подробнее о характеристиках сканированияпозже.

Шаг в сторону: Характеристики градиента

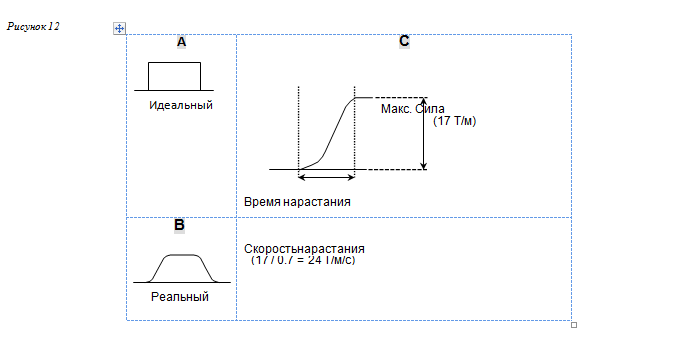
Идеально, при включении градиента немедленно достигается максимум мощности, а при выключении сразу уменьшается до нуля (Рисунок 12A). К сожалению, дело обстоит не так, поскольку мы живем не в идеальном мире. В действительности градиенту необходимо некоторое время, чтобы достичь максимума мощности при включении и нуля при выключении (Рисунок 12B). Время, необходимое для достижения максимальной мощности, называется временем нарастания (Рисунок 12C). Если максимальную мощность разделить на время нарастания, получится параметр, называемый скоростью нарастания. Эти параметры являются характеристиками градиентной системы.
Вам следует сравнивать эти значения, потому что они отличны для каждой системы:

1.Максимальная сила: как можно выше (минимальное поле наблюдения FOVи максимальнаяматрица).
2.Время нарастания: как можно короче (см. пункт3).
3.Скорость нарастания: как можно больше (минимальное TR, TE иETS).

Эксплуатационные показатели сканера, и поэтому область его возможного применения, главным образом определяются эксплуатационными характеристиками системы градиента. Другие предсказуемые трудности связаны с напряженностью поля B0, компьютерной системой и доступностью использования интерфейса пользователя.

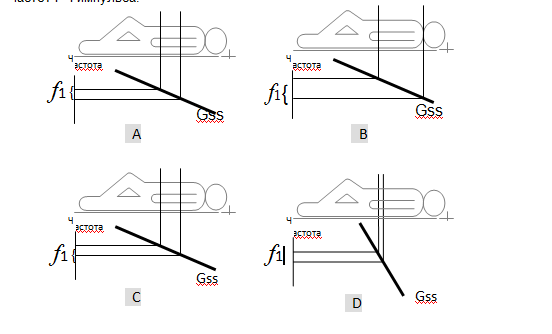
Шаг в сторону: толщина среза

На первом шаге кодирования сигнала с помощью срез-селектирующего градиента (Gss) определяется положение среза. В нашем примере толщина среза не играла роли. Однако в реальной жизни она очень важна.
Толщина среза определяется двумя факторами:

1.Крутизной наклона поляградиента.
2.Полосой частот 90º РЧимпульса.

На Рисунках 13A и 13B крутизна градиента одинаковая, в то время как полоса частот РЧ импульса разная. В качестве альтернативы, рисунки 13C и 13D показывают, что, изменяя крутизну градиента при постоянной полосе частот РЧ импульса, можно также изменять толщину среза.
Практически, толщина среза определяется комбинацией крутизны градиента и полосы частот РЧ импульса.

Рисунок 13

Источник:

1. ЭвертБлинк(Evert Blink), «ОсновыМРТ: Физика» (Basic MRI Physics)
2. Кретов Егор, «Разбираем Магнитно-резонансный томограф», https://habr.com/ru/post/405355/
3. Кучковой Павел, инженер Рустомограф

Нейронные сети обучаются с помощью тех или иных модификаций градиентного спуска, а чтобы применять его, нужно уметь эффективно вычислять градиенты функции потерь по всем обучающим параметрам. Казалось бы, для какого-нибудь запутанного вычислительного графа это может быть очень сложной задачей, но на помощь спешит метод обратного распространения ошибки.

Открытие метода обратного распространения ошибки стало одним из наиболее значимых событий в области искусственного интеллекта. В актуальном виде он был предложен в 1986 году Дэвидом Э. Румельхартом, Джеффри Э. Хинтоном и Рональдом Дж. Вильямсом и независимо и одновременно красноярскими математиками С. И. Барцевым и В. А. Охониным. С тех пор для нахождения градиентов параметров нейронной сети используется метод вычисления производной сложной функции, и оценка градиентов параметров сети стала хоть сложной инженерной задачей, но уже не искусством. Несмотря на простоту используемого математического аппарата, появление этого метода привело к значительному скачку в развитии искусственных нейронных сетей.

Суть метода можно записать одной формулой, тривиально следующей из формулы производной сложной функции: если $f(x) = g_m(g_{m-1}(ldots (g_1(x)) ldots))$, то $frac{partial f}{partial x} = frac{partial g_m}{partial g_{m-1}}frac{partial g_{m-1}}{partial g_{m-2}}ldots frac{partial g_2}{partial g_1}frac{partial g_1}{partial x}$. Уже сейчас мы видим, что градиенты можно вычислять последовательно, в ходе одного обратного прохода, начиная с $frac{partial g_m}{partial g_{m-1}}$ и умножая каждый раз на частные производные предыдущего слоя.

Backpropagation в одномерном случае

В одномерном случае всё выглядит особенно просто. Пусть $w_0$ — переменная, по которой мы хотим продифференцировать, причём сложная функция имеет вид

$$f(w_0) = g_m(g_{m-1}(ldots g_1(w_0)ldots)),$$

где все $g_i$ скалярные. Тогда

$$f'(w_0) = g_m'(g_{m-1}(ldots g_1(w_0)ldots))cdot g’_{m-1}(g_{m-2}(ldots g_1(w_0)ldots))cdotldots cdot g’_1(w_0)$$

Суть этой формулы такова. Если мы уже совершили forward pass, то есть уже знаем

$$g_1(w_0), g_2(g_1(w_0)),ldots,g_{m-1}(ldots g_1(w_0)ldots),$$

то мы действуем следующим образом:

• берём производную $g_m$ в точке $g_{m-1}(ldots g_1(w_0)ldots)$;

• умножаем на производную $g_{m-1}$ в точке $g_{m-2}(ldots g_1(w_0)ldots)$;

• и так далее, пока не дойдём до производной $g_1$ в точке $w_0$.

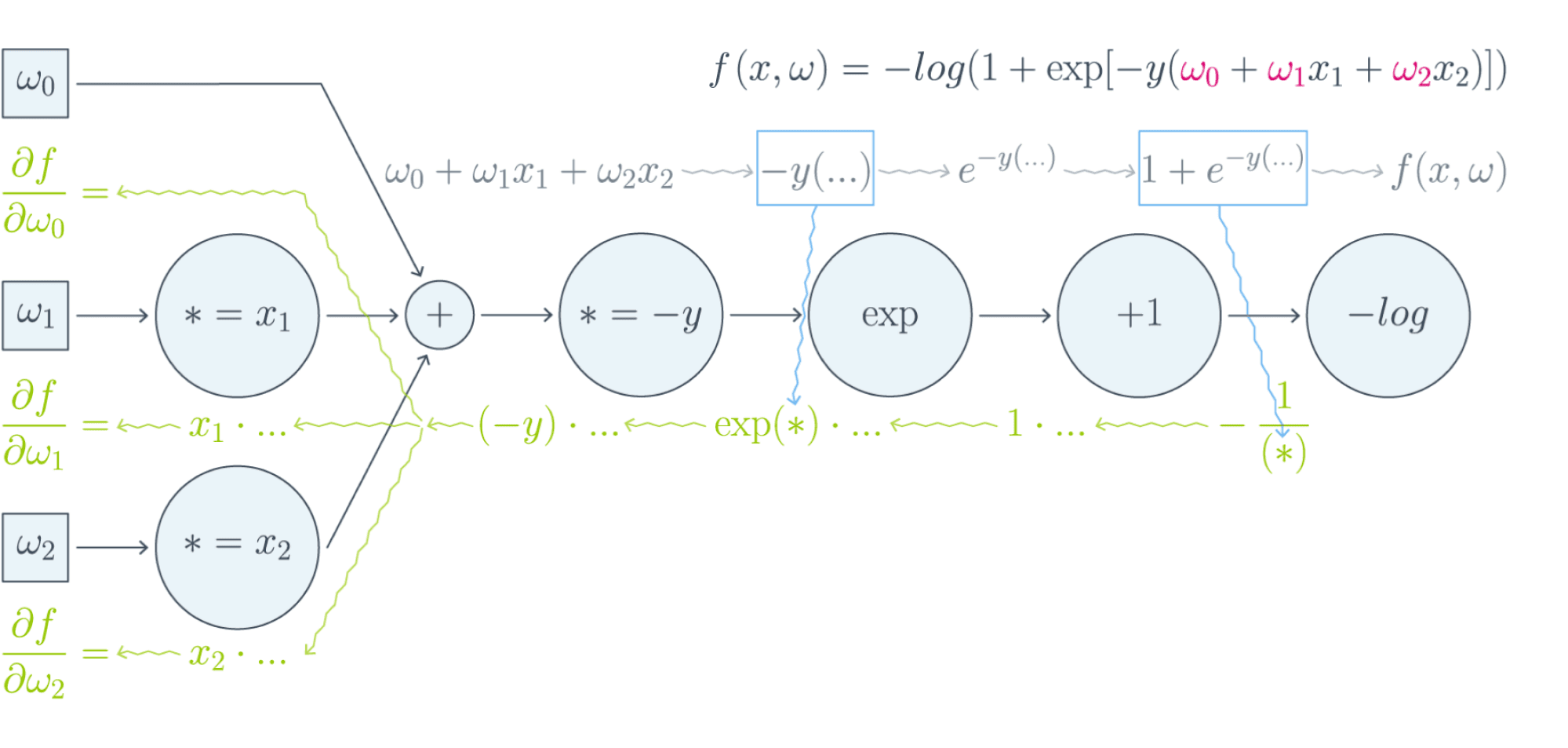
Проиллюстрируем это на картинке, расписав по шагам дифференцирование по весам $w_i$ функции потерь логистической регрессии на одном объекте (то есть для батча размера 1):

Собирая все множители вместе, получаем:

$$frac{partial f}{partial w_0} = (-y)cdot e^{-y(w_0 + w_1x_1 + w_2x_2)}cdotfrac{-1}{1 + e^{-y(w_0 + w_1x_1 + w_2x_2)}}$$

$$frac{partial f}{partial w_1} = x_1cdot(-y)cdot e^{-y(w_0 + w_1x_1 + w_2x_2)}cdotfrac{-1}{1 + e^{-y(w_0 + w_1x_1 + w_2x_2)}}$$

$$frac{partial f}{partial w_2} = x_2cdot(-y)cdot e^{-y(w_0 + w_1x_1 + w_2x_2)}cdotfrac{-1}{1 + e^{-y(w_0 + w_1x_1 + w_2x_2)}}$$

Таким образом, мы видим, что сперва совершается forward pass для вычисления всех промежуточных значений (и да, все промежуточные представления нужно будет хранить в памяти), а потом запускается backward pass, на котором в один проход вычисляются все градиенты.

Почему же нельзя просто пойти и начать везде вычислять производные?

В главе, посвящённой матричным дифференцированиям, мы поднимаем вопрос о том, что вычислять частные производные по отдельности — это зло, лучше пользоваться матричными вычислениями. Но есть и ещё одна причина: даже и с матричной производной в принципе не всегда хочется иметь дело. Рассмотрим простой пример. Допустим, что $X^r$ и $X^{r+1}$ — два последовательных промежуточных представления $Ntimes M$ и $Ntimes K$, связанных функцией $X^{r+1} = f^{r+1}(X^r)$. Предположим, что мы как-то посчитали производную $frac{partialmathcal{L}}{partial X^{r+1}_{ij}}$ функции потерь $mathcal{L}$, тогда

$$frac{partialmathcal{L}}{partial X^{r}_{st}} = sum_{i,j}frac{partial f^{r+1}_{ij}}{partial X^{r}_{st}}frac{partialmathcal{L}}{partial X^{r+1}_{ij}}$$

И мы видим, что, хотя оба градиента $frac{partialmathcal{L}}{partial X_{ij}^{r+1}}$ и $frac{partialmathcal{L}}{partial X_{st}^{r}}$ являются просто матрицами, в ходе вычислений возникает «четырёхмерный кубик» $frac{partial f_{ij}^{r+1}}{partial X_{st}^{r}}$, даже хранить который весьма болезненно: уж больно много памяти он требует ($N^2MK$ по сравнению с безобидными $NM + NK$, требуемыми для хранения градиентов). Поэтому хочется промежуточные производные $frac{partial f^{r+1}}{partial X^{r}}$ рассматривать не как вычисляемые объекты $frac{partial f_{ij}^{r+1}}{partial X_{st}^{r}}$, а как преобразования, которые превращают $frac{partialmathcal{L}}{partial X_{ij}^{r+1}}$ в $frac{partialmathcal{L}}{partial X_{st}^{r}}$. Целью следующих глав будет именно это: понять, как преобразуется градиент в ходе error backpropagation при переходе через тот или иной слой.

  Вы спросите себя: надо ли мне сейчас пойти и прочитать главу учебника про матричное дифференцирование?

Встречный вопрос. Найдите производную функции по вектору $x$:

$$f(x) = x^TAx, Ain Mat_{n}{mathbb{R}}text{ — матрица размера }ntimes n$$

А как всё поменяется, если $A$ тоже зависит от $x$? Чему равен градиент функции, если $A$ является скаляром? Если вы готовы прямо сейчас взять ручку и бумагу и посчитать всё, то вам, вероятно, не надо читать про матричные дифференцирования. Но мы советуем всё-таки заглянуть в эту главу, если обозначения, которые мы будем дальше использовать, покажутся вам непонятными: единой нотации для матричных дифференцирований человечество пока, увы, не изобрело, и переводить с одной на другую не всегда легко.

Мы же сразу перейдём к интересующей нас вещи: к вычислению градиентов сложных функций.

Градиент сложной функции

Напомним, что формула производной сложной функции выглядит следующим образом:

$$left[D_{x_0} (color{#5002A7}{u} circ color{#4CB9C0}{v}) right](h) = color{#5002A7}{left[D_{v(x_0)} u right]} left( color{#4CB9C0}{left[D_{x_0} vright]} (h)right)$$

Теперь разберёмся с градиентами. Пусть $f(x) = g(h(x))$ – скалярная функция. Тогда

$$left[D_{x_0} f right] (x-x_0) = langlenabla_{x_0} f, x-x_0rangle.$$

С другой стороны,

$$left[D_{h(x_0)} g right] left(left[D_{x_0}h right] (x-x_0)right) = langlenabla_{h_{x_0}} g, left[D_{x_0} hright] (x-x_0)rangle = langleleft[D_{x_0} hright]^* nabla_{h(x_0)} g, x-x_0rangle.$$

То есть $color{#FFC100}{nabla_{x_0} f} = color{#348FEA}{left[D_{x_0} h right]}^* color{#FFC100}{nabla_{h(x_0)}}g$ — применение сопряжённого к $D_{x_0} h$ линейного отображения к вектору $nabla_{h(x_0)} g$.

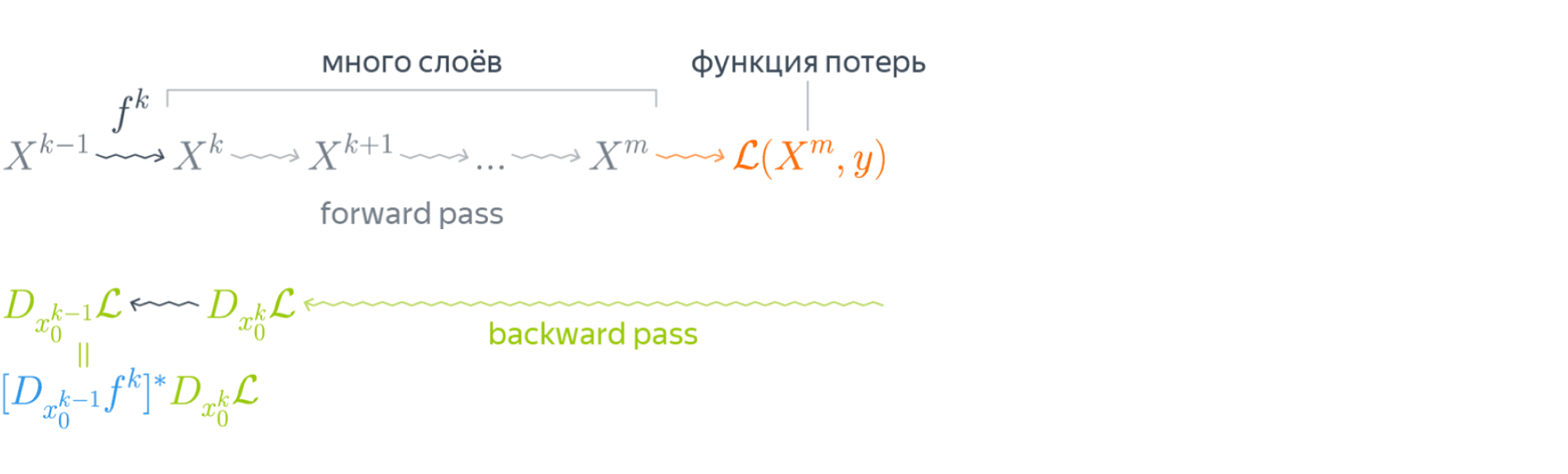
Эта формула — сердце механизма обратного распространения ошибки. Она говорит следующее: если мы каким-то образом получили градиент функции потерь по переменным из некоторого промежуточного представления $X^k$ нейронной сети и при этом знаем, как преобразуется градиент при проходе через слой $f^k$ между $X^{k-1}$ и $X^k$ (то есть как выглядит сопряжённое к дифференциалу слоя между ними отображение), то мы сразу же находим градиент и по переменным из $X^{k-1}$:

Таким образом слой за слоем мы посчитаем градиенты по всем $X^i$ вплоть до самых первых слоёв.

Далее мы разберёмся, как именно преобразуются градиенты при переходе через некоторые распространённые слои.

Градиенты для типичных слоёв

Рассмотрим несколько важных примеров.

Примеры

1. $f(x) = u(v(x))$, где $x$ — вектор, а $v(x)$ – поэлементное применение $v$:

   $$vbegin{pmatrix}
   x_1
   vdots
   x_N
   end{pmatrix}
   = begin{pmatrix}
   v(x_1)
   vdots
   v(x_N)
   end{pmatrix}$$

   Тогда, как мы знаем,

   $$left[D_{x_0} fright] (h) = langlenabla_{x_0} f, hrangle = left[nabla_{x_0} fright]^T h.$$

   Следовательно,

   $$begin{multline*}
   left[D_{v(x_0)} uright] left( left[ D_{x_0} vright] (h)right) = left[nabla_{v(x_0)} uright]^T left(v'(x_0) odot hright) =\[0.1cm]
   = sumlimits_i left[nabla_{v(x_0)} uright]_i v'(x_{0i})h_i
   = langleleft[nabla_{v(x_0)} uright] odot v'(x_0), hrangle.
   end{multline*},$$

   где $odot$ означает поэлементное перемножение. Окончательно получаем

   $$color{#348FEA}{nabla_{x_0} f = left[nabla_{v(x_0)}uright] odot v'(x_0) = v'(x_0) odot left[nabla_{v(x_0)} uright]}$$

   Отметим, что если $x$ и $h(x)$ — это просто векторы, то мы могли бы вычислять всё и по формуле $frac{partial f}{partial x_i} = sum_jbig(frac{partial z_j}{partial x_i}big)cdotbig(frac{partial h}{partial z_j}big)$. В этом случае матрица $big(frac{partial z_j}{partial x_i}big)$ была бы диагональной (так как $z_j$ зависит только от $x_j$: ведь $h$ берётся поэлементно), и матричное умножение приводило бы к тому же результату. Однако если $x$ и $h(x)$ — матрицы, то $big(frac{partial z_j}{partial x_i}big)$ представлялась бы уже «четырёхмерным кубиком», и работать с ним было бы ужасно неудобно.

2. $f(X) = g(XW)$, где $X$ и $W$ — матрицы. Как мы знаем,

   $$left[D_{X_0} f right] (X-X_0) = text{tr}, left(left[nabla_{X_0} fright]^T (X-X_0)right).$$

   Тогда

   $$begin{multline*}
   left[ D_{X_0W} g right] left(left[D_{X_0} left( ast Wright)right] (H)right) =
   left[ D_{X_0W} g right] left(HWright)=\
   = text{tr}, left( left[nabla_{X_0W} g right]^T cdot (H) W right) =\
   =
   text{tr} , left(W left[nabla_{X_0W} (g) right]^T cdot (H)right) = text{tr} , left( left[left[nabla_{X_0W} gright] W^Tright]^T (H)right)
   end{multline*}$$

   Здесь через $ast W$ мы обозначили отображение $Y hookrightarrow YW$, а в предпоследнем переходе использовалось следующее свойство следа:

   $$
   text{tr} , (A B C) = text{tr} , (C A B),
   $$

   где $A, B, C$ — произвольные матрицы подходящих размеров (то есть допускающие перемножение в обоих приведённых порядках). Следовательно, получаем

   $$color{#348FEA}{nabla_{X_0} f = left[nabla_{X_0W} (g) right] cdot W^T}$$

3. $f(W) = g(XW)$, где $W$ и $X$ — матрицы. Для приращения $H = W — W_0$ имеем

   $$
   left[D_{W_0} f right] (H) = text{tr} , left( left[nabla_{W_0} f right]^T (H)right)
   $$

   Тогда

   $$ begin{multline*}
   left[D_{XW_0} g right] left( left[D_{W_0} left(X astright) right] (H)right) = left[D_{XW_0} g right] left( XH right) =
   = text{tr} , left( left[nabla_{XW_0} g right]^T cdot X (H)right) =
   text{tr}, left(left[X^T left[nabla_{XW_0} g right] right]^T (H)right)
   end{multline*} $$

   Здесь через $X ast$ обозначено отображение $Y hookrightarrow XY$. Значит,

   $$color{#348FEA}{nabla_{X_0} f = X^T cdot left[nabla_{XW_0} (g)right]}$$

4. $f(X) = g(softmax(X))$, где $X$ — матрица $Ntimes K$, а $softmax$ — функция, которая вычисляется построчно, причём для каждой строки $x$

   $$softmax(x) = left(frac{e^{x_1}}{sum_te^{x_t}},ldots,frac{e^{x_K}}{sum_te^{x_t}}right)$$

   В этом примере нам будет удобно воспользоваться формализмом с частными производными. Сначала вычислим $frac{partial s_l}{partial x_j}$ для одной строки $x$, где через $s_l$ мы для краткости обозначим $softmax(x)_l = frac{e^{x_l}} {sum_te^{x_t}}$. Нетрудно проверить, что

   $$frac{partial s_l}{partial x_j} = begin{cases}
   s_j(1 — s_j), & j = l,
   -s_ls_j, & jne l
   end{cases}$$

   Так как softmax вычисляется независимо от каждой строчки, то

   $$frac{partial s_{rl}}{partial x_{ij}} = begin{cases}
   s_{ij}(1 — s_{ij}), & r=i, j = l,
   -s_{il}s_{ij}, & r = i, jne l,
   0, & rne i
   end{cases},$$

   где через $s_{rl}$ мы обозначили для краткости $softmax(X)_{rl}$.

   Теперь пусть $nabla_{rl} = nabla g = frac{partialmathcal{L}}{partial s_{rl}}$ (пришедший со следующего слоя, уже известный градиент). Тогда

   $$frac{partialmathcal{L}}{partial x_{ij}} = sum_{r,l}frac{partial s_{rl}}{partial x_{ij}} nabla_{rl}$$

   Так как $frac{partial s_{rl}}{partial x_{ij}} = 0$ при $rne i$, мы можем убрать суммирование по $r$:

   $$ldots = sum_{l}frac{partial s_{il}}{partial x_{ij}} nabla_{il} = -s_{i1}s_{ij}nabla_{i1} — ldots + s_{ij}(1 — s_{ij})nabla_{ij}-ldots — s_{iK}s_{ij}nabla_{iK} =$$

   $$= -s_{ij}sum_t s_{it}nabla_{it} + s_{ij}nabla_{ij}$$

   Таким образом, если мы хотим продифференцировать $f$ в какой-то конкретной точке $X_0$, то, смешивая математические обозначения с нотацией Python, мы можем записать:

   $$begin{multline*}
   color{#348FEA}{nabla_{X_0}f =}\
   color{#348FEA}{= -softmax(X_0) odot text{sum}left(
   softmax(X_0)odotnabla_{softmax(X_0)}g, text{ axis = 1}
   right) +}\
   color{#348FEA}{softmax(X_0)odot nabla_{softmax(X_0)}g}
   end{multline*}
   $$

Backpropagation в общем виде

Подытожим предыдущее обсуждение, описав алгоритм error backpropagation (алгоритм обратного распространения ошибки). Допустим, у нас есть текущие значения весов $W^i_0$ и мы хотим совершить шаг SGD по мини-батчу $X$. Мы должны сделать следующее:

1. Совершить forward pass, вычислив и запомнив все промежуточные представления $X = X^0, X^1, ldots, X^m = widehat{y}$.
2. Вычислить все градиенты с помощью backward pass.
3. С помощью полученных градиентов совершить шаг SGD.

Проиллюстрируем алгоритм на примере двуслойной нейронной сети со скалярным output’ом. Для простоты опустим свободные члены в линейных слоях.

Обучаемые параметры – матрицы $U$ и $W$. Как найти градиенты по ним в точке $U_0, W_0$?

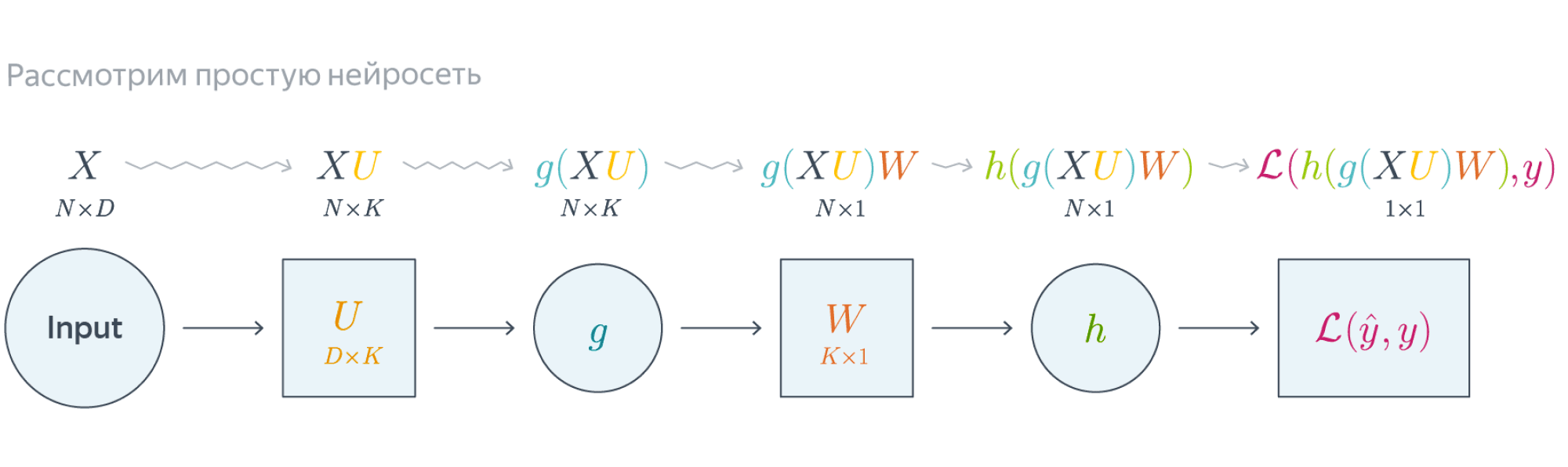
$$nabla_{W_0}mathcal{L} = nabla_{W_0}{left({vphantom{frac12}mathcal{L}circ hcircleft[Wmapsto g(XU_0)Wright]}right)}=$$

$$=g(XU_0)^Tnabla_{g(XU_0)W_0}(mathcal{L}circ h) = underbrace{g(XU_0)^T}_{ktimes N}cdot
left[vphantom{frac12}underbrace{h’left(vphantom{int_0^1}g(XU_0)W_0right)}_{Ntimes 1}odot
underbrace{nabla_{hleft(vphantom{int_0^1}g(XU_0)W_0right)}mathcal{L}}_{Ntimes 1}right]$$

Итого матрица $ktimes 1$, как и $W_0$

$$nabla_{U_0}mathcal{L} = nabla_{U_0}left(vphantom{frac12}
mathcal{L}circ hcircleft[Ymapsto YW_0right]circ gcircleft[ Umapsto XUright]
right)=$$

$$=X^Tcdotnabla_{XU^0}left(vphantom{frac12}mathcal{L}circ hcirc [Ymapsto YW_0]circ gright) =$$

$$=X^Tcdotleft(vphantom{frac12}g'(XU_0)odot
nabla_{g(XU_0)}left[vphantom{in_0^1}mathcal{L}circ hcirc[Ymapsto YW_0right]
right)$$

$$=ldots = underset{Dtimes N}{X^T}cdotleft(vphantom{frac12}
underbrace{g'(XU_0)}_{Ntimes K}odot
underbrace{left[vphantom{int_0^1}left(
underbrace{h’left(vphantom{int_0^1}g(XU_0)W_0right)}_{Ntimes1}odotunderbrace{nabla_{h(vphantom{int_0^1}gleft(XU_0right)W_0)}mathcal{L}}_{Ntimes 1}
right)cdot underbrace{W^T}_{1times K}right]}_{Ntimes K}
right)$$

Итого $Dtimes K$, как и $U_0$

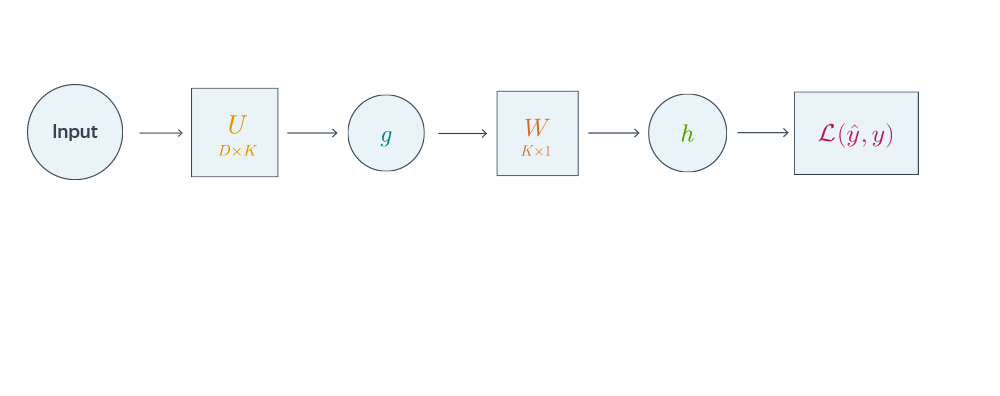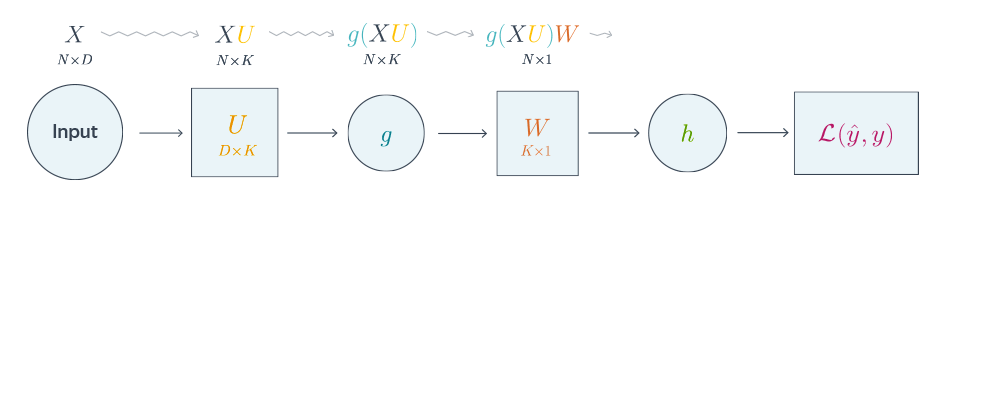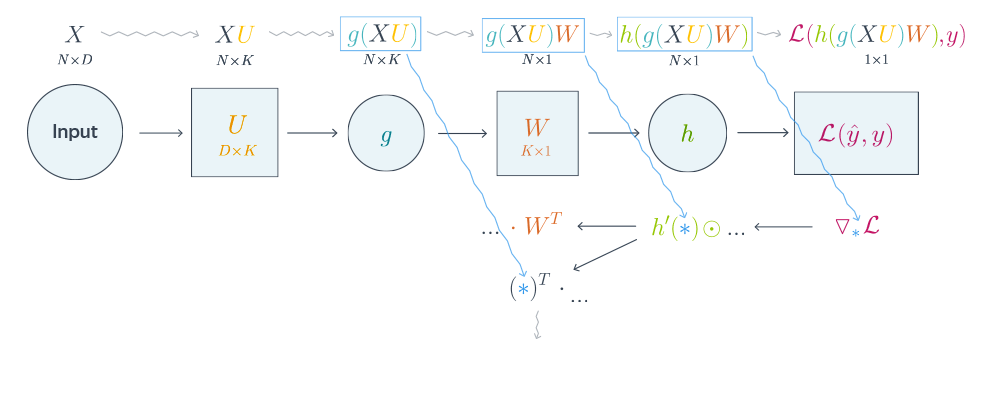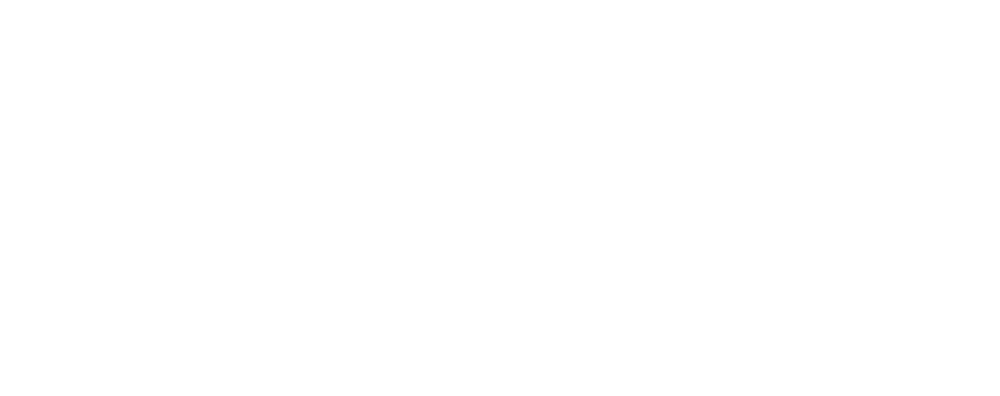
Схематически это можно представить следующим образом:

Backpropagation для двуслойной нейронной сети

Если вы не уследили за вычислениями в предыдущем примере, давайте более подробно разберём его чуть более конкретную версию (для $g = h = sigma$)Рассмотрим двуслойную нейронную сеть для классификации. Мы уже встречали ее ранее при рассмотрении линейно неразделимой выборки. Предсказания получаются следующим образом:

$$
widehat{y} = sigma(X^1 W^2) = sigmaBig(big(sigma(X^0 W^1 )big) W^2 Big).
$$

Пусть $W^1_0$ и $W^2_0$ — текущее приближение матриц весов. Мы хотим совершить шаг по градиенту функции потерь, и для этого мы должны вычислить её градиенты по $W^1$ и $W^2$ в точке $(W^1_0, W^2_0)$.

Прежде всего мы совершаем forward pass, в ходе которого мы должны запомнить все промежуточные представления: $X^1 = X^0 W^1_0$, $X^2 = sigma(X^0 W^1_0)$, $X^3 = sigma(X^0 W^1_0) W^2_0$, $X^4 = sigma(sigma(X^0 W^1_0) W^2_0) = widehat{y}$. Они понадобятся нам дальше.

Для полученных предсказаний вычисляется значение функции потерь:

$$
l = mathcal{L}(y, widehat{y}) = y log(widehat{y}) + (1-y) log(1-widehat{y}).
$$

Дальше мы шаг за шагом будем находить производные по переменным из всё более глубоких слоёв.

1. Градиент $mathcal{L}$ по предсказаниям имеет вид

   $$
   nabla_{widehat{y}}l = frac{y}{widehat{y}} — frac{1 — y}{1 — widehat{y}} = frac{y — widehat{y}}{widehat{y} (1 — widehat{y})},
   $$

   где, напомним, $ widehat{y} = sigma(X^3) = sigmaBig(big(sigma(X^0 W^1_0 )big) W^2_0 Big)$ (обратите внимание на то, что $W^1_0$ и $W^2_0$ тут именно те, из которых мы делаем градиентный шаг).

2. Следующий слой — поэлементное взятие $sigma$. Как мы помним, при переходе через него градиент поэлементно умножается на производную $sigma$, в которую подставлено предыдущее промежуточное представление:

   $$
   nabla_{X^3}l = sigma'(X^3)odotnabla_{widehat{y}}l = sigma(X^3)left( 1 — sigma(X^3) right) odot frac{y — widehat{y}}{widehat{y} (1 — widehat{y})} =
   $$

   $$
   = sigma(X^3)left( 1 — sigma(X^3) right) odot frac{y — sigma(X^3)}{sigma(X^3) (1 — sigma(X^3))} =
   y — sigma(X^3)
   $$

3. Следующий слой — умножение на $W^2_0$. В этот момент мы найдём градиент как по $W^2$, так и по $X^2$. При переходе через умножение на матрицу градиент, как мы помним, умножается с той же стороны на транспонированную матрицу, а значит:

   $$
   color{blue}{nabla_{W^2_0}l} = (X^2)^Tcdot nabla_{X^3}l = (X^2)^Tcdot(y — sigma(X^3)) =
   $$

   $$
   = color{blue}{left( sigma(X^0W^1_0) right)^T cdot (y — sigma(sigma(X^0W^1_0)W^2_0))}
   $$

   Аналогичным образом

   $$
   nabla_{X^2}l = nabla_{X^3}lcdot (W^2_0)^T = (y — sigma(X^3))cdot (W^2_0)^T =
   $$

   $$
   = (y — sigma(X^2W_0^2))cdot (W^2_0)^T
   $$

4. Следующий слой — снова взятие $sigma$.

   $$
   nabla_{X^1}l = sigma'(X^1)odotnabla_{X^2}l = sigma(X^1)left( 1 — sigma(X^1) right) odot left( (y — sigma(X^2W_0^2))cdot (W^2_0)^T right) =
   $$

   $$
   = sigma(X^1)left( 1 — sigma(X^1) right) odotleft( (y — sigma(sigma(X^1)W_0^2))cdot (W^2_0)^T right)
   $$

5. Наконец, последний слой — это умножение $X^0$ на $W^1_0$. Тут мы дифференцируем только по $W^1$:

   $$
   color{blue}{nabla_{W^1_0}l} = (X^0)^Tcdot nabla_{X^1}l = (X^0)^Tcdot big( sigma(X^1) left( 1 — sigma(X^1) right) odot (y — sigma(sigma(X^1)W_0^2))cdot (W^2_0)^Tbig) =
   $$

   $$
   = color{blue}{(X^0)^Tcdotbig(sigma(X^0W^1_0)left( 1 — sigma(X^0W^1_0) right) odot (y — sigma(sigma(X^0W^1_0)W_0^2))cdot (W^2_0)^Tbig) }
   $$

Итоговые формулы для градиентов получились страшноватыми, но они были получены друг из друга итеративно с помощью очень простых операций: матричного и поэлементного умножения, в которые порой подставлялись значения заранее вычисленных промежуточных представлений.

Автоматизация и autograd

Итак, чтобы нейросеть обучалась, достаточно для любого слоя $f^k: X^{k-1}mapsto X^k$ с параметрами $W^k$ уметь:

• превращать $nabla_{X^k_0}mathcal{L}$ в $nabla_{X^{k-1}_0}mathcal{L}$ (градиент по выходу в градиент по входу);
• считать градиент по его параметрам $nabla_{W^k_0}mathcal{L}$.

При этом слою совершенно не надо знать, что происходит вокруг. То есть слой действительно может быть запрограммирован как отдельная сущность, умеющая внутри себя делать forward pass и backward pass, после чего слои механически, как кубики в конструкторе, собираются в большую сеть, которая сможет работать как одно целое.

Более того, во многих случаях авторы библиотек для глубинного обучения уже о вас позаботились и создали средства для автоматического дифференцирования выражений (autograd). Поэтому, программируя нейросеть, вы почти всегда можете думать только о forward-проходе, прямом преобразовании данных, предоставив библиотеке дифференцировать всё самостоятельно. Это делает код нейросетей весьма понятным и выразительным (да, в реальности он тоже бывает большим и страшным, но сравните на досуге код какой-нибудь разухабистой нейросети и код градиентного бустинга на решающих деревьях и почувствуйте разницу).

Но это лишь начало

Метод обратного распространения ошибки позволяет удобно посчитать градиенты, но дальше с ними что-то надо делать, и старый добрый SGD едва ли справится с обучением современной сетки. Так что же делать? О некоторых приёмах мы расскажем в следующей главе.

Из названия статьи вы уже поняли, что именуется данная ошибка «Fatal error in gc». А суть этой ошибки: «Get Thread Context failed». Практически все пользователи, познакомившиеся с «Fatal error in gc» — игроманы, в хорошем смысле этого слова. То есть, на компьютере или ноутбуке установлен клиент какой-либо браузерной игры, какая игра – не важно. Естественно, из-за большой популярности игр:

• «Ground War: Tanks».
• «Metal War Online»
• «Contract Wars»
• «Cities: Skylines»
• «Prime World: Defenders»

— ошибка всплывает чаще всего именно в клиентах этих игр.

Список игр можно продолжать перечислять до бесконечности. Суть всего выше сказанного такова: ошибка «Fatal error in gc» появляется во время игры, в Клиент версии игры. Изначально игры браузерные, но разработчики этих самых игр, создают Клиент игры и ошибка выскакивает именно в Клиенте игры, а не в браузерной версии.

Что означает ошибка «Fatal error in gc» и как исправить ошибку «Fatal error in gc»?

Мы решили отследить историю возникновения данной ошибки у пользователей, а точнее у игроманов.

В 2010 году о данной проблеме ещё не слышали и не видели. Тогда, в далёком десятом году, вылетала ошибка «Fatal error in gc», но, правда, с надписью: «Too many heap sections», что явно не с нашей оперы. Наша, рассматриваемая проблема, появилась ровно через десять месяцев, в конце 10-ого, начале 11-ого годов.

В 2011 году начинают появляться призывы о помощи в решении проблемы с «Fatal error in gc» в играх «Wolf Quest» и «Prime World». В те далёкие времена начали появляться всплывающие окошки от виндовс с надписью «Неисправимая ошибка» или «Фатальная ошибка».

И, начиная с 2011 года, начали регулярно всплывать мольбы о помощи на различного рода игровых форумах. Ошибка «Fatal error in gc» появилась в 2013 году в играх: «King’s Bounty: Legions» и «Contra City».

И вот уже сейчас, спустя шесть лет (с 2011 по 2017), проблема остаётся трудно решаемой. Одни советуют одно, другие советуют второе. Как же решить проблему со всплывающей «Фатальной ошибкой»?

Как решить проблему: «Fatal error in gc: Get Thread Context failed»?

Сразу отметим, что причиной возникновения этого лага не есть антивирусники. Отключать, удалять и переустанавливать антивирусник, не важно Kaspersky Anti-Virus это или Dr.Web CureIt – это не решит проблему. Но, отказываться от совета или нет, решать вам: «Необходимо отключить антивирусник, а точнее Real-time shield защиту, потом почистить кеш и перезапусть игровой Клиент». Маловероятно, что проблема у вас решиться, но исключить данный вариант решения вопроса следует

Суть проблемы «Fatal error in gc: Get Thread Context failed» — это несовместимость игры с вашей ОС. Грубовато сказано, но зато доходчиво, ведь действительно проблема в совместимости, которую можно решать несколькими путями.

Решение вопроса с совместимостью

Для решения совместимости программы (игрового клиента) следует кликнуть по иконке игры или по файлу с разрешением .exe правой кнопкой мыши.

В появившемся окошке, выбираем пункт «Исправление проблем с совместимостью».

Дальнейшие действия очень просты. В появившемся окошке, вам необходимо будет определиться с выбором варианта решения проблемы с совместимостью.

Первый пункт. В первом варианте вам будет предложено решить проблему с совместимостью с помощью рекомендованных параметров. При выборе именно этого пункта решения вопроса совместимости, всё закончится довольно таки быстро. Windows решит проблему методом присвоения параметров, которые соответствуют режиму совместимости с Windows Windows 8.

Второй пункт «Диагностика программы» — это долгий путь, который будет закончен режимом совместимости Windows Windows XP. Попробуйте оба варианта совместимости и остановитесь на том варианте, который устраняет возникновение «Fatal error in gc».

Если вы знаете, как по другому решается проблема возникновения Fatal error in gc — пишите об этом в комментариях под этой статьёй.

Little Nightmares

Если Вы столкнулся с ошибкой «Fatal error» в игре Little Nightmares, то есть решение с использованием эмулятора.

Его можно скачать по ссылке ниже.

Инструкция по запуску через эмулятор.

А что делать если данный способ не помог, есть еще варианты?
Проц AMD phenom II x4 995, после всех манипуляций, уже в меню игры жуткие фризы и загрузка камня 99%.

А что делать если данный способ не помог, есть еще варианты?
Проц AMD phenom II x4 995, после всех манипуляций, уже в меню игры жуткие фризы и загрузка камня 99%.

У меня тоже процессор AMD Phenom II x4. Модель не помню. Какая у тебя видеокарта и сколько оперативной памяти? Всё делал как в видео?

Кастыль, не играбельно. Через N-ое время наичнает безбожно тормозить.

P.S: id игры при новом запуске меняется.
P.S: AMD Phenom II X4 970, 16 GB памяти, MSI R7 265 2GB

P.S: Не мучайтесь, делайте возврат денег.

Круто конечно, что и лицензия запускается через эмулятор, но кто-нибудь в курсе собираются разработчики это поправлять?

Ведь по факту толку от того что они юзают SSE4a никакого — лучше бы оптимизировали игру и поправили местами управление — местами очень неудобно.

Мы недавно уже писали об одной из ошибок FATAL ERROR в S.T.A.L.K.E.R.: Call of Pripyat, не подумайте, что это та же самая. Дело в том, что ошибки в этой игре не отображают не код, а значатся просто как FATAL ERROR. И методы смправления у этих багов разумеется совершенно разные. Различать эти баги можно исключительно по тексту, который вы увидите в табличке с ошибкой. В нашей статье мы разберем FATAL ERROR, сопровождающуюся следующим текстом:

[error]Expression : fatal error [error]Function : CInifile::Load [error]File : D:prog_repositorysources runkxrCoreXr_ini.cpp [error]Line : 274 [error]Description : [error]Arguments : Duplicate section ‘wpn_m16’ found.

Давайте мы расскажем вам, как избавиться от этого неприятного бага.

Метод устранения ошибки

Устранить ошибку не так уж и сложно, вам всего лишь нужно:

1. Зайти в папку с игрой.
2. Найти в ней папку gamedata и удалить ее.
3. Далее , если игра скачана в Steam, о найдите ее в библиотеке, щелкните правой кнопкой и выберите «Обновить кэш».
4. Также, если вы используете моды, то рекомендуется использовать только один мод оружия.

Радостная новость заключается в том, что переустановка игры не требуется и после этих нехитрых действий ошибка должна пропасть. Приятной игры!