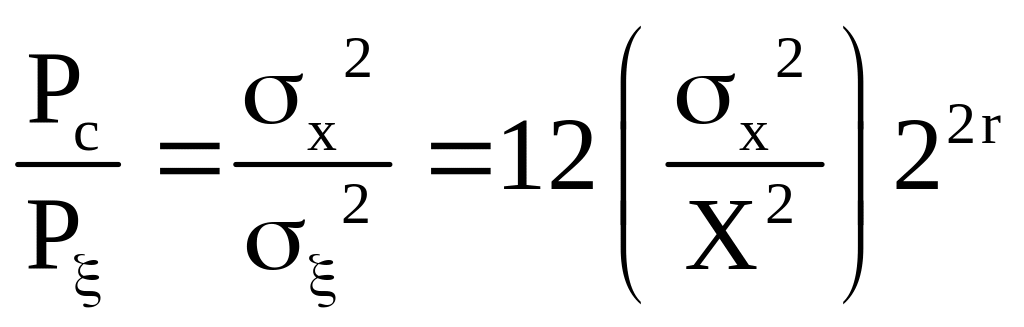Операция
квантования
сводится к тому, что всем отсчетам
входного сигнала x,
попавшим в некоторый интервал,
приписывается одно и то же значение
,
выражаемое двоичной кодовой комбинацией.
Если
кодовая комбинация содержит r
разрядов, то число дискретных уровней
выходного сигнала квантователя равно
.
Для
взаимно однозначного соответствия весь
диапазон изменения входного сигнала
X
= x
max
– x
min
должен быть разбит на такое же количество
уровней.
Величина
интервала разбиения – шаг
квантования
– представляет собой значение аналоговой
величины, на которую отличаются уровни
входного сигнала, представленные двумя
соседними кодовыми комбинациями.
При
наиболее распространенном равномерном
квантовании шаг квантования равен
(1.12)
Характеристикой
квантования
называется зависимость квантованного
значения
от значения непрерывной величины x.
Типичная
характеристика
квантователя
с постоянном шагом квантования
приведена на рисунке 1.16.

Рисунок 1.16 –
Характеристика квантования при постоянном
шаге квантования
На
рисунке 1.17 приведена временная диаграмма
работы квантователя, где точками отмечены
квантованные значения, и временная
диаграмма ошибки квантования
.
Временная последовательность ошибок
квантования случайного сигнала
представляет собой случайный процесс
с равномерным законом распределения.
Этот случайный процесс называют шумом
квантования.

Рисунок
1.17 – Временные зависимости сигналов
на входе (x)
и выходе (
)
квантователя
и
ошибки квантования
Из
рисувнка видно, что абсолютное значение
ошибки квантования не превышает Δ/2.
Закон
распределения этого случайного процесса
приведен на рисунке 1.18.

Рисунок 1.18 –
Плотность вероятности шума квантования
Определим дисперсию шума квантования

После подстановки
(2.1) в последнее соотношение получим
(1.13)
Из
(1.13) следует, что дисперсия шума квантования
зависит от характеристик квантователя
и не зависит от уровня сигнала.
Определим отношение сигнал/шум на выходе квантователя
,
где
Pc—
мощность сигнала,
–
мощность шума,
—
среднеквадратическое значение сигнала.
Это отношение в
децибелах равно
(1.14)
Из последнего соотношения
видно, что
-
каждое
добавление одного разряда в кодовом
слове увеличивает отношение сигнал/шум
на 6 дБ. -
с
уменьшением уровня входного сигнала
отношение сигнал/шум уменьшается.
1.6.
Квантователи с переменным шагом
квантования
(нелинейные
квантователи)
Недостаток
линейного квантователя, связанный с
уменьшением отношения сигнал/шум
квантования при уменьшении уровня
сигнала, можно устранить, если уменьшать
шаг квантования по мере уменьшения
уровня сигнала.
Характеристика
квантования с переменным шагом квантования
приведена на рисунке 1.19.
Такую
характеристику можно получить, если
последовательно включить нелинейный
преобразователь и линейный квантователь
(рисунок 1.19)
Чтобы
устранить нелинейные искажения,
обусловленные введением нелинейного
преобразователя, после квантователя
используют второй нелинейный
преобразователь квантованного сигнала
с характеристикой, обратной характеристике
первого. С помощью первого осуществляют
компрессию сигнала, а с помощью второго
– его экспандирование. В целом описанная
операция называется компандированием.
Результирующая сквозная характеристика
системы «компрессор-экспандер» остается
линейной.
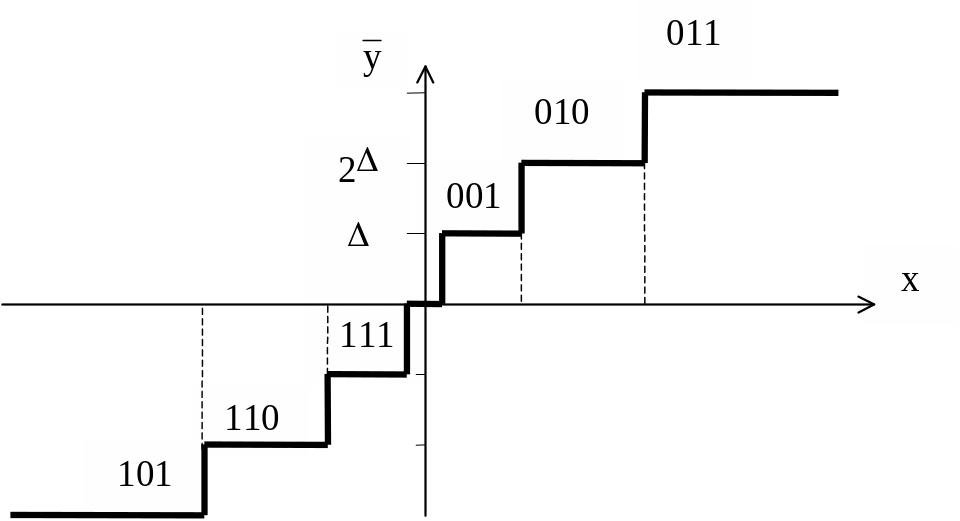
Рисунок
1.19 – Характеристика квантования при
переменном шаге квантования
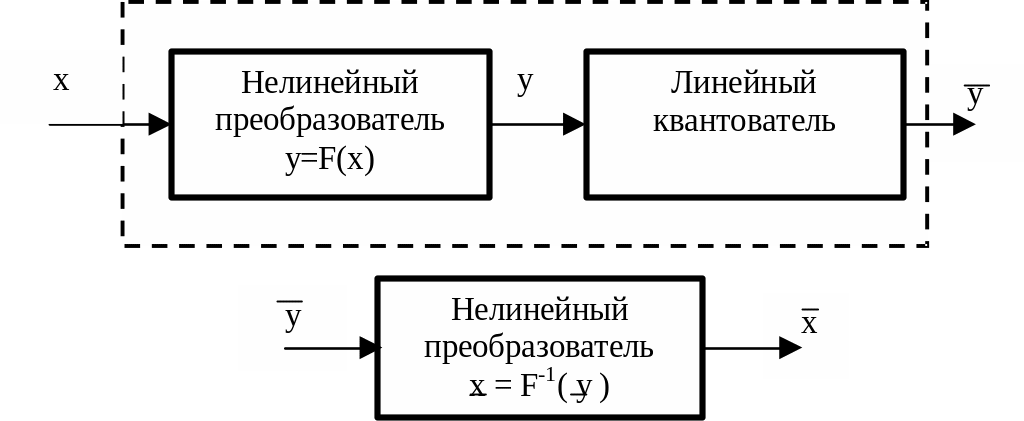
Рисунок
1.20 –Система «компрессор-экспандер»
В настоящее время
используются два закона компандирования:
μ-закон
(1.15) и А – закон (1.16):
(1.15)
где
=255,
,
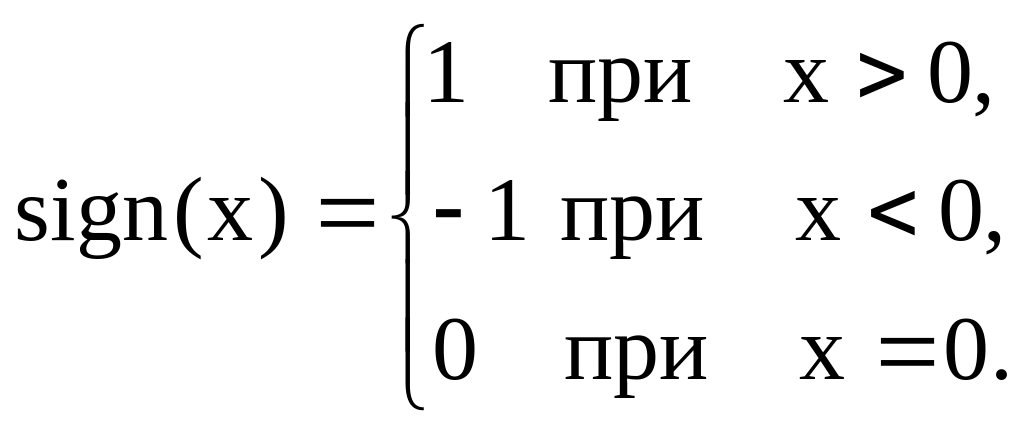
(1.16)
где
A
= 87.6.
Заключение
При дискретизации
аналогового сигнала возникают два
эффекта, касающиеся спектра сигнала:
-
Эффект
размножения спектра аналогового
сигнала, -
Эффект
наложения сгустков спектра дискретного
сигнала друг на друга.
Эффект
наложения спектров приводит к искажению
дискретного сигнала и невозможности
точного восстановления аналогового
сигнала из дискретного.
Спектр дискретного
сигнала представляет собой периодическую
функцию частоты, период которой равен
частоте дискретизации.
Если дискретизации
подвергается периодический аналоговый
сигнал с линейчатым спектром, то
размножение спектра осуществляется по
закону:
при
где
F
– частота спектральной составляющей
аналогового сигнала.
Амплитуды
спектральных составляющих дискретного
сигнала пропорциональны соответствующим
составляющим спектра аналогового
сигнала.
Размножение
спектра апериодического аналогового
сигнала осуществляется по этому же
закону, если рассматривать в качестве
F
характерные частоты непрерывного
спектра аналогового сигнала.
Эффект
наложения спектров при дискретизации
отсутствует, если выполняется условие
,
где
Fmax
– максимальная частота спектра
аналогового сигнала.
Если
дискретизации подвергается узкополосный
модулированный сигнал, а результатом
последующей цифровой обработки должно
быть выделение модулирующего сигнала,
то частота дискретизации может быть
выбрана существенно меньше, чем 2Fmax.
В этом случае
необходимо выполнить условия:
,
где
—
ширина спектра аналогового сигнала,
,
где
,
а f0
– частота несущей аналогового сигнала.
При
выполнении последнего условия частота
несущей, приведенная в интервал частот
от нуля до половины частоты дискретизации
(интервал Котельникова), равна четверти
частоты дискретизации.
Необходимость
квантования дискретного сигнала связана
с тем, что в вычислительных устройствах
значение сигнала должно быть представлено
числом конечной разрядности.
Операция
квантования
сводится к тому, что всем отсчетам
входного сигнала x,
попавшим в некоторый интервал,
приписывается одно и то же значение
,
выражаемое двоичной кодовой комбинацией.
Разность
между квантованным значением и значением
отсчета дискретного сигнала называется
ошибкой квантования. Временная
последовательность ошибок квантования
случайного сигнала представляет собой
случайный процесс с равномерным законом
распределения. Этот случайный процесс
называют шумом
квантования.
В
квантователе с постоянным шагом
квантования (линейном квантователе)
отношение сигнал/шум квантования зависит
от количества разрядов квантователя,
уровня сигнала и диапазона квантователя.
Каждое
добавление одного разряда в кодовом
слове увеличивает отношение сигнал/шум
на 6 дБ.
С
уменьшением уровня входного сигнала
отношение сигнал/шум уменьшается.
Последнее
обстоятельство является недостатком
линейного квантователя, который
устраняется в квантователе с переменным
шагом квантования (нелинейном квантователе)
за счет уменьшения шага квантования по
мере уменьшения абсолютного значения
уровня входного сигнала квантователя.
Контрольные
вопросы и задачи по теме №1:
1.
Что такое дискретизация аналогового
сигнала? Начертите временные диаграммы
синусоидального сигнала на входе и
выходе дискретизатора в случае, когда
частота синусоидального колебания
меньше половины частоты дискретизации.
2. Начертите
спектральные диаграммы синусоидального
сигнала на входе и выходе дискретизатора
в случае, когда частота синусоидального
колебания меньше половины частоты
дискретизации.
3.В
чем сущность эффекта наложения спектров?
Каким образом можно уменьшить ошибку
наложения?
4.Начертите
амплитудный спектр дискретной синусоиды,
если частота аналогового синусоидального
колебания на входе дискретизатора выше
частоты дискретизации.
5.
Из каких условий выбирается частота
дискретизации модулированного колебания,
если результатом последующей цифровой
обработки должно быть выделение
модулирующего колебания?
6.
Дискретизация синусоидального колебания
,
где f0=20МГц,
осуществляется с частотой FД
= 16 МГц. Чему равна частота дискретной
синусоиды?
7.
На входе аналогового ФНЧ действует
последовательность прямоугольных
импульсов. АЧХ фильтра показана на
рисунке 1.21. Выходной сигнал фильтра
подается на дискретизатор. Частота
дискретизации равна 20 кГц. Возникнет
ли эффект наложения спектров при
дискретизации?

8.
На входе дискретизатора действует
сигнал
,
где
F1=1
МГц, F2
= 2 МГц.
Частота дискретизации FД
= 8 МГц. Чему равен максимальный частотный
разнос между соседними составляющими
спектра дискретного сигнала?
9.
На входе дискретизатора действует
сигнал
,
где F=1
МГц, f0
= 15 МГц.
Частота дискретизации FД
= 12 МГц. Чему равен минимальный частотный
разнос между соседними составляющими
спектра дискретного сигнала?
10.На
рисунке 1.22 приведен спектр аналогового
сигнала. Начертите в относительном
масштабе спектр сигнала после дискретизации
в пределах интервала Котельникова (от
0 до половины частоты дискретизации),
если f0=28МГц,
fmin=25МГц,
fmax=31МГц,
а частота дискретизации равна FД=
16 МГц.
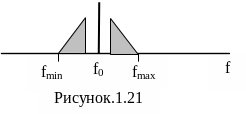
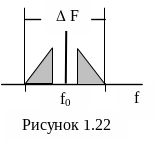
11.
На входе демодулятора действует
модулированный аналоговый сигнал,
спектр которого симметричен относительно
частоты несущей f0
= 445кГц (рисунок 1.22). Ширина спектра
.
При каком из двух значений частоты
дискретизации отсутствует эффект
наложения спектров: FД=20кГц,
FД=21кГц?
12. Поясните
сущность операции квантования дискретных
сигналов. Что такое шаг квантования?
Как зависит шаг квантования при
равномерном (линейном) квантовании от
количества разрядов и диапазона
квантователя?
13.
Дайте определение характеристике
квантования. Начертите характеристику
линейного квантователя.
14. Поясните механизм
возникновения шума квантования. Начертите
график вероятностного распределения
шума квантования. Как связана дисперсия
шума квантования с шагом квантования
и количеством разрядов квантователя
при равномерном квантовании?
15.
Как зависит отношение сигнал/шум на
выходе равномерного квантователя от
количества разрядов, диапазона
квантователя и среднеквадратичного
уровня входного сигнала?
16.
Начертите характеристику квантования
квантователя с неравномерным шагом
квантования (нелинейного квантователя).
17.Поясните сущность
алгоритма функционирования нелинейного
квантователя, состоящего из входного
нелинейного преобразователя и линейного
квантователя. Каким образом устраняются
нелинейные искажения выходного сигнала
при использовании нелинейного
квантователя?
18.Чем
отличается зависимость отношения
сигнал/шум на выходе нелинейного
квантователя от среднеквадратичного
уровня входного сигнала от аналогичной
зависимости для линейного квантователя?
19.
Отношение сигнал/шум на выходе линейного
квантователя равно 40 дБ. Каким станет
это отношение, если количество разрядов
увеличить на два при неизменном уровне
входного сигнала и неизменном диапазоне
квантователя?
Контрольная
карта ответов
Номер
ответа соответствует номеру контрольного
вопроса в предыдущем разделе.
6.
F
= f0
–FД
= 20-16 = 4 МГц
7.
FД
= 20 кГц, Fmax
= 8 кГц. Так как FД>
2 Fmax,
то эффект наложения не возникнет.
8.
Максимальный частотный разнос между
соседними составляющими спектра
дискретного сигнала равен 4 МГц
9.
Минимальный частотный разнос между
соседними составляющими спектра
дискретного сигнала равен 2 МГц.
10.

11.
Эффект наложения отсутствует при частоте
дискретизации FД
=20 кГц.
19.
Отношение сигнал/шум станет равным 52
дБ.
Список
литературы по теме № 1:
1.
В.Г.Иванова, А.И.Тяжев. Цифровая обработка
сигналов и сигнальные процессоры / Под
редакцией д.т.н., профессора Тяжева А.И.
— Самара, 2008г.
2.Куприянов
М.С., Матюшкин Б.Д. Цифровая обработка
сигналов: процессоры, алгоритмы, средства
проектирования. –2-е изд., перераб. и
доп.- СПб.: Политехника, 1999. –592с.
:
ил.
3.Л.Р.Рабинер,
Р.В.Шафер. Цифровая обработка речевых
сигналов. – М.: Радио и связь, 1981. – 495с.:
ил.
4.
А.И. Солонина, Д.А.
Улахович, С.М. Арбузов, Е.Б. Соловьёва.
Основы цифровой обработки сигналов.-
Изд. 2-е испр. и перераб. – СПб.: БХВ-Петербург,
2005.-768с.: ил.
5.А.Б.
Сергиенко. Цифровая обработка сигналов.
– СПб.: Питер, 2002.-2002.-608с.: ил.
24
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Когда я был в Питере, и мы сидели в кабаке, у нас с товарищами 



Поскольку дельта икс у нас совершенно чёткая, или скорее равная отрезкам оцифровки, то производная значения снятого с АЦП будет нынешнее значение минус предыдущее, делённое на период квантования: df/dt=(f(t1) -f(t2))/(t1 -t2). Для опытов я выбрал функцию гармонического синуса sin(x). В дальнейшем проверил и на остальных функциях, но это самая красивая и в нашем случае самая актуальная.
Изначальный график для экспериментов
Для начала я составил таблицу, над которой начал издеваться. Первая строчка [ t= ] — это время от старта работы условного АЦП, который наращивается с шагом квантования (последняя строчка). Вторая — [ SIN(t) ]синус вычесленный от этого кванта времени, формула которого примитивна: =SIN(B1). Третья — [ dSIN(t)/dt ] это численное нахождение производной. Формула её проста: =(C2-B2)/C5 (первая ячейка). Предпоследняя строчка это [ COS(t) ], это нахождения косинуса от перменной t. Она нужна для того, чтобы сравнивать с истинным значением косинуса вычисленную производную (если помните, производная синуса — это косинус). Последняя строка — это квантование, т.е. проще говоря шаг изменения t. Внизу строиться график, который строит гибкую линию по точкам. Сейчас у нас выбран самый оптимальный шаг квантования 0,5 . Здесь всё ясно, дальше я двух разделах покажу сначала ошибки квантования, и следственные ошибки производных, затем ошибки дифференцирования при ошибочных входных данных. Если ваш мозг не вспух и вы готовы дальше пуститься в дебри математики и электроники,
Ошибки квантования
Как видно из самой первой картинки, производная практически полностью соответствует графику косинуса. Если мы ещё уменьшим «частоту дискретизации», или в нашем случае шаг до dt=0,1, то получим вообще практически совпадающие кривые, которые я проиллюстрирую ниже:
Полученный график с шагом 0,1
Как видно, при этом шаге квантования график производной (фиолетовая кривая), практически полностью совпадает с графиком косинуса (красная кривая). Маркерами показанны точки квантования. В этом случае всё ясно, но давайте увеличим шаг, от 0,5 до 1
Полученный график с шагом 1
Видно, что производная, да и все графики начинают «плыть».
Продолжим увеличение квантования до 2:
Полученный график с шагом 2
Всё начинает плыть и уходить, но ещё отдалённо напоминает синус. Однако уже видно, что численно рассчитанная производная СОВЕРШЕННО не соответствует своему значению. Да и вообще находится в противофазе. Напоследок возьмём квантование равное 5 (в 10 раз больше исходного).
Полученный график с шагом 10
Видно что в этом случае мы наблюдаем полную ересь. И в данном случае можно сказать, что высокие частоты и шумы, могут хорошо подпортить реальное значение производной. Теперь же посмотрим как влияет погрешность снятого сигнала, на численный рассчёт производной.
Численное вычисление производной, при неточности снятого сигнала (шумах, наводках, высших гармониках)
Добавим теперь в формулу вычисления синуса некоторую погрешность снятия сигнала, для этого прибавим к формуле вычисления синуса некоторое случайное число: =SIN(C1)+СЛЧИС()*0,1 . Данная формула внесёт 10% погрешность от амплитудного значения в вычисление сигнала, просто добавляя некоторое случайное число от нуля до 0,1. Я покажу несколько вариантов с разной погрешностью. Сначала покажем сигнал с 5% погрешностью:
Полученный график с погрешностью 5%
Как видно из графика, ни на синус, ни на производную такая погрешность не оказывает должного влияния. Возьмём тогда погрешность в 10%
Полученный график с погрешностью 10%
Вот, ярко видно, что на графике синуса погрешность сказалось мало. А вот на графике производной очень даже, в особенности хорошо раскорячило её концы. На последок покажу что будет если построить график производной с 20% погрешностью:
Полученный график с погрешностью 20%
График отдалённо напоминает косинус. Видно куча убеганий и прочего. Надо учитывать, что это ПСЕВДОслучайная велечина, в реальной жизни всё может быть гораздо хуже. Но всё же лучше смоделировать данные фишки, чтобы представлять себе что же может твориться на АЦП.
Вывод: Считать численно производную по снятым значениям с АЦП можно и нужно. Но необходимо оценивать уровень внешних помех, которые могут влиять на сигнал, и очень сильно его портить. Желательно использовать фильтрацию сигнала, выделяя полезный сигнал. Филтрация может быть как аналоговая, так цифровая. Мне даже показали прекрасную формульную замену аналоговой фильтрацией прекрасной програмкой на си. И разумеется мы должны себе ЧЁТКО представлять какой сигнал цифруем, и не цифровать сигнал на пределах возможностей АЦП. 5 точек на период, как показала практика — не самый плохой вариант!
Template:Unreferenced
The difference between the actual analog value and quantized digital value due is called quantization error. This error is due either to rounding or truncation.
Many physical quantities are actually quantized by physical entities. Examples of fields where this limitation applies include electronics (due to electrons), optics (due to photons), biology (due to DNA), and chemistry (due to molecules). This is sometimes known as the «quantum noise limit» of systems in those fields. This is a different manifestation of «quantization error,» in which theoretical models may be analog but physics occurs digitally. Around the quantum limit, the distinction between analog and digital quantities vanishes.
Quantization noise model of quantization error[]
File:Quanterr.png Quantization noise. The difference between the blue and red signals in the upper graph is the quantization error, which is «added» to the original signal and is the source of noise.
Quantization noise is a model of quantization error introduced by quantization in the analog-to-digital conversion (ADC) process in telecommunication systems and signal processing. It is a rounding error between the analogue input voltage to the ADC and the output digitized value. The noise is non-linear and signal-dependent. It can be modelled in several different ways.
In an ideal analog-to-digital converter, where the quantization error is uniformly distributed between −1/2 LSB and +1/2 LSB, and the signal has a uniform distribution covering all quantization levels, the signal-to-noise ratio (SNR) can be calculated from
The most common test signals that fulfil this are full amplitude triangle waves and sawtooth waves.
In this case a 16-bit ADC has a maximum signal-to-noise ratio of 6.0206 · 16=96.33 dB.
When the input signal is a full-amplitude sine wave the distribution of the signal is no longer uniform, and the corresponding equation is instead
Here, the quantization noise is once again assumed to be uniformly distributed. When the input signal has a high amplitude and a wide frequency spectrum this is the case.[1]
In this case a 16-bit ADC has a maximum signal-to-noise ratio of 98.09 dB.
For complex signals in high-resolution ADCs this is an accurate model. For low-resolution ADCs, low-level signals in high-resolution ADCs, and for simple waveforms the quantization noise is not uniformly distributed, making this model inaccurate.[2] In these cases the quantization noise distribution is strongly affected by the exact amplitude of the signal.
Template:Listen
References[]
- ↑ Template:Cite book
- ↑ Template:Cite book
See also[]
- Round-off error
- Dither
- Analog to digital converter
- Quantization
- Quantization noise
- Discretization error
- Signal-to-noise ratio
- Bit resolution
- SQNR
External links[]
- Quantization noise in Digital Computation, Signal Processing, and Control, Bernard Widrow and István Kollár, 2007.
- The Relationship of Dynamic Range to Data Word Size in Digital Audio Processing
- Round-Off Error Variance — derivation of noise power of q²/12 for round-off error
- Dynamic Evaluation of High-Speed, High Resolution D/A Converters Outlines HD, IMD and NPR measurements, also includes a derivation of quantization noise
- Signal to quantization noise in quantized sinusoidal
de:Quantisierungsrauschen
es:Ruido de cuantificación
ja:量子化雑音
ja:量子化誤差
pl:Szum kwantyzacji
ru:Шум квантования
Template:Unreferenced
The difference between the actual analog value and quantized digital value due is called quantization error. This error is due either to rounding or truncation.
Many physical quantities are actually quantized by physical entities. Examples of fields where this limitation applies include electronics (due to electrons), optics (due to photons), biology (due to DNA), and chemistry (due to molecules). This is sometimes known as the «quantum noise limit» of systems in those fields. This is a different manifestation of «quantization error,» in which theoretical models may be analog but physics occurs digitally. Around the quantum limit, the distinction between analog and digital quantities vanishes.
Quantization noise model of quantization error[]
File:Quanterr.png Quantization noise. The difference between the blue and red signals in the upper graph is the quantization error, which is «added» to the original signal and is the source of noise.
Quantization noise is a model of quantization error introduced by quantization in the analog-to-digital conversion (ADC) process in telecommunication systems and signal processing. It is a rounding error between the analogue input voltage to the ADC and the output digitized value. The noise is non-linear and signal-dependent. It can be modelled in several different ways.
In an ideal analog-to-digital converter, where the quantization error is uniformly distributed between −1/2 LSB and +1/2 LSB, and the signal has a uniform distribution covering all quantization levels, the signal-to-noise ratio (SNR) can be calculated from
The most common test signals that fulfil this are full amplitude triangle waves and sawtooth waves.
In this case a 16-bit ADC has a maximum signal-to-noise ratio of 6.0206 · 16=96.33 dB.
When the input signal is a full-amplitude sine wave the distribution of the signal is no longer uniform, and the corresponding equation is instead
Here, the quantization noise is once again assumed to be uniformly distributed. When the input signal has a high amplitude and a wide frequency spectrum this is the case.[1]
In this case a 16-bit ADC has a maximum signal-to-noise ratio of 98.09 dB.
For complex signals in high-resolution ADCs this is an accurate model. For low-resolution ADCs, low-level signals in high-resolution ADCs, and for simple waveforms the quantization noise is not uniformly distributed, making this model inaccurate.[2] In these cases the quantization noise distribution is strongly affected by the exact amplitude of the signal.
Template:Listen
References[]
- ↑ Template:Cite book
- ↑ Template:Cite book
See also[]
- Round-off error
- Dither
- Analog to digital converter
- Quantization
- Quantization noise
- Discretization error
- Signal-to-noise ratio
- Bit resolution
- SQNR
External links[]
- Quantization noise in Digital Computation, Signal Processing, and Control, Bernard Widrow and István Kollár, 2007.
- The Relationship of Dynamic Range to Data Word Size in Digital Audio Processing
- Round-Off Error Variance — derivation of noise power of q²/12 for round-off error
- Dynamic Evaluation of High-Speed, High Resolution D/A Converters Outlines HD, IMD and NPR measurements, also includes a derivation of quantization noise
- Signal to quantization noise in quantized sinusoidal
de:Quantisierungsrauschen
es:Ruido de cuantificación
ja:量子化雑音
ja:量子化誤差
pl:Szum kwantyzacji
ru:Шум квантования
This example shows how to compute and compare the statistics of the signal quantization error when using various rounding methods.
First, a random signal is created that spans the range of the quantizer.
Next, the signal is quantized, respectively, with rounding methods ‘fix’, ‘floor’, ‘ceil’, ‘nearest’, and ‘convergent’, and the statistics of the signal are estimated.
The theoretical probability density function of the quantization error will be computed with ERRPDF, the theoretical mean of the quantization error will be computed with ERRMEAN, and the theoretical variance of the quantization error will be computed with ERRVAR.
Uniformly Distributed Random Signal
First we create a uniformly distributed random signal that spans the domain -1 to 1 of the fixed-point quantizers that we will look at.
q = quantizer([8 7]);
r = realmax(q);
u = r*(2*rand(50000,1) - 1); % Uniformly distributed (-1,1)
xi=linspace(-2*eps(q),2*eps(q),256);
Fix: Round Towards Zero.
Notice that with ‘fix’ rounding, the probability density function is twice as wide as the others. For this reason, the variance is four times that of the others.
q = quantizer('fix',[8 7]); err = quantize(q,u) - u; f_t = errpdf(q,xi); mu_t = errmean(q); v_t = errvar(q); % Theoretical variance = eps(q)^2 / 3 % Theoretical mean = 0 fidemo.qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
Estimated error variance (dB) = -46.8586 Theoretical error variance (dB) = -46.9154 Estimated mean = 7.788e-06 Theoretical mean = 0
Floor: Round Towards Minus Infinity.
Floor rounding is often called truncation when used with integers and fixed-point numbers that are represented in two’s complement. It is the most common rounding mode of DSP processors because it requires no hardware to implement. Floor does not produce quantized values that are as close to the true values as ROUND will, but it has the same variance, and small signals that vary in sign will be detected, whereas in ROUND they will be lost.
q = quantizer('floor',[8 7]); err = quantize(q,u) - u; f_t = errpdf(q,xi); mu_t = errmean(q); v_t = errvar(q); % Theoretical variance = eps(q)^2 / 12 % Theoretical mean = -eps(q)/2 fidemo.qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
Estimated error variance (dB) = -52.9148 Theoretical error variance (dB) = -52.936 Estimated mean = -0.0038956 Theoretical mean = -0.0039062
Ceil: Round Towards Plus Infinity.
q = quantizer('ceil',[8 7]); err = quantize(q,u) - u; f_t = errpdf(q,xi); mu_t = errmean(q); v_t = errvar(q); % Theoretical variance = eps(q)^2 / 12 % Theoretical mean = eps(q)/2 fidemo.qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
Estimated error variance (dB) = -52.9148 Theoretical error variance (dB) = -52.936 Estimated mean = 0.0039169 Theoretical mean = 0.0039062
Round: Round to Nearest. In a Tie, Round to Largest Magnitude.
Round is more accurate than floor, but all values smaller than eps(q) get rounded to zero and so are lost.
q = quantizer('nearest',[8 7]); err = quantize(q,u) - u; f_t = errpdf(q,xi); mu_t = errmean(q); v_t = errvar(q); % Theoretical variance = eps(q)^2 / 12 % Theoretical mean = 0 fidemo.qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
Estimated error variance (dB) = -52.9579 Theoretical error variance (dB) = -52.936 Estimated mean = -2.212e-06 Theoretical mean = 0
Convergent: Round to Nearest. In a Tie, Round to Even.
Convergent rounding eliminates the bias introduced by ordinary «round» caused by always rounding the tie in the same direction.
q = quantizer('convergent',[8 7]); err = quantize(q,u) - u; f_t = errpdf(q,xi); mu_t = errmean(q); v_t = errvar(q); % Theoretical variance = eps(q)^2 / 12 % Theoretical mean = 0 fidemo.qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
Estimated error variance (dB) = -52.9579 Theoretical error variance (dB) = -52.936 Estimated mean = -2.212e-06 Theoretical mean = 0
Comparison of Nearest vs. Convergent
The error probability density function for convergent rounding is difficult to distinguish from that of round-to-nearest by looking at the plot.
The error p.d.f. of convergent is
f(err) = 1/eps(q), for -eps(q)/2 <= err <= eps(q)/2, and 0 otherwise
while the error p.d.f. of round is
f(err) = 1/eps(q), for -eps(q)/2 < err <= eps(q)/2, and 0 otherwise
Note that the error p.d.f. of convergent is symmetric, while round is slightly biased towards the positive.
The only difference is the direction of rounding in a tie.
x=(-3.5:3.5)'; [x convergent(x) nearest(x)]
ans =
-3.5000 -4.0000 -3.0000
-2.5000 -2.0000 -2.0000
-1.5000 -2.0000 -1.0000
-0.5000 0 0
0.5000 0 1.0000
1.5000 2.0000 2.0000
2.5000 2.0000 3.0000
3.5000 4.0000 4.0000
Plot Helper Function
The helper function that was used to generate the plots in this example is listed below.
type(fullfile(matlabroot,'toolbox','fixedpoint','fidemos','+fidemo','qerrordemoplot.m')) %#ok<*NOPTS>
function qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
%QERRORDEMOPLOT Plot function for QERRORDEMO.
% QERRORDEMOPLOT(Q,F_T,XI,MU_T,V_T,ERR) produces the plot and display
% used by the example function QERRORDEMO, where Q is the quantizer
% whose attributes are being analyzed; F_T is the theoretical
% quantization error probability density function for quantizer Q
% computed by ERRPDF; XI is the domain of values being evaluated by
% ERRPDF; MU_T is the theoretical quantization error mean of quantizer Q
% computed by ERRMEAN; V_T is the theoretical quantization error
% variance of quantizer Q computed by ERRVAR; and ERR is the error
% generated by quantizing a random signal by quantizer Q.
%
% See QERRORDEMO for examples of use.
% Copyright 1999-2014 The MathWorks, Inc.
v=10*log10(var(err));
disp(['Estimated error variance (dB) = ',num2str(v)]);
disp(['Theoretical error variance (dB) = ',num2str(10*log10(v_t))]);
disp(['Estimated mean = ',num2str(mean(err))]);
disp(['Theoretical mean = ',num2str(mu_t)]);
[n,c]=hist(err);
figure(gcf)
bar(c,n/(length(err)*(c(2)-c(1))),'hist');
line(xi,f_t,'linewidth',2,'color','r');
% Set the ylim uniformly on all plots
set(gca,'ylim',[0 max(errpdf(quantizer(q.format,'nearest'),xi)*1.1)])
legend('Estimated','Theoretical')
xlabel('err'); ylabel('errpdf')
This example shows how to compute and compare the statistics of the signal quantization error when using various rounding methods.
First, a random signal is created that spans the range of the quantizer.
Next, the signal is quantized, respectively, with rounding methods ‘fix’, ‘floor’, ‘ceil’, ‘nearest’, and ‘convergent’, and the statistics of the signal are estimated.
The theoretical probability density function of the quantization error will be computed with ERRPDF, the theoretical mean of the quantization error will be computed with ERRMEAN, and the theoretical variance of the quantization error will be computed with ERRVAR.
Uniformly Distributed Random Signal
First we create a uniformly distributed random signal that spans the domain -1 to 1 of the fixed-point quantizers that we will look at.
q = quantizer([8 7]);
r = realmax(q);
u = r*(2*rand(50000,1) - 1); % Uniformly distributed (-1,1)
xi=linspace(-2*eps(q),2*eps(q),256);
Fix: Round Towards Zero.
Notice that with ‘fix’ rounding, the probability density function is twice as wide as the others. For this reason, the variance is four times that of the others.
q = quantizer('fix',[8 7]); err = quantize(q,u) - u; f_t = errpdf(q,xi); mu_t = errmean(q); v_t = errvar(q); % Theoretical variance = eps(q)^2 / 3 % Theoretical mean = 0 fidemo.qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
Estimated error variance (dB) = -46.8586 Theoretical error variance (dB) = -46.9154 Estimated mean = 7.788e-06 Theoretical mean = 0
Floor: Round Towards Minus Infinity.
Floor rounding is often called truncation when used with integers and fixed-point numbers that are represented in two’s complement. It is the most common rounding mode of DSP processors because it requires no hardware to implement. Floor does not produce quantized values that are as close to the true values as ROUND will, but it has the same variance, and small signals that vary in sign will be detected, whereas in ROUND they will be lost.
q = quantizer('floor',[8 7]); err = quantize(q,u) - u; f_t = errpdf(q,xi); mu_t = errmean(q); v_t = errvar(q); % Theoretical variance = eps(q)^2 / 12 % Theoretical mean = -eps(q)/2 fidemo.qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
Estimated error variance (dB) = -52.9148 Theoretical error variance (dB) = -52.936 Estimated mean = -0.0038956 Theoretical mean = -0.0039062
Ceil: Round Towards Plus Infinity.
q = quantizer('ceil',[8 7]); err = quantize(q,u) - u; f_t = errpdf(q,xi); mu_t = errmean(q); v_t = errvar(q); % Theoretical variance = eps(q)^2 / 12 % Theoretical mean = eps(q)/2 fidemo.qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
Estimated error variance (dB) = -52.9148 Theoretical error variance (dB) = -52.936 Estimated mean = 0.0039169 Theoretical mean = 0.0039062
Round: Round to Nearest. In a Tie, Round to Largest Magnitude.
Round is more accurate than floor, but all values smaller than eps(q) get rounded to zero and so are lost.
q = quantizer('nearest',[8 7]); err = quantize(q,u) - u; f_t = errpdf(q,xi); mu_t = errmean(q); v_t = errvar(q); % Theoretical variance = eps(q)^2 / 12 % Theoretical mean = 0 fidemo.qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
Estimated error variance (dB) = -52.9579 Theoretical error variance (dB) = -52.936 Estimated mean = -2.212e-06 Theoretical mean = 0
Convergent: Round to Nearest. In a Tie, Round to Even.
Convergent rounding eliminates the bias introduced by ordinary «round» caused by always rounding the tie in the same direction.
q = quantizer('convergent',[8 7]); err = quantize(q,u) - u; f_t = errpdf(q,xi); mu_t = errmean(q); v_t = errvar(q); % Theoretical variance = eps(q)^2 / 12 % Theoretical mean = 0 fidemo.qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
Estimated error variance (dB) = -52.9579 Theoretical error variance (dB) = -52.936 Estimated mean = -2.212e-06 Theoretical mean = 0
Comparison of Nearest vs. Convergent
The error probability density function for convergent rounding is difficult to distinguish from that of round-to-nearest by looking at the plot.
The error p.d.f. of convergent is
f(err) = 1/eps(q), for -eps(q)/2 <= err <= eps(q)/2, and 0 otherwise
while the error p.d.f. of round is
f(err) = 1/eps(q), for -eps(q)/2 < err <= eps(q)/2, and 0 otherwise
Note that the error p.d.f. of convergent is symmetric, while round is slightly biased towards the positive.
The only difference is the direction of rounding in a tie.
x=(-3.5:3.5)'; [x convergent(x) nearest(x)]
ans =
-3.5000 -4.0000 -3.0000
-2.5000 -2.0000 -2.0000
-1.5000 -2.0000 -1.0000
-0.5000 0 0
0.5000 0 1.0000
1.5000 2.0000 2.0000
2.5000 2.0000 3.0000
3.5000 4.0000 4.0000
Plot Helper Function
The helper function that was used to generate the plots in this example is listed below.
type(fullfile(matlabroot,'toolbox','fixedpoint','fidemos','+fidemo','qerrordemoplot.m')) %#ok<*NOPTS>
function qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
%QERRORDEMOPLOT Plot function for QERRORDEMO.
% QERRORDEMOPLOT(Q,F_T,XI,MU_T,V_T,ERR) produces the plot and display
% used by the example function QERRORDEMO, where Q is the quantizer
% whose attributes are being analyzed; F_T is the theoretical
% quantization error probability density function for quantizer Q
% computed by ERRPDF; XI is the domain of values being evaluated by
% ERRPDF; MU_T is the theoretical quantization error mean of quantizer Q
% computed by ERRMEAN; V_T is the theoretical quantization error
% variance of quantizer Q computed by ERRVAR; and ERR is the error
% generated by quantizing a random signal by quantizer Q.
%
% See QERRORDEMO for examples of use.
% Copyright 1999-2014 The MathWorks, Inc.
v=10*log10(var(err));
disp(['Estimated error variance (dB) = ',num2str(v)]);
disp(['Theoretical error variance (dB) = ',num2str(10*log10(v_t))]);
disp(['Estimated mean = ',num2str(mean(err))]);
disp(['Theoretical mean = ',num2str(mu_t)]);
[n,c]=hist(err);
figure(gcf)
bar(c,n/(length(err)*(c(2)-c(1))),'hist');
line(xi,f_t,'linewidth',2,'color','r');
% Set the ylim uniformly on all plots
set(gca,'ylim',[0 max(errpdf(quantizer(q.format,'nearest'),xi)*1.1)])
legend('Estimated','Theoretical')
xlabel('err'); ylabel('errpdf')