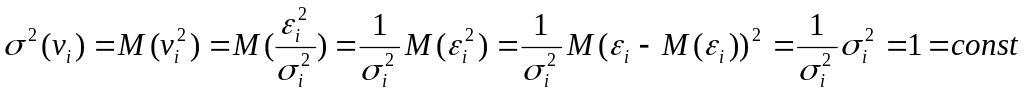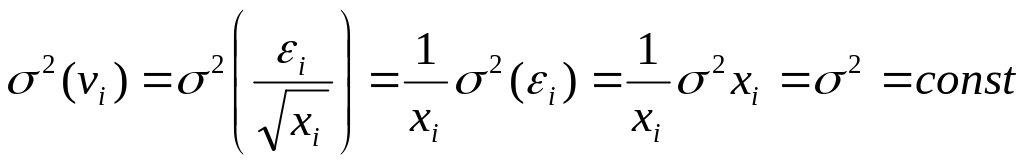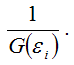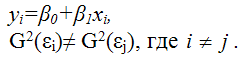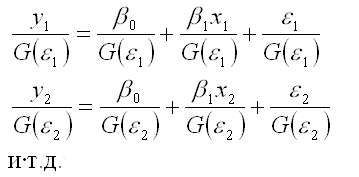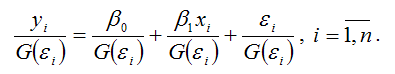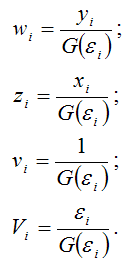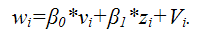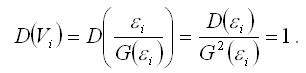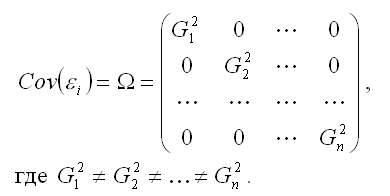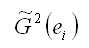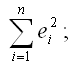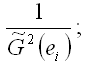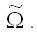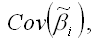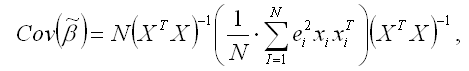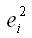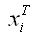При установлении
гетероскедастичности возникает
необходимость преобразования модели
с целью устранения данного недостатка.
Вид преобразования зависит от того,
известны или нет дисперсии
отклонений
.
Метод взвешенных
наименьших квадратов (ВНК) применяется
для известных для каждого наблюдения
значениях
.
В этом случае можно устранить
гетероскедастичность, разделив каждое
наблюдаемое значение на соответствующее
ему значение среднего квадратического
отклонения. В этом суть метода взвешенных
наименьших квадратов.
Для простоты
изложения опишем ВНК на примере парной
регрессии:
.
(5.8)
Разделим обе части
(5.8) на известное
:
.
(5.9)
Положив
,
получим уравнение регрессии без
свободного члена, но с дополнительной
объясняющей переменной Z
и с «преобразованным» отклонением
:
.
(5.10)
При этом для
выполняется условие гомоскедастичности.
Действительно,
.
Так как по предпосылке 10
МНК
,
то
,
и тогда
.
Следовательно,
для преобразованной модели (5.10) выполняются
предпосылки 10-50
МНК. В этом случае оценки, полученные
по МНК, будут наилучшими линейными
несмещенными оценками.
Для применения
ВНК необходимо знать фактические
значения дисперсий
отклонений. На практике такие значения
известны крайне редко. следовательно,
чтобы применить ВНК, необходимо сделать
реалистические предположения о значениях
.
Например, может
оказаться целесообразным предположить,
что дисперссии
отклонений
пропорциональны значениям
(рис. 5.4,а) или значениям
(рис. 5.4,б).
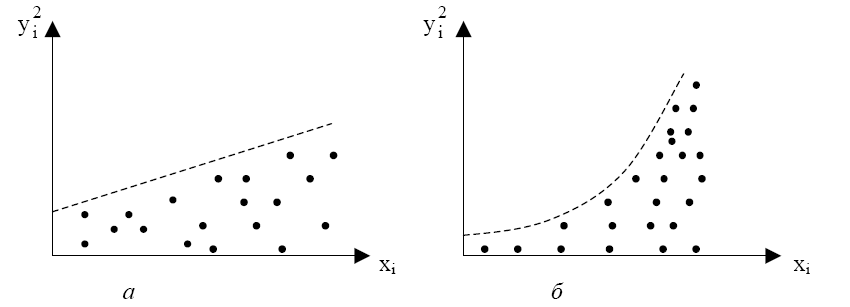
Рис.
5. 4
Дисперсии
пропорциональны
(рис 5.4,а):
(
— коэффициент пропорциональности).
Тогда уравнение
(5.8) преобразуется делением его левой и
правой частей на
:
.
(5.11)
Несложно показать,
что для случайных отклонений
выполняется условие гомоскедастичности.
Следовательно, в регрессии (5.11) применим
обычный МНК. Действительно, в силу
выполнимости предпосылки
имеем:
.
Таким образом,
оценив для (5.11) по МНК коэффициенты
и
,
затем возвращаются к исходному уравнению
регрессии (5.8).
4. Автокорреляция остатков, ее последствия. Обнаружение автокорреляции остатков
Автокорреляция
остатков обычно встречается в регрессионном
анализе при использовании данных
временных рядов. Поэтому в дальнейших
выкладках вместо символа i используется
символ t, отражающий момент наблюдения,
объем выборки при этом будем обозначать
символом T.
В экономических задачах значительно
чаще встречается так называемая
положительная
автокорреляция
(
),
нежели отрицательная
автокорреляция
(
).
В большинстве
случаев положительная автокорреляция
вызывается направленным постоянным
воздействием некоторых неучтенных в
модели факторов.
Среди основных
причин, вызывающих появление автокорреляции,
можно выделить ошибки спецификации,
инерцию в изменении экономических
показателей, эффект паутины, сглаживание
данных.
Последствия
автокорреляции в определенной степени
сходны с последствиями гетероскедастичности.
Среди них при применении МНК обычно
выделяют следующие:
-
Оценки параметров,
оставаясь линейными и несмещенными,
перестают быть эффективными. Следовательно,
они перестают обладать свойствами
наилучших линейных несмещенных оценок
(BLUE-оценок). -
Дисперсии оценок
являются смещенными. Часто дисперсии,
вычисляемые по стандартным формулам,
являются заниженными, что влечет за
собой увеличение-статистик.
Это может привести к признанию
статистически значимыми объясняющие
переменные, которые в действительности
таковыми могут и не являться. -
Оценка дисперсии
регрессии
является смещенной оценкой истинного
значения
,
во многих случаях занижая его. -
В силу вышесказанного
выводы по—
и-статистикам,
определяющим значимость коэффициентов
регрессии и коэффициента детерминации,
возможно, будут неверными. Вследствие
этого ухудшаются прогнозные качества
модели.
В силу неизвестности
значений параметров уравнения регрессии
неизвестными будут также и истинные
значения отклонений
.
Поэтому выводы об их независимости
осуществляются на основе оценок
,
полученных из эмпирического уравнения
регрессии. Рассмотрим возможные методы
определения автокорреляции.
-
Графический метод.
Существует несколько
вариантов графического определения
автокорреляции. Один из них, увязывающий
отклонения
с моментами
их получения (их порядковыми номерами
),
приведен на рис. 5.5. Это так называемые
последовательно-временные графики. В
этом случае по оси абсцисс обычно
откладываются либо время (момент)
получения статистических данных, либо
порядковый номер наблюдения, а по оси
ординат – отклонения
(либо оценки отклонений
).
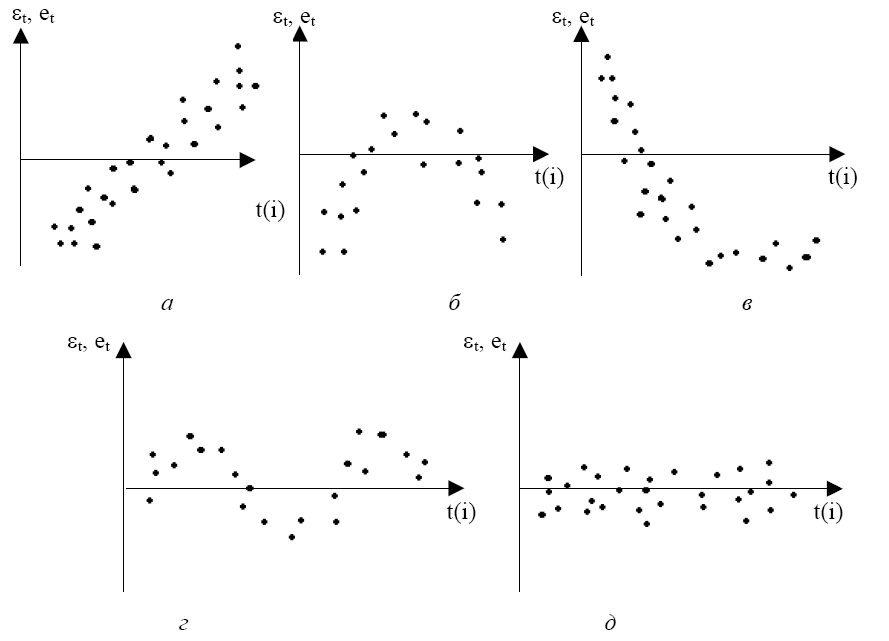
Рис.
5. 5
Естественно
предположить, что на рис. 5.5, а-г
имеются определенные связи между
отклонениями, т.е. автокорреляция имеет
место. Отсутствие зависимости на рис.
5.5,д
скорее всего свидетельствует об
отсутствии автокорреляции.
Например, на рис.
5.5,б
отклонения вначале в основном
отрицательные, затем положительные,
потом снова отрицательные. Это
свидетельствует о наличии между
отклонениями определенной зависимости.
Более того, можно утверждать, что в этом
случае имеет место положительная
автокорреляция остатков. Она становится
весьма наглядной, если график 5.5,б
дополнить графиком зависимости
от
(рис. 5.6).
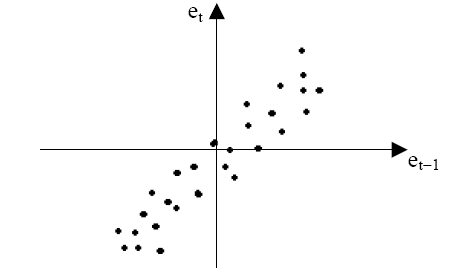
Рис.
5. 6
Подавляющее
большинство точек на этом графике
расположено в I
и III
четвертях декартовой системы координат,
подтверждая положительную зависимость
между соседними отклонениями.
Следует заметить,
что в современных компьютерных прикладных
программах для решения задач по
эконометрике аналитическое выражение
регрессии дополняется графическим
представлением результатов. На график
реальных колебаний зависимой переменной
накладывается график колебаний переменной
по уравнению регрессии. Сопоставив эти
два графика, можно выдвинуть гипотезу
о наличии автокорреляции остатков. Если
эти графики пересекаются редко, то можно
предположить наличие положительной
автокорреляции остатков.
-
метод рядов.
Этот метод достаточно
прост: последовательно определяются
знаки отклонений
.
Например,
(——)(+++++++)(—)(++++)(-),
т.е. 5 «-», 7 «+», 3
«-», 4 «+», 1 «-» при 20 наблюдениях.
Ряд
определяется как непрерывная
последовательность одинаковых знаков.
Количество знаков в ряду называется
длиной ряда.
Визуальное
распределение знаков свидетельствует
о неслучайном характере связей между
отклонениями. Если рядов слишком мало
по сравнению с количеством наблюдений
,
то вполне вероятна положительная
автокорреляция. Если же рядов слишком
мало, то вероятна отрицательная
автокорреляция. Для более детального
анализа предлагается следующая процедура.
Пусть
– объем выборки;
– общее количество
знаков «+» при
наблюдениях (количество положительных
отклонений
);
– общее количество
знаков «-» при
наблюдениях (количество положительных
отклонений
);
– количество
рядов.
При достаточно
большом количестве наблюдений (
)
и отсутствии автокорреляции СВ
имеет асимптотически нормальное
распределение с
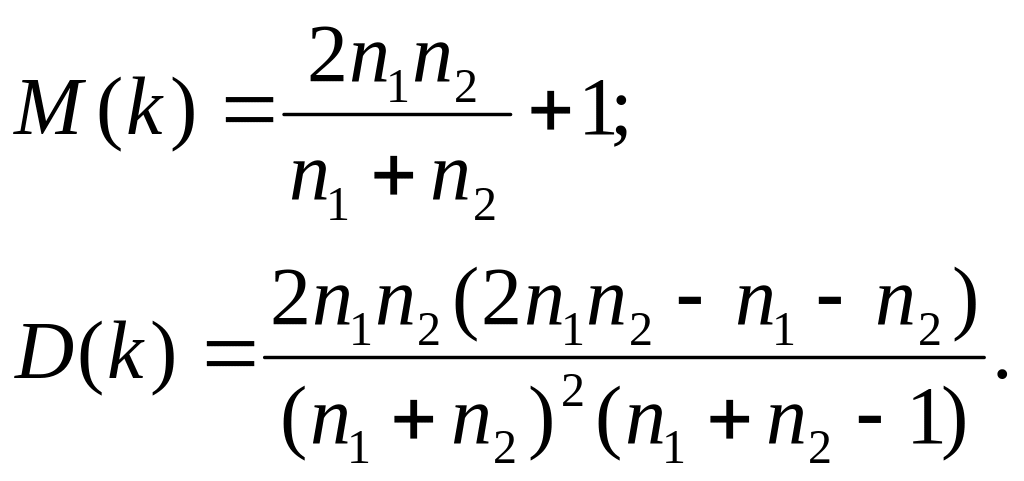
Тогда, если
,
то гипотеза об отсутствии автокорреляции
не отклоняется.
Для небольшого
числа наблюдений (
)
Свед и Эйзенхарт разработали таблицы
критических значений количества рядов
при
наблюдениях . Суть таблиц в следующем.
На пересечении
строки
и столбца
определяются нижнее
и верхнее
значения при уровне значимости
.
Если
,
то говорят об отсутствии автокорреляции.
Если
,
то говорят о положительной автокорреляции.
Если
,
то говорят об отрицательной автокорреляции.
В нашем примере
.
По таблицам определяем
.
Поскольку
,
то применяется предположение о наличии
положительной автокорреляции при уровне
значимости
.
-
Критерий
Дарбина-Уотсона.
Наиболее известным
критерием обнаружения автокорреляции
первого порядка является критерий
Дарбина-Уотсона. Общая схема критерия
Дарбина-Уотсона изложена в моделях
временных рядов (см.тема7,стр. ).
При установлении
автокорреляции необходимо в первую
очередь
проанализировать
правильность спецификации модели.Если
после ряда
усовершенсвований
регрессии автокорреляция по-прежнему
имеет место, то возможны определенные
преобразования, устраняющие автокорреляцию.
Среди них выделяется авторегрессионная
схема первого порядка AR(1).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Понимание гетероскедастичности в регрессионном анализе
17 авг. 2022 г.
читать 3 мин
В регрессионном анализе гетероскедастичность (иногда пишется как гетероскедастичность) относится к неравномерному разбросу остатков или ошибок. В частности, это относится к случаю, когда имеет место систематическое изменение разброса невязок по диапазону измеренных значений.
Гетероскедастичность является проблемой, потому что обычная регрессия методом наименьших квадратов (OLS) предполагает, что остатки поступают из совокупности с гомоскедастичностью , что означает постоянную дисперсию.
Когда в регрессионном анализе присутствует гетероскедастичность, его результатам становится трудно доверять. В частности, гетероскедастичность увеличивает дисперсию оценок коэффициента регрессии, но регрессионная модель этого не учитывает.
Это повышает вероятность того, что регрессионная модель объявит термин в модели статистически значимым, хотя на самом деле это не так.
В этом руководстве объясняется, как обнаружить гетероскедастичность, причины гетероскедастичности и потенциальные способы решения проблемы гетероскедастичности.
Как обнаружить гетероскедастичность
Самый простой способ обнаружить гетероскедастичность — использовать график сопоставления значения и остатка .
После того, как вы подгоните линию регрессии к набору данных, вы можете создать диаграмму рассеяния, которая показывает подобранные значения модели в сравнении с остатками этих подобранных значений.
На приведенной ниже диаграмме рассеяния показано типичное подобранное значение по сравнению с остаточным графиком , на котором присутствует гетероскедастичность.
Обратите внимание, как остатки становятся намного более разбросанными по мере того, как подобранные значения становятся больше. Эта форма «конуса» является явным признаком гетероскедастичности.
Что вызывает гетероскедастичность?
Гетероскедастичность возникает естественным образом в наборах данных с большим диапазоном наблюдаемых значений данных. Например:
- Рассмотрим набор данных, который включает годовой доход и расходы 100 000 человек в Соединенных Штатах. Для лиц с более низкими доходами изменчивость соответствующих расходов будет ниже, поскольку у этих людей, вероятно, достаточно денег только для оплаты самого необходимого. Для людей с более высокими доходами будет более высокая изменчивость соответствующих расходов, поскольку у этих людей есть больше денег, которые они могут потратить, если захотят. Некоторые люди с более высоким доходом предпочтут тратить большую часть своего дохода, в то время как некоторые могут предпочесть быть бережливыми и тратить только часть своего дохода, поэтому изменчивость расходов среди этих людей с более высоким доходом по своей сути будет выше.
- Рассмотрим набор данных, включающий население и количество цветочных магазинов в 1000 различных городах США. Для городов с небольшим населением может быть обычным наличие только одного или двух цветочных магазинов. Но в городах с большим населением будет гораздо большая вариабельность количества цветочных магазинов. В этих городах может быть от 10 до 100 магазинов. Это означает, что когда мы создаем регрессионный анализ и используем население для прогнозирования количества цветочных магазинов, по своей сути будет большая изменчивость остатков для городов с более высоким населением.
Некоторые наборы данных просто более склонны к гетероскедастичности, чем другие.
Как исправить гетероскедастичность
Существует три распространенных способа исправить гетероскедастичность:
1. Преобразуйте зависимую переменную
Один из способов исправить гетероскедастичность — каким-то образом преобразовать зависимую переменную. Одним из распространенных преобразований является просто получение журнала зависимой переменной.
Например, если мы используем численность населения (независимая переменная) для прогнозирования количества цветочных магазинов в городе (зависимая переменная), вместо этого мы можем попытаться использовать численность населения для прогнозирования логарифма количества цветочных магазинов в городе.
Использование журнала зависимой переменной, а не исходной зависимой переменной, часто приводит к исчезновению гетероскедастичности.
2. Переопределите зависимую переменную
Другой способ исправить гетероскедастичность — переопределить зависимую переменную. Один из распространенных способов сделать это — использовать скорость для зависимой переменной, а не необработанное значение.
Например, вместо использования численности населения для прогнозирования количества цветочных магазинов в городе мы можем вместо этого использовать численность населения для прогнозирования количества цветочных магазинов на душу населения.
В большинстве случаев это снижает изменчивость, которая естественным образом возникает среди больших групп населения, поскольку мы измеряем количество цветочных магазинов на человека, а не простое количество цветочных магазинов.
3. Используйте взвешенную регрессию
Другой способ исправить гетероскедастичность — использовать взвешенную регрессию. Этот тип регрессии присваивает вес каждой точке данных на основе дисперсии ее подобранного значения.
По сути, это дает небольшие веса точкам данных с более высокой дисперсией, что уменьшает их квадраты невязок. Когда используются правильные веса, это может устранить проблему гетероскедастичности.
Вывод
Гетероскедастичность — довольно распространенная проблема, когда дело доходит до регрессионного анализа, потому что многие наборы данных по своей природе склонны к непостоянной дисперсии.
Однако, используя график сравнения подобранного значения с остатком , можно довольно легко обнаружить гетероскедастичность.
А путем преобразования зависимой переменной, переопределения зависимой переменной или использования взвешенной регрессии проблему гетероскедастичности часто можно устранить.
Важное предположение о линейной регрессии заключается в том, что остатки не имеют гетероскедастичности. Проще говоря, дисперсия остатка не будет увеличиваться с установленным значением переменной отклика. В этой статье я объясню, почему важно обнаруживать гетероскедастичность? Как определить гетероскедастичность модели? Если существует, как исправить эту проблему с помощью кода R. Этот процесс иногда называютОстаточный анализ。
Почему важно определять гетероскедастичность?
Как только выПостроение модели линейной регрессииОбычно гетероскедастичность остатков должна быть обнаружена. Причина в том, что мы хотим проверить, может ли установленная модель объяснить некоторые шаблоны переменной отклика Y, и в конечном итоге она отображается в остатке. Если есть гетероскедастичность, полученная регрессионная модель неэффективна и нестабильна, и мы можем получить странные результаты предсказания позже.
Как определить гетероскедастичность?
Следующее строится через RcarsМодель регрессии, полученная из набора данных, используется для иллюстрации. Первый проходlm()Функция для построения модели:
lmMod <- lm(dist ~ speed, data=cars) # initial modelТеперь модель готова. Есть два способа определения гетероскедастичности:
-
Графический метод
-
Статистический тест
Графический метод
par(mfrow=c(2,2)) # init 4 charts in 1 panel
plot(lmMod)График выглядит следующим образом:
Нас интересуют две картинки в верхнем левом и нижнем левом углах. Верхний левый угол представляет собой график зависимости остатков от подгоночных значений. Нижний левый угол — это нормализованные остатки, нанесенные на график относительно установленных значений. Если гетероскедастичности нет вообще, вы должны увидеть совершенно случайную точку, точка равномерно распределена по всему диапазону оси X, и вы получите плоскую красную линию.
Однако в этом случае красная линия слегка изогнута от верхнего левого графика, и остаточная ошибка, по-видимому, увеличивается с увеличением значения подгонки. Поэтому предполагается, что гетероскедастичность существует.
Статистический тест
Иногда вам может понадобиться алгоритм для определения гетероскедастичности. Для того, чтобы автоматически оценить его существование и внести изменения. Существует два метода тестирования, чтобы определить, существует ли гетероскедастичность — тест Брейша-Пэгана и тест NCV.
Бреуш языческий тест
lmtest::bptest(lmMod) # Breusch-Pagan test
studentized Breusch-Pagan test
data: lmMod
BP = 3.2149, df = 1, p-value = 0.07297Инспекция NCV
car::ncvTest(lmMod) # Breusch-Pagan test
Non-constant Variance Score Test
Variance formula: ~ fitted.values
Chisquare = 4.650233 Df = 1 p = 0.03104933 Учитывая уровень значимости 0,05, значения P для обоих тестов малы. Следовательно, мы можем отвергнуть нулевую гипотезу о том, что дисперсия остатка постоянна, и сделать вывод, что гетероскедастичность существует, подтверждая тем самым приведенный выше графический вывод.
Как исправить гетероскедастичность?
Перестройте модель прогнозирования
Переменное преобразование, такое как преобразование Бокса-Кокса
Преобразование Бокса-Кокса
Преобразование Бокса-КоксаЭто математическое преобразование, которое превращает переменные в приблизительно нормальное распределение. Обычно преобразование Бокса-Кокса для переменной Y может решить эту проблему, и это именно то, что я хочу сделать.
library(caret)
distBCMod <- caret::BoxCoxTrans(cars$dist)
print(distBCMod)
Box-Cox Transformation
50 data points used to estimate Lambda
Input data summary:
Min. 1st Qu. Median Mean 3rd Qu. Max.
2.00 26.00 36.00 42.98 56.00 120.00
Largest/Smallest: 60
Sample Skewness: 0.759
Estimated Lambda: 0.5 Модельный объект, полученный преобразованием Бокса-Кокса, уже существует, теперь примените его кcar$distЗагрузите и добавьте новый фрейм данных.
cars <- cbind(cars, dist_new=predict(distBCMod, cars$dist)) # append the transformed variable to cars
head(cars) # view the top 6 rows
speed dist dist_new
1 4 2 0.8284271
2 4 10 4.3245553
3 7 4 2.0000000
4 7 22 7.3808315
5 8 16 6.0000000
6 9 10 4.3245553Для новой регрессионной модели преобразованные данные уже доступны. Теперь начните создавать модель и проверьте гетероскедастичность.
lmMod_bc <- lm(dist_new ~ speed, data=cars)
bptest(lmMod_bc)
studentized Breusch-Pagan test
data: lmMod_bc
BP = 0.011192, df = 1, p-value = 0.9157При значении P 0,91 мы не можем отклонить нулевую гипотезу (дисперсия остатка постоянна). Следовательно, дисперсия предполагаемых остатков одинакова. Точно так же используйте график, чтобы проверить гетероскедастичность.
plot(lmMod_bc)График выглядит следующим образом:
Линия вверху слева более плоская, а остатки распределены равномерно. Таким образом, проблема гетероскедастичности была решена.
Эта статья переведена и организована Xueqing Data Network, пожалуйста, обратитесь к оригинальному текстуHow to detect heteroscedasticity and rectify it?Автор Сельва Прабхакаран. Перепечатка, пожалуйста, укажите оригинальную ссылкуhttp://www.xueqing.cc/cms/article/113
Перепечатано по адресу: https://my.oschina.net/u/2605101/blog/603214.
60. Устранение гетероскедастичности остатков модели регрессии
Существует множество методов устранения гетероскедастичности остатков модели регрессии. Рассмотрим некоторые из них.
Наиболее простым методом устранения гетероскедастичности остатков модели регрессии является взвешивание параметров модели регрессии. В этом случае отдельным наблюдениям независимой переменой, характеризующимся максимальным среднеквадратическим отклонением случайной ошибки, придаётся больший вес, а остальным наблюдениям с минимальным среднеквадратическим отклонением случайной ошибки придаётся меньший вес. После данной процедуры свойство эффективности оценок неизвестных коэффициентов модели регрессии сохраняется.
Если для устранения гетероскедастичности был использован метод взвешивания, то в результате мы получим взвешенную модель регрессии с весами
Предположим, что на основе имеющихся данных была построена линейная модель парной регрессии, в которой было доказано наличие гетероскедастичности остатков
Рассмотрим подробнее процесс взвешивания для данной модели регрессии.
Разделим каждый член модели регрессии на среднеквадратическое отклонение случайной ошибки G(?i):
В общем виде процесс взвешивания для линейной модели парной регрессии выглядит следующим образом:
Для более наглядного представления полученной модели регрессии воспользуемся методом замен:
В результате получим преобразованный вид взвешенной модели регрессии:
Преобразованная взвешенная модель регрессии является двухфакторной моделью регрессии.
Дисперсию случайной ошибки взвешенной модели регрессии можно рассчитать по формуле:
Полученный результат доказывает постоянство дисперсий случайных ошибок преобразованной модели регрессии, т. е. о выполнении условия гомоскедастичности.
Главный недостаток метода взвешивания заключается в необходимости априорного знания среднеквадратических отклонений случайных ошибок модели регрессии. По той причине, что в большинстве случаев данная величина является неизвестной, приходится использовать другие методы, в частности методы коррекции гетероскедастичности.
Определение. Суть методов коррекции гетероскедастичности состоит в определении оценки ковариационной матрицы случайных ошибок модели регрессии:
Для определения оценок
используется метод Бреуше-Пайана, который реализуется в несколько этапов:
1) после получения оценок неизвестных коэффициентов модели регрессии рассчитывают остатки ei и показатель суммы квадратов остатков
2) рассчитывают оценку дисперсии остатков модели регрессии по формуле:
3) строят взвешенную модель регрессия, где весами являются оценка дисперсии остатков модели регрессии
4) если при проверке гипотез взвешенная модель регрессии является незначимой, то можно сделать вывод, что оценки матрицы ковариаций ? являются неточными.
Если вычислены оценки дисперсий остатков модели регрессии, то в этом случае можно использовать доступный обобщённый или взвешенный методы наименьших квадратов для вычисления оценок коэффициентов модели регрессии, которые отличаются только оценкой
Если гетероскедастичность остатков не поддаётся корректировке, то можно рассчитать оценки неизвестных коэффициентов модели регрессии с помощью классического метода наименьших квадратов, но затем подвергнуть корректировке ковариационную матрицу оценок коэффициентов
т. к. условие гетероскедастичности приводит к увеличению данной матрицы.
Ковариационная матрица оценок коэффициентов
может быть скорректирована методом Уайта:
где N – количество наблюдений;
X – матрица независимых переменных;
– квадрат остатков модели регрессии;
– транспонированная i-тая строка матрицы данных Х.
Корректировка ковариационной матрицы оценок коэффициентов
методом Уайта приводит к изменению t-статистики и доверительных интервалов для коэффициентов регрессии.
Данный текст является ознакомительным фрагментом.
Читайте также
11. Критерии оценки неизвестных коэффициентов модели регрессии
11. Критерии оценки неизвестных коэффициентов модели регрессии
В ходе регрессионного анализа была подобрана форма связи, которая наилучшим образом отражает зависимость результативной переменной у от факторной переменной х:y=f(x).Необходимо оценить неизвестные
14. Оценка коэффициентов модели парной регрессии с помощью выборочного коэффициента регрессии
14. Оценка коэффициентов модели парной регрессии с помощью выборочного коэффициента регрессии
Помимо метода наименьших квадратов, с помощью которого в большинстве случаев определяются неизвестные параметры модели регрессии, в случае линейной модели парной регрессии
15. Оценка дисперсии случайной ошибки модели регрессии
15. Оценка дисперсии случайной ошибки модели регрессии
При проведении регрессионного анализа основная трудность заключается в том, что генеральная дисперсия случайной ошибки является неизвестной величиной, что вызывает необходимость в расчёте её несмещённой
18. Характеристика качества модели регрессии
18. Характеристика качества модели регрессии
Качеством модели регрессии называется адекватность построенной модели исходным (наблюдаемым) данным.Для оценки качества модели регрессии используются специальные показатели.Качество линейной модели парной регрессии
35. Проверка гипотезы о значимости коэффициентов регрессии и модели множественной регрессии в целом
35. Проверка гипотезы о значимости коэффициентов регрессии и модели множественной регрессии в целом
Проверка значимости коэффициентов регрессии означает проверку основной гипотезы об их значимом отличии от нуля.Основная гипотеза состоит в предположении о незначимости
39. Модели регрессии, нелинейные по факторным переменным
39. Модели регрессии, нелинейные по факторным переменным
При исследовании социально-экономических явлений и процессов далеко не все зависимости можно описать с помощью линейной связи. Поэтому в эконометрическом моделировании широко используется класс нелинейных
40. Модели регрессии, нелинейные по оцениваемым коэффициентам
40. Модели регрессии, нелинейные по оцениваемым коэффициентам
Нелинейными по оцениваемым параметрам моделями регрессииназываются модели, в которых результативная переменная yi нелинейно зависит от коэффициентов модели ?0…?n.К моделям регрессии, нелинейными по
41. Модели регрессии с точками разрыва
41. Модели регрессии с точками разрыва
Определение. Моделями регрессии с точками разрыва называются модели, которые нельзя привести к линейной форме, т. е. внутренне нелинейные модели регрессии.Модели регрессии делятся на два класса:1) кусочно-линейные модели регрессии;2)
44. Методы нелинейного оценивания коэффициентов модели регрессии
44. Методы нелинейного оценивания коэффициентов модели регрессии
Функцией потерь или ошибок называется функционал вида
Также в качестве функции потерь может быть использована сумма модулей отклонений наблюдаемых значений результативного признака у от теоретических
46. Проверка гипотезы о значимости нелинейной модели регрессии. Проверка гипотезы о линейной зависимости между переменными модели регрессии
46. Проверка гипотезы о значимости нелинейной модели регрессии. Проверка гипотезы о линейной зависимости между переменными модели регрессии
На нелинейные модели регрессии, которые являются внутренне линейными, т. е. сводимыми к линейному виду, распространяются все
57. Гетероскедастичность остатков модели регрессии
57. Гетероскедастичность остатков модели регрессии
Случайной ошибкой называется отклонение в линейной модели множественной регрессии:?i=yi–?0–?1x1i–…–?mxmiВ связи с тем, что величина случайной ошибки модели регрессии является неизвестной величиной, рассчитывается
58. Тест Глейзера обнаружения гетероскедастичности остатков модели регрессии
58. Тест Глейзера обнаружения гетероскедастичности остатков модели регрессии
Существует несколько тестов на обнаружение гетероскедастичности остатков модели регрессии.Рассмотрим применение теста Глейзера на примере линейной модели парной регрессии.Предположим, что
59. Тест Голдфелда-Квандта обнаружения гетероскедастичности остатков модели регрессии
59. Тест Голдфелда-Квандта обнаружения гетероскедастичности остатков модели регрессии
Основным условием проведения теста Голдфелда-Квандта является предположение о нормальном законе распределения случайной ошибки ?i модели регрессии.Рассмотрим применение данного
61. Автокорреляция остатков модели регрессии. Последствия автокорреляции. Автокорреляционная функция
61. Автокорреляция остатков модели регрессии. Последствия автокорреляции. Автокорреляционная функция
Автокорреляцией называется корреляция, возникающая между уровнями изучаемой переменной. Это корреляция, проявляющаяся во времени. Наличие автокорреляции чаще всего
62. Критерий Дарбина-Уотсона обнаружения автокорреляции остатков модели регрессии
62. Критерий Дарбина-Уотсона обнаружения автокорреляции остатков модели регрессии
Помимо автокорреляционной и частной автокорреляционной функций для обнаружения автокорреляции остатков модели регрессии используется критерий Дарбина-Уотсона. Однако данный критерий
63. Устранение автокорреляции остатков модели регрессии
63. Устранение автокорреляции остатков модели регрессии
В связи с тем, что наличие в модели регрессии автокорреляции между остатками модели может привести к негативным результатам всего процесса оценивания неизвестных коэффициентов модели, автокорреляция остатков
Секунда теории
Гетероскедастичность – это ситуация, когда ошибка регрессии не удовлетворяет условию гомоскедастичности, т.е. дисперсия этой самой ошибки непостоянно. Это приводит при использовании метода наименьших квадратов к разным неприятным эффектам смещения значений оценок, что ставит под сомнение смысл всей проделанной на основании данного уравнения регрессии работы.
В странствиях по CRAN-у попался пакет skedastic, в котором реализованы 25 разных тестов гомоскедастичности – о нем и поговорим.
О тестах
Вдумчивый разбор математического основания всех реализованных тестов – это дело статьи в специализированном журнале, дело данной заметки – посмотреть, как они работают.
Возьмем из пакета UsingR данные о бриллиантах diamond и посмотрим уравнение регрессии (цена зависит от веса)
library(tidyverse)
library(ggplot2)
library(skedastic)
library(AER)
library(gvlma)
library(UsingR)
data(diamond)
ggplot(data = diamond, aes(x=carat, y=price)) + geom_point()
model_1 <- lm(price~carat, data=diamond)
summary(model_1)
gvlma(model_1)
ggplot(data = diamond, aes(x=carat, y=model_1$residuals)) + geom_point() + ylab("Error of model")На графике видна классическая линейная зависимость. Соответствующая модель значима и даже (по версии пакета gvlma) все условия Гаусса-Маркова выполняются
График ошибок говорит о том же самом:
Есть значительные основания полагать, что гетероскедастичности тут нет. Теперь посмотрим на результаты применения пакета skedastic (во всех тестах нулевая гипотеза: есть гомоскедастичность; при уровне значимости меньше заданного, допустим, 0.05, она будет отвергнута):
Собственно, тесты почти единодушны: 24 из 25 (кроме теста Хонды) указали, что нулевая гипотеза не может быть отвергнута, значит, можно смело говорить про гомоскедастичность.
Эксперимент
Самое интересное, правда, другое – вопрос о том, насколько эти тесты определяют гетероскедастичность, когда у нас она есть. Создадим искусственный датафрейм по формуле y = ax+b+e(1+s|x|) при разных значениях s. При s=0 у нас классическая гомоскедастичность (ошибки происходят из нормального распределения), при s=1 – классическая гетероскедастичность (когда дисперсия ошибок растет при увеличении х по модулю). Логично предположить, что нормальное поведение теста в этих случаях – обратная пропорциональность p-значения от значения s. Каждый тест проводился 100 раз на разных значениях a и b, его результаты потом усреднялись. Соответствующие графики представлены ниже:
Собственно, тестов, определяющий данный вид гетероскедастичности, всего 4 (из 25): Диблази-Боуманна, Уайта, Юса и Чжоу. Это говорит о том, что даже если вам тесты показали, что у вас все хорошо, это не значит, что оно так и есть. И это также повод внимательно посмотреть и определить области эффективности этих тестов.
Все материалы, в т.ч. статьи авторов-изобретателей тестов, есть на https://github.com/acheremuhin/Heteroscedacity