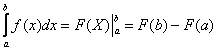Сегодня детально проанализируем алгоритм изменения порядка интегрирования в двойном интеграле. Под изменением порядка интегрирования имеем в виду, что задан двойной интеграл в котором интегрирование проводится сначала по «икс», а дальше полученный результат интегрируют по «игрек». Нужно поменять пределы интегрирования, а возможно и разбить на несколько областей интегрирование, для того, чтобы сначала интегрировать по «игрек», а далее по «иксу». В курсе высшей математики подобные примеры учат решать достаточно длительное время, но не во всех это выходит. Схема изменения порядка интегрирования будет расписана на готовых примерах с красиво выполненными рисунками областей интегрирования. Кто-то может подумать, что рисунки здесь ни к чему, но прочитав статью целиком Вы поймете, что без рисунков Вы не сможете понять как изменяются пределы интегрирования, и как их правильно расставлять.
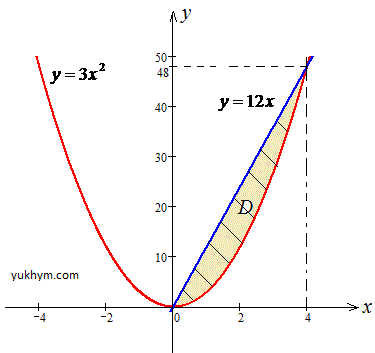
Пример 3.1 Изменить порядок интегрирования в двойном интеграле:
Решение: Построим область интегрирования ограниченую кривыми
0≤x≤4, 3x2≤y≤12x, где
y=3x2 — парабола с вершиной в точке O(0;0) и ветками вверх;
y=12x — прямая, которая проходит через начало координат O(0;0).
График области интегрирования приведен на рисунке.
В этом примере «игрек» изменяется от нижней кривой (параболы) к верхней (прямой), в это время «икс» пробегает значение от 0 до 4.
При изменении порядка интегрирования мы будем пробегать значение от первой кривой по «иксу» (прямой) ко второй (параболы), «игрек» в это время будет проходить значение от 0 ко второй точке пересечения заданных кривых.
Отсюда следует, что для изменения порядка интегрирования нужно найти точки пересечения кривых, дальше для изменения пределов нужно перейти от y(x) к x(y) для этих самых пределов.
Выражаем заданные функции y(x) через переменную y:
y=3x2, отсюда 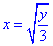
y=12x, отсюда x=y/12.
Найдем точки пересечения:
y=3x2=12x, отсюда
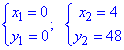
Расставим пределы в заданной области:
D: 0≤y≤48
Выполняем изменение порядка интегрирования
Вот и вся схема перехода от интегрирования по y,x к двойному интегралу по x,y.
Пример 3.2 Изменить порядок интегрирования:
Решение: Запишем область интегрирования для заданного примера
a/2≤x≤a 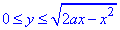
Превратим верхнюю кривую по y к каноническому виду
y=√(2ax-x2), y2=2ax-x2, x2-2ax+a2+y2=a2, (x-a)2+y2=a2 — верхний полукруг с центром в начале координат O(a;0) и радиусом a.
На рисунку наведем область интегрирования
Найдем запись функции через переменную y:
(x-a)^2+y^2=a^2, (x-a)^2 =a^2-y^2,
При изменении порядка интегрирования нашу область необходимо разбить на две подобласти:
D=D1+D2.
Расставим пределы в каждой области:
D1: 0≤y≤a√3/2, a/2≤x≤a;
D2: a√3/2≤y≤a, 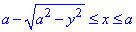
Дальше можем изменить порядок интегрирования
Внимательно пересмотрите фрагмент где область интегрирования разбивается на 2 участка, для чего это делается и от чего зависит.
Многие этого не понимают, поскольку не представляют что делаем, здесь же имеем график из которого видим, что в первой области «икс» изменяется от первой прямой x=a/2 ко второй x=a, во второй области переменная «икс» пробегает значение от полукруга к прямой x=a.
Пример 3.3 Изменить порядок интегрирования:
Решение: Область интегрирования ограничена кривыми
0≤y≤1, 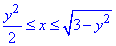
x=√(3-y2), x2=3-y2, x2+y2=(√3)2 — правый полукруг с центром в точке O(0;0) и радиусом R=√3.
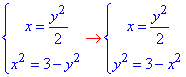
Для изменения порядка интегрирования выражаем функции через переменную x:
x=y2/2, y2=2x, y=√(2x);
x2=3-y2, y2=3-x2, y=√(3-x2).
Найдем точки пересечения графиков функций:
параболы с горизонтальной прямой
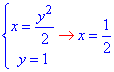
параболы с правой частью полукруга (І четверть)
Подставляем y2 из второго уравнения системы уравнений в первое x=1,5-0,5x2;
При решении получим x=1.
Выполняем построение и разбитие на нужные подобласти интегрирования
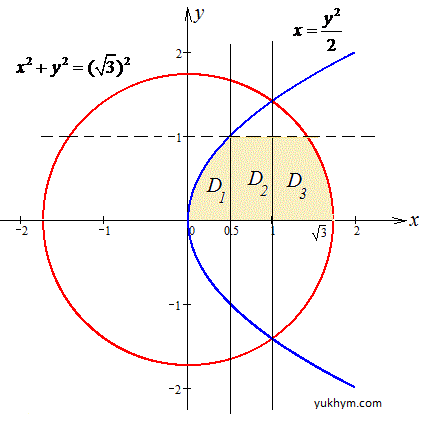
Для изменения порядка интегрирования нашу область разобьем на три подобласти:
D=D1+D2+D3.
Расставим пределы в каждой области:
D1: 0≤x≤0,5, 0≤y≤√(2x);
D2: 0,5≤x≤1, 0≤y≤1;
D3: 1≤x≤√3, 0≤y≤√(3-x2).
Внимательно разберитесь, как это сопоставить с областями на рисунку и почему именно такое разбитие здесь нужно выполнять.
Запишем как изменится интеграл при изменении порядка интегрирования
Думаю приведенных объяснений достаточно, чтобы самостоятельно научиться менять порядок интегрирования.
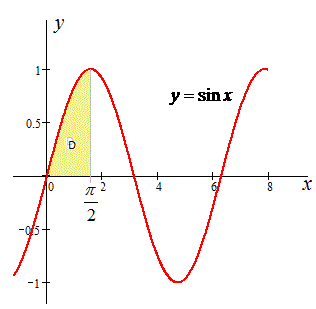
Пример 3.4 Изменить порядок интегрирования:
Решение: Построим область интегрирования, которая ограничена кривыми
0≤x≤π/2, 0≤y≤sin(x), где y=0 — ось абсцисс;
y=sin(x) — синусоида.
Выражаемый полученные функции через переменную y:
y=sin(x), отсюда x=arcsin(y);
y=0, отсюда x=0.
Графику кривых наведем на рисунку
Пределы интегрирования в заданной области поменяются на такие:
D: 0≤y≤1, 0≤x≤arcsin(y).
Записываем двойной интеграл с перечисленными пределами интегрирования
Имеем еще 5 готовых примеров на изменение порядка интегрирования, их Вы можете пересмотреть в следующей статье.
Для определенного интеграла справедливы все типы замен, что и для неопределенного интеграла, но иногда её проводить нельзя (о чём позже). Ну а основная новизна состоит в том, как поменять пределы интегрирования при замене? В примерах ниже я постараюсь привести такие типы замен, которые не встречались ранее:
Пример 5
Вычислить определенный интеграл
Во-первых, замечаем, что отрезок входит в область определения подынтегральной функции (подкоренное выражение больше нуля вообще при любом
).
И главный вопрос здесь не в определённом интеграле, а в том, какую подобрать замену. Смотрим в Таблицу интегралов (см. Приложения) и прикидываем, на что у нас больше всего похожа подынтегральная функция? Очевидно, что на длинный логарифм: . Но есть одна неувязочка: в табличном интеграле под корнем
, а в нашем – «икс» в четвёртой степени. И из этих рассуждений следует идея замены – неплохо бы нашу четвертую степень превратить в квадрат. Это реально.
Сначала готовим интеграл к замене:
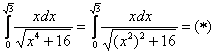
Из вышеуказанных соображений совершенно естественно напрашивается замена:
, после чего в знаменателе будет всё хорошо:
.
Выясняем, во что превратится оставшаяся часть подынтегрального выражения, для этого навешиваем дифференциалы на обе части:
раскрываем дифференциал слева:
и выражаем нужный нам кусок:
По сравнению с заменой в неопределенном интеграле, у нас добавляется дополнительный этап: находим новые переделы интегрирования.
Это достаточно просто. Смотрим на нашу замену и старые пределы интегрирования
,
.
Сначала подставляем в нижний предел интегрирования, то есть, ноль:
,
затем подставляем верхний предел интегрирования – корень из трёх:
И всего-то лишь…. Завершаем решение:
(1) В соответствии с проведённой заменой, записываем новый интеграл с новыми пределами интегрирования.
(2) Это простейший табличный интеграл, интегрируем по таблице. Константу лучше оставить за скобками, чтобы она не мешалась в дальнейших вычислениях. Справа отчеркиваем линию с указанием новых пределов интегрирования
– это подготовка для применения формулы Ньютона-Лейбница.
(3) Используем формулу Ньютона-Лейбница 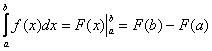
И особенно приятно, что никаких обратных замен проводить не нужно.
А сейчас пара интегралов для самостоятельного решения. Какие замены проводить – постарайтесь догадаться самостоятельно.
Пример 6
Вычислить определенные интегралы
а) 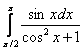
Решения и ответы в конце книги. Приложение Тригонометрические таблицы в помощь, в изучаемой теме этот справочный материал требуется довольно часто.
И теперь обещанный момент о правомерности замены. В определённой ситуации её проводить нельзя! Так, интеграл 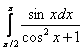
, однако верхний предел интегрирования («пи») не входит в область определения этого тангенса и поэтому данная подстановка нелегальна! Таким образом, функция-«замена» должна быть непрерывна во всех точках отрезка
интегрирования.


| Оглавление |
Полную и свежую версию данного курса в pdf-формате,
а также курсы по другим темам можно найти здесь.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин
Содержание:
- Рассмотрим двойной интеграл
- Как вычислить двойной интеграл?
Пример 1.
Изменить порядок интегрирования в интеграле:
Решение: В данном интеграле область интегрирования D — правильная область первого типа (рис. 10). По теореме 1 интеграл / записывается в виде двойного интеграла 










Для обоих интегралов переменная х принимает только отрицательные значения. Значит для точек 


Теперь, если рассмотреть область интегрирования D как правильную область второго типа, то согласно теореме 2 интеграл / записывается в виде

По этой ссылке вы найдёте полный курс лекций по высшей математике:
Пример 2.
Изменить порядок интегрирования в повторном» интеграле.

Решение:
Область интегрирования D ограничена линиями 



Пример 3.
Изменить порядок интегрирования в повторном интеграле

Решение:
Образец выполнения задания в Mathcad:
Зададим подынтегральную функцию и определим границы области интегрирования по пределам повторного интеграла:

Изменим порядок интегрирования. Для этого надо выразить уравнения границ в виде: 

Указание. Для того, чтобы задать уравнения границ в виде: 




Возможно вам будут полезны данные страницы:
Рассмотрим двойной интеграл





Тогда имеет место равенство 

Координаты 


Интеграл
называется двойным интегралом в криволинейных координатах.
Простейшим и важнейшим частным случаем криволинейных координат являются полярные координаты 


a 
При этом имеет место формула замены переменных в двойном интеграле при переходе к полярным координатам 
Расстановка пределов и вычисление двойного интеграла в криволинейных координатах выполняется аналогично случаю прямоугольных координат.
Как вычислить двойной интеграл?

по области D, ограниченной прямыми 
Решение:
Область D — параллелограмм АВСК (рис. 19 а). Хотя подынтегральная функция и область интегрирования просты, вычисление данного интеграла в прямоугольных координатах достаточно громоздко (убедитесь самостоятельно). Заметив, что уравнения прямых можно записать в виде 









Область D изображена на рис. 20 а. Заметим, что расставить пределы интегрирования в исходном интеграле не просто, однако подходящая замена переменных позволяет свести этот интеграл к интегралу по прямоугольнику.
Введем новые переменные при помощи равенств 






Таким образом, исходный интеграл в плоскости 

Граница области G описывается линиями
(так как одна из формул преобразования имеет вид
то линии
в плоскости
соответствует линия
в плоскости
),
(рис. 20 6).
Поэтому область G имеет вид 

Строим круг 






Таким образом, 
Лекции:
- Производная функции заданной неявно
- Методы определенного интегрирования
- Функция распределения
- Рациональные числа
- Матричные уравнения: пример решения
- Найти частные производные
- Уравнения с двумя переменными
- Матрицы
- Расстояние между скрещивающимися прямыми
- Нахождение промежутков возрастания и убывания функции
В определенном интеграле можно переставить верхний и нижний предел, сменив при этом знак:
Например,
в определенном интеграле перед
интегрированием
целесообразно
поменять пределы интегрирования на
«привычный» порядок:
–
в
таком виде интегрировать значительно
удобнее.
Как
и для неопределенного интеграла, для
определенного интеграла справедливы
свойства линейности:

–
это
справедливо не только для двух, но и для
любого количества функций.
В
определенном интеграле можно
проводить замену
переменной интегрирования,
правда, по сравнению с неопределенным
интегралом тут есть своя специфика, о
которой мы еще поговорим.
Для
определенного интеграла справедлива формула
интегрирования по частям:

Пример
1
Вычислить
определенный интеграл
Решение:
(1)
Выносим константу за знак интеграла.
(2)
Интегрируем по таблице с помощью самой
популярной формулы
.
Появившуюся константу
целесообразно
отделить от
и
вынести за скобку. Делать это не
обязательно, но желательно – зачем
лишние вычисления?
(3)
Используем формулу Ньютона-Лейбница
.
Сначала подставляем в
верхний
предел, затем – нижний предел. Проводим
дальнейшие вычисления и получаем
окончательный ответ.
Пример
2
Вычислить
определенный интеграл
Это
пример для самостоятельно решения,
решение и ответ в конце урока.
Немного
усложняем задачу:
Пример
3
Вычислить
определенный интеграл
Решение:

(1)
Используем свойства линейности
определенного интеграла.
(2)
Интегрируем по таблице, при этом все
константы выносим – они не будут
участвовать в подстановке верхнего и
нижнего предела.
(3)
Для каждого из трёх слагаемых применяем
формулу Ньютона-Лейбница:
СЛАБОЕ
ЗВЕНО в определенном интеграле – это
ошибки вычислений и часто встречающаяся
ПУТАНИЦА В ЗНАКАХ. Будьте внимательны!
Особое внимание заостряю на третьем
слагаемом:
–
первое место в хит-параде ошибок по
невнимательности, очень часто машинально
пишут
(особенно,
когда подстановка верхнего и нижнего
предела проводится устно и не расписывается
так подробно). Еще раз внимательно
изучите вышерассмотренный пример.
Следует
заметить, что рассмотренный способ
решения определенного интеграла – не
единственный. При определенном опыте,
решение можно значительно сократить.
Например, я сам привык решать подобные
интегралы так:
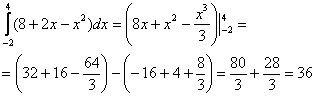
Здесь
я устно использовал правила линейности,
устно проинтегрировал по таблице. У
меня получилась всего одна скобка с
отчёркиванием пределов:
(в
отличие от трёх скобок в первом способе).
И в «целиковую» первообразную функцию,
я сначала подставил сначала 4, затем –2,
опять же выполнив все действия в уме.
Какие
недостатки у короткого способа решения?
Здесь всё не очень хорошо с точки зрения
рациональности вычислений, но лично
мне всё равно – обыкновенные дроби я
считаю на калькуляторе.
Кроме того,
существует повышенный риск допустить
ошибку в вычислениях, таким образом,
студенту-чайнику лучше использовать
первый способ, при «моём» способе решения
точно где-нибудь потеряется знак.
Несомненными
преимуществами второго способа является
быстрота решения, компактность записи
и тот факт, что первообразная
находится
в одной скобке.
Совет:
перед тем, как использовать формулу
Ньютона-Лейбница, полезно провести
проверку: а сама-то первообразная найдена
правильно?
Так,
применительно к рассматриваемому
примеру: перед тем, как в первообразную
функцию
подставлять
верхний и нижний пределы, желательно
на черновике проверить, а правильно ли
вообще найден неопределенный интеграл?
Дифференцируем:
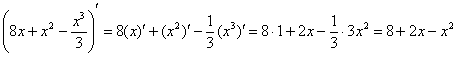
Получена
исходная подынтегральная функция,
значит, неопределенный интеграл найден
верно. Теперь можно и формулу
Ньютона-Лейбница применить.
Такая
проверка будет не лишней при вычислении
любого определенного интеграла.
Пример
4
Вычислить
определенный интеграл
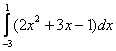
Это
пример для самостоятельно решения.
Попробуйте решить его коротким и
подробным способом.
Замена
переменной в определенном интеграле
Для
определенного интеграла справедливы
все типы замен, что и для неопределенного
интеграла. Таким образом, если с заменами
у Вас не очень, следует внимательно
ознакомиться с уроком Метод
замены в неопределенном интеграле.
В
этом параграфе нет ничего страшного
или сложного. Единственная новизна
состоит в вопросе, как поменять пределы
интегрирования при замене.
В
примерах я постараюсь привести такие
типы замен, которые еще нигде не
встречались на сайте.
Пример
5
Вычислить
определенный интеграл

Главный
вопрос здесь вовсе не в определенном
интеграле, а в том, как правильно провести
замену. Смотрим в таблицу
интегралов и
прикидываем, на что у нас больше всего
похожа подынтегральная функция? Очевидно,
что на длинный логарифм:
.
Но есть одна неувязочка, в табличном
интеграле под корнем
,
а в нашем – «икс» в четвёртой степени.
Из рассуждений следует и идея замены –
неплохо бы нашу четвертую степень
как-нибудь превратить в квадрат. Это
реально.
Сначала
готовим наш интеграл к замене:
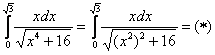
Из
вышеуказанных соображений совершенно
естественно напрашивается замена:
Таким
образом, в знаменателе будет всё
хорошо:
.
Выясняем,
во что превратится оставшаяся
часть
подынтегрального
выражения, для этого находим дифференциал
:
По
сравнению с заменой в неопределенном
интеграле у нас добавляется дополнительный
этап.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
|
13:57 Изменить порядок интегрирования в двойном интеграле |
|
Покажем на конкретных примерах:
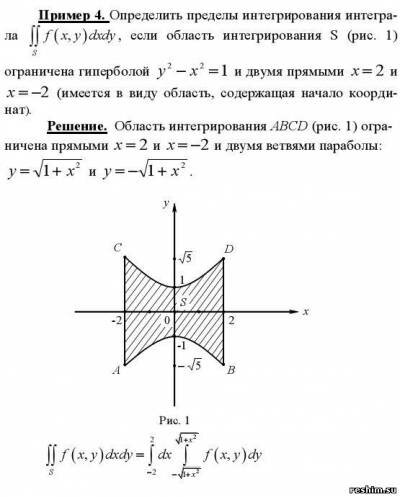
$$iint_{S}^{.} f(x,y)dxdy$$ если область интегрирования S (рис.1) ограничена гиперболой $y^2-x^2=1″ $ и двумя прямыми $x=2,x=-2″$ (имеется ввиду область содержащая начало координат)
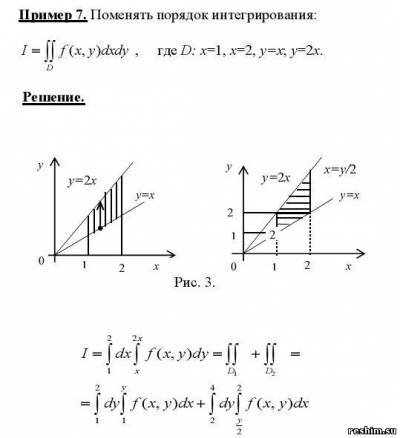
Пример 2. Поменять порядок интегрирования $I=iint_{D}^{.}fleft ( x,y right )dxdy,D:x=1,x=2,y=x,y=2x$
Пример 3. Изменить порядок интегрирования в двойном интеграле $I=int_{0}^{1}dxint_{-2sqrt{x}}^{2sqrt{x}}fleft ( x,y right )dy$
|
Категория: Вычислить интеграл | Просмотров: 168475 | | Теги: изменить порядок интегрирования, кратные интегралы | Рейтинг: 3.0/18 |


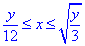
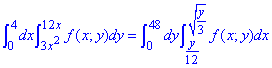
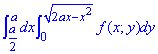
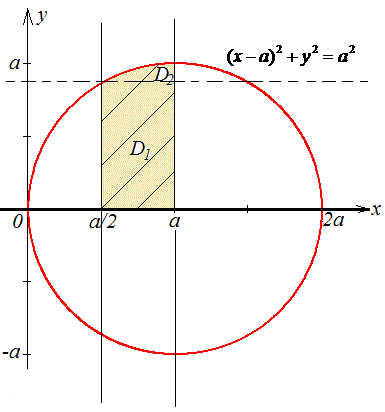
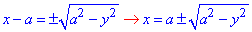
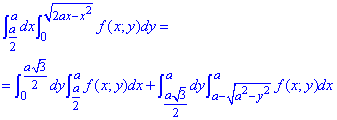
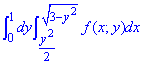
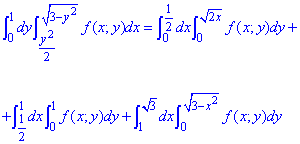
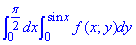
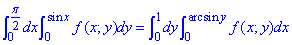
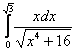
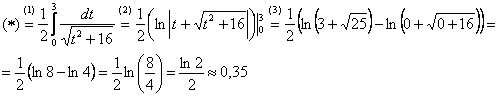







 (так как одна из формул преобразования имеет вид
(так как одна из формул преобразования имеет вид  то линии
то линии  в плоскости
в плоскости  соответствует линия
соответствует линия  в плоскости
в плоскости  ),
),  (рис. 20 6).
(рис. 20 6).