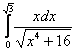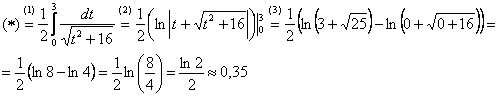Как изменить пределы интегрирования при замене переменной - Исправление ошибок и поиск оптимальных решений проблем

Для определенного интеграла справедливы все типы замен, что и для неопределенного интеграла, но иногда её проводить нельзя (о чём позже). Ну а основная новизна состоит в том, как поменять пределы интегрирования при замене? В примерах ниже я постараюсь привести такие типы замен, которые не встречались ранее:

Пример 5
Вычислить определенный интеграл

Во-первых, замечаем, что отрезок входит в область определения подынтегральной функции (подкоренное выражение больше нуля вообще при любом ).

И главный вопрос здесь не в определённом интеграле, а в том, какую подобрать замену. Смотрим в Таблицу интегралов (см. Приложения) и прикидываем, на что у нас больше всего похожа подынтегральная функция? Очевидно, что на длинный логарифм: . Но есть одна неувязочка: в табличном интеграле под корнем , а в нашем – «икс» в четвёртой степени. И из этих рассуждений следует идея замены – неплохо бы нашу четвертую степень превратить в квадрат. Это реально.
Сначала готовим интеграл к замене:
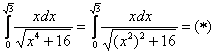
(прерываем решение для промежуточных действий)

Из вышеуказанных соображений совершенно естественно напрашивается замена:
, после чего в знаменателе будет всё хорошо: .

Выясняем, во что превратится оставшаяся часть подынтегрального выражения, для этого навешиваем дифференциалы на обе части:

раскрываем дифференциал слева:

и выражаем нужный нам кусок:

По сравнению с заменой в неопределенном интеграле, у нас добавляется дополнительный этап: находим новые переделы интегрирования.

Это достаточно просто. Смотрим на нашу замену и старые пределы интегрирования , .

Сначала подставляем в нижний предел интегрирования, то есть, ноль:
,
затем подставляем верхний предел интегрирования – корень из трёх:

И всего-то лишь…. Завершаем решение:

(1) В соответствии с проведённой заменой, записываем новый интеграл с новыми пределами интегрирования.

(2) Это простейший табличный интеграл, интегрируем по таблице. Константу лучше оставить за скобками, чтобы она не мешалась в дальнейших вычислениях. Справа отчеркиваем линию с указанием новых пределов интегрирования – это подготовка для применения формулы Ньютона-Лейбница.

(3) Используем формулу Ньютона-Лейбница 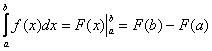и упрощаем результат по известной формуле.

И особенно приятно, что никаких обратных замен проводить не нужно.
А сейчас пара интегралов для самостоятельного решения. Какие замены проводить – постарайтесь догадаться самостоятельно.

Пример 6
Вычислить определенные интегралы
а) 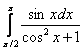, б)

Решения и ответы в конце книги. Приложение Тригонометрические таблицы в помощь, в изучаемой теме этот справочный материал требуется довольно часто.

И теперь обещанный момент о правомерности замены. В определённой ситуации её проводить нельзя! Так, интеграл 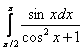, казалось бы, разрешим с помощью универсальной тригонометрической подстановки , однако верхний предел интегрирования («пи») не входит в область определения этого тангенса и поэтому данная подстановка нелегальна! Таким образом, функция-«замена» должна быть непрерывна во всех точках отрезка интегрирования.

1.5. А если подвести функцию под знак дифференциала?

1.3. Простейшие определённые интегралы

| Оглавление |

Полную и свежую версию данного курса в pdf-формате,
а также курсы по другим темам можно найти здесь.

Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!

С наилучшими пожеланиями, Александр Емелин

Источник

Теорема
2.
Пусть
функции

и φ(t)
удовлетворяют условиям:

функция

непрерывна на отрезке [a,
b];
функция
φ(t)
и
ее
производная непрерывны на отрезке

причем

3).

Тогда:

.
(*)

Доказательство.
Функция
непрерывна на [a,
b],
следовательно, у нее существует
первообразная F(x):

.
Функция
непрерывна
на
,
следовательно, имеет первообразную
G(t),

которая имеет вид G(t)=F(φ(t)),
ибо

К
определенным интегралам из формулы (*)
применим основную формулу интегрального
исчисления:

Однако,
последняя разность в силу условия 3)
равна
.
Это и доказывает формулу (*).

Пример
3.

Заметим,
что определенный интеграл от единичной
функции нет необходимости вычислять
по формуле Ньютона–Лейбница: он равен
разности верхнего и нижнего пределов
интегрирования.

Пример
4.

Замечание.
При
замене переменной в определенном
интеграле меняем и пределы интегрирования.
Возврат к первоначальной переменной
интегрирования не нужен.

III Интегрирование по частям в определенном интеграле

Теорема
3.
Пусть функции
и
непрерывны
вместе со своими производными на отрывке
[a,
b].
Тогда:

Доказательство.
Формулу дифференцирования
проинтегрируем по отрезку[a,
b]:

Но
первообразная для
есть сама функцияuv,
значит, по основной формуле

отсюда
и получаем утверждения теоремы.

Пример
5.

§7.
Замечания к теме

I

О
первообразных четной и нечетной функции

Рассмотрим
одну из первообразных непрерывной
функции
и
вычислим
:

Если
функция

четная,
то есть

,

то
получим

Значит,
первообразная
–
нечетная.
Если

же

функция

нечетная, то есть
),
то

что
означает четность первообразной
.
А так как всякая другая первообразная
имеет вид,
то получаем полезное свойство
первообразных:

одна
из первообразных четной функции нечетна;

все
первообразные нечетной функции четны.

II

Об
интегралах
по симметричным промежуткам

Формула
Ньютона – Лейбница и доказанное в
предыдущем пункте свойство приводят к
формулам:

Например,
без вычислений можно получить
,
так как подынтегральная функция нечетная,
а промежуток интегрирования симметричен
относительно нуля.

III

Об интегралах от периодических функций.

Пусть
функция

имеет период T:
.
Пользуясь аддитивностью определенного
интеграла,
запишем для любого
а:

и
в третьем интеграле сделаем замену
x=x+T.
Тогда y=x–T,
,иdx=dy:

Окончательно,

интеграл
от периодической функции по промежутку,
длина которого равна периоду, не зависит
от положения промежутка на числовой
оси.

Соседние файлы в папке MATANALIZ — 2

Источник

Замена переменной в определенном интеграле

Содержание:

Примеры с решением

Если функция непрерывна на отрезке а функция непрерывно дифференцируема на отрезке причем то

При вычислении конкретного интеграла с использованием уравнения Ньютона-Лейбница желательно не проводить четкого различия между этапами решения задачи (найти подынтегральное выражение в производной и найти приращение производной).

Примеры с решением

Пример 1.

Вычислить Применим подстановку Тогда

Следовательно,

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Теорема 12.5. Пусть дан интеграл непрерывная функция в интервале Пусть переменная интегрирования заменена по формуле причем:

{иначе говоря, значения отвечают соответственно верхнему и нижнему пределам интеграла);

непрерывна в интервале

— функция монотонна в интервале т.е. в этом интервале производная сохраняет знак.

Тогда справедлива формула

Доказательство. Пусть есть первообразная для подынтегральной функции исходного интеграла. Тогда согласно формуле (12.14) запишем

С другой стороны, рассмотрим функцию получаемую из заменой Она является сложной функцией от Возьмем производную от этой функции по Таким образом, эта производная равна подынтегральной функции в правой части формулы (12.16), т.е. для этой подынтегральной функции выражение есть первообразная, поэтому интеграл в правой части (12.16), согласно формуле Ньютона-Лейбница, равен

Правая часть этой формулы совпадает с правой частью формулы (12.17), следовательно, их левые части также равны, т.е. получаем формулу (12.16). Теорема доказана.

Итак, при замене переменной в определенном интеграле по формуле мы должны положить в интеграле и Кроме того, пределы и исходного интеграла для следует заменить соответствующими пределами для переменной а именно, и Чтобы установить пределы и для новой переменной, целесообразно выразить из формулы переменную через т.е. найти функцию обратную к х Тогда . После интегрирования возвращаться к старой переменной уже нет необходимости. Как и в случае неопределенных интегралов, подстановка переменных позволяет упростить интеграл путем его аппроксимации в табличной форме (табличной форме).

Возможно вам будут полезны данные страницы:

Пример 2.

Вычислить

Чтобы избавиться от корня, сделаем замену Тогда Нужно найти пределы для Для этого выразим через и получим При будем иметь а при получим Учтем, что 1 тогда

Лекции:

Формулы тригонометрии и их использование для преобразования тригонометрических выражений
Интегральный признак Коши
Правила дифференцирования
Построение графика функции
Признак Лейбница
Функции комплексного переменного
Преобразование подобия
Формулы производных
Изометрия
Определенный интеграл примеры решений

Источник

Материалы к практическому занятию по теме

«Замена переменной в определенном интеграле»

Краткие теоретические сведения

Если заданный интеграл с помощью алгебраических
преобразований трудно или невозможно привести к одному или нескольким табличным
интегралам, то для его вычисления применяют особые методы, одним из которых
является метод замены переменной (подстановки). Это наиболее часто
используемый метод. Он применяется, когда подынтегральная функция является
сложной функцией.

В основе метода лежит формула дифференцирования сложной
функции. Известно, что F¢(x)=f(x) и если существует функция F[g(t)],
причём функция g(t) дифференцируема, то

( F[g(t)] )¢ = F¢(x) g¢(t) = f(x) g¢(t) = f [g(t)] g¢(t).

Отсюда следует, что если ò f(x)dx = F(x)+ C, то ò f [g(t)] g¢(t)dt = F[g(t)]+ C.

Поскольку g(t)dt = dg(t), то предыдущее равенство можно записать в
следующем виде:

ò f [g(t)]dg(t) = F[g(t)]+ C.

При вычислении определенного интеграла методом замены
переменной (подстановки) определенный интеграл

преобразуется с помощью подстановки t=w(x) или x=g(t) в определенный интеграл относительно новой переменной t. При
этом старые пределы интегрирования a и b заменяются соответственно новыми пределами
интегрирования c и d, которые находятся из исходной подстановки. Из
первой подстановки новые пределы интегрирования вычисляются непосредственно: c=w(a), d=w(b). Из второй подстановки новые пределы интегрирования находятся путем
решения уравнений a=g(c), b=g(d) относительно c и d.

Таким образом, формула замены переменной в
определенном интеграле:

Подынтегральные функции непрерывны соответственно на отрезке [a;b] и на отрезке [c;d].

Правило интегрирования методом замены
переменной

1. Определяют, к какому табличному интегралу
приводится данный интеграл

(предварительно преобразовав подынтегральное
выражение, если нужно).

2. Определяют, какую часть подынтегральной функции
заменить новой переменной, и

записывают эту замену.

3. Находят дифференциалы обеих частей записи и
выражают дифференциал старой

переменной (или выражение, содержащее этот
дифференциал) через дифференциал

новой переменной.

4. Старые пределы интегрирования a и b
заменяют соответственно новыми пределами

интегрирования c и d,
которые находятся из исходной подстановки.

5. Записывают интеграл относительно новой переменной
и производят его

непосредственное вычисление.

Примеры вычисления определенных интегралов способом
подстановки

1. Вычислить определённый интеграл .

Решение. Пусть , тогда , .

Новые пределы интегрирования: , .

Следовательно, .

2. Вычислить определённый интеграл .

Решение. Пусть , тогда .

Новые пределы интегрирования: , .

Следовательно, .

3. Вычислить определённый интеграл .

Решение. Пусть , тогда .

Новые пределы интегрирования: , .

Следовательно, .

4. Вычислить определённый интеграл .

Решение. Преобразуем подкоренное выражение: .

Тогда пусть , а .

Новые пределы интегрирования: , .

Следовательно,

5. Вычислить определённый интеграл
.

Решение. Полагаем, что , тогда .

Находим пределы интегрирования: , , откуда

, . На
отрезке .

Следовательно,

6. Вычислить определённый интеграл .

Решение. Пусть , тогда .

Новые пределы интегрирования: , .

Следовательно,

Задания для решения на занятии

Вычислить интегралы методом замены переменной:

1) .
Ответ: .

2) .
Ответ: .

3) . Ответ:
.

4) .
Ответ: .

5) .
Ответ: .

6) . Ответ:
.

Задания для самостоятельной (внеаудиторной) работы

Вычислить интегралы методом замены переменной:

1) . Ответ:
.

2) . Ответ:
.

3) . Ответ:
.

4) Ответ: .

Задания для проверочной работы

1 вариант

Вычислите определенный интеграл методом замены
переменной

1. . 2. . 3. .

2 вариант

Вычислите определенный интеграл методом замены
переменной

1. . 2. . 3. .

Ответы: 1 вариант 2 вариант

1) 4 1) 2

2) 2)

3) 3)

Используемая литература:

1) Практические
занятия по математике:
учебное пособие / Н.В.Богомолов / Москва, «Высшая школа», 1990

2) Сборник задач по математике с решениями для техникумов / И.Л.Соловейчик, В.Т.Лисичкин / Москва,
«ОНИКС 21 век», «Мир и Образование», 2003

3) Математика:
учебник для студентов средних профессиональных учреждений / С.Г.Григорьев,
С.В.Иволгина, под редакцией В.А.Гусева / Москва, «Академия», 2010

Источник

I. Замена переменной в определенном интеграле.

Предварительно изучите по учебнику Г. М. Фихтенголь-ца главу XI, п° 186. Разберите примеры, решенные в этом пункте. Обратите особое внимание на выполнимость условий, при которых становится возможной замена переменной.

В теоретическом курсе доказывается, что определен-

рый интеграл при выполнении ряда условий мо-

экет быть заменен другим определенным интегралом

Замечание. При вычислении определенного интеграла с помощью замены переменной нет необходимости затем возпращаться к стар эй переменной (как мы это делали при вычислении неопределенного интеграла).

При этом используется замена переменной

Решение. Введем новую переменную t, положив Покажем, что функцияУдовлетворяет всем условиям теоремы о замене переменной в определенном интеграле. В самом деле,

I) функция, w______ определена и непрерывна

для всех значений t и, в частности, на некотором промежутке

, и ее значения не выходят за пределы промежутка, когда t изменяется в

3) существует вНепрерывная производная

Итак, указанная замена переменной законна. Тогда

для

Так как-, то, заменяя переменную в

определенном интеграле и учитывая четность подынтегральной функции, получим:

Указание. Для отыскания пределов интегрирования новой переменной t используйте равенствоНижний предел а найдется, если вместо х подставить значение нижнего (старого) предела:

Верхний предел р найдется, если вместо х подставить значение верхнего (старого) предела:

389. Вычислить интеграл:

Решение. Введем новую переменную t, связанную со старой переменной х соотношением Покажем, что такая замена переменной законна.

Действительно: I) функцияОпределена и

непрерывна на отрезке(так как она определена

и непрерывна на всей числовой поямой). и ее значения не выходят за пределы промежуткаКогда t изменя

ется в

3) существует вНепрерывная производная

Итак, вводим новую переменную t, полагая Тогда

Так какТо, заменяя переменную в опре-

390. Вычислить интеграл: ;.

Решение. Введем новую переменную t, положив х = te. (Почему возможна такая замена?) Тогда dx = = 6 tbdt. Найдем пределы интегрирования для новой переменной t:

Заменяя переменную в определенном интеграле, получим

Применяя соответствующую замену переменной, вычислить интегралы:

2. Интегрирование по частям в определенном интеграле.

Рассмотрите внимательно решение примеров, помещенных в п° 187. Обратите особое внимание на выполнение необходимых условий, при которых операция интегрирования по частям будет законна.

402. Вычислить интеграл:

Решение. ОбозначимЧерез и, аЧерез,

120

Эта операция является законной, так как в промежутке [I, 2] функции и и V являются непрерывными функциями и имеют непрерывные производные

В теоретическом курсе было показано, что при выполнении этих условий

Следовательно,

Интеграл снова берем по частям, полагая

(Мы пропускаем доказательство законности данной операции, так как оно аналогично доказательству, приведенному ранее.)

Получим:

Окончательно получим:

403. Вычислить интеграл

Решение. Обозначим х через и иЧерез dv,

Легко показать, что данная операция является законной: функции—функции непрерывные и име

ют в каждой точке промежутка [О, I] непрерывные производные. Следовательно,

Используя метод интегрирования по частям, вычислить следующие интегралы:

Метод интегрировайия по частям в определенном интеграле часто используется для получения удобных рекуррентных формул, позволяющих сводить данный интеграл к интегралу такого же типа, но более простому.

414. Вычислить интеграл: