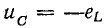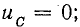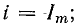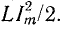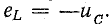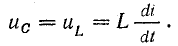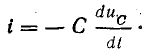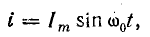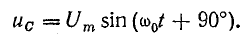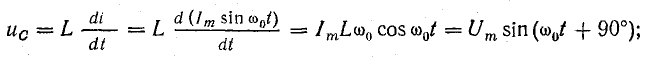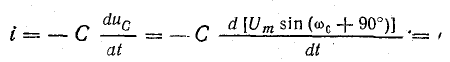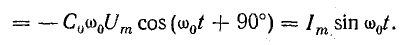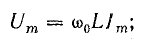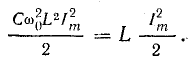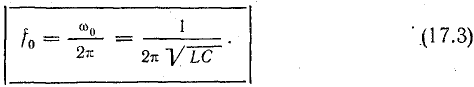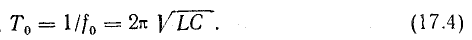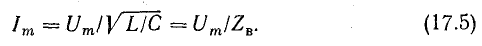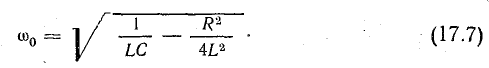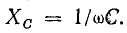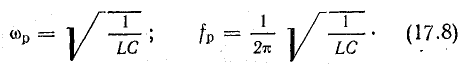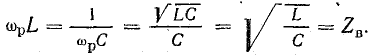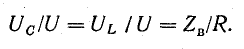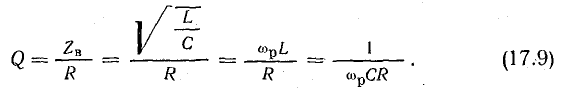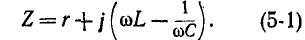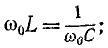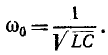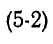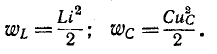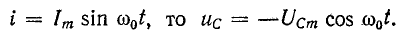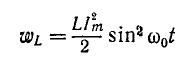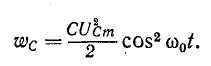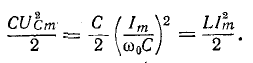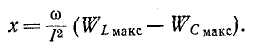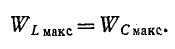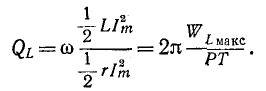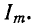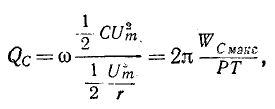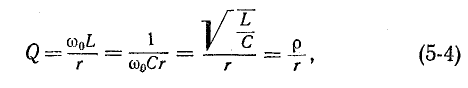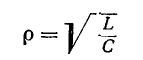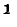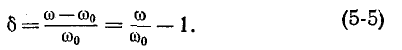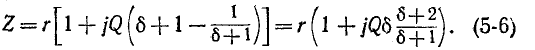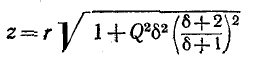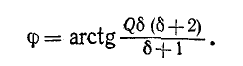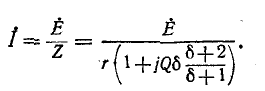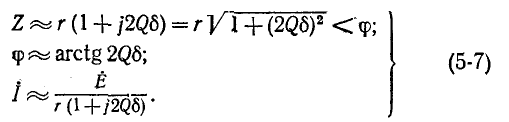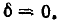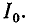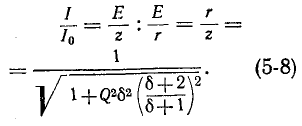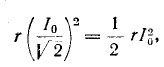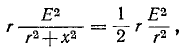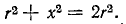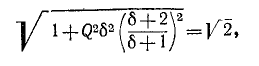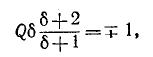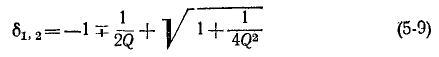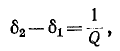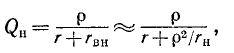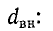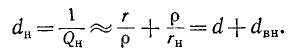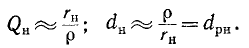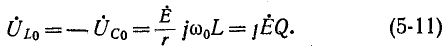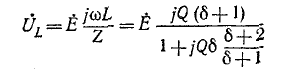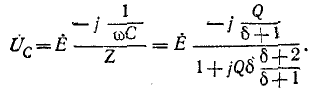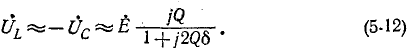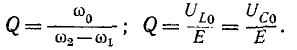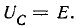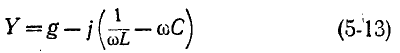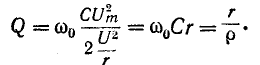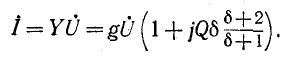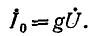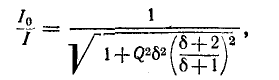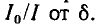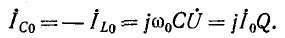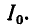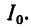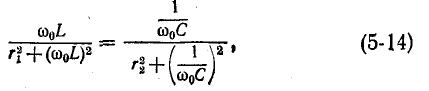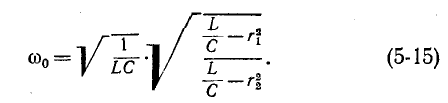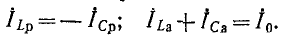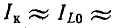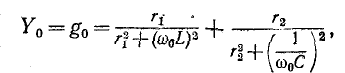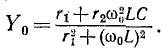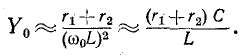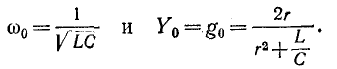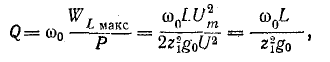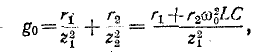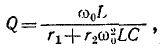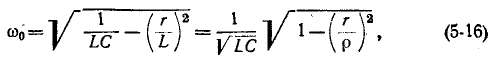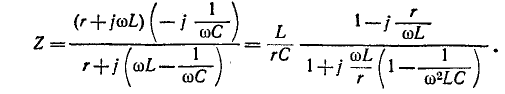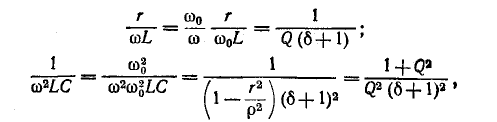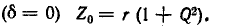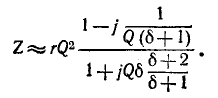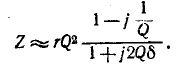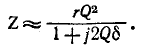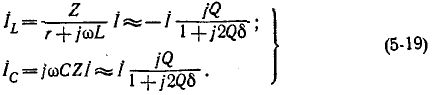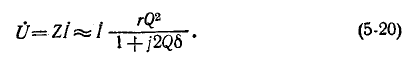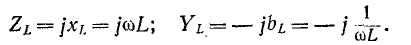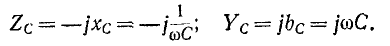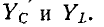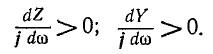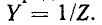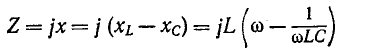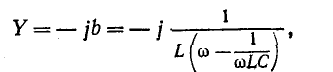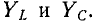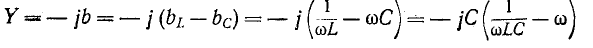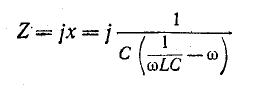Снижение резонансной частоты головок
Нижняя граница воспроизводимого громкоговорителем диапазона частот определяется основной резонансной частотой головки. К сожалению, в продаже очень редко бывают головки, имеющие основную резонансную частоту ниже 60-80 Гц. Поэтому для расширения диапазона рабочих частот акустических систем весьма актуальной представляется возможность снижения основной резонансной частоты используемых в них головок. Как известно, подвижная система головки (диффузор со звуковой катушкой) в области основного резонанса представляет собой простую колебательную систему, состоящую из массы и гибкости подвеса. Резонансная частота такой системы определяется формулой:
где т — масса диффузора, звуковой катушки и присоединенной массы воздуха, г;
С — гибкость подвеса, см/дин.
Таким образом, чтобы снизить основную резонансную частоту головки необходимо увеличить либо массу диффузора и звуковой катушки, либо гибкость их подвеса, либо то и другое вместе. Наиболее просто увеличить массу диффузора, укрепив на нем дополнительный груз. Однако увеличивать массу подвижной системы головки невыгодно, так как это снизит не только резонансную частоту, но и создаваемое головкой звуковое давление. Дело в том, что сила F, создаваемая током I в звуковой катушке динамической головки, равна
F=В*l*I,
где B — магнитная индукция в зазоре;
l — длина проводника звуковой катушки.
С другой стороны, согласно законам механики, эта сила равна
F=m*a,
где m — масса подвижной системы; a — колебательное ускорение.
Поскольку сила, приложенная к звуковой катушке, зависит для данной головки только от величины тока, то увеличив массу, мы во столько же раз уменьшим колебательное ускорение катушки и диффузора; а поскольку звуковое давление, создаваемое головкой в этой области частот, пропорционально ускорению диффузора, уменьшение ускорения равносильно снижению звукового давления. Если бы мы попытались вдвое снизить основную резонансную частоту головки, для этого потребовалось бы увеличить массу подвижной системы в четыре раза, и во столько же раз снизилось бы создаваемое головкой звуковое давление при неизменном токе в катушке. Кроме того, увеличение массы повысило бы добротность подвижной системы и увеличило резонансный пик, а с ним и неравномерность частотной характеристики, что, в свою очередь, ухудшило бы переходные характеристики громкоговорителя.
Следовательно, для снижения резонансной частоты головки целесообразнее увеличить гибкость подвеса диффузора и центрирующего диска, то есть уменьшить жесткость крепления подвижной системы. Делается это следующим образом. Прежде всего отклеивают или отрезают острым скальпелем или лезвием (по кольцу диффузородержателя) воротник диффузора. Затем отпаивают гибкие выводы звуковой катушки, отвинчивают кольцо центрирующего диска и гетинаксовый 0
Источник
Как понизить резонансную частоту динамика
Если тебе не жаль такого матюгальника то отдели экранирующий стакан и один внути приклеенный магнит.
ZoidBerg
а без разбирания можно как-то обойтись?
-20 dB m.ix писал: Простым способом.
Навешивается магнит.
Или снимается имеющийся.
Или он же переворачивается на 180*
Кхм. Ну, уменьшится отдача динамика. И что? На резонансную частоту-то это как повлияет? Резонансная частота останется таковой даже без магнитной системы, ибо сие есмь частота механического резонанса подвижной системы динамика. А зависит она в свою очередь как раз от жёсткости подвеса и массы этой самой системы.
ZoidBerg, таки, если жёсткостью подвеса не удаётся выйти на нужную частоту резонанса — может, массой попробовать? Типа, вклеить вместо картонного защитного колпачка металлический? За остальные характеристики (ширина полосы, искажения) не ручаюсь — не аудиофил, но резонанс таким методом варьировать очень даже удобно будет.
Может и можно, но я сомневаюсь.
Катушка в динамике это тот же колебательный контур.
Можно Фазовым инвертором поигратся — уменьшая-увеличивая длинну трубы. Это на низкие частоты.
ZoidBerg
я игрался с ФИ и это мало чего дало
вот я видел другой дин PJ и выяснил его особенности-наименьший вес диффа и очень мягкий ход
25 ГЕРЦ как неф делать
вот и хочу этот до такого же состояния довести и в упор столкнулся с мягкостью подвеса
могу предположить,что это вспененный бутил-каучук и мне это не о чем не говорит
вот и хз как его смягчить
ZoidBerg писал: вот и хз как его смягчить
Вырезать с другова такого же.
-20 dB m.ix писал: Вырезать с другова такого же.
Эт не вариант. На другом — мягче? Другое дело — уменьшить жёсткость центрирующей шайбы, прорезав в ней секторные окна. Минусы — разбирать дин таки придётся, во первых, и во вторых — вариант необратим, в случае провала придётся искать новое кольцо.
ZoidBerg, а насчёт массы — проверь таки вариант. Временно утяжелить диффузор можно, например, куском строительной «липучки». А в том гр-ле, о котором ты писал, малая масса диффузора как раз и компенсируется малой жёсткостью подвеса. С увеличением массы резонансная частота понижается, и с уменьшением жёсткости тоже понижается.
ZoidBerg
нет дин пока я портить не буду
а чем можно растворить ентот материал?
ДОБАВЛЕНО 27/12/2009 01:54
а,понял
завтра начну пробовать,а то сегодня ужо поздно будить соседей)))))))
-20 dB ZoidBerg писал: а чем можно растворить ентот материал?
Вот бы ещё знать, что там за материал. Плюс ко всему — многие синтет. материалы временно размягчаются, например, ацетоном. Но кто пробовал размягчить ацетоном, например, ПВХ трубку — знают, во что она превращается через пару дней. Т.е размягчается она прекрасно, прямо таки резиновой становится, но. улетучиваются делавшие её мягкой до размягчения ацетоном пластификаторы, и через день другой это уже не ПВХ, это больше по жёсткости полистирол напоминает. Так что размягчать «абы чем» не рекомендую.
ZoidBerg
я был прав это он и есть http://www.vestaplay.ru/velas-54.php
ДОБАВЛЕНО 27/12/2009 02:05
тока про этот материал ниче нет
ДОБАВЛЕНО 27/12/2009 02:08
кстати когда я на него капнул 646го подвес вспух в том месте,а потом выровнялся
ДОБАВЛЕНО 27/12/2009 02:11
ZoidBerg писал: кстати когда я на него капнул 646го подвес вспух в том месте,а потом выровнялся
. когда испарился 646-й, возможно, унеся с собой часть пластификатора.
Я выше о том и писал.
ZoidBerg
еще говорят,что если 646 смешать с машинным маслом и немного пропитать подвес-тоже смягчится
можа тогда пластификатор поменяется местами с маслом?)))
ДОБАВЛЕНО 27/12/2009 12:16
вот у того динамика PJ подвес — тот же материал подвеса,тока тоньше
тут еще нашел-можа дин мягчить 10 герцами на высоком уровне сигнала?
ДОБАВЛЕНО 27/12/2009 12:36
блю,10 герц разве не влиляют на психику?
-20 dB ZoidBerg писал: тут еще нашел-можа дин мягчить 10 герцами на высоком уровне сигнала?
Что-то сильно меня такой вариант «сомневает». А пальчиками промять-размассировать тогда не проще будет? Да и если подвес ДЕСЯТИЛЕТИЯМИ мнётся примерно таким образом по всему частотному диапазону, и не меняет резонансную частоту — с какого бы он вдруг размялся за час-день умышленного «массажа» на одной частоте?
ZoidBerg
кароче нам нужно найти способ уменьшить толщину подвеса
ДОБАВЛЕНО 27/12/2009 14:10
вобщем я ща ему час буду делать массаж подвеса-реально помогает!
Я б подвес не трогал, можно нарушить эластичность и он разсыпится со временем, а вот шайбу пропитав ацитоном в раёне складок, возможно поможет, только главное что б ацетон не попал на места склеивания, а то оторвётся на на десятигерцовом масаже 
ZoidBerg
массажем подвеса удалось снизить до 27 герц
ДОБАВЛЕНО 27/12/2009 16:15
останавливаться не хочу
ДОБАВЛЕНО 27/12/2009 16:24
реально сегодня дин офигенно раскачался!
раньше на полной громкости дин имел ход 3 см
теперь 5 см и больше не пробовал ,сейчас буду пробовать в корпусе
ZoidBerg
поставил в корпус, результат-класс
тока теперь ФИ надо подогнать на более высокую частоту!!
ЗЫ результат подтвердили соседи, стучащие изо всех сил в батареи и пол!!
в доме все трясется
-20 dB ZoidBerg писал: в доме все трясется
И разве-ж сие хорошо есмь? Это же паразитные резонансы, + стук слабоукреплённых резонирующих предметов. Стоило ли тогда мучаться с качеством? ИМХО, и уличный «колокол» смог бы дом трясти не хуже.
ZoidBerg
не,это в других комнатах,а в моей все чисто
тока теперь фи надо настроить под техно хотяб,ато щас 22 герца
реп самый низкий щас качаю хотя его не люблю
ДОБАВЛЕНО 27/12/2009 17:58
звуки грома ооочень реалистичные.
БЕЗЫМЯННЫЙ
Cдается мне что у этого HiEnda через 20 часов «прогрева» резонанс еще вдвое снизится 
ZoidBerg, КСВ комнаты по слухам 100Гц если ковров и шкафов не сторят в комнате.
ZoidBerg
вот как раз ковров у мя предостаточно висит
ДОБАВЛЕНО 27/12/2009 22:03
думаю фи так и оставлю,если S-90 докуплю-самое то будет
Если тебе не жаль такого матюгальника то отдели экранирующий стакан и один внути приклеенный магнит.
ZoidBerg
а без разбирания можно как-то обойтись?
-20 dB m.ix писал: Простым способом.
Навешивается магнит.
Или снимается имеющийся.
Или он же переворачивается на 180*
Кхм. Ну, уменьшится отдача динамика. И что? На резонансную частоту-то это как повлияет? Резонансная частота останется таковой даже без магнитной системы, ибо сие есмь частота механического резонанса подвижной системы динамика. А зависит она в свою очередь как раз от жёсткости подвеса и массы этой самой системы.
ZoidBerg, таки, если жёсткостью подвеса не удаётся выйти на нужную частоту резонанса — может, массой попробовать? Типа, вклеить вместо картонного защитного колпачка металлический? За остальные характеристики (ширина полосы, искажения) не ручаюсь — не аудиофил, но резонанс таким методом варьировать очень даже удобно будет.
Может и можно, но я сомневаюсь.
Катушка в динамике это тот же колебательный контур.
Можно Фазовым инвертором поигратся — уменьшая-увеличивая длинну трубы. Это на низкие частоты.
ZoidBerg
я игрался с ФИ и это мало чего дало
вот я видел другой дин PJ и выяснил его особенности-наименьший вес диффа и очень мягкий ход
25 ГЕРЦ как неф делать
вот и хочу этот до такого же состояния довести и в упор столкнулся с мягкостью подвеса
могу предположить,что это вспененный бутил-каучук и мне это не о чем не говорит
вот и хз как его смягчить
ZoidBerg писал: вот и хз как его смягчить
Вырезать с другова такого же.
-20 dB m.ix писал: Вырезать с другова такого же.
Эт не вариант. На другом — мягче? Другое дело — уменьшить жёсткость центрирующей шайбы, прорезав в ней секторные окна. Минусы — разбирать дин таки придётся, во первых, и во вторых — вариант необратим, в случае провала придётся искать новое кольцо.
ZoidBerg, а насчёт массы — проверь таки вариант. Временно утяжелить диффузор можно, например, куском строительной «липучки». А в том гр-ле, о котором ты писал, малая масса диффузора как раз и компенсируется малой жёсткостью подвеса. С увеличением массы резонансная частота понижается, и с уменьшением жёсткости тоже понижается.
ZoidBerg
нет дин пока я портить не буду
а чем можно растворить ентот материал?
ДОБАВЛЕНО 27/12/2009 01:54
а,понял
завтра начну пробовать,а то сегодня ужо поздно будить соседей)))))))
-20 dB ZoidBerg писал: а чем можно растворить ентот материал?
Вот бы ещё знать, что там за материал. Плюс ко всему — многие синтет. материалы временно размягчаются, например, ацетоном. Но кто пробовал размягчить ацетоном, например, ПВХ трубку — знают, во что она превращается через пару дней. Т.е размягчается она прекрасно, прямо таки резиновой становится, но. улетучиваются делавшие её мягкой до размягчения ацетоном пластификаторы, и через день другой это уже не ПВХ, это больше по жёсткости полистирол напоминает. Так что размягчать «абы чем» не рекомендую.
ZoidBerg
я был прав это он и есть http://www.vestaplay.ru/velas-54.php
ДОБАВЛЕНО 27/12/2009 02:05
тока про этот материал ниче нет
ДОБАВЛЕНО 27/12/2009 02:08
кстати когда я на него капнул 646го подвес вспух в том месте,а потом выровнялся
ДОБАВЛЕНО 27/12/2009 02:11
ZoidBerg писал: кстати когда я на него капнул 646го подвес вспух в том месте,а потом выровнялся
. когда испарился 646-й, возможно, унеся с собой часть пластификатора.
Я выше о том и писал.
ZoidBerg
еще говорят,что если 646 смешать с машинным маслом и немного пропитать подвес-тоже смягчится
можа тогда пластификатор поменяется местами с маслом?)))
ДОБАВЛЕНО 27/12/2009 12:16
вот у того динамика PJ подвес — тот же материал подвеса,тока тоньше
тут еще нашел-можа дин мягчить 10 герцами на высоком уровне сигнала?
ДОБАВЛЕНО 27/12/2009 12:36
блю,10 герц разве не влиляют на психику?
-20 dB ZoidBerg писал: тут еще нашел-можа дин мягчить 10 герцами на высоком уровне сигнала?
Что-то сильно меня такой вариант «сомневает». А пальчиками промять-размассировать тогда не проще будет? Да и если подвес ДЕСЯТИЛЕТИЯМИ мнётся примерно таким образом по всему частотному диапазону, и не меняет резонансную частоту — с какого бы он вдруг размялся за час-день умышленного «массажа» на одной частоте?
ZoidBerg
кароче нам нужно найти способ уменьшить толщину подвеса
ДОБАВЛЕНО 27/12/2009 14:10
вобщем я ща ему час буду делать массаж подвеса-реально помогает!
Я б подвес не трогал, можно нарушить эластичность и он разсыпится со временем, а вот шайбу пропитав ацитоном в раёне складок, возможно поможет, только главное что б ацетон не попал на места склеивания, а то оторвётся на на десятигерцовом масаже 
ZoidBerg
массажем подвеса удалось снизить до 27 герц
ДОБАВЛЕНО 27/12/2009 16:15
останавливаться не хочу
ДОБАВЛЕНО 27/12/2009 16:24
реально сегодня дин офигенно раскачался!
раньше на полной громкости дин имел ход 3 см
теперь 5 см и больше не пробовал ,сейчас буду пробовать в корпусе
ZoidBerg
поставил в корпус, результат-класс
тока теперь ФИ надо подогнать на более высокую частоту!!
ЗЫ результат подтвердили соседи, стучащие изо всех сил в батареи и пол!!
в доме все трясется
-20 dB ZoidBerg писал: в доме все трясется
И разве-ж сие хорошо есмь? Это же паразитные резонансы, + стук слабоукреплённых резонирующих предметов. Стоило ли тогда мучаться с качеством? ИМХО, и уличный «колокол» смог бы дом трясти не хуже.
ZoidBerg
не,это в других комнатах,а в моей все чисто
тока теперь фи надо настроить под техно хотяб,ато щас 22 герца
реп самый низкий щас качаю хотя его не люблю
ДОБАВЛЕНО 27/12/2009 17:58
звуки грома ооочень реалистичные.
БЕЗЫМЯННЫЙ
Cдается мне что у этого HiEnda через 20 часов «прогрева» резонанс еще вдвое снизится 
ZoidBerg, КСВ комнаты по слухам 100Гц если ковров и шкафов не сторят в комнате.
вот как раз ковров у мя предостаточно висит
ДОБАВЛЕНО 27/12/2009 22:03
думаю фи так и оставлю,если S-90 докуплю-самое то будет
Попробуем разобраться с ключевыми параметрами динамиков. Начнем с одного из самых основных параметров — с резонансной частоты(fs). Писал очень долго и муторно, сотни раз переделывал и переписывал, и получилось многабукафф:) Поэтому разбил на две части. Во второй части будет о том, как фс ведет себя при различных оформлениях и резонанс применительно к высокочастотникам.
От вас жду дополнений и исправлений! Попробуем вместе создать действительно хорошие тексты, доступно разъясняющие основы и физику звука. Надеюсь, не только мне хочется от и до во всем разобраться:) Текст не самый легкий, поэтому включаем думалку, и вперед:) Поехали!
Итак, резонансная частота. Разумеется, этот параметр не самодостаточный и для построения сколь угодно качественной системы знания одного его будет мало.
Динамик, как и любая колебательная система, имеет свою резонансную частоту. Это не незыблемая величина, она может довольно сильно меняться в зависимости от разных факторов. Например, температура упала => подвесы задубели – резонанс возрос. Закинули динамик в ЗЯ – резонанс возрос. Накидали на колпак сортирки с ПВА – резонанс упал.
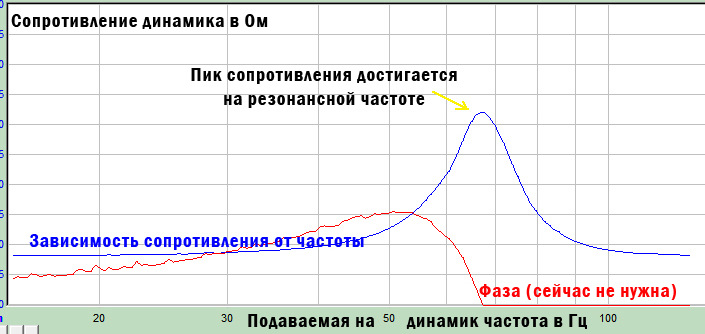
В документации к солидным динамикам всегда указывают эту величину, обозначается она Fs. Представляет собой некое значение частоты в герцах, при которой у динамика в свободном поле наблюдается резонанс. При замере динамик находится не в коробе (в идеале – на солидном удалении от любых отражающих поверхностей), он размят и замер делается при нормальной температуре. Легче всего этот резонанс определить по пику на графике зависимости сопротивления динамика от подаваемой на него частоты. Выглядит этот график примерно так:
Зная резонансную частоту, мы можем с большой долей вероятности определить, на каких частотах будет играть динамик. Динамик с резонансом в 120Гц – это отвратительный сабвуфер и очень плохой мидбас. Даже если он выглядит как сабвуфер и у него 12” дифф, огромный магнит и большая губа.
Кстати: Есть еще два параметра, которые могут полностью изменить картину – это добротность и линейный ход динамика. Например, если дин с частотой 30Гц (неплохо для саба) имеет линейный ход пару мм – это плохой саб. Сыграть красиво и низко он сможет, но очень не громко. Или если у дина с резонансом 30Гц добротность 0,15 – например, в закрытом ящике из него саба не получится. Слишком низкую добротность придется поднимать коробом, а вместе с ней в разы возрастет и результирующая частота. В общем, одной fs обойтись не удастся. Но сегодня говорим только о резонансной частоте.
Теперь смелое утверждение: динамику хорошо ВЫШЕ этой частоты. Чем выше рабочий диапазон динамика, тем более строго соблюдается это утверждение.
Например, пищалкам категорически противопоказано работать на своей Фс. Для них нужно обрезать сигнал так, чтобы на частоте резонанса они не играли вообще, пищалки должны работать значительно выше. Иначе и звук будет непотребный, и за сохранность железа никто не ответит.
Серединки и миды в крайнем случае могут работать до резонансной частоты. Если они не будут ее пересекать – это положительно отразится и на качестве звука, и на долговечности компонентов. Сабвуферы могут забираться и даже жить ниже ФС, но тут многое зависит от акустического оформления и помещения. Общая суть для сабов: чем ниже фс, тем более этот динамик сабовый. Если перед вами лежит 15-ти дюймовый дин с огромным магнитом и у него резонанс 68Гц — сабом он не станет никогда. Максимум, что из него можно будет сделать — это мидбас. Но никак не саб.
А теперь самое интересное: о чем нам может сказать Фс?
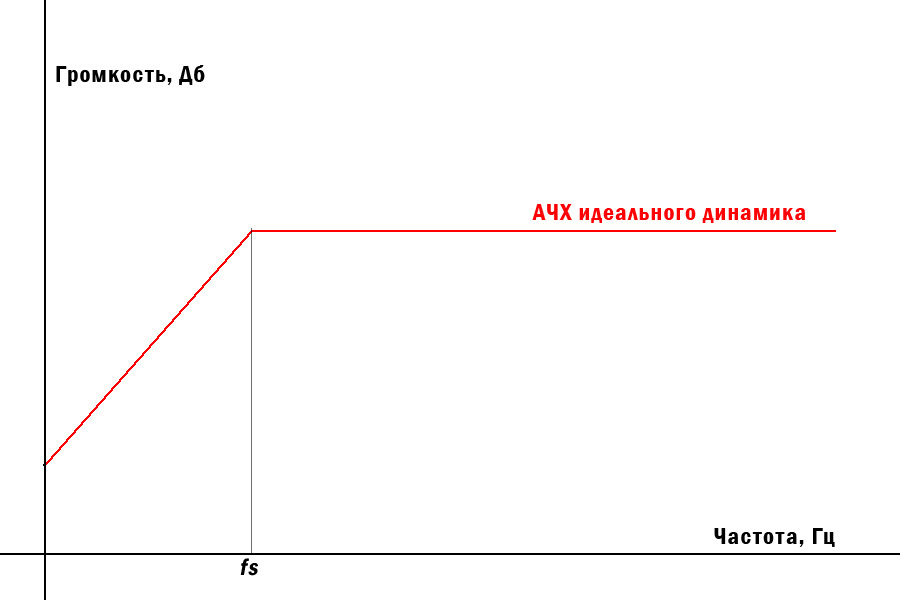
Если взять идеальный динамик, и прям перед ним повесить микрофон, АЧХ будет выглядеть примерно так:
Источник
-
Резонанс напряжений
Явление совпадения по фазе напряжения
и тока в R,L,C-цепи называется
электрическим резонансом.
В цепях переменного тока с последовательным
соединением R,L,C- элементов при равенствевозникает резонанс напряжений.
При
т.е. резонанс напряжений наступает при
равенстве реактивных сопротивлений.
Условием резонанса напряжений является
равенство
(6-43)
или
(6-44)
Поэтому в цепи переменного
тока резонанс напряжений может наступить:
-
если при постоянных LиCчастота сигнала,
подаваемого в цепь, изменяясь, становится
равной ν ==
;
()
-
если при постоянной частоте входного
сигнала и постоянной индуктивности
емкость конденсатора меняется и
становится равной: С =;
-
если при постоянной частоте входного
сигнала и постоянной емкости меняется
индуктивность и становится равной: L=;
-
если при постоянной частоте входного
сигнала изменение обеих величин LиCприводит к равенству:.
Таким образом, чтобы в цепи наступил
резонанс напряжений, необходимо
обеспечить определенное соотношение
между величинами ν, L,C,
т.е. резонанса в цепи можно добиться
путем регулирования (подбора) параметров
индуктивного и емкостного элементов,
а также с помощью изменения частоты
питающего тока. При резонансе частота
тока (напряжения) равна частоте
собственных колебаний цепи (контура).
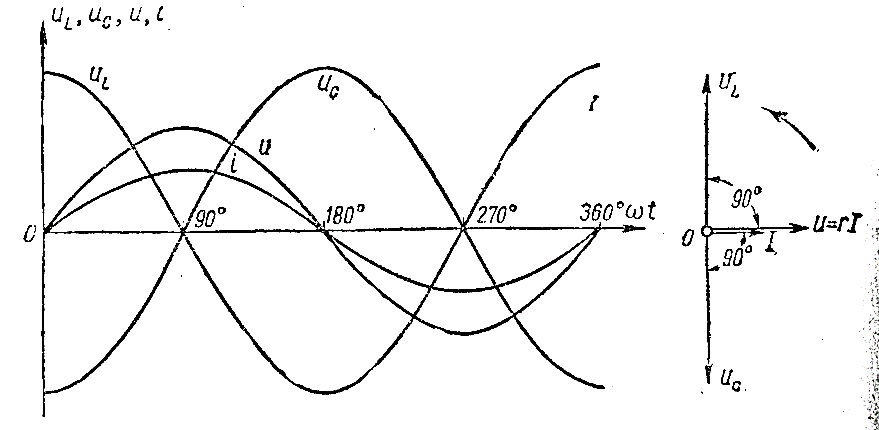
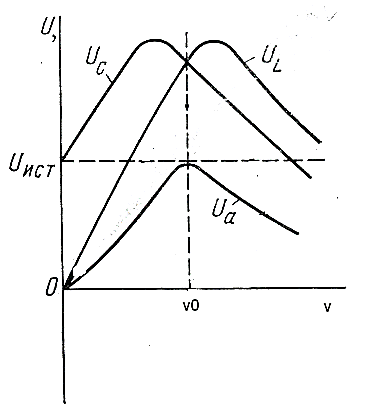
Рис. 77 Графики и векторная диаграмма
для резонанса напряжений.
При резонансе напряжений выражение
U==
(6-45)
так как .
Полное сопротивление цепи
Z==R, (6-46)
так как =
.
Полная мощность цепи
S==P, (6-47)
так как .
Фазовый сдвиг между током и напряжением
(6-48)
так как =
следовательно
.
Коэффициент мощности
= 1, (6-49)
так как Z=R
Таким образом, электрическая
цепь переменного тока в режиме резонанса
представляет собой чисто активную
нагрузку.
Зависимость параметров цепи от
частоты. Практический интерес
представляют соотношения между
параметрами цепи и их зависимость от
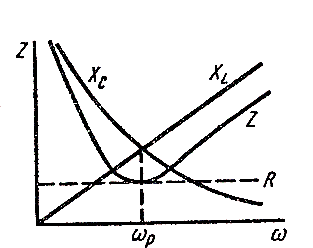
частоты тока. На рис.78 а показаны
а б
Рис.78
кривые R=R(v).
Т.к. активное сопротивление практически
от частоты не зависит то графикR=R(v)
представляет прямую параллельную оси
абсцисс. Индуктивное сопротивлениепрямо пропорционально, а емкостное
сопротивлениеобратно
пропорционально частоте тока.
До резонанса ,
при резонансе,
после резонанса.
При резонансе полное реактивное
сопротивление
=
Полное сопротивление цепи Z,
также зависит от частоты. До и после
резонанса оно растет за счет увеличенияили
.
При резонансеZ=R.
По закону Ома ток в последовательной
R,L,C– цепи
. (6-50)
При резонансе (XL
=XC)
и ток равен максимальному значению, в
то время как до (XL
<XC)
и после (XL
>XC)
резонанса он уменьшается. Приv=0,XC=
∞,I= 0. Аналогично приv=∞,XL=∞,I= 0. На рис. б показаны
графикиI(v).
Кривая зависимости тока от частоты
называется резонансной кривой. По
характеру изменения тока в R,L,C– цепи
легко установить состояние резонанса
в ней – максимальное значение тока в
цепи указывает на момент резонанса.
Рис. 79
Рис.80
Напряжение на резистивном элементе
изменяется пропорционально току: При резонансе, когда ток максимален,
напряжениеUaтакже максимально и равно напряжению
источника питанияUист
(рис. ). Приω= 0; ∞ токI= 0;Ua= 0. На рис.79а изображена зависимость
Напряжение на индуктивном элементе
пропорционально токуIи частоте
.
.
При увеличении частоты напряжение на
индуктивном элементе растет и при
частоте, близкой к резонансной, достигает
максимального значения; по мере
дальнейшего увеличения частоты ток, а
следовательно, и индуктивное напряжение
уменьшаются. При поэтому индуктивное напряжение равно
напряжению источника питания. Криваяизображена на рис. 79а .
Напряжение на емкостном элементеследовательно,
оно пропорционально токуIи обратно пропорционально частоте.
ПриПоэтому емкостное напряжение компенсирует
приложенное напряжение к цепи, т.е.При увеличении частоты напряжение
растет и при частоте, близкой к
резонансной, достигает максимального
значения; по мере дальнейшего увеличения
частоты ток и емкостное напряжение
уменьшаются. ПриКривая
изображена на рис. .
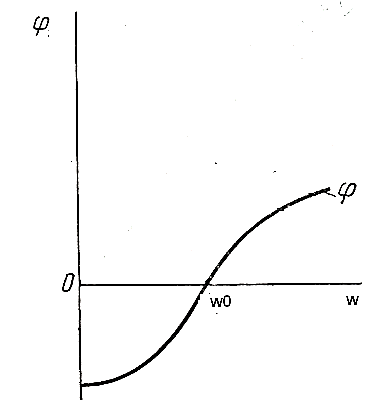
Сдвиг фаз определяется из
выражения
При т.е.
,
что соответствует.
При что соответствует
При т.е.
График зависимости
изображен на рис. 80 .
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Попробуем разобраться с ключевыми параметрами динамиков. Начнем с одного из самых основных параметров — с резонансной частоты(fs). Писал очень долго и муторно, сотни раз переделывал и переписывал, и получилось многабукафф:) Поэтому разбил на две части. Во второй части будет о том, как фс ведет себя при различных оформлениях и резонанс применительно к высокочастотникам.
От вас жду дополнений и исправлений! Попробуем вместе создать действительно хорошие тексты, доступно разъясняющие основы и физику звука. Надеюсь, не только мне хочется от и до во всем разобраться:) Текст не самый легкий, поэтому включаем думалку, и вперед:) Поехали!
Итак, резонансная частота. Разумеется, этот параметр не самодостаточный и для построения сколь угодно качественной системы знания одного его будет мало.
Динамик, как и любая колебательная система, имеет свою резонансную частоту. Это не незыблемая величина, она может довольно сильно меняться в зависимости от разных факторов. Например, температура упала => подвесы задубели – резонанс возрос. Закинули динамик в ЗЯ – резонанс возрос. Накидали на колпак сортирки с ПВА – резонанс упал.
В документации к солидным динамикам всегда указывают эту величину, обозначается она Fs. Представляет собой некое значение частоты в герцах, при которой у динамика в свободном поле наблюдается резонанс. При замере динамик находится не в коробе (в идеале – на солидном удалении от любых отражающих поверхностей), он размят и замер делается при нормальной температуре. Легче всего этот резонанс определить по пику на графике зависимости сопротивления динамика от подаваемой на него частоты. Выглядит этот график примерно так:
пример графика сопротивления динамика от частоты
Зная резонансную частоту, мы можем с большой долей вероятности определить, на каких частотах будет играть динамик. Динамик с резонансом в 120Гц – это отвратительный сабвуфер и очень плохой мидбас. Даже если он выглядит как сабвуфер и у него 12” дифф, огромный магнит и большая губа.
Кстати: Есть еще два параметра, которые могут полностью изменить картину – это добротность и линейный ход динамика. Например, если дин с частотой 30Гц (неплохо для саба) имеет линейный ход пару мм – это плохой саб. Сыграть красиво и низко он сможет, но очень не громко. Или если у дина с резонансом 30Гц добротность 0,15 – например, в закрытом ящике из него саба не получится. Слишком низкую добротность придется поднимать коробом, а вместе с ней в разы возрастет и результирующая частота. В общем, одной fs обойтись не удастся. Но сегодня говорим только о резонансной частоте.
Теперь смелое утверждение: динамику хорошо ВЫШЕ этой частоты. Чем выше рабочий диапазон динамика, тем более строго соблюдается это утверждение.
Например, пищалкам категорически противопоказано работать на своей Фс. Для них нужно обрезать сигнал так, чтобы на частоте резонанса они не играли вообще, пищалки должны работать значительно выше. Иначе и звук будет непотребный, и за сохранность железа никто не ответит.
Серединки и миды в крайнем случае могут работать до резонансной частоты. Если они не будут ее пересекать – это положительно отразится и на качестве звука, и на долговечности компонентов. Сабвуферы могут забираться и даже жить ниже ФС, но тут многое зависит от акустического оформления и помещения. Общая суть для сабов: чем ниже фс, тем более этот динамик сабовый. Если перед вами лежит 15-ти дюймовый дин с огромным магнитом и у него резонанс 68Гц — сабом он не станет никогда. Максимум, что из него можно будет сделать — это мидбас. Но никак не саб.
А теперь самое интересное: о чем нам может сказать Фс?
Если взять идеальный динамик, и прям перед ним повесить микрофон, АЧХ будет выглядеть примерно так:
Завал начинается как раз на частоте резонанса. А после резонанса играет относительно ровненько до тех пор, пока ему позволяет его конструкция.
Проверил это утверждение на практике. Взял три динамика и снял АЧХ (микрофон в паре см от диффа) и их Т/С параметры. Выглядят динамики так:
Полный размер
тестовые мидбасы
Параметры следующие:
Первый номер – резонанс 65 и очень острый пик сопротивления. Сам динамик бестолковый, у него добротность 1,7 (оттого такая острая форма импеданса), но его АЧХ из-за этого наиболее наглядна. Динамик от муз центра JVS, диаметр 18см по подвесу. Стоял в ФИ))) (!) И да, звук был гуано полнейшее.
№2 – 16 мидбас Каденс, резонанс под сотню, добротность 0,88
№3 – странный и бестолковый, но мощно выглядящий 16 мид, добротность 1, резонанс выше сотни герц.
А вот их АЧХ
Самая наглядная зеленая кривая от первого дина, там прям явный надлом на частоте резонанса. В остальных кривых тоже не сложно угадать точку перехода со спада в полку, и эта точка соответствует частоте резонанса.
Почему так происходит? Дело в том, что при понижении частоты ход динамика увеличивается при условии постоянной громкости. Другими словами: чтобы играть на одной и той же громкости и при этом понижать частоту, амплитуду колебаний диффузора придется увеличивать. И о чудо, это происходит автоматически! Но только до резонансной частоты.
Динамик умеет «автоматически» увеличивать амплитуду пропорционально падению частоты только выше резонансной частоты. Оттого ниже фс идет спад — дин просто не может выйти на нужную амплитуду для поддержания нужного уровня громкости.
Исходя из этой логики, динамику с высоким резонансом не нужен большой линейный ход. А так как динамики проектируют сбалансированными (хочется в это верить) – то так и получается на практике. Живой пример – широко распространенные в среде новичков ГДНы от С90 и прочих. По сути, они являются мидбасом, и играют почти до 400Гц. И когда его используют в роли саба, он очень быстро упирается в малый линейный ход. Ну не предназначен он отыгрывать 20-30Гц))) Конструктив другой. Личный пример: восстанавливал замятый колпак на таком динамике, попутно увеличив массу подвижки и снизив резонансную частоту.
Все получилось, по Т/С параметрам динамик стал прям сабом. И поет красиво, звук мощный такой… но ни о каком «валеве» и «давилове» и близко речи не стоит. Любой мистери, который изначально саб, может гораздо больше в плане громкости. Потому что спроектирован именно под это, и ход соответствует низкой частоте.
От чего зависит фс?
Масса подвижки – увеличение массы подвижной системы уменьшает резонансную частоту. Оттого динамики разной размерности с одинаковыми моторами будут отличаться по фс: как правило, диффузор бОльшего диаметра тяжелее, поэтому резонанс его будет ниже.
Жесткость подвеса – чем подвес более жесткий, тем выше резонанс.
Жесткость диффузора – с повышением жесткости диффа резонанс растет! Если диффузор мягкий и «желеобразный» то фс будет ниже, чем у точно такого же динамика, но с жестким дифом. Это очень видно, например, при установке тюнячих жестких колпаков.
И конечно от оформления. Но об этом во второй части.
Усилитель на Фс не влияет! Хотя, можно компенсировать спад АЧХ ниже частоты резонанса подъемом уровня сигнала на этих частотах. Но я не сторонник таких решений.
От проводов тоже не зависит, даже если они очень плохие или очень хорошие:)
Пожалуй, на этом остановимся, остальное во второй части. Ну, если тема покажется интересной.
Часть вторая
Содержание:
Резонанс в электрических цепях:
Явление резонанса можно наблюдать в любых колебательных системах, в том числе механических и электрических. Электрический резонанс возникает при определенных условиях в электрических цепях переменного тока, содержащих индуктивности и емкости.
Изучение электрического резонанса
Изучение электрического резонанса необходимо, так как это явление широко используется в технике электросвязи, а в установках сильного тока, где его возникновение специально не предусматривается, резонанс может оказаться опасным (могут возникнуть перенапряжения и пробой изоляции).
Колебательный контур
Для того чтобы понять резонансные явления, переходные процессы в электрических цепях переменного тока, которые рассматриваются далее, важно иметь представление о процессах в колебательном контуре, состоящем из идеальных катушки и конденсатора, т. е. в контуре без потерь.
Колебательный процесс в таком контуре заключается во взаимном преобразовании электрического и магнитного полей. При этом изменяется энергия полей, поэтому колебательный процесс в контуре с количественной стороны будем, как и раньше, характеризовать изменением энергии.
Ток и напряжение в колебательном контуре
Предположим, что конденсатор с емкостью С получил от источника запас энергии
В первую часть периода (0 — T/4) конденсатор разряжается и в цепи существует ток. В это время в обособленной цепи конденсатор играет роль источника энергии (рис. 17.1, б). В начальный момент ток равен нулю, далее он увеличивается. Увеличение тока в цепи вызывает возникновение э. д. с. самоиндукции eL и накопление энергии в магнитном поле катушки. Э. д. с. самоиндукции уравновешивает напряжение на конденсаторе:
Напряжение на конденсаторе в процессе разрядки уменьшается, поэтому вызываемый в цепи ток растет все медленнее, соответственно с этим уменьшается и э. д. с. самоиндукции, которая пропорциональна скорости изменения тока. Таким образом, к концу разрядки конденсатора (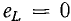
Рис. 17.1. К анализу колебательного контура
С этого момента ток начинает уменьшаться (но не прекращается), сохраняя свое направление. В следующую часть периода (от T/4 до T/2) направление тока сохраняется, потому что э. д. с. самоиндукции при уменьшении тока меняет свой знак, и роль источника энергии переходит к катушке. Уменьшающийся ток теперь является зарядным током конденсатора, заряжающегося в обратном направлении (рис. 17.1, в). Напряжение на конденсаторе увеличивается, уравновешивая теперь э. д. с. самоиндукции:
При увеличении напряжения на конденсаторе его зарядный ток уменьшается все быстрее, в результате чего э. д. с. eL увеличивается. Таким образом, к концу зарядки конденсатора напряжение на его обкладках достигает наибольшего значения, э. д. с. самоиндукции тоже максимальна, а ток становится равным нулю. Энергия магнитного поля снова перешла в энергию электрического поля . С этого момента рост э. д. с. самоиндукции прекращается и начинается ее уменьшение. Роль источника энергии снова переходит к конденсатору. Начинается третья часть периода (от Т/2 до 3T/4). В рассматриваемом процессе конденсатор второй раз становится источником энергии. Но по сравнению с первым он имеет обратную полярность, поэтому его разрядный ток изменяет направление и далее увеличивается. Снова энергия убывает в электрическом поле и накапливается в магнитном поле (рис. 17.1, г).
В момент времени t = 3T/4 напряжение на конденсаторе и э. д. с. самоиндукции становятся равными нулю, а ток — наибольшим. В последнем отрезке времени (от 3T/4 до Т) процесс протекает в том же порядке, что и во втором, но при обратном направлении тока (рис. 17.1, д).
В момент времени t = Т конденсатор заряжен в том же направлении и тем же количеством энергии, как и при t = 0. Ток переходит через нуль к положительным значениям и далее увеличивается. Процесс повторяется в порядке, рассмотренном ранее.
Характеристики колебательного контура
Энергетический процесс в колебательном контуре имеет периодический характер с периодом Т. Колебания в электрической цепи, не связанной с источником энергии, называют собственными или свободными.
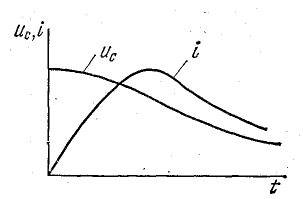
Этот процесс рассмотрен по графикам изменения тока i, напряжения uC и э.д.с. eL, которые приняты синусоидальными функциями времени.
Для такого предположения имеется полное основание, так как эти величины взаимно связаны соотношением
Вместе с тем ток в контуре пропорционален скорости изменения заряда конденсатора, причем он увеличивается, когда конденсатор разряжается. Следовательно,
Такая взаимная связь переменных величин говорит о синусоидальном законе изменения тока и напряжения, но при наличии сдвига фаз между ними на 90°, т. е. при
Это можно проверить:
Величину ω0 в уравнениях тока и напряжения называют угловой частотой собственных колебаний в контуре. Найдем ее, используя равенство наибольшего количества энергии в конденсаторе и катушке:
и связь между амплитудами тока и напряжения:
Сокращая, получим
Частота собственных колебаний
Период собственных колебаний
Из равенства (17.1) вытекает еще одно важное соотношение
Величина, стоящая в знаменателе, имеет размерность сопротивления и называется волновым сопротивлением контура:
Колебательный контур с потерями энергии
Незатухающие колебания в контуре получаются в предположении, что потери энергии отсутствуют, т. е. R = 0.
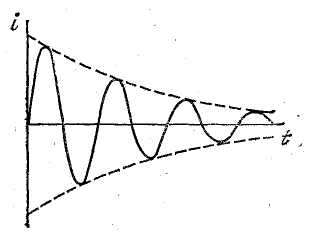
Если активное сопротивление контура не равно нулю, то запас энергии в контуре сокращается (энергия превращается в тепло), амплитуды тока и напряжения с каждым периодом убывают, как показано на рис. 17.2.
Более детальное исследование колебательного контура показывает, что частота собственных колебаний зависит от активного сопротивления:
При R = 0 это выражение совпадает с (17.2).
При 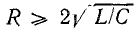
Рис. 17.2. График изменения тока в колебательном контуре с потерями
Рис. 17.3. Апериодический разряд конденсатора на катушку индуктивности
Резонанс напряжений
При рассмотрении различных режимов электрических цепей был отмечен случай равенства реактивных сопротивлений ХL = ХC при последовательном соединении элементов, содержащих индуктивность и емкость.
В этом случае электрическая цепь находится в режиме резонанса напряжений, который характеризуется тем, что реактивная мощность цепи равна нулю, ток и напряжение совпадают по фазе.
Условие возникновения резонанса
Резонанс напряжений возникает при определенной для данной цепи частоте источника энергии (частоте вынужденных колебании), которую называет резонансной частотой ωр.
При резонансной частоте, как будет показано далее, 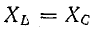
Режим электрической цепи при последовательном соединении участков с индуктивностью и емкостью, характеризующийся равенством индуктивного и емкостного сопротивлений, называют резонансом напряжений.
Резонанс напряжений рассмотрим, сначала на схеме идеализированной цепи (рис. 17.4, а), в которой последовательно с резистором R включены идеальные (без потерь) катушка L и конденсатор С.
Рис. 17.4. К вопросу о резонансе напряжений
Реактивные сопротивления ХL и ХC (рис. 17.4, б) зависят от частоты вынужденных колебаний ω:
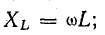
Приравнивая реактивные сопротивления и учитывая, что ω = ωр, получим
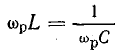
Отсюда резонансная частота
В данном случае выражение для резонансной частоты совпадает с формулой (17.3) для частоты собственных колебаний в контуре без потерь.
Основные соотношения между величинами, характеризующими режим электрической цепи и энергетические процессы. Нужно отметить, что в неразветвленной цепи обмен энергией между катушкой и конденсатором совершается через источник энергии, который восполняет потери энергии в активных сопротивлениях.
Резонансные кривые
Резонанс напряжений в цепи можно установить двумя путями: 1) изменением параметров L и С (одного из них или обоих вместе) при постоянной частоте источника или 2) изменением частоты источника энергии при постоянных L и С.
В связи с этим большой практический интерес представляют зависимости напряжений и токов на отдельных элементах цепи от частоты. Эти зависимости называют резонансными кривыми (рис. 17.4, в).
Реактивные сопротивления с изменением частоты меняются, как показано на рис. 17.4, б. При увеличении частоты ХL увеличивается пропорционально частоте, а ХC уменьшается по закону обратной пропорциональности.
Соответственно полное сопротивление Z цепи при резонансной частоте ωр оказывается наименьшим, равным активному сопротивлению R; при частоте 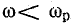
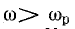
Такая зависимость полного сопротивления от частоты определяет характер изменения тока при постоянном напряжении в цепи (рис. 17.4, в). При 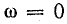
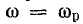
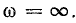
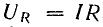
Напряжение на конденсаторе UC при 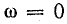
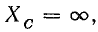
Индуктивное напряжение 

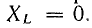
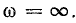
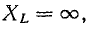
При частотах, меньших резонансной, реактивное сопротивление цепи имеет емкостный характер (отрицательно), поэтому и угол сдвига фаз в цепи отрицательный. Уменьшаясь с ростом частоты, он становится равным нулю при резонансе 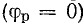
Добротность контура
При резонансе напряжений отношение напряжения на индуктивности или емкости к напряжению, приложенному к цепи (напряжению источника), равно отношению волнового сопротивления к активному. Действительно, при резонансе сопротивления реактивных элементов
Поэтому
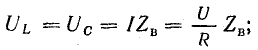
Из этого выражения следует, что при 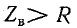
Такое превышение может оказаться значительным, если реактивные сопротивления много больше активного, и изоляция катушки или конденсатора может быть пробита. На практике подобный случай возможен, если на конце кабельной линии включается приемник, обладающий индуктивностью.
В радиотехнике качество резонансного контура считается тем выше, чем больше отношение 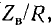
Чем меньше мощность потерь энергии в контуре (этому соответствует меньшая величина R), тем больше добротность контура.
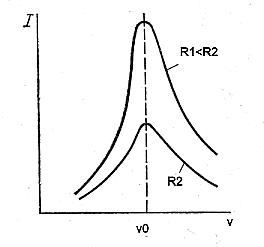
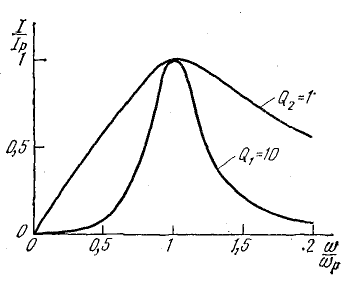
Большей величине добротности соответствует больший ток Iр при резонансе и более острая резонансная кривая.
На рис. 17.5 показаны две резонансные кривые тока, построенные в относительных единицах при двух величинах добротности. По горизонтальной оси отложены отношения изменяющейся частоты источника энергии к резонансной частоте ω/ωр, а по вертикальной —отношения тока при данной частоте к току при резонансной частоте I/Iр.
Рис. 17.5. Резонансные кривые при двух значениях добротности контура
Все рассуждения о резонансе напряжений в идеализированной цепи можно распространить и на цепи, содержащие последовательно соединенные катушку и конденсатор с потерями. Как известно, реальные катушки и конденсатор могут быть представлены схемами последовательного соединения активного и реактивного сопротивлений (рис. 17.5). Активные сопротивления катушки и конденсатора можно рассматривать как часть общего активного сопротивления цепи R, тогда схема на рис. 17.4, а будет пригодна и в этом случае.
Резонанс в электрических цепях
Резонансные (колебательные) цепи:
Резонансными или колебательными цепями называются электрические цепи, в которых могут возникать явления резонанса напряжений или токов.
Резонанс представляет собой такой режим пассивной электрической цепи, содержащей индуктивности и емкости, при котором реактивное сопротивление и реактивная проводимость цепи равны нулю; соответственно равна нулю реактивная мощность на выводах цепи.
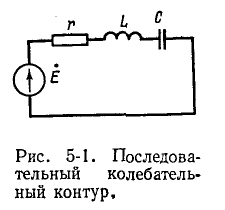
Резонанс напряжения наблюдается в электрической цепи с последовательным соединением участков, содержащих индуктивности и емкости. Неразветвленная цепь, состоящая из последовательно соединенных элементов r, L и С, рассмотренная, представляет собой один из простейших случаев такой цепи. В радиотехнике ее называют последовательным колебательным контуром.
При резонансе напряжений индуктивное сопротивление одной части цепи компенсируется емкостным сопротивлением другой ее части, последовательно соединенной с первой. В результате реактивное сопротивление и реактивная мощность на выводах цепи равны нулю.
В свою очередь резонанс токов наблюдается в электрической цепи с параллельным соединением участков, содержащих индуктивности и емкости. Один из простейших примеров такой цепи, состоящей из параллельно соединенных элементов r, L и С. В радиотехнике такую цепь называют параллельным колебательным контуром.
При резонансе токов индуктивная проводимость одной части цепи компенсируется емкостной проводимостью другой ее части, параллельно соединенной с первой. В результате реактивная проводимость и реактивная мощность на выводах цепи равны нулю.
Частоты, при которых наблюдается явление резонанса, называются резонансными частотами.
Исследование резонансных режимов в электрических цепях заключается в нахождении резонансных частот,
зависимостей различных величин от частоты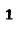
Резонансные цепи очень широко применяются в электротехнике и представляют собой неотъемлемую часть всякого радиотехнического устройства. Изучению явления резонанса, свойств и частотных характеристик простейших резонансных цепей посвящена данная глава.
Последовательный колебательный контур. Резонанс напряжений
Резонансная цепь с последовательным соединением r, L и С (рис. 5-1) является простейшей цепью для изучения явления резонанса напряжений и подробно рассматривается ниже. Комплексное сопротивление такой цепи зависит от частоты:
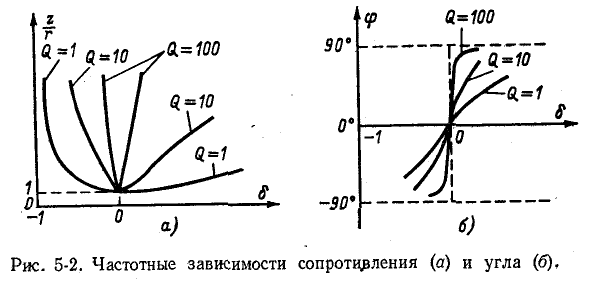
Резонанс напряжений наступает при частоте 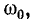
отсюда
Мгновенные энергии выражаются формулами:
Если принять
Поэтому
и
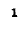
Максимальные значения этих энергий равны друг другу, так как
Это следует и из того, что реактивное сопротивление цепи, содержащей индуктивность и емкость, при любой схеме соединений пропорционально разности максимальных значений энергии, запасаемой в магнитном и электрическом полях:
Поэтому условию резонанса (х = 0) соответствует равенство
Мгновенные значения 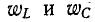
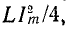
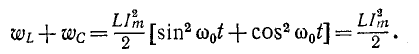
В рассматриваемом случае (резонанс напряжений, рис. 5-1) в цепи не происходит обмена энергии между источником и реактивными элементами цепи, а вся электрическая энергия, поступающая от источника, расходуется в сопротивлении r.
Мы уже встречались с понятием добротности индуктивной катушки 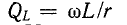
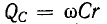
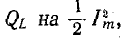
Здесь 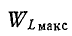
Аналогично рассуждая, т. е. умножив и разделив выражение 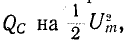
где 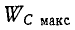
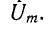
В случае резонансной цепи также пользуются понятием добротности цепи, подразумевая под этим в общем случае величину
здесь 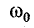
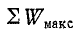
Знак 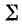
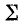
Для схемы рис. 5-1 на основании (5-3) получаем:
где
называется характеристическим (а также волновым) сопротивлением резонансного контура.
Условимся называть относительной расстройкой частоты по отношению к резонансной
частоте контура величину
Сопротивление контура согласно (5-1) и с учетом (5-2) и (5-4)
откуда, используя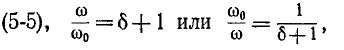
Следовательно, полное сопротивление цепи
и угол
Ток в цепи
При частоте, близкой к резонансной,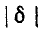
Выражения (5-7) практически достаточно точны при 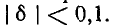
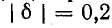
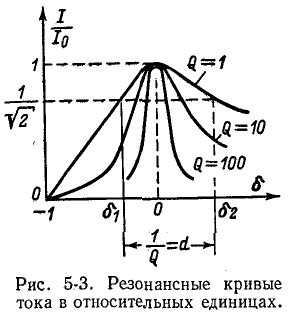
На рис. 5-2 кривые даны в относительных значениях: по оси абсцисс отложена относительная расстройка частоты 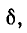
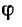
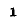
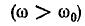
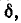
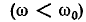
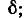
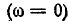
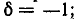
Полное сопротивление цепи минимально при резонансе напряжений при этом ток в цепи достигает своего максимального значения
На рис. 5-3 изображены резонансные кривые тока в относительных значениях: по оси абсцисс, как и на предыдущих графиках, отложены значения 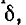
Чем выше добротность цепи Q, тем острее резонансные кривые. Таким образом, величина Q характеризует остроту резонансной кривой («остроту настройки»); согласно (5-3) чем больше отношение максимума энергии поля реактивного элемента к количеству теплоты, рассеиваемой за один период в резонансном контуре, тем острее резонансная кривая.
Резонансные кривые были построены здесь в зависимости от относительной расстройки частоты 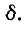
вывести расчетные выражения и построить резонансные кривые в зависимости от 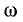
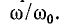
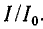
Полосу частот вблизи резонанса, на границах которой ток снижается до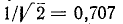
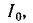
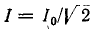
т. е. составляет половину мощности, расходуемой при резонансе. Поэтому полосу пропускания характеризуют как полосу, границы которой соответствуют половине максимальной мощности. На границах полосы пропускания резонансного контура активное и реактивное сопротивления равны 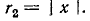
что дает
Соответственно и фазовый сдвиг между напряжением на выводах цепи и током составляет 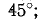
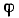
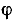
На основании (5-8) условие для границы полосы пропускания записывается в следующем виде:
или
откуда
(знак минус перед корнем, получающийся в результате решения квадратного уравнения, опускается, как не имеющий смысла). Индексы 1 и 2 и соответственно знаки минус и плюс в выражении (5-9) относятся к границам ниже и выше резонанса.
По определению полоса пропускания резонансного контура находится из условия
или
Величина d, обратная добротности контура, называется затуханием контура.
При достаточно высокой добротности резонансного контура 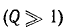
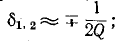
В радиотехнических устройствах к одному из реактивных элементов колебательного контура, например емкости, подключается нагрузка в виде сопротивления 
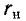
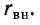
Так как обычно 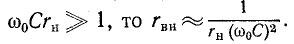
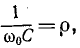
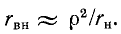
Таким образом, добротность нагруженного контура равна:
а затухание увеличивается на вносимое затухание
Если вносимое сопротивление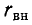
Внутреннее сопротивление источника э. д. с. 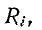
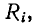
контура. Поэтому с точки зрения сокращения полосы пропускания последовательного колебательного контура выгоден источник напряжения с малым внутренним сопротивлением.
В условиях, близких к резонансу, напряжения на индуктивности и емкости могут быть весьма велики, что необходимо учитывать во избежание повреждения изоляции.
На рис. 5-4 показана векторная диаграмма тока и напряжений при резонансе. Напряжения на реактивных элементах при резонансе определяются из выражения
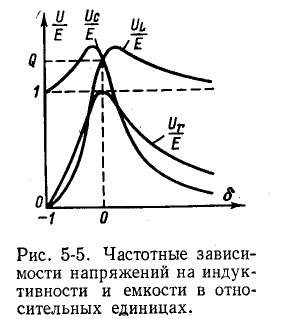
При Q > 1 эти напряжения превышают напряжение U — Е, приложенное к резонансному контуру. Однако значения, получаемые на основании (5-11), не являются максимальными: максимум напряжения 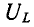
несколько выше (правее), а максимум Uc — ниже (левее) резонансной частоты (рис. 5-5).
Напряжение на индуктивности 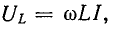
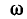
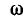
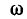
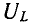
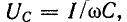
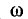
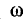
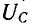
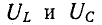
Эго также вытекает из анализа следующих ниже выражений, полученных с учетом (5-5) и (5-6):
и
Напряжение 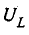
а напряжение
Пренебрегая 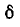
Возвращаясь к определению понятия добротности рассматриваемой резонансной цепи, мы видим, что наряду с формулами (5-3) и (5-4) добротность цепи характеризуется выражениями (5-10) и (5-11), а именно:
Последняя формула показывает, что добротность рассматриваемой цепи определяется как кратность перенапряжения на L и С при резонансной частоте.
Выше была рассмотрена неразветвленная электрическая цепь с последовательно соединенными r, L н С. Для исследования явления резонанса в более сложных разветвленных цепях, где резонанс напряжений может возникать на одной или нескольких частотах, наряду с аналитическим методом расчета, иллюстрированным выше, целесообразно также пользоваться методом геометрических мест.
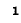
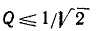
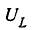
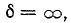
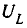
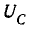
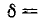

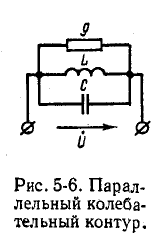
Параллельный колебательный контур и резонанс токов
Явление резонанса токов удобно изучать применительно к электрической цепи с параллельно соединенными r, L и С (рис. 5-6), так как при этом можно непосредственно воспользоваться результатами, полученными в предыдущем параграфе.
Действительно, выражение для комплексной проводимости такой цепи
по своей структуре аналогично выражению (5-1), причем резонансная частота определяется согласно (5-2).
Добротность резонансной цепи на основании (5-3)
По аналогии с предыдущим выражение (5-13) приводится к виду:
Сравнивая полученный результат с (5-6), убеждаемся в том, что выражение Y/g для схемы рис. 5-6 имеет тот же вид, что и выражение 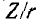
Поэтому кривые рис. 5-2 применимы и в данном случае: кривые рис. 5-2, а выражают зависимость от 6 Отношения y/g, а кривые рис. 5-2, б — зависимость угла —
Кривые рис. 5-2, а показывают, что при резонансе токов полная проводимость цепи минимальна, т. е. входное сопротивление достигает максимума.
При заданном напряжении 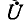
Этот ток достигает минимума при резонансной частоте, так как при этом
Следовательно, отношение. токов 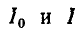
правая часть которого полностью совпадает с (5-8).
В связи с этим резонансные кривые рис. 5-3 выражают применительно к схеме рис. 5-6 зависимость
В случае резонанса токов токи в индуктивном и емкостном элементах схемы рис. 5-6 равны и противоположны по знаку:
Полученное выражение показывает, что добротность рассматриваемой цепи определяется как кратность токов в L и С по отношению к суммарному току
При Q > 1 эти токи превышают
Если параллельный колебательный контур питается от источника тока с внутренним сопротивлением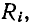
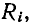
Для схемы рис. 5-6 при резонансе токов остается в силе вывод, сделанный в предыдущем параграфе о непрерывном обмене энергией между индуктивным и емкостным элементами при резонансе напряжений.
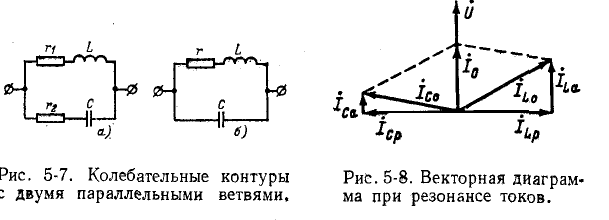
Схема рис. 5-6 является идеализированной, так как она не учитывает активных потерь в ветвях L и С. Поэтому рассмотрим другие схемы,’приняв во внимание активные сопротивления в ветвях L и С (рис. 5-7, а и б).
Условие резонанса токов для схемы рис. 5-7, а записывается в виде равенства реактивных проводимостей:
Откуда
Явление резонанса возможно при этом только в случае, если подкоренное выражение (5-15) имеет положительный
знак или, что то же, величины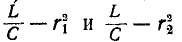
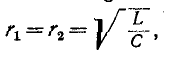
.
На рис. 5-8 показана векторная диаграмма при резонансе токов в цепи рис. 5-7, а. Токи в индуктивной и емкостной ветвях слагаются из активных 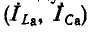
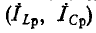
Чем меньше 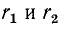
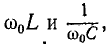
к 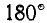
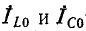
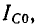
При резонансе вся цепь имеет только активную проводимость
откуда с учетом (5-14)
Для колебательного контура с малыми потерями можно пренебречь слагаемым 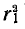
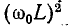
что 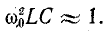
При 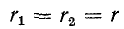
Кроме того, если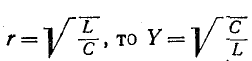
частоте (резонанс в такой цепи называют «безразличным» резонансом).
Легко убедиться в том, что и в. случае резонансной цепи с двумя параллельными ветвями (см. рис. 5-7) соблюдается условие 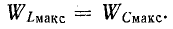
умножить обе части уравнения (5-14) на
Выше отмечалось, что в схеме с параллельно соединенными r, L и С (см. рис. 5-6) полная проводимость всей цепи имеет минимум при резонансной частоте.
Для схемы рис. 5-7, б нетрудно показать, что при изменении частоты о) или индуктивности L минимум полной проводимости цепи, а также минимум общего тока наступают не при резонансной частоте. В том же случае, когда переменным параметром является емкость С, проводимость и общий ток достигают минимума при резонансе токов.
Добротность параллельного колебательного контура рис. на основании (5-3) равна:
но
откуда
где резонансная частота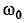
Часто в ветви с емкостью сопротивлением 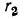
Рассмотрим этот случай (см. рис. 5-7, б).
Резонанасная частота такого контура согласно (5-15)
а добротность цепи в соответствии с полученным выше выражением
Из сопоставления (5-16) и (5-2) видно, что при одних и тех же параметрах r, L и С резонансные частоты для схем рис. 5-1 и 5-7, б отличаются множителем
При 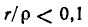
Общее сопротивление колебательного контура (см. рис, 5-7, б)
На основании соотношений (5-16) и (5-17) можно получить:
Учитывая также соотношения
получаем выражение для сопротивления колебательного контура:
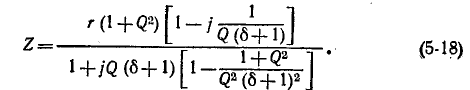
При резонансной частоте
В тех случаях, когда 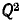
В режиме, близком к резонансу, когда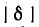
При высокой добротности колебательного контура
Приэтом токи в ветвях
Здесь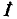
Напряжение на выводах цепи 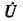
Приближенные выражения (5-19) и (5-20) аналогичны при заданном Q выражениям(5-12) и (5-7), выведенным для цепи рис. 5-1, при условии замены напряжений токами и обратно. Поэтому кривые сопротивлений, токов и напряжений, соответствующие схеме рис. 5-1, в известном масштабе приближенно выражают проводимости, напряжения и токи в схеме рис. 5-7, б.
Следует обратить внимание на то, что в схеме рис. 5-6 мгновенная мощность в цепи при резонансе токов равна мгновенной мощности, расходуемой в сопротивлении r; в схемах с двумя параллельными ветвями (рис. 5-7) мгновенная мощность на выводах цепи отлична от мгновенной мощности, расходуемой в сопротивлениях ветвей. Например, в тот момент, когда ток, входящий в цепь, проходит через нулевое значение, мгновенная мощность на выводах цепи равна нулю; в этот момент токи в ветвях, сдвинутые по фазе относительно суммарного тока цепи, отличны от нуля и поэтому мгновенная мощность, расходуемая в сопротивлениях ветвей, также не равна нулю. Объясняется это тем, что в схемах ~рис. 5-7, а и б энергия, накапливаемая реактивными элементами, периодически преобразуется частично в теплоту (в сопротивлениях ветвей), а затем вновь пополняется за счет энергии источника.
Для повышения крутизны резонансных характеристик, необходимой для более четкого разделения колебаний разных частот, в радиотехнике широко применяются двухконтурные резонансные цепи: два резонансных контура, настроенных каждый в отдельности на одну и ту же частоту, связываются индуктивно или электрически. В отличие от «одногорбой» резонансной кривой одиночного контура в связанных цепях получаются «двугорбые» кривые; например, ток в каждом контуре может иметь максимумы при двух частотах, расположенных ниже и выше резонансной частоты одиночного контура.
Частотные характеристики сопротивлений и проводимостей реактивных двухполюсников
Двухполюсником называется любая электрическая цепь или часть электрической цепи, имеющая два вывода. Ниже рассматриваются только линейные двухполюсники, т. е. такие, которые состоят из линейных элементов.
Различают двухполюсники активные и пассивные.
Активным называется двухполюсник, содержащий источники электрической энергии, которые не компенсируются взаимно внутри двухполюсника.
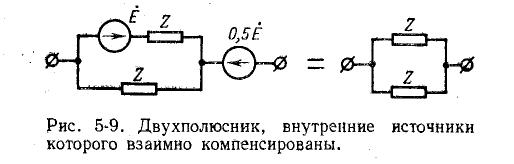
Пассивным называется двухполюсник, не содержащий источников электрической энергии; в случае линейного двухполюсника он может содержать источники электрической энергии, взаимно компенсирующиеся таким образом, что напряжение на его разомкнутых выводах равно нулю. Такой линейный двухполюсник относится к категории пассивных; его сопротивление, измеренное на выводах, не изменится, если источники электрической энергии внутри него заменить пассивными элементами — внутренними сопротивлениями источников э. д. с. или соответственно внутренними проводимостями источников тока. Пример двухполюсника, содержащего компенсированные источники, показан на рис. 5-9.
По числу элементов, входящих в двухполюсник, различают одноэлементный, двухэлементный и многоэлементный двухполюсники.
По характеру этих элементов двухполюсники делятся на реактивные, т. е. состоящие из индуктивностей и емкостей, и двухполюсники с потерями, содержащие активные сопротивления. Реактивные двухполюсники представляют собой идеализированные электрические системы, приближающиеся по своим свойствам к физически существующим цепям с малыми потерями.
Частотные характеристики сопротивлений или проводимостей двухполюсников, образующих электрическую цепь, предопределяют частотные и резонансные свойства цепи, т. е. зависимости амплитуд и фаз токов и напряжений от частоты.
Настоящий параграф посвящен изучению частотных характеристик пассивных реактивных двухполюсников.
Одноэлементные реактивные двухполюсники
Индуктивность и емкость представляют собой простейшие одноэлементные реактивные двухполюсники. Знак комплексного сопротивления и комплексной проводимости каждого из этих двухполюсников не зависит от частоты; этим они существенно отличаются от других, более сложных реактивных двухполюсников, содержащих неоднородные реактивные элементы, т. е. индуктивность и емкость в разных сочетаниях.
Комплексное сопротивление индуктивного элемента во всем спектре частот имеет положительный знак, а комплексная проводимость — отрицательный:
Комплексное сопротивление емкостного элемента во всем спектре частот имеет отрицательный знак, а комплексная проводимость — положительный:
В рассматриваемом случае реактивных двухполюсников комплексные сопротивления и проводимости являются мнимыми. Поэтому для сохранения знаков частотные ха-рактернстнкн сопротивлений и проводимостей удобно рисовать в прямоугольной системе координат, в которой вверх откладываются мнимые величины со знаком плюс, а вниз — со знаком минус.
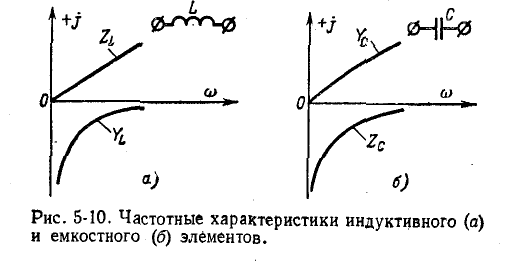
Частотные характеристики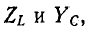
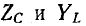
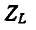
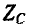
Следует заметить, что как сопротивления, так и проводимости рассматриваемых здесь одноэлементных реактивных двухполюсников возрастают (с учетом знака) по мере повышения частоты, т. е.
Это является общим свойством всех реактивных двухполюсников, а не только одноэлементных.
Двухполюсник, состоящий из последовательно или параллельно соединенных однородных элементов (индуктивностей или емкостей), относится к числу одноэлементных двухполюсников, так как последовательно или параллельно соединенные однородные элементы могут быть заменены одним эквивалентным реактивным элементом того же характера.
Двухэлементные реактивные двухполюсники
Двухэлементные двухполюсники, составленные из индуктивности и емкости, представляют собой простейшие резонансные цепи.
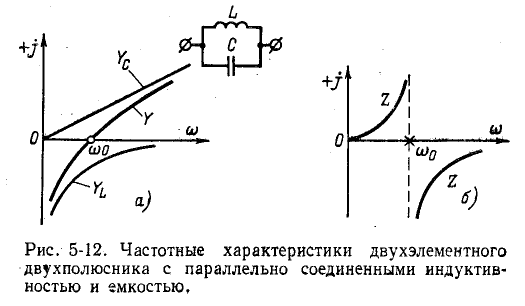
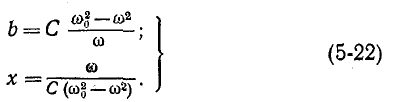
При последовательном соединении индуктивности и емкости алгебраически складываются комплексные сопротивления. На рис. 5-11, а жирной линией показана частотная характеристика двухполюсника, полученная в результате графического сложения кривых 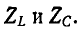
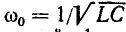
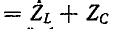
Частотная характеристика проводимости того же двухполюсника представляет собой функцию, обратную сопротивлению:
Кривая Y показана на рис. 5-11, б.
При резонансной частоте проводимость рассматриваемого двухполюсника обращается в бесконечность; эта точка носит название полюса функции Y и обозначается на чертеже крестиком
Частотные характеристики Z и Y, построенные таким образом1, соответствуют уравнениям:
и
или с учетом(5-2):
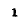
В области частот ниже резонансной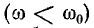
В области частот выше резонансной
При параллельном соединении индуктивности и емкости алгебраически складываются их комплексные проводимости. На рис. 5-12, а жирной линией показана частотная
характеристика двухполюсника, полученная в результате графического сложения
Частотная характеристика сопротивления того же двухполюсника представляет собой функцию, обратную проводимости: Z — 1/Y. Кривая Z показана на рис. 5-12, б.
Частота, при которой характеристика Y пересекает ось абсцисс (нуль функции У), а характеристика Z уходит в бесконечность (полюс функции Z), является резонансной частотой (резонанс токов).
Частотные характеристики, построенные на рис. 5-12, соответствуют уравнениям:
И
или с учетом (5-22)
В области частот ниже резонансной проводимость индуктивного элемента перекомпенсирует проводимость емкостного элемента и сопротивление двухполюсника получается, индуктивным. В области частот выше резонансной наблюдается обратное явление и сопротивление двухполюсника имеет емкостный характер.
Таким образом, в зависимости от частоты двухэлементный реактивный двухполюсник может иметь либо индуктивное, либо емкостное сопротивление. При этом, так же как и в случае одноэлементного реактивного двухполюсника, кривые Z и Y возрастают, т. е. производные от 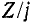
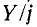
В отличие от сопротивлений одноэлементных двухполюсников, которые выражаются только через текущую частоту, сопротивления двухэлементных реактивных двухполюсников зависят также и от разности квадратов резонансной и текущей частот (формулы (5-21) и (5-22)1.
Как видно из выражений (5-21), для построения частотных характеристик двухполюсника, состоящего из последовательно соединенных элементов L и С, достаточно знать нуль функции Z или, что то же, полюс функции Y. Параметр L, входящий в (5-21), влияет только на выбор масштаба Z и Y по оси ординат.
Аналогично в соответствии с (5-22) для построения частотных характеристик двухполюсника, состоящего из параллельно соединенных элементов L и С, достаточно знать полюс Z или, что то же, нуль Y, причем параметр С влияет только на масштаб Z и Y.
Двухполюсники, имеющие одинаковые частотные характеристики Z или Y, эквивалентны.
Многоэлементный реактивный двухполюсник
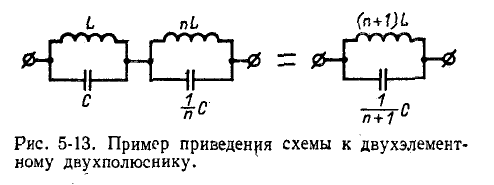
Многоэлементный реактивный двухполюсник может быть получен в результате различных сочетаний одноэлементных и двухэлементных двухполюсников. Пользуясь частотными характеристиками, приведенными выше, можно построить частотные характеристики для трех-, четырех- и много-элементных реактивных двухполюсников. При этом одно-
родные элементы (или группы элементов с одинаковыми резонансными частотами), соединенные параллельно или последовательно, должны быть сначала заменены одним элементом (или эквивалентной группой элементов, как это, например, показано на рис. 5-13).
Такие двухполюсники будем называть «приведенными».
Из свойства положительности производной 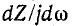
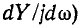
В общем случае, если при 
В противном случае порядок расположения резонансов обратный: первым наступает резонанс напряжений, вторым — резонанс токов и т. д.
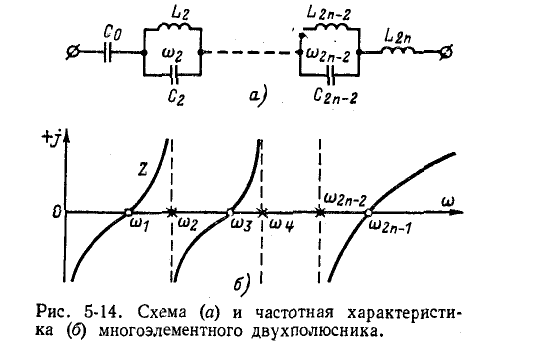
На рис. 5-14, а дана схема многоэлементного двухполюсника, а на рис. 5-14, б — соответствующая ему частотная характеристика сопротивления.
У реактивных двухполюсников сумма чисел полюсов и нулей (не считая точек 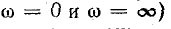
Расположение нулей и полюсов, как указывалось выше, поочередное, а все ветви частотной характеристики с увеличением 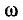
- Соединение звездой и треугольником в трехфазных цепях
- Принцип действия асинхронного и синхронного двигателей
- Метод симметричных составляющих
- Цепи периодического несинусоидального тока
- Расчет неразветвленной однородной магнитной цепи
- Энергия магнитного поля
- Синусоидальные Э.Д.С. и ток
- Электрические цепи с взаимной индуктивностью
Резонансные явления наблюдаются в колебательных системах, когда частота собственных колебаний элементов системы совпадает с частотой внешних (вынужденных) колебательных процессов. Данное утверждение справедливо и для цепей с циркулирующим переменным током. В таких электрических цепях при наличии определённых условий возникает резонанс напряжений, что влияет на параметры тока. Явление резонанса в электротехнике может быть полезным или вредным, в зависимости от ситуации, в которой происходит процесс.
Описание явления
Если в некой электрической цепи (см. рис. 1) имеются ёмкостные и индуктивные элементы, которые обладают собственными резонансными частотами, то при совпадении этих частот амплитуда колебаний резко возрастёт. То есть происходит резкий всплеск напряжений на этих элементах. Это может вызвать разрушение элементов электрической цепи.
Давайте рассмотрим на этом примере, какие явления будут происходить при подключении генератора переменного тока к контактам схемы. Заметим, что катушки и конденсаторы обладают свойствами, которые можно сравнить с аналогом реактивного резистора. В частности, дроссель в электрической цепи создаёт индуктивное сопротивление. Конденсатор является причиной ёмкостного сопротивления.
Индуктивный элемент вызывает сдвиг фаз, характеризующийся отставанием тока от напряжения на ¼ периода. Под действием конденсатора ток, наоборот, на ¼ периода опережает напряжение.
Другими словами, действие индуктивности противоположно действию на сдвиг фаз ёмкостного сопротивления. То есть катушки индуктивности и ёмкостные элементы по-разному воздействуют на генератор и по-своему корректируют фазовые соотношения между электрическим током и напряжением.
Формула
Общее реактивное сопротивление рассматриваемых нами элементов равно сумме сопротивлений каждого из них. С учётом противоположности действий можно записать: Xобщ = XL — Xc , где XL = ωL — индуктивное реактивное сопротивление, выражение Xc = 1/ωC — это ёмкостное реактивное сопротивление.
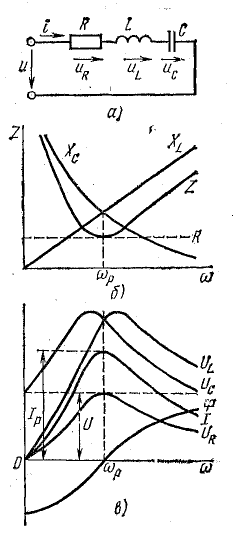
На рисунке 2 изображены графики зависимости полного сопротивления цепи и связанной с ним силы тока, от реактивного сопротивления индуктивного элемента. Обратите внимание на то, как падает полное сопротивление при уменьшении реактивной сопротивляемости RL (график б) и как при этом возрастает ток (график в).
Электрические цепи, состоящие из последовательно соединённых конденсаторов, пассивный резисторов и катушек индуктивности называют последовательными резонансными (колебательными) контурами (см. рис. 2). Существуют также параллельные контуры, в которых R, L, C элементы подключены параллельно (рис. 3).
В режиме резонанса мощность источника питания будет рассеиваться только на активных сопротивлениях (в том числе на активном сопротивлении катушки). Для резонансных контуров характерны потери только активной мощности, которая израсходуется на поддержание колебательного процесса. Реактивная мощность на L C — элементах при этом не расходуется. Ток в резонансном режиме принимает максимальное значение:
Величину Q принято называть термином «Добротность контура». Данный параметр показывает, во сколько раз напряжение, возникшее на контактах реактивных элементов, превышает входное напряжение U электрической сети. Для описания соотношения выходного и входного напряжений часто применяют коэффициент K. При резонансе:
K = Uвых / Uвх = UC0 / U = Q
Формулировка
На основании вышеописанных явлений, сформулируем определение резонансного напряжения: «Если общее падение напряжения на ёмкостно-индуктивных элементах равно нулю, а амплитуда тока – максимальна, то такое особое состояние системы называется резонансом напряжений». Для лучшего понимания явления, немного перефразируем определение: резонансом напряжений является состояние, когда напряжение на CL — цепочке больше чем на входе электрической цепи.
Описанное явление довольно распространено в электротехнике. Иногда с ним борются, а иногда специально создают условия для образования резонанса. Основными характеристиками всякого резонансного контура являются параметры добротности и частоты [ 1 ].
В случае, если XL = Xc – справедливо равенство: ωL = 1/ωC , отсюда получаем:
Если ω = ω0 – возникает резонанс напряжений. Частоты совпадают в том случае, когда индуктивное сопротивление сравняется с ёмкостным сопротивлением конденсатора. В таких случаях в цепи будет действовать только активное сопротивление R. Наличие реактивных элементов в схеме приводит к увеличению полного сопротивления цепи (Z):
где R – общее активное сопротивление.
Учитывая, что по закону Ома U = I/Z, можно утверждать, что общее напряжение в цепи зависит, в том числе, и от слагаемых индуктивного и ёмкостного сопротивлений.
Если бы в рассматриваемой схеме (рис. 1) отсутствовало активное сопротивление R, то значение полного сопротивления Z стремилось бы к 0. Следовательно, напряжение на реактивных элементах при этом возрастает до критического уровня.
Поскольку XL и Xc зависят от частоты входного напряжения, то для возникновения резонанса следует подобрать соответствующую частоту сети, или изменять параметры катушки, либо конденсатора до тех пор, пока резонансные частоты не совпадут. Любое нарушение условий резонанса немедленно приводит к выходу системы из резонансного режима с последующим падением напряжения.
Условия наступления
Резонансные явления наступают только при наличии следующих условий:
- Наличие минимального активного сопротивления на участке электрической цепи.
- Равенство реактивных сопротивлений, возникших на цепочке LC.
- Совпадение входной частоты источника питания с резонансной частотой колебательного контура.
При резонансе в контуре напряжения на его элементах могут повышаться на порядок и больше.
Примеры применения на практике
Классическим примером применения резонанса колебательных контуров является настройка радиоприёмника на частоту соответствующей радиостанции. В качестве рабочего элемента настроечного узла используется конденсатор с регулируемой ёмкостью. Вращение ручки настройки изменяет ёмкость конденсатора, а значит и резонансную частоту контура.
В момент совпадения резонансной частоты с рабочей частотой какой-либо радиостанции возникает резонанс напряжений, в результате которого резко возрастает амплитуда колебаний принятой радиоприёмником частоты. Специальные фильтры отделяют эти колебания от несущих радиочастот, а усилители усиливают полученные сигналы. В динамике появляются звуки, генерируемые передатчиком радиостанции.
Колебательные контуры, построенные на принципе последовательного соединения LC-элементов, применяются в цепях питания высокоомных нагрузок, потребляющих токи повышенного напряжения. Такие же устройства применяют в полосовых фильтрах.
Последовательный резонанс применяют при пониженных напряжениях сети. В этом случае используют реактивную энергию обмоток трансформатора, соединённых последовательно.
Конденсаторы и различные катушки индуктивности (рис. 5) входят в конструкцию практически всех аналоговых устройств. Они используются для настройки фильтров или для управления токами в отдельных узлах.
Важно знать, что резонансные контуры не увеличивают количество электрической энергии в цепях. Они лишь могут повышать напряжения, иногда до опасных значений. Постоянный ток не причиной резонансных явлений.
Наряду с полезными свойствами резонансных явлений, в практической электротехнике часто возникают ситуации, когда резонанс напряжений приносит вред. В основном это связано с нежелательным повышением параметров тока на участках цепей. Примером могут служить опасное резонансные явления в кабельных линиях без нагрузки, что может привести к пробоям изоляции. Чтобы этого не случилось, на концевых участках таких линий устанавливают балластные нагрузочные элементы.