Как понять, почему «плюс» на «минус» дает «минус» ?
Слушая учителя математики, большинство учеников воспринимают материал как аксиому. При этом мало кто пытается добраться до сути и разобраться, почему «минус» на «плюс» дает знак «минус», а при умножении двух отрицательных чисел выходит положительное.
Законы математики
Большинство взрослых не в силах объяснить ни себе, ни своим детям, почему так получается. Они твердо усвоили этот материал в школе, но при этом даже не попытались выяснить, откуда взялись такие правила. А зря. Зачастую современные дети не столь доверчивы, им необходимо докопаться до самой сути и понять, скажем, почему «плюс» на «минус» дает «минус». А иногда сорванцы специально задают каверзные вопросы, дабы насладиться моментом, когда взрослые не могут дать вразумительного ответа. И совсем уж беда, если впросак попадает молодой учитель.
Для объяснения правильности этого закона математики, необходимо сформулировать аксиомы кольца. Но для начала следует понять, что это такое. В математике кольцом принято называть множество, в котором задействованы две операции с двумя элементами. Но разбираться с этим лучше на примере.
Аксиома кольца
Существует несколько математических законов.
- Первый из них переместительный, согласно ему, C + V = V + C.
- Второй называется сочетательным (V + C) + D = V + (C + D).
Им же подчиняется и умножение (V х C) х D = V х (C х D).
Никто не отменял и правил, по которым открываются скобки (V + C) х D = V х D + C х D, также верно, что C х (V + D) = C х V + C х D.
Кроме того, установлено, что в кольцо можно ввести специальный, нейтральный по сложению элемент, при использовании которого будет верно следующее: C + 0 = C. Кроме того, для каждого C есть противоположный элемент, который можно обозначить, как (-C). При этом C + (-C) = 0.
Выведение аксиом для отрицательных чисел
Приняв приведенные выше утверждения, можно ответить на вопрос: «»Плюс» на «минус» дает какой знак?» Зная аксиому про умножение отрицательных чисел, необходимо подтвердить, что действительно (-C) х V = -(C х V). А также, что верно такое равенство: (-(-C)) = C.
Для этого придется вначале доказать, что у каждого из элементов существует лишь один ему противоположный «собрат». Рассмотрим следующий пример доказательства. Давайте попробуем представить, что для C противоположными являются два числа — V и D. Из этого следует, что C + V = 0 и C + D = 0, то есть C + V = 0 = C + D. Вспоминая о переместительных законах и о свойствах числа 0, можно рассмотреть сумму всех трех чисел: C, V и D. Попробуем выяснить значение V. Логично, что V = V + 0 = V + (C + D) = V + C + D, ведь значение C + D, как было принято выше, равняется 0. Значит, V = V + C + D.
Точно так же выводится и значение для D: D = V + C + D = (V + C) + D = 0 + D = D. Исходя из этого, становится ясно, что V = D.
Для того чтобы понять, почему все же «плюс» на «минус» дает «минус», необходимо разобраться со следующим. Так, для элемента (-C) противоположными являются C и (-(-C)), то есть между собой они равны.
Тогда очевидно, что 0 х V = (C + (-C)) х V = C х V + (-C) х V. Из этого следует, что C х V противоположно (-)C х V, значит, (-C) х V = -(C х V).
Для полной математической строгости необходимо еще подтвердить, что 0 х V = 0 для любого элемента. Если следовать логике, то 0 х V = (0 + 0) х V = 0 х V + 0 х V. А это значит, что прибавление произведения 0 х V никак не меняет установленную сумму. Ведь это произведение равняется нулю.
Зная все эти аксиомы, можно вывести не только, сколько «плюс» на «минус» дает, но и что получается при умножении отрицательных чисел.
Умножение и деление двух чисел со знаком «-»
Если не углубляться в математические нюансы, то можно попробовать более простым способом объяснить правила действий с отрицательными числами.
Допустим, что C — (-V) = D, исходя из этого, C = D + (-V), то есть C = D — V. Переносим V и получаем, что C + V = D. То есть C + V = C — (-V). Этот пример объясняет, почему в выражении, где идут два «минуса» подряд, упомянутые знаки следует поменять на «плюс». Теперь разберемся с умножением.
(-C) х (-V) = D, в выражение можно добавить и вычесть два одинаковых произведения, которые не поменяют его значения: (-C) х (-V) + (C х V) — (C х V) = D.
Вспомная о правилах работы со скобками, получаем:
1) (-C) х (-V) + (C х V) + (-C) х V = D;
2) (-C) х ((-V) + V) + C х V = D;
3) (-C) х 0 + C х V = D;
Из этого следует, что C х V = (-C) х (-V).
Аналогично можно доказать, что и в результате деления двух отрицательных чисел выйдет положительное.
Общие математические правила
Конечно, такое объяснение не подойдет для школьников младших классов, которые только начинают учить абстрактные отрицательные числа. Им лучше объяснять на видимых предметах, манипулируя знакомым им термином зазеркалья. Например, придуманные, но не существующие игрушки находятся именно там. Их и можно отобразить со знаком «-». Умножение двух зазеркальных объектов переносит их в еще один мир, который приравнивается к настоящему, то есть в результате мы имеем положительные числа. А вот умножение абстрактного отрицательного числа на положительное лишь дает знакомый всем результат. Ведь «плюс» умножить на «минус» дает «минус». Правда, в младшем школьном возрасте дети не слишком-то пытаются вникнуть во все математические нюансы.
Хотя, если смотреть правде в глаза, для многих людей даже с высшим образованием так и остаются загадкой многие правила. Все принимают как данность то, что преподают им учителя, не затрудняясь вникать во все сложности, которые таит в себе математика. «Минус» на «минус» дает «плюс» – об этом знают все без исключения. Это верно как для целых, так и для дробных чисел.
Решение простых линейных уравнений
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие уравнения
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.
Например, возьмем выражение 2 + 4 = 6. При вычислении левой части получается верное числовое равенство, то есть 6 = 6.
Уравнением можно назвать выражение 2 + x = 6, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Корень уравнения — то самое число, которое при подстановке на место неизвестной уравнивает выражения справа и слева.
Решить уравнение значит найти все возможные корни или убедиться, что их нет.
Решить уравнение с двумя, тремя и более переменными — это два, три и более значения переменных, которые обращают данное выражение в верное числовое равенство.
Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.
Какие бывают виды уравнений
Уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные.
Особенность преобразований алгебраических уравнений в том, что в левой части должен остаться многочлен от неизвестных, а в правой — нуль.
| Линейное уравнение выглядит так | ах + b = 0, где a и b — действительные числа.
Что поможет в решении:
|
|---|---|
| Квадратное уравнение выглядит так: | ax 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0. |
Числовой коэффициент — число, которое стоит при неизвестной переменной.
Кроме линейных и квадратных есть и другие виды уравнений, с которыми мы познакомимся в следующий раз:
Онлайн-курсы по математике за 7 класс помогут закрепить новые знания на практике с талантливым преподавателем.
Как решать простые уравнения
Чтобы научиться решать простые линейные уравнения, нужно запомнить формулу и два основных правила.
1. Правило переноса. При переносе из одной части в другую, член уравнения меняет свой знак на противоположный.
Для примера рассмотрим простейшее уравнение: x+3=5
Начнем с того, что в каждом уравнении есть левая и правая часть.
Перенесем 3 из левой части в правую и меняем знак на противоположный.
Можно проверить: 2 + 3 = 5. Все верно. Корень равен 2.
Решим еще один пример: 6x = 5x + 10.
Перенесем 5x из правой части в левую. Знак меняем на противоположный, то есть на минус.
Приведем подобные и завершим решение.
2. Правило деления. В любом уравнении можно разделить левую и правую часть на одно и то же число. Это может ускорить процесс решения. Главное — быть внимательным, чтобы не допустить глупых ошибок.
Применим правило при решении примера: 4x=8.
При неизвестной х стоит числовой коэффициент — 4. Их объединяет действие — умножение.
Чтобы решить уравнение, нужно сделать так, чтобы при неизвестной x стояла единица.
Разделим каждую часть на 4. Как это выглядит:
Теперь сократим дроби, которые у нас получились и завершим решение линейного уравнения:
Рассмотрим пример, когда неизвестная переменная стоит со знаком минус: −4x = 12
- Разделим обе части на −4, чтобы коэффициент при неизвестной стал равен единице.
−4x = 12 | : (−4)
x = −3
Если знак минус стоит перед скобками, и по ходу вычислений его убрали — важно не забыть поменять знаки внутри скобок на противоположные. Этот простой факт позволит не допустить обидные ошибки, особенно в старших классах.
Напомним, что не у каждого линейного уравнения есть решение — иногда корней просто нет. Изредка среди корней может оказаться ноль — ничего страшного, это не значит, что ход решения оказался неправильным. Ноль — такое же число, как и остальные.
Способов решения линейных уравнений немного, нужно запомнить только один алгоритм, который будет эффективен для любой задачки.
| Алгоритм решения простого линейного уравнения |
|---|
|
Чтобы быстрее запомнить ход решения и формулу линейного уравнения, скачайте или распечатайте алгоритм — храните его в телефоне, учебнике или на рабочем столе.
Примеры линейных уравнений
Теперь мы знаем, как решать линейные уравнения. Осталось попрактиковаться на задачках, чтобы чувствовать себя увереннее на контрольных. Давайте решать вместе!
Пример 1. Как правильно решить уравнение: 6х + 1 = 19.
- Перенести 1 из левой части в правую со знаком минус.
Разделить обе части на множитель, стоящий перед переменной х, то есть на 6.
Пример 2. Как решить уравнение: 5(х − 3) + 2 = 3 (х − 4) + 2х − 1.
5х − 15 + 2 = 3х − 12 + 2х − 1
Сгруппировать в левой части члены с неизвестными, а в правой — свободные члены. Не забываем при переносе из одной части уравнения в другую поменять знаки на противоположные у переносимых членов.
5х − 3х − 2х = −12 − 1 + 15 − 2
Приведем подобные члены.
Ответ: х — любое число.
Пример 3. Решить: 4х = 1/8.
- Разделим обе части уравнения на множитель стоящий перед переменной х, то есть на 4.
Пример 4. Решить: 4(х + 2) = 6 − 7х.
- 4х + 8 = 6 − 7х
- 4х + 7х = 6 − 8
- 11х = −2
- х = −2 : 11
- х = −2/11
Ответ: −2/11 или −(0,18). О десятичных дробях можно почитать в другой нашей статье.
Пример 5. Решить:
- 3(3х — 4) = 4 · 7х + 24
- 9х — 12 = 28х + 24
- 9х — 28х = 24 + 12
- -19х = 36
- х = 36 : (-19)
- х = — 36/19
Пример 6. Как решить линейное уравнение: х + 7 = х + 4.
5х — 15 + 2 = 3х — 2 + 2х — 1
Сгруппировать в левой части неизвестные члены, в правой — свободные члены:
Приведем подобные члены.
Ответ: нет решений.
Пример 7. Решить: 2(х + 3) = 5 − 7х.
Правила знаков
Минус и плюс – это признаки отрицательных и положительных чисел в математике. Они по-разному взаимодействую с собой, поэтому при выполнении каких-либо действий с числами, например, деление, умножение, вычитание, сложение и т.д., необходимо учитывать правила знаков. Без этих правил вы никогда не сможете решить даже самую простую алгебраическую или геометрическую задачу. Без знания этих правил, вы не сможете изучить не только математику, но и физику, химию, биологию, и даже географию.
Рассмотрим подробней основные правила знаков.
Деление.
Если мы делим «плюс» на «минус», то получаем всегда «минус». Если мы делим «минус» на «плюс», то получаем всегда также «минус». Если мы делим «плюс» на «плюс», то получаем «плюс». Если же мы делим «минус» на «минус», то получим, как ни странно, также «плюс».
Умножение.
Если мы умножаем «минус» на «плюс», то получаем всегда «минус». Если мы умножаем «плюс» на «минус», то получаем всегда также «минус». Если мы умножаем «плюс» на «плюс», то получаем положительно число, то есть «плюс». Тоже самое касается и двух отрицательных чисел. Если мы умножаем «минус» на «минус», то получим «плюс».
Вычитание и сложение.
Они базируются уже на других принципах. Если отрицательное число будет больше по модулю, чем наше положительное, то результат, конечно же, будет отрицательный. Наверняка, вам интересно, что же такое модуль и зачем он тут вообще. Все очень просто. Модуль – это значение числа, но без знака. Например -7 и 3. По модулю -7 будет просто 7 , а 3 так и останется 3. В итоге мы видим, что 7 больше, то есть выходит, что наше отрицательное число больше. Вот и выйдет -7+3 = -4. Можно сделать еще проще. Просто на первое место ставить положительное число, и выйдет 3-7 = -4, возможно кому-то так более понятно. Вычитание действуют полностью по такому же принципу.
источники:
http://skysmart.ru/articles/mathematic/reshenie-prostyh-linejnyh-uravnenij
http://mateshka.ru/math/arithmetic/pravila-znakov.html
Реле и его использование в автосигнализациях
Как сделать из «минуса» «плюс» и наоборот? Как подцепиться к электроприводу? Как открыть багажник с брелока сигнализации? Как заблокировать запуск двигателя? На все эти вопросы есть ответ: с помощью реле.
Зная, как работает реле, Вы сможете осуществить различные схемы подключения к электропроводке автомобиля.
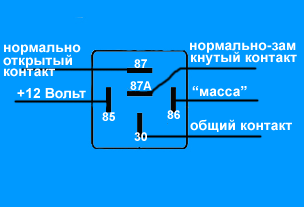
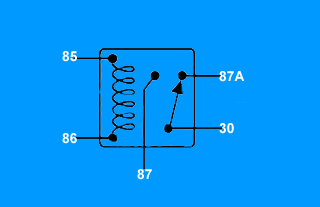
Обычно реле имеет 5 контактов (бывают и 4-хконтактные и 7-ми и т.д.). Если Вы посмотрите на реле внимательно, то увидите, что все контакты подписаны. Каждый контакт имеет своё обозначение. 30, 85, 86, 87 и 87А. На рисунке видно где, какой контакт.
Контакты 85 и 86 — это катушка. Контакт 30 — общий контакт, контакт 87А — нормально-замкнутый контакт, контакт 87 — нормально-разомкнутый контакт.
В состоянии покоя, т.е., когда на катушке нет питания, контакт 30 замкнут с контактом 87А. При одновременной подаче питания на контакты 85 и 86 (на один контакт «плюс» на другой — «минус», без разницы куда что) катушка «возбуждается», то есть срабатывает. Тогда контакт 30 отмыкается от контакта 87А и соединяется с контактом 87. Вот и весь принцип действия. Вроде бы ничего сложного.
Реле часто приходит на выручку во время установки дополнительного оборудования. Давайте рассмотрим простейшие примеры применения реле.
Блокировка двигателя
В качестве блокируемой цепи может быть что угодно, лишь бы машина не заводилась при разорванной цепи (стартер, зажигание, бензонасос, питание форсунок и т.д.).
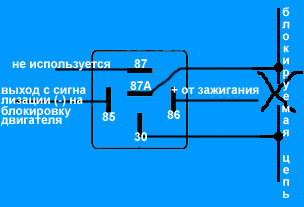
Один контакт питания катушки (пусть 85) соединяем с проводом сигнализации, на котором появляется «минус» при постановке в охрану. На другой контакт катушки (пусть 86) подаём +12 Вольт при включении зажигания. Контакты 30 и 87А подцепляем в разрыв блокируемой цепи. Теперь, если попытаться завести автомобиль при включенной охране, контакт 30 разомкнётся с контактом 87А и не даст завести двигатель.
Эта схема используется, если у вас «минус» с сигнализации на блокировку выходит при постановке в охрану. Если у вас «минус» с сигнализации на блокировку выходит при снятии с охраны, тогда вместо контакта 87А используем контакт 87, т.е. разрыв цепи теперь будет на контактах 87 и 30. При таком подключении реле будет всегда в рабочем состоянии (разомкнутом) при работающем двигателе.
Инвертируем полярность сигнала (с «минуса» делаем «плюс» и наоборот) и подключаемся к слаботочным транзисторным выходам сигнализации
Допустим, нам надо получить «минус», но у нас есть только «плюсовой» сигнал (например, у автомобиля положительные концевики, а у сигнализации нет входа положительных концевиков, а есть только вход отрицательных). На помощь опять приходит реле.
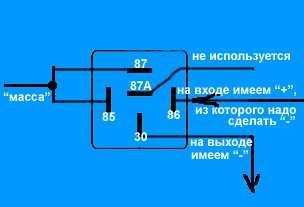
Подаём на один из контактов катушки (86) наш «плюс» (с концевиков автомобиля). На другой контакт катушки (85) и на контакт 87 подаём «минус». В итоге на выходе (контакт 30) получаем нужный нам «минус».
Если нам надо, наоборот, из «минуса» получить «плюс», то маленько меняем подключение. На контакт 86 подаём исходный «минус», а на контакты 85 и 87 подаём «плюс». В итоге на выходе (контакт 30) получаем нужный нам «плюс».
Если нам надо из слаботочного отрицательного выхода сигнализации (в сигнализации такие выходы могут называться по-разному и их назначение тоже различное: выход на 3-е зажигание, выход на открытие багажника, выход на закрытие стёкол и т.д.) сделать хороший мощный «минус» или «плюс», то тоже используем эту схему.
На контакт 85 подаём выход с сигнализации. На контакт 86 подаём «плюс». На контакт 87 подаём сигнал той полярности, который нам надо получить на выходе. В итоге на контакте 30 мы имеем ту полярность, которая на контакте 87.
Открытие багажника с брелока автосигнализации
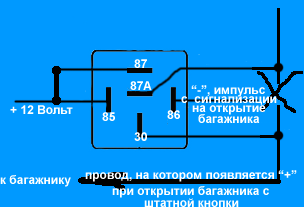
Если в автомобиле стоит электрический привод багажника, то можно подключиться к нему автосигнализацией для открытия его с брелока сигнализации. Если с сигнализации выходит слаботочный сигнал на открытие багажника (а чаще всего так и есть), то используем эту схему.
Прежде всего, находим провод на привод багажник, где появляется +12 Вольт при открытии багажника. Разрезаем этот провод. Тот конец разрезанного провода, который идёт к приводу, подцепляем к контакту 30. Другой конец провода подцепляем к контакту 87А. Выход с сигнализации подцепляем к контакту 86. Контакты 87 и 85 подцепляем на +12 Вольт.
Теперь, при подаче сигнала с сигнализации на открытие багажника, реле сработает и на провод электропривода багажника пойдёт «плюс». Привод сработает, и багажник откроется.
Это лишь немногие схемы подключения с использованием реле. Ещё немного схем с использованием реле можете найти на сайте в категории схемы хитрушек и в разделе схемы подключения к центральному замку.
Источник
Как из плюса сделать минус через реле
_________________
+7911 200 -2820 11-17 мск
» Можно я лягу?»(C)
JLCPCB, всего $2 за прототип печатной платы! Цвет — любой!
Зарегистрируйтесь и получите два купона по 5$ каждый:https://jlcpcb.com/cwc
Карма: 8
Рейтинг сообщений: 59
Зарегистрирован: Пт фев 17, 2017 11:18:07
Сообщений: 394
Откуда: Ставрополь-Донское
Рейтинг сообщения: 0
Карма: 109
Рейтинг сообщений: 7302
Зарегистрирован: Сб сен 13, 2014 16:27:32
Сообщений: 33408
Откуда: СпиртоГонск созвездия Омега
Рейтинг сообщения: 0
Создать интеллектуальный пожарный датчик, который будет не только оповещать о возгорании, а способен легко интегрироваться в системы умного дома или предприятия и выполнять ряд дополнительных действий, возможно с компонентами STMicroelectronics: высокопроизводительным радиочастотным трансивером S2-LP и малопотребляющим усилителем TSV629x. Рассмотрим подробнее это решение, отладочные комплекты и программный пакет ST.
Chevrolet Lanos Черный металлик ver.2.0
Как из минуса сделать плюс и наоборот
ArteClab
Был 4 дня назад
Максим Викторович, 42 года
Я езжу на Volkswagen Passat Синий немец! и Chevrolet Lanos Черный металлик ver.2.0
Красноярск, Россия
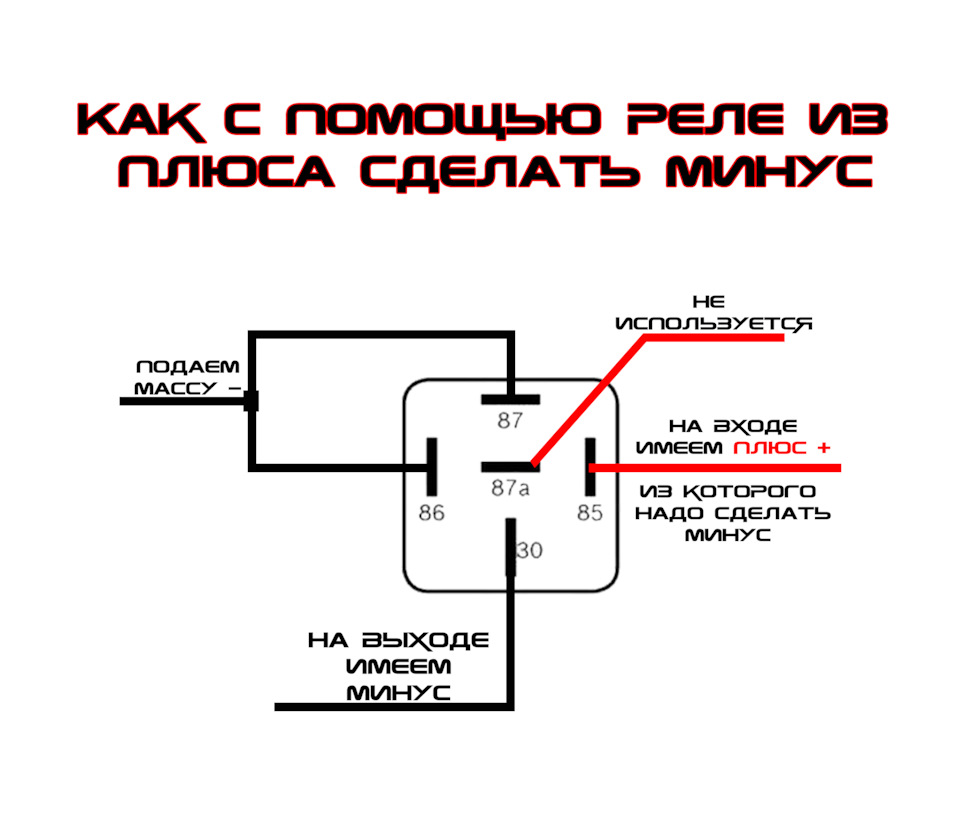
На заметку! Допустим, нам надо получить «минус», но у нас есть только «плюсовой» сигнал . На помощь опять приходит 5-и контактное реле. Схема проста
Полный размер
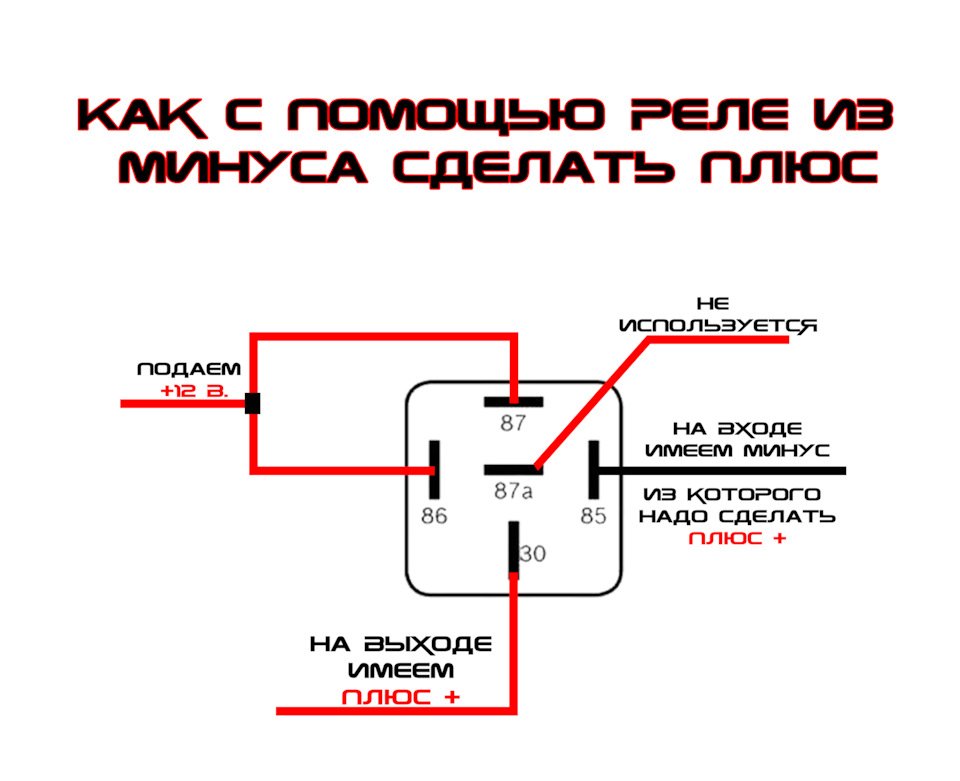
И наоборот нужно получить плюс имея минус…
Полный размер
Всем удачи!
30 октября 2020
Метки: электроника
2
Ранее Пришло время замены сцепления…
Разместить рекламу
Реклама
Машины в продаже
Кропоткин
Chevrolet Lanos, 2007
240 000 ₽
Екатеринбург
Chevrolet Lanos, 2008
185 000 ₽
Азов
Chevrolet Lanos, 2008
190 000 ₽
Кемерово
Chevrolet Lanos, 2007
195 000 ₽
Посмотреть больше машин на Дроме
Комментарии
2
Войдите или зарегистрируйтесь, чтобы писать комментарии, задавать вопросы и участвовать в обсуждении.
Войти
Зарегистрироваться
Dinarmus
Я езжу на KIA Rio (3G)
Можно по этой схеме подключить би лэд линзы? Управление по минусу. Постоянный+
5 месяцев
DekorPro44
Я езжу на Opel Zafira B
Нужная вещь при подключении камеры заднего вида
2 года
«Враг моего врага — мой друг».
Проще всего ответить: «Потому что таковы правила действий над отрицательными числами». Правила, которые мы учим в школе и применяем всю жизнь. Однако учебники не объясняют, почему правила именно такие. Мы сначала постараемся понять это, исходя из истории развития арифметики, а потом ответим на этот вопрос с точки зрения современной математики.
Давным-давно людям были известны только натуральные числа: 1, 2, 3, … Их использовали для подсчета утвари, добычи, врагов и т. д. Но числа сами по себе довольно бесполезны — нужно уметь с ними обращаться. Сложение наглядно и понятно, к тому же сумма двух натуральных чисел — тоже натуральное число (математик сказал бы, что множество натуральных чисел замкнуто относительно операции сложения). Умножение — это, по сути, то же сложение, если мы говорим о натуральных числах. В жизни мы часто совершаем действия, связанные с этими двумя операциями (например, делая покупки, мы складываем и умножаем), и странно думать, что наши предки сталкивались с ними реже — сложение и умножение были освоены человечеством очень давно. Часто приходится и делить одни величины на другие, но здесь результат не всегда выражается натуральным числом — так появились дробные числа.
Без вычитания, конечно, тоже не обойтись. Но на практике мы, как правило, вычитаем из большего числа меньшее, и нет нужды использовать отрицательные числа. (Если у меня есть 5 конфет и я отдам сестре 3, то у меня останется 5 – 3 = 2 конфеты, а вот отдать ей 7 конфет я при всем желании не могу.) Этим можно объяснить, почему люди долго не пользовались отрицательными числами.
В индийских документах отрицательные числа фигурируют с VII века н.э.; китайцы, видимо, начали употреблять их немного раньше. Их применяли для учета долгов или в промежуточных вычислениях для упрощения решения уравнений — это был лишь инструмент для получения положительного ответа. Тот факт, что отрицательные числа, в отличие от положительных, не выражают наличие какой-либо сущности, вызывал сильное недоверие. Люди в прямом смысле слова избегали отрицательных чисел: если у задачи получался отрицательный ответ, считали, что ответа нет вовсе. Это недоверие сохранялось очень долго, и даже Декарт — один из «основателей» современной математики — называл их «ложными» (в XVII веке!).
Рассмотрим для примера уравнение 7x – 17 = 2x – 2. Его можно решать так: перенести члены с неизвестным в левую часть, а остальные — в правую, получится 7x – 2x = 17 – 2, 5x = 15, x = 3. При таком решении нам даже не встретились отрицательные числа.
Но можно было случайно сделать и по-другому: перенести слагаемые с неизвестным в правую часть и получить 2 – 17 = 2x – 7x, (–15) = (–5)x. Чтобы найти неизвестное, нужно разделить одно отрицательное число на другое: x = (–15)/(–5). Но правильный ответ известен, и остается заключить, что (–15)/(–5) = 3.
Что демонстрирует этот нехитрый пример? Во-первых, становится понятна логика, которой определялись правила действий над отрицательными числами: результаты этих действий должны совпадать с ответами, которые получаются другим путем, без отрицательных чисел. Во-вторых, допуская использование отрицательных чисел, мы избавляемся от утомительного (если уравнение окажется посложнее, с большим числом слагаемых) поиска того пути решения, при котором все действия производятся только над натуральными числами. Более того, мы можем больше не думать каждый раз об осмысленности преобразуемых величин — а это уже шаг в направлении превращения математики в абстрактную науку.
Правила действий над отрицательными числами сформировались не сразу, а стали обобщением многочисленных примеров, возникавших при решении прикладных задач. Вообще, развитие математики можно условно разбить на этапы: каждый следующий этап отличается от предыдущего новым уровнем абстракции при изучении объектов. Так, в XIX веке математики поняли, что у целых чисел и многочленов, при всей их внешней непохожести, есть много общего: и те, и другие можно складывать, вычитать и перемножать. Эти операции подчиняются одним и тем же законам — как в случае с числами, так и в случае с многочленами. А вот деление целых чисел друг на друга, чтобы в результате снова получались целые числа, возможно не всегда. То же самое и с многочленами.
Потом обнаружились другие совокупности математических объектов, над которыми можно производить такие операции: формальные степенные ряды, непрерывные функции… Наконец, пришло понимание, что если изучить свойства самих операций, то потом результаты можно будет применять ко всем этим совокупностям объектов (такой подход характерен для всей современной математики).
В итоге появилось новое понятие: кольцо. Это всего-навсего множество элементов плюс действия, которые можно над ними производить. Основополагающими здесь являются как раз правила (их называют аксиомами), которым подчиняются действия, а не природа элементов множества (вот он, новый уровень абстракции!). Желая подчеркнуть, что важна именно структура, которая возникает после введения аксиом, математики говорят: кольцо целых чисел, кольцо многочленов и т. д. Отталкиваясь от аксиом, можно выводить другие свойства колец.
Мы сформулируем аксиомы кольца (которые, естественно, похожи на правила действий с целыми числами), а затем докажем, что в любом кольце при умножении минуса на минус получается плюс.
Кольцом называется множество с двумя бинарными операциями (т. е. в каждой операции задействованы два элемента кольца), которые по традиции называют сложением и умножением, и следующими аксиомами:
- сложение элементов кольца подчиняется переместительному (A + B = B + A для любых элементов A и B) и сочетательному (A + (B + C) = (A + B) + C) законам; в кольце есть специальный элемент 0 (нейтральный элемент по сложению) такой, что A + 0 = A, и для любого элемента A есть противоположный элемент (обозначаемый (–A)), что A + (–A) = 0;
- умножение подчиняется сочетательному закону: A·(B·C) = (A·B)·C;
- сложение и умножение связаны такими правилами раскрытия скобок: (A + B)·C = A·C + B·C и A·(B + C) = A·B + A·C.
Заметим, что кольца, в самой общей конструкции, не требуют ни перестановочности умножения, ни его обратимости (т. е. делить можно не всегда), ни существования единицы — нейтрального элемента по умножению. Если вводить эти аксиомы, то получаются другие алгебраические структуры, но в них будут верны все теоремы, доказанные для колец.
Теперь докажем, что для любых элементов A и B произвольного кольца верно, во-первых, (–A)·B = –(A·B), а во-вторых (–(–A)) = A. Из этого легко следуют утверждения про единицы: (–1)·1 = –(1·1) = –1 и (–1)·(–1) = –((–1)·1) = –(–1) = 1.
Для этого нам потребуется установить некоторые факты. Сперва докажем, что у каждого элемента может быть только один противоположный. В самом деле, пусть у элемента A есть два противоположных: B и С. То есть A + B = 0 = A + C. Рассмотрим сумму A + B + C. Пользуясь сочетательным и переместительным законами и свойством нуля, получим, что, с одной стороны, сумма равна B: B = B + 0 = B + (A + C) = A + B + C, а с другой стороны, она равна C: A + B + C = (A + B) + C = 0 + C = C. Значит, B = C.
Заметим теперь, что и A, и (–(–A)) являются противоположными к одному и тому же элементу (–A), поэтому они должны быть равны.
Первый факт получается так: 0 = 0·B = (A + (–A))·B = A·B + (–A)·B, то есть (–A)·B противоположно A·B, значит, оно равно –(A·B).
Чтобы быть математически строгими, объясним еще, почему 0·B = 0 для любого элемента B. В самом деле, 0·B = (0 + 0) B = 0·B + 0·B. То есть прибавление 0·B не меняет сумму. Значит, это произведение равно нулю.
А то, что в кольце ровно один ноль (ведь в аксиомах сказано, что такой элемент существует, но ничего не сказано про его единственность!), мы оставим читателю в качестве несложного упражнения.
Ответил: Евгений Епифанов