Как можно изменить электроемкость конденсатора

Электроемкость проводников

Проводники умеют не только проводить через себя электрический ток, но и накапливать заряд. Эта способность характеризуется таким параметром, как электроемкость.

Получай лайфхаки, статьи, видео и чек-листы по обучению на почту

Конденсаторы

Способность накапливать заряд — полезная штука, поэтому люди придумали конденсаторы. Это такие устройства, которые помогают применять электрическую емкость проводников в практических целях.

Конденсатор состоит из двух или более проводящих пластин (обкладок), разделенных диэлектриком. Между проводящими пластинами образуется электрическое поле, все силовые линии которого идут от одной обкладки к другой.

Зарядка конденсатора — это процесс накопления заряда на двух его обкладках. Заряды на них равны по величине и противоположны по знаку.

Электроемкость конденсатора измеряется отношением заряда на одной из обкладок к разности потенциалов между обкладками:

По закону сохранения заряда, если обкладки заряженного конденсатора соединить проводником, то заряды нейтрализуются, переходя с одной обкладки на другую. Так происходит разрядка конденсатора.

Любой конденсатор имеет предел напряжения. Если оно окажется слишком большим, то случится пробой диэлектрика, то есть разрядка произойдет прямо сквозь диэлектрик. Такой конденсатор больше работать не будет.

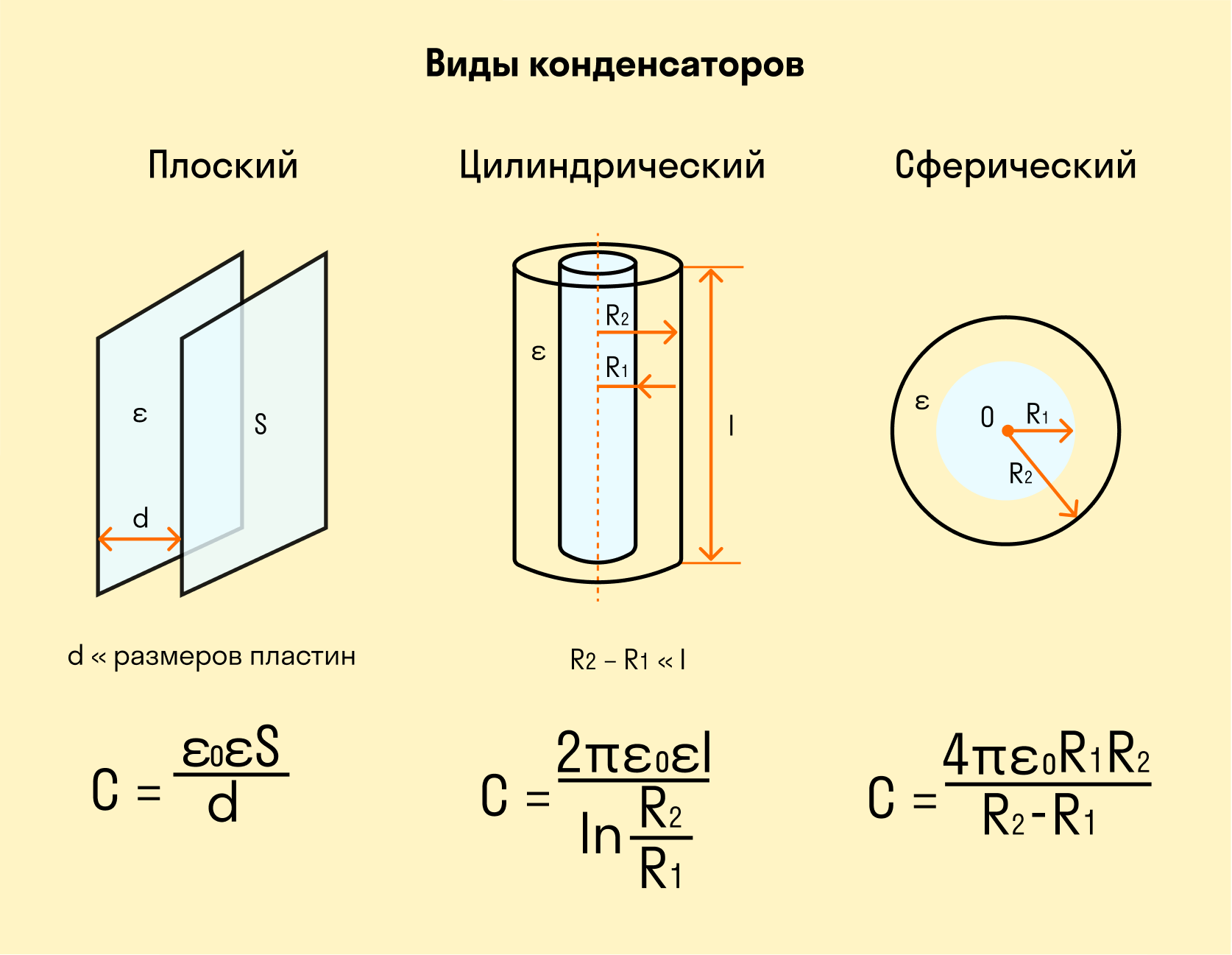
Виды конденсаторов

Особенность электроемкости в том, что она зависит от формы проводника. Для каждого вида проводников есть своя формула расчета электроемкости.

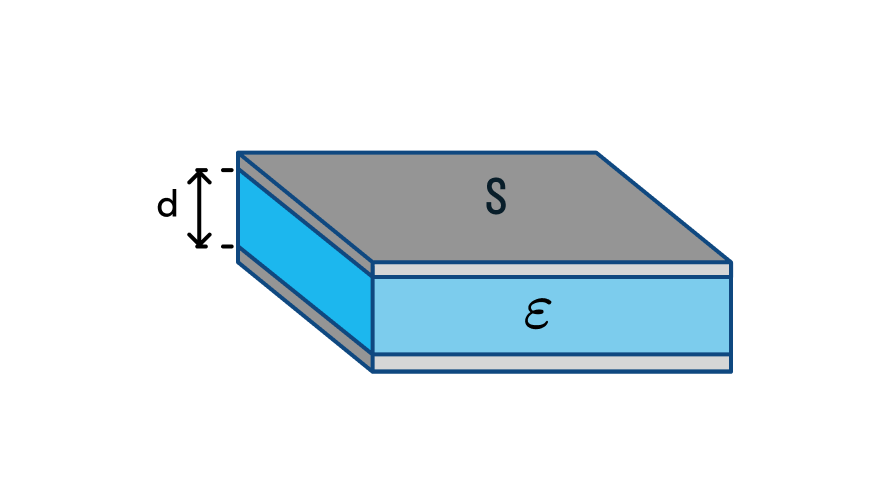
Проще всего вычислить электроемкость плоского конденсатора. Плоский конденсатор состоит из двух металлических пластин, между которыми помещают диэлектрическое вещество.

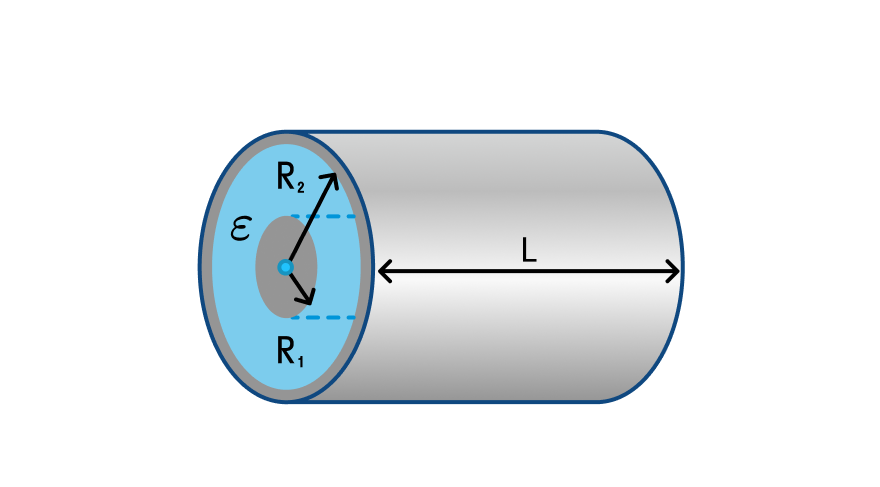
Самый популярный конденсатор — цилиндрический. Он состоит из двух металлических цилиндров, вложенных друг в друга, и диэлектрика, которым заполнено пространство между ними. Рассмотрим формулу электроемкости такого конденсатора.

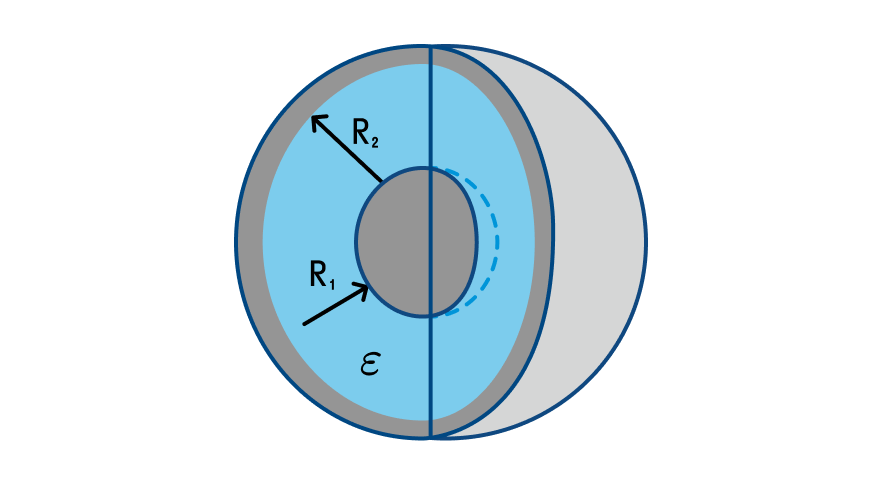
Сферический конденсатор состоит из двух проводящих сфер, вложенных друг в друга, и непроводящей жидкости, которой заполнено пространство между ними.

Подытожим все, что узнали, на картинке-шпаргалке:

Энергия конденсатора

У конденсатора, как и у любой системы заряженных тел, есть энергия. Чтобы зарядить конденсатор, необходимо совершить работу по разделению отрицательных и положительных зарядов. По закону сохранения энергии эта работа будет как раз равна энергии конденсатора.

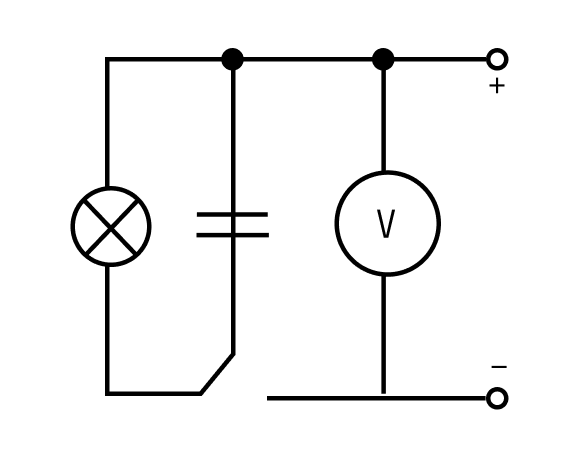
Доказать, что заряженный конденсатор обладает энергией, несложно. Для этого понадобится электрическая цепь, содержащая в себе лампу накаливания и конденсатор. При разрядке конденсатора вспыхнет лампа — это будет означать, что энергия конденсатора превратилась в тепло и энергию света.

Чтобы вывести формулу энергии плоского конденсатора, нам понадобится формула энергии электростатического поля.

В случае с конденсатором d будет представлять собой расстояние между пластинами.

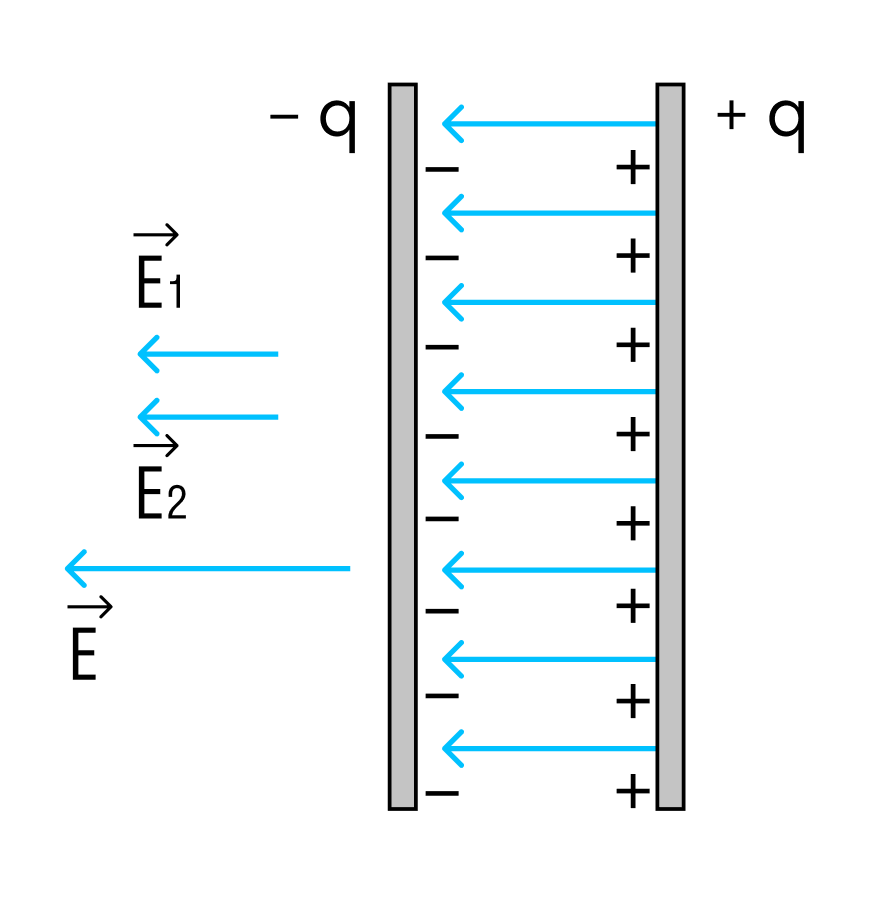
Заряд на пластинах конденсатора равен по модулю, поэтому можно рассматривать напряженность поля, создаваемую только одной из пластин.

Напряженность поля одной пластины равна Е/2, где Е — напряженность поля в конденсаторе.

В однородном поле одной пластины находится заряд q, распределенный по поверхности другой пластины.

Тогда энергия конденсатора равна:

W_p = qEd/2

Разность потенциалов между обкладками конденсатора можно представить, как произведение напряженности на расстояние:

U = Ed

Поэтому:

W_p = qU/2

Эта энергия равна работе, которую совершит электрическое поле при сближении пластин.

Заменив в формуле разность потенциалов или заряд с помощью выражения для электроемкости конденсатора C = q/U, получим три различных формулы энергии конденсатора:

Эти формулы справедливы для любого конденсатора.

Применение конденсаторов

Конденсатор есть в каждом современном устройстве. Разберем два самых наглядных примера.

Пример раз — вспышка

Без конденсатора вспышка в фотоаппарате работала бы не так, как мы привыкли, а с большими задержками, и к тому же быстро разряжала бы аккумулятор. Конденсатор в этом случае работает как батарейка. Он накапливает заряд от аккумулятора и хранит его до востребования. Когда нам нужна вспышка, конденсатор разряжается, чтобы она сработала и вылетела птичка.

Пример два — тачскрин

Тачскрин на телефоне работает по принципу, схожему с конденсатором. В самом смартфоне, конечно, тоже есть множество конденсаторов, но этот принцип куда интереснее.

Дело в том, что тело человека тоже умеет проводить электричество — у него даже есть сопротивление и электроемкость. Так что можно считать человеческий палец пластиной конденсатора — тело же проводник, почему бы и нет. Но если поднести палец к металлической пластине, получится плохой конденсатор.

В экран телефона встроена матрица из микроскопических пластинок. Когда мы подносим палец к одной из них, получается своего рода конденсатор. Когда перемещаем палец ближе к другой пластинке — еще один конденсатор. Телефон постоянно проверяет пластинки, и если обнаруживает, что у какой-то из них внезапно изменилась электроемкость, значит, рядом есть палец. Координаты пластинки с изменившейся электроемкостью передаются операционной системе телефона, а она уже решает, что с этими координатами делать.

Кстати, то же самое можно проделать, если взять обычную сосиску и поводить ей по экрану смартфона. Тачскрин будет реагировать на все контакты, как реагирует на человеческий палец.

Это не единственный вариант реализации тачскрина, но один из лучших на сегодняшний день. В айфоне используется именно он.

Изучать физику на примерах из реальной жизни может быть очень даже интересно. Попробуйте и убедитесь сами на классическом курсе по физике для 10 класса.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Проводники
различной формы и различного размера,
заряженные одинаковым количеством
электричества, приобретают различные
потенциалы. Это является следствием
того, что такие проводники обладают
различной электроемкостью. При одной
и той же форме большую емкость будут
иметь тела больших размеров. Так,
например, емкость шара прямо пропорциональна
его емкости.

Емкость
тел зависит от близости окружающих
предметов и их физических свойств. При
приближении к проводнику другого
проводника его емкость увеличивается.

В
международной системе единиц за единицу
емкости принята емкость такого проводника,
потенциал которого при увеличении
заряда на 1 кулон повышается на 1 вольт.
Эта единица называется фарадой (Ф).

1фарад=1кулон/1вольт.

Это
очень большая величина. На практике
применяются меньшие единицы: микрофарада
(мкФ), равная 10^-6Ф и пикофарада (пФ), равная
10^-12 Ф.

Два
проводника, изолированные один от
другого и помещенные в непосредственной
близости, образуют конденсатор. Емкость
конденсатора зависит от площади
поверхности проводников, которые
выполняются в виде пластин. Для увеличения
емкости увеличивают число пластин,
соединяя их вместе с одной стороны (рис
1 а)

Пластины
называют обкладками конденсатора. Они
могут быть самых различных форм.

Емкость
конденсатора С численно равна заряду,
который ему надо сообщить, чтобы разность
потенциалов между его обкладками
равнялась 1 вольту: C=q/(₂—₁)=q/U
(1.3)

Электрическое
поле конденсатора сосредоточено между
обкладками и поэтому окружающие
конденсатор тела практически не влияют
на его емкость.

При
введении между обкладками конденсатора
диэлектрика его емкость увеличивается.
Степень увеличения емкости зависит от
типа диэлектрика, т.е. от его диэлектрической
проницаемости:

=C/C₀,

где,
C₀
— емкость конденсатора с воздушным
диэлектриком; С — емкость того же
конденсатора с твердым или жидким
диэлектриком.

Емкость
конденсатора зависит также от расстояния
d между его обкладками. Формула для
определения емкости плоского конденсатора
с двумя пластинами, учитывающая все
выше перечисленные факторы, имеет вид:
C=S/(4d)*1/(9e11)
(Ф) (1.4)

Здесь
S — площадь одной из пластин, см^2, d-
расстояние между пластинами (толщина
диэлектрика) , см,
—
диэлектрическая проницаемость.

Для
увеличения площади обкладок последние
выполняются в виде двух полосок фольги,
свернутых в рулон и изолированных друг
от друга бумажной лентой. При этом
увеличиваются габариты конденсатора.

Уменьшение
расстояния между обкладками конденсатора
с целью увеличения его емкости наиболее
эффективным сказывается в электролитических
(оксидных) конденсаторах, в которых в
качестве диэлектрика используется
тонкая пленка окисла аммония. Однако
уменьшение d уменьшает электрическую
прочность конденсатора (т.е. из-за
избежания электрического пробоя,
выводящего конденсатор из строя)
снижается его рабочее напряжение.

Наиболее
эффективным способом увеличения емкости
конденсаторов является применение в
них диэлектриков с большим значением
диэлектрической постоянной
(например
керамический).

Для
увеличения емкости конденсаторы соединяю
параллельно (рис1
б).
При этом общая емкость полученной
батареи равна суме емкостей всех входящих
в нее конденсаторов: С_пар=С₁+С₂+С_3.
При последовательном соединении
конденсаторов общая емкость С_посл
оказывается меньше наименьшей емкости
входящих в батарею конденсаторов и
может быть определено по формуле:

1/C_посл=1/C₁+1/C₂+1/C₃

Рис.
1

Содержание книги

Предыдующая страница

§16. Превращение энергии в электрических и магнитных явлениях

16.7 Изменение энергии конденсатора при изменении его емкости.

Энергия конденсатора зависит от его емкости. Емкость конденсатора можно изменять, когда он заряжен — при этом будет изменяться его энергия. При рассмотрении этих процессов можно выделить два принципиально различных случая: первый — изменение емкости происходит при неизменных зарядах на обкладках; второй – емкость конденсатора изменяется при постоянном напряжении между обкладками (в этом случае конденсатор подключен к источнику постоянной ЭДС).

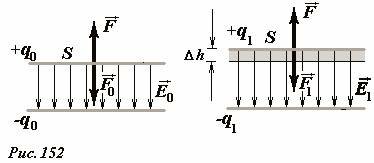
Рассмотрим теперь превращения энергии при изменении емкости плоского конденсатора, образованного двумя параллельными одинаковыми платинами площади S. Размеры пластин будем считать значительно превышающими расстояние между ними, что позволяет пренебречь краевыми эффектами, то есть считать электрическое поле (~vec E) однородным (Рис. 152). Пусть конденсатор заряжен, так что заряды каждой пластины одинаковы по модулю и равны q и противоположны по знаку, поверхностная плотность заряда на каждой пластине равна (~sigma = frac{q}{S}). Напряженность поля между пластинами в этом случае равна

(~E = frac{sigma}{varepsilon_0} = frac{q}{varepsilon_0 S}) , (1)

причем заряды каждой пластины создают поле, напряженность которого в два раза меньше напряженности суммарного поля (1); разность потенциалов между пластинами равна

(~Delta varphi = U = Eh = frac{qh}{varepsilon_0 S}) . (2)

Так заряды пластин разноименные, то пластины будут притягиваться друг к другу с некоторой силой F. Сила, действующая на одну пластину, равна произведению ее заряда на напряженность поля, создаваемого зарядом второй пластины,

(~F = q frac{E}{2} = frac{q^2}{2 varepsilon_0 S}) . (3)

Этой формуле можно придать иной вид, если выразить силу через напряженность электрического поля с помощью формулы (1)

(~F = frac{q^2}{2 varepsilon_0 S} = frac{varepsilon_0 E^2}{2} S) . (4)

Важно отметить, что давление электрического поля на проводящую платину в точности равно объемной плотности энергии поля

(~p = frac{F}{S} = frac{varepsilon_0 E^2}{2} = w) . (5)

Чтобы изменить (для определенности увеличить см. Рис. 152) расстояние между пластинами, к ним необходимо приложить внешнюю силу F₀, превышающую по модулю силе электрического притяжения. При перемещении пластины (увеличении расстояния) на величину Δh эта внешняя сила совершит положительную работу.

Если пластины конденсатора изолированы, то электрический заряд и, как следствие, напряженность поля и сила притяжения не зависят от расстояния между пластинами. Поэтому работа внешней силы по перемещению пластины на расстояние Δh будет минимальна, когда эта сила равна силе притяжения между пластинами, при этом

(~A = F_0 Delta h = frac{varepsilon_0 E^2}{2} S Delta h) . (6)

Благодаря этой работе возрастает энергия электрического поля – при неизменной напряженности и плотности энергии возрастает объем, занятый полем ((Delta V = S Delta h)), что выражается формулой

(~A = Delta W = w Delta V) . (7)

При увеличении расстояния между пластинами емкость конденсатора изменяется (уменьшается). Изменение энергии конденсатора можно также рассчитать, с помощью формулы для его энергии, причем следует выразить энергию через не изменяющийся в данном случае заряд конденсатора, то есть

(~Delta W = W_1 — W_0 = frac{q^2}{2 C_1} — frac{q^2}{2 C_0} = frac{q^2}{2} left(frac{h_1}{varepsilon_0 S} — frac{h_0}{varepsilon_0 S}right) = frac{q^2 Delta h}{2 varepsilon_0 S}) . (8)

Эта формула равносильна полученным выше выражениям для изменения энергии. Таким образом, в рассмотренном процессе превращения энергии понятны: работа внешней силы увеличивает энергию электрического поля конденсатора.

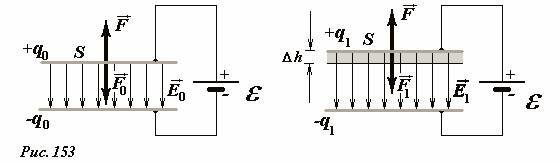
Рассмотрим теперь этот же процесс при условии, что обкладки конденсатора подключены к источнику постоянной ЭДС (Рис. 153). В этом случае при изменении расстояния между пластинами, остается неизменным напряжение U = ε между ними.

В этом случае разноименно заряженные пластины также притягиваются, поэтому для увеличения расстояния между ними внешняя сила также совершает положительную работу, однако при этом энергия конденсатора уменьшается, а не растет! Действительно, при постоянном напряжении между пластинами, изменение энергии конденсатора рассчитывается по формуле

(~Delta W_C = W_1 — W_0 = frac{C_1 U^2}{2} — frac{C_0 U^2}{2} = frac{U^2}{2} left(frac{varepsilon_0 S}{h_1} — frac{varepsilon_0 S}{h_0}right) = frac{varepsilon_0 S U^2}{2} left(frac{1}{h_1} — frac{1}{h_0}right)) . (9)

Так как h₁ > h₀ , то C₁ < C₀ и ΔW_C < 0.

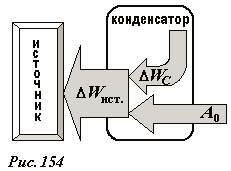
Но и в этом случае нарушения закона сохранения энергии нет, переданная системе энергия (равная совершенной работе) не «теряется» — конденсатор не является замкнутой системой, он же подключен к источнику ЭДС. При увеличении расстояния между пластинами емкость конденсатора уменьшается, поэтому уменьшается заряд на пластинах, которому некуда деться, кроме как вернуться назад, в источник. Их возращению препятствуют сторонние силы (вспомните – сторонние силы источника стремятся «вытолкнуть заряды из источника), поэтому при возвращении зарядов энергия источника повышается. Таким образом, при раздвигании пластин конденсатора происходит подзарядка источника, а энергия, переданная посредством совершенной работы, переходит в энергию источника. Кроме того, энергия поля в конденсаторе также уменьшается, поэтому эта «потеря» энергии также переходит в источник. Иными словами, при перемещении пластины внешняя сила не только совершает работу по подзарядке источника, но и «заставляет» электрическое поле вернуть часть своей энергии. Схематически потоки энергии в этом процессе показаны на Рис. 154.

Подтвердим проведенные рассуждения расчетами энергетического баланса и покажем, что он точно выполняется. Силу притяжения между пластинами (4) выразим через постоянное напряжение между пластинами

(~F = frac{varepsilon_0 E^2}{2} S = frac{varepsilon_0}{2} left(frac{U}{h}right)^2 S = frac{varepsilon_0 U^2 S}{2 h^2}) . (10)

В данном случае эта сила зависит от расстояния между пластинами. Поэтому для расчета работы необходимо разбить процесс движения пластины на малые участки и затем просуммировать работы на этих участках. Чтобы избежать этой громоздкой математической процедуры, будем считать, что смещение Δh мало настолько, что можно пренебречь изменением силы притяжения. В этом приближении работа внешней силы будет равна

(~delta A_0 = F Delta h = frac{varepsilon_0 U^2 S}{2 h^2_0} Delta h) . (11)

Преобразуем также выражение для изменения энергии конденсатора с учетом малости смещения. Запишем (h_1 = h_0 + Delta h) и подставим в формулу (9)

(~Delta W_C = W_1 — W_0 = frac{varepsilon_0 S U^2}{2} left(frac{1}{h_0 + Delta h} — frac{1}{h_0}right) = -frac{varepsilon_0 S U^2}{2} frac{Delta h}{h_0(h_0 + Delta h)} approx -frac{varepsilon_0 S U^2}{2} frac{Delta h}{h^2_0}) . (12)

Наконец, найдем работу по зарядке источника, которая равна произведению «вернувшегося» заряда на ЭДС источника (которая равна напряжению конденсатора):

(~Delta W_{ist} = U(q_0 — q_1) = U(C_0 U — C_1 U) = U^2 left(frac{varepsilon_0 S}{h_0} — frac{varepsilon_0 S}{h_0 + Delta h}right) = varepsilon_0 S U^2 left(frac{1}{h_0} — frac{1}{h_0 + Delta h}right) approx frac{varepsilon_0 S U^2 Delta h}{h^2_0}) .

Итак, проведенный расчет полностью подтверждает сделанные ранее заключения: увеличение энергии источника (что равносильно — работа по его подзарядке) равно сумме работы внешней силы и уменьшения энергии поля конденсатора

(~Delta W_{ist} = delta A_0 + (-Delta W_C)) .

Задание для самостоятельной работы.

1. Докажите, что в рассмотренном процессе энергетический баланс выполняется при любом (не малом) смещении пластины.

Признавая, что «аналогии ничего не доказывают, но много объясняют», рассмотрим гидростатическую аналогию преобразования энергии при изменении «емкости» сосуда. Как мы указывали, аналогом электрического заряда может служить объем жидкости, налитой в сосуд, аналогом изменения потенциала – изменение уровня жидкости, тогда аналогом электроемкости вертикального сосуда служит площадь его дна. Таким образом, изменению емкости должно соответствовать изменение площади поперечного сечения сосуда. Представим себе сосуд в форме параллелепипеда (аквариума), одна из стенок которого может двигаться – при ее смещении изменяется площадь сосуда, то есть изменяется его «емкость». При уменьшении площади сосуда уменьшается «емкость». В рассмотренных электростатических примерах – уменьшению емкости конденсатора соответствует увеличению расстояния между его пластинами.

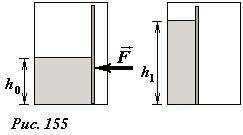
Пусть теперь в нашем сосуде находится некоторый объем жидкости, уровень которой равен h₀ (Рис. 155 ). Чтобы сместить подвижную стенку, к ней необходимо приложить некоторую внешнюю силу F. Если объем жидкости в сосуде сохраняется, то при смещении стенки ее уровень повышается, следовательно, увеличивается ее энергия. Понятно, что увеличение потенциальной энергии жидкости равно работе внешней силы.

Сравните: при неизменном объеме жидкости (электрическом заряде) уменьшение площади сосуда (емкости конденсатора) под действием внешней силы приводит к возрастанию уровня жидкости (разности потенциалов) и гидростатической энергии жидкости (электростатической энергии поля).

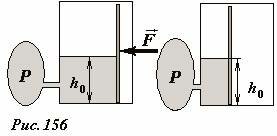
Если конденсатор подключен к источнику постоянной ЭДС, то его напряжение поддерживается постоянным. В гидростатической аналогии необходимо в этом случае говорить о постоянной высоте уровня жидкости в сосуде. В качестве устройства, поддерживающего постоянный уровень можно предложить, например, резиновый сосуд («грушу»), жидкость в которой поддерживается при постоянном давлении. Если теперь наш сосуд «переменной емкости» подключить к источнику постоянного давления (резиновой груше), то получим аналог конденсатора, подключенного к источнику постоянной ЭДС (Рис.156) При смещении подвижной стенки в этом случае внешняя сила также совершает положительную работу, но потенциальная энергия жидкости в сосуде уменьшается, так как уменьшается ее объем при неизменной высоте уровня. Под действием этой внешней силы часть жидкости из сосуда заталкивается в резиновую грушу, при этом энергия последней возрастает. Увеличение ее энергии равно сумме работы внешней силы и уменьшения потенциальной энергии жидкости в сосуде.

Сравниваем: при постоянном уровне жидкости в сосуде (напряжении конденсатора) уменьшение площади дна (емкости конденсатора) под действием внешней силы приводит к возвращению части жидкости (электрического заряда) в резиновый сосуд, поддерживаемый при постоянном давлении (источник постоянной ЭДС). При этом увеличение энергии жидкости в резиновом сосуде постоянного давления (источника ЭДС) равно сумме работы внешней силы и уменьшения потенциальной энергии жидкости в сосуде (энергии конденсатора).

Задание для самостоятельной работы.

1. Докажите, что в рассмотренных гидростатических аналогиях энергетический баланс выполняется точно.

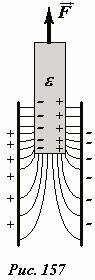
Электроемкость конденсатора зависит также от диэлектрической проницаемости вещества, находящегося между обкладками. Поэтому емкость конденсатора можно изменять, меняя вещество, находящееся между обкладками. Пусть, например, между обкладками плоского конденсатора находится диэлектрическая пластинка. Если конденсатор заряжен, то для извлечения пластинки необходимо приложить к ней внешнюю силу и совершить положительную работу. Механизм возникновения силы, действующей на пластинку со стороны электрического поля, проиллюстрирован на Рис. 157. При ее смещении изначально однородное распределение зарядов на обкладках конденсатора и поляризационных зарядов на пластинке искажается. Как следствие этого перераспределения зарядов искажается и электрическое поле, поэтому возникаю силы, стремящиеся втянуть пластинку внутрь конденсатора.

Расчет этих сил сложен, но энергетические характеристики происходящих процессов могут быть найдены без особого труда. С формальной точки зрения, не важно чем вызваны изменения емкости конденсатора, поэтому можно воспользоваться всеми рассуждениями и выводами предыдущего раздела, как для случая изолированного конденсатора (при сохранении заряда), так для конденсатора подключенного к источнику постоянной ЭДС.

Чрезвычайно интересными и практически важными являются энергетические характеристики процессов поляризации диэлектриков, однако их расчет представляет собой весьма сложную задачу. Для решения возникающих здесь проблем требует привлечения сведения о строении вещества. Некоторые из этих вопросов мы рассмотрим в следующем году после ознакомления с основами теории строения вещества.

Следующая страница

Конденсатор. Энергия электрического поля

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: электрическая ёмкость, конденсатор, энергия электрического поля конденсатора.

Предыдущие две статьи были посвящены отдельному рассмотрению того, каким образом ведут себя в электрическом поле проводники и каким образом — диэлектрики. Сейчас нам понадобится объединить эти знания. Дело в том, что большое практическое значение имеет совместное использование проводников и диэлектриков в специальных устройствах — конденсаторах.

Но прежде введём понятие электрической ёмкости.

к оглавлению ▴

Ёмкость уединённого проводника

Предположим, что заряженный проводник расположен настолько далеко от всех остальных тел, что взаимодействие зарядов проводника с окружающими телами можно не принимать во внимание. В таком случае проводник называется уединённым.

Потенциал всех точек нашего проводника, как мы знаем, имеет одно и то же значение , которое называется потенциалом проводника. Оказывается, что потенциал уединённого проводника прямо пропорционален его заряду. Коэффициент пропорциональности принято обозначать , так что

Величина называется электрической ёмкостью проводника и равна отношению заряда проводника к его потенциалу:

(1)

Например, потенциал уединённого шара в вакууме равен:

где — заряд шара, — его радиус. Отсюда ёмкость шара:

(2)

Если шар окружён средой-диэлектриком с диэлектрической проницаемостью , то его потенциал уменьшается в раз:

Соответственно, ёмкость шара в раз увеличивается:

(3)

Увеличение ёмкости при наличии диэлектрика — важнейший факт. Мы ещё встретимся с ним при рассмотрении конденсаторов.

Из формул (2) и (3) мы видим, что ёмкость шара зависит только от его радиуса и диэлектрической проницаемости окружающей среды. То же самое будет и в общем случае: ёмкость уединённого проводника не зависит от его заряда; она определяется лишь размерами и формой проводника, а также диэлектрической проницаемостью среды, окружающей проводник. От вещества проводника ёмкость также не зависит.

В чём смысл понятия ёмкости? Ёмкость показывает, какой заряд нужно сообщить проводнику, чтобы увеличить его потенциал на В. Чем больше ёмкость — тем, соответственно, больший заряд требуется поместить для этого на проводник.

Единицей измерения ёмкости служит фарад (Ф). Из определения ёмкости (1) видно, что Ф = Кл/В.

Давайте ради интереса вычислим ёмкость земного шара (он является проводником!). Радиус считаем приближённо равным км.

мкФ.

Как видите, Ф — это очень большая ёмкость.

Единица измерения ёмкости полезна ещё и тем, что позволяет сильно сэкономить на обозначении размерности диэлектрической постоянной . В самом деле, выразим из формулы (2):

Следовательно, диэлектрическая постоянная может измеряться в Ф/м:

Ф.

Так легче запомнить, не правда ли?

к оглавлению ▴

Ёмкость плоского конденсатора

Ёмкость уединённого проводника на практике используется редко. В обычных ситуациях проводники не являются уединёнными. Заряженный проводник взаимодействует с окружающими телами и наводит на них заряды, а потенциал поля этих индуцированных зарядов (по принципу суперпозиции!) изменяет потенциал самого проводника. В таком случае уже нельзя утверждать, что потенциал проводника будет прямо пропорционален его заряду, и понятие ёмкости проводника самого по себе фактически утрачивает смысл.

Можно, однако, создать систему заряженных проводников, которая даже при накоплении на них значительного заряда почти не взаимодействует с окружающими телами. Тогда мы сможем снова говорить о ёмкости — но на сей раз о ёмкости этой системы проводников.

Наиболее простым и важным примером такой системы является плоский конденсатор. Он состоит из двух параллельных металлических пластин (называемых обкладками), разделённых слоем диэлектрика. При этом расстояние между пластинами много меньше их собственных размеров.

Для начала рассмотрим воздушный конденсатор, у которого между обкладками находится воздух

Пусть заряды обкладок равны и . Именно так и бывает в реальных электрических схемах: заряды обкладок равны по модулю и противоположны по знаку. Величина — заряд положительной обкладки — называется зарядом конденсатора.

Пусть — площадь каждой обкладки. Найдём поле, создаваемое обкладками в окружающем пространстве.

Поскольку размеры обкладок велики по сравнению с расстоянием между ними, поле каждой обкладки вдали от её краёв можно считать однородным полем бесконечной заряженной плоскости:

Здесь — напряжённость поля положительной обкладки, — напряженность поля отрицательной обкладки, — поверхностная плотность зарядов на обкладке:

На рис. 1 (слева) изображены векторы напряжённости поля каждой обкладки в трёх областях: слева от конденсатора, внутри конденсатора и справа от конденсатора.

Рис. 1. Электрическое поле плоского конденсатора

Согласно принципу суперпозиции, для результирующего поля имеем:

Нетрудно видеть, что слева и справа от конденсатора поле обращается в нуль (поля обкладок погашают друг друга):

Внутри конденсатора поле удваивается:

или

(4)

Результирующее поле обкладок плоского конденсатора изображено на рис. 1 справа. Итак:

Внутри плоского конденсатора создаётся однородное электрическое поле, напряжённость которого находится по формуле (4). Снаружи конденсатора поле равно нулю, так что конденсатор не взаимодействует с окружающими телами.

Не будем забывать, однако, что данное утверждение выведено из предположения, будто обкладки являются бесконечными плоскостями. На самом деле их размеры конечны, и вблизи краёв обкладок возникают так называемые краевые эффекты: поле отличается от однородного и проникает в наружное пространство конденсатора. Но в большинстве ситуаций (и уж тем более в задачах ЕГЭ по физике) краевыми эффектами можно пренебречь и действовать так, словно утверждение, выделенное курсивом, является верным без всяких оговорок.

Пусть расстояние между обкладками конденсатора равно . Поскольку поле внутри конденсатора является однородным, разность потенциалов между обкладками равна произведению на (вспомните связь напряжения и напряжённости в однородном поле!):

(5)

Разность потенциалов между обкладками конденсатора, как видим, прямо пропорциональна заряду конденсатора. Данное утверждение аналогично утверждению «потенциал уединённого проводника прямо пропорционален заряду проводника», с которого и начался весь разговор о ёмкости. Продолжая эту аналогию, определяем ёмкость конденсатора как отношение заряда конденсатора к разности потенциалов между его обкладками:

(6)

Ёмкость конденсатора показывает, какой заряд ему нужно сообщить, чтобы разность потенциалов между его обкладками увеличилась на В. Формула (6), таким образом, является модификацией формулы (1) для случая системы двух проводников — конденсатора.

Из формул (6) и (5) легко находим ёмкость плоского воздушного конденсатора:

(7)

Она зависит только от геометрических характеристик конденсатора: площади обкладок и расстояния между ними.
Предположим теперь, что пространство между обкладками заполнено диэлектриком с диэлектрической проницаемостью . Как изменится ёмкость конденсатора?

Напряжённость поля внутри конденсатора уменьшится в раз, так что вместо формулы (4) теперь имеем:

(8)

Соответственно, напряжение на конденсаторе:

(9)

Отсюда ёмкость плоского конденсатора с диэлектриком:

(10)

Она зависит от геометрических характеристик конденсатора (площади обкладок и расстояния между ними) и от диэлектрической проницаемости диэлектрика, заполняющего конденсатор.

Важное следствие формулы (10): заполнение конденсатора диэлектриком увеличивает его ёмкость.

к оглавлению ▴

Энергия заряженного конденсатора

Заряженный конденсатор обладает энергией. В этом можно убедиться на опыте. Если зарядить конденсатор и замкнуть его на лампочку, то (при условии, что ёмкость конденсатора достаточно велика) лампочка ненадолго загорится.

Следовательно, в заряженном конденсаторе запасена энергия, которая и выделяется при его разрядке. Нетрудно понять, что этой энергией является потенциальная энергия взаимодействия обкладок конденсатора — ведь обкладки, будучи заряжены разноимённо, притягиваются друг к другу.

Мы сейчас вычислим эту энергию, а затем увидим, что существует и более глубокое понимание происхождения энергии заряженного конденсатора.

Начнём с плоского воздушного конденсатора. Ответим на такой вопрос: какова сила притяжения его обкладок друг к другу? Величины используем те же: заряд конденсатора , площадь обкладок .

Возьмём на второй обкладке настолько маленькую площадку, что заряд этой площадки можно считать точечным. Данный заряд притягивается к первой обкладке с силой

где — напряжённость поля первой обкладки:

Следовательно,

Направлена эта сила параллельно линиям поля (т. е. перпендикулярно пластинам).

Результирующая сила притяжения второй обкладки к первой складывается из всех этих сил , с которыми притягиваются к первой обкладке всевозможные маленькие заряды второй обкладки. При этом суммировании постоянный множитель вынесется за скобку, а в скобке просуммируются все и дадут . В результате получим:

(11)

Предположим теперь, что расстояние между обкладками изменилось от начальной величины до конечной величины . Сила притяжения пластин совершает при этом работу:

Знак правильный: если пластины сближаются , то сила совершает положительную работу, так как пластины притягиваются друг к другу. Наоборот, если удалять пластины , то работа силы притяжения получается отрицательной, как и должно быть.

С учётом формул (11) и (7) имеем:

где

Это можно переписать следующим образом:

где

(12)

Работа потенциальной силы притяжения обкладок оказалась равна изменению со знаком минус величины . Это как раз и означает, что — потенциальная энергия взаимодействия обкладок, или энергия заряженного конденсатора.

Используя соотношение , из формулы (12) можно получить ещё две формулы для энергии конденсатора (убедитесь в этом самостоятельно!):

(13)

(14)

Особенно полезными являются формулы (12) и (14).

Допустим теперь, что конденсатор заполнен диэлектриком с диэлектрической проницаемостью . Сила притяжения обкладок уменьшится в раз, и вместо (11) получим:

При вычислении работы силы , как нетрудно видеть, величина войдёт в ёмкость , и формулы (12) — (14) останутся неизменными. Ёмкость конденсатора в них теперь будет выражаться по формуле (10).

Итак, формулы (12) — (14) универсальны: они справедливы как для воздушного конденсатора, так и для конденсатора с диэлектриком.

к оглавлению ▴

Энергия электрического поля

Мы обещали, что после вычисления энергии конденсатора дадим более глубокое истолкование происхождения этой энергии. Что ж, приступим.

Рассмотрим воздушный конденсатор и преобразуем формулу (14) для его энергии:

Но — объём конденсатора. Получаем:

(15)

Посмотрите внимательно на эту формулу. Она уже не содержит ничего, что являлось бы специфическим для конденсатора! Мы видим энергию электрического поля , сосредоточенного в некотором объёме .

Энергия конденсатора есть не что иное, как энергия заключённого внутри него электрического поля.

Итак, электрическое поле само по себе обладает энергией. Ничего удивительного для нас тут нет. Радиоволны, солнечный свет — это примеры распространения энергии, переносимой в пространстве электромагнитными волнами.

Величина — энергия единицы объёма поля — называется объёмной плотностью энергии. Из формулы (15) получим:

(16)

В этой формуле не осталось вообще никаких геометрических величин. Она даёт максимально чистую связь энергии электрического поля и его напряжённости.

Если конденсатор заполнен диэлектриком, то его ёмкость увеличивается в раз, и вместо формул (15) и (16) будем иметь:

(17)

(18)

Как видим, энергия электрического поля зависит ещё и от диэлектрической проницаемости среды, в которой поле находится.
Замечательно, что полученные формулы для энергии и плотности энергии выходят далеко за пределы электростатики: они справедливы не только для электростатического поля, но и для электрических полей, меняющихся во времени.