Как можно изменить механическую энергию - Исправление ошибок и поиск оптимальных решений проблем

Энергия: что это такое

Если мы погуглим определение слова «Энергия», то скорее всего найдем что-то про формы взаимодействия материи. Это верно, но совершенно непонятно.

Поэтому давайте условимся здесь и сейчас, что энергия — это запас, который пойдет на совершение работы.

Энергия бывает разных видов: механическая, электрическая, внутренняя, гравитационная и так далее. Измеряется она в Джоулях (Дж) и чаще всего обозначается буквой E.

Получай лайфхаки, статьи, видео и чек-листы по обучению на почту

Практикующий детский психолог Екатерина Мурашова

Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков

Механическая энергия

Механическая энергия — это энергия, связанная с движением объекта или его положением, способность совершать механическую работу.

Она представляет собой совокупность кинетической и потенциальной энергии. Кинетическая энергия — это энергия действия. Потенциальная — ожидания действия.

Представьте, что вы взяли в руки канцелярскую резинку, растянули ее и отпустили. Из растянутого положения резинка просто «полетит», как только вы ей позволите это сделать. В этом процессе в момент натяжения резинка обладает потенциальной энергией, а в момент полета — кинетической.

Еще один примерчик: лыжник скатывается с горы. В самом начале — на вершине — у него максимальная потенциальная энергия, потому что он в режиме ожидания действия (ждущий режим 😂), а внизу горы он уже явно двигается, а не ждет, когда с ним это случится — получается, внизу горы кинетическая энергия.

Кинетическая энергия

Еще разок: кинетическая энергия — это энергия действия. Величина, которая очевиднее всего характеризует действие — это скорость. Соответственно, в формуле кинетической энергии точно должна присутствовать скорость.

Кинетическая энергия

Е_к — кинетическая энергия [Дж]

m — масса тела [кг]

v — скорость [м/с]

Чем быстрее движется тело, тем больше его кинетическая энергия. И наоборот — чем медленнее, тем меньше кинетическая энергия.

Задачка раз

Определить кинетическую энергию собаченьки массой 10 кг, если она бежала за мячом с постоянной скоростью 2 м/с.

Решение:

Формула кинетической энергии

Подставляем значения

Дж

Ответ: кинетическая энергия пёсы равна 20 Дж.

Задачка два

Найти скорость бегущего по опушке гнома, если его масса равна 20 кг, а его кинетическая энергия — 40 Дж

Решение:

Формула кинетической энергии

Выразим скорость:

Подставляем значения

Ответ: гном бежал со скоростью 2 м/с.

Онлайн-уроки физики в Skysmart не менее увлекательны, чем наши статьи!

Потенциальная энергия

В отличие от кинетической энергии, потенциальная чаще всего тем меньше, чем скорость больше. Потенциальная энергия — это энергия ожидания действия.

Например, потенциальная энергия у сжатой пружины будет очень велика, потому что такая конструкция может привести к действию, а следовательно — к увеличению кинетической энергии. То же самое происходит, если тело поднять на высоту. Чем выше мы поднимаем тело, тем больше его потенциальная энергия.

Потенциальная энергия деформированной пружины

Е_п — потенциальная энергия [Дж]

k — жесткость [Н/м]

x — удлинение пружины [м]

Потенциальная энергия в поле тяжести

Е_п = mgh

Еп — потенциальная энергия [Дж]

m — масса тела [кг]

g — ускорение свободного падения [м/с²]

h — высота [м]

На планете Земля g ≃ 9,8 м/с²

Задачка раз

Найти потенциальную энергию рака массой 0,1 кг, который свистит на горе высотой 2500 метров. Ускорение свободного падения считать равным 9,8 м/с².

Решение:

Формула потенциальной энергии Е_п = mgh

Подставляем значения

E_п = 0,1 · 9,8 · 2500 = 2450 Дж

Ответ: потенциальная энергия рака, свистящего на горе, равна 2450 Дж.

Задачка два

Найти высоту горки, с которой собирается скатиться лыжник массой 65 кг, если его потенциальная энергия равна 637 кДж. Ускорение свободного падения считать равным 9,8 м/с².

Решение:

Формула потенциальной энергии Е_п = mgh

Выразим высоту:

Переведем 637 кДж в Джоули.

637 кДж = 637000 Дж

Подставляем значения

Ответ: высота горы равна 1000 метров.

Задачка три

Два шара разной массы подняты на разную высоту относительно поверхности стола (см. рисунок). Сравните значения потенциальной энергии шаров E₁ и E₂. Считать, что потенциальная энергия отсчитывается от уровня крышки стола.

Решение:

Потенциальная энергия вычисляется по формуле: E = mgh

По условию задачи

m₁ = m

h₁ = 2h

m₂ = 2m

h₂ = h

Таким образом, получим, что

E₁ = mg2h = 2mgh,

а E₂ = 2mgh,

то есть E₁ = E₂.

Ответ: E₁ = E₂.

Закон сохранения энергии

В физике и правда ничего не исчезает бесследно. Чтобы это как-то выразить, используют законы сохранения. В случае с энергией — Закон сохранения энергии.

Закон сохранения энергии

Полная механическая энергия замкнутой системы остается постоянной.

Полная механическая энергия — это сумма кинетической и потенциальной энергий. Математически этот закон описывается так:

Закон сохранения энергии

Е_{полн. мех.} = Е_п + E_к = const

Е_{полн. мех.} — полная механическая энергия системы [Дж]

Е_п — потенциальная энергия [Дж]

Е_к — кинетическая энергия [Дж]

const — постоянная величина

Задачка раз

Мяч бросают вертикально вверх с поверхности Земли. Сопротивление воздуха пренебрежимо мало. Как изменится высота подъёма мяча при увеличении начальной скорости мяча в 2 раза?

Решение:

Должен выполняться закон сохранения энергии:

В начальный момент времени высота равна нулю, значит Е_п = 0. В этот же момент времени Е_к максимальна.

В конечный момент времени все наоборот — кинетическая энергия равна нулю, так как мяч уже не может лететь выше, а вот потенциальная максимальна, так как мяч докинули до максимальной высоты.

Это можно описать соотношением:

Е_п1 + Е_к1 = Е_п2 + Е_к2

0 + Е_к1 = Е_п2 + 0

Е_к1 = Е_п2

Разделим на массу левую и правую часть

Из соотношения видно, что высота прямо пропорциональна квадрату начальной скорости, значит при увеличении начальной скорости мяча в два раза, высота должна увеличиться в 4 раза.

Ответ: высота увеличится в 4 раза

Задачка два

Тело массой m, брошенное с поверхности земли вертикально вверх с начальной скоростью v₀, поднялось на максимальную высоту h₀. Сопротивление воздуха пренебрежимо мало. Чему будет равна полная механическая энергия тела на некоторой промежуточной высоте h?

Решение

По закону сохранения энергии полная механическая энергия изолированной системы остаётся постоянной. В максимальной точке подъёма скорость тела равна нулю, а значит, оно будет обладать исключительно потенциальной энергией Е_мех = Е_п = mgh₀.

Таким образом, на некоторой промежуточной высоте h, тело будет обладать и кинетической и потенциальной энергией, но их сумма будет иметь значение Е_мех = mgh₀.

Ответ: Е_мех = mgh₀.

Задачка три

Мяч массой 100 г бросили вертикально вверх с поверхности земли с начальной скоростью 6 м/с. На какой высоте относительно земли мяч имел скорость 2 м/с? Сопротивлением воздуха пренебречь.

Решение:

Переведем массу из граммов в килограммы:

m = 100 г = 0,1 кг

У поверхности земли полная механическая энергия мяча равна его кинетической энергии:

Дж

На высоте h потенциальная энергия мяча есть разность полной механической энергии и кинетической энергии:

Дж

Ответ: мяч имел скорость 2 м/с на высоте 1,6 м

Переход механической энергии во внутреннюю

Внутренняя энергия — это сумма кинетической энергии хаотичного теплового движения молекул и потенциальной энергии их взаимодействия. То есть та энергия, которая запасена у тела за счет его собственных параметров.

Часто механическая энергия переходит во внутреннюю. Происходит этот процесс путем совершения механической работы над телом. Например, если сгибать и разгибать проволоку — она будет нагреваться.

Или если кинуть мяч в стену, часть энергии при ударе перейдет во внутреннюю.

Задачка

Какая часть начальной кинетической энергии мяча при ударе о стену перейдет во внутреннюю, если полная механическая энергия вначале в два раза больше, чем в конце?

Решение:

В самом начале у мяча есть только кинетическая энергия, то есть Е_мех = Е_к.

В конце механическая энергия равна половине начальной, то есть Е_мех/2 = Е_к/2

Часть энергии уходит во внутреннюю, значит Е_полн = Е_мех/2 + Е_внутр

Е_мех = Е_мех/2 + Е_внутр

Е_мех/2 = Е_внутр

Е_внутр = Е_к/2

Ответ: во внутреннюю перейдет половина начальной кинетической энергии

Закон сохранения энергии в тепловых процессах

Чтобы закон сохранения энергии для тепловых процессов был сформулирован, было сделано два важных шага. Сначала французский математик и физик Жан Батист Фурье установил один из основных законов теплопроводности. А потом Сади Карно определил, что тепловую энергию можно превратить в механическую.

Вот что сформулировал Фурье:

При переходе теплоты от более горячего тела к более холодному температуры тел постепенно выравниваются и становятся едиными для обоих тел — наступает состояние термодинамического равновесия.

Таким образом, первым важным открытием было открытие того факта, что все протекающие без участия внешних сил тепловые процессы необратимы.

Дальше Карно установил, что тепловую энергию, которой обладает нагретое тело, непосредственно невозможно превратить в механическую энергию для производства работы. Это можно сделать, только если часть тепловой энергии тела с большей температурой передать другому телу с меньшей температурой и, следовательно, нагреть его до более высокой температуры.

Закон сохранения энергии в тепловых процессах

При теплообмене двух или нескольких тел абсолютное количество теплоты, которое отдано более нагретым телом, равно количеству теплоты, которое получено менее нагретым телом.

Математически его можно описать так:

Уравнение теплового баланса

Q_отд = Q_пол

Q_отд — отданное системой количество теплоты [Дж]

Q_пол — полученное системой количество теплоты [Дж]

Данное равенство называется уравнением теплового баланса. В реальных опытах обычно получается, что отданное более нагретым телом количество теплоты больше количества теплоты, полученного менее нагретым телом:

Это объясняется тем, что некоторое количество теплоты при теплообмене передаётся окружающему воздуху, а ещё часть — сосуду, в котором происходит теплообмен.

Чтобы разобраться в задачках, читайте нашу статью про агрегатные состояния вещества.

Задачка раз

Сколько граммов спирта нужно сжечь в спиртовке, чтобы нагреть на ней воду массой 580 г на 80 °С, если учесть, что на нагревание пошло 20% затраченной энергии.

Удельная теплота сгорания спирта 2,9 · 10₇ Дж/кг, удельная теплоёмкость воды 4200 Дж/(кг · °С).

Решение:

При нагревании тело получает количество теплоты

Q = cmΔt ,

где c — удельная теплоемкость вещества

При сгорании тела выделяется энергия

Q_сгор = q · m_сгор,

где q — удельная теплота сгорания топлива

По условию задачи нам известно, что на нагревание воды пошло 20% энергии, полученной при горении спирта.

То есть:

Ответ: масса сгоревшего топлива равна 33,6 г.

Задачка два

Какое минимальное количество теплоты необходимо для превращения в воду 500 г льда, взятого при температуре −10 °С? Потерями энергии на нагревание окружающего воздуха пренебречь. Удельная теплоемкость льда равна 2100 Дж/кг · ℃, удельная теплота плавления льда равна 3,3 · 10⁵ Дж/кг.

Решение:

Для нагревания льда до температуры плавления необходимо:

Q_нагрев = cmΔt

Q_нагрев = 2100 · 0,5 · (10 − 0) = 10 500 Дж

Для превращения льда в воду:

Q_пл = λm

Q_пл = 3,3 · 10⁵ · 0,5 = 165 000 Дж

Таким образом, для превращения необходимо затратить:

Q = Q_нагрев + Q_пл = 10 500 + 165 000 = 175 500 Дж = 175,5 кДж

Ответ: чтобы превратить 0,5 кг льда в воду при заданных условиях необходимо 175,5 кДж тепла.

Источник

Энергия.

Работа.
Мощность.
Механическая энергия.
Кинетическая энергия.
Потенциальная энергия тела вблизи поверхности Земли.
Потенциальна яэнергия деформированной пружины.
Закон сохранения механической энергии.
Закон изменения механической энергии.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: работа силы, мощность, кинетическая энергия, потенциальная энергия, закон сохранения механической энергии.

Мы приступаем к изучению энергии — фундаментального физического понятия. Но предварительно нужно разобраться с другой физической величиной — работой силы.

к оглавлению ▴

Работа.

Пусть на тело действует постоянная сила vec F и тело, двигаясь прямолинейно по горизонтальной поерхности, совершило перемещение vec s . Сила vec F не обязательно является непосредственной причиной перемещения (так, сила тяжести не является непосредственной причиной перемещения шкафа, который передвигают по комнате).

Предположим сначала, что векторы силы и перемещения сонаправлены (рис. 1; остальные силы, действующие на тело, не указаны)

Рис. 1.A=Fs

В этом простейшем случае работа определяется как произведение модуля силы на модуль перемещения:

A=Fs . (1)

Единицей измерения работы служит джоуль (Дж): Дж=Н cdot м. Таким образом, если под действием силы 1 Н тело перемещается на 1 м, то сила совершает работу 1 Дж.

Работа силы, перпендикулярной перемещению, по определению считается равной нулю. Так, в данном случае сила тяжести и сила реакции опоры не совершают работы.

Пусть теперь вектор силы образует с вектором перемещения острый угол alpha (рис. 2).

Разложим силу vec F на две составляющие: $vec F _{parallel }$ (параллельную перемещению) и $vec F _{perp }$ (перпендикулярную перемещению). Работу совершает только $vec F _{parallel }$ . Поэтому для работы силы vec F получаем:

$A=vec F _{parallel }s=Fcosalpha cdot s$ . Итак,

. (2)

Если вектор силы образует с вектором перемещения тупой угол alpha , то работа по-прежнему определяется формулой (2). В этом случае работа оказывается отрицательной.

Например, работа силы трения скольжения, действующей на тело в рассмотренных ситуациях, будет отрицательной, так как сила трения направлена противоположно перемещению. В этом случае имеем:

$alpha=180^{circ}, cos alpha=-1$ , и для работы силы трения получаем:

$A_{TP}=-F_{TP}s=-mu mgs$ ,

где — масса тела, — коэффициент трения между телом и опорой.

Соотношение (2) означает, что работа является скалярным произведением векторов силы и перемещения:

Это позволяет вычислять работу через координаты данных векторов:

$A=F_{displaystyle x}s_{displaystyle x}+F_{displaystyle y}s_{displaystyle y}+F_{displaystyle z}s_{displaystyle z}$ .

Пусть на тело действуют несколько сил $vec F_{1},vec F_{2},..,vec F_{n}$ и vec F — равнодействующая этих сил. Для работы силы vec F имеем:

$A=vec F vec s=(vec F_{1}+vec F_{2}+...+vec F_{n})vec s=vec F_{1}vec s+vec F_{2}vec s+...+vec F_{n}vec s$ ,

или

$A=A_{1}+A_{2}+...+A_{n}$ ,

где $A_{1}, A_{2},...,A_{n}$ — работы сил $F_{1}, F_{2},...,F_{n}$ . Итак, работа равнодействующей приложенных к телу сил равна сумме работ каждой силы в отдельности.

к оглавлению ▴

Мощность.

Часто имеет значение быстрота, с которой совершается работа. Скажем, на практике важно знать, какую работу сможет выполнить данное устройство за фиксированное время.

Мощность — это величина, характеризующая скорость совершения работы. Мощность есть отношение работы ко времени , за которое эта работа совершена:

$N=frac{displaystyle A}{displaystyle t}$ .

Мощность измеряется в ваттах (Вт). 1 Вт = 1 Дж/с, то есть 1 Вт — это такая мощность, при которой работа в 1 Дж совершается за 1 с.

Предположим, что силы, действующие на тело, уравновешены, и тело движется равномерно и прямолинейно со скоростью vec v . В этом случае существует полезная формула для мощности, развиваемой одной из действующих сил vec F .

За время тело совершит перемещение . Работа силы vec F будет равна:

Отсюда получаем мощность:

или

где alpha -угол между векторами силы и скорости.

Наиболее часто эта формула используется в ситуации, когда vec F — сила «тяги» двигателя автомобиля (которая на самом деле есть сила трения ведущих колёс о дорогу). В этом случае , и мы получаем просто:

N=Fv .

к оглавлению ▴

Механическая энергия.

Энергия является мерой движения и взаимодействия любых объектов в природе. Имеются различные формы энергии: механическая, тепловая, электромагнитная, ядерная. . .

Опыт показывает, что энергия не появляется ниоткуда и не исчезает бесследно, она лишь переходит из одной формы в другую. Это самая общая формулировка закона сохранения энергии.

Каждый вид энергии представляет собой некоторое математическое выражение. Закон сохранения энергии означает, что в каждом явлении природы определённая сумма таких выражений остаётся постоянной с течением времени.

Измеряется энергия в джоулях, как и работа.

Механическая энергия является мерой движения и взаимодействия механических объектов (материальных точек, твёрдых тел).

Мерой движения тела является кинетическая энергия. Она зависит от скорости тела. Мерой взаимодействия тел является потенциальная энергия. Она зависит от взаимного расположения тел.

Механическая энергия системы тел равна сумме кинетической энергии тел и потенциальной энергии их взаимодействия друг с другом.

к оглавлению ▴

Кинетическая энергия.

Кинетической энергией тела (принимаемого за материальную точку) называется величина

$K=frac{displaystyle mv^{displaystyle 2}}{displaystyle 2}$ ,

где — масса тела, — его скорость.

Кинетической энергией системы из тел называется сумма кинетических энергий каждого тела:

$K=frac{displaystyle m_{displaystyle 1}v_{displaystyle 1}^{displaystyle 2}}{displaystyle 2}+frac{displaystyle m_{displaystyle 2}v_{displaystyle 2}^{displaystyle 2}}{displaystyle 2}+...+frac{displaystyle m_{displaystyle N}v_{displaystyle N}^{displaystyle 2}}{displaystyle 2}$ .

Если тело движется под действием силы vec F , то кинетическая энергия тела, вообще говоря, меняется со временем. Оказывается, именение кинетической энергии тела за некоторый промежуток времени равно работе силы vec F . Покажем это для случая прямолинейного равноускоренного движения.

Пусть $vec{v_{1}}$ — начальная скорость, $vec{v_{2}}$ — конечная скорость тела. Выберем ось вдоль траектории тела (и, соответственно, вдоль вектора силы vec F ). Для работы силы vec F получаем:

$A=vec{F}vec{s}=F_{x}s_{displaystyle s}=ma_{displaystyle x}s_{displaystyle x}= ma_{displaystyle x}frac{{v_{displaystyle 2x}}^{displaystyle 2}-{v_{displaystyle 1x}}^{displaystyle 2}}{displaystyle 2a_{displaystyle x}}=frac{{displaystyle mv_{displaystyle 2x}}^{displaystyle 2}-{displaystyle mv_{displaystyle 1x}}^{displaystyle 2}}{displaystyle 2}$ .

(мы воспользовались формулой для $s_{x}$ , выведенной в статье «Равноускоренное движение»). Заметим теперь, что в данном случае проекция скорости отличается от модуля скорости разве что знаком; поэтому ${v_{displaystyle 1x}}^{displaystyle 2}={v_{displaystyle 1}}^{displaystyle 2}$ и ${v_{displaystyle 2x}}^{displaystyle 2}={v_{displaystyle 2}}^{displaystyle 2}$ . В результате имеем:

$A=frac{displaystyle mv_{displaystyle 2}^{displaystyle 2}}{displaystyle 2}-frac{displaystyle mv_{displaystyle 1}^{displaystyle 2}}{displaystyle 2}=K_{displaystyle 2}-K_{displaystyle 1}=Delta K$ ,

что и требовалось.

На самом деле соотношение справедливо и в самом общем случае криволинейного движения под действием переменной силы.

Теорема о кинетической энергии. Изменение кинетической энергии тела равно работе, совершённой приложенными к телу внешними силами за рассматриваемый промежуток времени.

Если работа внешних сил положительна, то кинетическая энергия увеличивается (, тело разгоняется).

Если работа внешних сил отрицательна, то кинетическая энергия уменьшается (, тело замедляет движение). Пример — торможение под действием силы трения, работа которой отрицательна.

Если же работа внешних сил равна нулю, то кинетическая энергия тела за это время не меняется. Нетривиальный пример — равномерное движение по окружности, совершаемое грузом на нити в горизонтальной плоскости. Сила тяжести, сила реакции опоры и сила натяжения нити всегда перпендикулярны скорости, и работа каждой из этих сил равна нулю в течение любого промежутка времени. Соответственно, кинетическая энергия груза (а значит, и его скорость) остаётся постоянной в процессе движения.

Задача. Автомобиль едет по горизонтальной дороге со скоростью и начинает резко тормозить. Найти путь , пройденный автомобилем до полной остановки, если коэффициент трения шин о дорогу равен .

Решение. Начальная кинетическая энергия автомобиля $K_{displaystyle 1}=frac{displaystyle mv^{displaystyle 2}}{displaystyle 2}$ , конечная кинетическая энергия $K_{displaystyle 2}=0$ . Изменение кинетической энергии $Delta K=K_{displaystyle 2}-K_{displaystyle 1}=-frac{displaystyle mv^{displaystyle 2}}{displaystyle 2}$ .

На автомобиль действуют сила тяжести m vec g , реакция опоры vec N и сила трения vec f . Сила тяжести и реакция опоры, будучи перпендикулярны перемещению автомобиля, работы не совершают. Работа силы трения:

Из теоремы о кинетической энергии теперь получаем:

$Delta K=A Rightarrow - frac{displaystyle mv^{displaystyle 2}}{displaystyle 2}=- mu mgs Rightarrow s=frac{displaystyle v^{displaystyle 2}}{displaystyle 2 mu g}$ .

к оглавлению ▴

Потенциальная энергия тела вблизи поверхности Земли.

Рассмотрим тело массы , находящееся на некоторой высоте над поверхностью Земли. Высоту считаем много меньше земного радиуса. Изменением силы тяжести в процессе перемещения тела пренебрегаем.

Если тело находится на высоте , то потенциальная энергия тела по определению равна:

W=mgh

где — ускорение свободного падения вблизи поверхности Земли.

Высоту не обязательно отсчитывать от поверхности Земли. Как мы увидим ниже (формулы (3), (4)), физическим смыслом обладает не сама по себе потенциальная энергия, но её изменение. А изменение потенциальной энергии не зависит от уровня отсчёта. Выбор нулевого уровня потенциальной энергии в конкретной задаче диктуется исключительно соображениями удобства.

Найдём работу, совершаемую силой тяжести при перемещении тела. Предположим, что тело перемещается по прямой из точки , находящейся на высоте $h_{1}$ , в точку , находящуюся на высоте $h_{2}$ (рис. 3).

Рис. 3.A=mg(h1-h2)[/math]

Угол между силой тяжести m vec g и перемещением тела vec s обозначим alpha . Для работы силы тяжести получим:

Но, как видно из рис. 3, $s cos alpha=h_{1}-h_{2}$ . Поэтому

$A=mg(h_{1}-h_{2})=mgh_{1}-mgh_{2}$ ,

или

$A=W_{1}-W_{2}$ . (3)

Учитывая, что $W_{1}-W_{2}=-(W_{2}-W_{1})=- Delta W$ , имеем также:

. (4)

Можно доказать, что формулы (3) и (4) справедливы для любой траектории, по которой тело перемещается из точки в точку , а не только для прямолинейного отрезка.

Работа силы тяжести не зависит от формы траектории, по которой перемещается тело, и равна разности значений потенциальной энергии в начальной и конечной точках траектории. Иными словами, работа силы тяжести всегда равна изменению потенциальной энергии с противоположным знаком. В частности, работа силы тяжести по любому замкнутому пути равна нулю.

Сила называется консервативной, если при перемещении тела работа этой силы не зависит от формы траектории, а определяется только начальным и конечным положением тела. Сила тяжести, таким образом, является консервативной. Работа консервативной силы по любому замкнутому пути равна нулю. Только в случае консервативной силы возможно ввести такую величину, как потенциальная энергия.

к оглавлению ▴

Потенциальна яэнергия деформированной пружины.

Рассмотрим пружину жёсткости . Начальная деформация пружины равна $x_{1}$ . Предположим,
что пружина деформируется до некоторой конечной величины деформации $x_{2}$ . Чему равна при этом работа силы упругости пружины?

В данном случае силу на перемещение не умножишь, так как сила упругости меняется в процессе деформации пружины. Для нахождения работы переменной силы требуется интегрирование. Мы не будем приводить здесь вывод, а сразу выпишем конечный результат.

Оказывается, сила упругости пружины также является консервативной. Её работа зависит лишь от величин $x_{1}$ и $x_{2}$ и определяется формулой:

$A=frac{kx_{displaystyle 1}^{displaystyle 2}}{displaystyle 2}-frac{displaystyle kx_{displaystyle 2}^{displaystyle 2}}{displaystyle 2}$ .

Величина

$W=frac{displaystyle kx^{displaystyle 2}}{displaystyle 2}$

называется потенциальной энергией деформированной пружины (x — величина деформации).

Следовательно,

$A=W_{1}-W_{2}=- Delta W$ ,

что полностью аналогично формулам (3) и (4).

к оглавлению ▴

Закон сохранения механической энергии.

Консервативные силы называются так потому, что сохраняют механическую энергию замкнутой системы тел.

Механическая энергия тела равна сумме его кинетической и потенциальной энергий:

E=K+W .

Механическая энергия системы тел равна сумме их кинетических энергий и потенциальной энергии их взаимодействия друг с другом.

Предположим, что тело совершает движение под действием силы тяжести и/или силы упругости пружины. Будем считать, что трения нет. Пусть в начальном положении кинетическая и потенциальная энергии тела равны $K_{1}$ и $W_{1}$ , в конечном положении — $K_{2}$ и $W_{2}$ . Работу внешних сил при перемещении тела из начального положения в конечное обозначим .

По теореме о кинетической энергии

$K_{2}-K_{1}=A$ .

Но работа консервативных сил равна разности потенциальных энергий:

$A=W_{1}-W_{2}$ .

Отсюда получаем:

$K_{2}-K_{1}=W_{1}-W_{2}$ ,

или

$K_{1}+W_{1}=K_{2}+W_{2}$ .

Левая и правая части данного равенства представляют собой механическую энергию тела в начальном и конечном положении:

$E_{1}=E_{2}$ .

Следовательно, при движении тела в поле силы тяжести и/или на пружине механическая энергия тела остаётся неизменной при отсутствии трения. Справедливо и более общее утверждение.

Закон сохранения механической энергии. Если в замкнутой системе действуют только консервативные силы, то механическая энергия системы сохраняется.

При этих условиях могут происходить лишь превращения энергии: из кинетической в потенциальную и наоборот. Общий запас механической энергии системы остаётся постоянным.

к оглавлению ▴

Закон изменения механической энергии.

Если между телами замкнутой системы имеются силы сопротивления (сухое или вязкое трение), то механическая энергия системы будет уменьшаться. Так, автомобиль останавливается в результате торможения, колебания маятника постепенно затухают и т. д. Силы трения неконсервативны: работа силы трения очевидным образом зависит от пути, по которому перемещается тело между данными точками. В частности, работа силы трения по замкнутому пути не равна нулю.

Снова рассмотрим движение тела в поле силы тяжести и/или на пружине. Вдобавок на тело действует сила трения, которая за рассматриваемый промежуток времени совершает отрицательную работу $A_{TP}$ . Работу консервативных сил (тяжести и упругости) по-прежнему обозначаем .

Изменение кинетической энергии тела равно работе всех внешних сил:

$K_{2}-K_{1}=A+A_{TP}$ .

Но $A=W_{1}-W_{2}$ , следовательно

$K_{2}-K_{1}=W_{1}-W_{2}+A_{TP}$ .

Отсюда

$K_{2}+W_{2}-(K_{1}+W_{1})=A_{TP}$ ,

или

$E_{2}-E_{1}=A_{TP}$ .

В левой части стоит величина $Delta E=E_{2}-E_{1}$ — изменение механической энергии тела:

$Delta E=A_{TP}$ .

Итак,при движении тела в поле силы тяжести и/или на пружине изменение механической энергии тела равно работе силы трения. Так как работа силы трения отрицательна,изменение механической энергии также отрицательно: механическая энергия убывает.
Справедливо и более общее утверждение.

Закон изменения механической энергии. Изменение механической энергии замкнутой системы равно работе сил трения, действующих внутри системы.

Ясно, что закон сохранения механической энергии является частным случаем данного утверждения.

Конечно, убыль механической энергии не противоречит общефизическому закону сохранения энергии. В данном случае механическая энергия превращается в энергию теплового движения частиц вещества и их потенциальную энергию взаимодействия друг с другом, т. е. переходит во внутреннюю энергию тел системы.

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Энергия.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
07.02.2023

Источник

$begingroup$

I was reading this chapter on conservation of energy and I couldn’t think of a suitable example for the argument given in the image attached. Now for friction to increase the mechanical energy of a system it has to be an external force as internal forces can’t change the total mechanical energy. But every example that I could think of, Friction was only decreasing the Mechanical energy of the system.

newtonian-mechanics
forces
energy-conservation
work
friction

Qmechanic♦

182k38 gold badges469 silver badges2095 bronze badges

asked Dec 11, 2021 at 12:55

VMnM7VMnM7

112 bronze badges

$endgroup$

$begingroup$
Can you think of situations where the speed (kinetic energy) or height (potential energy) of an object is increased as a result of friction ?
$endgroup$

Dec 11, 2021 at 13:23
$begingroup$
Friction cannot create kinetic or potential energy. However it can change types of energy. Consider a car engine that is production rotational energy that is transferred to the axel again rotational energy. If the tires are not slipping, it is the friction between the tires and the road that converts the rotational energy into liner kinetic energy. Again this is not creation of mechanical just the conversion of rotational kinetic energy into linear kinetic energy.
$endgroup$

Dec 11, 2021 at 13:49
$begingroup$
@Michael I agree. But if we consider the whole car to be a system, then the mechanical energy is conserved and not increased. Hence friction is not increasing the mechanical energy rather changing the form of energy as your rightly mentioned. But what will be the scenario in which it increases the mechanical energy? Or you are saying that there will be no such scenario?
$endgroup$

Dec 11, 2021 at 14:18
$begingroup$
@gandalf61 Nope. It either came out to be negative or zero.
$endgroup$

Dec 11, 2021 at 14:21

Источник

$begingroup$

newtonian-mechanics
forces
energy-conservation
work
friction

Qmechanic♦

182k38 gold badges469 silver badges2095 bronze badges

asked Dec 11, 2021 at 12:55

VMnM7VMnM7

112 bronze badges

$endgroup$

$begingroup$
Can you think of situations where the speed (kinetic energy) or height (potential energy) of an object is increased as a result of friction ?
$endgroup$

Dec 11, 2021 at 13:23
$begingroup$
Friction cannot create kinetic or potential energy. However it can change types of energy. Consider a car engine that is production rotational energy that is transferred to the axel again rotational energy. If the tires are not slipping, it is the friction between the tires and the road that converts the rotational energy into liner kinetic energy. Again this is not creation of mechanical just the conversion of rotational kinetic energy into linear kinetic energy.
$endgroup$

Dec 11, 2021 at 13:49
$begingroup$
@Michael I agree. But if we consider the whole car to be a system, then the mechanical energy is conserved and not increased. Hence friction is not increasing the mechanical energy rather changing the form of energy as your rightly mentioned. But what will be the scenario in which it increases the mechanical energy? Or you are saying that there will be no such scenario?
$endgroup$

Dec 11, 2021 at 14:18
$begingroup$
@gandalf61 Nope. It either came out to be negative or zero.
$endgroup$

Dec 11, 2021 at 14:21

Источник

Вы уже знаете, что механическая энергия тела (кинетическая и потенциальная) может изменяться. Внутренняя энергия тела также не является постоянной величиной, она может менять свое значение.

Внутренняя энергия зависит от температуры: при ее повышении внутренняя энергия увеличивается. Происходит это за счет увеличения средней скорости движения молекул и возрастания их кинетической энергии.

При понижении температуры внутренняя энергия, наоборот, понижается. Значит, внутренняя энергия тела меняется при изменении скорости движения молекул.

На данном уроке мы выясним, каким способом можно изменить скорость движения молекул. Таким образом, мы определим, при каких условиях происходит изменение внутренней энергии и дадим определения новым понятиям.

Совершение работы над телом

Рассмотрим опыт, представленный на рисунке 1.

Рисунок 1. Изменение внутренней энергии тела путем совершения работы над ним

У нас есть металлическая трубка, закрепленная на подставке. Наливаем в трубку немного эфира.

Эфир — бесцветная летучая жидкость. Часто употребляется в технике и медицине для дезинфекции. Имеет температуру кипения около $35 degree C$.

Закрываем пробкой. Обвиваем вокруг трубки веревку, и начинаем быстро двигать ее в разные стороны. Что произойдет?

После некоторого времени наших манипуляций с веревкой, эфир закипит. Его пар вытолкнет пробку.

Такой способ используется при разведении огня в диких условиях. Древние люди обладали им в совершенстве. При вращении сухой кусок дерева нагревался более чем на $250 degree C$ и загорался.

Внутренняя энергия эфира изменилась — она увеличилась. Он не только нагрелся, но и закипел. Натирая трубку веревкой, мы совершали механическую работу.

Также тела нагреваются при деформациях. То есть при ударах (вспомните опыт из прошлого урока с шаром из свинца), разгибании, сгибании (можно провести простой опыт, сгибая медную проволоку) и др.

Внутреннюю энергию тела можно увеличить, совершая над телом работу.

Когда нам холодно, мы начинаем дрожать — происходят мышечные сокращения. Таким образом наш организм увеличивает температуру тела — за счет работы мышц увеличивается внутренняя энергия.

Совершение работы самим телом

Рассмотрим опыт, представленный на рисунке 2.

Рисунок 2. Изменение внутренней энергии тела путем совершения работы самим телом

У нас имеется стеклянный сосуд, который закрывается пробкой. В пробке есть специальное отверстие. Через него с помощью насоса начнем закачивать в сосуд воздух.

Через некоторое время пробка вылетит. В этот момент можно заметить как образуется туман. Это означает, что воздух в сосуде стал холоднее.

Вытолкнув пробку, сжатый воздух в сосуде совершил работу. При этом температура воздуха понизилась. Так мы можем сказать, что его внутренняя энергия тоже уменьшилась.

Если работу совершает само тело, то его его внутренняя энергия уменьшается.

Внутреннюю энергию тела можно изменить путем совершения работы.

Теплопередача

Можно ли изменить внутреннюю энергию тела без совершения работы?

Мы часто наблюдаем ситуации, когда увеличивается температура тела. Например, закипание воды в чайнике, воздух нагревается от батарей отопления в квартире, нагреваются предметы, оставленные на солнце. Работа во всех этих примерах не совершается.

Попробуем объяснить увеличение внутренней энергии в таких случаях на следующем примере. Опустим обычную металлическую ложку в стакан с горячей водой (рисунок 3).

Рисунок 3. Изменение внутренней энергии тела без совершения работы

Что будет происходить?

Температура горячей воды намного больше температуры холодной ложки. Значит, кинетическая энергия молекул воды больше кинетической энергии частиц металлической ложки
Молекулы воды начинают взаимодействовать с частицами металла — передают им часть своей кинетической энергии
Энергия молекул воды уменьшается, энергия частиц металла увеличивается
Температура воды уменьшается, температура ложки увеличивается
Вскоре им температуры выравниваются

Внутреннюю энергию тела можно изменить путем теплопередачи.

Теплопередача — это процесс изменения внутренней энергии без совершения работы самими телом или над ним.

Происходит между телами с разной температурой
Идет в направлении от тел с более высокой температурой к телам с более низкой
Заканчивается, когда температуры тел выравниваются (становятся равны друг другу)

В мороз многие водоплавающие птицы (например, утки) охотно залезают в воду. В такую погоду температура воды выше температуры воздуха, что позволяет птицам не замерзать.

Способы изменения внутренней энергии тела

Итак,

внутреннюю энергию можно изменить двумя способами: совершая механическую работу или теплопередачей.

Существует три вида теплопередачи:

Теплопроводность
Конвекция
Излучение

Виды теплопередачи будут изучены нами в следующих уроках.

Источник

Если
частица массы m
движется со скоростью v,
то ее кинетическая
энергия
может быть представлена в виде

.
(1.3.57)

Кинетическая
энергия системы
частиц – величина аддитивная и
представляет собой сумму кинетических
энергий всех частиц системы:

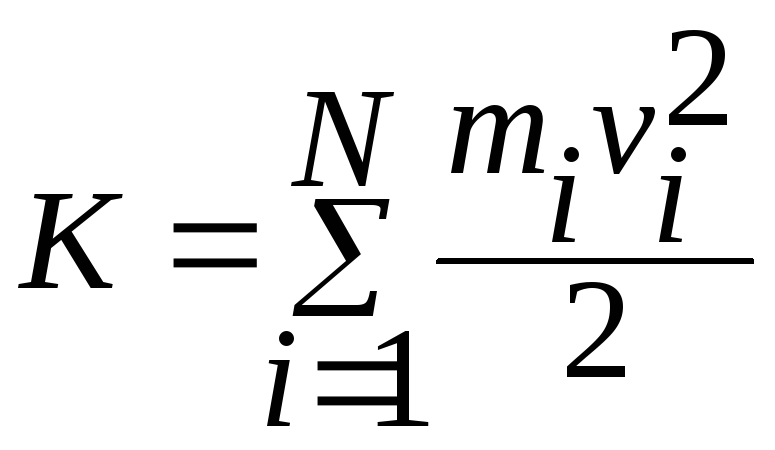
где
N
– число частиц в системе, m_i
– масса i-той
частицы, v_i
– скорость i-той
частицы.

*
Сила,
работа которой не зависит от формы и
длины пути (от
траектории точки приложения силы),
называется консервативной
силой.
Математически условие консервативности
силы выражается в виде:

что
означает:

*
циркуляция
консервативной силы по любому замкнутому
контуру равна нулю.

Из
определения консервативной силы следует:

работу
консервативной силы можно представить
как убыль некоторой скалярной функции

,
зависящей только от положения тела
(частицы), которая называется потенциальной
энергией:

Последняя
формула является определением
потенциальной энергии:

*
Потенциальная
энергия определена с точностью до
произвольной постоянной.

Так
как определена только разность
потенциальной энергии, то к выражению
для потенциальной энергии можно добавить
или вычесть любую постоянную величину.
Поэтому в каждом конкретном случае
договариваются о начале отсчета
потенциальной энергии (в какой именно
точке считают U
= 0).

Полная
механическая энергия частицы
– это сумма ее кинетической и потенциальной
энергий:

Если на частицу
действуют только консервативные силы,
то с одной стороны dA
= – dU
, с другой (из второго закона Ньютона):
dA
= dK

– dU
= dK,

d(K
+ U)
= dE=0 

Е = const
(1.3.58)

Выражение
(1.3.58) – это закон сохранения полной
механической энергии, который гласит:

*
механическая
энергия частицы, подверженной действию
только консервативных сил, сохраняется.

Неконсервативные
силы
– силы, работа которых зависит от длины
и формы пути. То есть, работа неконсервативных
сил на замкнутом пути не равна нулю, с
ними не связана потенциальная энергия.

Примеры:
сила трения скольжения, сила вязкого
трения.

Работа
силы трения скольжения зависит не от
перемещения тела, а от длины пути: A_тр
= – Nl,
и не равна
нулю при возвращении тела в исходную
точку.

Если
на частицу действуют как консервативные,
так и неконсервативные силы, то полная
механическая энергия этой частицы
сохраняться
не будет:

dE
= d(K
+ U)
= dA_неконс.
(1.3.59)

Выражение
(1.3.59) является математическим выражением
закона
изменения полной механической энергии:

*
Изменение полной механической энергии
частицы равно работе всех действующих
на нее неконсервативных сил:

Потенциальная
энергия системы
частиц
складывается из собственной
потенциальной энергии
U_соб
(энергия взаимодействия частиц системы
между собой) и внешней
потенциальной энергии
U_внешн:

U_сист
= U_соб
+ U_внешн,

где

Здесь
U_ij
– потенциальная энергия взаимодействия
i-той
и j-той
частиц системы; коэффициент 1/2
учитывает тот факт, что каждое слагаемое
в двойной сумме учитывается дважды.

Если
на каждую частицу системы действуют,
кроме внутренних, также внешние силы,
пусть тоже консервативные, то их работа
равна убыли внешней энергии dA
= – dU_внешн,

где .

Здесь
U_i
– потенциальная энергия i-той
частицы во внешнем поле. Она зависит от
положений всех частиц во внешнем поле
и является аддитивной (в отличие от
собственной энергии U_соб).

В
таком случае, полная механическая
энергия системы частиц запишется так:

E
= K_сист
+ U_соб
+ U_внешн.

*
Консервативной
называется система, полная механическая
энергия которой сохраняется:
E_сист
= сonst.
В такой
системе отсутствуют любые неконсервативные
силы (и внешние, и внутренние).

Заметим,
что консервативность системы и закон
сохранения энергии никак не связаны с
замкнутостью системы.

Закон
изменения полной механической энергии
системы:

*
Изменение
полной механической энергии системы
равно суммарной работе всех неконсервативных
сил:

dE_сист
= dA_неконс.

Кинетическая
энергия вращающегося вокруг закрепленной
оси твердого тела:

,
(1.3.60)

где
m_i
– масса i-той
частицы, R_i
– радиус окружности, по которой вращается
i-тая
частица, 
– угловая скорость вращения тела.

Продифференцируем
по времени формулу (1.3.60) и получим закон
изменения кинетической энергии
вращающегося вокруг закрепленной оси
твердого тела:

то
есть,

*
скорость
изменения кинетической энергии
вращательного движения равна мощности
результирующего момента сил относительно
оси вращения.

Отсюда

dK_вращ= M_zdt
= M_zd  K

K₂
– K₁
= 
M_zd,

то
есть,

*
изменение
кинетической энергии вращательного
движения равно работе момента сил.

Движение
твердого тела, при котором центр масс
перемещается в фиксированной плоскости,
а ось вращения тела, проходящая через
его центр масс, остается перпендикулярной
к этой плоскости, называется плоским
движением.
Типичным примером такого движения
является качение симметричного тела.

Это
движение можно свести к совокупности
поступательного движения и вращения
вокруг неподвижной
(закрепленной) оси.

Кинетическая
энергия тела, совершающего плоское
движение, запишется в виде

.
(1.3.61)

Здесь
V_С
– скорость движения центра масс тела.

Пример
22. Однородный
диск массы 1 кг и радиуса 1 м катится без
трения и проскальзывания. Скорость
центра масс диска составляет 1 м/с. Найти
кинетическую энергию диска.

Дано:
m
= 1 кг;

R
= 1 м;

V_C
= 1 м/с.

Найти:
К_плоск.

Решение.
Данное движение диска является плоским,
поэтому для кинетической энергии диска
запишем формулу (1.3.61):

Найдем
момент инерции диска, вращающегося
относительно оси, проходящей через его
центр масс из (1.3.52):

I_C
= (1/2)
mR²,

а
угловую скорость вращения диска из
(5.17): v
= R.

Имеем:

=
=

=
0,75 (Дж).

Ответ:
0,75 Дж.

Пример
23. Небольшая
шайба массы 1 кг, имея начальную скорость
10 м/с, останавливается, пройдя путь,
равный 5 м. Найти силу трения, действующую
на шайбу.

Дано:
m
= 1 кг;

V₀
= 1 м/с;

S
= 5 м.

Найти:
F_тр.

Решение.
В силу того, что во время движения на
шайбу действует сила трения, полная
механическая энергия шайбы изменяется,
причем из (1.3.59) имеем:

dE
= d(K
+ U)
= dA_неконс или
в интегральной форме, расшифровывая
работу силы трения,

Е
= A_неконс
= F_тр
Scos
= – F_тр
S,
(1.3.62)

так
как вектор силы трения противонаправлен
перемещению шайбы, то есть 
= 180,
cos180
= – 1.

Запишем,
чему равно изменение полной механической
энергии шайбы, используя (1.3.62):

,
откуда

= 10
(Н).

Ответ: 10 Н.

Пример 24.
Резиновая шайба массы 1 кг, двигаясь со
скоростью 1 м/с, соскальзывает с горки
высотой 1 м и приобретает скорость V
у подножия горки. Во время движения над
шайбой была совершена работа сил трения
А_тр
= 1 Дж. Считая, что ускорение свободного
падения составляет 10 м/с²,
найти скорость шайбы V.

Дано:
m
= 1 кг;

V₀
= 1 м/с;

А_тр
= 1 Дж;

g
= 10 м/с².

Найти: V.

Решение. Поскольку
во время движения шайбы на нее по условию
задачи действует сила трения, полная
механическая энергия шайбы изменяется.
Запишем закон изменения полной
механической энергии в интегральной
форме:

E
= Е₂
– Е₁
= A_тр.

Изменение
полной механической энергии:

,
откуда выразим
скорость, которую приобретает шайба у
подножия горки:

= 4,36 (м/с).

Ответ:
4,36 м/с.

Источник

Энергия: что это такое

Механическая энергия

Кинетическая энергия

Потенциальная энергия

Закон сохранения энергии

Переход механической энергии во внутреннюю

Закон сохранения энергии в тепловых процессах

Энергия.

Работа.

Мощность.

Механическая энергия.

Кинетическая энергия.

Потенциальная энергия тела вблизи поверхности Земли.

Потенциальна яэнергия деформированной пружины.

Закон сохранения механической энергии.

Закон изменения механической энергии.

Совершение работы над телом

Совершение работы самим телом

Теплопередача

Способы изменения внутренней энергии тела

Читайте также: