Как можно изменить момент силы маятника обербека

Лабораторная
работа № M-2

ИЗУЧЕНИЕ
ЗАКОНОВ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
НА
КРЕСТООБРАЗНОМ МАЯТНИКЕ ОБЕРБЕКА

1 Цель работы

Целью
работы является изучение законов
вращательного движения, определение
момента инерции J
маятника Обербека.

2 Оборудование
и принадлежности

Маятник Обербека,
секундомер, набор грузов.

3
Теоретическая часть

3.1
Основные определения и законы динамики
вращательного движения

Моментом
инерции
J
материальной точки массой m
относительно оси вращения называется
величина, равная произведению массы
точки на квадрат расстояния её до
рассматриваемой оси:
.

Моментом
инерции системы точек
(тела) относительно оси вращения
называется физическая величина, равная
сумме произведений масс n
материальных точек системы на квадрат
их расстояний до рассматриваемой оси:

. (1)

В
случае непрерывного распределения масс
эта сумма сводится к интегралу
,
где интегрирование производится по
всему объему тела. Величина r
в этом случае есть функция положения
точки с координатами x,
y,
z.

Если
известен момент инерции J_с
тела относительно оси, проходящей через
его центр масс, то момент инерции J
относительно любой другой параллельной
оси определяется теоремой Штейнера.

Теорема
Штейнера:
момент инерции тела J
относительно любой оси вращения равен
моменту его инерции J_с
относительно параллельной оси, проходящей
через центр масс C
тела, сложенному с произведением массы
тела на квадрат расстояния а
между осями:
.

Моментом
силы

относительно неподвижной точки О
называется физическая величина,
определяемая векторным произведением
радиус-вектора
,
проведенного из точки О в точку А
приложения силы, на силу
.
В векторном
виде
.

Рисунок 1 – Момент
силы

—
псевдовектор, его направление определяется
по правилу правого винта (рисунок 1).

Модуль момента
силы

.
(2)

Здесь
α
– угол между

и
,
rsinα=l
– кратчайшее расстояние между линией
действия силы и осью вращения и называется
плечом силы.

Основное
уравнение динамики вращательного
движения
твердого тела относительно неподвижной
оси: сумма моментов сил, действующих на
тело относительно оси, равно произведению
момента инерции этого тела относительно
той же оси на угловое ускорение,
приобретаемое телом

, (3)

в
векторной форме

.

Моментом
импульса

материальной точки А относительно
неподвижной точки О называется физическая
величина, определяемая векторным
произведением:

,

где

—
радиус-вектор, проведенный из точки О
в точку А;

—
импульс материальной точки.

—
псевдовектор, его направление определяется
по правилу правого винта.

Рассмотрим
абсолютно твердое тело, вращающееся
около неподвижной оси. Мысленно разобьем
это тело на маленькие объемы с элементарными
массами m_i,
находящиеся на расстоянии r_i
от оси вращения. При вращении эти объемы
будут иметь различные линейные
скорости

.

Момент
импульса твердого тела относительно
оси есть
сумма моментов импульса отдельных
частиц:

.
(4)

Скорость
поступательного движения


связана с угловой скоростью ω
следующим соотношением:.
При этом для абсолютно твердого тела
угловая скорость вращения составляющих
его частиц одинакова.

С
учетом этого, используя (1), запишем (4) в
виде
.

Т.о.
момент импульса твердого тела относительно
оси равен произведению момента инерции
тела относительно той же оси на угловую
скорость тела

.
(5)

Продифференцируем
уравнение (5) по времени:

.
(6)

Т.е.
основное
уравнение динамики вращательного
движения
твердого тела относительно неподвижной
оси (3) запишется в виде:

,

—
производная момента импульса твердого
тела относительно оси вращения равна
моменту сил относительно той же оси.

В
векторной форме
.

В
замкнутой системе момент внешних сил

и
,
откуда

или

, (7)

—
это выражение представляет собой закон
сохранения момента импульса.

Закон
сохранения момента импульса:
момент импульса замкнутой системы
сохраняется, т.е. не изменяется с течением
времени.

Рисунок 2 – Опыт
со скамьей Жуковского

Продемонстрировать
сохранение момента импульса можно с
помощью скамьи Жуковского (рисунок 2).
Человек, стоящий на скамье, которая без
трения вращается вокруг вертикальной
оси, держит в руках гири и вращается с
угловой скоростью ω₁
.
Если человек опустит руки, то его момент
инерции уменьшится, в результате чего
возрастет угловая скорость ω₂
его вращения. Закон сохранения момента
импульса для этого опыта: J₁ω₁=J₂ω₂
.

3.2
Описание экспериментальной установки

Маятник Обербека
(рисунок 3) состоит из четырех спиц 1
укрепленных на втулке 2 под прямым углом
друг к другу. На ту же втулку насажаны
два шкива 3 и 4 различных радиусов (r₁
и r₂).
Вся эта система может свободно вращаться
вокруг горизонтальной оси. Момент
инерции маятника Обербека можно менять,
передвигая грузы 5 вдоль спиц. Момент
сил, создается грузом 6 массой m,
подвешенным к нити 7, которая навита на
один из шкивов и перекинута через блок
8. Под действием момента сил система
будет вращаться равноускоренно с
постоянным угловым ускорением .
В нерабочем состоянии маятник удерживается
от вращения фиксирующим элементом 9.
Перемещение груза можно определять по
вертикальной шкале 10.

Рисунок
3 – Маятник Обербека

Момента
инерции J
маятника Обербека можно определить
теоретически как сумму моментов инерции
составляющих его частей относительно
оси вращения согласно (1) или экспериментально,
применяя понятия и законы динамики
вращательного движения.

Вращение
маятника Обербека под действием момента
результирующей силы М
подчиняется
основному уравнению динамики вращательного
движения (3).

Груз
m
движется равноускоренно. Измеряя время
t,
в течение которого груз m
из состояния покоя опустится на
расстояние h,
можно найти ускорение груза:

.
(8)

Угловое
ускорение
.
Если считать, что нить не проскальзывает
по ободу шкива, то ускорение груза будет
равно ускорению точек на ободе шкива,
а = r

= r,
отсюда:

, (9)

где
r
– радиус шкива.

Если
через F_н
обозначить силу натяжения нити, то
момент силы натяжения нити согласно
(2) равен:

М _н=
F_н
· r (10)

Силу
F_н
можно найти
из уравнения движения груза:

mg — F_н
=
ma
(11)

F_н
= m (g – a)
(12)

Момент
силы трения М_тр
обычно оказывается довольно велик и
способен существенно исказить результаты
опыта. Поэтому в (3) представим момент
силы, действующей на маятник Обербека,
как результирующую моментов сил натяжения
нити и трения:

М_н
– М_тр
=

=

(13)

Если
вращение равноускоренное и подчиняется
уравнению (13), то графически зависимость
углового ускорения от момента сил,
действующих на систему, будет представлять
собой прямую линию, проходящую через
точку с координатами [М_тр;
0] (рисунок 4). Коэффициент пропорциональности
и есть искомый момент инерции маятника
Обербека:

(14)

Таким
образом, если по экспериментальным
значениям удается построить график
функции
в
виде прямой наклонной линии, то можно
говорить о соблюдении основного уравнения
динамики вращательного движения (3).

Рисунок
4 – Зависимость углового ускорения от
момента сил, действующих на систему

Обратите
внимание, что экспериментальные точки
вследствие влияния погрешностей
измерений могут и не лежать на одной
прямой. Поэтому следует провести такую
усредненную прямую линию, для которой
отклонения точек в обе стороны будут
приблизительно одинаковыми. Прямая не
пересекает начало координат, так как
на систему действует момент силы трения.
Если масса m
груза, подвешенного на нити, мала, то
система может оставаться в равновесии.
Другими словами, вращение маятника
начнется только тогда, когда момент
силы натяжения М_н
будет больше момента сил трения М_тр.

4 Порядок выполнения
работы

1. Ознакомьтесь
   с параметрами системы, приведенными в
   таблице 1.

2. Убедитесь,
   что нить 7 навита на шкив 4 с бόльшим
   радиусом r₂
   и перекинута через блок 8 (рисунок 3).

3. Поверните
   фиксирующий элемент 9 и убедитесь, что
   маятник может свободно вращаться вокруг
   горизонтальной оси.

4. Укрепите
   на нити груз массой m₁
   и, осторожно вращая маятник, установите
   груз так, чтобы его нижний торец находился
   на отметке «0» на вертикальной шкале
   10.

5. С
   помощью секундомера определите время
   t₁,
   за которое груз опустится на расстояние
   h.
   Погасите вращение маятника с помощью
   фиксирующего элемента. Соблюдайте
   правила техники безопасности!

6. Занесите
   значение t₁
   в таблицу 2.

7. Повторите
   опыт для этого груза еще два раза,
   занесите в таблицу 1 значения t₂,
   t₃.

8. Повторите
   пункты 1-6 для грузов массами m₂,
   
   m₃,
   
   m₄,
   занесите в таблицу 1 результаты измерений.

9. Приведите систему
   в исходное состояние.

5
Обработка результатов

1. Вычислите
   среднее арифметическое значение времени
   движения каждого груза.

2. Для
   каждого груза по формуле (8) определите
   ускорение а.

3. Определите
   угловые ускорения 
   по формуле (9).

4. Принимая
   ускорение свободного падения g
   равным 9,81 м/с²,
   определите силу натяжения нити
   F_н
   (12)
   и момент этой силы М_н
   (10).
   Радиусы шкивов приведены в таблице 1.

5. По
   расчетным значениям постройте график
   зависимости
   .
   Сравните
   с рисунком 4. Сделайте вывод о характере
   вращения и соблюдении уравнения динамики
   вращательного движения (3).

6. По
   графику зависимости
   
   определите
   значение момента сил трения М_тр
   .
   Он будет соответствовать точке
   пересечения прямой с осью абсцисс.
   Запишите это значение.

7. По
   формуле (14) определите значение момента
   инерции J
   маятника
   Обербека. Заполните таблицу 2 результатов
   измерений.

Таблица 1 — Параметры
системы

Таблица
2 – Результаты измерений

1. Определите
   среднее значение момента инерции J_ср
   маятника
   Обербека.

2. Определите
   относительные погрешности прямых
   измерений _h,
   _t
   и _m,
   зная, что относительная погрешность
   величины Х

1. По
   наибольшей величине _max
   определите абсолютную погрешность
   .

2. Представьте
   ответ в виде
   ,
   кгм²
   .

6 Контрольные
вопросы

1. Что
   называется моментом инерции материальной
   точки, тела (системы материальных точек)
   относительно оси вращения?

2. От
   чего зависит момент инерции маятника
   Обербека в данной работе?

3. Изменится
   ли момент инерции маятника Обербека в
   данной работе при изменении радиуса
   шкива?

4. Основное
   уравнение динамики вращения тела вокруг
   неподвижной оси.

5. Сформулируйте
   закон сохранения момента импульса.
   Приведите примеры.

6. Решите
   приведенные ниже тестовые задания.

Задание 1

Задание
2

Задание
3

Задание
4

Если
момент инерции тела увеличить в 2 раза
и скорость его вращения увеличить в 2
раза, то момент импульса тела…

• Увеличится
  в
  раз

• Не
  изменится

• Увеличится
  в 4 раза

• Увеличится
  в 8 раз

Задание
5

Человек
сидит в центре вращающейся по инерции
вокруг вертикальной оси карусели и
держит в руках горизонтально длинный
шест за его середину. Если человек
повернет шест вертикально, то частота
вращения карусели в конечном состоянии…

• Не
  изменится

• Уменьшится

• Увеличится

Задание
6

Момент
импульса тела относительно неподвижной
оси изменяется по закону
.
Укажите график, правильно отражающий
зависимость от времени величины момента
сил, действующих на тело.

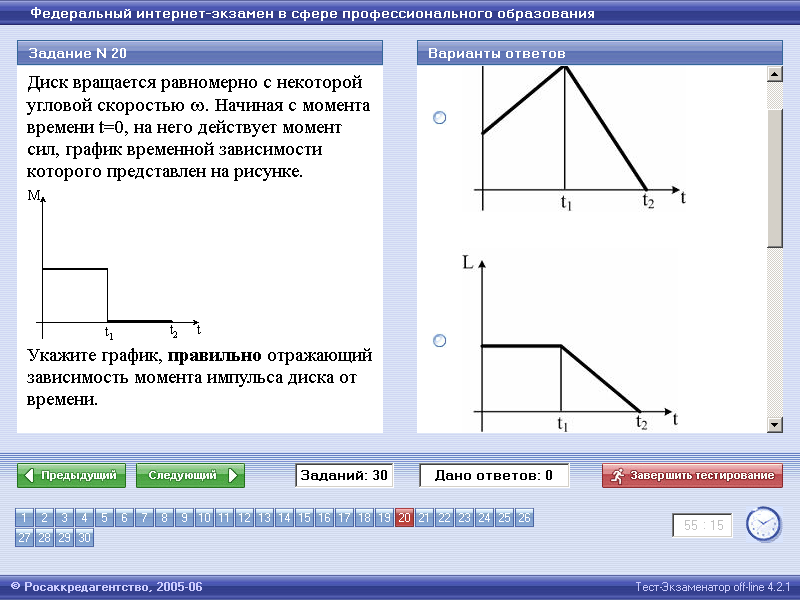
Задание
7

7

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Маятник Обербека состоит из шкива и стержней, укрепленных на одной неподвижной
горизонтальной оси, проходящей через центр симметрии системы. Относительно этой оси маятник может вращаться. На стержни насажены одинаковые
по массе грузы , которые
могут перемещаться и закрепляться в нужном положении. Передвижение грузов приводит к изменению момента инерции маятника. К шкиву
крепится гибкая нить, к свободному концу которой подвешивается груз массой . При поступательном движении груза момент силы натяжения приводит маятник во вращение.

I. Теоретическое введение.

Основной закон динамики твердого тела, вращающегося вокруг неподвижной оси, имеет вид:

где – алгебраическая сумма моментов сил, действующих на тело относительно оси вращения,

– момент инерции тела относительно той же оси,

– угловое ускорение.

Маятник Обербека вращается под действием момента силы натяжения нити (–сила натяжения,
— плечо этой силы, равное
радиусу шкива) и моменты силы трения .

Момент инерции маятника равен ,где — момент инерции системы без грузов (для
каждого маятника известен), — расстояние от
центра тяжести грузов до
оси вращения,
– число грузов , равное 3 или 4.

Уравнение (1) перепишем в виде:

Груз под действием силы натяжения нити и силы тяжести поступательного движения вниз. Пренебрегая растяжением нити, запишем II закон Ньютона в проекции на ось OY:

,

отсюда

Ускорение можно
найти из опыта. Нить наматывается на шкив, грузу предоставляется
возможность из состояния покоя пройти
расстояние , равное длине
нити. Одновременно измеряется время движения
груза. Из формулы кинематики рассчитывается ускорение:

Если нить перемещается по шкиву без проскальзывания, то тангенциальное ускорение
точек на поверхности шкива совпадает с ускорением .

Поэтому угловое ускорение маятника равно

Момент силы трения определим из закона сохранения энергии

Груз опускается
до нижней точки и затем поднимается на меньшую
высоту .
Убыль потенциальной энергии равна работе силы трения.

где —
изменение угла поворота шкива.

Перепишем (6):

, отсюда .

Обозначим

(7)

Тогда

(8)

Подставив (3), (5), (8) в (2), получим

(9),

II. Приложение.

Динамика вращательного движения

Краткие теоретические сведения

1. Момент инерции материальной точки

,

где — масса точки;

— расстояние до
оси вращения.

2. Моменты инерции тел правильной
   геометрической формы относительно оси,
   проходящей через центр:

В таблице —
радиус тел, — длина
стержня (ось перпендикулярна стержню)

3. Теорема Штейнера

Момент инерции тела относительно
произвольной оси равен

, где

— момент инерции
этого тела относительно оси, проходящей через
центр тяжести тела параллельно заданной оси;

— расстояние
между осями;

— масса тела.

4. Кинетическая энергия тела, вращающегося
   вокруг неподвижной оси:

, где

— момент инерции;

— угловая
скорость.

5. Момент силы, действующей в плоскости,
   перпендикулярной оси вращения

, где

— сила,

— плечо силы
(кратчайшее расстояние от оси вращения до линии
действия силы).

6. Момент импульса твердого тела

.

III. Практическая часть.

Порядок выполнения работы.
Выберите груз . Установите грузы на маятнике в
одно из двух возможных положений. Проведите
эксперимент, замерив при этом время опускания
груза и
расстояние недохода груза до первоначального
положения. Результаты занесите в протокол
испытаний и рассчитайте остальные величины.
Изменяя положение грузов и массу груза проведите
остальные опыты

Внимание!!! Перед выполнением работы посмотрите указания по выполнению лабораторных работ.

Для измерения времени опускания груза применяется секундомер.

Назначение кнопок секундомера показано на рисунке.

Часто задаваемые вопросы.

1. Как выбрать груз ? Для того чтобы выбрать груз
надо навести указатель мыши на него и нажать
левую кнопку мыши.

2. Как изменить положение грузов на маятнике Положение грузов на маятнике меняется путем нажатия левой кнопки мыши на маятнике.

Изучение основного закона динамики вращательного движения на маятнике Обербека

Экспериментальная проверка основного закона динамики вращательного движения твердого тела.

ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ

Набор грузов с известными массами.

Метровая линейка или рулетка.

ВЫВОД РАСЧЕТНОЙ ФОРМУЛЫ

Маятник Обербека представляет собой систему, состоящую из шкива и ступицы со спицами (рис. 1). Система может вращаться относительно неподвижной оси, проходящей через центр симметрии системы. На каждую из спиц насажены равные по массе грузы m, передвигая которые можно менять момент инерции системы. Грузы закрепляются на спицах винтами, масса которых входит в массу грузов. К шкиву крепится упругая нить, к свободному концу которой крепится груз массой m₀. Натяжение нити создает момент силы, приводящий маятник во вращение.

Основной закон динамики вращательного движения твердого тела имеет вид:

,

где M – алгебраическая сумма моментов сил, действующих на тело, относительно оси вращения; I – момент инерции тела относительно оси вращения; 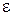– угловое ускорение.

Для маятника Обербека основной закон динамики вращательного движения принимает вид:

, (1)

где Т – сила натяжения нити, – момент силы трения системы, I₀ – момент инерции маятника Обербека без грузов, n – число грузов массой m, – расстояние от центра груза m до оси вращения (рис. 2), r – радиус шкива, равный для всех установок 5,9 см.

Экспериментальная проверка основного закона динамики вращательного движения на маятнике Обербека заключается в независимом определении левой и правой части соотношения (1) и их сравнении.

Из второго закона Ньютона для груза m₀ выразим силу натяжения нити

, (2)

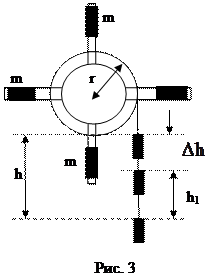
где 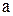– ускорение поступательного движения груза, g –ускорение свободного падения.

Для экспериментального определения силы натяжения нити необходимо знать массу груза и найти ускорение груза .

Масса груза известна. При необходимости массу можно определить с помощью технических весов.

Ускорение груза можно определить из эксперимента. Замотаем нить, на конце которой закреплен груз , на шкив маятника. Предоставим возможность грузу из состояния покоя пройти расстояние h за время t. Ускорение груза

Момент силы трения определим, оценив работу сил трения. Для этого предоставим грузу возможность опускаться с высоты , равной длине нити. Груз , опустившись до конца, затем поднимается на высоту (рис. 3). Убыль потенциальной энергии груза равна работе сил трения

. (3)

В экспериментальной установке силы трения действуют внутри системы, и момент силы трения можно считать постоянным. Работу сил трения можно вычислить по закону

, (4)

, (5)

где – угол поворота маятника, – число оборотов.

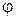
Из (3), (4) с учетом соотношения (5), получим

, (6)

. (7)

Зная длину нити и , можно определить коэффициент , а затем момент силы трения .

В правую часть (1) входят неизвестные величины и . Длину можно измерить экспериментально. При отсутствии проскальзывания нити по шкиву тангенциальное ускорение точек на поверхности шкива совпадает с ускорением поступательного движения груза , а угловое ускорение равно

. (8)

Соотношение (1) с учетом (2), (6) и (8) принимает вид

(9)

Это уравнение проверим экспериментально.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1. Запишите значение момента инерции I₀, число спиц n, массу груза m, радиус шкива r в таблицу (см. образец, табл.1).

2. Измерьте длину нити h с помощью рулетки или метровой линейки.

3. Грузы на спицах маятника установите в крайние положения и измерьте длину – расстояние от центра грузов m до оси вращения.

4. Подберите груз m₀ не менее 100 г.

5. Закрутите полностью нить на шкив маятника и отпустите груз без толчка, одновременно включив секундомер.

6. В крайнем нижнем положении груза m₀ фиксируйте время падения и дайте возможность закрутиться нити. В максимальной точке подъема груза m₀ остановите маятник и измерьте расстояние h. Чтобы убедиться в правильности фиксации времени падения, опыт проведите 5 раз.

7. Сдвиньте грузы m на спицах ближе к оси вращения и измерьте расстояние . Повторите опыт по измерению времени падения t и h для груза m₀.

8. Подберите груз m₀ меньше 100 г и проведите опыты как в предыдущих пунктах 5–7.

9. По результатам опытов вычислите ускорение груза, коэффициент , левую и правую части (9) для каждого из четырех проведенных опытов.

10. Результаты измерений и расчета занесите в таблицу (см. образец, табл.1).

11. Сравните результаты всех полученных четырех опытов. Установите, в каком опыте получается наименьшее расхождение между левой и правой частями (9). Попытайтесь проанализировать причины разных расхождений во всех опытах.

h, м	, м	m0, кг	t, с	, м	а, м/с 2		Левая часть (кг·м 2 /с 2 )	Правая часть (кг·м 2 /с 2 )
n=	g=9,8 м/с 2	m0=0,255 кг	r=0,059 м	I0= кг·м 2

1. Сформулируйте основную идею работы. Какие физические законы применяются для решения задач работы?

2. Выведите рабочую формулу для проверки основного закона динамики вращательного движения твердого тела.

3. Как при помощи маятника Обербека изменить момент инерции системы? момент внешней силы?

4. Запишите и сформулируйте основной закон динамики вращательного движения твердого тела относительно закрепленной оси. Сопоставьте его со вторым законом Ньютона, проведите аналогию.

5. Опишите экспериментальную установку. Из каких основных частей она состоит?

6. Как можно оценить момент сил трения, действующих в системе?

7. Что называется моментом инерции тела относительно оси и каков его физический смысл?

8. Запишите и сформулируйте теорему Штейнера.

9. Что называется моментом силы относительно оси? Как он направлен?

10. Какие предположения сделаны в данной работе относительно физических свойств нити? Обоснуйте их.

11. Какие величины используют для описания вращательного движения?

12. Чему равен момент импульса тела относительно оси?

13. Проведите аналогию между величинами и формулами для поступательного и вращательного движения твердого тела.

14. Могут ли единицы измерения различных физических величин иметь одинаковую размерность?

15. Как спортсмен, прыгая с трамплина в воду, управляет скоростью своего вращения?

БИБЛИОГРАФИЧЕСКИЙ СПИСОК ЛИТЕРАТУРЫ

1. Савельев, И. В. Курс физики. В 3-х т. Т. 1. Механика. Молекулярная физика./ И. В. Савельев.- М.: Наука, 1989.- 352 с.

2. Иродов, И. Е. Механика. Основные законы./ И. Е. Иродов.- М.: Лаборатория Базовых Знаний, 2001.- 256 с.

3. Волков, В. Н. Физика. В 3-х т. Т. 1. Механика. Молекулярная физика./ В. Н. Волков, Г. И. Рыбакова, М. Н. Шипко; Иван. гос. энерг. ун-т.- Иваново, 1993.- 230 с.

Динамика вращательного движения (на установке маятник Обербека)

Лабораторная работа М-8

ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ (на установке Маятник ОБЕРБЕКА)

Экспериментальное исследование динамики вращательного движения твёрдого тела на установке «Маятник Обербека»; экспериментальное определение момента инерции и момента силы трения.

2. ПОДГОТОВКА К РАБОТЕ

Изучите теоретический материал по учебникам [1], [2]: понятия абсолютно твёрдого тела (АТТ), момента силы, момента инерции; теорему Штейнера; закон вращательного движения АТТ. Ознакомьтесь с устройством лабораторного стенда, с методом косвенного измерения момента инерции и момента силы трения. Подготовьте ответы на вопросы для допуска.

3. КРАТКАЯ ТЕОРИЯ

Абсолютно твердое тело (АТТ) – это тело, деформациями которого можно пренебречь в условиях данной задачи.

Момент силы — величина, характеризующая внешнее воздействие на тело и определяющая изменение его вращательного движения. Относительно неподвижной точки О (рис.1) момент силы равен векторному произведению:

, (1)

где радиус-вектор, проведённый из точки вращения О в точку приложения силы, — угол между векторами и .

Момент силы относительно оси вращения z (рис.1) – это проекция вектора на эту ось.

Инерционность (инертные свойства) АТТ по отношению к вращающему воздействию момента характеризуется моментом инерции относительно оси вращения z . Величина равна сумме:

, (2)

где mi ­ — элементарные массы, на которые можно условно разбить АТТ, — их кратчайшие расстояния от оси z.

В случае тонкого стержня длиной и массой , вращающегося вокруг оси, проходящей через его центр масс, перпендикулярно стержню:

. (3)

При переносе оси вращения на расстояние d параллельно оси, проходящей через центр масс, величина рассчитывается по теореме Штейнера:

, (4)

где m — полная масса АТТ.

Для АТТ с неподвижной осью вращения z выполняется уравнение динамики вращательного движения:

, (5)

где — сумма моментов внешних сил относительно оси z, — момент инерции относительно этой же оси, — угловая скорость, — угловое ускорение.

4. ОПИСАНИЕ УСТАНОВКИ И МЕТОДИКА ПРОВЕДЕНИЯ ЭКСПЕРИМЕНТА

Устройство маховика Обербека (МО) показано на рис. 2. Вращающееся на горизонтальной оси тело выполнено в виде крестовины 1 с четырьмя стержнями, на которые надеты грузы 2. Положение грузов можно изменять. Такая конструкция позволяет регулировать величину момента инерции тела без изменения его полной массы. Крестовина с грузами приводится во вращение дополнительным грузом 3, массу которого можно изменять. Груз 3 закреплён на нити 4, наматываемой на шкив 5 и перекинутой через блок 6. Расстояние, проходимое по вертикали грузом 3, отсчитывается по шкале на вертикальной штанге 8. Для отсчёта верхней координаты груза 3 служит фиксатор 7. Время движения груза 3 измеряется электронным секундомером, снабжённым фотодатчиком 9. На оси вращения крестовины имеется электромагнитный тормоз, который автоматически останавливает движение МО в момент пересечения луча фотодатчика 9 грузом 3.

Покажем, каким образом на основе прямых измерений пути h и времени t движения груза 3 можно косвенно определить динамические параметры вращения МО.

Будем считать, что вращающиеся элементы МО представляют собой абсолютно твёрдые тела (закон (5) выполняется), действующие силы постоянны (движение равноускоренное), нить 4 — невесома и нерастяжима, а масса блока 6 – пренебрежимо мала.

В соответствии со схемой МО, представленной на рис. 3, уравнение вращательного движения крестовины имеет вид:

, (6)

— (7)

момент силы натяжения нити T0, — момент силы трения, r – радиус шкива 5 (направления векторов и показаны на рис. 3). В силу невесомости нити и блока 6 (рис. 2) модули сил натяжения нитей равны между собой: Т0= Т’= Т.

Для груза 3 массой m:

(8)

. (9)

Из кинематических соображений ускорение груза 3 равно:

. (10)

Поскольку нить нерастяжима, ускорения a и β связаны соотношением:

. (11)

Принимая грузы 2 с массами за материальные точки, полный момент инерции МО можно приближённо рассчитывать по формуле:

, (12)

где -расстояние грузов 2 до оси , -момент инерции всех остальных вращающихся элементов МО.

Сделаем выводы из полученных соотношений.

Из формулы (6) следует, что экспериментальный график должен быть прямой линией типас угловым коэффициентом:

, (13)

при этом отрезок, отсекаемый на оси ординат, равен

. (14)

График зависимости в соответствии с формулой (12) будет также прямой линией ,

где ; . (15)

5. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

5.1. Подготовка установки к работе (выполняет лаборант)

5.1.1. С помощью винтов на нижней платформе стенда отрегулировать вертикальное положение штанги 8. При этом груз 3 при опускании на нити должен проходить по центру отверстия фотодатчика 9, не задевая его стенок.

5.1.2. Включить секундомер в сеть 220 В. При этом кнопка на задней панели секундомера должна находиться в выключенном состоянии (шкала времени не освещена).

5.2. Измерение зависимости времени движения груза от его массы

5.2.1. Перемещая фиксатор 7 по шкале 8 и грузы 2 по стержням крестовины, установить величины и , указанные в первой и второй строках табл. 1 для вашей бригады. Величина , где — координата луча фотодатчика; — координата верхней кромки фиксатора; величина отсчитывается по сантиметровым делениям на стержнях, с добавлением расстояния 2 см от закрепляемого конца стержня до оси крестовины.

5.2.2. С использованием наборных грузов произвести трёхкратные измерения времени движения груза 3 в зависимости от величин его массы , указанных в табл. 1. Измерения проводятся в следующем порядке:

а) при выключенном секундомере вручную намотать нить на шкив 5 до совмещения нижней поверхности груза 3 с верхней кромкой фиксатора 7;

б) поддерживая крестовину, включить секундомер нажатием кнопки на его задней панели (при этом срабатывает электромагнитный тормоз на оси крестовины, и на шкале секундомера появляются нулевые показания);

в) кратковременным нажатием кнопки «Пуск» на передней панели секундомера привести МО в движение;

г) сразу после автоматической остановки движения МО записать показание со шкалы секундомера и выключить его кнопкой на его задней панели.

5.2.3. Полученные результаты записать в табл. 2.

5.3. Измерение зависимости времени движения груза от положения грузов на стержнях крестовины

5.3.1. Не изменяя величины , установить массу груза 3, указанную в третьей строке табл. 1 для вашей бригады.

5.3.2. В порядке, описанном в пункте 5.2.2., произвести однократные измерения времени при различных расстояниях грузов 2 от оси крестовины. Рекомендуемые величины указаны в табл. 3. Результаты записать в табл. 3.

6. ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ

И ОФОРМЛЕНИЕ ОТЧЁТА

6.1. Обработка результатов измерений пункта 5.2

6.1.1. По данным табл. 2 рассчитать средние значения и занести результаты в табл. 2.

6.1.2. Подставляя величины в формулы (10) и (11), рассчитать и записать в табл. 2 значения ускорений и . Радиус шкива r записан на установке.

6.1.3. По формуле (7) с учетом (9) определить величины моментов и записать их в табл. 2.

6.1.4. По данным табл. 2 построить график зависимости . Обработайте зависимость по методу наименьших квадратов (МНК). Для этого надо открыть папку «Обработка результатов ЛР» на рабочем столе компьютера и файл «Расчёт МНК». Результаты расчёта опытных величин и (см. формулы (13) и (14)) и соответствующие погрешности записать в табл. 2.

6.2. Обработка результатов измерений пункта 5.3

6.2.1. С использованием формул (6)-(11) можно получить формулу для расчета момента инерции (проверьте вывод самостоятельно):

(16)

По данным ti из табл. 3 по формуле (16) рассчитать значения . Занести результаты в табл. 3.

6.2.2. Обработайте полученную зависимость Iz(R2) по методу наименьших квадратов. Для этого необходимо открыть папку «Обработка результатов ЛР», расположенную на рабочем столе лабораторного компьютера, и открыть файл «Расчет y=Аx+В МНК. xls». Результаты расчёта опытных величин и (см. формулы (15)) с соответствующими погрешностями записать в табл.3.

6.2.3. Проведите сравнение значений , полученных в пунктах 6.1.4 и 6.2.2 при одинаковых значениях . Сравнить полученное значение с величиной, указанной на поверхностях грузов 2.

6.2.4. По известным значениям массы и длины стержней крестовины с помощью теоремы Штейнера рассчитайте их момент инерции. Оцените их вклад в величину , полученную в п. 6.2.2.

6.2.5. Сделайте выводы по полученным экспериментальным результатам.

7. ВОПРОСЫ ДЛЯ ДОПУСКА К ЛАБОРАТОРНОЙ РАБОТЕ

7.1. Дайте определения момента силы и момента инерции. Каким образом в установке можно регулировать и измерять эти величины?

7.2. Каким образом можно рассчитать момент инерции твёрдого тела при параллельном переносе оси вращения от центра масс на некоторое расстояние ? Как рассчитать момент инерции четырёх стержней крестовины со снятыми грузами при их известных массах и длинах?

7.3. Сформулируйте закон динамики вращательного движения абсолютно твёрдого тела? При каких условиях тело будет вращаться равноускоренно? Каковы направления векторов моментов вращающих сил в установке? Как определить моменты этих сил относительно оси вращения?

7.4. Какие приближения использованы в формуле (12) для расчёта момента инерции? При каком предположении можно считать движение равноускоренным?

7.5. Каким образом можно изменять момент инерции крестовины? Какой вращающий момент создает сила натяжения нити?

7.6. Каким образом зависит время опускания груза 3 от начальной высоты , его массы , расстояний грузов на крестовине от её оси, от момента силы трения?

7.7. Каково соотношение между ускорениями и ? Какие свойства нити 4 (рис. 2) необходимы для выполнения этого соотношения?

7.8. Как на основе формул (7) и (9) можно приближённо рассчитать момент силы натяжения нити, вращающей МО, если ускорение груза 3 будет намного меньше ускорения свободного падения?

Лабораторные работы по физике

ИЗУЧЕНИЕ ЗАКОНОВ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ НА МАЯТНИКЕ ОБЕРБЕКА

Цель работы: 1) изучение кинематических и динамических характеристик вращательного движения;

2) экспериментальное определение момента инерции крестовины маятника Обербека и момента сил трения;

3) проверка справедливости закона сохранения (превращения) энергии механической системы.

Схема экспериментальной установки

1 – ось вращения;

Основным элементом маятника Обербека (рис. 1) является крестовина, способная свободно вращаться вокруг неподвижной горизонтальной оси 1. Крестовина состоит из четырех стержней 2 с грузами-насадками 3, расположенными симметрично относительно оси вращения. С крестовиной жестко скреплен шкив 4 радиусом R. На шкив намотана нить 5, перекинутая через легкий блок 6. К свободному концу нити привязан груз 7, массу которого m можно изменять в процессе опытов. Для измерения высоты h расположения груза над полом служит линейка 8, а для измерения времени его падения – секундомер 9.

Если поднятый на высоту h груз отпустить, то он начнет падать с ускорением , которое определяется вторым законом Ньютона. На груз действуют две силы: сила тяжести и сила натяжения нити (сопротивлением воздуха в данном случае можно пренебречь). Уравнение основного закона динамики:

в проекциях на направление движения груза имеет вид:

Пренебрегая массами нити 5 и блока 6, можно считать, что нить действует на поверхность шкива касательной силой , равной по модулю силе : | | = | | = Fн . Касательная сила создает вращающий момент , по модулю равный произведению модуля силы на ее плечо, т.е. на радиус шкива R: Мн = Fн R. С учетом (1) вращающий момент силы натяжения нити равен

Под действием момента крестовина начинает вращаться с угловым ускорением . При этом на оси вращения возникают, хотя и незначительные, силы трения. Эти силы создают тормозящий момент , направленный противоположно угловому ускорению. С учетом направления моментов сил натяжения и трения алгебраическая запись уравнения основного закона динамики вращательного движения имеет вид

J e = Мн – Мтр , (3)

где J – момент инерции крестовины маятника Обербека относительно оси вращения.

Известно, что момент инерции зависит только от распределения массы тела относительно оси. Для крестовины маятника величина J определяется в основном положением грузов-насадок 3 на стержнях 2. Если их положение в ходе опытов не изменяется, то и момент инерции остается постоянным. Момент сил трения также можно считать практически неизменным. Поэтому зависимость углового ускорения e от момента силы натяжения Мн , согласно уравнению (3), имеет линейный характер. Определив опытным путем значения e при различных Мн и обработав соответствующим образом полученную экспериментальную зависимость e (Мн), с помощью этого уравнения можно найти неизвестные величины J и Мтр . Рассмотрим теперь методику измерения углового ускорения e и момента силы натяжения Мн .

Так как нить 5 практически нерастяжима, все ее точки, включая точки на поверхности шкива, движутся с одинаковым ускорением , равным по модулю ускорению падающего груза : | | = | | = a. Груз падает с высоты h равноускоренно; при этом за время t он проходит путь

Измерив высоту h и время падения груза t, можем найти ускорение

Если известны масса груза т и радиус шкива R, то по формуле (2) можно рассчитать момент силы натяжения нити Мн .

Угловое ускорение вращения шкива, а следовательно, и крестовины и тангенциальное (касательное) ускорение точек на поверхности шкива связаны известным соотношением

Таким образом, зная массу груза т, радиус шкива R и высоту h, с которой падает груз, а также измерив время его падения t, можно экспериментально определить величины e и Мн .

Рассмотрим теперь превращение энергии в вышеописанном опыте. Поднятый на высоту h груз обладает потенциальной энергией

кинетическая энергия системы «груз + крестовина» при этом равна нулю. В момент падения груза на пол его потенциальная энергия обращается в ноль, но за счет ее уменьшения груз приобретает кинетическую энергию

а крестовина – кинетическую энергию вращения

где v – скорость груза в момент падения; w – угловая скорость вращения крестовины к этому моменту.

Итак, начальное значение полной механической энергии рассматриваемой системы равно W0 = Wp , а конечное W = Wk1 + Wk2 . Изменение энергии:

Как известно, изменение полной механической энергии консервативной системы равно нулю, а при наличии неконсервативных сил – их работе. В данной системе действуют неконсервативные силы трения, работа которых равна

где j – угол поворота крестовины за время падения груза. Знак « – » отражает тот факт, что работа сил трения и сопротивления всегда отрицательна (угол между направлениями силы и перемещения равен 180 ° ). Итак, закон сохранения (превращения) энергии в данном случае можно записать как

С учетом соотношений (6)-(9) уравнение (10) примет вид:

Для экспериментальной проверки справедливости уравнения (11) необходимо знать все входящие в него величины. К ним относятся, во-первых, заранее известные ускорение свободного падения g, масса груза т и высота h; во-вторых, определяемые путем обработки экспериментальной зависимости момент инерции крестовины J и момент сил трения Мтр ; в-третьих, кинематические характеристики системы v, w и j . Остановимся на определении последних.

Скорость груза в момент его падения на пол найдем исходя из закономерностей равноускоренного движения:

Такую же по величине скорость имеют и точки на поверхности шкива. Используя связь между линейной и угловой скоростями, получим

Так как линейное расстояние, пройденное точками на поверхности шкива, равно перемещению груза за тот же промежуток времени, угол j (в радианах) может быть рассчитан как

Порядок измерений и обработки результатов

1. Запишите радиус шкива R , выразив его в метрах, в тетрадь (R=17мм).

2. Занесите во второй столбец таблицы 1 значение массы груза т (в кг).

3. Вращая крестовину, намотайте нить на шкив так, чтобы нижняя поверхность груза 7 оказалась на заданной высоте h над полом, запишите значение высоты в тетрадь (значение h задает преподаватель или спишите с экрана монитора).

4. Отпустив крестовину, одновременно включите секундомер, а в момент касания грузом пола – выключите. Запишите время падения в третий столбец таблицы 1.

5. Повторите пп. 3 и 4 с тем же грузом еще два раза. Рассчитайте и занесите в таблицу среднее из трех значений времени t.

6. Увеличивая массу груза согласно рекомендациям, выполните пп. 2-5 еще пять раз.

7. Для каждого из шести проделанных опытов рассчитайте ускорение а по формуле (4), подставляя в нее среднее из трех измеренных значений времени падения t. Величину а (с точностью не менее чем до трех значащих цифр) запишите в четвертый столбец таблицы 1.

8. По формулам (2) и (5) вычислите значения момента силы натяжения нити Мн и углового ускорения e . Результаты занесите в соответствующие столбцы табл. 1.

9. Руководствуясь правилами [1], постройте график зависимости углового ускорения от момента силы натяжения (в данной работе необходимо, чтобы начало координат совпадало с нулевыми значениями откладываемых величин e и Мн). Нанесите на график экспериментально полученные точки.

10. Одним из описанных ниже способов* обработайте линейную экспериментальную зависимость e (Мн) и найдите значения момента инерции крестовины J и момента сил трения Мтр. Запишите эти значения в тетрадь.

11. Для одного из проделанных опытов рассчитайте по формулам (12)-(14) скорость груза v, угловую скорость вращения w и угол поворота j крестовины маятника Обербека в момент падения груза на пол.

12. Вычислите значения левой и правой частей уравнения закона сохранения энергии (11). Сравнив эти значения между собой, сделайте выводы.

Обработка зависимости e (Мн)

Угловое ускорение крестовины e и момент силы натяжения нити Мн связаны уравнением основного закона динамики вращательного движения (3). Зависимость e (Мн) можно представить в виде

где . Таким образом, определив коэффициенты линейной зависимости (15) K и b, легко найти момент инерции J и момент сил трения Мтр :

Обработку экспериментальной зависимости e (Мн) можно провести либо графически, либо методом наименьших квадратов.

Графический способ. По экспериментальным точкам проведите сглаживающую прямую. Из уравнения (3) следует, что угловое ускорение e обращается в нуль при Мн = Мтр . Таким образом, момент сил трения Мтр определяется (с учетом масштаба!) отрезком, отсекаемым проведенной прямой на оси абсцисс (рис. 2).

Величина K в уравнении (15) представляет собой угловой коэффициент прямой, т.е. тангенс угла ее наклона к оси абсцисс. Согласно (16), момент инерции J есть величина, обратная K, – значит, его можно найти как котангенс этого угла. Выбрав на сглаживающей прямой две достаточно удаленные друг от друга точки, рассчитайте значение J как отношение отрезков

причем величины отрезков D Мн и D e должны быть взяты с учетом масштаба графика и выражены в соответствующих единицах измерения: D Мн – в Н × м, а D e – в рад/с2 или в с – 2. Только в этом случае результат будет правильным, и момент инерции будет иметь размерность кг × м2.

Метод наименьших квадратов. (Подробно этот метод рассмотрен в [1]). Изучив данный материал, заполните два последних столбца табл. 1. Найдите суммы значений величин в последних четырех столбцах и занесите их в строку « S = ». Вычислите коэффициенты K и b зависимости (15); результаты расчетов запишите в тетрадь. Для определения момента инерции крестовины J и момента сил трения Мтр воспользуйтесь соотношениями (16). На графике зависимости e (Мн) проведите прямую по двум точкам, координаты которых рассчитайте по найденным значениям коэффициентов. Убедитесь в правильности проведенных расчетов (прямая должна «наилучшим» образом пройти через экспериментальные точки).

Какие величины характеризуют вращательное движение?

Что характеризует момент инерции твердого тела относительно оси вращения? Как он рассчитывается?

Сформулируйте и докажите теорему Штейнера.

Как изменится кинетика опускания гири, если грузы на крестовине передвинуть ближе (дальше) к оси вращения.

Дайте определение момента силы. Какие моменты сил действуют на крестовину маятника Обербека в этой работе.

Запишите математически и сформулируйте главный закон динамики вращательного движения.

Покажите, что в пренебрежении трением, расчетная формула для момента инерции маятника Обербека будет иметь вид:
.

Запишите и поясните закон сохранения (превращения) механической энергии в этой работе.