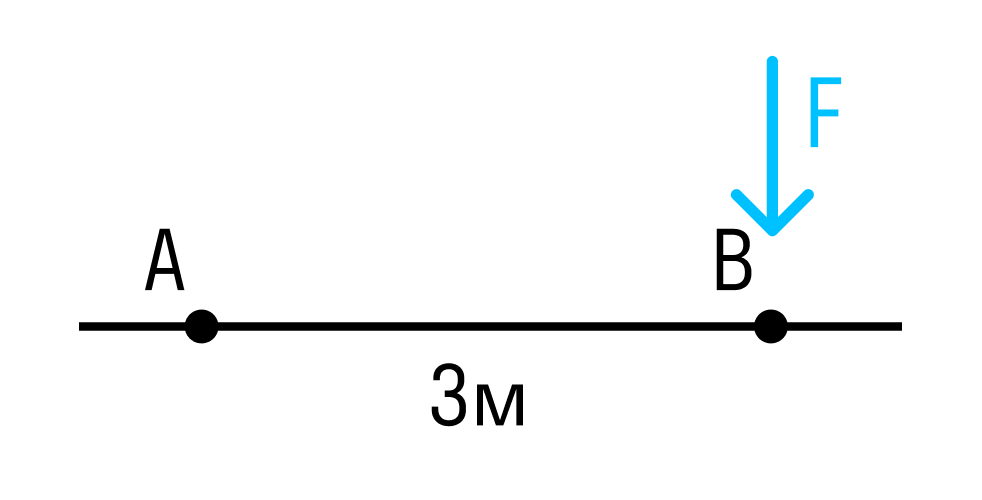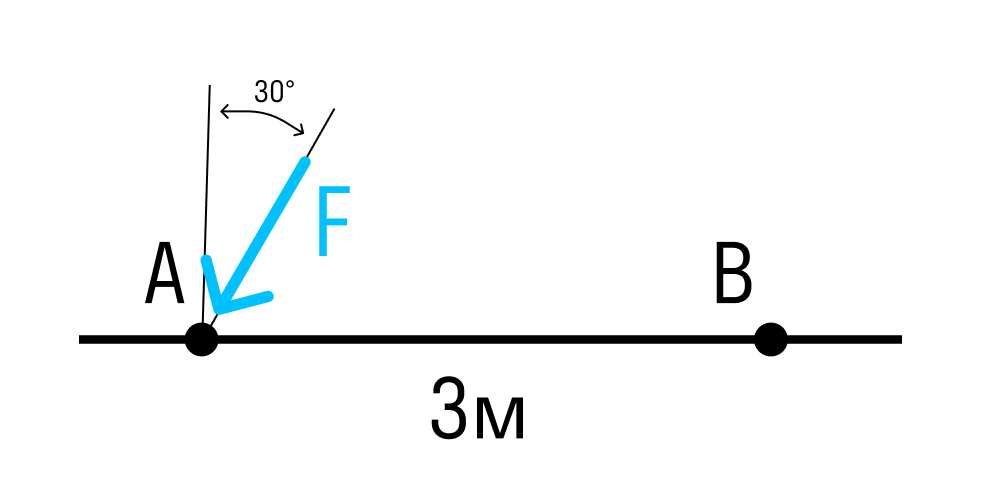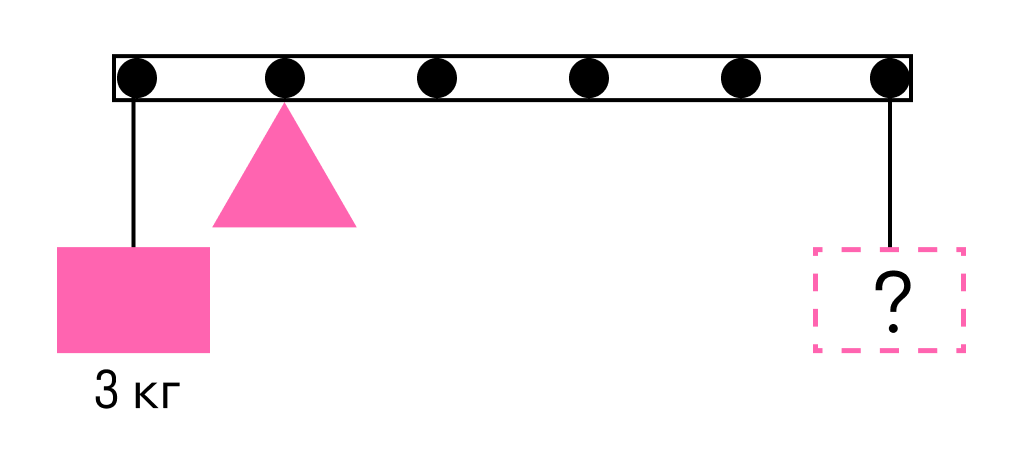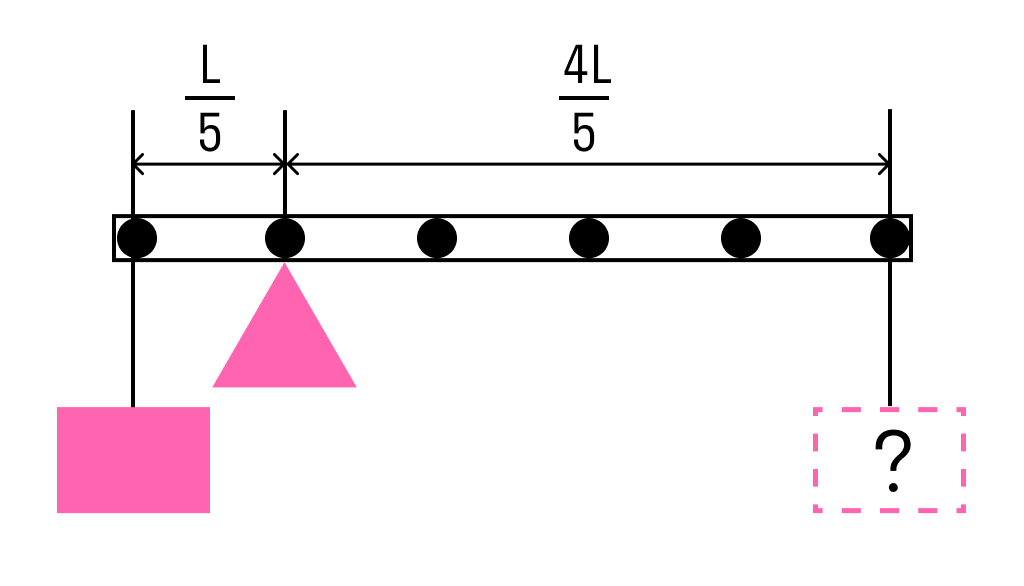Как можно изменить момент силы не меняя величину силы - Исправление ошибок и поиск оптимальных решений проблем

5.1 Момент силы относительно центра (или
точки)

В
ведем
важное понятие о моменте силы относительно
точки. Точку, относительно которой
берется момент, называют центром
момента, а момент силы относительно
этой точки – моментом относительно
центра.

Если под действием приложенной силы
тело может вращаться вокруг некоторой
закрепленной точки, то момент силы
относительно этой точки будет
характеризовать вращательный эффект
силы. Вращательное действие силы на
тело будет зависеть от модуля силы,
расстояния линии действия силы до точки
закрепления и от направления вращения
в этой плоскости.

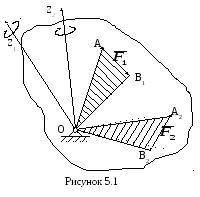
Так, например, если к телу, закрепленному
неподвижно в точке О (рисунок 5.1), приложена
в точке A₁ сила
,
то тело будет вращаться вокруг оси OZ₁,
перпендикулярно плоскости треугольника
OA₁B₁,
в направлении, указанном на рисунке.
Если к этому же телу приложена сила

в точке A₂, то тело
будет вращаться вокруг оси OZ₂,
перпендикулярно к плоскости треугольника
OA₂B₂.

Мерой вращательного действия силы
на тело с закрепленной точкой является
момент силы относительно точки.

Алгебраическая величина момента
силы относительно точки, определяется
произведением модуля силы на ее плечо.

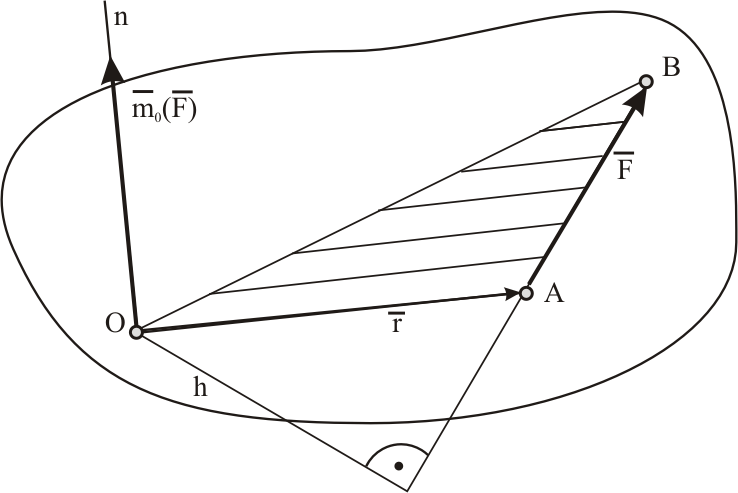
Рассмотрим силу F,
приложенную в точке А (рисунок 5.2). Из
некоторого центра О опустим перпендикуляр
на линию действия силы
;
длину h этого перпендикуляра
называют плечом силы

относительно центра О.

Рисунок 5.2

Момент силы относительно центра О
определяется:

1) модулем момента, равным произведению
F·h;

2) положением в пространстве плоскости
ОАВ («плоскости поворота»), проходящей
через центр О и силу
;

3) направлением поворота в этой плоскости.

Из геометрии известно, что положение
плоскости в пространстве определяется
направлением нормали «n»
(перпендикуляра) к этой плоскости. Таким
образом, момент силы относительно центра
характеризуется не только его числовым
значением, но и направлением в пространстве,
т.е. является величиной векторной.

Моментом силы F
относительно центра О называется
приложенный в центре О вектор
,
модуль которого равен произведению
модуля силы

на ее плечо h и
который направлен перпендикулярно
плоскости, проходящей через центр О и
силу, в ту сторону, откуда сила видна
стремящейся повернуть тело вокруг
центра О против хода часовой стрелки
(рисунок 5.3).

Согласно этому определению

(5.1)

Этот результат следует из того, что пл.
Δ ОАВ= АВ·h/2=Fh/2.
Измеряется момент силы в Ньютон-метрах
(Нм). Выведем формулу, для вектора-момента
силы

относительно точки О. Для этого рассмотрим
векторное произведение

векторов

и

(рисунок 5.3). Как известно из векторной
алгебры, это будет вектор, перпендикулярный
к плоскости, в которой расположены
векторы

и
,
и направленный в такую сторону, чтобы
с его конца видеть поворот от

к

кратчайшим путем против хода часовой
стрелки. Модуль этого вектора

или
.

Поэтому

или
, (5.2)

где

– радиус-вектор точки А, проведенный
из центра О.

Таким образом, вектор-момент силы
относительно точки равен векторному
произведению радиуса-вектора точки
приложения силы на вектор силы.

Обозначая алгебраическое значение
момента силы относительно точки О через
,
будет иметь

(5.3)

Из формулы (5.3) следует, момент силы
относительно точки, лежащей на линии
действия этой силы, равен нулю (т.к. h=0).

Пример.

Вычислить моменты сил
,
относительно точки O.

Решение

Вектор

направлен перпендикулярно плоскости
OAEN, т.е. по прямой OL.
,
т.к. линия действия силы

проходит через точку O.

Векторы

и

перпендикулярны к плоскости ОВDN,
но направлены в противоположные стороны.
Вектор

перпендикулярен к плоскости ОАВL
и направлен по прямой ON.

5.2 Пара сил. Момент пары сил

Парой
сил называется система двух равных по
модулю, параллельных и направленных в
противоположные стороны сил, действующих
на абсолютно твердое тело (рисунок 5.3,
а).

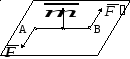
а) б)

Рисунок 5.3

Система сил
,
,
образующих пару, не находится в равновесии
(эти силы не направлены вдоль одной
прямой). В то же время пара сил не имеет
равнодействующей, т.к. равнодействующая
любой системы сил равна ее главному
вектору
,
т.е. сумме этих сил, но для пары сил
,
поэтому свойства пары сил, как особой
меры механического взаимодействия тел,
рассмотрим отдельно.

Плоскость, проходящая через линии
действия пары сил называется плоскостью
действия пары. Расстояние
d между линиями
действия сил пары называется
плечом пары. Действие
пары сил на твердое тело сводится к
вращательному эффекту, который
характеризуется величиной, называемой
моментом пары. Этот момент
определяется:

1) Его модулем, равным произведению F·d;

2) положением в пространстве плоскости
действия пары;

3) направлением поворота пары в этой
плоскости.

Таким образом, как и момент силы
относительно центра, это величина
векторная. Поэтому моментом пары сил
называется вектор

(или
),
модуль которого равен произведению
модуля одной из сил пары на ее плечо и
который направлен перпендикулярно
плоскости действия пары в ту сторону,
откуда пара видна стремящейся повернуть
тело против хода часовой стрелки
(рисунок 5.3, б).

Следует отметить, что так как плечо силы

относительно точки А равно d
(рисунок 5.3, а), а плоскость, проходящая
через точку А и силу
,
совпадает с плоскостью действия пары,
то одновременно
.

В отличие от момента силы

может быть приложен в любой точке (такой
вектор называется свободным).
Измеряется момент пары, как и момент
силы, в Н·м.

Покажем, что моменту пары можно дать
другое выражение: момент пары равен
сумме моментов относительно любого
центра О сил, образующих пару, т.е.

(5.4)

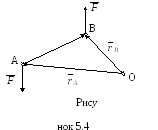
Для доказательства проведем из
произвольной точки О (рисунок 5.4)
радиусы-векторы

и
.

Тогда согласно формуле (5.2), учитывая,
что
,
получим
;

и, следовательно,

Так как
,
то справедливость (5.4) доказана. Отсюда
следует, что

или

(5.5)

т.е. момент пары равен моменту одной
из ее сил относительно точки приложения
другой силы. Отметим еще, что модуль
момента пары

(5.5^/)

Так как действие пары сил на твердое
тело определяется значением суммы
моментов сил пары относительно любого
центра О, то из формулы (5.4) следует, что
две пары сил, имеющие одинаковые
моменты, эквивалентны, т.е. оказывают
на тело одинаковое механическое действие.
Это означает, что две пары сил, независимо
от того, где каждая из них расположена
в данной плоскости (или в параллельных
плоскостях) и чему равны в отдельности
модули их сил и их плечи, если моменты
имеют одно и то же значение
,
будут эквивалентны. Так как выбор центра
О произволен, то вектор

можно считать приложенным в любой точке,
т.е. это свободный вектор.

В дальнейшем будем на чертеже вместо
пары изображать полностью ее характеризующий
вектор
.
При этом модуль

определяет модуль момента пары [формула
(5.5)], а направление

определяет плоскость действия пары и
направление поворота в этой плоскости.

Из формулы (5.4) следует, еще, что если на
тело действует несколько пар с моментами
;
….,
то сумма моментов всех сил, образующих
эти пары относительно любого центра
будет равна
++…+,
а следовательно, вся совокупность этих
пар эквивалентна одной паре с моментом

(5.6)

Этот результат выражает теорему о
сложении пар.

Из формулы (5.6) следует, при равновесии
системы пар, действующих на твердое
тело, должно быть

или
(5.6^/)

Таким образом, отметим следующие свойства
пар сил:

1) Пары сил, лежащие в одной плоскости,
эквивалентны, если их моменты численно
равны и одинаковы по знаку.

2) Пару сил, не изменяя ее действия на
твердое тело, можно переносить в любое
место в плоскости ее действия, поворачивать
ее плечо на любой угол, не изменяя
величины ее момента и направления
вращения.

3) Пары сил в пространстве эквивалентны,
если их моменты геометрически равны.

4) Не изменяя действия пары сил на твердое
тело, пару сил можно переносить в любую
плоскость, параллельную плоскости ее
действия, а также изменять ее силы и
плечо, сохраняя неизменным модуль и
направление ее момента. Таким образом,
вектор-момент пары можно переносить в
любую точку, т.е. вектор-момент пары сил
является свободным вектором.

5) Геометрическая сумма моментов
составляющих пар равна моменту
эквивалентной им пары сил:

или

(5.7)

6) Пары сил, произвольно расположенные
в пространстве, взаимно уравновешиваются
в том случае, если геометрическая сумма
их моментов равна нулю, т.е. условие
равновесия пар сил в пространстве имеет
вид:

(5.8)

7) Момент пары сил эквивалентной системе
пар сил на плоскости, равен алгебраической
сумме моментов составляющих пар:

(5.9)

Пары сил, расположенные в одной
плоскости, взаимно уравновешиваются,
если алгебраическая сумма их моментов
равна нулю.

(5.10)

Т.е. выражение 5.10 является условием
равновесия пар сил на плоскости, а (5.8)
– в пространстве.

Вопросы
для самоконтроля

Момент силы относительно точки

Что называется моментом силы относительно
точки?
Как направлен вектор момента силы
относительно точки?
Запишите формулу, по которой определяется
алгебраический момент силы относительно
точки.
Какой площадью можно определить числовое
значение момента силы относительно
заданной точки?
Изменится ли момент силы относительно
данной точки при переносе силы вдоль
линии ее действия?
В каком случае момент силы относительно
данной точки равен нулю?
Определите геометрическое место точек
пространства, относительно которых
моменты данной силы:
1. геометрически равны;
2. равны по модулю.
Определите момент силы относительно
точки O, если F=200H;
OA=0.5м (рисунок 5.5).

Рисунок 5.5

9. Определить моменты сил

и

относительно координатных осей, если

КН,

КН, ОА = 0,4 м; ОВ = 0,6 м; ОС = 0,3 м (рисунок
5.5).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Плоская система сил

Система сил, действующих на плоскости, называется плоской системой сил. Особенностью плоской системы сил заключается в том, что линии действия этих сил уже не пересекаются в одной точке.

Одним из важнейших понятий плоской системы сил является понятие пары сил.

Пара сил

Парой сил называется система двух, равных по модулю, параллельных и направленных в противоположные стороны сил, действующих на абсолютно твердое тело.

Пара сил может быть обозначена как . Плечом пары сил называется длина перпендикуляра, проведенного к линиям действия сил, составляющих пару.

Согласно аксиоме №1 пара сил не находится в равновесии и не имеет равнодействующую.

Момент пары сил. Моментом пары сил является сумма моментов сил составляющих пару относительно произвольного центра .

Вычисление алгебраического момента пары сил. Для вычисления алгебраического момента пары сил, удобно воспользоваться результатом следующей теоремы.

Теорема. Алгебраическая сумма моментов сил, составляющих пару, относительно любого центра, лежащего в плоскости действия пары сил не зависит от выбора этого центра. Момент пары сил равен произведению одной из сил, составляющих пару на плечо пары.

Доказательство.

Пусть в плоскости действует пара сил, как показано на рис.С.24.

Обозначим плечо силы vec F относительно центра буквой . Тогда плечо силы относительно центра будет равно величине (a + b) , где является плечом пары сил.

Тогда, согласно определению алгебраического момента пары сил и в соответствии с правилом знаков для момента силы относительно центра можно записать

${M_o} = F cdot (a + b) - F cdot a = F cdot b$ (С.7)

Таким образом, алгебраический момент пары сил не зависит от расстояния до центра и равен произведению модуля силы vec F на плечо пары.

Что и требовалось доказать.

В дальнейшем необходимо рассмотреть следующие теоремы, выражающие основные свойства пар сил и устанавливающие условие эквивалентности двух пар сил.

Теорема. Две пары сил, лежащие в одной плоскости и имеющие численно равные моменты и одинаковое направление вращения, эквивалентны.

Доказательство.

Пусть на абсолютно твердое тело действует пара сил $left{ {{{vec F}_1},{{vec F}_2}} right}$ , причем ${vec F_1} = - {vec F_2}$ . Будем считать, что сила ${vec F_1}$ приложена в точке , а сила ${vec F_2}$ приложена в точке (рис.С.25).

Доказательство теоремы проведем в несколько этапов.

1. Проведем прямую линию , соединяющую точки и , а также параллельные прямые ${a_1}$ и ${a_2}$ , являющиеся линиями действия сил ${vec F_1}$ и ${vec F_2}$ .

2. Проведем две произвольные параллельные прямые ${b_1}$ и ${b_2}$ , проходящие соответственно через точки и .

3. Разложим силу ${vec F_1}$ по направлениям $({b_2},c)$ , а силу ${vec F_2}$ по направлениям $({b_1},c)$ (рис.С.26).

Получим ${vec F_1} = {vec Q_1} + {vec P_1}$ и ${vec F_2} = {vec Q_2} + {vec P_2}$ .

4. Согласно теореме Вариньона

$mo{m_A}({vec F_1}) = mo{m_A}({vec P_1}) + mo{m_A}({vec Q_1})$

Причем $mo{m_A}({vec Q_1}) equiv 0$ , так как линия действия силы ${vec Q_1}$ (линия ) проходит через точку .

Таким образом, $mo{m_A}({vec F_1}) = mo{m_A}({vec P_1})$ .

Аналогичным образом получаем, что $mo{m_B}({vec F_2}) = mo{m_B}({vec P_2})$ .

Из последних формул следует, что момент пары сил $left{ {{{vec F}_1},{{vec F}_2}} right}$ эквивалентен моменту пары сил $left{ {{{vec P}_1},{{vec P}_2}} right}$ . Что и требовалось доказать.

Из доказанной теоремы вытекают два важных следствия.

Следствие 1. У данной пары сил, не изменяя оказываемого действия, можно менять величину и направление сил, а также длину плеча, сохраняя при этом величину момента силы.

Следствие 2. Данную пару сил, не изменяя оказываемого действия, можно переносить куда угодно в плоскости действия пары. Следовательно, действие пары на тело не зависит от положения пары в ее плоскости. Таким образом, момент пары является свободным вектором!

Теперь необходимо разобраться со следующей важной проблемой. Можно ли, не меняя оказываемого действия, переносить силу, приложенную к заданной точке абсолютно твердого тела параллельно самой себе в любую другую точку ?

На этот вопрос отвечает следующая теорема.

Источник

Сила: что это за величина

В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или замедляется, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причиной любого действия или взаимодействия является сила.

Сила — это физическая векторная величина, является мерой действия тела на другое тело.

Она измеряется в ньютонах — это единица измерения названа в честь Исаака Ньютона.

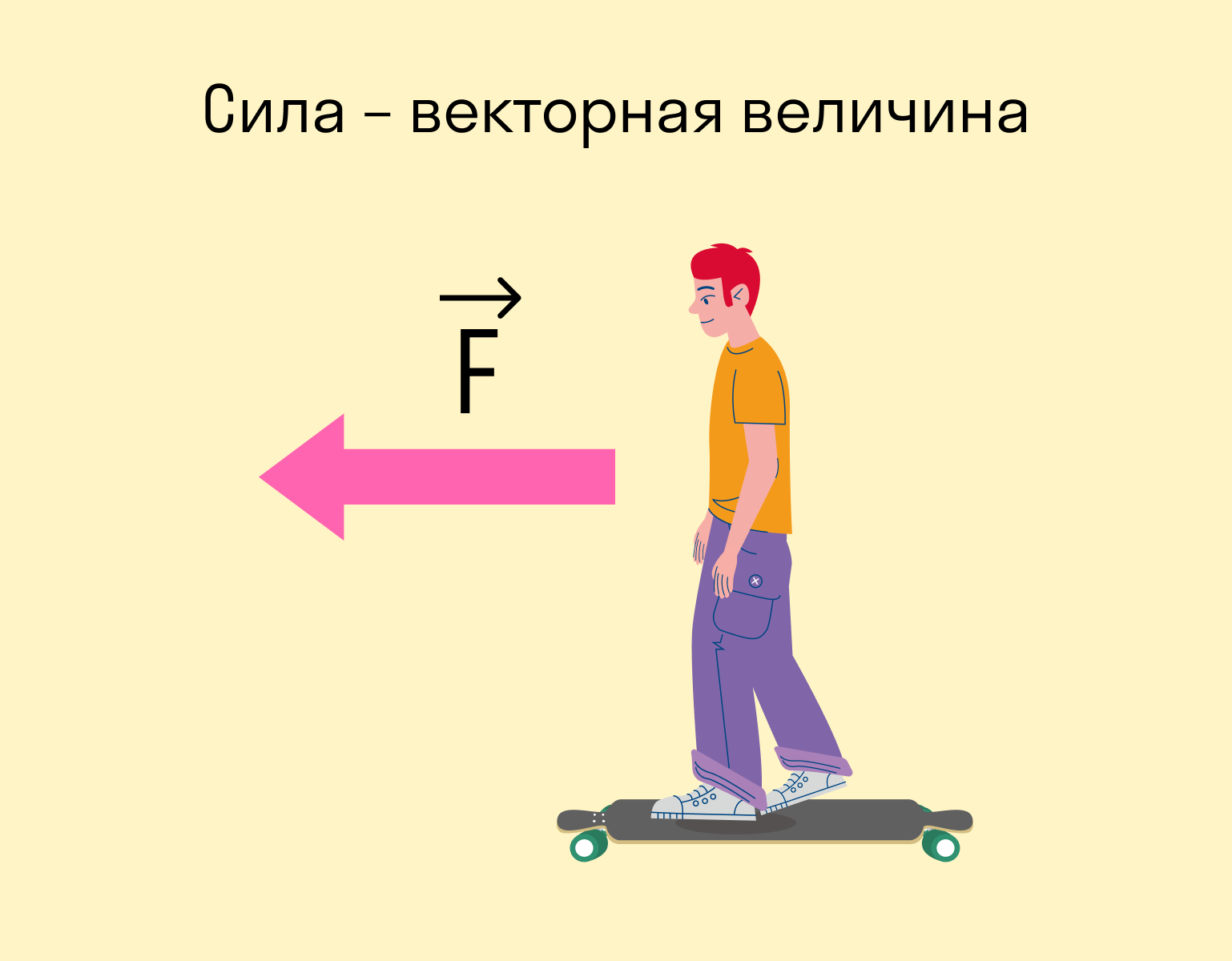
Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат.

Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В данном случае результат выражается в направлении движения.

Получай лайфхаки, статьи, видео и чек-листы по обучению на почту

Пятерка по физике у тебя в кармане!

Решай домашку по физике на изи. Подробные решения помогут разобраться в сложной теме и получить пятерку!

Плечо силы

Для начала давайте разберемся, что такое плечо силы — оно нам сегодня очень пригодится.

Представьте человека. Совершенно обычного. Если он совершенно обычный, у него точно будут плечи — без них получится уже какой-то инопланетянин. Если мы прочертим прямую вдоль линии плеча, а потом еще одну — вдоль линии руки — мы получим две пересекающиеся прямые. Угол между такими прямыми будет равен 90 градусов, а значит эти линии перпендикулярны.

Как анатомическое плечо перпендикулярно руке, так и в физике плечо перпендикулярно, только уже линии действия силы.

То есть перпендикуляр, проведенный от точки опоры до линии, вдоль которой действует сила — это плечо силы.

Попробуйте курсы подготовки к ЕГЭ по физике с опытным преподавателем в онлайн-школе Skysmart!

Рычаг

В каждом дворе есть качели, для которых нужны два качающихся (если в вашем дворе таких нет, посмотрите в соседнем). Большая доска ставится посередине на точку опоры. По сути своей, качели — это рычаг.

Рычаг — простейший механизм, представляющий собой балку, вращающуюся вокруг точки опоры.

Хорошо, теперь давайте найдем плечо этой конструкции. Возьмем правую часть качелей. На качели действует сила тяжести правого качающегося, проведем перпендикуляр от линии действия силы до точки опоры. Получилась, что плечо совпадает с рычагом, разве что рычаг — это вся конструкция, а плечо — половина.

Давайте попробуем опустить качели справа, тогда что получим: рычаг остался тем же самым по длине, но вот сместился на некоторый угол, а вот плечо осталось на том же месте. Если направление действия силы не меняется, как и точка опоры, то перпендикуляр между ними невозможно изменить.

Правило равновесия рычага

Рычаг находится в равновесии тогда, когда силы, действующие на него, обратно пропорциональны плечам этих сил.

F₁, F₂ — силы, действующие на рычаг

l₁, l₂ — плечи этих сил

Момент силы

При решении задач на различные силы нам обычно хватало просто сил. Сила действует всегда линейно (ну в худшем случае под углом), поэтому очень удобно пользоваться законами Ньютона, приравнивать разные силы. Это работало с материальными точками, но не будет так просто применяться к телам, у которых есть форма и размер.

Вот мы приложили силу к краю палки, но при этом не можем сказать, что на другом ее конце будут то же самое ускорение и та же самая сила. Для этого мы вводим такое понятие, как момент силы.

Момент силы — это произведение силы на плечо. Для определения физического смысла можно сказать, что момент — это вращательное действие.

Момент силы

M = Fl

M — момент силы [Н*м]
F — сила [Н]
l — плечо [м]

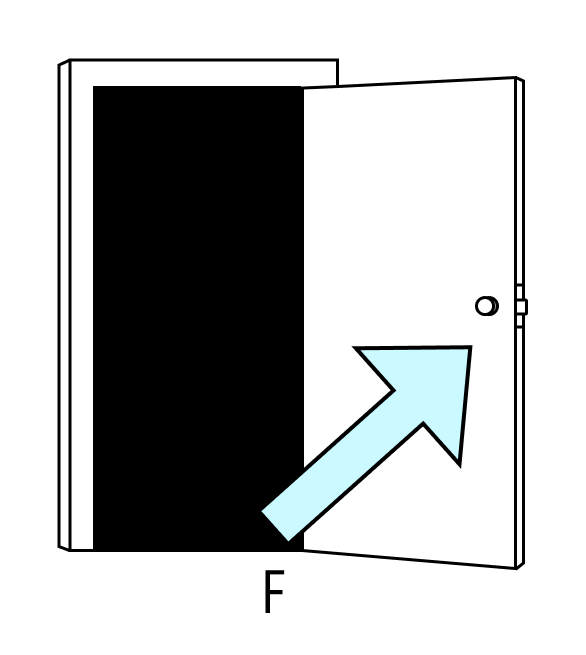
Для примера представьте, что вы забыли, как открывать двери. Стоите перед дверью и раздумываете, как легче это сделать.

Для начала приложим силу к краю двери — туда, где самый длинный рычаг. Открылась!

А что если толкнуть дверь ближе к креплению — там, где плечо намного короче? Для этого придется приложить силу большего значения.

Вывод: чтобы повернуть дверь, нужен крутящий момент определенного значения. Чем больше плечо силы, тем меньше значение силы, которую нужно приложить — и наоборот. Поэтому нам легче толкать дверь там, где плечо силы больше.

Похожая история с гаечным ключом. Чтобы закрутить гайку, нужно взяться за ручку подальше от гайки. За счет увеличения плеча мы уменьшаем значение силы, которую нужно приложить.

Расчет момента силы

Сейчас рассмотрим несколько вариантов того, как момент может рассчитываться. По идее просто нужно умножить силу на плечо, но поскольку мы имеем дело с векторами, все не так просто.

Если сила расположена перпендикулярно оси стержня, мы просто умножаем модуль силы на плечо.

Расстояние между точками A и B — 3 метра.

Момент силы относительно точки A:

МА=F×AB=F×3м

Если сила расположена под углом к оси стержня, умножаем проекцию силы на плечо.

Обратите внимание, что такие задания могут встретиться только у учеников не раньше 9 класса!

Момент силы относительно точки B:

MB=F×cos30×AB=F×cos30×3м

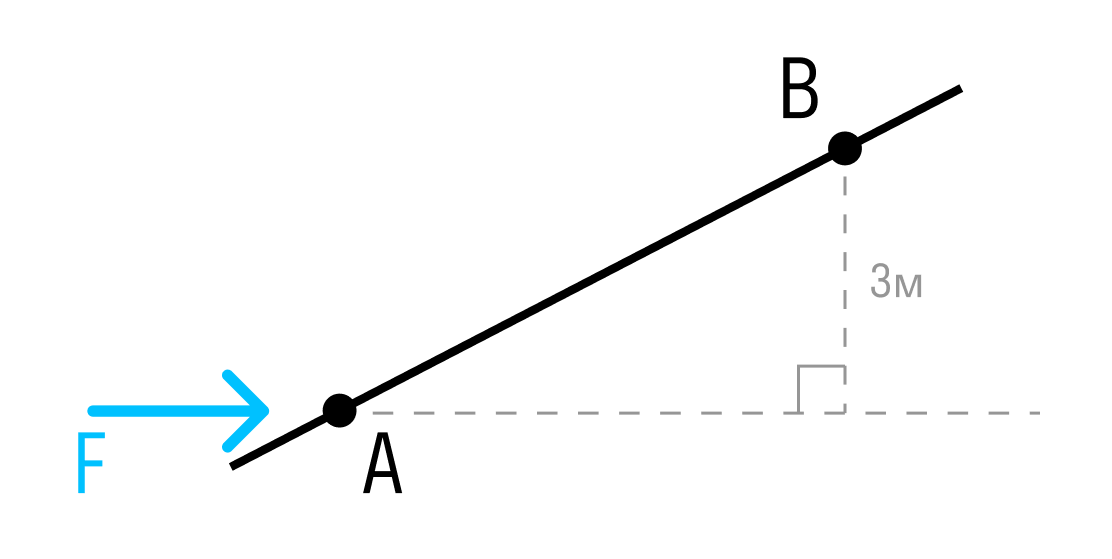
Если известно самое короткое расстояние от точки до линии действия силы, момент рассчитывается как произведение силы на это расстояние (плечо).

Момент силы относительно точки B:

MB=F×3м

Правило моментов

Вернемся к нашим баранам качелям. Силы, с которыми мы действуем на разные стороны этих качелей могут быть разными, но вот моменты должны быть одинаковыми.

Правило моментов говорит о том, что если рычаг не вращается, то сумма моментов сил, поворачивающих рычаг против часовой стрелки, равна сумме моментов сил, поворачивающих рычаг по часовой стрелке.

Это условие выполняется относительно любой точки.

Правило моментов

M₁ + M₂ +…+ M_n = M’₁ + M’₂ +…+ M’_n

M₁ + M₂ +…+ M_n — сумма моментов сил, поворачивающих рычаг по часовой стрелке [Н*м]

M’₁ + M’₂ +…+ M’_n — сумма моментов сил, поворачивающих рычаг против часовой стрелке [Н*м]

Давайте рассмотрим этот закон на примере задач.

Задача 1

К левому концу невесомого стержня прикреплен груз массой 3 кг.

Стержень расположили на опоре, отстоящей от его левого конца на 0,2 длины стержня. Чему равна масса груза, который надо подвесить к правому концу стержня, чтобы он находился в равновесии?

Решение:

Одним из условий равновесия стержня является то, что полный момент всех внешних сил относительно любой точки равен нулю. Рассмотрим моменты сил относительно точки опоры. Момент, создаваемый левым грузом равен

он вращает стержень против часовой стрелки. Момент, создаваемый правым грузом:

— он вращает по часовой.

Приравнивая моменты, получаем, что для равновесия к правому концу стержня необходимо подвесить груз массой

M = m : 4 = 3 : 4 = 0,75 кг

Ответ: для равновесия к правому концу стержня необходимо подвесить груз массой 0,75 кг

Задача 2

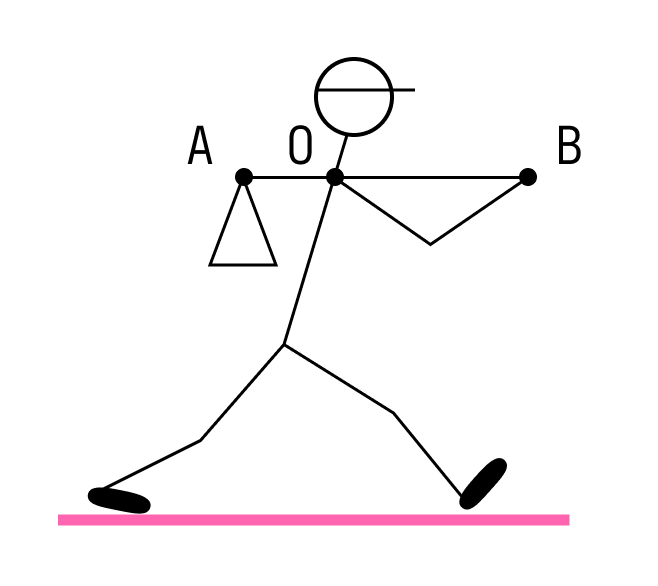
Путешественник несёт мешок с вещами на лёгкой палке. Чтобы удержать в равновесии груз весом 80 Н, он прикладывает к концу B палки вертикальную силу 30 Н. OB = 80 см. Чему равно OA?

Решение:

По правилу рычага:

где FA и FB — силы, приложенные соответственно к точкам A и B. Выразим длину OA:

Ответ: расстояние ОА равно 30 см

Задача 3

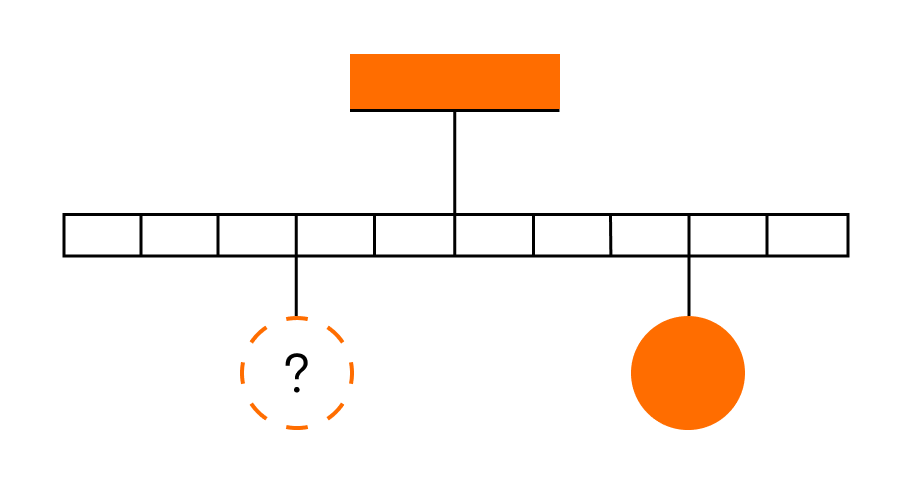
Тело массой 0,2 кг подвешено к правому плечу невесомого рычага (см. рисунок). Груз какой массы надо подвесить ко второму делению левого плеча рычага для достижения равновесия?

Решение:

По правилу рычага

Отсюда

Ответ: Масса груза равна 0,3 кг

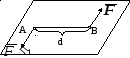
Задача 4 — a.k.a самая сложная задачка

Под действием силы тяжести mg груза и силы F рычаг, представленный на рисунке, находится в равновесии. Вектор силы F перпендикулярен рычагу, груз на плоскость не давит. Расстояния между точками приложения сил и точкой опоры, а также проекции этих расстояний на вертикальную и горизонтальную оси указаны на рисунке.

Если модуль силы F равен 120 Н, то каков модуль силы тяжести, действующей на груз?

Решение:

Одним из условий равновесия рычага является то, что полный момент всех внешних сил относительно любой точки равен нулю. Рассмотрим моменты сил относительно опоры рычага. Момент, создаваемый силой F, равен F*5 м и он вращает рычаг по часовой стрелке. Момент, создаваемый грузом относительно этой точки — mg*0,8 м, он вращает против часовой. Уточним, что 0,8 м — это расстояние от центра тяжести груза до опоры, т. е. перпендикуляр до оси вращения. Приравнивая моменты, получаем выражение для модуля силы тяжести

Ответ: модуль силы тяжести, действующей на груз равен 750 Н

Источник

Рассмотрим, как определяется момент силы относительно оси. Стремление силы вращать тело вокруг неподвижной оси зависит от величины силы, ее наклона и расстояния от оси.

Из опыта известно, что силы, проходящие через ось, и силы, параллельные оси, НЕ МОГУТ ВЫЗВАТЬ ВРАЩЕНИЯ ТЕЛА вокруг этой оси. Посмотрим на рисунок.

Ни сила Р₁, линия действия которой пересекает ось Oz, ни сила Р₂, параллельная оси, не смогут повернуть тело вокруг этой оси.

Для вращательного эффекта силы относительно закрепленной оси вводится понятие момента силы относительно оси М_z(Р). Вращательный эффект силы относительно оси и выражается ее моментом.

Пусть на тело в какой-то точке действует произвольная сила Р, не параллельная оси вращения Oz и не пересекающая эту ось. Проведем плоскость H, перпендикулярную оси Oz и проходящую через начало вектора силы. Разложим заданную силу Р на две составляющие: Р₁, расположенную в плоскости H, и Р₂, параллельную оси Oz.

Составляющая Р₂, параллельная оси Oz момента относительно этой оси не создает. Составляющая Р₁, действующая в плоскости H, создает момент относительно оси Oz или, что то же самое, относительно точки О. Момент силы Р₁ измеряется произведением модуля самой силы на длину а перпендикуляра, опущенного из точки О на направление этой силы, т. е.

В выражение момента силы относительно оси входит не вся сила, а только ее составляющая, лежащая в плоскости, перпендикулярной оси вращения.

Знак момента по общему правилу определяется направлением вращения тела: (+) при движении по часовой стрелке, (—) при движении против часовой стрелки (правило условно). При определении знака момента наблюдатель должен непременно находиться со стороны положительного направления оси. На рисунке вверху момент силы Р относительно оси Oz положителен, так как для наблюдателя, смотрящего со стороны положительного направления оси (сверху), тело под действием заданной силы представляется вращающимся вокруг оси по ходу часовой стрелки.

На рисунке внизу момент силы Р относительно оси Oz — величина отрицательная.

Рассмотрим частный случай.

В частном случае момент силы Р, расположенной в плоскости H, относительно оси Oz, перпендикулярной этой плоскости, определится произведением полной величины силы Р на ее плечо l относительно точки пересечения оси Oz и плоскости H

Итак, для определения момента силы относительно оси нужно спроектировать силу на плоскость, перпендикулярную оси, и найти момент проекции силы на плоскость относительно точки пересечения оси с этой плоскостью.

Моментом силы относительно точки называется произведение величины силы на длину перпендикуляра, опущенного из точки на линию действия силы (рис. а).

Если бы тело было закреплено в точке О, то сила Р стремилась бы вращать тело вокруг этой точки. Точка О, относительно которой берется момент, называется центром

момента, а перпендикуляр а называется плечом силы относительно центра момента.

Таким образом,

М = сила×плечо.

Момент силы Р относительно О обозначается

М₀(Р) = Ра.

Моменты сил измеряют в ньютонометрах (Нм) или килограммометрах (кГм) или в соответствующих кратных и дольных единицах, как и моменты пар.

Принято считать момент положительным, если сила стремится вращать тело по часовой стрелке (рис. а), и отрицательным — против часовой стрелки (рис. б).

Установленное правило знаков для моментов сил, как и для моментов пар, условно.

Когда линия действия силы проходит через данную точку, ее момент относительно этой точки равен нулю, так как в рассматриваемом случае плечо равно нулю а = 0 (рис. в).

Между моментом пары и моментом силы есть одно существенное различие. У момента пары сил величина и направление не зависят от положения этой пары в пространстве. У момента силы величина и направление (знак) момента силы зависят от положения точки, относительно которой определяется момент.

Пары, подобно силам, можно складывать.

Пара, заменяющая собой действие данных пар, называется результирующей. Результирующая нескольких пар эквивалентна заданным парам.

Определение по данным парам их результирующей пары называется сложением пар.

Сложим две пары, расположенные в одной плоскости.

Имеем пары P₁P‘₁ и Р₂Р’₂ с плечами а и b (см. рис.), т. е.

М₁ = — P₁а,

М₂ = P₂b

Приведем данные пары к одному плечу, не изменяя величины моментов каждой пары. Некоторый отрезок АВ = с (см. рис.выше) примем за общее плечо преобразованных пар.

Обозначим силы эквивалентных пар как Q₁ ,Q’₁ и Q₂ ,Q’₂ ; тогда

М₁ = — P₁а = —Q₁c;

М₂ = P₂b = Q₂c

Складывая силы, приложенные в точках А и В, найдем их равнодействующие

R’ = Q’₁ — Q’₂

R = Q₁ — Q₂

Обозначим эти уравнения буквой (а)

Равнодействующие R и R’, равные по величине и направленные в противоположные стороны, образуют пару сил RR’ ; момент которой

М = —Rc. (б)

Пара RR’ представляет результирующую пару. Подставив в уравнение (б) значение R из уравнения (а), получим

М = —Rc = — ( Q₁ — Q₂)с = Q₂c —Q₁c,

а так как

М₂ = Q₂c и М₁ = —Q₁c,

то

М = М₁ + М₂

Таким образом, приходим к заключению, что момент результирующей пары равен алгебраической сумме моментов составляющих пар.

Аналогичное доказательство применимо к любому количеству пар, лежащих в одной плоскости. Поэтому при произвольном числе слагаемых пар, лежащих в одной плоскости или параллельных плоскостях, момент результирующей пары определится по формуле

На основании приведенного правила сложения пар устанавливается условие равновесия системы пар, лежащих в одной плоскости, а именно:

для равновесия системы пар необходимо и достаточно, чтобы момент результирующей пары равнялся нулю или чтобы алгебраическая сумма моментов пар равнялась нулю:

В соответствии с определением эквивалентных систем сил (см. — здесь), две пары сил считают эквивалентными в том случае, если после замены одной пары другой парой механическое состояние тела не изменяется, т. е. не изменяется движение тела или не нарушается его равновесие.

Эффект действия пары сил на твердое тело не зависит от ее положения в плоскости. Таким образом, пару сил можно переносить в плоскости ее действия в любое положение.

Рассмотрим еще одно свойство пары сил, которое является основой для сложения пар.

Не нарушая состояния тела, можно как угодно изменять величины сил и плечо пары, только бы момент пары оставался неизменным.

Рассмотрим пару сил РР’ плечом а (рис. а).

Заменим эту пару новой парой QQ’ с плечом b (рис. 6) так, чтобы момент пары остался тем же.

Момент заданной пары сил M₁ = Ра. Момент новой пары сил М₂ = Qb. По определению пары сил эквивалентны, т. е. производят одинаковые действия, если их моменты равны.

Если, изменив величину сил и плечо новой пары, мы сохраним равенство их моментов M₁= М₂ или Ра = Qb, то состояние тела от такой замены не нарушится.

Итак, вместо заданной пары РР’ с плечом а мы получили эквивалентную пару QQ’ с плечом b.

Система двух равных и параллельных сил, направленных в противоположные стороны и не лежащих на одной прямой, называется парой сил. Примером такой системы сил могут служить усилия, передаваемые от рук шофера на рулевое колесо автомобиля.

Пара сил имеет очень большое значение в практике. Именно поэтому свойства пары как специфической меры механического взаимодействия тел изучается отдельно.

Сумма сил пары равна нулю

Р — Р’ = 0 (рис. а),

т. е. пара сил не имеет равнодействующей. Несмотря на это тело под действием пары сил не находится в равновесии.

Действие пары сил на твердое тело, как показывает опыт, состоит в том, что она стремится вращать это тело.

Способность пары сил производить вращение количественно определяется моментом пары, равным произведению силы на кратчайшее расстояние (взятое по перпендикуляру к силам) между линиями действия сил.

Обозначим момент пары М, а кратчайшее расстояние между силами а, тогда абсолютная величина момента (рис. а)

М = Ра = Р’а.

Кратчайшее расстояние между линиями действия сил называется плечом пары, поэтому можно сказать, что момент пары сил по абсолютной величине равен произведению одной из сил пары на ее плечо.

Эффект действия пары сил полностью определяется ее моментом. Поэтому пару сил можно изображать дугообразной стрелкой, указывающей направление вращения (см.рис.).

Так как пара сил не имеет равнодействующей, ее нельзя уравновесить одной силой.

В Международной системе единиц (СИ) силу измеряют в ньютонах, а плечо в метрах. Соответственно момент пары в системе СИ измеряется в ньютонометрах (н·м) или в единицах, кратных ньютонометру: кн·м, Мн·м и т. д.

Будем считать момент пары сил положительным, если пара стремится повернуть тело по направлению хода часовой стрелки (рис. а) и отрицательным, если пара стремится вращать тело против хода часовой стрелки (рис. б).

Принятое правило знаков для моментов пар условно; можно было бы принять противоположное правило. При решении задач во избежание путаницы всегда нужно принимать одно определенное правило знаков.

Задачи на равновесие встречаются не только в механике, но и в других дисциплинах. Для их решения используют различные методы: аналитический, основанный на уравнениях равновесия, графический и графоаналитический, основанные на применении геометрического условия равновесия.

Использование геометрического условия равновесия дает наиболее простое решение для системы трех сходящихся сил. При наличии в системе четырех и более сил рациональнее применять аналитический метод, который является самым универсальным и применяется чаще всего.

При аналитическом методе решение всех задач ведется по следующему плану:

первый этап — выделяют объект равновесия, т. е. тело или точку, равновесие которых в данной задаче следует рассмотреть;

второй этап — к выделенному объекту равновесия прикладывают заданные силы;

третий этап — выделенную точку или тело освобождают от связей и вместо них прикладывают реакции этих связей;

четвертый этап — выбирают координатные оси и составляют уравнения равновесия;

пятый этап — решают уравнения равновесия;

шестой этап — проверяют правильность решения.

Надежный способ проверки — повторное решение задачи при другом выборе системы координат.

Когда для решения задач используют геометрические условия равновесия, например замкнутость силового многоугольника для сходящейся системы сил, первые три этапа сохраняются.

Когда в задачах статики встречается не отдельное тело, а система или группа тел, приведенная методика решения в целом сохраняется. Равновесие каждого тела рассматривают отдельно и затем решают составленные для всех тел уравнения равновесия.

Остановимся еще на одном важном вопросе. В задачах статики часто приходится определять усилия в стержнях. Необходимо установить, как действуют растягивающие и сжимающие силы в стержнях на точки крепления стержней или узлы.

Рассмотрим некоторые случаи.

Когда стержень MN растянут (рис. а), его реакции на точки крепления направлены от этих точек М и N внутрь стержня. Когда стержень сжат, его реакции направлены к точкам закрепления, т. о. наружу (рис. б).

Следовательно, можно сказать, что в растянутом стержне реакции направлены от узлов, а в сжатом — к узлам.

Здесь можно отметить аналогию с деформированной пружиной (рис. в, г, д).

Здесь на схемах приведен случай недеформированной пружины и растянутой пружины. Теперь рассмотрим случай, когда пружина сжата:

Иногда при аналитическом решении задач бывает трудно определить направления реакций стержней. В этих случаях стержни удобно считать растянутыми, и реакции стержней направлять от узлов (от прикрепляемого стержнем тела). Если решение задачи даст значение реакции со знаком минус, значит, в действительности имеет место не растяжение, а сжатие. Таким образом, реакции растянутых стержней будут положительными, а сжатых — отрицательными.

Сходящаяся система сил находится в равновесии в случае замкнутости силового многоугольника. Величина равнодействующей при этом равна нулю (R = 0).

Проекции равнодействующей системы сходящихся сил на координатные оси равны суммам проекций составляющих сил на те же оси, т. е.

Модуль равнодействующей определится по формуле:

Оба слагаемых, стоящих под знаком корня, во всех случаях положительны как величины, возведенные в квадрат. Поэтому R = 0 только при выполнении условий:

Таким образом, равнодействующая плоской системы сходящихся сил равна нулю только в том случае, когда алгебраические суммы проекций ее слагаемых на каждую из двух координатных осей равны нулю.

Формулы Σх=0 (сумма проекций всех сил на ось Х равна нулю), Σy=0 (сумма проекций всех сил на ось Y равна нулю) называют уравнениями равновесия плоской системы сходящихся сил и используют при аналитическом решении задач.

Следовательно, для решения задач на равновесие плоской системы сходящихся сил мы имеем два уравнения. Эти уравнения позволяют определить две неизвестные величины.

Если же задача содержит неизвестные в количестве, превышающем число уравнений равновесия, то эту задачу нельзя решить методами статики абсолютно твердого тела. Задачи подобного типа называют статически неопределимыми. Их решение возможно только при отказе от допущения об абсолютной твердости тел; помимо уравнений равновесия для решения их составляют дополнительные уравнения, основанные на рассмотрении деформаций тел. Методы решения таких задач рассматриваются в курсе сопротивления материалов.

Равнодействующая системы сходящихся сил может быть найдена через проекции составляющих.

Рассмотрим ее определение на примере системы сил , изображенной на рис. а.

Равнодействующая этих сходящихся сил построена на рис. б:

Проектируя все силы на оси Ох и Оу и используя теорему о проекции векторной суммы получаем:

Модуль равнодействующей силы через ее проекции определяется по формуле

Подставив в это уравнение значение проекций R_x и R_y, найдем

Направление R определим по косинусам углов, которые эта сила образует с координатными осями:

Заданы сходящиеся силы (рис. а).

Геометрическая сумма, или равнодействующая, этих сил

определяется замыкающей стороной силового многоугольника (рис. б).

Спроектируем все вершины силового многоугольника ABCDEKL на ось х и обозначим их проекции соответственно а, b, с, d, е, k, l.

Проекции сил на ось х изобразятся отрезками:

P_1x = ab; P_2x= bc; P_3x= cd;

P_4x =—de; P_5x= ek; P_6x= kl.

Сумму проекций можно представить в следующем виде:

Так как al есть проекция равнодействующей силы на ось х, т.е. al = R_x, то

или

где n — число слагаемых векторов.

Следовательно, проекция векторной суммы на какую-либо ось равна алгебраической сумме проекций слагаемых векторов на ту же ось.

В плоскости геометрическую сумму сил можно спроектировать на две координатные оси, а в пространстве соответственно на три.

На плоскости сила может быть представлена как векторная сумма двух взаимно перпендикулярных сил и , которые по модулю равны абсолютным значениям соответствующих проекций

Здесь имеем случай разложения силы на две составляющие по координатным осям. Отличие проекции силы от ее составляющей заключается в том, что проекция силы на ось — величина скалярная, а составляющая — величина векторная.

При рассмотрении силы в пространстве приходится проектировать ее на три координатные оси. Установим, как определяются в пространстве проекции и составляющие произвольной силы , приложенной в точке А.

Первоначально сила проектируется на координатные плоскости, например, на плоскость хОу и на плоскость yOz. Эти проекции будем снабжать двумя индексами: проекцию на плоскость хОу обозначим , а проекцию на плоскость yOz обозначим .

Проекции сил на координатные плоскости представляют собой векторные величины. Каждую из проекций на координатные плоскости и легко спроектировать на две координатные оси, в плоскости которых она лежит. При этом получим три проекции силы , и .

Сила может быть представлена диагональю прямоугольного параллелепипеда, построенного на составляющих , и (см.рис. выше), которые по модулю равны соответствующим проекциям. Следовательно, модуль и направление силы в пространстве определятся по формулам: