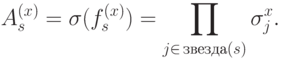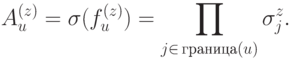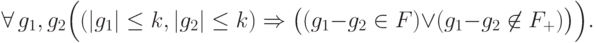Как найти синдром ошибки - Исправление ошибок и поиск оптимальных решений проблем

Вычисление
синдрома для циклических кодов является
довольно простой процедурой.

Пусть
U(x)
и r(х)
‑
полиномы, соответствующие переданному
кодовому слову и принятой последовательности.

Разделив
r(x)
на g(x),
получим

r(x)
= q(x)
g(x)
+ s(x),
(1.73)

где
— q(x)
— частное от деления, s(x)
— остаток от деления.

Если
r(x)
является кодовым полиномом, то он делится
на g(x)
без остатка, то есть s(x)
= 0.

Следовательно,
s(x)

0
является условием наличия ошибки в
принятой последовательности, то есть
синдромом принятой последовательности.

Синдром
s(x)
имеет в общем случае вид

S(x)
= S₀
+ S₁
x + … + S_n-

k-1
x^n-k-1
. (1.74)

Очевидно,
что схема вычисления синдрома является
схемой деления, подобной схемам
кодирования рис. 1.10 или 1.11 .

При
наличии в принятой последовательности
r

хотя бы одной ошибки вектор синдрома S
будет иметь, по крайней мере, один
нулевой элемент, при этом факт наличия
ошибки легко обнаружить, объединив по
ИЛИ
выходы всех ячеек регистра синдрома.

Покажем,
что синдромный многочлен S(x)
однозначно связан с многочленом ошибки
e(x),
а
значит, с его помощью можно не только
обнаруживать, но и локализовать ошибку
в принятой последовательности.

Пусть

e(x)
= e₀
+ e₁
x
+ e₂
x²
+ … + e_n_-1
xⁿ^-1
(1.75)

— полином
вектора ошибки.

Тогда
полином принятой последовательности

r(x)
= U(x)
+ e(x).
(1.76)

Прибавим
в этом выражении слева и справа U(x),
а также учтем, что

r(x)
= q(x)
g(x) + S(x), U(x) = m(x)
g(x), (1.77)

тогда

,
(1.78)

то
есть синдромный
полином S(x)
есть
остаток от
деления полинома ошибки e(x)
на порождающий полином g(x).

Отсюда следует, что по синдрому S(x)
можно однозначно определить вектор
ошибки e(x), а следовательно,
исправить эту ошибку.

На рис. 1.14 приведена схема синдромного
декодера с исправлением однократной
ошибки для циклического (7,4)-кода.
По своей структуре она подобна схеме,
приведенной на рис. 1.6, с той лишь разницей,
что вычисление синдрома принятой
последовательности производится здесь
не умножением на проверочную матрицу,
а делением на порождающий полином. При
этом она сохраняет и недостаток, присущий
всем синдромным декодерам: необходимость
иметь запоминающее устройство, ставящее
в соответствие множеству возможных
синдромов S множество векторов
ошибок e. Цикличность структуры
кода в этом случае не учитывается.

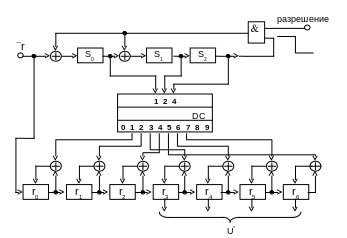
Рис.
1.14

1.3.4. Неалгебраические методы декодирования циклических кодов

Все
методы декодирования линейных блочных
кодов можно разбить на две группы:
алгебраические
и неалгебраические.

В
основе алгебраических методов лежит
решение систем уравнений, задающих
значение и расположение ошибок.
Рассмотренные синдромные декодеры
относятся именно к этой группе методов.

При
неалгебраических методах та же цель
достигается с помощью простых структурных
понятий теории кодирования, позволяющих
находить комбинации ошибок более простым
путем.

Одним
из неалгебраических методов является
декодирование с использованием алгоритма
Меггитта,
пригодного для исправления как одиночных,
так и l-кратных
ошибок (на практике l

3).

При
декодировании в соответствии с алгоритмом
Меггитта также вычисляется синдром
принятой последовательности S(x),
однако используется он иначе, нежели в
рассмотренных ранее синдромных декодерах.

Идея,
лежащая в основе декодера Меггитта,
очень проста и основывается на следующих
свойствах циклических кодов:

—
существует взаимно-однозначное
соответствие между множеством всех
исправляемых ошибок и множеством
синдромов;

—
если S(x)
— синдромный многочлен, соответствующий
многочлену ошибок е(x),

то xS(x)
mod
g(x)
— синдромный многочлен, соответствующий
x
e(x) mod (xⁿ
+ 1).

Равенство
а(x)
= b(x) mod p(x)
читается как “а(x),
сравнимо с b(x)
по модулю р(x)”
и означает, что а(x)
и b(x)
имеют одинаковые остатки от деления на
полином p(x).

Таким
образом, второе
условие
означает, что если
комбинация ошибок циклически сдвинута
на одну позицию вправо, то для получения
нового синдрома нужно сдвинуть содержимое
регистра сдвига с обратными связями,
содержащего S(x),

также на одну позицию вправо.

Следовательно,
основным
элементом декодера Меггитта является
сдвиговый регистр. Структурная схема
декодера Меггитта для циклических кодов
произвольной длины приведена
на рис. 1.15.

Рис.
1.15

Декодер
работает следующим образом. Перед
началом работы содержимое всех разрядов
регистров равно нулю. Принимаемая
последовательность r
в
течение первых n
тактов вводится в буферный регистр и
одновременно с этим в (n—k)-разрядном
сдвиговом регистре с обратными связями
производится ее деление на порождающий
полином g(x).

Через
n
тактов
в буферном регистре оказывается принятое
слово r
,
a в регистре синдрома — остаток от
деления вектора ошибки на порождающий
полином.

Вычисленный
синдром сравнивается со всеми табличными
синдромами, и в случае совпадения с
одним из них старший разряд буферного
регистра исправляется путем прибавления
к его значению единицы.

После
этого синдромный и буферный регистры
один раз циклически сдвигаются. Это
реализует умножение S(x)
на
x
и деление на g(x).
Содержимое ячеек синдромного регистра
теперь равно остатку от деления xS(x)
на g(x)
или синдрому ошибки x
е(x) mod (Хⁿ
+ 1).

Если
новый синдром совпадает с одним их
табличных, то исправляется очередная
ошибка и т.д. Через n
тактов
все позиции будут, таким образом,
исправлены.

Рассмотрим
работу декодера Меггитта для циклического
(7,4)-кода,
исправляющего одиночную ошибку. Схема
декодера изображена на рис. 1.16.

Рис.
1.16

Принцип
работы декодера заключается в том, что
независимо
от того, в какой позиции произошла
ошибка, осуществляется ее сдвиг в
последнюю ячейку буферного регистра с
соответствующим пересчетом синдрома
и ее исправление в этой позиции.

Полином
ошибки в старшем разряде для (7,4)-кода
Хемминга имеет вид е₆(x)
= x⁶,
соответствующий ему синдромный полином
S₆(x)
= 1 + x³
(
S
= (101)),
детектор ошибки настроен на это значение
синдрома.

Пусть,
например, передана последовательность
U
= (1001011),
ей соответствует кодовый полином U(x)
= 1 + x³
+ x⁵
+ x⁶.
Произошла ошибка в третьей позиции е(x)
= x³,
принятый вектор имеет вид r
= (1000011),
его полином r(x)
= 1 + x⁵
+ x⁶.

Kогда
принятая последовательность полностью
входит в буферный регистр, в регистре
синдрома оказывается синдром,
соответствующий ошибке е(x)
= x³S₃
= (110).
Поскольку он не совпадает с табличным
для е₆,
на выходе детектора ошибок будет 0
и исправления не происходит.

Далее
производятся однократный циклический
сдвиг принятой последовательности в
буферном регистре, однократное деление
синдрома x∙S₃
на порождающий полином в регистре с
обратными связями и проверка на совпадение
синдрома с заданным.

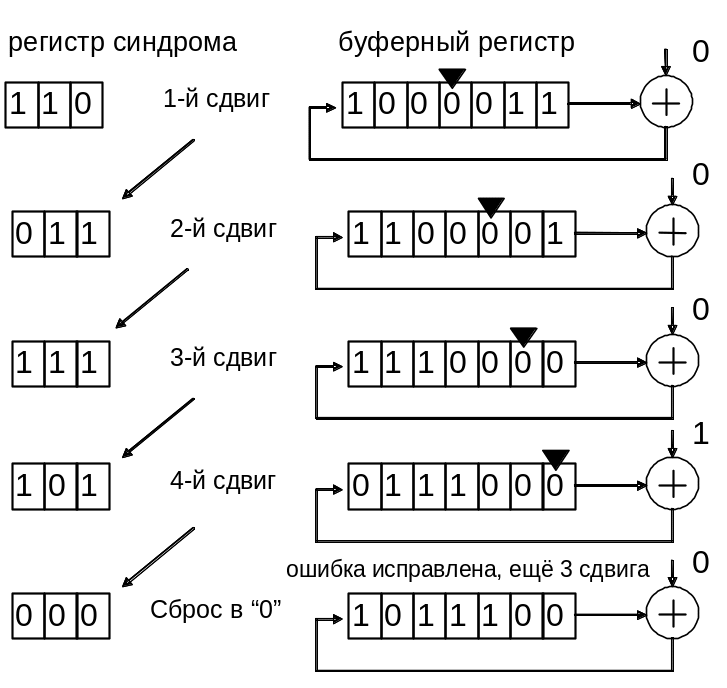
Последовательность
состояний регистров декодера в процессе
декодирования показана на рис. 1.17.

Рис.
1.17

Т
аким
образом, исправление ошибки в декодере
Меггитта осуществляется за 2n
тактов: в течение n
тактов производится ввод принятой
последовательности в буферный регистр,
в течение l
тактов
— исправление ошибки, и еще в течение
n
— l
— восстановление
буферного регистра в исходное состояние
с исправленным словом. Простота декодера
достигается увеличением времени
декодирования.

Следует
отметить, что в связи с успехами в
разработке БИС и устройств памяти в
значительной степени снимается вопрос
о размерах таблиц, связывающих значения
синдрома и вектора ошибки (для синдромных
декодеров) и даже значения кодовых слов
и принятых последовательностей (для
декодера максимального правдоподобия).
Поэтому в перспективе возможно снижение
интереса к кодам, обладающим специальной
структурой, и к методам их декодирования.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
#
#
#
#
#
#
10.06.2015684.82 Кб13P4.pdf
#
#
#
#

Источник

Торические коды.

Приведем важный пример симплектического кода. Он строится так. Пусть есть квадратная решетка размера на торе. Сопоставим каждому ее ребру по q-биту. Таким образом, всего имеется n=r^2 q-битов. Проверочные операторы будут двух типов.

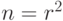
Рис.
14.1.

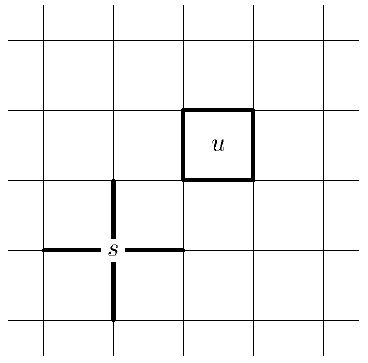
Тип I задается вершинами. Выберем некоторую вершину и сопоставим ей проверочный оператор

$A^{(x)}_s=sigma(f^{(x)}_s)=prod_{jin,mathrm {text{звезда}}(s)}^{} sigma^x_j.$

Тип II задается гранями. Выберем некоторую грань и сопоставим ей проверочный оператор

$A^{(z)}_u=sigma(f^{(z)}_u)=prod_{jin, mathrm {text{граница}}(u)}^{} sigma^z_j.$

Операторы $A^{(x)}_s$ и $A^{(z)}_u$ коммутируют, поскольку граница и звезда всегда пересекаются по четному числу ребер. (Перестановочность оператор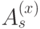ов одного типа очевидна.)

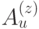
Хотя мы указали 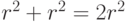проверочных операторов (по одному на грань и на вершину), между ними есть соотношения. Произведение всех $A^{(x)}$ -операторов, как и произведение всех $A^{(z)}$ -операторов, равны тождественному. Можно показать, что других соотношений нет. Поэтому , а . Поэтому торический код позволяет закодировать два q-бита. Посмотрим, чему равно кодовое расстояние для торического кода.

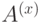
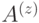
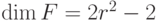
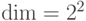
Для торического кода имеются естественные разложения

$F=F^{(x)}oplus F^{(z)},qquad F_+=F_+^{(x)}oplus F_+^{(z)}$

на подпространства, соответствующие проверочным операторам, состоящим только из 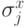, либо только из . Такие коды называются CSS кодами (по фамилиям авторов, впервые рассмотревших этот класс кодов [25, 44]). В случае торического кода элементы подпространств $F^{(z)}$ , $F_+^{(z)}$ имеют вид ; им можно сопоставить 1-цепи, т.е. формальные линейные комбинации ребер с коэффициентами . 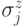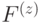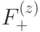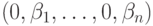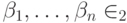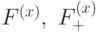Элементам подпространств $F^{(x)}_{ms}, F_+^{(x)}$ сопоставляются 1-коцепи. Рассмотрим вектор $f^{(z)}_uin F^{(z)}_{ms}$ , отвечающий грани с номером . Ему будет сопоставлена 1-цепь, являющаяся границей этой грани. Легко видеть, что пространство $F^{(z)}$ состоит из всех 1-границ. Аналогично, векторам $f_s^{(x)}$ будут сопоставляться 1-кограницы, порождающие все пространство 1-кограниц.

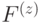
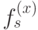
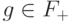
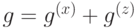
Возьмем произвольный элемент gin F_+ , $g=g^{(x)}+g^{(z)}$ . Условия коммутирования запишутся следующим образом:

$begin{multiline} omega(f_s^{(x)},g)=0quad Longleftrightarrowquad omega(f_s^{(x)},g^{(z)})=0, \ omega(f_u^{(z)},g)=0quad Longleftrightarrowquad omega(f_u^{(z)},g^{(x)})=0. end{multiline}$

Чтобы выполнялось 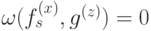$omega(f_s^{(x)},g^{(z)}_{ms})=0$ , нужно, чтобы в любой звезде было четное число ребер с ненулевыми весами из $g^{(z)}$ . Другими словами, $g^{(z)}$ — это 1-цикл (с коэффициентами в ZZ_2 ). Аналогично, $g^{(x)}$ должен быть 1-коциклом.

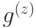
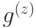
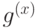
Итак, пространства 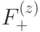$F_+^{(z)}$ , $F_+^{(x)}$ состоят из 1-циклов и 1-коциклов, а пространства $F^{(z)}$ , $F^{(x)}$ состоят из 1-границ и 1-кограниц. Следовательно, кодовое расстояние есть минимальная мощность (количество ненулевых коэффициентов) по циклам, не являющимся границами, и коциклам, не являющимся кограницами. Легко видеть, что этот минимум равен (нужны либо цикл, либо разрез, не гомологичные 0). Это означает, что торический код исправляет ошибок.

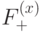
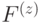
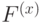
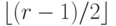
Будем обозначать коды описанного вида через TOR(r) .

Замечание. Торические коды являются очень важным примером, обладающим рядом замечательных свойств. В частности, это коды с локальными проверками. Последовательность кодов называется кодами с локальными проверками, если выполнены следующие условия:

каждый проверочный оператор действует на ограниченное константой число q-битов;
каждый q-бит входит в ограниченное константой число проверочных операторов;
кодовое расстояние неограниченно возрастает.

Такие коды представляют интерес для задачи построения вычислительных схем, устойчивых к ошибкам. При исправлении ошибок могут происходить новые ошибки. Но для кодов с локальными проверками схемы исправления ошибок имеют фиксированную глубину, поэтому одна ошибка при работе такой схемы портит ограниченное число q-битов.

Процедура исправления ошибок.

Определение 14.6 и теорема 14.2 указывают только на принципиальную возможность восстановить исходное состояние системы после действия ошибки. На примере симплектических кодов покажем, как реализовать процедуру исправления ошибки.

Рассмотрим частный случай, к которому все сводится. Пусть имеются две ошибки, заданные операторами , . Тогда ( |c|=1 ). Назовем синдромом ошибки g_1 вектор (для g_2 — аналогично).

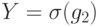
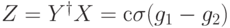
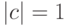
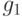
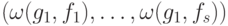
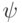
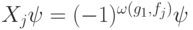
Возьмем вектор . Обозначим . Проверочные операторы действуют на ketpsi так: $X_jketpsi=(-1)^{omega(g_1,f_j)}ketpsi$ . Поэтому, измеряя собственные числа X_j на состоянии , можно измерить синдром.

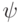
Рис.
14.2.

Если кодовое расстояние равно , то выполнено

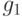
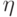
Условие означает эквивалентность ошибок g_1 и g_2 , т.е. для любого вектора keteta из кодового подпространства. Условие равносильно тому, что синдромы ошибок g_1 и g_2 не совпадают. Итак, либо ошибки эквивалентны, либо их можно различить по синдрому. Следовательно, по синдрому можно определить ошибку с точностью до эквивалентности, т.е. по модулю подпространства .

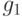
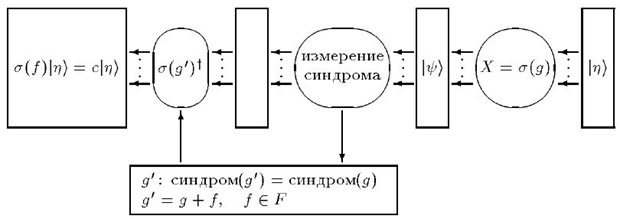
Теперь ясно, как нужно исправлять ошибку. После того как определен синдром, применим оператор, обратный к оператору восстановленной по синдрому ошибки. Получим состояние, отличающееся от исходного лишь на фазовый множитель. Вся процедура изображена на рис. 14.2.

Выше рассмотрен случай ошибки типа 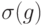. На самом деле ошибка состоит в действии преобразования матриц плотности вида

$T=sum_{|h|leq k,|h'|leq k}^{} b_{h,h'} sigma(h)cdotsigma(h')^dagger.$

В качестве упражнения читателю предлагается проверить, как работает приведенная выше схема в случае такого общего преобразования матриц плотности.

Задача 14.6. Постройте полиномиальный алгоритм определения ошибки по синдрому для торического кода.

Источник

Авторы
Резюме
Файлы
Ключевые слова
Литература

Барсагаев А.А.

1

Калмыков М.И.

1 Федеральное государственное автономное образовательное учреждение высшего профессионального образования «Северо-Кавказский федеральный университет»

В работе рассмотрены вопросы, связанные с анализом корректирующих способностей модулярных полиномиальных кодов (МПК). Данные коды позволяют осуществлять обработку данных в реальном масштабе времени за счет использования малоразрядных данных. При этом обработка информации осуществляется параллельно по вычислительным трактам и независимо друг от друга. Такое свойство МПК позволяет осуществлять процедуры поиска и коррекции ошибок. Для повышения корректирующих способностей кодов в МПК вводят дополнительные контрольные основания. С целью определения местоположения и глубины ошибки используются позиционные характеристики. В статье представлен алгоритм поиска и коррекции ошибок с использованием псевдоортогональных базисов модулярных полиномиальных кодов.

модулярные полиномиальные коды

параллельные вычисления

остатки

псевдоортогональные базисы

коррекция ошибок.

1. Бережной В.В., Калмыков И.А., Червяков Н.И., Щелкунова Ю.О., Шилов А.А. Нейросетевая реализация в полиномиальной системе классов вычетов операций ЦОС повышенной разрядности // Нейрокомпьютеры: разработка и применение. – 2004. – № 5-6. – С. 94.

2. Бережной В.В., Калмыков И.А., Червяков Н.И., Щелкунова Ю.О., Шилов А.А. Архитектура отказоустойчивой нейронной сети для цифровой обработки сигналов // Нейрокомпьютеры: разработка и применение. – 2004. – № 12. – С. 51-57.

3. Емарлукова Я.В., Калмыков И.А., Зиновьев А.В. Высокоскоростные систолические отказоустойчивые процессоры цифровой обработки сигналов для инфотелекоммуникационных систем // Инфокоммуникационные технологии. Самара. – 2009. – №2. – С. 31-37.

4. Калмыков И.А., Червяков Н.И., Щелкунова Ю.О., Шилов А.А. Нейросетевая реализация в полиномиальной системе классов вычетов операций ЦОС повышенной разрядности // Нейрокомпьютеры: разработка и применение. – 2004. – № 5-6. – С. 94.

5. Калмыков И.А., Чипига А.Ф. Структура нейронной сети для реализации цифровой обработки сигналов повышенной разрядности // Вестник Ставропольского государственного университета. – 2004. – Т.38. – С. 46.

6. Калмыков И.А., Петлеванный С.В., Сагдеев А.К., Емарлукова Я.В. Устройство для преобразования числа из полиномиальной системы классов вычетов в позиционный код с коррекцией ошибки // Патент России № 2309535. 31.03.2006. Бюл. № 30 от 27.10.2007.

7. Калмыков И.А., Гахов В.Р., Емарлукова Я.В. Устройство обнаружения и коррекции ошибок в кодах полиномиальной системы классов вычетов // Патент России № 2300801. 30.06.2005. Бюл. № 16 от 10.06.2007.

8. Хайватов А.Б., Калмыков И.А. Математическая модель отказоустойчивых вычислительных средств, функционирующих в полиномиальной системе классов вычетов // Инфокоммуникационные технологии. – 2007. – Т.5. – №3. – С.39-42.

9. Червяков Н.И., Калмыков И.А., Щелкунова Ю.О., Бережной В.В. Математическая модель нейронной сети для коррекции ошибок в непозиционном коде расширенного поля Галуа // Нейрокомпьютеры: разработка и применение. – 2003. – № 8-9. – С. 10-17.

10. Чипига А.А., Калмыков И.А., Лободин М.В. Устройство спектрального обнаружения и коррекции в кодах полиномиальной системы классов вычетов // Патент России № 2301441. Бюл. № 17 от 20.06.2007.

Введение

В последние годы цифровая обработка сигналов (ЦОС) занимает доминирующее положение в системах и средствах передачи и обработки информации в связи с неоспоримыми достоинствами – точность, гибкость и высокая скорость обработки. Кроме того, с развитием средств вычислительной техники системы ЦОС становятся все дешевле и компактнее. Эффективность ЦОС полностью определяется объемом вычислений, которые получаются при реализации математической модели процесса цифровой обработки сигнала с помощью специализированного процессора (СП). Снижение объема вычислений приводит к уменьшению аппаратурных затрат при реализации систем ЦОС или к повышению производительности вычислительного устройства. Таким образом, выбор алгебраической системы оптимальной с точки зрения минимума объема вычислений при реализации методов ЦОС является актуальной и важной.

Постановка задачи исследований. Как правило, в подавляющем большинстве приложений задачи ЦОС сводится к нахождению значений ортогонального преобразования конечной реализации сигнала для большого числа точек, что предопределяет повышенные требования к скорости обработки и разрядности вычислительного устройства. Решить данную проблему можно за счет перехода от одномерных вычислений к многомерным. В основу данного преобразования положена китайская теорема об остатках (КТО) [1-5].

Особое место среди таких систем занимает модулярная полиномиальная система класса вычетов, с помощью которых возможна организация ортогональных преобразований сигналов в расширенных полях Галуа . Если исходное число А представить в полиномиальной форме, а в качестве оснований выбрать минимальные многочлены поля Галуа, то справедливо

A (z) = (α1 (z), α2 (z).., αn (z)), (1)

где αi (z) ≡ A (z mod pi(z); pi (z) – минимальный многочлен.

Применение модулярных полиномиальных кодов позволяет свести операции в кольце полиномов к соответствующим операциям над остатками [1-6]. В этом случае

, (1)

где и — модулярный код в кольце полиномов; ; ; — операции сложения, вычитания и умножения в GF(p); l = 1, …,n.

Таким образом, основным достоинством непозиционных кодов является, то, что данные представляются в виде малоразрядных остатков, которые обрабатываются по параллельным вычислительным трактам. Это позволяет повысить скорость вычислений, что и предопределяет интерес к полиномиальным непозиционным кодам в различных областях применения [1-6].

В работах [1-5] предлагается для эффективной реализации ортогональных преобразований с высокой точностью и скоростью вычислений реализация дискретного преобразования Фурье (ДПФ) в кольце полиномов. В этом случае, если имеется кольцо полиномов P(z), с коэффициентами в виде элементов поля GF(p), то данное кольцо разлагается в сумму

, (2)

где Pl(z) – локальное кольцо полиномов, образованное неприводимым полиномом pl(z) над полем GF(p); l=1, …, n.

При этом в кольце полиномов можно организовать ортогональное преобразование, представляющее собой полиномиальное ДПФ, вида

, (3)

где , l=1,2,…,m; k=0,1,…d-1.

При этом должны выполняться следующие условия:

1. — первообразный элемент порядка d для локального кольца Pl(z).

2. d имеет мультипликативный обратный элемент d*.

Если отмеченные условия выполняются, то получается циклическая группа, которая имеет порядок d. В этом случае ортогональное преобразование является полиномиальным ДПФ для кольца вычетов P(z) если существуют преобразования над конечным кольцом Pl(z)

Поэтому ДПФ над Pl(z) можно обобщить над кольцом P(z), если конечное кольцо Pl(z) содержит корень d-ой степени из единицы и d имеет мультипликативный обратный элемент d*, такой что справедливо

. (4)

Основным достоинством системы класса вычетов является сравнительная простота выполнения модульных операций (сложения, вычитания, умножения). Формальные правила выполнения таких операций в МПК позволяют существенно повысить скорость вычислительных устройств ЦОС [5].

Кроме модульных операций, позволяющих повысить скорость обработки информации, модулярные коды позволяют обнаруживать и исправлять ошибки, возникающие в процессе функционирования СП. Если в качестве рабочих оснований выбрать k минимальных многочленов МПК (k<n), то данные основания определяют рабочий диапазон

. (5)

Если , то такой полином считается разрешенным и не содержит ошибок. В противном случае, полином, представленный в модулярном полиномиальном коде, содержит ошибки [6-10].

Для определения местоположения и глубины ошибки в полиномиальной системе классов вычетов используются позиционные характеристики. В работе [9] представлен алгоритм вычисления такой характеристики как интервальный номер. Синдром ошибки для полиномиального кода вычисляется в работе [8]. В работе [7] показана математическая модель поиска ошибочного основания с использованием алгоритма нулевизации. Структура устройства спектрального обнаружения и коррекции в кодах полиномиальной системы классов вычетов приведена в работе [10].

Одной из характеристик, использующемой при выполнении процедур поиска и коррекции ошибок в модулярных кодах, является след полинома. Для получения данной характеристики используются псевдоортогональные полиномы. Они представляют собой ортогональные полиномы, у которых нарушена ортогональность по нескольким основаниям. Известно, что если в псевдоортогональных полиномах нарушена ортогональность по контрольным основаниям, то данные полиномы являются ортогональными полиномами безизбыточной системы оснований полиномиальной системы классов вычетов.

Для получения псевдоортогональных полиномов проведем расширение системы оснований p1(z), …, pk(z) на r контрольных оснований pk+1(z), …, pk+r(z) и представим ортогональные полиномы в виде:

(6)

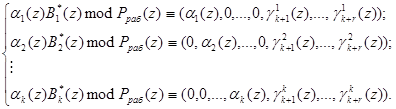
Выражение (6) определяет значения псевдоортогональных полиномов, у которых нарушена ортогональность по контрольным основаниям.

Согласно китайской теореме об остатках

, (7)

полином можно представить в виде:

. (8)

Тогда каждое слагаемое выражения (4) представляет собой

, (9)

где Bi*(z) – ортогональный базис безизбыточной системы оснований МПК.

Подставив выражение (6) в равенство (8), и учитывая, что в процессе выполнения операции не бывает выход за пределы Pраб(z), получаем

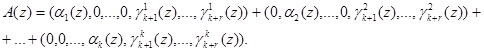
Следовательно, справедливо

(9)

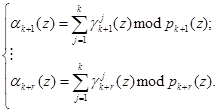
Таким образом, на основании (9) и воспользовавшись значениями псевдоортогональных полиномов, определяемых равенством (6), можно вычислить значения остатков по контрольным основаниям согласно

. (10)

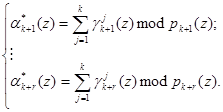
Затем на основании полученных значений и значений, поступающих на вход устройства коррекции ошибок, можно определить синдром ошибки согласно выражения

(11)

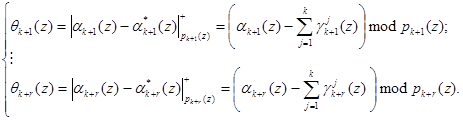
Если разность равна нулю, т.е. , то исходный полином является разрешенным и не содержит ошибки. В противном случае модулярная комбинация является запрещенной. Тогда в зависимости от величины синдрома ошибки осуществляется коррекция ошибки, т.е.

(12)

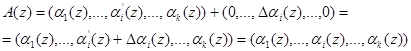
где— вектор ошибки модулярного кода; — глубина ошибки по i-му модулю МПК.

В работе [6] представлена структура устройства для преобразования числа из полиномиальной системы классов вычетов в позиционный код с коррекцией ошибки, в процессе функционирования которого используется данный алгоритм. Следует отметить, что этот алгоритм поиска и коррекции ошибок позволяет осуществить поиск и коррекцию всех однократных ошибок с использованием двух контрольных оснований и 90 процентов двоичных ошибок.

Вывод. В работе показана возможность осуществления цифровой обработки сигналов с использованием математической модели ЦОС, обладающей свойством кольца и поля. Применение полиномиальных кодов позволяет повысить скорость обработки данных за счет применения малоразрядных остатков и их параллельной архитектуре вычислений. Кроме того, МПК могут использоваться для повышения отказоустойчивости вычислительных систем. В работе рассмотрен алгоритм вычислений позиционной характеристики на основе ортогональных базисов, у которых нарушена ортогональность по контрольным основаниям.

Патент России № 2301441. Бюл. № 17 от 20.06.2007.

Библиографическая ссылка

Барсагаев А.А., Калмыков М.И. АЛГОРИТМЫ ОБНАРУЖЕНИЯ И КОРРЕКЦИИ ОШИБОК В МОДУЛЯРНЫХ ПОЛИНОМИАЛЬНЫХ КОДАХ // Международный журнал экспериментального образования. – 2014. – № 3-1.
– С. 103-106;

URL: https://expeducation.ru/ru/article/view?id=4672 (дата обращения: 11.02.2023).

Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»

(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)

Источник

1.3.4. Неалгебраические методы декодирования циклических кодов

Торические коды.

Процедура исправления ошибок.

Библиографическая ссылка

Читайте также: