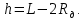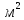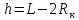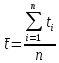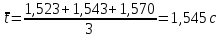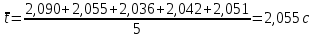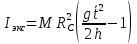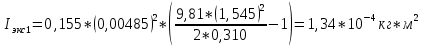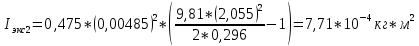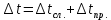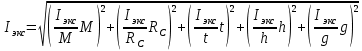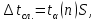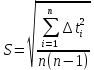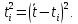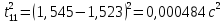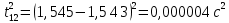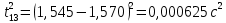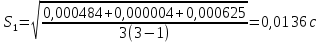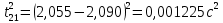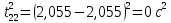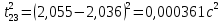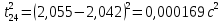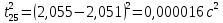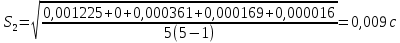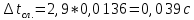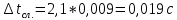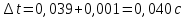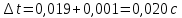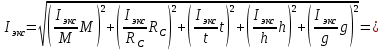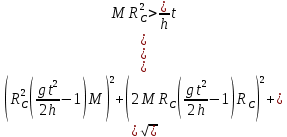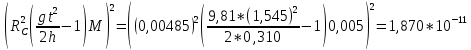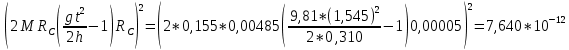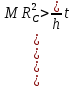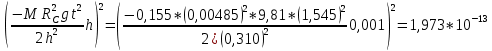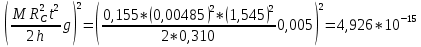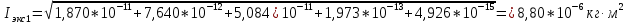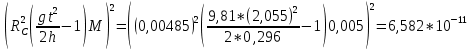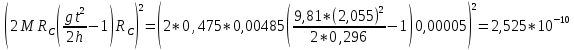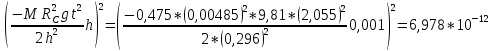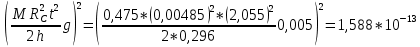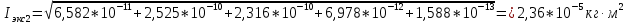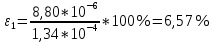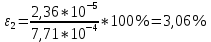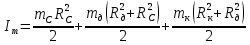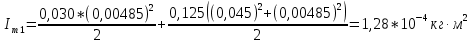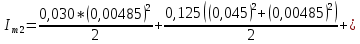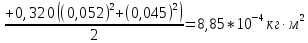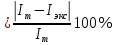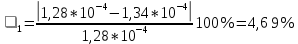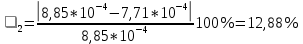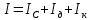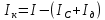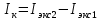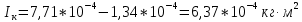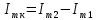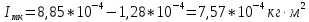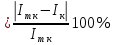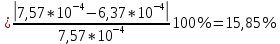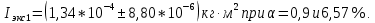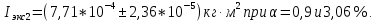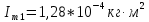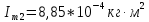Маятник Максвелла. Внешний вид и параметры лабораторной установки. Определение момента инерции маятника Максвелла
Страницы работы
Фрагмент текста работы
Санкт-Петербургский государственный университет
аэрокосмического приборостроения
Рейтинг за работу
Преподаватель
Отчёт по лабораторной работе №3
по курсу общая физика
«Маятник Максвелла»
ОФ43.2205_1.03_ЛР
Работу выполнил студент
группы 1564 кс
Санкт-Петербург
2005
1. Цель работы: определение момента инерции маятника Максвелла.
2. Описание
лабораторной установки.
На вертикальной
стойке крепятся два кронштейна. Верхний неподвижный кронштейн снабжён воротком 1
для крепления и регулировки бифилярного подвеса, электромагнитом 2 для
фиксирования маятника в верхнем положении и фотодатчиком 3, включающий
секундомер. На подвижном кронштейне закреплён фотодатчик 4, включающий
секундомер. Шкала секундомера 5 вынесена на лицевую панель прибора.
Кнопка «Сеть»
включает питание установки, кнопка «сброс» производит обнуление показаний
секундомера. При нажатии на кнопку «Пуск» отключается электромагнит, и маятник
приходит в движение.
Массу и момент
инерции маятника можно менять при помощи сменных колец, надеваемых на диск.
Длина нити должна быть такой, чтобы нижняя кромка маятника была на 1-2 мм ниже
оптической оси нижнего фотодатчика. Ось маятника должна быть горизонтальной.
Длина нити (высота падения) определяется по шкале, нанесённой на вертикальной
стойке.
Параметры установки:
радиус оси Rоси = 5 мм, радиус нити Rнити = 0,6 мм, радиус диска R1 = 42,5 мм, внешний радиус кольца R2 = 52,5 мм, масса диска mD
= 125 г, масса первого кольца m1 = 390 г, масса второго кольца m2 = 264 г.
Таблица технических характеристик приборов.
|
Прибор |
Тип |
Предел |
Цена |
Класс |
|
Секундомер |
МК-2 |
99,999 |
0,001 |
1 |
|
Линейка |
— |
44 мм |
1 мм |
0,5 |
θh = 2 мм.
θt = 0,001 с.
3. Рабочие формулы.
1.) tср. = (t1 + t2 + … +
tN)/N,
где tср. – среднее
значение времени падения; t1 – время падения при первом измерении; tN – время падения при последнем измерении; N
– количество измерений.
2.) I = m·(r + rн)2·[(g·t2/2·h0) — 1], где I – момент инерции маятника Максвелла; m –
масса маятника; r – радиус оси маятника; rн – радиус нити; g – ускорение свободного падения; t – время
падения маятника; h0 – высота падения маятника.
3.) Iср.взв.
= I1 + I2 + … + IN/N, где Iср.взв. – среднее взвешенное значение момента инерции.
4.) ID = mD·RD2/2, где ID
– момент инерции диска; mD
– масса диска; RD — радиус диска.
5.) IК = mК·(RК12 + RК22)/2, где IК – момент инерции кольца; mК – масса кольца; RК1 – внутренний радиус кольца; RК2 – внешний радиус кольца.
6.) Iтеор. = [mD·R12 + mК·(R12 + R22)]/2, где I – теоретическое выражение для
маятника Максвелла; R1 – радиус диска; R2 – внешний радиус кольца.
4. Результаты
измерений и вычислений.
Таблица 1. m =
33 + 125 = 158 г, h = 20 + 1 = 21 см.
|
№ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
t, |
0,909 |
0,912 |
0,898 |
0,92 |
0,901 |
0,915 |
0,914 |
0,899 |
0,916 |
0,915 |
|
tср., с |
0,91 |
|||||||||
|
I, кг·м2 |
9,08·10-5 |
|||||||||
|
St, с |
0,008 |
|||||||||
|
St, с |
0,0025 |
|||||||||
|
Δt, с |
0,007 |
|||||||||
|
ID, кг·м2 |
11,289·10—5 |
Таблица 2. m =
33 + 125 + 390 = 548 г, h = 20 см.
|
№ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
t, |
1,401 |
1,394 |
1,504 |
1,414 |
1,394 |
1,395 |
1,425 |
1,468 |
1,422 |
1,417 |
|
tср., с |
1,423 |
|||||||||
|
I, |
83,539·10-5 |
|||||||||
|
St, с |
0,036 |
|||||||||
|
St, с |
0,0114 |
|||||||||
|
Δt, с |
0,027 |
|||||||||
|
ID, кг·м2 |
11,289·10—5 |
|||||||||
|
IК, кг·м2 |
88,969·10-5 |
|||||||||
|
Iтеор., кг·м2 |
100,258·10-5 |
Таблица 3. m =
33 + 125 + 264 = 422 г, h = 20 см.
|
№ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
t, |
1,362 |
1,496 |
1,358 |
1,345 |
1,356 |
1,363 |
1,383 |
1,37 |
1,352 |
1,383 |
|
tср., с |
1,377 |
|||||||||
|
I, |
60,155·10-5 |
|||||||||
|
St, с |
0,044 |
|||||||||
|
St, с |
0,014 |
|||||||||
|
Δt, с |
0,033 |
|||||||||
|
ID, кг·м2 |
11,289·10—5 |
|||||||||
|
IК, кг·м2 |
60,225·10-5 |
|||||||||
|
Iтеор., кг·м2 |
71,514·10-5 |
Таблица 4. m =
33 + 125 + 264 = 422 г, h = 18 см.
|
№ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
t, |
1,301 |
1,282 |
1,301 |
1,3 |
1,295 |
1,294 |
1,301 |
1,304 |
1,294 |
1,293 |
|
tср., с |
1,297 |
|||||||||
|
I, |
59,297·10-5 |
|||||||||
|
St, с |
0,006 |
|||||||||
|
St, с |
0,0019 |
|||||||||
|
Δt, с |
0,005 |
|||||||||
|
ID, кг·м2 |
11,289·10—5 |
|||||||||
|
Iтеор., кг·м2 |
71,514·10-5 |
Таблица 5. m =
33 + 125 + 264 = 422 г, h = 15 см.
|
№ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
t, |
1,144 |
1,152 |
1,149 |
1,148 |
1,173 |
1,148 |
1,142 |
1,145 |
1,145 |
1,168 |
|
tср., с |
1,151 |
|||||||||
|
I, |
55,949·10-5 |
|||||||||
|
St, с |
0,011 |
|||||||||
|
St, с |
0,0035 |
|||||||||
|
Δt, с |
0,009 |
|||||||||
|
ID, кг·м2 |
11,289·10—5 |
|||||||||
|
Iтеор., кг·м2 |
71,514·10-5 |
Iср.взв.
= 58,467·10-5 (кг·м2).
5. Примеры
вычислений.
1.) tср. = (t1 + t2 + t3 + t4 + t5 + t6 + t7 + t8 + t9 + + t10)/10 = (0,909 + 0,912 + 0,898 + 0,92 + 0,901 + + 0,915 + 0,914 +
0,899 + 0,916 + 0,915)/10 =9,099/10 = = 0,91 (с).
2.) I = m·(r + rн)2·[(g·t2/2·h0) — 1] =
158·10-3·(5·10-3 + + 0,6·10-3)2·[(9,8·0,912/2·21·10-2)
— 1] = 9,08·10-5 (кг·м2).
3.) Iср.взв. = I3
+ I4 +I5/3 = 60,155·10-5 + 59,297·10-5
+ + 55,949·10-5/3 = 58,467·10-5 (кг·м2).
4.) ID = mD·RD2/2 = 125·10-3·(42,5·10-3)2/2 = =
0,125·1806,25·10—6/2 = 11,289·10—5 (кг·м2).
5.) IК = mК·(RК12 + RК22)/2=
390·10-3·[(42,5·10-3)2 + + (52,5·10-3)2]/2
= 0,39·[1806,25·10-6 + 2756,25·10-6]/2= = 0,39·4562,5·10-6/2
= 88,969·10-5 (кг·м2).
6.) Iтеор. = [mD·R12
+ mК·(R12 + R22)]/2=[125·10-3·(42,5·10-3)2
+ + 390·10-3·[(42,5·10-3)2 + (52,5·10-3)2]]/2
= [0,125 x x 1806,25·10-6 + 0,39·[1806,25·10-6 +
2756,25·10-6]]/2 = = [225,781·10-6 + 0,39·4562,5·10-6]/2
= = [225,781·10-6 + 1779,375·10-6]/2 =
2005,156·10-6/2 = = 1002,578·10-6 = 100,258·10-5
(кг·м2).
6. Вычисление
погрешностей.
1.) St = √((t1—tср.)2 + (tN—tср.)2/N-1), где St – средняя квадратичная погрешность значения времени.
2.) St = St/√N, где St – случайная погрешность
удельного сопротивления.
3.) Δt = θt + kSt, где Δt – полная
погрешность удельного сопротивления.
Примеры вычислений:
1.) St = √((t1-tср.)2 + (tN-tср.)2/N-1) = √((0,909 — 0,91)2 + + (0,912 — 0,91)2(0,898
— 0,91)2 + (0,92 – 0,91)2 + + (0,901 – 0,91)2
+ (0,915 – 0,91)2 + (0,914 – 0,91)2 + + (0,899 – 0,91)2
+ (0,916–0,91)2 + (0,915 – 0,91)2/10 — 1 = √(0,000001 + 0,000004
+ 0,000144 + 0,0001 + + 0,000081 + 0,000025 + 0,000016 + 0,000121 + 0,000036+
+ 0,000025/9 = √0,000553/9 = √0,0000614 = 0,0078358 = = 0,008 (с).
2.) St = St/√N = 0,008/√10 = 0,008/3,162 = 0,0025 (с).
3.) Δt = θt
+ kSt = 0,001 + 2,3·0,0025 = 0,007 (с).
8. Окончательные
результаты, их обсуждение или несовпадение.
В данной лабораторной работе были
проведены исследования маятника Максвелла; рассчитаны среднее время падения
маятника, и по нему момент инерции, проведена обработка результатов измерений;
было произведено исследование зависимости момента инерции маятника от высоты, с
которой происходит падение маятника.
Из проделанных опытов и вычислений видно,
что момент инерции маятника не зависит от высоты падения маятника, так как чем
больше высота, тем больше время падения маятника. А на момент инерции маятника
влияет масса маятника, радиус оси и радиус нити. Также из формулы для момента
инерции маятника Максвелла:
I = m·(r + rн)2·[(g·t2/2·h0) — 1] следует, что при изменении высоты
меняется и время падения, но соотношение остаётся прежним, поэтому высота не
влияет на момент инерции маятника Максвелла.
В лабораторной работе мы рассчитываем
момент инерции по двум формулам:
1.) Экспериментальное значение момента
инерции:
I = m·(r + rн)2·[(g·t2/2·h0) — 1];
2.) Теоретическое
выражение для момента инерции маятника:
Iтеор. = [mD·R12 + mК·(R12 + R22)]/2.
Моменты инерции,
посчитанные по этим формулам, различаются между собой
Похожие материалы
- Отчет по лабораторной работе №1 Бипризма Френеля
- Определение электрического сопротивления. Экспериментальная проверка закона Ома. Определение удельного сопротивления нихрома
- Столкновение шаров. Проверка законов сохранения импульса и энергии, определение деформации шаров и силы удара
Информация о работе
Тип:
Отчеты по лабораторным работам
Рис. 1
Задание 1:определить
ускорение свободного падения при помощи
оборотного маятника с предельной
относительной погрешностью,
не превышающей 5 %.
Задание 2:определить ускорение
свободного падения при помощи
математического маятника с предельной
относительной погрешностью,
не превышающей 5 %.
Оборудование и принадлежности:установка для проведения измерений,
линейка.
ОПИСАНИЕ УСТАНОВКИ
Общий вид оборотного маятника показан
на рис.1. Основание 1 оснащено регулируемыми
ножками 2, которые позволяют производить
выравнивание прибора. В основании
закреплена колонка 3, на которой
зафиксирован верхний кронштейн 4 и
нижний кронштейн 5 с фотоэлектрическим
датчиком 6. С одной стороны кронштейна
4 находится математический маятник 7, с
другой — оборотный маятник 8.
Оборотный маятник выполнен в виде
стального стержня, на котором фиксируются
две повернутые лезвиями друг к другу
опорные призмы 11 и две чечевицы (подвижных
груза) 12а и 12б.
На стержне через 10 мм нанесены кольцевые
углубления, служащие для определения
приведенной длины Lоборотного
маятника (расстояние между опорными
призмами). Призмы и чечевицы можно
перемещать вдоль стержня и фиксировать
в любом положении. Эти элементы выполнены
таким образом, что расстояние между
ними является кратным 10 мм, а фиксирующие
воротки размещены так, чтобы при помощи
кольцевых углублений их можно было бы
фиксировать в нужном положении.
Нижний кронштейн 5 вместе с фотоэлектрическим
датчиком можно перемещать вдоль колонки
3 и фиксировать в произвольно выбранном
положении.
ЭЛЕМЕНТЫ ТЕОРИИ
Рис. 2
Общие сведения.Физическим
маятником называется твердое тело,
способное совершать колебания под
действием силы тяжести относительно
горизонтальной оси (рис. 2). К таким
колебаниям применимо основное уравнение
динамики вращательного движения твёрдого
тела, которое в проекции на ось вращенияZимеет вид:
(1)
где Mz–
проекция момента силы тяжести на ось
Z, I– момент
инерции маятника относительно оси
колебаний,z– проекция углового ускорения на осьZ. Учитывая, чтоMz= –mgasin, z=d2/dt2,
получим:
, (2)
где m– масса маятника,a–
расстояние от оси вращения до центра
масс маятника,– угловое перемещение маятника (угол
отклонения маятника от положения
равновесия). Угловое перемещение –
векторная величина, его направление
определяется по правилу буравчика. В
данном случае векторы
и
направлены в противоположные стороны,
поэтому выражение дляMzзаписано со знаком минус.
При малых углах отклонения sin
,
в этом случае уравнение (2) можно записать
в виде:
+
(3)
Уравнение (3) представляет собой уравнение
гармонических колебаний переменной
величины ,
квадрат угловой частоты которых равен
коэффициенту передво втором слагаемом. То есть
(4)
Решение уравнения (3) можно записать в
виде
(t) = ocos(t
+ o), (5)
где o– угловая амплитуда колебаний,o– начальная фаза колебаний.
Из вышеизложенного следует, что колебания
физического маятника (как и математического
маятника) не являются гармоническими.
Они будут мало отличаться от гармонических
колебаний лишь в том случае, когда
выполняется условие sin
,
то есть, когда угол отклонения маятника
от положения равновесия небольшой.
Из формулы (4) находим период колебаний
физического маятника:
(6)
Период колебаний математического
маятника длиной L вычисляется по формуле:
(7)
Сравнивая формулы (6) и (7), приходим к
выводу, что математический маятник,
длина которого
, (8)
будет совершать колебания с тем же
периодом, что и данный физический
маятник. Точка, находящаяся на расстоянии
L(рис. 1) от оси вращения физического
маятника на прямой, проходящей через
его центр масс перпендикулярно оси
вращения, называется центром качания
физического маятника. ВеличинаL,
вычисляемая по формуле (8), называется
приведенной длиной физического маятника.
По теореме Гюйгенса – Штейнера
I = Io
+ ma2, (9)
где Io–
момент инерции физического маятника
относительно оси, проходящей через его
центр масс параллельно оси колебаний.
Подставив (9) в (8), получим:
(10)
Рис.
3
Из (10) следует, что приведенная длина
физического маятника больше расстояния
от оси вращения до центра масс маятника
на величину (рис. 2, 3)
. (11)
Подвесим маятник на оси, параллельной
прежней и проходящей через центр качания
С(рис. 3). В этом случае приведенная
длина маятника
(12)
По теореме Гюйгенса – Штейнера
Подставив это выражение в (12), а также
учитывая, чтоa1 = Io/ma
= L— a,получим:
.
Так как приведенная длина физического
маятника относительно новой оси не
изменилась, то и период его колебаний
на новой оси также не изменился.
Следовательно, данная ось и параллельная
ей ось, проходящая через центр качания
маятника, обладают свойством взаимности.
Ускорение свободного падения можно
вычислить по формуле
. (13)
При определении ускорения свободного
падения с помощью оборотного маятника
необходимо, изменяя его момент инерции
(передвигая чечевицу 12а), добиться того,
чтобы расстояние между опорными призмами
стало равным приведенной длине оборотного
маятника. Измерив LиT, по формуле
(13) находимg.
Для определения ускорения свободного
падения с помощью математического
маятника необходимо измерить его длину
L, соответствующий ей период колебанийT, и по формуле (13) вычислитьg.
Чтобы повысить точность измерения
периода колебаний T, необходимо
измерить времяtдляn колебаний
(обычно n= 10). Тогда
. (14)
Соседние файлы в папке Механика старые
- #
- #
- #
- #
- #
- #
- #
- #
- #


Подборка по базе: лабараторная работа № 1.docx, Контрольная работа по ПОПД для 3-х курсов (восстановлен).docx, курсовая работа Лецензирование и сертефикация.rtf, СТРб_1803_Лабораторная работа_2.docx, Практическая работа №1. Абдуваитов.doc, Практическая работа №3. Абдуваитов.doc, Практическая работа № 1.doc, Практическая работа1 .docx, Контрольная работа по ВМТС.docx, Практическая работа в Тотал Коммандер .docx
Лабораторная работа № 1.8
МАЯТНИК МАКСВЕЛЛА
Цель работы: определение момента инерции маятника Максвелла.
Задание к работе:
К работе допущен:
Расчеты выполнил:
Работу защитил:
Введение
Момент инерции твердого тела – важная физическая характеристика. Он является мерой инертности тела при вращательном движении. Момент инерции твердого тела J относительно оси вращения равен сумме произведений элементарных масс Δ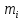
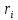
Маятник Максвелла представляет собой массивный диск 1, насаженный на стержень 2 и подвешенный бифилярно с помощью нитей 3 к горизонтальной опоре (рис. 1). Если, накрутив нити на концы стержня, поднять маятник на некоторую высоту h (рис. 1) относительно положения равновесия 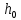
Рис.1. Маятник Максвелла
Определение момента инерции маятника Максвелла в данной лабораторной работе основано на использовании закона сохранения механической энергии.
где М – масса маятника; v – скорость поступательного движения центра масс маятника; 
Решая уравнение (1) относительно I, получаем:
Поскольку поступательное движение центра масс маятника равноускоренное, то при нулевой начальной скорости:
где t – время, за которое маятник опустился с высоты h до нижнего положения.
Если считать, что раскручивание нитей со стержня происходит без проскальзывания, то угловая скорость связана с линейной скоростью центра масс маятника соотношением:
где 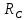
Подставляя (3) и (4) в (2), получаем выражение для определения момента инерции маятника, содержащее параметры, которые можно определить опытным путем:
Таким образом, измерив массу маятника М, радиус стержня 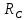
По свойству аддитивности момент инерции маятника I равен сумме моментов инерции диска 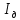
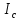
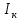
Так как маятник состоит из тел правильной формы, моменты инерции которых известны, формулу (6) можно представить в виде:
где 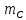
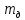
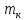
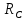
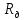
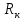
Таким образом, зная массы диска, стрежня, сменных колец и их радиусы по формуле (7) можно теоретически вычислить момент инерции маятника.
1. Описание установки
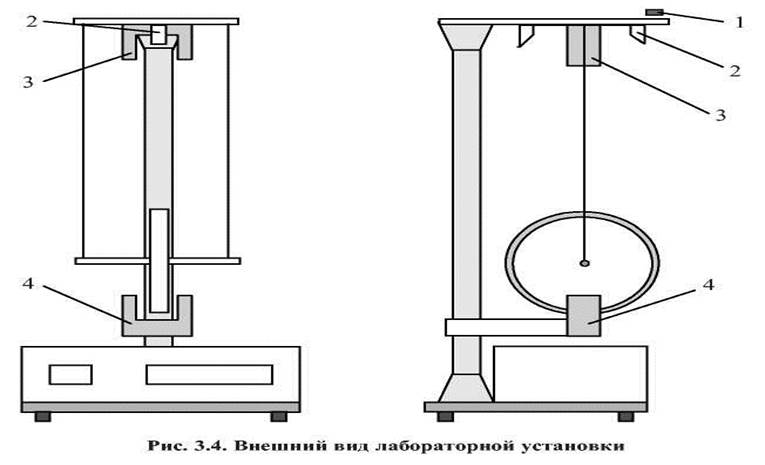
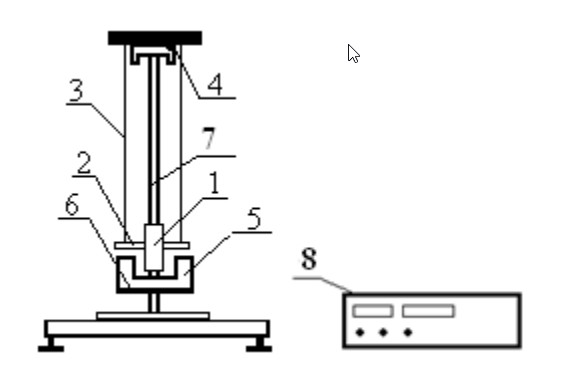
Установка включает в себя маятник Максвелла, электронный блок и набор сменных колец. Общий вид установки представлен на рис.2.
Рис.2. Общий вид установки
Маятник представляет собой диск 1 закрепленный на стержне 2, подвешенный на бифилярном подвесе 3. На диск крепятся сменные кольца. Установка состоит из основания, на вертикальной стойке которого размещены верхний 4 и подвижный нижний 5 кронштейны. Верхний кронштейн 4 снабжен устройством для крепления и регулировки подвеса 3. На вертикальной стойке нанесена миллиметровая шкала 7, по которой определяют высоту h. В кронштейне 5 закреплен фотоэлектрический датчик, фиксирующий положение маятника в нижнем положении, по достижении которого останавливается счетчик времени. На передней панели электронного блока 8 имеются индикаторы единиц измерения и времени, кнопки управления: «СБРОС», «СТОП» и «ПУСК».
Технические характеристики установки:
- Масса стержня
; радиус стержня
.
- Масса диска
; радиус диска
.
- Массы сменных колец
,
; внешний радиус сменных колец
.
2. Порядок выполнения измерений
Упражнение 1.
- Определить массу маятника без сменного кольца М. Результат записать в табл. 1. Установить между фотодатчиками, находящимися в кронштейнах 4 и 5, расстояние L заданное преподавателем при помощи шкалы 10. Вычислить расстояние h:
- Вращая маятник, зафиксировать его в исходном верхнем положении. Одновременно отпустить маятник и нажать кнопку «ПУСК» на электронном блоке, произвести отсчет времени t. Занести результаты измерений в табл. 1.
- Повторить п.2 заданное преподавателем количество раз.
Таблица 1
| № | М,
кг |
ΔМ,
кг |
h,
м |
Δh,
м |
t,
c |
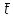 , ,
c |
Δt,
c |
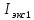 , ,
кг∙ |
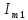 , ,
кг∙ |
Δ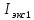 , ,
кг∙ |
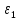 ,% ,% |
| 1 | 0,155 | 0,005 | 0,310 | 0,001 | 1,456 | 1,545 | 0,040 | 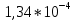 |
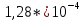 |
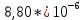 |
6,57 |
| 2 | 1,251 | ||||||||||
| 3 | 1,523 | ||||||||||
| 4 | 1,543 | ||||||||||
| 5 | 1,570 |
Упражнение 2.
- Надеть на диск сменное кольцо, масса которого задана преподавателем. Определить массу получившегося маятника М. Результат записать в табл. 2 Вычислить расстояние h:
- Вращая маятник, зафиксировать его в исходном верхнем положении. Одновременно отпустить маятник и нажать кнопку «ПУСК» на электронном блоке, произвести отсчет времени t. Занести результаты измерений в табл. 2.
- Повторить п.2 заданное преподавателем количество раз.
Таблица 2
| № | М,
кг |
ΔМ,
кг |
h,
м |
Δh,
м |
t,
c |
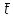 , ,
c |
Δt,
c |
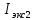 , ,
кг∙ |
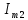 , ,
кг∙ |
Δ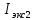 , ,
кг∙ |
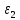 ,% ,% |
| 1 | 0,475 | 0,005 | 0,296 | 0,001 | 2,090 | 2,055 | 0,020 | 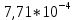 |
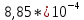 |
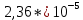 |
3,06 |
| 2 | 2,055 | ||||||||||
| 3 | 2,036 | ||||||||||
| 4 | 2,042 | ||||||||||
| 5 | 2,051 |
3. Обработка результатов измерений
3.1. Рассчитать среднее время движения маятника можно по формуле:
Значения времени, полученного в результате первого и второго опыта в упр. 1 считаю как промах и не учитываю при вычислении.
3.2. По формуле (5) можно рассчитать момент инерции маятника 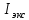
3.3. Вычислить абсолютную ошибку времени, абсолютную и
относительную ошибки момента инерции можно по формулам:
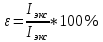
3.3.1. Сначала вычислю абсолютную погрешность времени.
3.3.1.1. Погрешность прибора можно определить по цене деления. Так как прибор измеряет время с точностью до 1 мс, то 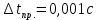
3.3.1.2. Случайная погрешность определяется по формуле:
где 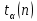
Следовательно, перед началом вычислений надо найти недостающие величины.
3.3.1.2.1. Коэффициент Стьюдента (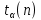
3.3.1.2.2. S вычисляется по формуле:
Δ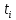
Δ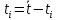
следовательно:
Δ
Δ
Δ
Δ
Δ
Δ
Δ
Δ
Δ
3.3.1.2.3. Теперь можно вычислить 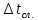
3.3.1.3. Абсолютная погрешность равна:
3.3.2. Теперь вычислю абсолютную погрешность момента инерции.
Так как g – табличная величина, то в качестве абсолютной погрешности принимается половина разряда последней значащей цифры числа, т.е.
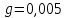
Для упр. 1:
Для упр. 2:
3.3.3. Теперь вычислю относительную погрешность момента инерции.
3.4. По формуле (7) можно рассчитать теоретический момент инерции маятника 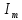
3.5. Сравниваю экспериментальное и теоретическое значения момента инерции, вычислив разницу между ними в процентах:
3.6. На основе полученных экспериментальных значений рассчитаю момент инерции кольца 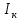
откуда
Так как значение 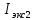
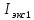
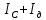
3.7. На основе полученных теоретический значений рассчитаю момент инерции кольца 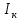
3.8. Сравниваю экспериментальное и теоретическое значения момента инерции кольца, вычислив разницу между ними в процентах:
Заключение
Определил момент инерции маятника Максвелла. Для этого рассчитал теоретические значения инерции и провел опыты, чтобы рассчитать экспериментальные значения:
Также вычислил теоретическое и экспериментальное значение инерции кольца:
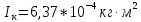
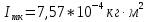




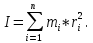
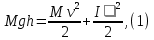
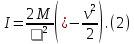
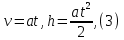
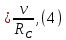
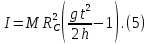
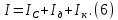
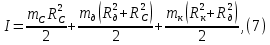
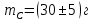 ; радиус стержня
; радиус стержня 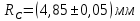 .
.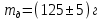 ; радиус диска
; радиус диска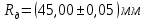 .
.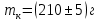 ,
, 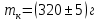 ; внешний радиус сменных колец
; внешний радиус сменных колец 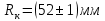 .
.