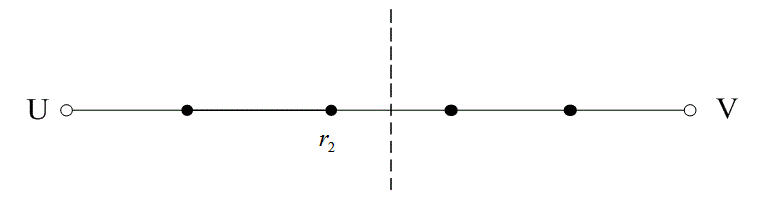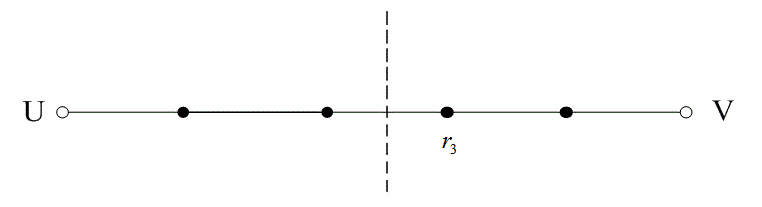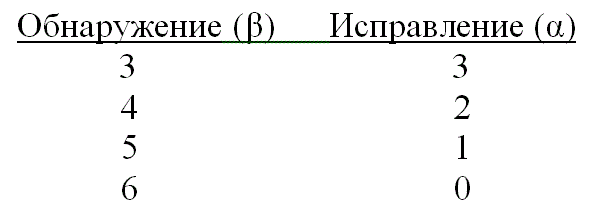Построение кодов обнаружения ошибок (защитных кодов)
В процессе
преобразования информации, представленной
в закодированной форме, часто возникают
ошибки, связанные со сбоями в работе
технических средств преобразования
информации ,а также допущенные людьми
при работе с компьютером и оргтехникой.
Построение кодов
обнаружения ошибок основано на трех
основных принципах:
1) Использование
признаков делимости
2) Запрещение
использования определенной части
кодовых слов.
3) Запрещение
использования определенных символов.
1. Построение кодов обнаружения ошибок с использованием признака делимости числа
Суть
данного способа построения кодов
обнаружения ошибок состоит в следующем:
допустим необходимо построить код
обнаружения ошибок для табельного
номера, состоящего из четырех цифр:
5621 а)
в данном случае выбирается число М,
называемое модулем (желательно простое
целое число) и исходное кодовое число
делится на модуль М. Например, М=9
5621
: 9
54
22
18
41
36
5
и
остаток от деления (в данном случае
равный 5) дописывается справа от исходного
кодового слова. Таким образом, табельный
номер примет вид 56215,
где первые четыре разряда информационные,
а последний контрольный.
б)
контроль по модулю «10». Допустим,
необходимо построить код обнаружения
ошибок для номенклатурного номера
материала 62154. Находим сумму чисел:
6+2+1+5+4=18.
Далее
определяется ближайшее, большее 18, число
кратное 10. Это число 20. Определяется
разность этих чисел 20-18=2. Полученное
значение и является контрольным разрядом.
Таким образом, будет обрабатываться
на всех стадиях число 621542,
содержащее 5 информационных разрядов
и 1 контрольный. В данном случае
присутствует избыточная информация,
введение которой оправдано необходимостью
контроля правильности преобразования
информации. Однако, данный способ не
позволяет обнаружить ошибки, связанные
с перестановкой цифр.
Для
этого существует способ построения
кодов обнаружения ошибок с
учетом весовых коэффициентов.
Суть которого в том, что на каждый разряд
числа «навешивается» весовой коэффициент.
Далее применяется контроль по модулю
«10», только с использованием весовых
коэффициентов числа.
Например, требуется
построить код инвентарного номера
оборудования 190624. Для каждого разряда
числа вводится весовой коэффициент,
причем, чем старше разряд, тем больше
коэффициент. Данное число имеет весовые
коэффициенты:
6
5 4 3 2 1
1
9 0 6 2 4
Находится
сумма цифр числа, умноженных на весовые
коэффициенты: 1*6+9*5+0*4+6*3+2*2+4*1=77.
Находится разность между ближайшим
большим числом, кратным 10, и данным
числом 80-77=3 и эта разность дописывается
к исходному кодовому числу в качестве
контрольного разряда: 1906243.
Построение
защитных кодов для информации,
представленной в двоичном коде
Одним
из основных способов контроля двоичной
информации является контроль «на
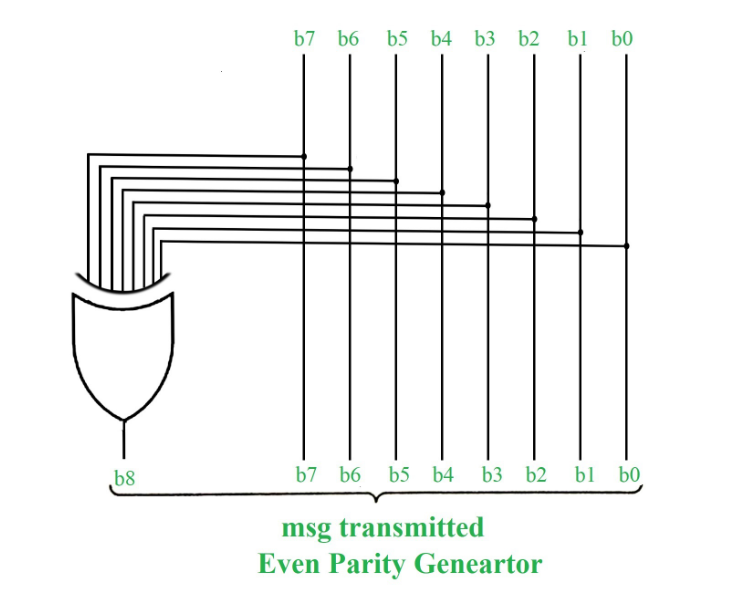
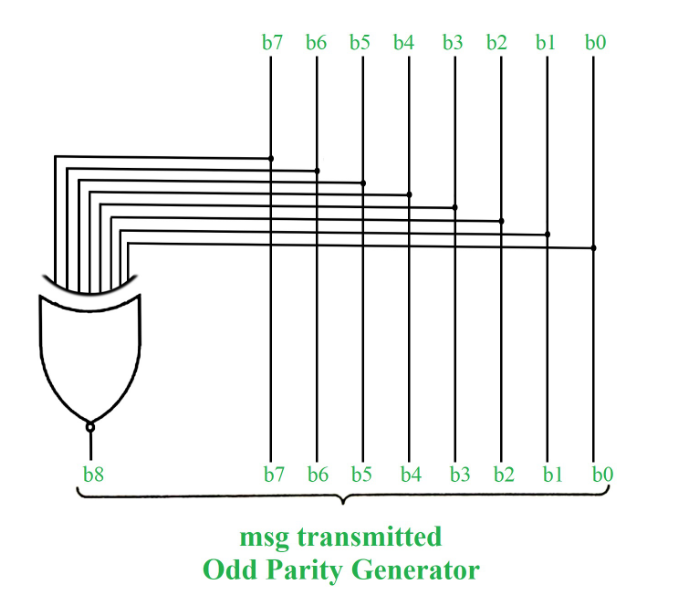
ЧЕТ». В
исходном кодовом числе подсчитывается
количество единиц, если оно является
нечетным, в качестве контрольного
разряда к числу приписывается 1,
если четным — 0.
В полученном кодовом слове число единиц
должно быть обязательно четным.
Например: а)
110011 — исходное кодовое слово
1100110
— кодовое слово с контрольным разрядом
б)
11001 — исходное кодовое слово
110011
— кодовое слово с контрольным разрядом
Коды
обнаружения ошибок, построенные по
принципу применения кодовых словарей
Данный способ
построения кодов обнаружения ошибок
заключается в использовании слов,
входящих в специальным образом
составленные кодовые словари. Только
данные слова являются разрешенными,
все остальные запрещенными для
использования. Если кодовое слово,
подлежащее преобразованию, содержится
в кодовом словаре, значит информация
преобразуется без ошибок, если данного
слова в кодовом словаре нет, значит
выдается сообщение об ошибке. Кодовые
словари могут быть построены на 10 и на
100 слов.
Пример построения
кодового словаря на 10 слов:01 12 23 34 45 56 67
78 89 90. Все остальные двузначные слова
являются запрещенными. В данном случае
коэффициент использования информационной
емкости кода равен: 10/99=0,1.
Здесь
10- количество слов в словаре , 99 —
максимально возможное количество цифр
в словаре.
Например, если
получено при передаче информации слово
13, то выдается сообщение об ошибке, т.к.
данное слово в кодовом словаре
отсутствует. В
случае одиночной ошибки она может быть
исправлена: это может быть либо слово
23,либо — 12.
Кодовый словарь
на 100 слов строится следующим образом:
|
Десятки |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
0 1 2 3 4 5 6 7 8 9 |
001 012 023 034 045 056 067 078 089 090 |
102 113 124 135 146 157 168 179 180 191 |
203 214 225 236 247 258 269 270 281 292 |
304 315 326 337 348 359 360 371 382 393 |
405 416 427 438 449 450 461 472 483 494 |
506 517 528 539 540 551 562 573 584 595 |
607 618 629 630 641 652 663 674 685 696 |
708 719 720 731 742 753 764 775 786 797 |
809 810 821 832 843 854 865 876 887 898 |
900 912 923 934 945 956 967 978 989 999 |
Проверка
правильности переданных кодовых слов
выполняется несколькими способами.
Основные способы контроля приведены
ниже:
-
похожие
по написанию цифры кодового слова (3 и
8, 5 и 6, 9 и 0, 6 и 9 и т.д.) ; -
ошибки,
совершенные при вводе с клавиатуры
(рядом расположенные клавиши: с 1 рядом
2 и 4, с 5 – рядом 2, 4 и 6 и т.д.); -
перестановка
цифр числа при вводе с клавиатуры.
Коды
обнаружения ошибок, построенные по
принципу запрещения использования
определенной части символов
Очень часто в
процессе преобразования информации
возникают ошибки, связанные с нечетким
заполнением первичных документов или
с нажатием на устройствах передачи или
подготовки данных ошибочно рядом
расположенной клавиши. При нечетком
заполнении документов бывает сложно
различить похожие по начертанию цифры
4 и 7, 0 и 6, 0 и 9. Для избежания подобного
рода ошибок, а также устранения возможности
ошибок при нажатии рядом расположенных
на клавиатуре клавиш запрещается
использовать для построения кодовых
слов следующие символы: например: 0,6,9.
Все остальные символы являются
разрешенными. В случае, если в процессе
преобразования информации возникает
кодовое слово, содержащее разрешенные
символы, выдается сообщение об ошибке.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Improve Article
Save Article
Improve Article
Save Article
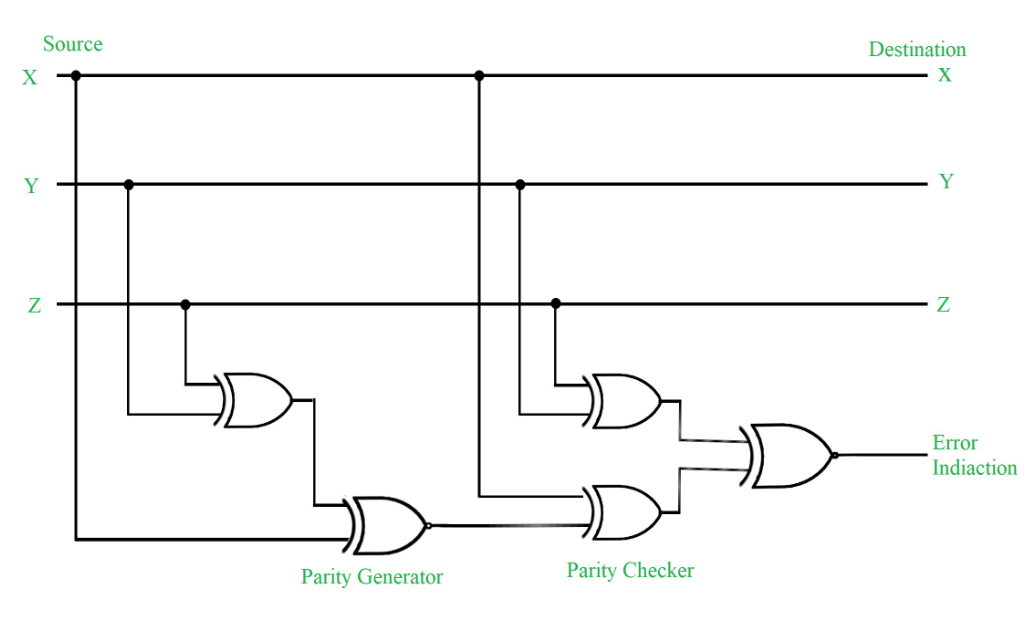
Error Detection Codes :
The binary information is transferred from one location to another location through some communication medium. The external noise can change bits from 1 to 0 or 0 to 1.This changes in values are called errors. For efficient data transfer, there should be an error detection and correction codes. An error detection code is a binary code that detects digital errors during transmission. A famous error detection code is a Parity Bit method.
Parity Bit Method :
A parity bit is an extra bit included in binary message to make total number of 1’s either odd or even. Parity word denotes number of 1’s in a binary string. There are two parity system-even and odd. In even parity system 1 is appended to binary string it there is an odd number of 1’s in string otherwise 0 is appended to make total even number of 1’s.
In odd parity system, 1 is appended to binary string if there is even a number of 1’s to make an odd number of 1’s. The receiver knows that whether sender is an odd parity generator or even parity generator. Suppose if sender is an odd parity generator then there must be an odd number of 1’s in received binary string. If an error occurs to a single bit that is either bit is changed to 1 to 0 or O to 1, received binary bit will have an even number of 1’s which will indicate an error.
The limitation of this method is that only error in a single bit would be identified.
| Message (XYZ) | P(Odd) | P(Even) |
|---|---|---|
| 000 | 1 | 0 |
| 001 | 0 | 1 |
| 010 | 0 | 1 |
| 011 | 1 | 0 |
| 100 | 0 | 1 |
| 101 | 1 | 0 |
| 110 | 1 | 0 |
| 111 | 0 | 1 |
Figure – Error Detection with Odd Parity Bit
Points to Remember :
- In 1’s complement of signed number +0 and -0 has two different representation.
- The range of signed magnitude representation of an 8-bit number in which 1-bit is used as a signed bit as follows -27 to +27.
- Floating point number is said to be normalized if most significant digit of mantissa is one. For example, 6-bit binary number 001101 is normalized because of two leading 0’s.
- Booth algorithm that uses two n bit numbers for multiplication gives results in 2n bits.
- The booth algorithm uses 2’s complement representation of numbers and work for both positive and negative numbers.
- If k-bits are used to represent exponent then bits number = (2k-1) and range of exponent = – (2k-1 -1) to (2k-1).
Improve Article
Save Article
Improve Article
Save Article
Error Detection Codes :
The binary information is transferred from one location to another location through some communication medium. The external noise can change bits from 1 to 0 or 0 to 1.This changes in values are called errors. For efficient data transfer, there should be an error detection and correction codes. An error detection code is a binary code that detects digital errors during transmission. A famous error detection code is a Parity Bit method.
Parity Bit Method :
A parity bit is an extra bit included in binary message to make total number of 1’s either odd or even. Parity word denotes number of 1’s in a binary string. There are two parity system-even and odd. In even parity system 1 is appended to binary string it there is an odd number of 1’s in string otherwise 0 is appended to make total even number of 1’s.
In odd parity system, 1 is appended to binary string if there is even a number of 1’s to make an odd number of 1’s. The receiver knows that whether sender is an odd parity generator or even parity generator. Suppose if sender is an odd parity generator then there must be an odd number of 1’s in received binary string. If an error occurs to a single bit that is either bit is changed to 1 to 0 or O to 1, received binary bit will have an even number of 1’s which will indicate an error.
The limitation of this method is that only error in a single bit would be identified.
| Message (XYZ) | P(Odd) | P(Even) |
|---|---|---|
| 000 | 1 | 0 |
| 001 | 0 | 1 |
| 010 | 0 | 1 |
| 011 | 1 | 0 |
| 100 | 0 | 1 |
| 101 | 1 | 0 |
| 110 | 1 | 0 |
| 111 | 0 | 1 |
Figure – Error Detection with Odd Parity Bit
Points to Remember :
- In 1’s complement of signed number +0 and -0 has two different representation.
- The range of signed magnitude representation of an 8-bit number in which 1-bit is used as a signed bit as follows -27 to +27.
- Floating point number is said to be normalized if most significant digit of mantissa is one. For example, 6-bit binary number 001101 is normalized because of two leading 0’s.
- Booth algorithm that uses two n bit numbers for multiplication gives results in 2n bits.
- The booth algorithm uses 2’s complement representation of numbers and work for both positive and negative numbers.
- If k-bits are used to represent exponent then bits number = (2k-1) and range of exponent = – (2k-1 -1) to (2k-1).
Дисциплина: ТЕХНОЛОГИИ ФИЗИЧЕСКОГО УРОВНЯ
ПЕРЕДАЧИ ДАННЫХ
Занятие №10
Методы обнаружения и коррекции ошибок
при передаче информации в компьютерных сетях.
ПЛАН ЗАНЯТИЯ:
1. Обнаружение и коррекция ошибок
2. Методы обнаружения ошибок
3. Методы коррекции ошибок
4. Вопросы
Обнаружение и коррекция ошибок
Надежную передачу
информации обеспечивают различные методы. Основной
принцип работы протоколов, которые
обеспечивают надежность передачи информации —
повторная передача искаженных или потерянных
пакетов.
Такие протоколы
основаны на том, что приемник в состоянии распознать факт искажения информации
в принятом кадре информации.
Еще одним, более
эффективным подходом, чем повторная передача пакетов,
является использование самокорректирующихся
кодов, которые позволяют не только
обнаруживать, но и исправлять ошибки в
принятом кадре.
Методы обнаружения ошибок
Методы
обнаружения ошибок основаны на передаче в составе блока данных
избыточной служебной информации, по которой можно судить с некоторой степенью
вероятности о достоверности принятых данных. В
сетях с коммутацией пакетов такой
единицей информации может быть PDU
любого уровня, для определенности будем
считать, что мы контролируем кадры.
Избыточную
служебную информацию принято называть контрольной суммой,
или контрольной последовательностью
кадра (Frame Check Sequence, FCS).
Контрольная сумма
вычисляется как функция от основной информации, причем не
обязательно путем суммирования.
Принимающая
сторона повторно вычисляет контрольную сумму кадра по
известному алгоритму и в случае ее совпадения
с контрольной суммой, вычисленной
передающей стороной, делает вывод о том,
что данные были переданы через сеть
корректно.
Рассмотрим
несколько распространенных алгоритмов вычисления контрольной
суммы, отличающихся вычислительной
сложностью и способностью обнаруживать
ошибки в данных.
Контроль по
паритету.
Контроль по
паритету представляет собой наиболее простой метод контроля
данных. В то же время это наименее мощный
алгоритм контроля, так как с его помощью
можно обнаруживать только одиночные
ошибки в проверяемых данных.
Метод заключается в
суммировании по модулю 2 всех битов контролируемой информации.
Нетрудно заметить, что для информации,
состоящей из нечетного числа единиц,
контрольная сумма всегда равна 1, а при четном
числе единиц — 0.
Например, для данных 100101011 результатом контрольного суммирования будет
значение 1. Результат суммирования также
представляет собой один дополнительный бит
данных, который пересылается вместе с
контролируемой информацией. При искажении в
процессе пересылки любого одного бита исходных
данных (или контрольного разряда)
результат суммирования будет отличаться
от принятого контрольного разряда, что
говорит об ошибке.
Однако двойная
ошибка, например 110101010, будет неверно принята за
корректные данные.
Поэтому контроль по паритету применяется к небольшим порциям
данных, как правило, к каждому байту, что дает
коэффициент избыточности для этого
метода 1/8.
Метод редко
используется в компьютерных сетях из-за значительной
избыточности и невысоких диагностических
возможностей.
Вертикальный и
горизонтальный контроль по паритету
Вертикальный и
горизонтальный контроль по паритету представляет собой
модификацию описанного метода. Его отличие
состоит в том, что исходные данные
рассматриваются в виде матрицы, строки
которой составляют байты данных.
Контрольный разряд
подсчитывается отдельно для каждой строки и для каждого столбца
матрицы. Этот метод позволяет обнаруживать
большую часть двойных ошибок, однако он
обладает еще большей избыточностью. На
практике этот метод сейчас также почти не
применяется при передаче информации по сети.
Циклический избыточный контроль
Циклический
избыточный контроль (Cyclic Redundancy Check, CRC) является в
настоящее время наиболее популярным методом
контроля в вычислительных сетях (и не
только в сетях, например, этот метод широко
применяется при записи данных на гибкие и
жесткие диски).
Метод основан на
представлении исходных данных в виде одного многоразрядного
двоичного числа.
Например, кадр стандарта Ethernet, состоящий из 1024 байт, рассматривается как
одно число, состоящее из 8192 бит. Контрольной
информацией считается остаток от
деления этого числа на известный делитель R.
Обычно в качестве делителя выбирается
семнадцати- или тридцатитрехразрядное число,
чтобы остаток от деления имел длину 16
разрядов (2 байт) или 32 разряда (4 байт).
При получении кадра
данных снова вычисляется остаток от деления на тот же делитель R, но при этом к
данным кадра добавляется и содержащаяся в нем контрольная сумма.
Если остаток от
деления на R равен нулю, то делается вывод об отсутствии ошибок в полученном
кадре, в противном случае кадр считается искаженным.
Этот метод
обладает более высокой вычислительной сложностью, но его
диагностические возможности гораздо выше, чем
у методов контроля по паритету.
Этот метод
позволяет обнаруживать все одиночные ошибки, двойные ошибки и
ошибки в нечетном числе битов.
Метод обладает
также невысокой степенью избыточности. Например, для кадра
Ethernet размером 1024 байт контрольная
информация длиной 4 байт составляет только
0,4 %.
Методы коррекции ошибок
Техника
кодирования, которая позволяет приемнику не только понять, что
присланные данные содержат ошибки, но и
исправить их, называется прямой
коррекцией ошибок — (Forward Error Correction, FEC).
Коды, которые
обеспечивают прямую коррекцию ошибок, требуют введения большей избыточности в
передаваемые данные, чем коды, только обнаруживающие ошибки.
При применении
любого избыточного кода не все комбинации кодов являются
разрешенными. Например, контроль по паритету
делает разрешенными только половину
кодов.
Если мы
контролируем три информационных бита, то разрешенными 4-битными
кодами с дополнением до нечетного количества
единиц будут:
000 1, 001 0, 010 0, 011 1, 100
0, 101 1, 110 1, 111 0
То есть всего 8 кодов из 16 возможных.
Для того чтобы
оценить количество дополнительных битов, требуемых для
исправления ошибок, нужно знать так
называемое расстояние Хемминга между
разрешенными комбинациями кода.
Расстоянием
Хемминга называется минимальное число битовых разрядов, в
которых отличается любая пара разрешенных
кодов.
Для схем контроля
по паритету расстояние Хемминга равно 2.
Можно доказать, что если мы сконструировали
избыточный код с расстоянием
Хемминга, равным N, то
такой код будет в состоянии распознавать (N-1)-кратные
ошибки
и исправлять (N-1)/2-кратные
ошибки.
Так как коды с
контролем по паритету имеют расстояние Хемминга, равное 2, то
они могут только обнаруживать однократные
ошибки и не могут исправлять ошибки.
Коды Хемминга
эффективно обнаруживают и исправляют изолированные ошибки,
то есть отдельные искаженные биты,
которые разделены большим количеством
корректных битов.
Однако при
появлении длинной последовательности искаженных битов (пульсации
ошибок) коды Хемминга не работают.
Пульсации ошибок
характерны для беспроводных каналов, в которых применяют
сверточные коды.
Поскольку для распознавания наиболее вероятного корректного кода в
этом методе задействуется решетчатая
диаграмма, то такие коды еще называют
решетчатыми.
Эти коды
используются не только в беспроводных каналах, но и в модемах.
Методы прямой коррекции ошибок особенно
эффективны для технологий
физического уровня, которые не поддерживают
сложные процедуры повторной передачи
данных в случае их искажения.
Вопросы
:
1. Что называется контрольной
последовательностью кадра?
2. Что представляет собой контроль по
паритету?
3. Что представляет собой вертикальный и
горизонтальный контроль по паритету?
4. Что представляет собой циклический избыточный
контроль?
5. Что называется прямой коррекцией ошибок?
6. Что называется расстоянием Хемминга?
7. Какие коды называются решетчатыми?
8. Где используются решетчатые коды?

Как нетрудно догадаться, ко всему этому причастны корректирующие коды. Собственно, ECC так и расшифровывается — «error-correcting code», то есть «код, исправляющий ошибки». А CRC — это один из алгоритмов, обнаруживающих ошибки в данных. Исправить он их не может, но часто это и не требуется.
Давайте же разберёмся, что это такое.
Для понимания статьи не нужны никакие специальные знания. Достаточно лишь понимать, что такое вектор и матрица, как они перемножаются и как с их помощью записать систему линейных уравнений.
Внимание! Много текста и мало картинок. Я постарался всё объяснить, но без карандаша и бумаги текст может показаться немного запутанным.
Каналы с ошибкой
Разберёмся сперва, откуда вообще берутся ошибки, которые мы собираемся исправлять. Перед нами стоит следующая задача. Нужно передать несколько блоков данных, каждый из которых кодируется цепочкой двоичных цифр. Получившаяся последовательность нулей и единиц передаётся через канал связи. Но так сложилось, что реальные каналы связи часто подвержены ошибкам. Вообще говоря, ошибки могут быть разных видов — может появиться лишняя цифра или какая-то пропасть. Но мы будем рассматривать только ситуации, когда в канале возможны лишь замены нуля на единицу и наоборот. Причём опять же для простоты будем считать такие замены равновероятными.
Ошибка — это маловероятное событие (а иначе зачем нам такой канал вообще, где одни ошибки?), а значит, вероятность двух ошибок меньше, а трёх уже совсем мала. Мы можем выбрать для себя некоторую приемлемую величину вероятности, очертив границу «это уж точно невозможно». Это позволит нам сказать, что в канале возможно не более, чем ошибок. Это будет характеристикой канала связи.
Для простоты введём следующие обозначения. Пусть данные, которые мы хотим передавать, — это двоичные последовательности фиксированной длины. Чтобы не запутаться в нулях и единицах, будем иногда обозначать их заглавными латинскими буквами (,
,
, …). Что именно передавать, в общем-то неважно, просто с буквами в первое время будет проще работать.
Кодирование и декодирование будем обозначать прямой стрелкой (), а передачу по каналу связи — волнистой стрелкой (
). Ошибки при передаче будем подчёркивать.
Например, пусть мы хотим передавать только сообщения и
. В простейшем случае их можно закодировать нулём и единицей (сюрприз!):
Передача по каналу, в котором возникла ошибка будет записана так:
Цепочки нулей и единиц, которыми мы кодируем буквы, будем называть кодовыми словами. В данном простом случае кодовые слова — это и
.
Код с утроением
Давайте попробуем построить какой-то корректирующий код. Что мы обычно делаем, когда кто-то нас не расслышал? Повторяем дважды:
Правда, это нам не очень поможет. В самом деле, рассмотрим канал с одной возможной ошибкой:
Какие выводы мы можем сделать, когда получили ? Понятно, что раз у нас не две одинаковые цифры, то была ошибка, но вот в каком разряде? Может, в первом, и была передана буква
. А может, во втором, и была передана
.
То есть, получившийся код обнаруживает, но не исправляет ошибки. Ну, тоже неплохо, в общем-то. Но мы пойдём дальше и будем теперь утраивать цифры.
Проверим в деле:
Получили . Тут у нас есть две возможности: либо это
и было две ошибки (в крайних цифрах), либо это
и была одна ошибка. Вообще, вероятность одной ошибки выше вероятности двух ошибок, так что самым правдоподобным будет предположение о том, что передавалась именно буква
. Хотя правдоподобное — не значит истинное, поэтому рядом и стоит вопросительный знак.
Если в канале связи возможна максимум одна ошибка, то первое предположение о двух ошибках становится невозможным и остаётся только один вариант — передавалась буква .
Про такой код говорят, что он исправляет одну ошибку. Две он тоже обнаружит, но исправит уже неверно.
Это, конечно, самый простой код. Кодировать легко, да и декодировать тоже. Ноликов больше — значит передавался ноль, единичек — значит единица.
Если немного подумать, то можно предложить код исправляющий две ошибки. Это будет код, в котором мы повторяем одиночный бит 5 раз.
Расстояния между кодами
Рассмотрим поподробнее код с утроением. Итак, мы получили работающий код, который исправляет одиночную ошибку. Но за всё хорошее надо платить: он кодирует один бит тремя. Не очень-то и эффективно.
И вообще, почему этот код работает? Почему нужно именно утраивать для устранения одной ошибки? Наверняка это всё неспроста.
Давайте подумаем, как этот код работает. Интуитивно всё понятно. Нолики и единички — это две непохожие последовательности. Так как они достаточно длинные, то одиночная ошибка не сильно портит их вид.
Пусть мы передавали , а получили
. Видно, что эта цепочка больше похожа на исходные
, чем на
. А так как других кодовых слов у нас нет, то и выбор очевиден.
Но что значит «больше похоже»? А всё просто! Чем больше символов у двух цепочек совпадает, тем больше их схожесть. Если почти все символы отличаются, то цепочки «далеки» друг от друга.
Можно ввести некоторую величину , равную количеству различающихся цифр в соответствующих разрядах цепочек
и
. Эту величину называют расстоянием Хэмминга. Чем больше это расстояние, тем меньше похожи две цепочки.
Например, , так как все цифры в соответствующих позициях равны, а вот
.
Расстояние Хэмминга называют расстоянием неспроста. Ведь в самом деле, что такое расстояние? Это какая-то характеристика, указывающая на близость двух точек, и для которой верны утверждения:
- Расстояние между точками неотрицательно и равно нулю только, если точки совпадают.
- Расстояние в обе стороны одинаково.
- Путь через третью точку не короче, чем прямой путь.
Достаточно разумные требования.
Математически это можно записать так (нам это не пригодится, просто ради интереса посмотрим):
.
Предлагаю читателю самому убедиться, что для расстояния Хэмминга эти свойства выполняются.
Окрестности
Таким образом, разные цепочки мы считаем точками в каком-то воображаемом пространстве, и теперь мы умеем находить расстояния между ними. Правда, если попытаться сколько нибудь длинные цепочки расставить на листе бумаги так, чтобы расстояния Хэмминга совпадали с расстояниями на плоскости, мы можем потерпеть неудачу. Но не нужно переживать. Всё же это особое пространство со своими законами. А слова вроде «расстояния» лишь помогают нам рассуждать.
Пойдём дальше. Раз мы заговорили о расстоянии, то можно ввести такое понятие как окрестность. Как известно, окрестность какой-то точки — это шар определённого радиуса с центром в ней. Шар? Какие ещё шары! Мы же о кодах говорим.
Но всё просто. Ведь что такое шар? Это множество всех точек, которые находятся от данной не дальше, чем некоторое расстояние, называемое радиусом. Точки у нас есть, расстояние у нас есть, теперь есть и шары.
Так, скажем, окрестность кодового слова радиуса 1 — это все коды, находящиеся на расстоянии не больше, чем 1 от него, то есть отличающиеся не больше, чем в одном разряде. То есть это коды:
Да, вот так странно выглядят шары в пространстве кодов.
А теперь посмотрите. Это же все возможные коды, которые мы получим в канале в одной ошибкой, если отправим ! Это следует прямо из определения окрестности. Ведь каждая ошибка заставляет цепочку измениться только в одном разряде, а значит удаляет её на расстояние 1 от исходного сообщения.
Аналогично, если в канале возможны две ошибки, то отправив некоторое сообщение , мы получим один из кодов, который принадлежит окрестности
радиусом 2.
Тогда всю нашу систему декодирования можно построить так. Мы получаем какую-то цепочку нулей и единиц (точку в нашей новой терминологии) и смотрим, в окрестность какого кодового слова она попадает.
Сколько ошибок может исправить код?
Чтобы код мог исправлять больше ошибок, окрестности должны быть как можно шире. С другой стороны, они не должны пересекаться. Иначе если точка попадёт в область пересечения, непонятно будет, к какой окрестности её отнести.
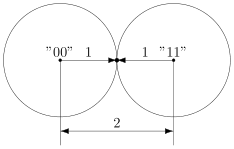
В коде с удвоением между кодовыми словами и
расстояние равно 2 (оба разряда различаются). А значит, если мы построим вокруг них шары радиуса 1, то они будут касаться. Это значит, точка касания будет принадлежать обоим шарам и непонятно будет, к какому из них её отнести.
Именно это мы и получали. Мы видели, что есть ошибка, но не могли её исправить.
Что интересно, точек касания в нашем странном пространстве у шаров две — это коды и
. Расстояния от них до центров равны единице. Конечно же, в обычно геометрии такое невозможно, поэтому рисунки — это просто условность для более удобного рассуждения.
В случае кода с утроением, между шарами будет зазор.
Минимальный зазор между шарами равен 1, так как у нас расстояния всегда целые (ну не могут же две цепочки отличаться в полутора разрядах).
В общем случае получаем следующее.
Этот очевидный результат на самом деле очень важен. Он означает, что код с минимальным кодовым расстоянием будет успешно работать в канале с
ошибками, если выполняется соотношение
Полученное равенство позволяет легко определить, сколько ошибок будет исправлять тот или иной код. А сколько код ошибок может обнаружить? Рассуждения такие же. Код обнаруживает ошибок, если в результате не получится другое кодовое слово. То есть, кодовые слова не должны находиться в окрестностях радиуса
других кодовых слов. Математически это записывается так:
Рассмотрим пример. Пусть мы кодируем 4 буквы следующим образом.
Чтобы найти минимальное расстояние между различными кодовыми словами, построим таблицу попарных расстояний.
| A | B | C | D | |
|---|---|---|---|---|
| A | — | 3 | 3 | 4 |
| B | 3 | — | 4 | 3 |
| C | 3 | 4 | — | 3 |
| D | 4 | 3 | 3 | — |
Минимальное расстояние , а значит
, откуда получаем, что такой код может исправить до
ошибок. Обнаруживает же он две ошибки.
Рассмотрим пример:
Чтобы декодировать полученное сообщение, посмотрим, к какому символу оно ближе всего.
Минимальное расстояние получилось для символа , значит вероятнее всего передавался именно он:
Итак, этот код исправляет одну ошибку, как и код с утроением. Но он более эффективен, так как в отличие от кода с утроением здесь кодируется уже 4 символа.
Таким образом, основная проблема при построении такого рода кодов — так расположить кодовые слова, чтобы они были как можно дальше друг от друга, и их было побольше.
Для декодирования можно было бы использовать таблицу, в которой указывались бы все возможные принимаемые сообщения, и кодовые слова, которым они соответствуют. Но такая таблица получилась бы очень большой. Даже для нашего маленького кода, который выдаёт 5 двоичных цифр, получилось бы варианта возможных принимаемых сообщений. Для более сложных кодов таблица будет значительно больше.
Попробуем придумать способ коррекции сообщения без таблиц. Мы всегда сможем найти полезное применение освободившейся памяти.
Интерлюдия: поле GF(2)
Для изложения дальнейшего материала нам потребуются матрицы. А при умножении матриц, как известно мы складываем и перемножаем числа. И тут есть проблема. Если с умножением всё более-менее хорошо, то как быть со сложением? Из-за того, что мы работаем только с одиночными двоичными цифрами, непонятно, как сложить 1 и 1, чтобы снова получилась одна двоичная цифра. Значит вместо классического сложения нужно использовать какое-то другое.
Введём операцию сложения как сложение по модулю 2 (хорошо известный программистам XOR):
Умножение будем выполнять как обычно. Эти операции на самом деле введены не абы как, а чтобы получилась система, которая в математике называется полем. Поле — это просто множество (в нашем случае из 0 и 1), на котором так определены сложение и умножение, чтобы основные алгебраические законы сохранялись. Например, чтобы основные идеи, касающиеся матриц и систем уравнений по-прежнему были верны. А вычитание и деление мы можем ввести как обратные операции.
Множество из двух элементов с операциями, введёнными так, как мы это сделали, называется полем Галуа GF(2). GF — это Galois field, а 2 — количество элементов.
У сложения есть несколько очень полезных свойств, которыми мы будем пользоваться в дальнейшем.
Это свойство прямо следует из определения.
А в этом можно убедиться, прибавив к обеим частям равенства. Это свойство, в частности означает, что мы можем переносить в уравнении слагаемые в другую сторону без смены знака.
Проверяем корректность
Вернёмся к коду с утроением.
Для начала просто решим задачу проверки, были ли вообще ошибки при передаче. Как видно, из самого кода, принятое сообщение будет кодовым словом только тогда, когда все три цифры равны между собой.
Пусть мы приняли вектор-строку из трёх цифр. (Стрелочки над векторами рисовать не будем, так как у нас почти всё — это вектора или матрицы.)
Математически равенство всех трёх цифр можно записать как систему:
Или, если воспользоваться свойствами сложения в GF(2), получаем
Или
В матричном виде эта система будет иметь вид
где
Транспонирование здесь нужно потому, что — это вектор-строка, а не вектор-столбец. Иначе мы не могли бы умножать его справа на матрицу.
Будем называть матрицу проверочной матрицей. Если полученное сообщение — это корректное кодовое слово (то есть, ошибки при передаче не было), то произведение проверочной матрицы на это сообщение будет равно нулевому вектору.
Умножение на матрицу — это гораздо более эффективно, чем поиск в таблице, но у нас на самом деле есть ещё одна таблица — это таблица кодирования. Попробуем от неё избавиться.
Кодирование
Итак, у нас есть система для проверки
Её решения — это кодовые слова. Собственно, мы систему и строили на основе кодовых слов. Попробуем теперь решить обратную задачу. По системе (или, что то же самое, по матрице ) найдём кодовые слова.
Правда, для нашей системы мы уже знаем ответ, поэтому, чтобы было интересно, возьмём другую матрицу:
Соответствующая система имеет вид:
Чтобы найти кодовые слова соответствующего кода нужно её решить.
В силу линейности сумма двух решений системы тоже будет решением системы. Это легко доказать. Если и
— решения системы, то для их суммы верно
что означает, что она тоже — решение.
Поэтому если мы найдём все линейно независимые решения, то с их помощью можно получить вообще все решения системы. Для этого просто нужно найти их всевозможные суммы.
Выразим сперва все зависимые слагаемые. Их столько же, сколько и уравнений. Выражать надо так, чтобы справа были только независимые. Проще всего выразить .
Если бы нам не так повезло с системой, то нужно было бы складывая уравнения между собой получить такую систему, чтобы какие-то три переменные встречались по одному разу. Ну, или воспользоваться методом Гаусса. Для GF(2) он тоже работает.
Итак, получаем:
Чтобы получить все линейно независимые решения, приравниваем каждую из зависимых переменных к единице по очереди.
Всевозможные суммы этих независимых решений (а именно они и будут кодовыми векторами) можно получить так:
где равны либо нулю или единице. Так как таких коэффициентов два, то всего возможно
сочетания.
Но посмотрите! Формула, которую мы только что получили — это же снова умножение матрицы на вектор.
Строчки здесь — линейно независимые решения, которые мы получили. Матрица называется порождающей. Теперь вместо того, чтобы сами составлять таблицу кодирования, мы можем получать кодовые слова простым умножением на матрицу:
Найдём кодовые слова для этого кода. (Не забываем, что длина исходных сообщений должна быть равна 2 — это количество найденных решений.)
Итак, у нас есть готовый код, обнаруживающий ошибки. Проверим его в деле. Пусть мы хотим отправить 01 и у нас произошла ошибка при передаче. Обнаружит ли её код?
А раз в результате не нулевой вектор, значит код заподозрил неладное. Провести его не удалось. Ура, код работает!
Для кода с утроением, кстати, порождающая матрица выглядит очень просто:
Подобные коды, которые можно порождать и проверять матрицей называются линейными (бывают и нелинейные), и они очень широко применяются на практике. Реализовать их довольно легко, так как тут требуется только умножение на константную матрицу.
Ошибка по синдрому
Ну хорошо, мы построили код обнаруживающий ошибки. Но мы же хотим их исправлять!
Для начала введём такое понятие, как вектор ошибки. Это вектор, на который отличается принятое сообщение от кодового слова. Пусть мы получили сообщение , а было отправлено кодовое слово
. Тогда вектор ошибки по определению
Но в странном мире GF(2), где сложение и вычитание одинаковы, будут верны и соотношения:
В силу особенностей сложения, как читатель сам может легко убедиться, в векторе ошибки на позициях, где произошла ошибка будет единица, а на остальных ноль.
Как мы уже говорили раньше, если мы получили сообщение с ошибкой, то
. Но ведь векторов, не равных нулю много! Быть может то, какой именно ненулевой вектор мы получили, подскажет нам характер ошибки?
Назовём результат умножения на проверочную матрицу синдромом:
И заметим следующее
Это означает, что для ошибки синдром будет таким же, как и для полученного сообщения.
Разложим все возможные сообщения, которые мы можем получить из канала связи, по кучкам в зависимости от синдрома. Тогда из последнего соотношения следует, что в каждой кучке будут вектора с одной и той же ошибкой. Причём вектор этой ошибки тоже будет в кучке. Вот только как его узнать?
А очень просто! Помните, мы говорили, что у нескольких ошибок вероятность ниже, чем у одной ошибки? Руководствуясь этим соображением, наиболее правдоподобным будет считать вектором ошибки тот вектор, у которого меньше всего единиц. Будем называть его лидером.
Давайте посмотрим, какие синдромы дают всевозможные 5-элементные векторы. Сразу сгруппируем их и подчеркнём лидеров — векторы с наименьшим числом единиц.
В принципе, для корректирования ошибки достаточно было бы хранить таблицу соответствия синдрома лидеру.
Обратите внимание, что в некоторых строчках два лидера. Это значит для для данного синдрома два паттерна ошибки равновероятны. Иными словами, код обнаружил две ошибки, но исправить их не может.
Лидеры для всех возможных одиночных ошибок находятся в отдельных строках, а значит код может исправить любую одиночную ошибку. Ну, что же… Попробуем в этом убедиться.
Вектор ошибки равен , а значит ошибка в третьем разряде. Как мы и загадали.
Ура, всё работает!
Что же дальше?
Чтобы попрактиковаться, попробуйте повторить рассуждения для разных проверочных матриц. Например, для кода с утроением.
Логическим продолжением изложенного был бы рассказ о циклических кодах — чрезвычайно интересном подклассе линейных кодов, обладающим замечательными свойствами. Но тогда, боюсь, статья уж очень бы разрослась.
Если вас заинтересовали подробности, то можете почитать замечательную книжку Аршинова и Садовского «Коды и математика». Там изложено гораздо больше, чем представлено в этой статье. Если интересует математика кодирования — то поищите «Теория и практика кодов, контролирующих ошибки» Блейхута. А вообще, материалов по этой теме довольно много.
Надеюсь, когда снова будет свободное время, напишу продолжение, в котором расскажу про циклические коды и покажу пример программы для кодирования и декодирования. Если, конечно, почтенной публике это интересно.
6.5.1. Весовой коэффициент двоичных векторов и расстояние между ними
6.5.2. Минимальное расстояние для линейного кода
6.5.3. Обнаружение и исправление ошибок
6.5.3.1. Распределение весовых коэффициентов кодовых слов
6.5.3.2.Одновременное обнаружение и исправление ошибок
6.5.4. Визуализация пространства 6-кортежей
6.5.5. Коррекция со стиранием ошибок
6.5.1. Весовой коэффициент двоичных векторов и расстояние между ними
Конечно же, понятно, что правильно декодировать можно не все ошибочные комбинации. Возможности кода для исправления ошибок в первую очередь определяются его структурой. Весовой коэффициент Хэмминга (Hamming weight) w(U) кодового слова U определяется как число ненулевых элементов в U. Для двоичного вектора это эквивалентно числу единиц в векторе. Например, если U=100101101, то w(U) = 5. Расстояние Хэмминга (Hamming distance) между двумя кодовыми словами U и V, обозначаемое как d(U, V), определяется как количество элементов, которыми они отличаются.
U=100101101
V=011110100
d(U,V)=6
Согласно свойствам сложения по модулю 2, можно отметить, что сумма двух двоичных векторов является другим двоичным вектором, двоичные единицы которого расположены на тех позициях, которыми эти векторы отличаются.
U + V=111011001
Таким образом, можно видеть, что расстояние Хэмминга между двумя векторами равно весовому коэффициенту Хэмминга их суммы, т.е. d(U, V) = w(U + V). Также видно, что весовой коэффициент Хэмминга кодового слова равен его расстоянию Хэмминга до нулевого вектора.
6.5.2. Минимальное расстояние для линейного кода
Рассмотрим множество расстояний между всеми парами кодовых слой в пространстве Vn. Наименьший элемент этого множества называется минимальным расстоянием кода и обозначается dmin. Как вы думаете, почему нас интересует именно минимальное расстояние, а не максимальное? Минимальное расстояние подобно наиболее слабому звену в цепи, оно дает нам меру минимальных возможностей кода и, следовательно, характеризует его мощность.
Как обсуждалось ранее, сумма двух произвольных кодовых слов дает другой элемент пространства кодовых слов. Это свойство линейных кодов формулируется просто: если U и V — кодовые слова, то и W = U + V тоже должно быть кодовым словом. Следовательно, расстояние между двумя кодовыми словами равно весовому коэффициенту третьего кодового слова, т.е. d(U, V) = w(U + V) = w(W). Таким образом, минимальное расстояние линейного кода можно определить, не прибегая к изучению расстояний между всеми комбинациями пар кодовых слов. Нам нужно лишь определить вес каждого кодового слова (за исключением нулевого вектора) в подпространстве; минимальный вес соответствует минимальному расстоянию dmin. Иными словами, dmin соответствует наименьшему из множества расстояний между нулевым кодовым словом и всеми остальными кодовыми словами.
6.5.3. Обнаружение и исправление ошибок
Задача декодера после приема вектора r заключается в оценке переданного кодового слова Ui. Оптимальная стратегия декодирования может быть выражена в терминах алгоритма максимального правдоподобия (см. приложение Б); считается, что передано было слово Ui, если
(6.41)
Поскольку для двоичного симметричного канала (binary symmetric channel — BSC) правдоподобие Ui относительно r обратно пропорционально расстоянию между r и U, можно сказать, что передано было слово Ui, если
(6.42)
Другими словами, декодер определяет расстояние между r и всеми возможными переданными кодовыми словами Uj, после чего выбирает наиболее правдоподобное Uj, для которого
(6.43)
где М = 2k — это размер множества кодовых слов. Если минимум не один, выбор между минимальными расстояниями является произвольным. Наше обсуждение метрики расстояний будет продолжено в главе 7.
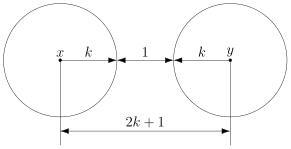
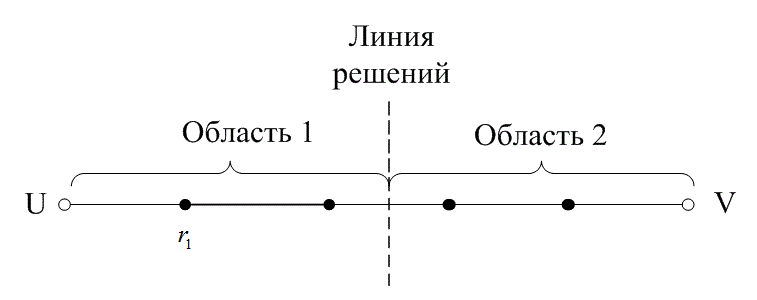
На рис. 6.13 расстояние между двумя кодовыми словами U и V показано как расстояние Хэмминга. Каждая черная точка обозначает искаженное кодовое слово. На рис. 6.13, а проиллюстрирован прием вектора r1 находящегося на расстоянии 1 от кодового слова U и на расстоянии 4 от кодового слова V. Декодер с коррекцией ошибок, следуя стратегии максимального правдоподобия, выберет при принятом векторе r1 кодовое слово U. Если r1 получился в результате появления одного ошибочного бита в переданном векторе кода U, декодер успешно исправит ошибку. Но если же это произошло в результате 4-битовой ошибки в векторе кода V, декодирование будет ошибочным. Точно так же, как показано на рис. 6.13, б, двойная ошибка при передаче U может привести к тому, что в качестве переданного вектора будет ошибочно определен вектор r2, находящийся на расстоянии 2 от вектора U и на расстоянии 3 от вектора кода V. На рис. 6.13 показана ситуация, когда в качестве переданного вектора ошибочно определен вектор r3, который находится на расстоянии 3 от вектора кода U и на расстоянии 2 от вектора V. Из рис. 6.13 видно, что если задача состоит только в обнаружении ошибок, а не в их исправлении, то можно определить искаженный вектор — изображенный черной точкой и представляющий одно-, двух-, трех- и четырехбитовую ошибку. В то же время пять ошибок при передаче могут привести к приему кодового слова V, когда в действительности было передано кодовое слово U; такую ошибку невозможно будет обнаружить.
Из рис. 6.13 можно видеть, что способность кода к обнаружению и исправлению ошибок связана с минимальным расстоянием между кодовыми словами. Линия решения на рисунке служит той же цели, что и в процессе демодуляции, — для разграничения областей решения.
а)
б)
в)
Рис. 6.13. Возможности определения и исправления ошибок: а) принятый вектор r1; б) принятый вектор r2; в) принятый вектор r3
В примере, приведенном на рис. 6.13, критерий принятия решения может быть следующим: выбрать U, если r попадает в область 1, и выбрать V, если r попадает в область 2. Выше показывалось, что такой код (при dmin = 5) может исправить две ошибки. Вообще, способность кода к исправлению ошибок t определяется, как максимальное число гарантированно исправимых ошибок на кодовое слово, и записывается следующим образом [4].
(6.44)
Здесь означает наибольшее целое, не превышающее х. Часто код, который исправляет все искаженные символы, содержащие ошибку в t или меньшем числе бит, также может исправлять символы, содержащие t +1 ошибочных бит. Это можно увидеть на рис. 6.11. В этом случае dmin = 3, поэтому из уравнения (6.44) можно видеть, что исправимы все ошибочные комбинации из t = 1 бит. Также исправима одна ошибочная комбинация, содержащая / +1 (т.е. 2) ошибочных бит. Вообще, линейный код (n, k), способный исправлять все символы, содержащие t ошибочных бит, может исправить всего 2n—k ошибочных комбинаций. Если блочный код с возможностью исправления символов, имеющих ошибки в t бит, применяется для исправления ошибок в двоичном симметричном канале с вероятностью перехода р, то вероятность ошибки сообщения Рм(вероятность того, что декодер совершит неправильное декодирование и п-битовый блок содержит ошибку) можно оценить сверху, используя уравнение (6.18).
(6.45)
Оценка переходит в равенство, если декодер исправляет все ошибочные комбинации, содержащие до t ошибочных бит включительно, но не комбинации с числом ошибочных бит, большим t. Такие декодеры называются декодерами с ограниченным расстоянием. Вероятность ошибки в декодированном бите РB зависит от конкретного кода и декодера. Приближенно ее можно выразить следующим образом [5].
(6.46)
В блочном коде, прежде чем исправлять ошибки, необходимо их обнаружить. (Или же код может использоваться только для определения наличия ошибок.) Из рис. 6.13 видно, что любой полученный вектор, который изображается черной точкой (искаженное кодовое слово), можно определить как ошибку. Следовательно, возможность определения наличия ошибки дается следующим выражением.
(6.47)
Блочный код с минимальным расстоянием dmin гарантирует обнаружение всех ошибочных комбинаций, содержащих dmin — 1 или меньшее число ошибочных бит. Такой код также способен обнаружить и большую ошибочную комбинацию, содержащую dmin или более ошибок. Фактически код (n, k) может обнаружить 2n – 2k ошибочных комбинаций длины п. Объясняется это следующим образом. Всего в пространстве 2n n-кортежей существует 2n -1 возможных ненулевых ошибочных комбинаций. Даже правильное кодовое слово — это потенциальная ошибочная комбинация. Поэтому всего существует 2k -1 ошибочных комбинаций, которые идентичны 2k -1 ненулевым кодовым словам. При появлении любая из этих 2k — 1 ошибочных комбинаций изменяет передаваемое кодовое слово Uj на другое кодовое слово Uj. Таким образом, принимается кодовое слово Uj и его синдром равен нулю. Декодер принимает Uj за переданное кодовое слово, и поэтому декодирование дает неверный результат. Следовательно, существует 2k -1 необнаружимых ошибочных комбинаций. Если ошибочная комбинация не совпадает с одним из 2k кодовых слов, проверка вектора r с помощью синдромов дает ненулевой синдром и ошибка успешно обнаруживается. Отсюда следует, что существует ровно 2n-2k выявляемых ошибочных комбинаций. При больших n, когда 2k<<2n, необнаружимой будет только незначительная часть ошибочных комбинаций.
6.5.3.1. Распределение весовых коэффициентов кодовых слов
Пусть Aj — количество кодовых слов с весовым коэффициентом j в линейном коде (п, k). Числа A0,A1,…,An называются распределением весовых коэффициентов этого кода. Если код применяется только для обнаружения ошибок в двоичном симметричном канале, то вероятность того, что декодер не сможет определить ошибку, можно рассчитать, исходя из распределения весовых коэффициентов кода [5].
(6.48)
где р — вероятность перехода в двоичном симметричном канале. Если минимальное расстояние кода равно dmin значения от А1 до , равны нулю.
Пример 6.5. Вероятность необнаруженной ошибки в коде
Пусть код (6,3), введенный в разделе 6.4.3, используется только для обнаружения наличия ошибок. Рассчитайте вероятность необнаруженной ошибки, если применяется двоичный симметричный канал, а вероятность перехода равна 10-2.
Решение
Распределение весовых коэффициентов этого кода выглядит следующим образом: A0=1, А1= А2 = 0, A3 = 4, A5 = 0, A6 = 0. Следовательно, используя уравнение (6.48), можно записать следующее.
Для р = 10-2 вероятность необнаруженной ошибки будет равна 3,9 х 10-6.
6.5.3.2. Одновременное обнаружение и исправление ошибок
Возможностями исправления ошибок с максимальным гарантированным (t), где t определяется уравнением (6.44), можно пожертвовать в пользу определения класса ошибок. Код можно использовать для одновременного исправления α и обнаружения β ошибок, причем , а минимальное расстояние кода дается следующим выражением [4].
(6.49)
При появлении t или меньшего числа ошибок код способен обнаруживать и исправлять их. Если ошибок больше t, но меньше е+1, где е определяется уравнением (6.47), код может определять наличие ошибок, но исправить может только некоторые из них. Например, используя код с dmin = 7. можно выполнить обнаружение и исправление со следующими значениями α и β.
Заметим, что исправление ошибки подразумевает ее предварительное обнаружение. В приведенном выше примере (с тремя ошибками) все ошибки можно обнаружить и исправить. Если имеется пять ошибок, их можно обнаружить, но исправить можно только одну из них.
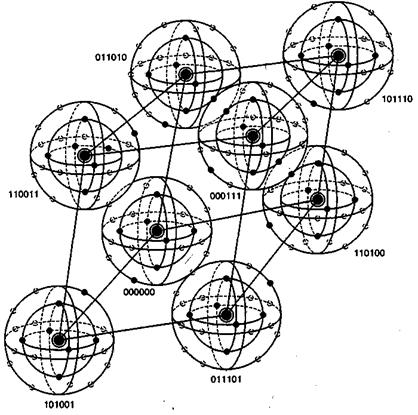
6.5.4. Визуализация пространства 6-кортежей
На рис. 6.14 визуально представлено восемь кодовых слов, фигурирующих в примере из раздела 6.4.3. Кодовые слова образованы посредством линейных комбинаций из трех независимых 6-кортежей, приведенных в уравнении (6.26); сами кодовые слова образуют трехмерное подпространство. На рисунке показано, что такое подпространство полностью занято восемью кодовыми словами (большие черные круги); координаты подпространства умышленно выбраны неортогональными. На рис. 6.14 предпринята попытка изобразить все пространство, содержащее шестьдесят четыре 6-кортежей, хотя точно нарисовать или составить такую модель невозможно. Каждое кодовое слово окружают сферические слои или оболочки. Радиус внутренних непересекающихся слоев — это расстояние Хэмминга, равное 1; радиус внешнего слоя — это расстояние Хэмминга, равное 2. Большие расстояния в этом примере не рассматриваются. Для каждого кодового слова два показанных слоя заняты искаженными кодовыми словами. На каждой внутренней сфере существует шесть таких точек (всего 48 точек), представляющих шесть возможных однобитовых ошибок в векторах, соответствующих каждому кодовому слову. Эти кодовые слова с однобитовыми возмущениями могут быть соотнесены только с одним кодовым словом; следовательно, такие ошибки могут быть исправлены. Как видно из нормальной матрицы, приведенной на рис. 6.11, существует также одна двухбитовая ошибочная комбинация, которая также поддается исправлению. Всего существует разных двухбитовых ошибочных комбинаций, которыми может быть искажено любое кодовое слово, но исправить можно только одну из них (в нашем примере это ошибочная комбинация 010001). Остальные четырнадцать двухбитовых ошибочных комбинаций описываются векторами, которые нельзя однозначно сопоставить с каким-либо одним кодовым словом; эти не поддающиеся исправлению ошибочные комбинации дают векторы, которые эквивалентны искаженным векторам двух или большего числа кодовых слов. На рисунке все (56) исправимые кодовые слова с одно- и двухбитовыми искажениями показаны маленькими черными кругами. Искаженные кодовые слова, не поддающиеся исправлению, представлены маленькими прозрачными кругами.
Рис, 6.14. Пример восьми кодовых слов в пространстве 6-кортежей
При представлении свойств класса кодов, известных как совершенные коды (perfect code), рис. 6.14 весьма полезен. Код, исправляющий ошибки в t битах, называется совершенным, если нормальная матрица содержит все ошибочные комбинации из t или меньшего числа ошибок и не содержит иных образующих элементов классов смежности (отсутствует возможность исправления остаточных ошибок). В контексте рис. 6.14 совершенный код с коррекцией ошибок в t битах — это такой код, который (при использовании обнаружения по принципу максимального правдоподобия) может исправить все искаженные кодовые слова, находящиеся на расстоянии Хэмминга t (или ближе) от исходного кодового слова, и не способен исправить ни одну из ошибок, находящихся на расстоянии, превышающем t.
Кроме того, рис. 6.14 способствует пониманию основной цели поиска хороших кодов. Предпочтительным является пространство, максимально заполненное кодовыми словами (эффективное использование введенной избыточности), а также желательно, чтобы кодовые слова были по возможности максимально удалены друг от друга. Очевидно, что эти цели противоречивы.
6.5.5. Коррекция со стиранием ошибок
Приемник можно сконструировать так, чтобы он объявлял символ стертым, если последний принят неоднозначно либо обнаружено наличие помех или кратковременных сбоев. Размер входного алфавита такого канала равен Q, а выходного —Q + 1; лишний выходной символ называется меткой стирания (erasure flag), или просто стиранием (erasure). Если демодулятор допускает символьную ошибку, то для ее исправления необходимы два параметра, определяющие ее расположение и правильное значение символа. В случае двоичных символов эти требования упрощаются — нам необходимо только расположение ошибки. В то же время, если демодулятор объявляет символ стертым (при этом правильное значение символа неизвестно), расположение этого символа известно, поэтому декодирование стертого кодового слова может оказаться проще исправления ошибки. Код защиты от ошибок можно использовать для исправления стертых символов или одновременного исправления ошибок и стертых символов. Если минимальное расстояние кода равно dmin, любая комбинация из ρ или меньшего числа стертых символов может быть исправлена при следующем условии [6].
(6.50)
Предположим, что ошибки появляются вне позиций стирания. Преимущество исправления посредством стираний качественно можно выразить так: если минимальное расстояние кода равно dmin, согласно уравнению (6.50), можно восстановить dmin-1 стирание. Поскольку число ошибок, которые можно исправить без стирания информации, не превышает (dmin-1)/2, то преимущество исправления ошибок посредством стираний очевидно. Далее, любую комбинацию из α ошибок и γ стираний можно исправить одновременно, если, как показано в работе [6],
(6.51)
Одновременное исправление ошибок и стираний можно осуществить следующим образом. Сначала позиции из у стираний замещаются нулями, и получаемое кодовое слово декодируется обычным образом. Затем позиции из у стираний замещаются единицами, и декодирование повторяется для этого варианта кодового слова. После обработки обоих кодовых слов (одно с подставленными нулями, другое — с подставленными единицами) выбирается то из них, которое соответствует наименьшему числу ошибок, исправленных вне позиций стирания. Если удовлетворяется неравенство (6.51), то описанный метод всегда дает верное декодирование.
Пример 6.6. Коррекция со стиранием ошибок
Рассмотрим набор кодовых слов, представленный в разделе 6.4.3.
000000 110100 011010 101110 101001 011101 110011 000111
Пусть передано кодовое слово 110011, в котором два крайних слева разряда приемник объявил стертыми. Проверьте, что поврежденную последовательность хx0011 можно исправить.
Решение
Поскольку , код может исправить
= 2 стирания. В этом легко убедиться из рис. 6.11 или приведенного выше перечня кодовых слов, сравнивая 4 крайних правых разряда xx00l1 с каждым из допустимых кодовых слов. Действительно переданное кодовое слово — это ближайшее (с точки зрения расстояния Хэмминга) к искаженной последовательности.

 Сотни
Сотни