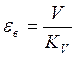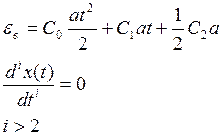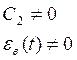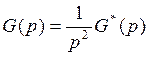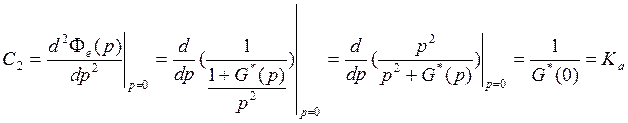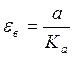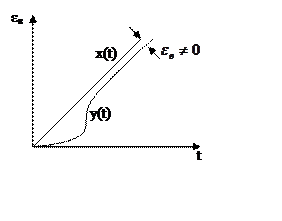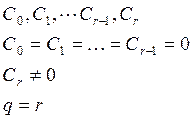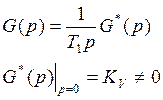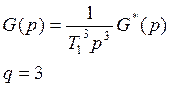Коэффициент ошибки тау

Рассматриваемый метод может применяться как для задающего так и для возмущающего воздействий. Не снижая общности рассуждений, рассмотрим случай, когда имеется только задающее воздействие.

Если функция времени имеет произвольную форму, но достаточно плавную вдали от начальной точки процесса в том смысле, что через некоторое время существенное значение имеет только конечное число производных

то ошибку системы можно определить следующим образом. Из формулы (5.20) можно найти изображение ошибки

где — передаточная функция замкнутой системы по ошибке, — изображение задающего воздействия.

Разложим передаточную функцию по ошибке в выражении (8.18) в ряд по возрастающим степеням комплексной величины :

сходящийся при малых значениях , т. е. при достаточно больших значениях времени что соответствует установившемуся процессу изменения регулируемой величины при заданной форме управляющего воздействия.

Переходя в выражении (8.19) к оригиналу, получаем формулу для установившейся ошибки

Величины называются коэффициентами ошибок. Они могут определяться согласно общему правилу разложения функции в ряд Тейлора по формулам

Так как передаточная функция по ошибке представляет собой дробнорациональную функцию, то коэффициенты ошибок можно более просто получить делением числителя на знаменатель и сравнением получающегося ряда с выражением (8.19).

Коэффициент может быть отличным от нуля только в статических системах и то только в тех случаях, когда не принимаются меры по устранению первой составляющей статической ошибки посредством масштабирования или использования неединичных обратных связей (см. § 9.3).

В системах с астатизмом первого порядка а коэффициент связан с добротностью по скорости соотношением

В системах с астатизмом второго порядка

а коэффициент связан с добротностью по ускорению соотношением

При исследовании ошибки от возмущающего воздействия можно получить все коэффициенты не равными нулю при астатизме любого порядка, так как астатизму по задающему воздействию может соответствовать наличие статической ошибки по возмущению.

Если задающее воздействие имеет ограниченное число производных, то ряд (8.20) будет иметь ограниченное число членов. Предположение, что коэффициенты ошибок представляют собой постоянные числа, обусловливает применение этого метода для сравнительно медленно меняющихся входных воздействий или , когда можно пренебречь влиянием переходной составляющей процесса и рассматривать только вынужденное движение системы.

Пример. Определим первые три коэффициента ошибки по задающему воздействию, если передаточная функция разомкнутой системы имеет вид

Передаточная функция по ошибке

Деля числитель на знаменатель, получаем ряд

Сравнение этого ряда с (8.19) дает

Так, например, если задающее воздействие в этой системе меняется по закону

то установившаяся ошибка будет

Показатели качества сау

Количественные оценки
качества, так называемые прямые показатели
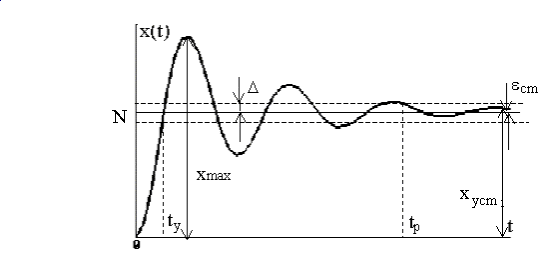
качества, определяются по кривой
переходного процесса (рис.16).

Рис.16. Переходная
функция и показатели качества

Используются следующие
прямые показатели качества:

1. величина
   перерегулирования
   ,

;

характеризует
максимальное отклонение регулируемой
величины от ее установившегося значения,
которое может быть определено в
соответствии с теоремой о конечном
значении оригинала

;

1. время
   переходного процесса или время
   регулирования t_p
   – наименьшее значение времени, после
   которого имеет место неравенство

,

где

— заданная величина, обычно лежащая в
пределах =0,02÷0,05;

3)
статическая ошибка _сm
–
величина отклонения установившегося
значения регулируемой величины x()
от требуемого значения
N

или
,
гдеE(p)– изображение ошибки;

4)
время регулирования t_р
– промежуток времени, по истечении
которого регулируемая величина первый
раз достигает установившегося значения.

Для определения
качества системы могут использоваться
и другие показатели, соответствующие
решаемой задаче, например, число колебаний
регулируемой величины за время
регулирования, частота и период колебаний
и т.д.

Во всех случаях
необходимо построить переходную функцию.

Коэффициенты ошибок

Точность САУ в
установившемся режиме, при относительно
медленно изменяющихся воздействиях,
может быть оценена с помощью коэффициентов
ошибок. Изображение ошибки определяется
выражением

,

где
—
передаточная функция по ошибке.

Разложим передаточную
функцию системы по ошибке в степенной
ряд в окрестности точки p=0.
Отметим, что приp0,tи именно
поэтому мы говорим о точности в
установившемся режиме.

Обозначим:
и получим

,
(8)

.

Учитывая, что оператор
p, умноженный на
изображение самой величины, является
символом дифференцирования, можно для
оригиналов записать

.
(9)

Выражение (9) определяет
зависимость ошибки регулирования от
различных составляющих входного
воздействия, коэффициенты K_iполучили название коэффициентов ошибок:

• K₀— коэффициент ошибки по положению;

• K₁—
  коэффициент ошибки по скорости;

• K₂– коэффициент ошибки по ускорению и
  т.д.

Из (8) следует, что

.

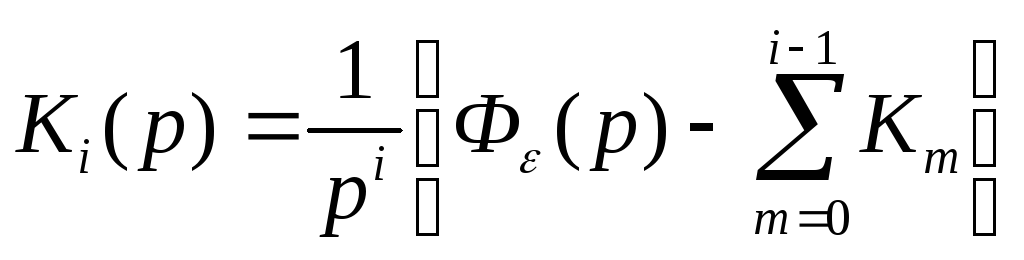
Численные значения
коэффициентов ошибок определяются из
этого выражения при p0.

.

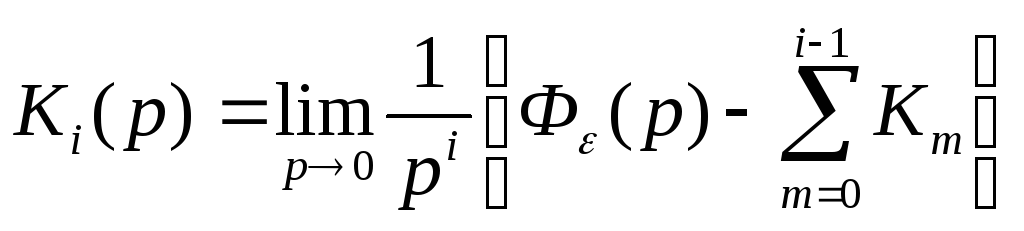
Очевидно, что К₀=Ф_(0).

Входное воздействие
можно представить в виде степенного
ряда

,

где g₀– постоянная величина, характеризующая
начальное значение, g₁=const – скорость
изменения входного воздействия, g₂=const – ускорение и т.д.

Тогда

.

Пусть передаточная
функция разомкнутой системы имеет вид

,

где - порядок астатизма системы. Для
передаточной функции замкнутой системы
по ошибке получим

.

Изображение ошибки
запишется в виде

.

Отсюда следует, что
если порядок астатизма больше порядка
старшей производной воздействия, т.е.
>m, то ошибка в
установившемся режиме будет равна нулю.
Если=m, то установившаяся
ошибка будет равна постоянной величине,
называемой статической ошибкой. И если<m, то при tи. В отношении
коэффициентов ошибок последнее выражение
позволяет сделать следующие выводы.

1). Если система
статическая, т.е.=0,
то существуют все составляющие ошибки
и все коэффициенты ошибок не равны нулю,
т.к.К₀ = Ф_(0)
0.

2).Система с астатизмом
1-го порядка, 
=1, не имеет ошибки по положению иК₀=0.

3).Система с астатизмом
2-го порядка, 
=2, не имеет ошибок по положению и по
скорости иК₀ =0,К₁=0.

Этот список можно
продолжить. Таким образом, повышение
порядка астатизма повышает точность
системы в установившемся режиме. Но
повышение порядка астатизма снижает
запасы устойчивости, т.к. введение
интегрирующих звеньев увеличивает
фазовое запаздывание (снижает частоту
). Поэтому на
практике порядок астатизма выше второго
не применяют, а чаще всего ограничиваются
астатизмом первого порядка, используя
для повышения точности другие способы.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

C₁V –
скоростная ошибка, ошибка от скорости.

С₁
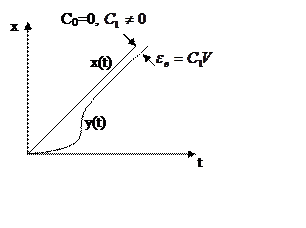
– коэффициент скоростной ошибки.

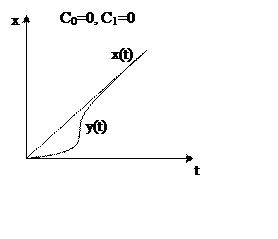q=1, I
порядок астатизма                            Данная система называется системой
с астатизмом второго порядка и она содержит в разомкнутой системе 2 и более
интеграторов.

Определим коэффициент С₁ для системы с
первым порядком астатизма

K_V – Добротность
системы по скорости.

— статический
коэффициент усиления позиционной части

разомкнутой системы.

Можно сказать, что общее значение

5.2.3 Режим изменения задающей величины с постоянным
ускорением.

Пусть

— ускорение

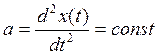
Чтобы система имела  необходимо,
чтоб С₀, С₁=0, иначе ошибка будет неограниченно расти.

Установившееся значение ошибки

С₂ – коэффициент ошибки от ускорения

Система с ошибкой от ускорения

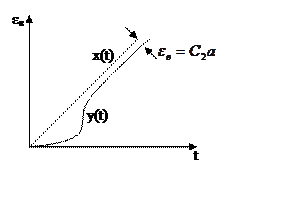Система
с астатизмом второго порядка (q=2), содержит в разомкнутом виде два интегрирующих
звена.

 — позиционная часть разомкнутой
системы.

Система без ошибки от ускорения

Если в системе С₂=0, ε_в=0, то
это система без ошибки от ускорения.

                                                      Система
с астатизмом выше второго порядка

                                                      q>2

         Свяжем С₂ с передаточной функцией
разомкнутой системы

— коэффициент
усиления позиционной части разомкнутой системы, добротность системы по
ускорению.

5.2.4 Связь астатизма системы с ЛАЧХ разомкнутой
системы.

Порядок астатизма – целое число q, которое равно
порядку в описании входного сигнала , при котором
установившаяся ошибка постоянна и отлична от нуля.

1.

2.

3.

                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                   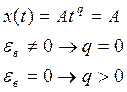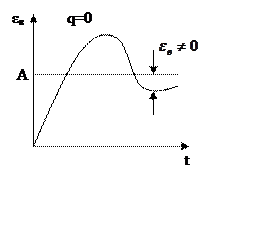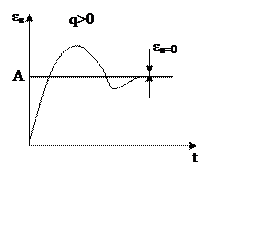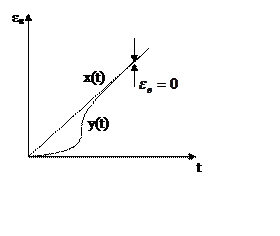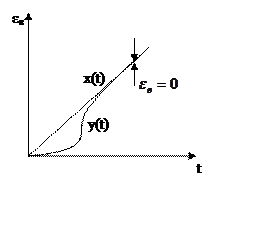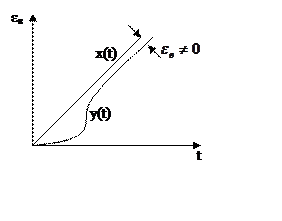q=2                                                                   
q>2

На практике астатизм выше второго порядка (q>2)
не применяется, поэтому мы их не рассматриваем.

5.2.5 Способы определения порядка астатизма

1. По коэффициентам ошибок

2. По количеству интегрирующих звеньев в передаточной
функции разомкнутой системы.

 — позиционная
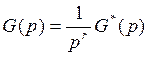
часть системы

Система имеет r интеграторов и q=r

3.По наклону ЛАЧХ в низкочастотной области.

Предположим, что передаточная функция разомкнутой
системы имеет вид

Тогда
ЛАЧХ будет иметь следующий вид.

Пусть 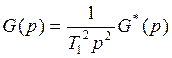, где

 — позиционная
часть

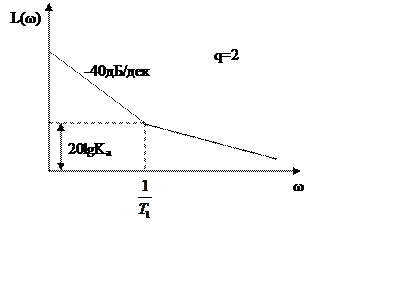Этот случай в жизни практически не встречается

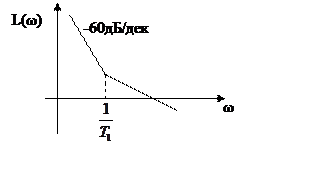
В итоге, астатизм системы определяется по ЛАЧХ
следующим образом

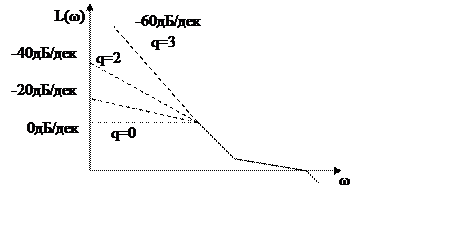5.2.6 Исследование точности в условиях действия
управляющих и возмущающих сигналов

В общем случае на систему действуют как управляющие
(задающие), так и возмущающие сигналы.