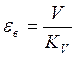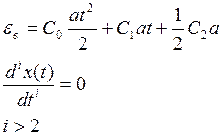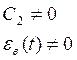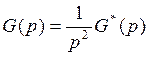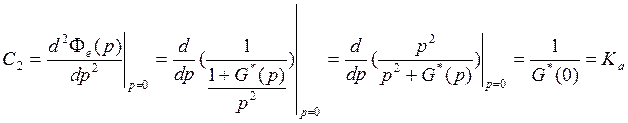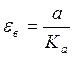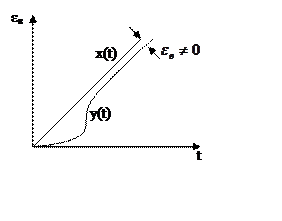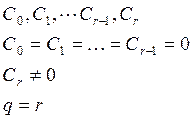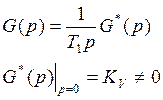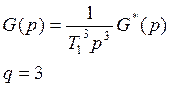Коэффициент скоростной ошибки - Исправление ошибок и поиск оптимальных решений проблем

Расчеты скоростной ошибки εСт регулирования

Входной сигнал x(t)=Vtи изображением его является.
В соответствии с (1.56) скоростную ошибкуε_СКследует вычислять по
формуле

(1.58)

1). Пусть в (1.58) значение порядка νастатизма САУ равно нулю:ν=0. Такая
САУ называется статической. Тогда
скоростная ошибкаε_СКбудет равна

В статической САУ скоростная ошибка
ε_СКбесконечно большая
и, поэтому, такая САУ неработоспособна.

2). Пусть в (1.58) значение порядка νастатизма САУ равно 1:ν=1. Такая САУ
называется астатической 1-го порядка.
Тогда скоростная ошибкаε_СКбудет равна

В астатической САУ 1-го порядка имеется
скоростная ошибка ε_СК,
которую можно только уменьшить путем
увеличения общего коэффициента усиленияКразомкнутой САУ, но обратить в
ноль ее нельзя.

3). Пусть в (1.58) значение порядка νастатизма САУ равно 2:ν=2. Такая САУ
называется астатической 2-го порядка.
Тогда скоростная ошибкаε_СКбудет равна

В астатической САУ 2-го порядка скоростная
ошибка ε_СКравна нулю,
т.е САУ является абсолютно точной.

Выводы по расчетам статической и скоростной ошибок регулирования:

1. Ошибки регулирования могут быть
уменьшены путем увеличения общего
коэффициента усиления Ки порядка
астатизмаνразомкнутой САУ.

2. При увеличении Кошибки регулирования
только уменьшаются. но не обращаются в
ноль.

3. При увеличении νСАУ становится
абсолютно точной — ошибка регулирования
становится нулевой.

3.6. Типовые регуляторы. Влияние п-, и- и д-регуляторов на прямые показатели качества сау: устойчивость, ошибки регулирования, колебательность, перерегулирование и быстродействие.

Для обеспечения при работе САУ заданных
показателей качества в ее структуру
вводят корректирующие устройства и
регуляторы. Корректирующие устройства
имеют передаточную функцию произвольного
вида. Регуляторами называются устройства,
передаточная функция которых имеет
стандартный вид.

Существуют три базовых простейших
регулятора – пропорциональный (П),
интегральный (И) и дифференциальный
(Д):

— П-регулятор имеет передаточную функцию
;

— И-регулятор имеет передаточную
функцию ;

— Д-регулятор имеет передаточную
функцию .

Из трех простейших можно получить еще
четыре составных регулятора:

— ПИ-регулятор с передаточной функцией ;

— ПД-регулятор с передаточной функцией ;

— ИД-регулятор с передаточной функцией ;

— ПИД-регулятор с передаточной функцией .

На практике широко применяются регуляторы
ПИ- и ПИД-типов. Регуляторы ПД- и ИД-типов
применяются редко из-за их низкой
помехоустойчивости (см. тему 1.17).

Простейшие
регуляторы обеспечивают улучшение
только некоторых показателей качества
САУ, а составные обеспечивают улучшение
работы САУ по комплексу показателей
качества. В практике проектирования
САУ и их эксплуатации крайне важно
понимание того, какие показатели качества
улучшает каждый из простейших регуляторов.

Будем рассматривать структурную схему
САУ, в которой регулятор и объект
управления включены последовательно
(рис.1.48а). Все характеристики САУ с
регулятором будем помечать индексом
СР, а без регулятора (рис.1.48б) –
индексомБР.

Из построений вытекают следующие
изменения косвенных показателей качества
ω_сриγ:

— частота среза ω_срувеличится;

— запас по фазе γуменьшится.

Прямые
показатели качестваσ,t₁иt_ППв
соответствии с соотношениями (1.59)
изменятся следующим образом:

— перерегулирование σувеличится,
возможна даже потеря устойчивости;

— быстродействие САУ по моменту t₁первой установки возрастет;

— об изменении t_ППничего определенного сказать нельзя,
так какt_ППуменьшается при увеличенииω_сри увеличивается при уменьшенииγ.

Качественные изменения графика
переходного процесса отображены на
рис.1.50.

При использовании П-регулятора порядок
астатизма САУ не изменяется, поэтому
ни одна из существующих ненулевых ошибок
регулирования не обратится в ноль, а
может быть только уменьшена за счет
того, что коэффициент передачи k_Прегулятора будет взят большим единицы.

д). Эксплуатационные качества П-регулятора
являются наилучшими из всех простейших
регуляторов, так как П-регулятор не
обладает повышенной чувствительностью
к помехам (не ухудшает соотношение
«сигнал-помеха» для проходящего
через него сигнала), а его выходной
сигнал не подвержен дрейфу.

Выводы по применению П-регулятора
в САУ

Достоинства П-регулятора:

1. Повышает быстродействие САУ, оцениваемое
временем первой установки.

2. Эксплуатационные качества являются
наилучшими и, поэтому, в любом стандартном
регуляторе содержится П-часть.

Недостатки П-регулятора:

1. Увеличивает перерегулирование САУ.

2. Не обращает в ноль ни одну из ошибок
регулирования исходной САУ.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

C₁V –
скоростная ошибка, ошибка от скорости.

С₁
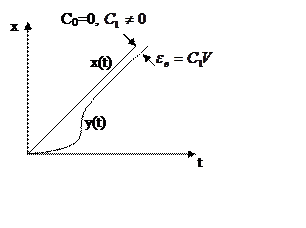
– коэффициент скоростной ошибки.

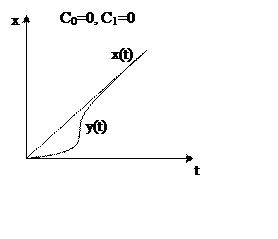q=1, I
порядок астатизма Данная система называется системой
с астатизмом второго порядка и она содержит в разомкнутой системе 2 и более
интеграторов.

Определим коэффициент С₁ для системы с
первым порядком астатизма

K_V – Добротность
системы по скорости.

— статический
коэффициент усиления позиционной части

разомкнутой системы.

Можно сказать, что общее значение

5.2.3 Режим изменения задающей величины с постоянным
ускорением.

Пусть

— ускорение

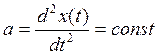
Чтобы система имела необходимо,
чтоб С₀, С₁=0, иначе ошибка будет неограниченно расти.

Установившееся значение ошибки

С₂ – коэффициент ошибки от ускорения

Система с ошибкой от ускорения

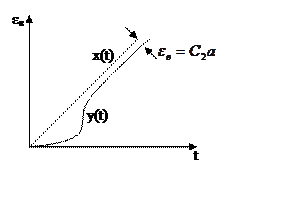Система
с астатизмом второго порядка (q=2), содержит в разомкнутом виде два интегрирующих
звена.

— позиционная часть разомкнутой
системы.

Система без ошибки от ускорения

Если в системе С₂=0, ε_в=0, то
это система без ошибки от ускорения.

Система
с астатизмом выше второго порядка

q>2

Свяжем С₂ с передаточной функцией
разомкнутой системы

— коэффициент
усиления позиционной части разомкнутой системы, добротность системы по
ускорению.

5.2.4 Связь астатизма системы с ЛАЧХ разомкнутой
системы.

Порядок астатизма – целое число q, которое равно
порядку в описании входного сигнала , при котором
установившаяся ошибка постоянна и отлична от нуля.

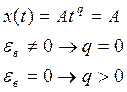
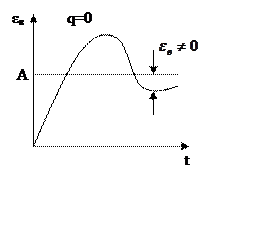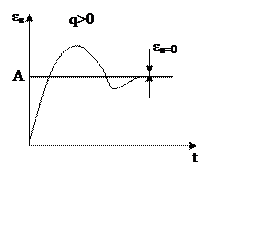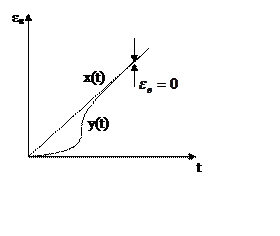
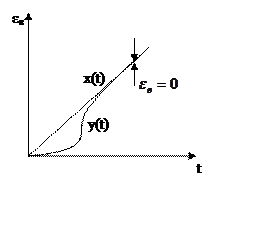
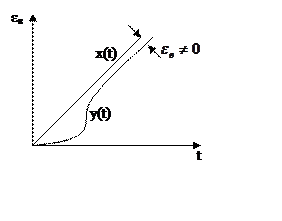q=2
q>2

На практике астатизм выше второго порядка (q>2)
не применяется, поэтому мы их не рассматриваем.

5.2.5 Способы определения порядка астатизма

1. По коэффициентам ошибок

2. По количеству интегрирующих звеньев в передаточной
функции разомкнутой системы.

— позиционная
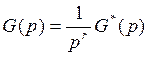
часть системы

Система имеет r интеграторов и q=r

3.По наклону ЛАЧХ в низкочастотной области.

Предположим, что передаточная функция разомкнутой
системы имеет вид

Тогда
ЛАЧХ будет иметь следующий вид.

Пусть 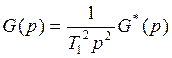, где

— позиционная
часть

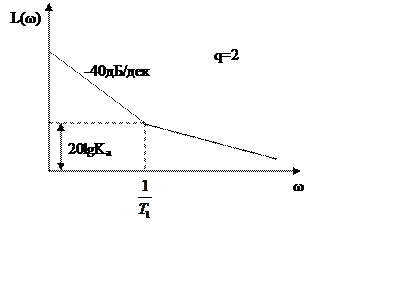Этот случай в жизни практически не встречается

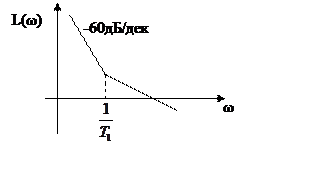
В итоге, астатизм системы определяется по ЛАЧХ
следующим образом

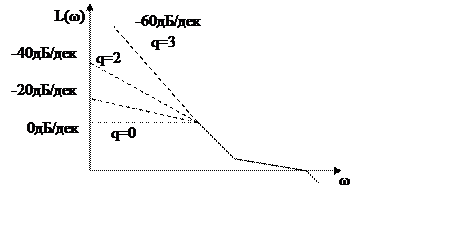5.2.6 Исследование точности в условиях действия
управляющих и возмущающих сигналов

В общем случае на систему действуют как управляющие
(задающие), так и возмущающие сигналы.

Источник

Как отмечалось, ошибка САУ в установившемся режиме является одним из показателей качества системы. В случае медленно изменят ющихся задающего или возмущающего воздействий ошибку системы в установившемся режиме удобно определять с помощью коэффициентов ошибок.

Ошибка следящей системы вызываемая изменением задающего воздействия а в соответствии с (2.61), может быть определена

с помощью передаточной функции системы по ошибке

Предположим, что можно разложить в степенной ряд относительно сходящийся, по крайней мере, при малых значениях

Тогда, согласно (4.22), можно записать

Этот ряд сходится в окрестности точки Поэтому будет сходиться и оригинал ряда (4.24) при т. е. ряд, в который можно разложить ошибку системы в установившемся режиме:

Отсюда видно, что в общем случае ошибка системы в установившемся режиме состоит из ряда слагаемых, пропорциональных как входному сигналу так и его производным. Слагаемые, входящие в ряд ошибок, обычно называют так: — ошибкой по положению (по сигналу); — ошибкой, вызываемой скоростью; — ошибкой, вызываемой ускорением задающего воздействия и т.д., а постоянные — коэффициентами ошибок. Ошибки в установившихся режимах, вызываемые изменяющимся задающим воздействием, называются динамическими. Зная коэффициенты ошибок и закон изменения задающего воздействия а с помощью формулы (4.25) можно определить ошибку системы в установившемся режиме.

Коэффициенты ошибок выразим через параметры системы. Передаточная функция системы по ошибке связана с передаточной функцией разомкнутой системы выражением

Учитывая, что передаточная функция системы с астатизмом порядка в разомкнутом состоянии имеет вид

где передаточная функция по ошибке в соответствии с выражением (4.26) будет равна:

где коэффициенты с равны сумме коэффициентов при одинаковых степенях

При (статическая система):

При (астатическая система с астатизмом порядка):

На основании (4.23) и (4.27) можно записать

откуда

Раскрывая скобки в правой части полученного выражения и приравнивая коэффициенты правой и левой частей при одинаковых степенях можно получить систему уравнений, из которой затем можно определить коэффициенты ошибок через коэффициенты с и о уравнения САУ. Значения коэффициентов ошибок будут различными для систем с различными порядками астатизма. Найдем сначала коэффициенты ошибок для статической системы

Приравнивая члены левой и правой частей выражения (4.31) при одинаковых степенях и учитывая, что получаем следующую систему уравнений:

из которой можно определить коэффициенты ошибок для статической системы. Из первого уравнения находим или, если принять во внимание, что а также, что для случая в соответствии с формулой то

Из второго уравнения находим

Аналогично можно определить и другие коэффициенты ошибок.

Таблица 4.3. (см. скан) Коэффициенты ошибок статической и астатических систем

Коэффициенты ошибок астатической системы с астатизмом первого порядка могут быть найдены из системы уравнений, полученной из выражения (4.31) приравниванием коэффициентов его левой и правой частей при одинаковых степенях при учете, что

Из первого уравнения из второго уравнения с учетом (4.29):

Аналогично определяются остальные коэффициенты ошибок.

В табл. 4.3 приводятся несколько первых коэффициентов ошибок Для статической и астатических систем первого и второго порядков астатизма. В качестве примера определим установившиеся ошибки САУ, обладающих различными порядками астатизма при разных задающих воздействиях.

Пример 3. Задающее воздействие изменяется по закону ступенчатой функции а (табл. 4.4). Определить установившиеся ошибки в следящих системах, имеющих порядок астатизма

1. Определяем производные

Таблица 4.4. Характер реакций систем на различные задающие воздействия

2. С учетом (4.34) выражение (4.25) для ошибки принимает вид

т. е. при ступенчатом воздействии появляется только ошибка по положению.

3. Для определения в статической системе подставляем из табл. 4.3 значение в формулу (4.35): т. е. при ступенчатом задающем воздействии в статической системе возникает постоянная ошибка по положению. Эта ошибка при данном будет тем меньше, чем больше системы.

4. Установившиеся ошибки в астатических системах с астатизмом порядка и с астатизмом 2-го порядка т. е. ошибка по положению, а следовательно, и вся установившаяся ошибка в астатических системах при ступенчатом задающем воздействии равна нулю.

Реакции следящих систем с порядками астатизма на ступенчатое задающее воздействие изображены в табл. 4.4.

Пример 4. Задающее воздействие изменяется по закону а (см. табл. 4.4). Определить в следящих системах с порядком астатизма

1. Определяем производные от

Учитывая, что вторая и более высокие производные от а равны нулю, формула (4.25) примет вид

т. е. при линейно возрастающем задающем воздействии возможно появление в системе динамических ошибок по положению и по скорости.

3. Для определения в статической системе подставляем из табл. 4.3 значения в формулу (4.36):

т. е. в статической системе имеются ошибки по положению и по скорости. Ошибка

по положению при изменении задающего воздействия с постоянной скоростью возрастает во времени и поэтому системы стремится к бесконечности.

4. Установившаяся ошибка астатической системы с астатизмом порядка

т. е. в системе с астатизмом порядка ошибка по положению равна нулю (так как Скоростная ошибка постоянна. Она пропорциональна скорости изменения задающего воздействия и обратно пропорциональна коэффициенту усиления системы в разомкнутом состоянии Выражение (4.37) для скоростной ошибки, полученное с помощью коэффициентов ошибок, совпадает с ранее полученной формулой (2.75).

5. Установившаяся ошибка астатической системы с астатизмом порядка т. е. в системе с астатизмом порядка при изменении с постоянной скоростью равна нулю. Это объясняется тем, что коэффициенты ошибок , следовательно, ошибка по положению и по скорости в этой системе равны нулю.

Реакции следящих систем на задающее воздействие а изображены в табл. 4.4.

Пример 5. Задающее воздействие где — начальное значение — начальное значение скорости изменения а — ускорение а Определить в следящих системах с порядками астатизма

1. Определяем производные от а

2. С учетом (4.38) выражение (4.25) принимает вид

т. е. при равноускоренном изменении задающего воздействия возможно появление в системе динамических ошибок по положению, скоростной ошибки и ошибки по ускорению.

3. Установившиеся динамические ошибки:

в статической системе