Коэффициент поверхностного натяжения
Определение и формула коэффициента поверхностного натяжения
Имеется другое определение коэффициента поверхностного натяжения — энергетическое. Оно исходит из того, что если площадь поверхности жидкости увеличивается, то некоторое количество молекул из ее объема поднимается на слой поверхности. С этой целью внешние силы совершают работу () против сил сцепления молекул. Величина данной работы будет пропорциональна изменению площади поверхности жидкости (
):
где коэффициентом пропорциональности является коэффициент поверхностного натяжения.
Тогда коэффициент поверхностного натяжения можно определить как физическую величину, равную работе, которая необходима для увеличения площади поверхности жидкости при изотермическом процессе не единицу:
Коэффициент поверхностного натяжения — это положительная физическая величина ().
Молекулы поверхностного слоя жидкости имеют избыточную, в сравнении с молекулами внутренних слоев, потенциальную энергию. Потенциальную энергию поверхностного слоя можно вычислить как:
где S — площадь поверхности жидкости.
Свойства коэффициента поверхностного натяжения
Для чистых жидкостей при увеличении температуры коэффициент поверхностного натяжения уменьшается.
Величина коэффициента связана с силами межмолекулярного взаимодействия. Он может принимать различные значения. У летучих (хорошо испаряющихся) жидкостей
меньше, чем у нелетучих.
Коэффициент поверхностного натяжения воды зависит от концентрации примесей в ней. Так, при добавлении в воду биологически активных веществ (паста, мыло) поверхностное натяжение воды уменьшается.
Коэффициент поверхностного натяжения можно найти, используя капилляры. Для этого капилляр опускают в сосуд с водой и измеряют высоту подъема жидкости (h). При этом коэффициент находят, применяя формулу:
где — плотность жидкости,
— радиус капилляра,
— краевой угол,
— ускорение свободного падения.
Вообще говоря, поверхностное натяжение существует на границе твердых, жидких и газообразных тел. Но чаще рассматривают поверхностное натяжение на границе газ — жидкость.
Коэффициент поверхностного натяжения входит в известную формулу Лапласа, которая определяет добавочного давление (), которое вызывает кривизна поверхности жидкости:
где и
— радиусы кривизны двух взаимно перпендикулярных сечений поверхности жидкости.
Единицы измерения
Основной единицей измерения коэффициента поверхностного натяжения в системе СИ является:
Н/м = Дж/м2
Примеры решения задач
Поверхностное натяжение.
Это
напряженное состояние поверхностного
слоя жидкости, вызванное силами
взаимодействия между молекулами,
находящимися в верхнем слое жидкости.
рис.19
Сила
поверхностного натяжения
– горизонтальная составляющая всех
сил, действующих на молекулу, находящуюся
в поверхностном слое жидкости.
Рассмотрим
молекулу жидкости, находящуюся в
поверхностном слое, и другую молекулу,
которая находится внутри объема
жидкости(рис.19). Равнодействующая всех
сил, действующих на молекулу, находящуюся
внутри объема жидкости, равна нулю, так
как эта молекула со всех сторон окружена
такими же молекулами, и между ними
действуют силы взаимного притяжения.
А равнодействующая всех сил, действующих
на молекулу, находящуюся в поверхностном
слое жидкости, не равна нулю и направлена
внутрь объема жидкости. Это объясняется
тем, что сверху молекула поверхностного
слоя жидкости окружена молекулами
воздуха, расстояние между которыми
значительно больше чем расстояние между
молекулами жидкости, а значит и силы
притяжения между молекулами воздуха и
жидкости меньше сил взаимодействия
между молекулами самой жидкости, которыми
рассматриваемая молекула окружена
снизу. Поэтому каждая молекула
поверхностного слоя жидкости втягивается
внутрь объема жидкости, и, таким образом,
на поверхности создается особый слой
молекул, находящийся в напряженном
состоянии.
Пленка
поверхностного натяжения всегда
стремится сократить площадь поверхности.
— коэффициент
поверхностного натяжения
— длина контура,
ограничивающего поверхность жидкости
Поверхностно
активные вещества
Существуют такие
вещества, называемые поверхностно
активными, которые могут изменять
коэффициент поверхностного натяжения
жидкостей. К таким веществам относятся,
например, мыло, которое уменьшает
коэффициент поверхностного натяжения
воды. Также по отношению к воде поверхностно
активными являются нефть, спирт, эфир
и многие другие жидкие и твердые вещества.
1.2. Жидкость в капиллярах.
Капиллярные
явления. Капиллярами
называют сосуды с маленьким поперечным
сечением (внутренний диаметр меньше
1мм). Важная особенность капилляров
заключается в том, что поверхность
жидкости в них искривлена за счет
смачивания и несмачивания.
Искривленная
форма поверхности жидкости в капиллярной
трубке носит название мениска.
Мениск
в зависимости от смачивания несмачивания
бывает соответственно:
вогнутым
и выпуклым
Изогнутость
поверхности жидкости в капилляре
обусловлена поверхностным натяжением.
с
несмачивание
рис.20
Под
искривленной поверхностью жидкости в
капилляре действует добавочное давление,
обусловленное поверхностным натяжением.
Добавочное давление стремится сделать
изогнутую поверхность жидкости плоской.
Кроме
того, действует гидравлическое или
нормальное давление – давление жидкости
на дно сосуда. Нормальное давление
направлено всегда вниз, к дну сосуда. А
дополнительное давление при смачивании
направлено вверх. Поэтому в капиллярной
трубке при смачивании гидравлическое
давление меньше на величину
.
И, чтобы скомпенсировать действие
дополнительного давления, жидкость в
капилляре поднимается на определенную
высоту (рис.20). При несмачивании
дополнительное давление направлено
вниз и совпадает с гидравлическим.
Поэтому это давление больше на величину.
Не смачиваемая жидкость опускается в
капилляре на некоторую высоту, чтобы
скомпенсировать действие добавочного
давления. Высота поднятия смачивающей
жидкости в капилляре определяется по
формуле:
Борелли-Жюрена
Высота
зависит от поверхности натяжения, от
рода жидкости, от радиуса капилляра.
Добавочное
давление под искривленной поверхностью
жидкости определяется по формуле
Лапласса.
и
— радиусы кривизны двух взаимно
перпендикулярных сечений поверхности
жидкости.
Если
поверхность жидкости имеет сферическую
форму, то формула Лапласа принимает
вид:
Дополнительное
давление под искривленной поверхностью
жидкости прямо пропорционально
коэффициенту поверхностного натяжения
жидкости и обратно пропорционально
радиусу кривизны поверхности жидкости.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Понятие и характеристики поверхностного натяжения
С явлением поверхностного натяжения жидкости мы сталкиваемся каждый день:
- капли воды стремятся принять форму, близкую к шарообразной (а в невесомости они совсем шарообразные);
- струя воды из-под крана стремится к цилиндрической форме;
- булавка не тонет на поверхности воды в стакане;
- многие насекомые могут скользить по поверхности воды.
Силы поверхностного натяжения действуют вдоль поверхности жидкости, стремясь сократить ее площадь. Как будто жидкость заключена в упругую пленку, которая стремится сжать свое содержимое.
Потенциальная энергия взаимного притяжения молекул жидкости примерно равна их кинетической энергии. Это позволяет веществу сохранять объем (но не форму), и этот объем ограничивается поверхностью жидкости.
На молекулу жидкости, которая находится внутри, действуют силы притяжения со стороны других молекул, и они уравновешивают друг друга. А на ту молекулу, что находится на поверхности, действуют силы притяжения не только со стороны других молекул жидкости, но и со стороны газа (внешней среды). Эти вторые значительно меньше первых, поэтому равнодействующая сила притяжения направлена внутрь жидкости, что способствует удержанию молекулы на поверхности.
Поверхностное натяжение — это величина, которая показывает стремление жидкости сократить свою свободную поверхность, то есть уменьшить избыток своей потенциальной энергии на границе раздела с газообразной фазой.
Чем больше площадь поверхности жидкости, тем больше молекул, которые обладают избыточной потенциальной энергией, и тем больше поверхностная энергия. Этот факт можно записать в виде следующего соотношения:
Поверхностная энергия жидкости
W = σS
W — поверхностная энергия жидкости [Дж]
S — площадь свободной поверхности [м2]
σ — коэффициент поверхностного натяжения [Н/м]
Отсюда мы можем вывести формулу коэффициента поверхностного натяжения.
Коэффициент поверхностного натяжения — это физическая величина, которая характеризует данную жидкость и численно равна отношению поверхностной энергии к площади свободной поверхности жидкости.
Коэффициент поверхностного натяжения
σ = W/S
W — поверхностная энергия жидкости [Дж]
S — площадь свободной поверхности [м2]
σ — коэффициент поверхностного натяжения [Н/м]
Коэффициент поверхностного натяжения жидкости зависит:
- от природы жидкости;
- температуры жидкости;
- свойств газа, который граничит с данной жидкостью;
- наличия поверхностно-активных веществ (например, мыло или стиральный порошок), которые уменьшают поверхностное натяжение.
Коэффициент поверхностного натяжения не зависит от площади свободной поверхности жидкости, хотя может быть рассчитан с ее помощью.
Если на жидкость не действуют другие силы или их действие мало, жидкость будет стремиться принимать форму сферы, как капля воды или мыльный пузырь. Так же ведет себя вода в невесомости. Жидкость ведет себя так, как будто по касательной к ее поверхности действуют силы, стягивающие эту поверхность. Эти силы называются силами поверхностного натяжения.
Сила поверхностного натяжения
F = σl
F — сила поверхностного натяжения [Н]
l — длина контура, ограничивающего поверхность жидкости [м]
σ — коэффициент поверхностного натяжения [Н/м]
В химической промышленности в воду часто добавляют специальные реагенты-смачиватели, не дающие ей собираться в капли на какой-либо поверхности. Например, их добавляют в жидкие средства для посудомоечных машин. Попадая в поверхностный слой воды, молекулы таких реагентов заметно ослабляют силы поверхностного натяжения, вода не собирается в капли и не оставляет на поверхности пятен после высыхания.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Пятерка по физике у тебя в кармане!
Решай домашку по физике на изи. Подробные решения помогут разобраться в сложной теме и получить пятерку!
Поверхностное натяжение некоторых жидкостей на границе с воздухом
|
Вещество |
Температура, °C |
Поверхностное натяжение, 10−3 Н/м |
|
Хлорид натрия (водный раствор) |
20 |
82,55 |
|
Хлорид натрия |
801 |
115 |
|
Глицерин |
30 |
64,7 |
|
Олово |
400 |
518 |
|
Азотная кислота 70% |
20 |
59,4 |
|
Анилин |
20 |
42,9 |
|
Ацетон |
20 |
23,7 |
|
Бензол |
20 |
29,0 |
|
Вода |
20 |
72,86 |
|
Глицерин |
20 |
59,4 |
|
Нефть |
20 |
26 |
|
Ртуть |
20 |
486,5 |
|
Серная кислота 85% |
20 |
57,4 |
|
Спирт этиловый |
20 |
22,8 |
|
Уксусная кислота |
20 |
27,8 |
|
Этиловый эфир |
20 |
16,9 |
|
Раствор мыла |
20 |
43 |
Пример решения задачи
Тонкое алюминиевое кольцо радиусом 7,8 см соприкасается с мыльным раствором. Каким усилием можно оторвать кольцо от раствора? Температуру раствора считать комнатной. Масса кольца 7 г. Коэффициент поверхностного натяжения мыльного раствора при комнатной температуре равен 4 × 10-2 Н/м.
Решение
Выполним рисунок:
На кольцо действуют сила тяжести, сила поверхностного натяжения и внешняя сила, с которой отрывают кольцо от раствора.
Так как кольцо соприкасается с раствором и внешней и внутренней сторонами, то сила поверхностного натяжения удваивается:
Fs = 2σl
Контур, ограничивающий поверхность жидкости, имеет форму окружности. Значит, его длина будет равна:
l = 2πR
Подставляем в формулу силы поверхностного натяжения:
Fs = 4σπR
Условие отрыва кольца от поверхности раствора имеет вид второго закона Ньютона для инерциальных систем отсчета:
F = mg + Fs
Подставляем силу поверхностного натяжения:
F = mg + 4σπR
И вычисляем:
F = 0,007 × 10 + 4 × 4 × 10-2 × 3,14 × 7,8 × 10-2 = 0,11 Н
Ответ: Для того, чтобы оторвать кольцо от раствора, необходимо приложить силу в 0,11 Н.
Важность поверхностного натяжения
Выше мы уже показали, что поверхностное натяжение встречается в повседневной жизни достаточно часто. Но на самом деле оно встречается еще чаще!
В некоторых отраслях промышленности поверхностное натяжение используют как простой показатель загрязнения продуктов. Поскольку оно определяется на молекулярном уровне, любое изменение компонентов вещества может привести к изменению этого показателя. То есть если мы знаем, каким должно быть поверхностное натяжение совершенно чистого вещества, то по отклонению от этой нормы мы можем установить уровень его загрязнения.
Не только человек, но и представители живой природы используют физические явления в своих целях. Например, за счет поверхностного натяжения насекомые водомерки могут перемещаться по водной глади, не промочив лапки. Конечности водомерки отталкивают воду и захватывают воздух, что позволяет насекомым продавливать поверхность воды, не нарушая ее.
За счет поверхностного натяжения возникает такое любопытное явление, как ламинарное течение. Это упорядоченный режим течения вязкой жидкости или газа, при котором соседние слои жидкости не перемешиваются. Выглядит ламинарная струя так, как будто вода застыла.
И это еще не все: поверхностное натяжение позволяет предметам плавать, благодаря ему выживают и развиваются экосистемы, и даже состав воды стабилен только за счет этого явления. Без него вода бы постоянно находилась на границе двух агрегатных состояний: испарялась и вновь конденсировалась, так как молекулы легко выскакивали бы с ее поверхности.
Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!
Содержание:
Поверхностное натяжение жидкости:
В отличие от газов жидкости имеют свободную поверхность. Молекулы, расположенные на поверхности жидкости, и молекулы внутри жидкости находятся в разных условиях:
a) молекулы внутри жидкости окружены другими молекулами жидкости со всех сторон. Молекула 1 внутри жидкости испытывает действие соседних молекул со всех сторон, поэтому равнодействующая сил притяжения, действующих на нее, равна нулю (f; молекула 1);
b) молекулы на поверхности жидкости испытывают действие со стороны соседних молекул жидкости только сбоку и снизу. Притяжение со стороны молекул газа (пара жидкости или воздуха) над жидкостью во много раз слабее, чем со стороны молекул жидкости, поэтому не принимаются во внимание (f; молекула 2). В результате каждая из равнодействующих сил
Сила поверхностного натяжения
Сила поверхностного натяжения — это сила, направленная по касательной к поверхности жидкости, перпендикулярно к линии, ограничивающей поверхность жидкости, и стремящаяся сократить площадь поверхности жидкости. Сила поверхностного натяжения прямо пропорциональна длине границы соприкосновения свободной поверхности жидкости с твердым телом:
Здесь 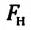
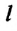
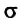
Коэффициент поверхностного натяжения
Коэффициент поверхностного натяжения — численно равен силе поверхностного натяжения, приходящейся на единицу длины линии, ограничивающей поверхность жидкости:
Значение коэффициента поверхностного натяжения зависит от вида жидкости и ее температуры, то есть с увеличением температуры жидкости коэффициент его поверхностного натяжения уменьшается и при критической температуре равен нулю. Единица коэффициента поверхностного натяжения в СИ:
Смачивающая и несмачивающая жидкость. При внимательном рассмотрении можно увидеть искривление поверхности жидкости на границе между жидкостью и твердым телом.
Мениск — это искривление свободной поверхности жидкости в месте ее соприкосновении с поверхностью твердого тела (или другой жидкости). Угол между поверхностью мениска и поверхностью твердого тела называется краевым углом.
Значение краевого угла 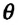
Смачивающая жидкость —это жидкость, у которой краевой угол острый. Сила взаимного притяжения между молекулами смачивающей жидкости и твердого тела больше, чем силы взаимного притяжения между молекулами самой жидкости. В результате свободная поверхность жидкости в сосуде становится вогнутой, например, вода в стеклянном сосуде — смачивающая жидкость (g).
Несмачивающая жидкость — это жидкость, у которой краевой угол тупой. Сила взаимного притяжения между молекулами несмачивающей жидкости и твердого тела меньше, чем сила взаимного притяжения между молекулами самой жидкости. В результате свободная поверхность жидкости в сосуде бывает выпуклой, например, ртуть в стеклянном сосуде — несмачивающая жидкость (i).
Капиллярные явления
В повседневной жизни встречаются и используются тела, с легкостью впитывающие в себя воду, например, полотенце, промокательная бумага, сахар, кирпич, растения и др. Это свойство в телах объясняется существованием в них большого количества очень узких трубочек — капилляров.
Капилляр — это узкая трубка (канал) диаметром меньше 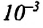
Капиллярными явлениями называют явления подъема смачивающей и опускания несмачивающей жидкости по капилляру относительно общего уровня жидкости под действием сил поверхностного натяжения (j).
В таблице 6.4 дана зависимость между величинами, характеризующими жидкость, поднимающуюся в капилляре.
Таблица 6.4
|
Характеристики жидкости, поднимающейся в капилляре |
Формула |
| Вес жидкости, поднимающейся в капилляре |
Где |
| Масса жидкости, поднимающейся в капилляре | 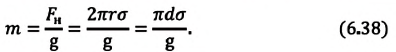 |
| Высота жидкости, поднимающейся в капилляре |
Если жидкость полностью смачиваемая, то получаем в Где |
| Давление жидкости, поднимающейся в капилляре | 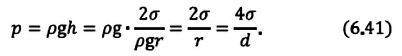 |
Поверхностное натяжение жидкости
Некоторые виды пауков могут передвигаться по поверхности воды не проваливаясь, как будто эта поверхность покрыта невидимой тонкой пленкой. такое же впечатление создается, если наблюдать за вытеканием воды из маленького отверстия — вода течет не тоненькой струйкой, а образует капли. Бумажная салфетка впитывает воду, едва коснувшись ее поверхности. какая сила является причиной всех этих явлений?
Каковы особенности поверхностного слоя жидкости
На свободной поверхности жидкости молекулы находятся в особых условиях, отличающихся от условий, в которых находятся молекулы внутри жидкости. Рассмотрим две молекулы — А и Б (рис. 33.1): молекула А находится внутри жидкости, а молекула Б — на ее поверхности. Молекула А окружена другими молекулами жидкости равномерно, поэтому силы, действующие на молекулу А со стороны молекул, попадающих в сферу межмолекулярного взаимодействия, скомпенсированы, то есть их равнодействующая равна нулю.
Молекула Б с одной стороны окружена молекулами жидкости, а с другой — молекулами газа. Со стороны жидкости на нее действует гораздо больше молекул, чем со стороны газа, поэтому равнодействующая F межмолекулярных сил направлена в глубь жидкости. Чтобы молекула из глубины попала в поверхностный слой, нужно совершить работу против межмолекулярных сил. Это означает, что молекулы поверхностного слоя жидкости (по сравнению с молекулами внутри жидкости) обладают избыточной потенциальной энергией. Эта избыточная энергия является частью внутренней энергии жидкости и называется поверхностной энергией (Wпов). Очевидно, что чем больше площадь S поверхности жидкости, тем больше поверхностная энергия: W S пов = σ , где σ (сигма) — коэффициент пропорциональности, который называют поверхностным натяжением жидкости.
Поверхностное натяжение жидкости — физическая величина, которая характеризует данную жидкость и равна отношению поверхностной энергии к площади поверхности жидкости:
Единица поверхностного натяжения в СИ — ньютон на метр:
Поверхностное натяжение жидкости определяется силами межмолекулярного взаимодействия, поэтому оно зависит:
- от природы жидкости: у летучих жидкостей (эфир, спирт, бензин) поверхностное натяжение меньше, чем у нелетучих (ртуть, жидкие металлы);
- температуры жидкости: чем выше температура жидкости, тем меньше поверхностное натяжение;
- присутствия в составе жидкости поверхностно активных веществ — их наличие уменьшает поверхностное натяжение;
- свойств газа, с которым жидкость граничит. В таблицах обычно приводят значение поверхностного натяжения на границе жидкости и воздуха при определенной температуре (табл. 1).
Таблица 1
Поверхностное натяжение σ некоторых жидкостей
Что такое сила поверхностного натяжения
Поскольку поверхностный слой жидкости обладает избыточной потенциальной энергией (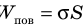
Наличие сил поверхностного натяжения делает поверхность жидкости похожей на натянутую резиновую пленку, однако упругие силы в резиновой пленке зависят от площади ее поверхности (от того, насколько пленка деформирована), а поверхность жидкости всегда «натянута» одинаково, то есть силы поверхностного натяжения не зависят от площади поверхности жидкости. Наличие сил поверхностного натяжения можно доказать с помощью такого опыта. Если проволочный каркас с закрепленной на нем нитью опустить в мыльный раствор, каркас затянется мыльной пленкой, а нить приобретет произвольную форму (рис. 33.2, а).
Если осторожно проткнуть иглой мыльную пленку по одну сторону от нити, сила поверхностного натяжения мыльного раствора, действующая с другой стороны, натянет нить (рис. 33.2, б). Опустим в мыльный раствор проволочную рамку, одна из сторон которой подвижна. На рамке образуется мыльная пленка (рис. 33.3). Будем растягивать эту пленку, действуя на перекладину (подвижную сторону рамки) с некоторой силой 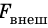
Если под действием этой силы перекладина переместится на ∆x , то внешние силы совершат работу: 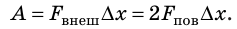
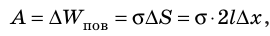
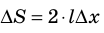
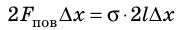
Таким образом, поверхностное натяжение σ численно равно силе поверхностного натяжения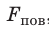
С одним из методов определения поверхностного натяжения жидкости вы ознакомитесь, выполняя лабораторную работу № 7.
- Заказать решение задач по физике
Где проявляется поверхностное натяжение
В жизни вы постоянно сталкиваетесь с проявлениями сил поверхностного натяжения. Так, благодаря ему на поверхности воды удерживаются легкие предметы (рис. 33.4) и некоторые насекомые.
Рис. 33.4. Монетка удерживается на поверхности воды благодаря силе поверхностного натяжения. (Чтобы провести такой опыт, монетку нужно потереть между пальцев и осторожно опустить на поверхность воды.)
Когда вы ныряете, ваши волосы расходятся во все стороны, но как только вы окажетесь над водой, волосы слипнутся, так как в этом случае площадь свободной поверхности воды намного меньше, чем при раздельном расположении прядей в воде. По этой же причине можно лепить фигуры из влажного песка: вода, обволакивая песчинки, прижимает их друг к другу.
Рис. 33.5. Капля удерживается около небольшого отверстия до тех пор, пока сила поверхностного натяжения уравновешивает силу тяжести
Стремлением жидкости уменьшить площадь поверхности объясняется и тот факт, что в условиях невесомости вода принимает форму шара, — при заданном объеме шарообразной форме соответствует наименьшая площадь поверхности. Форму шара приобретают тонкие мыльные пленки (мыльные пузыри). Поверхностным натяжением объясняется образование пены: пузырек газа, достигнув поверхности жидкости, имеет над собой тонкий слой жидкости; если пузырек мал, то архимедовой силы недостаточно, чтобы разорвать двойной поверхностный слой, и пузырек «застревает» вблизи поверхности. Благодаря поверхностному натяжению жидкость не выливается из маленького отверстия тоненькой струйкой, а капает (рис. 33.5), дождь не проливается через ткань зонта или палатки и т. д.
Почему одни жидкости собираются в капли, а другие растекаются
Наличие сил поверхностного натяжения проявляется в сферической форме мелких капелек росы, в каплях воды, разбегающихся по раскаленной плите, в капельках ртути на поверхности стекла. Однако при соприкосновении с твердым телом сферическая форма капли, как правило, не сохраняется. Форма свободной поверхности жидкости зависит также от сил взаимодействия молекул жидкости с молекулами твердого тела.
Если силы взаимодействия между молекулами жидкости больше, чем силы взаимодействия между молекулами жидкости и твердого тела, жидкость не смачивает поверхность твердого тела (рис. 33.6). Например, ртуть не смачивает стекло, а вода не смачивает покрытую сажей поверхность.
Рис. 33.6. Капля несмачивающей жидкости принимает форму, близкую к сферической, а поверхность жидкости вблизи стенки сосуда является выпуклой
Если же капельку ртути поместить на цинковую пластину, то капелька будет стремиться растечься по поверхности пластины; так же ведет себя и капелька воды на стекле (рис. 33.7). Если силы взаимодействия между молекулами жидкости меньше сил взаимодействия между молекулами жидкости и твердого тела, жидкость смачивает поверхность твердого тела.
Рис. 33.7. Капля смачивающей жидкости стремится растечься по поверхности твердого тела, а вблизи стенки сосуда поверхность жидкости принимает вогнутую форму
Почему жидкость поднимается в капиллярах
В природе часто встречаются тела, пронизанные многочисленными мелкими капиллярами (от лат. capillaris — волосяной) — узкими каналами произвольной формы. Такую структуру имеют бумага, дерево, почва, многие ткани и строительные материалы. В цилиндрических капиллярах искривленная поверхность жидкости представляет собой часть сферы, которую называют мениском. У смачивающей жидкости образуется вогнутый мениск (рис. 33.8, а), а у несмачивающей — выпуклый (рис. 33.8, б).
Рис. 33.8. капиллярные явления: а — смачивающая жидкость поднимается по капилляру; б — несмачивающая жидкость опускается в капилляре
Поверхность жидкости стремится к минимуму потенциальной энергии, а искривленная поверхность обладает большей площадью по сравнению с площадью сечения капилляра, поэтому поверхность жидкости стремится выровняться и под ней возникает избыточное (отрицательное или положительное) давление — лапласово давление (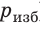
Под вогнутой поверхностью (жидкость смачивает капилляр) лапласово давление отрицательное и жидкость втягивается в капилляр. Так поднимаются влага и питательные вещества в стеблях растений, керосин по фитилю, влага в почве. Вследствие лапласового давления салфетки или ткань впитывают воду, брюки в дождливую погоду сильно намокают снизу и т. д. Под выпуклой поверхностью (жидкость не смачивает капилляр) лапласово давление положительное и жидкость в капилляре опускается. Чем меньше радиус капилляра, тем больше высота подъема (или опускания) жидкости (см. задачу ниже).
Пример решения задачи
Капиллярную трубку радиусом r одним концом опустили в жидкость, смачивающую внутреннюю поверхность капилляра. На какую высоту поднимется жидкость в капилляре, если плотность жидкости ρ, а ее поверхностное натяжение σ ? Чему равно лапласово давление под вогнутой поверхностью капилляра? Смачивание считайте полным.
Решение:
На жидкость в капилляре действуют сила тяжести и сила поверхностного натяжения (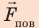
Поиск математической модели, решение
Поскольку m V = ρ , а объем воды в цилиндрическом капилляре 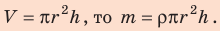
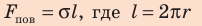
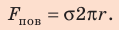

где R — радиус кривизны мениска (при полном смачивании r=R).
Ответ: (Данные выводы следует запомнить!)
Выводы:
- Свойства паров в физике
- Кипение жидкостей в физике
- Электромагнитные явления в физике
- Электромагнитные волны и их свойства
- Расчет количества теплоты при нагревании и охлаждении
- Удельная теплота сгорания топлива
- Плавление и кристаллизация в физике
- Испарение жидкостей в физике
Поверхностное натяжение
Свойство поверхности жидкости сокращаться можно истолковать как существование сил, стремящихся сократить эту поверхность. Молекула M1 (рис. 2), расположенная на поверхности жидкости, взаимодействует не только с молекулами, находящимися внутри жидкости, но и с молекулами, находящимися на поверхности жидкости, расположенными в пределах сферы молекулярного действия. Для молекулы M1 равнодействующая (~vec R) молекулярных сил, направленных вдоль свободной поверхности жидкости, равна нулю, а для молекулы M2, расположенной у границы поверхности жидкости, (~vec R ne 0) и (~vec R) направлена по нормали к границам свободной поверхности и по касательной к самой поверхности жидкости.
Рис. 2
Равнодействующая сил, действующих на все молекулы, находящиеся на границе свободной поверхности, и есть сила поверхностного натяжения. В целом она действует так, что стремится сократить поверхность жидкости.
Можно предположить, что сила поверхностного натяжения (~vec F) прямо пропорциональна длине l границы поверхностного слоя жидкости, ведь на всех участках поверхностного слоя жидкости молекулы находятся в одинаковых условиях:
(~F sim l .)
Действительно, рассмотрим вертикальный прямоугольный каркас (рис. 3, а, б), подвижная сторона которого уравновешена. После извлечения рамки из раствора мыльной пленки подвижная часть перемещается из положения 1 в положение 2. Учитывая, что пленка представляет собой тонкий слой жидкости и имеет две свободные поверхности, найдем работу, совершаемую при перемещении поперечины на расстояние h = a1a2: A = 2Fh, где F — сила, действующая на каркас со стороны каждого поверхностного слоя. С другой стороны, (~A = alpha Delta S = alpha cdot 2lh).
Рис. 3
Следовательно, (~2Fh = alpha cdot 2lh Rightarrow F = alpha l), откуда (~alpha = frac Fl).
Согласно этой формуле единицей коэффициента поверхностного натяжения в СИ является ньютон на метр (Н/м).
Коэффициент поверхностного натяжения α численно равен силе поверхностного натяжения, действующей на единицу длины границы свободной поверхности жидкости. Коэффициент поверхностного натяжения зависит от природы жидкости, от температуры и от наличия примесей. При увеличении температуры он уменьшается. При критической температуре, когда исчезает различие между жидкостью и паром, α = 0.
Примеси в основном уменьшают (некоторые увеличивают) коэффициент поверхностного натяжения.
Таким образом, за счет сил поверхностного натяжения поверхностный слой жидкости всегда находится в состоянии натяжения. Однако это состояние существенно отличается от натяжения упругой резиновой пленки. Упругая пленка растягивается за счет увеличения расстояния между частицами, при этом сила натяжения возрастает, при растяжении же жидкой пленки расстояние между частицами не меняется, а увеличение поверхности достигается в результате перехода молекул из толщи жидкости в поверхностный слой. Поэтому при увеличении поверхности жидкости сила поверхностного натяжения не изменяется (она не зависит от площади поверхности).
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 180-181.
ПОВЕРХНОСТНОЕ НАТЯЖЕНИЕ ЖИДКОСТЕЙ
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Введение
В окружающем нас мире наряду с тяготением, упругостью и трением действует еще одна сила, на которую мы обычно не обращаем внимание. Эта сила действует вдоль касательной к поверхностям всех жидкостей. Силу, которая действует вдоль поверхности жидкости перпендикулярно линии, ограничивающей эту поверхность, стремится сократить её до минимума, называют силой поверхностного натяжения. Она сравнительно мала, ее действие никогда не вызывает мощных эффектов. Тем не менее, мы не можем налить воду в стакан, вообще ничего не можем проделать с какой-либо жидкостью без того, чтобы не привести в действие силы поверхностного натяжения. К эффектам, называемым поверхностным натяжением, мы настолько привыкли, что не замечаем их. Удивительно разнообразны проявления поверхностного натяжения жидкости в природе и технике. В природе и в нашей жизни они играют немаловажную роль. Без них мы не могли бы писать гелиевыми ручками, картриджив принтерах сразу же ставили бы большую кляксу, опорожнив весь свой резервуар. Нельзя было бы намылить руки – пена не образовалась бы. Слабый дождик промочил бы нас насквозь, а радугу нельзя было бы видеть ни при какой погоде. Поверхностное натяжение собирает воду в капли и благодаря поверхностному натяжению можно выдуть мыльный пузырь. Используя правило «Вовремя удивляться» бельгийского профессора Плато для исследователей, рассмотрим в работе необычные опыты.
Цель работы: экспериментально проверить проявления поверхностного натяжения жидкости, определить коэффициент поверхностного натяжения жидкостей методом отрыва капель
Задачи:
-
Изучить учебную, научно-популярную литературу, использовать материалы в сети «Интернет» по теме «Поверхностное натяжение»;
-
проделать опыты, доказывающие, что собственная форма жидкости – шар;
-
провести эксперименты с уменьшением и увеличением поверхностного натяжения;
-
сконструировать и собрать экспериментальную установку, с помощью которой определить коэффициент поверхностного натяжения некоторых жидкостей методом отрыва капель.
-
обработать полученные данные и сделать вывод.
Объект исследования: жидкости.
Основная часть. Поверхностное натяжение
М
Рис 1. Г. Галилей
ногочисленные наблюдения и опыты показывают, что жидкость может принимать такую форму, при которой ее свободная поверхность имеет наименьшую площадь. В своем стремлении сократиться поверхностная пленка придавала бы жидкости сферическую форму, если бы не притяжение к Земле. Чем меньше капля, тем большую роль играют силы поверхностного натяжения. Поэтому маленькие капельки росы на листьях деревьев, на траве близки по форме к шару, при свободном падении дождевые капли почти строго шарообразны. Стремление жидкости сокращаться до возможного минимума, можно наблюдать на многих явлениях, которые кажутся удивительными. Еще Галилей задумывался над вопросом: почему капли росы, которые он видел по утрам на листьях капусты, принимают шарообразную форму? Утверждение, что жидкость не имеет своей формы, оказывается не совсем точным. Собственная форма жидкости – шар, как наиболее ёмкая форма. Молекулы вещества в жидком состоянии расположены почти вплотную друг к другу. В отличие от твердых кристаллических тел, в которых молекулы образуют упорядоченные структуры во всем объеме кристалла и могут совершать тепловые колебания около фиксированных центров, молекулы жидкости обладают большей свободой. Каждая молекула жидкости, также как и в твердом теле, «зажата» со всех сторон соседними молекулами и совершает тепловые колебания около некоторого положения равновесия. Однако время от времени любая молекула может переместиться в соседнее вакантное место. Такие перескоки в жидкостях происходят довольно часто; поэтому молекулы не привязаны к определенным центрам, как в кристаллах, и могут перемещаться по всему объему жидкости. Этим объясняется текучесть жидкостей. Из-за сильного взаимодействия между близко расположенными молекулами они могут образовывать локальные (неустойчивые) упорядоченные группы, содержащие несколько молекул. 1
Рис 2. Пример ближнего порядка молекул жидкости и дальнего порядка молекул кристаллического вещества: 1 – вода; 2 – лед
А как можно объяснить самопроизвольное сокращение поверхности жидкости? Молекулы на поверхности и в глубине жидкости находятся в разных условиях. На каждую молекулу внутри жидкости действуют силы притяжения со стороны соседних молекул, окружающих ее со всех сторон. Результирующая этих сил равна нулю. Над поверхностью жидкости находится пар, плотность которого во много раз меньше плотности жидкости, и взаимодействием молекул пара с молекулами жидкости можно пренебречь. Молекулы, которые находятся на поверхности жидкости, притягиваются только молекулами, находящимися внутри жидкости. Под действием этих сил молекулы поверхностного слоя втягиваются внутрь, число молекул на поверхности уменьшается, площадь поверхности сокращается. Но не все молекулы могут с поверхности уйти внутрь жидкости, этому препятствуют силы отталкивания, возникающие при уменьшении расстояний между молекулами. При определенных расстояниях между молекулами, втягиваемыми внутрь, и молекулами, находящимися под поверхностью, силы взаимодействия становятся равными нулю, процесс сокращения поверхности прекращается. На поверхности остается такое число молекул, при котором ее площадь оказывается минимальной для данного объема жидкости. Так как жидкость текуча, она принимает такую форму, при которой число молекул на поверхности минимально, а минимальную поверхность при данном объеме имеет шар, то есть капля жидкости принимает форму, близкую шаровой.Проще всего уловить характер сил поверхностного натяжения, наблюдая образование капли. Всмотритесь внимательно, как постепенно растет капля, образуется сужение – шейка, — и капля отрывается. Не нужно много фантазии, чтобы представить себе, что вода как бы заключена в эластичный мешочек, и этот мешочек разрывается, когда вес превышает его прочность. В действительности, конечно, ничего кроме воды, в капле нет, но сам поверхностный слой воды ведёт себя, как растянутая эластичная пленка. Такое же впечатление производит пленка мыльного пузыря.
Опыт №1
С
Рис . 3
тремление жидкости к минимуму потенциальной энергии можно наблюдать с помощью мыльных пузырей. Мыльная пленка представляет собой двойной поверхностный слой. Если выдуть мыльный пузырь, а потом прекратить надувание, то он станет уменьшаться в объёме, выжимая из себя струю воздуха.
Фото 1
Поверхностное натяжение – явление молекулярного давления на жидкость, вызываемое притяжением молекул поверхностного слоя к молекулам внутри жидкости5
Опыт Плато (1849г.)
П
Рис. 4. Ж.Плато
оводом, побудившим бельгийского профессора к опытам, был случай. Нечаянно он налил в смесь спирта и воды небольшое количество масла, и оно приняло форму шара. Размышляя над этим фактом, Плато наметил ряд опытов, которые впоследствии блестяще были выполненными его друзьями и учениками. В своем дневнике он написал для исследователей правило: «Вовремя удивляться». Я решила исследовать опыт Плато, но в другом варианте: использовать в опыте подсолнечное масло и подкрашенную марганцовую воду.
Опыт, доказывающий, что однородная жидкость принимает форму с минимальной свободной поверхностью
Вариант опыта Плато №2
1) В мензурку налили подсолнечное масло.
2) Глазной пипеткой капнули в подсолнечное масло каплю подкрашенной марганцовой воды диаметром приблизительно 5мм.
3
Фото 2
) Наблюдали шарики воды разного размера, медленно падающие на дно и принимающие овальную приплюснутую форму (Фото 2).
5) Наблюдали, как капля принимает правильную форму шара (Фото 2).
Вывод: Жидкость, притягивая молекулы поверхностного слоя, сжимает саму себя. Овальная приплюснутая форма объясняется тем, что вес капли, которая не смешивается с маслом, больше выталкивающей силы. Правильная форма шара объясняется тем, что капля плавает внутри масла: вес капли уравновешивается выталкивающей силой.
При свободном падении, в состоянии невесомости капли дождя практически имеют форму шара. В космическом корабле шарообразную форму принимает и достаточно большая масса жидкости.
Коэффициент поверхностного натяжения
В отсутствии внешней силы вдоль поверхности жидкости действует сила поверхностного натяжения, которая сокращает до минимума площадь поверхности пленки. Сила поверхностного натяжения – сила, направленная по касательной к поверхности жидкости, перпендикулярно участку контура, ограничивающего поверхность, в сторону ее сокращения.
F = Ơ ℓ
Ơ = F / ℓ
Ơ — коэффициент поверхностного натяжения – это отношение модуля F силы поверхностного натяжения, действующей на границу поверхностного слоя ℓ, к этой длине есть величина постоянная, не зависящая от длины ℓ. Коэффициент поверхностного натяжения зависит от природы граничащих сред и от температуры. Его выражают в ньютонах на метр (Н / м).
Опыты с уменьшением и увеличением
п
Фото 3
оверхностного натяжения
Опыт №3
-
В широкий стеклянный сосуд налили воду.
-
На поверхность бросили кусочки пенопласта.
-
Прикоснулись к центру поверхности воды кусочком мыла.
-
Кусочки пенопласта начинают двигаться от центра к краям сосуда (Фото 3).
-
Капали в центр сосуда бензином, спиртом, моющим средством «Fairy».
Вывод: Поверхностное натяжение данных веществ меньше, чем у воды.
Эти вещества используются для удаления грязи, жирных пятен, сажи, т.е. не растворимых в воде веществ.Из-за достаточно высокого поверхностного натяжения вода сама по себе не обладает очень хорошим чистящим действием. Например, вступая в контакт с пятном, молекулы воды притягиваются друг к другу больше, чем к частицам нерастворимой грязи.Мыло и синтетические моющие средства (СМС) содержат вещества, уменьшающие поверхностное натяжение воды. Первое мыло, самое простое моющее средство, было получено на Ближнем Востоке более 5000 лет назад. Поначалу оно использовалось, главным образом, для стирки и обработки язв и ран. И только в 1 веке н.э. человек стал мыться с мылом.
В начале 1-го века мыло появилось на свет.
От грязи спасло человека и стал он чистым с юных лет.
Я говорю вам про мыло, что вскоре породило: шампунь, гель, порошок.
Стал чистым мир, как хорошо!
Рис 5. Ф. Гюнтер
Моющими средствами называются натуральные и синтетические вещества с очищающим действием, в особенности мыло и стиральные порошки, применяемые в быту, промышленности и сфере обслуживания. Мыло получают в результате химического взаимодействия жира и щелочи. Скорее всего, оно было открыто по чистой случайности, когда над костром жарили мясо, и жир стекал на золу, обладающую щелочными свойствами. Производство мыла имеет давнюю историю, а вот первое синтетическое моющее средство (СМС) появилось в 1916г., его изобрел немецкий химик Фриц Гюнтер для промышленных целей. Бытовые СМС, более или менее безвредные для рук, стали выпускаться 1933г. С тех пор разработан целый ряд синтетических моющих средств (СМС) узкого назначения, а их производство стало важной отраслью химической промышленности.
Именно из-за поверхностного натяжения вода сама по себе не обладает достаточным чистящим действием. Вступая в контакт с пятном, молекулы воды притягиваются друг к другу, вместо того чтобы захватывать частицы грязи, другими словами они не смачивают грязь.
Мыло и синтетические моющие средства содержат вещества, повышающие смачивающие свойства воды за счет уменьшения силы поверхностного натяжения. Эти вещества называются поверхностно-активными (ПАВ), поскольку действуют на поверхности жидкости.
Рис. 6
Сейчас производство СМС стало важной отраслью химической промышленности. Эти вещества называют поверхностно-активным веществом (ПАВ), поскольку действуют на поверхности жидкости. Молекулы ПАВ можно представить в виде головастиков. Головами они «цепляются» за воду, а «хвостами» за жир. Когда ПАВ смешивают с водой, их молекулы на поверхности обращены «головами» вниз, а «хвостами» наружу. Раздробив таким образом поверхность воды, эти молекулы значительно уменьшают эффект поверхностного натяжения, тем самым помогая воде проникнуть в ткань. Этими же «хвостиками» молекулы ПАВ (Рис 6) захватывают попадающиеся им молекулы жира.2
Опыт №4
Фото 4
Фото 6
1.Налили в блюдце молоко так, чтобы оно закрыло дно (Фото 4)
2. Капнули на поверхность молока 2 капля зеленки
3. Наблюдали, как зеленка «увлекается» от центра к краям. Две капли зеленки покрывают большую часть поверхности молока! (Фото 5)
Вывод: поверхностное натяжение зеленки, намного меньше, чем молока.
4. На поверхность зеленки капнули жидкость для мытья посуды «Fairy», мы увидели, как эта жидкость растеклась по всей поверхности.(Фото 6)
Вывод: поверхностное натяжение моющего средства меньше, чем зеленки.
Фото 5
Опыт№5
-
В широкий стеклянный сосуд налили воду.
-
На поверхность бросили кусочки пенопласта.
-
Прикоснулись к центру поверхности воды кусочком сахара.
-
К
Фото 7
усочки пенопласта начинают двигаться от краев сосуда к центру (Фото 7).
Вывод: поверхностное натяжение водного раствора сахара больше, чем чистой воды.
Опыт№6
Удаление с поверхности ткани жирового пятна
Смочили бензином ватку и этой ваткой смочили края пятна (а не само пятно). Бензин уменьшает поверхностное натяжение, поэтому жир собирается к центру пятна и оттуда его можно удалить, этой же ваткой если же смачивать, само пятно, то оно может увеличиться в размерах вследствие уменьшения поверхностного натяжения.
Для экспериментального определения значения поверхностного натяжения жидкости можно использовать процесс образования и отрыва капель, вытекающих из капельницы.
Краткая теория методаотрыва капель
Малый объем жидкости сам по себе принимает форму, близкую к шару, так как благодаря малой массе жидкости мала и сила тяжести, действующая на нее. Этим объясняется шарообразная форма небольших капель жидкости. На рис.1 приведены фотографии, на которых показаны различные стадии процесса образования и отрыва капли. Фотография получена с помощью скоростной киносъемки, капля растет медленно, можно считать, что в каждый момент времени она находится в равновесии. Поверхностное натяжение вызывает сокращение поверхности капли, оно стремится придать капле сферическую форму. Сила тяжести располагает центр тяжести капли как можно ниже. В результате капля оказывается вытянутой (рис.7а).
Рис. 7. а б в г
Процесс образования и отрыва капель
Чем больше капля, тем большую роль играет потенциальная энергия силы тяжести. Основная масса по мере роста капли собирается внизу и у капли образуется шейка (рис.7б). Сила поверхностного натяжения направлена вертикально по касательной к шейке и она уравновешивает силу тяжести, действующую на каплю. Теперь достаточно капле совсем немного увеличиться и силы поверхностного натяжения уже не уравновешивают силу тяжести. Шейка капли быстро сужается (рис.7в) и в результате капля отрывается (рис.7г).
Метод измерения коэффициента поверхностного натяжения некоторых жидкостей основывается на взвешивании капель. В случае медленного вытекания жидкости из малого отверстия размер образующихся капель зависит от плотности жидкости, коэффициента поверхностного натяжения, размера и формы отверстия, а также от скорости истечения. При медленном вытекании смачивающей жидкости из вертикальной цилиндрической трубки образующаяся капля имеет форму, показанную на рисунке 8. Радиус r шейки капли связан с наружным радиусом трубки R соотношением r = kR (1)
где k – коэффициент, зависящий от размеров трубки и скорости вытекания.
В
R
момент отрыва вес капли должен быть равен равнодействующей сил поверхностного натяжения, действующих по длине, равной протяженности контура шейки в самой ее узкой части. Таким образом, можно записать
m
r
g=ơl
Рис. 8
mg = 2πrơ (2)
Подставляя величину радиуса шейки r из равенства (1) и решая его, получим
Ơ =mg/2πkR (3)
Для определения массы капли, некоторое число n капель взвешивают в стакане известного веса. Если масса стаканчика без капель и с каплями будет соответственно М0 и М, то масса одной капли
m = (M-M0)/n
Подставляя последнее выражение в формулу (3) и вводя вместо радиуса трубки ее диаметр d, получим расчетную формулу
ơ = ((M-M0)g)/πkdn 3 (4)
Исследовательская работа «Определение коэффициента поверхностного натяжения некоторых жидкостей методом отрыва капель»
Цель исследования: определить коэффициент поверхностного натяжения жидкости методом отрыва капель некоторых жидкостей. Приборы: установка для измерения коэффициента поверхностного натяжения, весы, разновес, стаканчик, штангенциркуль, секундомер. Материалы: моющие средства: «Fairy», «Aos», молоко, спирт, бензин, растворы порошков: «Миф», «Persil», шампуни «Fruttis», «Pantene», «Schauma» и «Fruttis», гели для душа «Sensen», «Монпансье» и «Discover».
Описание прибора.
Для определения коэффициента поверхностного натяжения собрали установку, состоящую из штатива, на котором установили бюретку с исследуемой жидкостью. На конце бюретки укрепили наконечник-трубку, на конце которой образуется капля. Взвешивание капель производили в специальном стаканчике.
Ход исследования
-
С помощью штангенциркуля измерили диаметр наконечника-трубки три раза и вычислили среднее значение d.
-
Взвесили на весах чистый сухой стаканчик (М0).
-
С помощью краника бюретки добились скорости вытекания капель
15 капель в минуту.
-
Отлили из бюретки в стаканчик 60 капель жидкости, считая точно количество отлитых капель.
-
Взвесили стаканчик с жидкостью. (М)
-
Подставили полученные значения в формулу ơ = ((M-M0)g)/πkdn
-
Вычислили коэффициент поверхностного натяжения.
-
Провели опыт три раза
-
Вычислили среднее значение коэффициента поверхностного натяжения.
Коэффициент поверхностного натяжения в системе СИ измеряется в Н/м.
Таблица №1
Результаты определения коэффициента поверхностного натяжения (Н/м)
|
Жидкость |
Коэффициент поверхностного натяжения |
|
|
Измеренное |
Табличное |
|
|
Спирт этиловый |
23 |
22 |
|
Бензин |
24 |
21 |
|
Молоко (2,5) |
45 |
— |
|
Молоко (коровье домашнее) |
41 |
— |
|
Раствор порошка «Миф» |
32 |
— |
|
Раствор порошка «Persil» |
36 |
— |
|
Моющее средство «Fairy» |
45 |
— |
|
Моющее средство «Aos» |
53 |
— |
Вывод: Из исследованных кухонных моющих средств, при всех остальных одинаковых параметрах, влияющих на качество «отмывания», лучше использовать средство «Fairy». Из исследованных стиральных порошков «Миф», т.к. именно их растворы обладают наименьшим поверхностным натяжением. Следовательно, первое средство («Fairy») лучше помогает смывать нерастворимые в воде жиры с посуды, являясь эмульгатором – средством, облегчающим получение эмульсий (взвесей мельчайших частиц жидкого вещества в воде). Второе («Миф») лучше отстирывает бельё, проникая в поры между волокнами тканей. Заметим, что при использовании кухонных моющих средств, мы заставляем вещество (в частности жир) хотя бы на некоторое время растворится в воде, т.к. происходит «дробление» его на мельчайшие частицы. За это время рекомендуется смыть нанесенное моющее средство струей чистой воды, а не ополаскивать посуду через какое-то время в ёмкости. Кроме того исследовали поверхностное натяжение шампуней и гелей для душа. Из-за достаточно высокой вязкости этих жидкостей сложно точно определить коэффициент поверхностного натяжения их, но зато можно сравнить. Были исследованы (методом отрыва капель) шампуни «Pantene», «Schauma» и «Fruttis», а также гели для душа «Sensen», «Монпансье» и «Discover».
Вывод:
-
Поверхностное натяжение уменьшается в шампунях на ряду «Fruttis» — «Schauma» — «Pantene», в гелях – в ряду «Монпансье» — «Discover» — «Senses».
-
Поверхностное натяжение шампуней меньше поверхностного натяжения гелей (Например «Pantene» < «Senses» на 65 мН/м), что оправдывает их назначение: шампуни – для мытья волос, гели – для мытья тела.
-
При всех остальных одинаковых характеристиках, влияющих на качество мытья, из исследованных шампуней лучше использовать «Pantene» (Рис. 9), из исследованных гелей для душа – «Senses»(Рис.10).
Рис. 9
Рис . 10
Метод отрыва капель, не будучи очень точным, однако, используется в медицинской практике. Этим методом определяют в диагностических целях поверхностное натяжение спинномозговой жидкости, желчи и т.д.
Заключение
Выводы:
1. Получены экспериментальные подтверждения теоретических выводов, доказывающие, что однородная жидкость принимает форму с минимальной свободной поверхностью
2. Проведены эксперименты с уменьшением и увеличением поверхностного натяжения, результаты которых доказали, чтомыло и синтетические моющие средства содержат вещества, повышающие смачивающие свойства воды за счет уменьшения силы поверхностного натяжения.
3. Для определения коэффициента поверхностного натяжения жидкостей
а) изучена краткая теория метода отрыва капель;
б) сконструирована и собрана экспериментальная установка;
в) вычислены средние значения коэффициента поверхностного натяжения различных жидкостей, сделаны выводы.
4. Результаты экспериментов и исследования представлены в виде таблицы и фотографий.
Работа над проектом позволила мне приобрести более широкие знания по разделу физики «Поверхностное натяжение».
Мне хочется закончить свой проект словами великого ученого физика
А. Эйнштейна:
«Мне достаточно испытать ощущение вечной тайны жизни, осознавать и интуитивно постигать чудесную структуру всего сущего и активно бороться, чтобы схватить пусть даже самую малую крупинку разума, который проявляется в Природе»
Список использованных источников и литературы
-
http://www.physics.ru/
-
http://greenfuture.ru/
-
http://www.agym.spbu.ru/
-
Буховцев Б.Б., Климонтович Ю. Л., Мякишев Г.Я., Физика, учебник для 9 класса средней школы — 4-е издание – М.: Просвещение, 1988 г. – 271 с.
-
Касьянов В.А., Физика, 10 класс, учебник для общеобразовательных учебных заведений, М.: Дрофа, 2001г. – 410 с.
-
Пинский А.А. Физика: учебник. Пособие для 10 классов с углубленным изучением физики. М.: Просвещение, 1993г. – 416 с.
-
Юфанова И.Л. Занимательные вечера по физике в средней школе: книга для учителя. — М.: Просвещение, 1990г. -215с
-
Чуянов В.Я., Энциклопедический словарь юного физика, М.: Педагогика, 1984г. – 350 с.
11http://www.physics.ru/
2 http://greenfuture.ru
3 www.agym.spbu.ru
16
Просмотров работы: 8452
Surface tension experimental demonstration with soap
Surface tension is the tendency of liquid surfaces at rest to shrink into the minimum surface area possible. Surface tension is what allows objects with a higher density than water such as razor blades and insects (e.g. water striders) to float on a water surface without becoming even partly submerged.
At liquid–air interfaces, surface tension results from the greater attraction of liquid molecules to each other (due to cohesion) than to the molecules in the air (due to adhesion).[1]
There are two primary mechanisms in play. One is an inward force on the surface molecules causing the liquid to contract.[2][3] Second is a tangential force parallel to the surface of the liquid.[3] This tangential force is generally referred to as the surface tension. The net effect is the liquid behaves as if its surface were covered with a stretched elastic membrane. But this analogy must not be taken too far as the tension in an elastic membrane is dependent on the amount of deformation of the membrane while surface tension is an inherent property of the liquid–air or liquid–vapour interface.[4]
Because of the relatively high attraction of water molecules to each other through a web of hydrogen bonds, water has a higher surface tension (72.8 millinewtons (mN) per meter at 20 °C) than most other liquids. Surface tension is an important factor in the phenomenon of capillarity.
Surface tension has the dimension of force per unit length, or of energy per unit area.[4] The two are equivalent, but when referring to energy per unit of area, it is common to use the term surface energy, which is a more general term in the sense that it applies also to solids.
In materials science, surface tension is used for either surface stress or surface energy.
Causes[edit]
Diagram of the cohesive forces on molecules of a liquid
Due to the cohesive forces, a molecule located away from the surface is pulled equally in every direction by neighbouring liquid molecules, resulting in a net force of zero. The molecules at the surface do not have the same molecules on all sides of them and therefore are pulled inward. This creates some internal pressure and forces liquid surfaces to contract to the minimum area.[2]
There is also a tension parallel to the surface at the liquid-air interface which will resist an external force, due to the cohesive nature of water molecules.[2][3]
The forces of attraction acting between molecules of the same type are called cohesive forces, while those acting between molecules of different types are called adhesive forces. The balance between the cohesion of the liquid and its adhesion to the material of the container determines the degree of wetting, the contact angle and the shape of meniscus. When cohesion dominates (specifically, adhesion energy is less than half of cohesion energy) the wetting is low and the meniscus is convex at a vertical wall (as for mercury in a glass container). On the other hand, when adhesion dominates (adhesion energy more than half of cohesion energy) the wetting is high and the similar meniscus is concave (as in water in a glass).
Surface tension is responsible for the shape of liquid droplets. Although easily deformed, droplets of water tend to be pulled into a spherical shape by the imbalance in cohesive forces of the surface layer. In the absence of other forces, drops of virtually all liquids would be approximately spherical. The spherical shape minimizes the necessary «wall tension» of the surface layer according to Laplace’s law.
Water droplet lying on a damask. Surface tension is high enough to prevent seeping through the textile
Another way to view surface tension is in terms of energy. A molecule in contact with a neighbor is in a lower state of energy than if it were alone. The interior molecules have as many neighbors as they can possibly have, but the boundary molecules are missing neighbors (compared to interior molecules) and therefore have a higher energy. For the liquid to minimize its energy state, the number of higher energy boundary molecules must be minimized. The minimized number of boundary molecules results in a minimal surface area.[5]
As a result of surface area minimization, a surface will assume the smoothest shape it can (mathematical proof that «smooth» shapes minimize surface area relies on use of the Euler–Lagrange equation). Since any curvature in the surface shape results in greater area, a higher energy will also result.
Physics[edit]
Physical units[edit]
Surface tension, represented by the symbol γ (alternatively σ or T), is measured in force per unit length. Its SI unit is newton per meter but the cgs unit of dyne per centimeter is also used. For example,[6]
Definition[edit]
This diagram illustrates the force necessary to increase the surface area. This force is proportional to the surface tension.
Surface tension can be defined in terms of force or energy.
In terms of force[edit]
Surface tension γ of a liquid is the force per unit length. In the illustration on the right, the rectangular frame, composed of three unmovable sides (black) that form a «U» shape, and a fourth movable side (blue) that can slide to the right. Surface tension will pull the blue bar to the left; the force F required to hold the movable side is proportional to the length L of the immobile side. Thus the ratio F/L depends only on the intrinsic properties of the liquid (composition, temperature, etc.), not on its geometry. For example, if the frame had a more complicated shape, the ratio F/L, with L the length of the movable side and F the force required to stop it from sliding, is found to be the same for all shapes. We therefore define the surface tension as
The reason for the
1/2 is that the film has two sides (two surfaces), each of which contributes equally to the force; so the force contributed by a single side is γL = F/2.
In terms of energy[edit]
Surface tension γ of a liquid is the ratio of the change in the energy of the liquid to the change in the surface area of the liquid (that led to the change in energy). This can be easily related to the previous definition in terms of force:[7] if F is the force required to stop the side from starting to slide, then this is also the force that would keep the side in the state of sliding at a constant speed (by Newton’s Second Law). But if the side is moving to the right (in the direction the force is applied), then the surface area of the stretched liquid is increasing while the applied force is doing work on the liquid. This means that increasing the surface area increases the energy of the film. The work done by the force F in moving the side by distance Δx is W = FΔx; at the same time the total area of the film increases by ΔA = 2LΔx (the factor of 2 is here because the liquid has two sides, two surfaces). Thus, multiplying both the numerator and the denominator of γ = 1/2F/L by Δx, we get
This work W is, by the usual arguments, interpreted as being stored as potential energy. Consequently, surface tension can be also measured in SI system as joules per square meter and in the cgs system as ergs per cm2. Since mechanical systems try to find a state of minimum potential energy, a free droplet of liquid naturally assumes a spherical shape, which has the minimum surface area for a given volume.
The equivalence of measurement of energy per unit area to force per unit length can be proven by dimensional analysis.[8]
Effects[edit]
Water[edit]
Several effects of surface tension can be seen with ordinary water:
- Beading of rain water on a waxy surface, such as a leaf. Water adheres weakly to wax and strongly to itself, so water clusters into drops. Surface tension gives them their near-spherical shape, because a sphere has the smallest possible surface area to volume ratio.
- Formation of drops occurs when a mass of liquid is stretched. The animation (below) shows water adhering to the faucet gaining mass until it is stretched to a point where the surface tension can no longer keep the drop linked to the faucet. It then separates and surface tension forms the drop into a sphere. If a stream of water were running from the faucet, the stream would break up into drops during its fall. Gravity stretches the stream, then surface tension pinches it into spheres.[9]
- Flotation of objects denser than water occurs when the object is nonwettable and its weight is small enough to be borne by the forces arising from surface tension.[5] For example, water striders use surface tension to walk on the surface of a pond in the following way. The nonwettability of the water strider’s leg means there is no attraction between molecules of the leg and molecules of the water, so when the leg pushes down on the water, the surface tension of the water only tries to recover its flatness from its deformation due to the leg. This behavior of the water pushes the water strider upward so it can stand on the surface of the water as long as its mass is small enough that the water can support it. The surface of the water behaves like an elastic film: the insect’s feet cause indentations in the water’s surface, increasing its surface area[10] and tendency of minimization of surface curvature (so area) of the water pushes the insect’s feet upward.
- Separation of oil and water (in this case, water and liquid wax) is caused by a tension in the surface between dissimilar liquids. This type of surface tension is called «interface tension», but its chemistry is the same.
- Tears of wine is the formation of drops and rivulets on the side of a glass containing an alcoholic beverage. Its cause is a complex interaction between the differing surface tensions of water and ethanol; it is induced by a combination of surface tension modification of water by ethanol together with ethanol evaporating faster than water.
-
A. Water beading on a leaf
-
B. Water dripping from a tap
-
C. Water striders stay at the top of liquid because of surface tension
-
D. Lava lamp with interaction between dissimilar liquids: water and liquid wax
Surfactants[edit]
Surface tension is visible in other common phenomena, especially when surfactants are used to decrease it:
- Soap bubbles have very large surface areas with very little mass. Bubbles in pure water are unstable. The addition of surfactants, however, can have a stabilizing effect on the bubbles (see Marangoni effect). Note that surfactants actually reduce the surface tension of water by a factor of three or more.
- Emulsions are a type of colloid in which surface tension plays a role. Tiny fragments of oil suspended in pure water will spontaneously assemble themselves into much larger masses. But the presence of a surfactant provides a decrease in surface tension, which permits stability of minute droplets of oil in the bulk of water (or vice versa).
Surface curvature and pressure[edit]
Surface tension forces acting on a tiny (differential) patch of surface. δθx and δθy indicate the amount of bend over the dimensions of the patch. Balancing the tension forces with pressure leads to the Young–Laplace equation
If no force acts normal to a tensioned surface, the surface must remain flat. But if the pressure on one side of the surface differs from pressure on the other side, the pressure difference times surface area results in a normal force. In order for the surface tension forces to cancel the force due to pressure, the surface must be curved. The diagram shows how surface curvature of a tiny patch of surface leads to a net component of surface tension forces acting normal to the center of the patch. When all the forces are balanced, the resulting equation is known as the Young–Laplace equation:[11]
where:
- Δp is the pressure difference, known as the Laplace pressure.[12]
- γ is surface tension.
- Rx and Ry are radii of curvature in each of the axes that are parallel to the surface.
The quantity in parentheses on the right hand side is in fact (twice) the mean curvature of the surface (depending on normalisation).
Solutions to this equation determine the shape of water drops, puddles, menisci, soap bubbles, and all other shapes determined by surface tension (such as the shape of the impressions that a water strider’s feet make on the surface of a pond).
The table below shows how the internal pressure of a water droplet increases with decreasing radius. For not very small drops the effect is subtle, but the pressure difference becomes enormous when the drop sizes approach the molecular size. (In the limit of a single molecule the concept becomes meaningless.)
| Droplet radius | 1 mm | 0.1 mm | 1 μm | 10 nm |
|---|---|---|---|---|
| Δp (atm) | 0.0014 | 0.0144 | 1.436 | 143.6 |
Floating objects[edit]
Cross-section of a needle floating on the surface of water. Fw is the weight and Fs are surface tension resultant forces.
When an object is placed on a liquid, its weight Fw depresses the surface, and if surface tension and downward force become equal then it is balanced by the surface tension forces on either side Fs, which are each parallel to the water’s surface at the points where it contacts the object. Notice that small movement in the body may cause the object to sink. As the angle of contact decreases, surface tension decreases. The horizontal components of the two Fs arrows point in opposite directions, so they cancel each other, but the vertical components point in the same direction and therefore add up[5] to balance Fw. The object’s surface must not be wettable for this to happen, and its weight must be low enough for the surface tension to support it. If m denotes the mass of the needle and g acceleration due to gravity, we have
Liquid surface[edit]
To find the shape of the minimal surface bounded by some arbitrary shaped frame using strictly mathematical means can be a daunting task. Yet by fashioning the frame out of wire and dipping it in soap-solution, a locally minimal surface will appear in the resulting soap-film within seconds.[8][13]
The reason for this is that the pressure difference across a fluid interface is proportional to the mean curvature, as seen in the Young–Laplace equation. For an open soap film, the pressure difference is zero, hence the mean curvature is zero, and minimal surfaces have the property of zero mean curvature.
Contact angles[edit]
The surface of any liquid is an interface between that liquid and some other medium.[note 1] The top surface of a pond, for example, is an interface between the pond water and the air. Surface tension, then, is not a property of the liquid alone, but a property of the liquid’s interface with another medium. If a liquid is in a container, then besides the liquid/air interface at its top surface, there is also an interface between the liquid and the walls of the container. The surface tension between the liquid and air is usually different (greater) than its surface tension with the walls of a container. And where the two surfaces meet, their geometry must be such that all forces balance.[8][11]
Forces at contact point shown for contact angle greater than 90° (left) and less than 90° (right)
Where the two surfaces meet, they form a contact angle, θ, which is the angle the tangent to the surface makes with the solid surface. Note that the angle is measured through the liquid, as shown in the diagrams above. The diagram to the right shows two examples. Tension forces are shown for the liquid–air interface, the liquid–solid interface, and the solid–air interface. The example on the left is where the difference between the liquid–solid and solid–air surface tension, γls − γsa, is less than the liquid–air surface tension, γla, but is nevertheless positive, that is
In the diagram, both the vertical and horizontal forces must cancel exactly at the contact point, known as equilibrium. The horizontal component of fla is canceled by the adhesive force, fA.[8]
The more telling balance of forces, though, is in the vertical direction. The vertical component of fla must exactly cancel the difference of the forces along the solid surface, fls − fsa.[8]
| Liquid | Solid | Contact angle |
|||
|---|---|---|---|---|---|
| water |
|
0° | |||
| ethanol | |||||
| diethyl ether | |||||
| carbon tetrachloride | |||||
| glycerol | |||||
| acetic acid | |||||
| water | paraffin wax | 107° | |||
| silver | 90° | ||||
| methyl iodide | soda-lime glass | 29° | |||
| lead glass | 30° | ||||
| fused quartz | 33° | ||||
| mercury | soda-lime glass | 140° |
Since the forces are in direct proportion to their respective surface tensions, we also have:[11]
where
- γls is the liquid–solid surface tension,
- γla is the liquid–air surface tension,
- γsa is the solid–air surface tension,
- θ is the contact angle, where a concave meniscus has contact angle less than 90° and a convex meniscus has contact angle of greater than 90°.[8]
This means that although the difference between the liquid–solid and solid–air surface tension, γls − γsa, is difficult to measure directly, it can be inferred from the liquid–air surface tension, γla, and the equilibrium contact angle, θ, which is a function of the easily measurable advancing and receding contact angles (see main article contact angle).
This same relationship exists in the diagram on the right. But in this case we see that because the contact angle is less than 90°, the liquid–solid/solid–air surface tension difference must be negative:
Special contact angles[edit]
Observe that in the special case of a water–silver interface where the contact angle is equal to 90°, the liquid–solid/solid–air surface tension difference is exactly zero.
Another special case is where the contact angle is exactly 180°. Water with specially prepared Teflon approaches this.[11] Contact angle of 180° occurs when the liquid–solid surface tension is exactly equal to the liquid–air surface tension.
Liquid in a vertical tube[edit]
An old style mercury barometer consists of a vertical glass tube about 1 cm in diameter partially filled with mercury, and with a vacuum (called Torricelli’s vacuum) in the unfilled volume (see diagram to the right). Notice that the mercury level at the center of the tube is higher than at the edges, making the upper surface of the mercury dome-shaped. The center of mass of the entire column of mercury would be slightly lower if the top surface of the mercury were flat over the entire cross-section of the tube. But the dome-shaped top gives slightly less surface area to the entire mass of mercury. Again the two effects combine to minimize the total potential energy. Such a surface shape is known as a convex meniscus.
We consider the surface area of the entire mass of mercury, including the part of the surface that is in contact with the glass, because mercury does not adhere to glass at all. So the surface tension of the mercury acts over its entire surface area, including where it is in contact with the glass. If instead of glass, the tube was made out of copper, the situation would be very different. Mercury aggressively adheres to copper. So in a copper tube, the level of mercury at the center of the tube will be lower than at the edges (that is, it would be a concave meniscus). In a situation where the liquid adheres to the walls of its container, we consider the part of the fluid’s surface area that is in contact with the container to have negative surface tension. The fluid then works to maximize the contact surface area. So in this case increasing the area in contact with the container decreases rather than increases the potential energy. That decrease is enough to compensate for the increased potential energy associated with lifting the fluid near the walls of the container.
Illustration of capillary rise and fall. Red=contact angle less than 90°; blue=contact angle greater than 90°
If a tube is sufficiently narrow and the liquid adhesion to its walls is sufficiently strong, surface tension can draw liquid up the tube in a phenomenon known as capillary action. The height to which the column is lifted is given by Jurin’s law:[8]
where
- h is the height the liquid is lifted,
- γla is the liquid–air surface tension,
- ρ is the density of the liquid,
- r is the radius of the capillary,
- g is the acceleration due to gravity,
- θ is the angle of contact described above. If θ is greater than 90°, as with mercury in a glass container, the liquid will be depressed rather than lifted.
Puddles on a surface[edit]
Profile curve of the edge of a puddle where the contact angle is 180°. The curve is given by the formula:[11]
where
Small puddles of water on a smooth clean surface have perceptible thickness.
Pouring mercury onto a horizontal flat sheet of glass results in a puddle that has a perceptible thickness. The puddle will spread out only to the point where it is a little under half a centimetre thick, and no thinner. Again this is due to the action of mercury’s strong surface tension. The liquid mass flattens out because that brings as much of the mercury to as low a level as possible, but the surface tension, at the same time, is acting to reduce the total surface area. The result of the compromise is a puddle of a nearly fixed thickness.
The same surface tension demonstration can be done with water, lime water or even saline, but only on a surface made of a substance to which water does not adhere. Wax is such a substance. Water poured onto a smooth, flat, horizontal wax surface, say a waxed sheet of glass, will behave similarly to the mercury poured onto glass.
The thickness of a puddle of liquid on a surface whose contact angle is 180° is given by:[11]
where
- h is the depth of the puddle in centimeters or meters.
- γ is the surface tension of the liquid in dynes per centimeter or newtons per meter.
- g is the acceleration due to gravity and is equal to 980 cm/s2 or 9.8 m/s2
- ρ is the density of the liquid in grams per cubic centimeter or kilograms per cubic meter
Illustration of how lower contact angle leads to reduction of puddle depth
In reality, the thicknesses of the puddles will be slightly less than what is predicted by the above formula because very few surfaces have a contact angle of 180° with any liquid. When the contact angle is less than 180°, the thickness is given by:[11]
For mercury on glass, γHg = 487 dyn/cm, ρHg = 13.5 g/cm3 and θ = 140°, which gives hHg = 0.36 cm. For water on paraffin at 25 °C, γ = 72 dyn/cm, ρ = 1.0 g/cm3, and θ = 107° which gives hH2O = 0.44 cm.
The formula also predicts that when the contact angle is 0°, the liquid will spread out into a micro-thin layer over the surface. Such a surface is said to be fully wettable by the liquid.
The breakup of streams into drops[edit]
Breakup of an elongated stream of water into droplets due to surface tension.
In day-to-day life all of us observe that a stream of water emerging from a faucet will break up into droplets, no matter how smoothly the stream is emitted from the faucet. This is due to a phenomenon called the Plateau–Rayleigh instability,[11] which is entirely a consequence of the effects of surface tension.
The explanation of this instability begins with the existence of tiny perturbations in the stream. These are always present, no matter how smooth the stream is. If the perturbations are resolved into sinusoidal components, we find that some components grow with time while others decay with time. Among those that grow with time, some grow at faster rates than others. Whether a component decays or grows, and how fast it grows is entirely a function of its wave number (a measure of how many peaks and troughs per centimeter) and the radii of the original cylindrical stream.
Gallery[edit]
-
Breakup of a moving sheet of water bouncing off of a spoon.
-
Photo of flowing water adhering to a hand. Surface tension creates the sheet of water between the flow and the hand.
-
Surface tension prevents a coin from sinking: the coin is indisputably denser than water, so it must be displacing a volume greater than its own for buoyancy to balance mass.
-
An aluminium coin floats on the surface of the water at 10 °C. Any extra weight would drop the coin to the bottom.
-
A daisy. The entirety of the flower lies below the level of the (undisturbed) free surface. The water rises smoothly around its edge. Surface tension prevents water from displacing the air between the petals and possibly submerging the flower.
-
A metal paper clip floats on water. Several can usually be carefully added without overflow of water.
-
A metal paperclip floating on water. A grille in front of the light has created the ‘contour lines’ which show the deformation in the water surface caused by the metal paper clip.
Thermodynamics[edit]
Thermodynamic theories of surface tension[edit]
J.W. Gibbs developed the thermodynamic theory of capillarity based
on the idea of surfaces of discontinuity.[14] Gibbs considered the case of a sharp mathematical surface being placed somewhere within the microscopically fuzzy physical interface that exists between two homogeneous substances. Realizing that the exact choice of the surface’s location was somewhat arbitrary, he left it flexible. Since the interface exists in thermal and chemical equilibrium with the substances around it (having temperature T and chemical potentials μi), Gibbs considered the case where the surface may have excess energy, excess entropy, and excess particles, finding the natural free energy function in this case to be 

Gibbs’ placement of a precise mathematical surface in a fuzzy physical interface.
Considering a given subvolume 







For sufficiently macroscopic and gently curved surfaces, the surface free energy must simply be proportional to the surface area:[14][15]
for surface tension 

As stated above, this implies the mechanical work needed to increase a surface area A is dW = γ dA, assuming the volumes on each side do not change. Thermodynamics requires that for systems held at constant chemical potential and temperature, all spontaneous changes of state are accompanied by a decrease in this free energy 
Gibbs and other scientists have wrestled with the arbitrariness in the exact microscopic placement of the surface.[16] For microscopic surfaces with very tight curvatures, it is not correct to assume the surface tension is independent of size, and topics like the Tolman length come into play. For a macroscopic sized surface (and planar surfaces), the surface placement does not have a significant effect on γ however it does have a very strong effect on the values of the surface entropy, surface excess mass densities, and surface internal energy,[14]: 237 which are the partial derivatives of the surface tension function 
Gibbs emphasized that for solids, the surface free energy may be completely different from surface stress (what he called surface tension):[14]: 315 the surface free energy is the work required to form the surface, while surface stress is the work required to stretch the surface. In the case of a two-fluid interface, there is no distinction between forming and stretching because the fluids and the surface completely replenish their nature when the surface is stretched. For a solid, stretching the surface, even elastically, results in a fundamentally changed surface. Further, the surface stress on a solid is a directional quantity (a stress tensor) while surface energy is scalar.
Fifteen years after Gibbs, J.D. van der Waals developed the theory of capillarity effects based on the hypothesis of a continuous variation of density.[17] He added to the energy density the term 
Thermodynamics of bubbles[edit]
The pressure inside an ideal spherical bubble can be derived from thermodynamic free energy considerations.[15] The above free energy can be written as:
where 

For a spherical bubble, the volume and surface area are given simply by
and
Substituting these relations into the previous expression, we find
which is equivalent to the Young–Laplace equation when Rx = Ry.
Influence of temperature[edit]
Temperature dependence of the surface tension between the liquid and vapor phases of pure water
Temperature dependency of the surface tension of benzene
Surface tension is dependent on temperature. For that reason, when a value is given for the surface tension of an interface, temperature must be explicitly stated. The general trend is that surface tension decreases with the increase of temperature, reaching a value of 0 at the critical temperature. For further details see Eötvös rule. There are only empirical equations to relate surface tension and temperature:
- Eötvös:[21][22][23]
Here V is the molar volume of a substance, TC is the critical temperature and k is a constant valid for almost all substances.[21] A typical value is k = 2.1×10−7 J K−1 mol−2⁄3.[21][23] For water one can further use V = 18 ml/mol and TC = 647 K (374 °C).[24] A variant on Eötvös is described by Ramay and Shields:[25]
where the temperature offset of 6 K provides the formula with a better fit to reality at lower temperatures.
- Guggenheim–Katayama:[22]
γ° is a constant for each liquid and n is an empirical factor, whose value is 11/9 for organic liquids. This equation was also proposed by van der Waals, who further proposed that γ° could be given by the expression
where K2 is a universal constant for all liquids, and PC is the critical pressure of the liquid (although later experiments found K2 to vary to some degree from one liquid to another).[22]
Both Guggenheim–Katayama and Eötvös take into account the fact that surface tension reaches 0 at the critical temperature, whereas Ramay and Shields fails to match reality at this endpoint.
Influence of solute concentration[edit]
Solutes can have different effects on surface tension depending on the nature of the surface and the solute:
- Little or no effect, for example sugar at water|air, most organic compounds at oil/air
- Increase surface tension, most inorganic salts at water|air
- Non-monotonic change, most inorganic acids at water|air
- Decrease surface tension progressively, as with most amphiphiles, e.g., alcohols at water|air
- Decrease surface tension until certain critical concentration, and no effect afterwards: surfactants that form micelles
What complicates the effect is that a solute can exist in a different concentration at the surface of a solvent than in its bulk. This difference varies from one solute–solvent combination to another.
Gibbs isotherm states that:
- Γ is known as surface concentration, it represents excess of solute per unit area of the surface over what would be present if the bulk concentration prevailed all the way to the surface. It has units of mol/m2
- C is the concentration of the substance in the bulk solution.
- R is the gas constant and T the temperature
Certain assumptions are taken in its deduction, therefore Gibbs isotherm can only be applied to ideal (very dilute) solutions with two components.
Influence of particle size on vapor pressure[edit]
The Clausius–Clapeyron relation leads to another equation also attributed to Kelvin, as the Kelvin equation. It explains why, because of surface tension, the vapor pressure for small droplets of liquid in suspension is greater than standard vapor pressure of that same liquid when the interface is flat. That is to say that when a liquid is forming small droplets, the equilibrium concentration of its vapor in its surroundings is greater. This arises because the pressure inside the droplet is greater than outside.[25]
Molecules on the surface of a tiny droplet (left) have, on average, fewer neighbors than those on a flat surface (right). Hence they are bound more weakly to the droplet than are flat-surface molecules.
- Pv° is the standard vapor pressure for that liquid at that temperature and pressure.
- V is the molar volume.
- R is the gas constant
- rk is the Kelvin radius, the radius of the droplets.
The effect explains supersaturation of vapors. In the absence of nucleation sites, tiny droplets must form before they can evolve into larger droplets. This requires a vapor pressure many times the vapor pressure at the phase transition point.[25]
This equation is also used in catalyst chemistry to assess mesoporosity for solids.[26]
The effect can be viewed in terms of the average number of molecular neighbors of surface molecules (see diagram).
The table shows some calculated values of this effect for water at different drop sizes:
| P/P0 for water drops of different radii at STP[22] | ||||
|---|---|---|---|---|
| Droplet radius (nm) | 1000 | 100 | 10 | 1 |
| P/P0 | 1.001 | 1.011 | 1.114 | 2.95 |
The effect becomes clear for very small drop sizes, as a drop of 1 nm radius has about 100 molecules inside, which is a quantity small enough to require a quantum mechanics analysis.
Methods of measurement[edit]
Because surface tension manifests itself in various effects, it offers a number of paths to its measurement. Which method is optimal depends upon the nature of the liquid being measured, the conditions under which its tension is to be measured, and the stability of its surface when it is deformed. An instrument that measures surface tension is called tensiometer.
- Du Noüy ring method: The traditional method used to measure surface or interfacial tension. Wetting properties of the surface or interface have little influence on this measuring technique. Maximum pull exerted on the ring by the surface is measured.[21]
- Wilhelmy plate method: A universal method especially suited to check surface tension over long time intervals. A vertical plate of known perimeter is attached to a balance, and the force due to wetting is measured.
- Spinning drop method: This technique is ideal for measuring low interfacial tensions. The diameter of a drop within a heavy phase is measured while both are rotated.
- Pendant drop method: Surface and interfacial tension can be measured by this technique, even at elevated temperatures and pressures. Geometry of a drop is analyzed optically. For pendant drops the maximum diameter and the ratio between this parameter and the diameter at the distance of the maximum diameter from the drop apex has been used to evaluate the size and shape parameters in order to determine surface tension.
- Bubble pressure method (Jaeger’s method): A measurement technique for determining surface tension at short surface ages. Maximum pressure of each bubble is measured.
- Drop volume method: A method for determining interfacial tension as a function of interface age. Liquid of one density is pumped into a second liquid of a different density and time between drops produced is measured.
- Capillary rise method: The end of a capillary is immersed into the solution. The height at which the solution reaches inside the capillary is related to the surface tension by the equation discussed below.[27].]]
- Stalagmometric method: A method of weighting and reading a drop of liquid.
- Sessile drop method: A method for determining surface tension and density by placing a drop on a substrate and measuring the contact angle (see Sessile drop technique).[28]
- Du Noüy–Padday method: A minimized version of Du Noüy method uses a small diameter metal needle instead of a ring, in combination with a high sensitivity microbalance to record maximum pull. The advantage of this method is that very small sample volumes (down to few tens of microliters) can be measured with very high precision, without the need to correct for buoyancy (for a needle or rather, rod, with proper geometry). Further, the measurement can be performed very quickly, minimally in about 20 seconds.
- Vibrational frequency of levitated drops: The natural frequency of vibrational oscillations of magnetically levitated drops has been used to measure the surface tension of superfluid 4He. This value is estimated to be 0.375 dyn/cm at T = 0 K.[29]
- Resonant oscillations of spherical and hemispherical liquid drop: The technique is based on measuring the resonant frequency of spherical and hemispherical pendant droplets driven in oscillations by a modulated electric field. The surface tension and viscosity can be evaluated from the obtained resonant curves.[30][31][32]
- Drop-bounce method: This method is based on aerodynamic levitation with a split-able nozzle design. After dropping a stably levitated droplet onto a platform, the sample deforms and bounces back, oscillating in mid-air as it tries to minimize its surface area. Through this oscillation behavior, the liquid’s surface tension and viscosity can be measured. [33]
- By smartphone: Some smartphones can be used to measure the surface tension of a transparent liquid. The method is based on measuring the wavelength of capillary waves of known frequency. The smartphone is placed on top of a cup with the liquid. Then smartphone’s vibro-motor excites (through the cup) capillary ripples on the surface of the liquid, which are captured by smartphone’s camera.[34]
Values[edit]
Data table[edit]
| Liquid | Temperature (°C) | Surface tension, γ |
|---|---|---|
| Acetic acid | 20 | 27.60 |
| Acetic acid (45.1%) + Water | 30 | 40.68 |
| Acetic acid (10.0%) + Water | 30 | 54.56 |
| Acetone | 20 | 23.70 |
| Blood | 22 | 55.89 |
| Diethyl ether | 20 | 17.00 |
| Ethanol | 20 | 22.27 |
| Ethanol (40%) + Water | 25 | 29.63 |
| Ethanol (11.1%) + Water | 25 | 46.03 |
| Glycerol | 20 | 63.00 |
| n-Hexane | 20 | 18.40 |
| Hydrochloric acid 17.7 M aqueous solution | 20 | 65.95 |
| Isopropanol | 20 | 21.70 |
| Liquid helium II | −273 | 0.37[36] |
| Liquid nitrogen | −196 | 8.85 |
| Liquid oxygen | −182 | 13.2 |
| Mercury | 15 | 487.00 |
| Methanol | 20 | 22.60 |
| Molten Silver chloride | 650 | 163[37] |
| Molten Sodium chloride/Calcium chloride (47/53 mole %) | 650 | 139[38] |
| n-Octane | 20 | 21.80 |
| Sodium chloride 6.0 M aqueous solution | 20 | 82.55 |
| Sucrose (55%) + water | 20 | 76.45 |
| Water | 0 | 75.64 |
| Water | 25 | 71.97 |
| Water | 50 | 67.91 |
| Water | 100 | 58.85 |
| Toluene | 25 | 27.73 |
Surface tension of water[edit]
The surface tension of pure liquid water in contact with its vapor has been given by IAPWS[39] as
where both T and the critical temperature TC = 647.096 K are expressed in kelvins. The region of validity the entire vapor–liquid saturation curve, from the triple point (0.01 °C) to the critical point. It also provides reasonable results when extrapolated to metastable (supercooled) conditions, down to at least −25 °C. This formulation was originally adopted by IAPWS in 1976 and was adjusted in 1994 to conform to the International Temperature Scale of 1990.
The uncertainty of this formulation is given over the full range of temperature by IAPWS.[39] For temperatures below 100 °C, the uncertainty is ±0.5%.
Surface tension of seawater[edit]
Nayar et al.[40] published reference data for the surface tension of seawater over the salinity range of 20 ≤ S ≤ 131 g/kg and a temperature range of 1 ≤ t ≤ 92 °C at atmospheric pressure. The range of temperature and salinity encompasses both the oceanographic range and the range of conditions encountered in thermal desalination technologies. The uncertainty of the measurements varied from 0.18 to 0.37 mN/m with the average uncertainty being 0.22 mN/m.
Nayar et al. correlated the data with the following equation
where γsw is the surface tension of seawater in mN/m, γw is the surface tension of water in mN/m, S is the reference salinity[41] in g/kg, and t is temperature in degrees Celsius. The average absolute percentage deviation between measurements and the correlation was 0.19% while the maximum deviation is 0.60%.
The International Association for the Properties of Water and Steam (IAPWS) has adopted this correlation as an international standard guideline.[42]
See also[edit]
- Anti-fog
- Capillary wave — short waves on a water surface, governed by surface tension and inertia
- Cheerio effect — the tendency for small wettable floating objects to attract one another.
- Cohesion
- Dimensionless numbers
- Bond number or Eötvös number
- Capillary number
- Marangoni number
- Weber number
- Dortmund Data Bank — contains experimental temperature-dependent surface tensions
- Electrodipping force
- Electrowetting
- Electrocapillarity
- Eötvös rule — a rule for predicting surface tension dependent on temperature
- Fluid pipe
- Hydrostatic equilibrium—the effect of gravity pulling matter into a round shape
- Interface (chemistry)
- Meniscus — surface curvature formed by a liquid in a container
- Mercury beating heart — a consequence of inhomogeneous surface tension
- Microfluidics
- Sessile drop technique
- Sow-Hsin Chen
- Specific surface energy — same as surface tension in isotropic materials.
- Spinning drop method
- Stalagmometric method
- Surface pressure
- Surface science
- Surface tension biomimetics
- Surface tension values
- Surfactants — substances which reduce surface tension.
- Szyszkowski equation — calculating surface tension of aqueous solutions
- Tears of wine — the surface tension induced phenomenon seen on the sides of glasses containing alcoholic beverages.
- Tolman length — leading term in correcting the surface tension for curved surfaces.
- Wetting and dewetting
Explanatory notes[edit]
- ^ In a mercury barometer, the upper liquid surface is an interface between the liquid and a vacuum containing some molecules of evaporated liquid.
References[edit]
- ^ «Surface Tension — an overview | ScienceDirect Topics». www.sciencedirect.com. Archived from the original on 2021-12-30. Retrieved 2021-12-30.
- ^ a b c «Surface Tension (Water Properties) – USGS Water Science School». US Geological Survey. July 2015. Archived from the original on October 7, 2015. Retrieved November 6, 2015.
- ^ a b c Berry, M V (1971). «The molecular mechanism of surface tension» (PDF). Physics Education. 6 (2): 79–84. Bibcode:1971PhyEd…6…79B. doi:10.1088/0031-9120/6/2/001. S2CID 250797804. Archived (PDF) from the original on 31 December 2021. Retrieved 8 July 2020.
- ^ a b Halliday, David; Resnick, Robert; Krane, Kenneth S. (2010-04-20). Physics, Volume 2. John Wiley & Sons. p. 342. ISBN 978-0-471-40194-0. Archived from the original on 2022-09-22. Retrieved 2021-03-19.
- ^ a b c White, Harvey E. (1948). Modern College Physics. van Nostrand. ISBN 978-0-442-29401-4.
- ^ Bush, John W. M. (April 2004). «MIT Lecture Notes on Surface Tension, lecture 1» (PDF). Massachusetts Institute of Technology. Archived (PDF) from the original on March 8, 2022. Retrieved April 1, 2007.
- ^ «Mechanical definition of surface tension». MIT. Archived from the original on April 12, 2013. Retrieved Dec 16, 2013.
- ^ a b c d e f g h Sears, Francis Weston; Zemanski, Mark W. (1955) University Physics 2nd ed. Addison Wesley
- ^ Bush, John W. M. (May 2004). «MIT Lecture Notes on Surface Tension, lecture 5» (PDF). Massachusetts Institute of Technology. Archived (PDF) from the original on February 26, 2007. Retrieved April 1, 2007.
- ^ Bush, John W. M. (May 2004). «MIT Lecture Notes on Surface Tension, lecture 3» (PDF). Massachusetts Institute of Technology. Archived (PDF) from the original on February 26, 2007. Retrieved April 1, 2007.
- ^ a b c d e f g h Pierre-Gilles de Gennes; Françoise Brochard-Wyart; David Quéré (2002). Capillarity and Wetting Phenomena—Drops, Bubbles, Pearls, Waves. Alex Reisinger. Springer. ISBN 978-0-387-00592-8.
- ^ Butt, Hans-Jürgen; Graf, Karlheinz; Kappl, Michael (2006). Physics and Chemistry of Interfaces. Wiley. p. 9. ISBN 978-3-527-60640-5.
- ^ Aaronson, Scott (March 2005) NP-complete Problems and Physical Reality Archived 2018-02-23 at the Wayback Machine. ACM SIGACT News
- ^ a b c d Gibbs, J.W. (2002) [1876–1878], «On the Equilibrium of Heterogeneous Substances», in Bumstead, H.A.; Van Nameeds, R.G. (eds.), The Scientific Papers of J. Willard Gibbs, vol. 1, Woodbridge, CT: Ox Bow Press, pp. 55–354, ISBN 978-0918024770
- ^ a b Landau; Lifshitz (1980). Course of Theoretical Physics Volume 5: Statistical Physics I (3 ed.). Pergamon. pp. 517–537.
- ^ Rusanov, A (2005). «Surface thermodynamics revisited». Surface Science Reports. 58 (5–8): 111–239. Bibcode:2005SurSR..58..111R. doi:10.1016/j.surfrep.2005.08.002. ISSN 0167-5729.
- ^ van der Waals, J.D. (1979) [1893], translated by Rowlinson, J.S., «The thermodynamic theory of capillarity under the hypothesis of a continuous variation of density», J. Stat. Phys., 20 (2): 197–200, Bibcode:1979JSP….20..197R, doi:10.1007/BF01011513, S2CID 122954999
- ^ Cahn, J.W.; Hilliard, J.E. (1958), «Free energy of a nonuniform system. I. Interfacial free energy», J. Chem. Phys., 28 (2): 258–266, Bibcode:1958JChPh..28..258C, doi:10.1063/1.1744102
- ^ Langer, J.S.; Bar-On, M.; Miller, H.D. (1975), «New computational method in the theory of spinodal decomposition», Phys. Rev. A, 11 (4): 1417–1429, Bibcode:1975PhRvA..11.1417L, doi:10.1103/PhysRevA.11.1417
- ^
Gorban, A.N.; Karlin, I. V. (2016), «Beyond Navier–Stokes equations: capillarity of ideal gas», Contemporary Physics (Review article), 58 (1): 70–90, arXiv:1702.00831, Bibcode:2017ConPh..58…70G, doi:10.1080/00107514.2016.1256123, S2CID 55317543 - ^ a b c d «Surface Tension by the Ring Method (Du Nouy Method)» (PDF). PHYWE. Archived (PDF) from the original on 2007-09-27. Retrieved 2007-09-08.
- ^ a b c d Adam, Neil Kensington (1941). The Physics and Chemistry of Surfaces, 3rd ed. Oxford University Press.
- ^ a b «Physical Properties Sources Index: Eötvös Constant». Archived from the original on 2011-07-06. Retrieved 2008-11-16.
- ^ Vargaftik, N. B.; Volkov, B. N.; Voljak, L. D. (1983). «International Tables of the Surface Tension of Water» (PDF). Journal of Physical and Chemical Reference Data. 12 (3): 817. Bibcode:1983JPCRD..12..817V. doi:10.1063/1.555688. Archived from the original (PDF) on 2016-12-21. Retrieved 2017-07-13.
- ^ a b c Moore, Walter J. (1962). Physical Chemistry, 3rd ed. Prentice Hall.
- ^ Ertl, G.; Knözinger, H. and Weitkamp, J. (1997). Handbook of heterogeneous catalysis, Vol. 2, p. 430. Wiley-VCH, Weinheim. ISBN 3-527-31241-2
- ^ Calvert, James B. «Surface Tension (physics lecture notes)». University of Denver. Archived from the original on 2007-09-15. Retrieved 2007-09-08.
- ^ «Sessile Drop Method». Dataphysics. Archived from the original on August 8, 2007. Retrieved 2007-09-08.
- ^ Vicente, C.; Yao, W.; Maris, H.; Seidel, G. (2002). «Surface tension of liquid 4He as measured using the vibration modes of a levitated drop». Physical Review B. 66 (21): 214504. Bibcode:2002PhRvB..66u4504V. doi:10.1103/PhysRevB.66.214504.
- ^ Zografov, Nikolay (2014). «Droplet oscillations driven by an electric field». Colloids and Surfaces A: Physicochemical and Engineering Aspects. 460: 351–354. doi:10.1016/j.colsurfa.2013.12.013.
- ^ Tankovsky, N. (2013). «Electrically Driven Resonant Oscillations of Pendant Hemispherical Liquid Droplet and Possibility to Evaluate the Surface Tension in Real Time». Zeitschrift für Physikalische Chemie. 227 (12): 1759–1766. doi:10.1524/zpch.2013.0420. S2CID 101722165.
- ^ Tankovsky, Nikolay (2011). «Oscillations of a Hanging Liquid Drop, Driven by Interfacial Dielectric Force». Zeitschrift für Physikalische Chemie. 225 (4): 405–411. doi:10.1524/zpch.2011.0074. S2CID 101625925.
- ^ Sun, Yifan; Muta, Hiroaki; Ohishi, Yuji (June 2021). «Novel Method for Surface Tension Measurement: the Drop-Bounce Method». Microgravity Science and Technology. 33 (3): 32. Bibcode:2021MicST..33…32S. doi:10.1007/s12217-021-09883-7.
- ^ Yue, Shichao; Katabi, Dina (2021). «Liquid testing with your smartphone». Communications of the ACM. 64 (10): 75–83. doi:10.1145/3481038. ISSN 0001-0782.
- ^ Lange’s Handbook of Chemistry (1967) 10th ed. pp 1661–1665 ISBN 0-07-016190-9 (11th ed.)
- ^ Brouwer, W; Pathria, R. K (1967). «On the Surface Tension of Liquid Helium II». Physical Review. 163 (1): 200–205. Bibcode:1967PhRv..163..200B. doi:10.1103/PhysRev.163.200.
- ^ Moser, Z; Gasior, W; Rzyman, K (1982). «Activities and Surface Tension of Liquid AgCl-KCl Solutions». Journal of the Electrochemical Society. 129 (3): 502–506. doi:10.1149/1.2131529.
- ^ Addison, C; Coldrey, J (1960). «Influence of Surface Reactions on the Interface Between Liquid Sodium and Molten Sodium Chloride + Calcium Chloride Mixtures». Transactions of the Faraday Society. 56: 840–845. doi:10.1039/tf9605600840.
- ^ a b International Association for the Properties of Water and Steam (June 2014). «Revised Release on Surface Tension of Ordinary Water Substance». Archived from the original on 2016-04-04. Retrieved 2016-02-20.
- ^ Nayar, K. G; Panchanathan, D; McKinley, G. H; Lienhard, J. H (November 2014). «Surface tension of seawater» (PDF). J. Phys. Chem. Ref. Data. 43 (4): 43103. Bibcode:2014JPCRD..43d3103N. doi:10.1063/1.4899037. hdl:1721.1/96884. Archived from the original on 2022-09-22. Retrieved 2018-04-20.
- ^ Millero, Frank J; Feistel, Rainer; Wright, Daniel G; McDougall, Trevor J (January 2008). «The composition of Standard Seawater and the definition of the Reference-Composition Salinity Scale». Deep-Sea Research Part I. 55 (1): 50. Bibcode:2008DSRI…55…50M. doi:10.1016/j.dsr.2007.10.001.
- ^ Guideline on the Surface Tension of Seawater (PDF) (Technical report). International Association for the Properties of Water and Steam. October 2019. IAPWS G14-19. Archived (PDF) from the original on 2020-03-26. Retrieved 2020-03-26.
External links[edit]
- «Why is surface tension parallel to the interface?». Physics Stack Exchange. Retrieved 2021-03-19.
- Berry, M V (1971-03-01). «The molecular mechanism of surface tension». Physics Education. 6 (2): 79–84. doi:10.1088/0031-9120/6/2/001. ISSN 0031-9120.
- Marchand, Antonin; Weijs, Joost H.; Snoeijer, Jacco H.; Andreotti, Bruno (2011-09-26). «Why is surface tension a force parallel to the interface?». American Journal of Physics. 79 (10): 999–1008. doi:10.1119/1.3619866. ISSN 0002-9505. arXiv: https://arxiv.org/abs/1211.3854
- On surface tension and interesting real-world cases
- Surface Tensions of Various Liquids
- Calculation of temperature-dependent surface tensions for some common components
- Surface tension calculator for aqueous solutions containing the ions H+, NH+
4, Na+, K+, Mg2+, Ca2+, SO2−
4, NO−
3, Cl−, CO2−
3, Br− and OH−. - T. Proctor Hall (1893) New methods of measuring surface tension in liquids, Philosophical Magazine (series 5, 36: 385–415), link from Biodiversity Heritage Library.
- The Bubble Wall[permanent dead link] (Audio slideshow from the National High Magnetic Field Laboratory explaining cohesion, surface tension and hydrogen bonds)
- C. Pfister: Interface Free Energy. Scholarpedia 2010 (from first principles of statistical mechanics)
- Surface and Interfacial Tension
- «Molten salts mixture surface tension». The Journal of Chemical Thermodynamics. 3 (2): 259–265. March 1971. doi:10.1016/S0021-9614(71)80111-8.
Surface tension experimental demonstration with soap
Surface tension is the tendency of liquid surfaces at rest to shrink into the minimum surface area possible. Surface tension is what allows objects with a higher density than water such as razor blades and insects (e.g. water striders) to float on a water surface without becoming even partly submerged.
At liquid–air interfaces, surface tension results from the greater attraction of liquid molecules to each other (due to cohesion) than to the molecules in the air (due to adhesion).[1]
There are two primary mechanisms in play. One is an inward force on the surface molecules causing the liquid to contract.[2][3] Second is a tangential force parallel to the surface of the liquid.[3] This tangential force is generally referred to as the surface tension. The net effect is the liquid behaves as if its surface were covered with a stretched elastic membrane. But this analogy must not be taken too far as the tension in an elastic membrane is dependent on the amount of deformation of the membrane while surface tension is an inherent property of the liquid–air or liquid–vapour interface.[4]
Because of the relatively high attraction of water molecules to each other through a web of hydrogen bonds, water has a higher surface tension (72.8 millinewtons (mN) per meter at 20 °C) than most other liquids. Surface tension is an important factor in the phenomenon of capillarity.
Surface tension has the dimension of force per unit length, or of energy per unit area.[4] The two are equivalent, but when referring to energy per unit of area, it is common to use the term surface energy, which is a more general term in the sense that it applies also to solids.
In materials science, surface tension is used for either surface stress or surface energy.
Causes[edit]
Diagram of the cohesive forces on molecules of a liquid
Due to the cohesive forces, a molecule located away from the surface is pulled equally in every direction by neighbouring liquid molecules, resulting in a net force of zero. The molecules at the surface do not have the same molecules on all sides of them and therefore are pulled inward. This creates some internal pressure and forces liquid surfaces to contract to the minimum area.[2]
There is also a tension parallel to the surface at the liquid-air interface which will resist an external force, due to the cohesive nature of water molecules.[2][3]
The forces of attraction acting between molecules of the same type are called cohesive forces, while those acting between molecules of different types are called adhesive forces. The balance between the cohesion of the liquid and its adhesion to the material of the container determines the degree of wetting, the contact angle and the shape of meniscus. When cohesion dominates (specifically, adhesion energy is less than half of cohesion energy) the wetting is low and the meniscus is convex at a vertical wall (as for mercury in a glass container). On the other hand, when adhesion dominates (adhesion energy more than half of cohesion energy) the wetting is high and the similar meniscus is concave (as in water in a glass).
Surface tension is responsible for the shape of liquid droplets. Although easily deformed, droplets of water tend to be pulled into a spherical shape by the imbalance in cohesive forces of the surface layer. In the absence of other forces, drops of virtually all liquids would be approximately spherical. The spherical shape minimizes the necessary «wall tension» of the surface layer according to Laplace’s law.
Water droplet lying on a damask. Surface tension is high enough to prevent seeping through the textile
Another way to view surface tension is in terms of energy. A molecule in contact with a neighbor is in a lower state of energy than if it were alone. The interior molecules have as many neighbors as they can possibly have, but the boundary molecules are missing neighbors (compared to interior molecules) and therefore have a higher energy. For the liquid to minimize its energy state, the number of higher energy boundary molecules must be minimized. The minimized number of boundary molecules results in a minimal surface area.[5]
As a result of surface area minimization, a surface will assume the smoothest shape it can (mathematical proof that «smooth» shapes minimize surface area relies on use of the Euler–Lagrange equation). Since any curvature in the surface shape results in greater area, a higher energy will also result.
Physics[edit]
Physical units[edit]
Surface tension, represented by the symbol γ (alternatively σ or T), is measured in force per unit length. Its SI unit is newton per meter but the cgs unit of dyne per centimeter is also used. For example,[6]
Definition[edit]
This diagram illustrates the force necessary to increase the surface area. This force is proportional to the surface tension.
Surface tension can be defined in terms of force or energy.
In terms of force[edit]
Surface tension γ of a liquid is the force per unit length. In the illustration on the right, the rectangular frame, composed of three unmovable sides (black) that form a «U» shape, and a fourth movable side (blue) that can slide to the right. Surface tension will pull the blue bar to the left; the force F required to hold the movable side is proportional to the length L of the immobile side. Thus the ratio F/L depends only on the intrinsic properties of the liquid (composition, temperature, etc.), not on its geometry. For example, if the frame had a more complicated shape, the ratio F/L, with L the length of the movable side and F the force required to stop it from sliding, is found to be the same for all shapes. We therefore define the surface tension as
The reason for the
1/2 is that the film has two sides (two surfaces), each of which contributes equally to the force; so the force contributed by a single side is γL = F/2.
In terms of energy[edit]
Surface tension γ of a liquid is the ratio of the change in the energy of the liquid to the change in the surface area of the liquid (that led to the change in energy). This can be easily related to the previous definition in terms of force:[7] if F is the force required to stop the side from starting to slide, then this is also the force that would keep the side in the state of sliding at a constant speed (by Newton’s Second Law). But if the side is moving to the right (in the direction the force is applied), then the surface area of the stretched liquid is increasing while the applied force is doing work on the liquid. This means that increasing the surface area increases the energy of the film. The work done by the force F in moving the side by distance Δx is W = FΔx; at the same time the total area of the film increases by ΔA = 2LΔx (the factor of 2 is here because the liquid has two sides, two surfaces). Thus, multiplying both the numerator and the denominator of γ = 1/2F/L by Δx, we get
This work W is, by the usual arguments, interpreted as being stored as potential energy. Consequently, surface tension can be also measured in SI system as joules per square meter and in the cgs system as ergs per cm2. Since mechanical systems try to find a state of minimum potential energy, a free droplet of liquid naturally assumes a spherical shape, which has the minimum surface area for a given volume.
The equivalence of measurement of energy per unit area to force per unit length can be proven by dimensional analysis.[8]
Effects[edit]
Water[edit]
Several effects of surface tension can be seen with ordinary water:
- Beading of rain water on a waxy surface, such as a leaf. Water adheres weakly to wax and strongly to itself, so water clusters into drops. Surface tension gives them their near-spherical shape, because a sphere has the smallest possible surface area to volume ratio.
- Formation of drops occurs when a mass of liquid is stretched. The animation (below) shows water adhering to the faucet gaining mass until it is stretched to a point where the surface tension can no longer keep the drop linked to the faucet. It then separates and surface tension forms the drop into a sphere. If a stream of water were running from the faucet, the stream would break up into drops during its fall. Gravity stretches the stream, then surface tension pinches it into spheres.[9]
- Flotation of objects denser than water occurs when the object is nonwettable and its weight is small enough to be borne by the forces arising from surface tension.[5] For example, water striders use surface tension to walk on the surface of a pond in the following way. The nonwettability of the water strider’s leg means there is no attraction between molecules of the leg and molecules of the water, so when the leg pushes down on the water, the surface tension of the water only tries to recover its flatness from its deformation due to the leg. This behavior of the water pushes the water strider upward so it can stand on the surface of the water as long as its mass is small enough that the water can support it. The surface of the water behaves like an elastic film: the insect’s feet cause indentations in the water’s surface, increasing its surface area[10] and tendency of minimization of surface curvature (so area) of the water pushes the insect’s feet upward.
- Separation of oil and water (in this case, water and liquid wax) is caused by a tension in the surface between dissimilar liquids. This type of surface tension is called «interface tension», but its chemistry is the same.
- Tears of wine is the formation of drops and rivulets on the side of a glass containing an alcoholic beverage. Its cause is a complex interaction between the differing surface tensions of water and ethanol; it is induced by a combination of surface tension modification of water by ethanol together with ethanol evaporating faster than water.
-
A. Water beading on a leaf
-
B. Water dripping from a tap
-
C. Water striders stay at the top of liquid because of surface tension
-
D. Lava lamp with interaction between dissimilar liquids: water and liquid wax
Surfactants[edit]
Surface tension is visible in other common phenomena, especially when surfactants are used to decrease it:
- Soap bubbles have very large surface areas with very little mass. Bubbles in pure water are unstable. The addition of surfactants, however, can have a stabilizing effect on the bubbles (see Marangoni effect). Note that surfactants actually reduce the surface tension of water by a factor of three or more.
- Emulsions are a type of colloid in which surface tension plays a role. Tiny fragments of oil suspended in pure water will spontaneously assemble themselves into much larger masses. But the presence of a surfactant provides a decrease in surface tension, which permits stability of minute droplets of oil in the bulk of water (or vice versa).
Surface curvature and pressure[edit]
Surface tension forces acting on a tiny (differential) patch of surface. δθx and δθy indicate the amount of bend over the dimensions of the patch. Balancing the tension forces with pressure leads to the Young–Laplace equation
If no force acts normal to a tensioned surface, the surface must remain flat. But if the pressure on one side of the surface differs from pressure on the other side, the pressure difference times surface area results in a normal force. In order for the surface tension forces to cancel the force due to pressure, the surface must be curved. The diagram shows how surface curvature of a tiny patch of surface leads to a net component of surface tension forces acting normal to the center of the patch. When all the forces are balanced, the resulting equation is known as the Young–Laplace equation:[11]
where:
- Δp is the pressure difference, known as the Laplace pressure.[12]
- γ is surface tension.
- Rx and Ry are radii of curvature in each of the axes that are parallel to the surface.
The quantity in parentheses on the right hand side is in fact (twice) the mean curvature of the surface (depending on normalisation).
Solutions to this equation determine the shape of water drops, puddles, menisci, soap bubbles, and all other shapes determined by surface tension (such as the shape of the impressions that a water strider’s feet make on the surface of a pond).
The table below shows how the internal pressure of a water droplet increases with decreasing radius. For not very small drops the effect is subtle, but the pressure difference becomes enormous when the drop sizes approach the molecular size. (In the limit of a single molecule the concept becomes meaningless.)
| Droplet radius | 1 mm | 0.1 mm | 1 μm | 10 nm |
|---|---|---|---|---|
| Δp (atm) | 0.0014 | 0.0144 | 1.436 | 143.6 |
Floating objects[edit]
Cross-section of a needle floating on the surface of water. Fw is the weight and Fs are surface tension resultant forces.
When an object is placed on a liquid, its weight Fw depresses the surface, and if surface tension and downward force become equal then it is balanced by the surface tension forces on either side Fs, which are each parallel to the water’s surface at the points where it contacts the object. Notice that small movement in the body may cause the object to sink. As the angle of contact decreases, surface tension decreases. The horizontal components of the two Fs arrows point in opposite directions, so they cancel each other, but the vertical components point in the same direction and therefore add up[5] to balance Fw. The object’s surface must not be wettable for this to happen, and its weight must be low enough for the surface tension to support it. If m denotes the mass of the needle and g acceleration due to gravity, we have
Liquid surface[edit]
To find the shape of the minimal surface bounded by some arbitrary shaped frame using strictly mathematical means can be a daunting task. Yet by fashioning the frame out of wire and dipping it in soap-solution, a locally minimal surface will appear in the resulting soap-film within seconds.[8][13]
The reason for this is that the pressure difference across a fluid interface is proportional to the mean curvature, as seen in the Young–Laplace equation. For an open soap film, the pressure difference is zero, hence the mean curvature is zero, and minimal surfaces have the property of zero mean curvature.
Contact angles[edit]
The surface of any liquid is an interface between that liquid and some other medium.[note 1] The top surface of a pond, for example, is an interface between the pond water and the air. Surface tension, then, is not a property of the liquid alone, but a property of the liquid’s interface with another medium. If a liquid is in a container, then besides the liquid/air interface at its top surface, there is also an interface between the liquid and the walls of the container. The surface tension between the liquid and air is usually different (greater) than its surface tension with the walls of a container. And where the two surfaces meet, their geometry must be such that all forces balance.[8][11]
Forces at contact point shown for contact angle greater than 90° (left) and less than 90° (right)
Where the two surfaces meet, they form a contact angle, θ, which is the angle the tangent to the surface makes with the solid surface. Note that the angle is measured through the liquid, as shown in the diagrams above. The diagram to the right shows two examples. Tension forces are shown for the liquid–air interface, the liquid–solid interface, and the solid–air interface. The example on the left is where the difference between the liquid–solid and solid–air surface tension, γls − γsa, is less than the liquid–air surface tension, γla, but is nevertheless positive, that is
In the diagram, both the vertical and horizontal forces must cancel exactly at the contact point, known as equilibrium. The horizontal component of fla is canceled by the adhesive force, fA.[8]
The more telling balance of forces, though, is in the vertical direction. The vertical component of fla must exactly cancel the difference of the forces along the solid surface, fls − fsa.[8]
| Liquid | Solid | Contact angle |
|||
|---|---|---|---|---|---|
| water |
|
0° | |||
| ethanol | |||||
| diethyl ether | |||||
| carbon tetrachloride | |||||
| glycerol | |||||
| acetic acid | |||||
| water | paraffin wax | 107° | |||
| silver | 90° | ||||
| methyl iodide | soda-lime glass | 29° | |||
| lead glass | 30° | ||||
| fused quartz | 33° | ||||
| mercury | soda-lime glass | 140° |
Since the forces are in direct proportion to their respective surface tensions, we also have:[11]
where
- γls is the liquid–solid surface tension,
- γla is the liquid–air surface tension,
- γsa is the solid–air surface tension,
- θ is the contact angle, where a concave meniscus has contact angle less than 90° and a convex meniscus has contact angle of greater than 90°.[8]
This means that although the difference between the liquid–solid and solid–air surface tension, γls − γsa, is difficult to measure directly, it can be inferred from the liquid–air surface tension, γla, and the equilibrium contact angle, θ, which is a function of the easily measurable advancing and receding contact angles (see main article contact angle).
This same relationship exists in the diagram on the right. But in this case we see that because the contact angle is less than 90°, the liquid–solid/solid–air surface tension difference must be negative:
Special contact angles[edit]
Observe that in the special case of a water–silver interface where the contact angle is equal to 90°, the liquid–solid/solid–air surface tension difference is exactly zero.
Another special case is where the contact angle is exactly 180°. Water with specially prepared Teflon approaches this.[11] Contact angle of 180° occurs when the liquid–solid surface tension is exactly equal to the liquid–air surface tension.
Liquid in a vertical tube[edit]
An old style mercury barometer consists of a vertical glass tube about 1 cm in diameter partially filled with mercury, and with a vacuum (called Torricelli’s vacuum) in the unfilled volume (see diagram to the right). Notice that the mercury level at the center of the tube is higher than at the edges, making the upper surface of the mercury dome-shaped. The center of mass of the entire column of mercury would be slightly lower if the top surface of the mercury were flat over the entire cross-section of the tube. But the dome-shaped top gives slightly less surface area to the entire mass of mercury. Again the two effects combine to minimize the total potential energy. Such a surface shape is known as a convex meniscus.
We consider the surface area of the entire mass of mercury, including the part of the surface that is in contact with the glass, because mercury does not adhere to glass at all. So the surface tension of the mercury acts over its entire surface area, including where it is in contact with the glass. If instead of glass, the tube was made out of copper, the situation would be very different. Mercury aggressively adheres to copper. So in a copper tube, the level of mercury at the center of the tube will be lower than at the edges (that is, it would be a concave meniscus). In a situation where the liquid adheres to the walls of its container, we consider the part of the fluid’s surface area that is in contact with the container to have negative surface tension. The fluid then works to maximize the contact surface area. So in this case increasing the area in contact with the container decreases rather than increases the potential energy. That decrease is enough to compensate for the increased potential energy associated with lifting the fluid near the walls of the container.
Illustration of capillary rise and fall. Red=contact angle less than 90°; blue=contact angle greater than 90°
If a tube is sufficiently narrow and the liquid adhesion to its walls is sufficiently strong, surface tension can draw liquid up the tube in a phenomenon known as capillary action. The height to which the column is lifted is given by Jurin’s law:[8]
where
- h is the height the liquid is lifted,
- γla is the liquid–air surface tension,
- ρ is the density of the liquid,
- r is the radius of the capillary,
- g is the acceleration due to gravity,
- θ is the angle of contact described above. If θ is greater than 90°, as with mercury in a glass container, the liquid will be depressed rather than lifted.
Puddles on a surface[edit]
Profile curve of the edge of a puddle where the contact angle is 180°. The curve is given by the formula:[11]
where
Small puddles of water on a smooth clean surface have perceptible thickness.
Pouring mercury onto a horizontal flat sheet of glass results in a puddle that has a perceptible thickness. The puddle will spread out only to the point where it is a little under half a centimetre thick, and no thinner. Again this is due to the action of mercury’s strong surface tension. The liquid mass flattens out because that brings as much of the mercury to as low a level as possible, but the surface tension, at the same time, is acting to reduce the total surface area. The result of the compromise is a puddle of a nearly fixed thickness.
The same surface tension demonstration can be done with water, lime water or even saline, but only on a surface made of a substance to which water does not adhere. Wax is such a substance. Water poured onto a smooth, flat, horizontal wax surface, say a waxed sheet of glass, will behave similarly to the mercury poured onto glass.
The thickness of a puddle of liquid on a surface whose contact angle is 180° is given by:[11]
where
- h is the depth of the puddle in centimeters or meters.
- γ is the surface tension of the liquid in dynes per centimeter or newtons per meter.
- g is the acceleration due to gravity and is equal to 980 cm/s2 or 9.8 m/s2
- ρ is the density of the liquid in grams per cubic centimeter or kilograms per cubic meter
Illustration of how lower contact angle leads to reduction of puddle depth
In reality, the thicknesses of the puddles will be slightly less than what is predicted by the above formula because very few surfaces have a contact angle of 180° with any liquid. When the contact angle is less than 180°, the thickness is given by:[11]
For mercury on glass, γHg = 487 dyn/cm, ρHg = 13.5 g/cm3 and θ = 140°, which gives hHg = 0.36 cm. For water on paraffin at 25 °C, γ = 72 dyn/cm, ρ = 1.0 g/cm3, and θ = 107° which gives hH2O = 0.44 cm.
The formula also predicts that when the contact angle is 0°, the liquid will spread out into a micro-thin layer over the surface. Such a surface is said to be fully wettable by the liquid.
The breakup of streams into drops[edit]
Breakup of an elongated stream of water into droplets due to surface tension.
In day-to-day life all of us observe that a stream of water emerging from a faucet will break up into droplets, no matter how smoothly the stream is emitted from the faucet. This is due to a phenomenon called the Plateau–Rayleigh instability,[11] which is entirely a consequence of the effects of surface tension.
The explanation of this instability begins with the existence of tiny perturbations in the stream. These are always present, no matter how smooth the stream is. If the perturbations are resolved into sinusoidal components, we find that some components grow with time while others decay with time. Among those that grow with time, some grow at faster rates than others. Whether a component decays or grows, and how fast it grows is entirely a function of its wave number (a measure of how many peaks and troughs per centimeter) and the radii of the original cylindrical stream.
Gallery[edit]
-
Breakup of a moving sheet of water bouncing off of a spoon.
-
Photo of flowing water adhering to a hand. Surface tension creates the sheet of water between the flow and the hand.
-
Surface tension prevents a coin from sinking: the coin is indisputably denser than water, so it must be displacing a volume greater than its own for buoyancy to balance mass.
-
An aluminium coin floats on the surface of the water at 10 °C. Any extra weight would drop the coin to the bottom.
-
A daisy. The entirety of the flower lies below the level of the (undisturbed) free surface. The water rises smoothly around its edge. Surface tension prevents water from displacing the air between the petals and possibly submerging the flower.
-
A metal paper clip floats on water. Several can usually be carefully added without overflow of water.
-
A metal paperclip floating on water. A grille in front of the light has created the ‘contour lines’ which show the deformation in the water surface caused by the metal paper clip.
Thermodynamics[edit]
Thermodynamic theories of surface tension[edit]
J.W. Gibbs developed the thermodynamic theory of capillarity based
on the idea of surfaces of discontinuity.[14] Gibbs considered the case of a sharp mathematical surface being placed somewhere within the microscopically fuzzy physical interface that exists between two homogeneous substances. Realizing that the exact choice of the surface’s location was somewhat arbitrary, he left it flexible. Since the interface exists in thermal and chemical equilibrium with the substances around it (having temperature T and chemical potentials μi), Gibbs considered the case where the surface may have excess energy, excess entropy, and excess particles, finding the natural free energy function in this case to be 

Gibbs’ placement of a precise mathematical surface in a fuzzy physical interface.
Considering a given subvolume 







For sufficiently macroscopic and gently curved surfaces, the surface free energy must simply be proportional to the surface area:[14][15]
for surface tension 

As stated above, this implies the mechanical work needed to increase a surface area A is dW = γ dA, assuming the volumes on each side do not change. Thermodynamics requires that for systems held at constant chemical potential and temperature, all spontaneous changes of state are accompanied by a decrease in this free energy 
Gibbs and other scientists have wrestled with the arbitrariness in the exact microscopic placement of the surface.[16] For microscopic surfaces with very tight curvatures, it is not correct to assume the surface tension is independent of size, and topics like the Tolman length come into play. For a macroscopic sized surface (and planar surfaces), the surface placement does not have a significant effect on γ however it does have a very strong effect on the values of the surface entropy, surface excess mass densities, and surface internal energy,[14]: 237 which are the partial derivatives of the surface tension function 
Gibbs emphasized that for solids, the surface free energy may be completely different from surface stress (what he called surface tension):[14]: 315 the surface free energy is the work required to form the surface, while surface stress is the work required to stretch the surface. In the case of a two-fluid interface, there is no distinction between forming and stretching because the fluids and the surface completely replenish their nature when the surface is stretched. For a solid, stretching the surface, even elastically, results in a fundamentally changed surface. Further, the surface stress on a solid is a directional quantity (a stress tensor) while surface energy is scalar.
Fifteen years after Gibbs, J.D. van der Waals developed the theory of capillarity effects based on the hypothesis of a continuous variation of density.[17] He added to the energy density the term 
Thermodynamics of bubbles[edit]
The pressure inside an ideal spherical bubble can be derived from thermodynamic free energy considerations.[15] The above free energy can be written as:
where 

For a spherical bubble, the volume and surface area are given simply by
and
Substituting these relations into the previous expression, we find
which is equivalent to the Young–Laplace equation when Rx = Ry.
Influence of temperature[edit]
Temperature dependence of the surface tension between the liquid and vapor phases of pure water
Temperature dependency of the surface tension of benzene
Surface tension is dependent on temperature. For that reason, when a value is given for the surface tension of an interface, temperature must be explicitly stated. The general trend is that surface tension decreases with the increase of temperature, reaching a value of 0 at the critical temperature. For further details see Eötvös rule. There are only empirical equations to relate surface tension and temperature:
- Eötvös:[21][22][23]
Here V is the molar volume of a substance, TC is the critical temperature and k is a constant valid for almost all substances.[21] A typical value is k = 2.1×10−7 J K−1 mol−2⁄3.[21][23] For water one can further use V = 18 ml/mol and TC = 647 K (374 °C).[24] A variant on Eötvös is described by Ramay and Shields:[25]
where the temperature offset of 6 K provides the formula with a better fit to reality at lower temperatures.
- Guggenheim–Katayama:[22]
γ° is a constant for each liquid and n is an empirical factor, whose value is 11/9 for organic liquids. This equation was also proposed by van der Waals, who further proposed that γ° could be given by the expression
where K2 is a universal constant for all liquids, and PC is the critical pressure of the liquid (although later experiments found K2 to vary to some degree from one liquid to another).[22]
Both Guggenheim–Katayama and Eötvös take into account the fact that surface tension reaches 0 at the critical temperature, whereas Ramay and Shields fails to match reality at this endpoint.
Influence of solute concentration[edit]
Solutes can have different effects on surface tension depending on the nature of the surface and the solute:
- Little or no effect, for example sugar at water|air, most organic compounds at oil/air
- Increase surface tension, most inorganic salts at water|air
- Non-monotonic change, most inorganic acids at water|air
- Decrease surface tension progressively, as with most amphiphiles, e.g., alcohols at water|air
- Decrease surface tension until certain critical concentration, and no effect afterwards: surfactants that form micelles
What complicates the effect is that a solute can exist in a different concentration at the surface of a solvent than in its bulk. This difference varies from one solute–solvent combination to another.
Gibbs isotherm states that:
- Γ is known as surface concentration, it represents excess of solute per unit area of the surface over what would be present if the bulk concentration prevailed all the way to the surface. It has units of mol/m2
- C is the concentration of the substance in the bulk solution.
- R is the gas constant and T the temperature
Certain assumptions are taken in its deduction, therefore Gibbs isotherm can only be applied to ideal (very dilute) solutions with two components.
Influence of particle size on vapor pressure[edit]
The Clausius–Clapeyron relation leads to another equation also attributed to Kelvin, as the Kelvin equation. It explains why, because of surface tension, the vapor pressure for small droplets of liquid in suspension is greater than standard vapor pressure of that same liquid when the interface is flat. That is to say that when a liquid is forming small droplets, the equilibrium concentration of its vapor in its surroundings is greater. This arises because the pressure inside the droplet is greater than outside.[25]
Molecules on the surface of a tiny droplet (left) have, on average, fewer neighbors than those on a flat surface (right). Hence they are bound more weakly to the droplet than are flat-surface molecules.
- Pv° is the standard vapor pressure for that liquid at that temperature and pressure.
- V is the molar volume.
- R is the gas constant
- rk is the Kelvin radius, the radius of the droplets.
The effect explains supersaturation of vapors. In the absence of nucleation sites, tiny droplets must form before they can evolve into larger droplets. This requires a vapor pressure many times the vapor pressure at the phase transition point.[25]
This equation is also used in catalyst chemistry to assess mesoporosity for solids.[26]
The effect can be viewed in terms of the average number of molecular neighbors of surface molecules (see diagram).
The table shows some calculated values of this effect for water at different drop sizes:
| P/P0 for water drops of different radii at STP[22] | ||||
|---|---|---|---|---|
| Droplet radius (nm) | 1000 | 100 | 10 | 1 |
| P/P0 | 1.001 | 1.011 | 1.114 | 2.95 |
The effect becomes clear for very small drop sizes, as a drop of 1 nm radius has about 100 molecules inside, which is a quantity small enough to require a quantum mechanics analysis.
Methods of measurement[edit]
Because surface tension manifests itself in various effects, it offers a number of paths to its measurement. Which method is optimal depends upon the nature of the liquid being measured, the conditions under which its tension is to be measured, and the stability of its surface when it is deformed. An instrument that measures surface tension is called tensiometer.
- Du Noüy ring method: The traditional method used to measure surface or interfacial tension. Wetting properties of the surface or interface have little influence on this measuring technique. Maximum pull exerted on the ring by the surface is measured.[21]
- Wilhelmy plate method: A universal method especially suited to check surface tension over long time intervals. A vertical plate of known perimeter is attached to a balance, and the force due to wetting is measured.
- Spinning drop method: This technique is ideal for measuring low interfacial tensions. The diameter of a drop within a heavy phase is measured while both are rotated.
- Pendant drop method: Surface and interfacial tension can be measured by this technique, even at elevated temperatures and pressures. Geometry of a drop is analyzed optically. For pendant drops the maximum diameter and the ratio between this parameter and the diameter at the distance of the maximum diameter from the drop apex has been used to evaluate the size and shape parameters in order to determine surface tension.
- Bubble pressure method (Jaeger’s method): A measurement technique for determining surface tension at short surface ages. Maximum pressure of each bubble is measured.
- Drop volume method: A method for determining interfacial tension as a function of interface age. Liquid of one density is pumped into a second liquid of a different density and time between drops produced is measured.
- Capillary rise method: The end of a capillary is immersed into the solution. The height at which the solution reaches inside the capillary is related to the surface tension by the equation discussed below.[27].]]
- Stalagmometric method: A method of weighting and reading a drop of liquid.
- Sessile drop method: A method for determining surface tension and density by placing a drop on a substrate and measuring the contact angle (see Sessile drop technique).[28]
- Du Noüy–Padday method: A minimized version of Du Noüy method uses a small diameter metal needle instead of a ring, in combination with a high sensitivity microbalance to record maximum pull. The advantage of this method is that very small sample volumes (down to few tens of microliters) can be measured with very high precision, without the need to correct for buoyancy (for a needle or rather, rod, with proper geometry). Further, the measurement can be performed very quickly, minimally in about 20 seconds.
- Vibrational frequency of levitated drops: The natural frequency of vibrational oscillations of magnetically levitated drops has been used to measure the surface tension of superfluid 4He. This value is estimated to be 0.375 dyn/cm at T = 0 K.[29]
- Resonant oscillations of spherical and hemispherical liquid drop: The technique is based on measuring the resonant frequency of spherical and hemispherical pendant droplets driven in oscillations by a modulated electric field. The surface tension and viscosity can be evaluated from the obtained resonant curves.[30][31][32]
- Drop-bounce method: This method is based on aerodynamic levitation with a split-able nozzle design. After dropping a stably levitated droplet onto a platform, the sample deforms and bounces back, oscillating in mid-air as it tries to minimize its surface area. Through this oscillation behavior, the liquid’s surface tension and viscosity can be measured. [33]
- By smartphone: Some smartphones can be used to measure the surface tension of a transparent liquid. The method is based on measuring the wavelength of capillary waves of known frequency. The smartphone is placed on top of a cup with the liquid. Then smartphone’s vibro-motor excites (through the cup) capillary ripples on the surface of the liquid, which are captured by smartphone’s camera.[34]
Values[edit]
Data table[edit]
| Liquid | Temperature (°C) | Surface tension, γ |
|---|---|---|
| Acetic acid | 20 | 27.60 |
| Acetic acid (45.1%) + Water | 30 | 40.68 |
| Acetic acid (10.0%) + Water | 30 | 54.56 |
| Acetone | 20 | 23.70 |
| Blood | 22 | 55.89 |
| Diethyl ether | 20 | 17.00 |
| Ethanol | 20 | 22.27 |
| Ethanol (40%) + Water | 25 | 29.63 |
| Ethanol (11.1%) + Water | 25 | 46.03 |
| Glycerol | 20 | 63.00 |
| n-Hexane | 20 | 18.40 |
| Hydrochloric acid 17.7 M aqueous solution | 20 | 65.95 |
| Isopropanol | 20 | 21.70 |
| Liquid helium II | −273 | 0.37[36] |
| Liquid nitrogen | −196 | 8.85 |
| Liquid oxygen | −182 | 13.2 |
| Mercury | 15 | 487.00 |
| Methanol | 20 | 22.60 |
| Molten Silver chloride | 650 | 163[37] |
| Molten Sodium chloride/Calcium chloride (47/53 mole %) | 650 | 139[38] |
| n-Octane | 20 | 21.80 |
| Sodium chloride 6.0 M aqueous solution | 20 | 82.55 |
| Sucrose (55%) + water | 20 | 76.45 |
| Water | 0 | 75.64 |
| Water | 25 | 71.97 |
| Water | 50 | 67.91 |
| Water | 100 | 58.85 |
| Toluene | 25 | 27.73 |
Surface tension of water[edit]
The surface tension of pure liquid water in contact with its vapor has been given by IAPWS[39] as
where both T and the critical temperature TC = 647.096 K are expressed in kelvins. The region of validity the entire vapor–liquid saturation curve, from the triple point (0.01 °C) to the critical point. It also provides reasonable results when extrapolated to metastable (supercooled) conditions, down to at least −25 °C. This formulation was originally adopted by IAPWS in 1976 and was adjusted in 1994 to conform to the International Temperature Scale of 1990.
The uncertainty of this formulation is given over the full range of temperature by IAPWS.[39] For temperatures below 100 °C, the uncertainty is ±0.5%.
Surface tension of seawater[edit]
Nayar et al.[40] published reference data for the surface tension of seawater over the salinity range of 20 ≤ S ≤ 131 g/kg and a temperature range of 1 ≤ t ≤ 92 °C at atmospheric pressure. The range of temperature and salinity encompasses both the oceanographic range and the range of conditions encountered in thermal desalination technologies. The uncertainty of the measurements varied from 0.18 to 0.37 mN/m with the average uncertainty being 0.22 mN/m.
Nayar et al. correlated the data with the following equation
where γsw is the surface tension of seawater in mN/m, γw is the surface tension of water in mN/m, S is the reference salinity[41] in g/kg, and t is temperature in degrees Celsius. The average absolute percentage deviation between measurements and the correlation was 0.19% while the maximum deviation is 0.60%.
The International Association for the Properties of Water and Steam (IAPWS) has adopted this correlation as an international standard guideline.[42]
See also[edit]
- Anti-fog
- Capillary wave — short waves on a water surface, governed by surface tension and inertia
- Cheerio effect — the tendency for small wettable floating objects to attract one another.
- Cohesion
- Dimensionless numbers
- Bond number or Eötvös number
- Capillary number
- Marangoni number
- Weber number
- Dortmund Data Bank — contains experimental temperature-dependent surface tensions
- Electrodipping force
- Electrowetting
- Electrocapillarity
- Eötvös rule — a rule for predicting surface tension dependent on temperature
- Fluid pipe
- Hydrostatic equilibrium—the effect of gravity pulling matter into a round shape
- Interface (chemistry)
- Meniscus — surface curvature formed by a liquid in a container
- Mercury beating heart — a consequence of inhomogeneous surface tension
- Microfluidics
- Sessile drop technique
- Sow-Hsin Chen
- Specific surface energy — same as surface tension in isotropic materials.
- Spinning drop method
- Stalagmometric method
- Surface pressure
- Surface science
- Surface tension biomimetics
- Surface tension values
- Surfactants — substances which reduce surface tension.
- Szyszkowski equation — calculating surface tension of aqueous solutions
- Tears of wine — the surface tension induced phenomenon seen on the sides of glasses containing alcoholic beverages.
- Tolman length — leading term in correcting the surface tension for curved surfaces.
- Wetting and dewetting
Explanatory notes[edit]
- ^ In a mercury barometer, the upper liquid surface is an interface between the liquid and a vacuum containing some molecules of evaporated liquid.
References[edit]
- ^ «Surface Tension — an overview | ScienceDirect Topics». www.sciencedirect.com. Archived from the original on 2021-12-30. Retrieved 2021-12-30.
- ^ a b c «Surface Tension (Water Properties) – USGS Water Science School». US Geological Survey. July 2015. Archived from the original on October 7, 2015. Retrieved November 6, 2015.
- ^ a b c Berry, M V (1971). «The molecular mechanism of surface tension» (PDF). Physics Education. 6 (2): 79–84. Bibcode:1971PhyEd…6…79B. doi:10.1088/0031-9120/6/2/001. S2CID 250797804. Archived (PDF) from the original on 31 December 2021. Retrieved 8 July 2020.
- ^ a b Halliday, David; Resnick, Robert; Krane, Kenneth S. (2010-04-20). Physics, Volume 2. John Wiley & Sons. p. 342. ISBN 978-0-471-40194-0. Archived from the original on 2022-09-22. Retrieved 2021-03-19.
- ^ a b c White, Harvey E. (1948). Modern College Physics. van Nostrand. ISBN 978-0-442-29401-4.
- ^ Bush, John W. M. (April 2004). «MIT Lecture Notes on Surface Tension, lecture 1» (PDF). Massachusetts Institute of Technology. Archived (PDF) from the original on March 8, 2022. Retrieved April 1, 2007.
- ^ «Mechanical definition of surface tension». MIT. Archived from the original on April 12, 2013. Retrieved Dec 16, 2013.
- ^ a b c d e f g h Sears, Francis Weston; Zemanski, Mark W. (1955) University Physics 2nd ed. Addison Wesley
- ^ Bush, John W. M. (May 2004). «MIT Lecture Notes on Surface Tension, lecture 5» (PDF). Massachusetts Institute of Technology. Archived (PDF) from the original on February 26, 2007. Retrieved April 1, 2007.
- ^ Bush, John W. M. (May 2004). «MIT Lecture Notes on Surface Tension, lecture 3» (PDF). Massachusetts Institute of Technology. Archived (PDF) from the original on February 26, 2007. Retrieved April 1, 2007.
- ^ a b c d e f g h Pierre-Gilles de Gennes; Françoise Brochard-Wyart; David Quéré (2002). Capillarity and Wetting Phenomena—Drops, Bubbles, Pearls, Waves. Alex Reisinger. Springer. ISBN 978-0-387-00592-8.
- ^ Butt, Hans-Jürgen; Graf, Karlheinz; Kappl, Michael (2006). Physics and Chemistry of Interfaces. Wiley. p. 9. ISBN 978-3-527-60640-5.
- ^ Aaronson, Scott (March 2005) NP-complete Problems and Physical Reality Archived 2018-02-23 at the Wayback Machine. ACM SIGACT News
- ^ a b c d Gibbs, J.W. (2002) [1876–1878], «On the Equilibrium of Heterogeneous Substances», in Bumstead, H.A.; Van Nameeds, R.G. (eds.), The Scientific Papers of J. Willard Gibbs, vol. 1, Woodbridge, CT: Ox Bow Press, pp. 55–354, ISBN 978-0918024770
- ^ a b Landau; Lifshitz (1980). Course of Theoretical Physics Volume 5: Statistical Physics I (3 ed.). Pergamon. pp. 517–537.
- ^ Rusanov, A (2005). «Surface thermodynamics revisited». Surface Science Reports. 58 (5–8): 111–239. Bibcode:2005SurSR..58..111R. doi:10.1016/j.surfrep.2005.08.002. ISSN 0167-5729.
- ^ van der Waals, J.D. (1979) [1893], translated by Rowlinson, J.S., «The thermodynamic theory of capillarity under the hypothesis of a continuous variation of density», J. Stat. Phys., 20 (2): 197–200, Bibcode:1979JSP….20..197R, doi:10.1007/BF01011513, S2CID 122954999
- ^ Cahn, J.W.; Hilliard, J.E. (1958), «Free energy of a nonuniform system. I. Interfacial free energy», J. Chem. Phys., 28 (2): 258–266, Bibcode:1958JChPh..28..258C, doi:10.1063/1.1744102
- ^ Langer, J.S.; Bar-On, M.; Miller, H.D. (1975), «New computational method in the theory of spinodal decomposition», Phys. Rev. A, 11 (4): 1417–1429, Bibcode:1975PhRvA..11.1417L, doi:10.1103/PhysRevA.11.1417
- ^
Gorban, A.N.; Karlin, I. V. (2016), «Beyond Navier–Stokes equations: capillarity of ideal gas», Contemporary Physics (Review article), 58 (1): 70–90, arXiv:1702.00831, Bibcode:2017ConPh..58…70G, doi:10.1080/00107514.2016.1256123, S2CID 55317543 - ^ a b c d «Surface Tension by the Ring Method (Du Nouy Method)» (PDF). PHYWE. Archived (PDF) from the original on 2007-09-27. Retrieved 2007-09-08.
- ^ a b c d Adam, Neil Kensington (1941). The Physics and Chemistry of Surfaces, 3rd ed. Oxford University Press.
- ^ a b «Physical Properties Sources Index: Eötvös Constant». Archived from the original on 2011-07-06. Retrieved 2008-11-16.
- ^ Vargaftik, N. B.; Volkov, B. N.; Voljak, L. D. (1983). «International Tables of the Surface Tension of Water» (PDF). Journal of Physical and Chemical Reference Data. 12 (3): 817. Bibcode:1983JPCRD..12..817V. doi:10.1063/1.555688. Archived from the original (PDF) on 2016-12-21. Retrieved 2017-07-13.
- ^ a b c Moore, Walter J. (1962). Physical Chemistry, 3rd ed. Prentice Hall.
- ^ Ertl, G.; Knözinger, H. and Weitkamp, J. (1997). Handbook of heterogeneous catalysis, Vol. 2, p. 430. Wiley-VCH, Weinheim. ISBN 3-527-31241-2
- ^ Calvert, James B. «Surface Tension (physics lecture notes)». University of Denver. Archived from the original on 2007-09-15. Retrieved 2007-09-08.
- ^ «Sessile Drop Method». Dataphysics. Archived from the original on August 8, 2007. Retrieved 2007-09-08.
- ^ Vicente, C.; Yao, W.; Maris, H.; Seidel, G. (2002). «Surface tension of liquid 4He as measured using the vibration modes of a levitated drop». Physical Review B. 66 (21): 214504. Bibcode:2002PhRvB..66u4504V. doi:10.1103/PhysRevB.66.214504.
- ^ Zografov, Nikolay (2014). «Droplet oscillations driven by an electric field». Colloids and Surfaces A: Physicochemical and Engineering Aspects. 460: 351–354. doi:10.1016/j.colsurfa.2013.12.013.
- ^ Tankovsky, N. (2013). «Electrically Driven Resonant Oscillations of Pendant Hemispherical Liquid Droplet and Possibility to Evaluate the Surface Tension in Real Time». Zeitschrift für Physikalische Chemie. 227 (12): 1759–1766. doi:10.1524/zpch.2013.0420. S2CID 101722165.
- ^ Tankovsky, Nikolay (2011). «Oscillations of a Hanging Liquid Drop, Driven by Interfacial Dielectric Force». Zeitschrift für Physikalische Chemie. 225 (4): 405–411. doi:10.1524/zpch.2011.0074. S2CID 101625925.
- ^ Sun, Yifan; Muta, Hiroaki; Ohishi, Yuji (June 2021). «Novel Method for Surface Tension Measurement: the Drop-Bounce Method». Microgravity Science and Technology. 33 (3): 32. Bibcode:2021MicST..33…32S. doi:10.1007/s12217-021-09883-7.
- ^ Yue, Shichao; Katabi, Dina (2021). «Liquid testing with your smartphone». Communications of the ACM. 64 (10): 75–83. doi:10.1145/3481038. ISSN 0001-0782.
- ^ Lange’s Handbook of Chemistry (1967) 10th ed. pp 1661–1665 ISBN 0-07-016190-9 (11th ed.)
- ^ Brouwer, W; Pathria, R. K (1967). «On the Surface Tension of Liquid Helium II». Physical Review. 163 (1): 200–205. Bibcode:1967PhRv..163..200B. doi:10.1103/PhysRev.163.200.
- ^ Moser, Z; Gasior, W; Rzyman, K (1982). «Activities and Surface Tension of Liquid AgCl-KCl Solutions». Journal of the Electrochemical Society. 129 (3): 502–506. doi:10.1149/1.2131529.
- ^ Addison, C; Coldrey, J (1960). «Influence of Surface Reactions on the Interface Between Liquid Sodium and Molten Sodium Chloride + Calcium Chloride Mixtures». Transactions of the Faraday Society. 56: 840–845. doi:10.1039/tf9605600840.
- ^ a b International Association for the Properties of Water and Steam (June 2014). «Revised Release on Surface Tension of Ordinary Water Substance». Archived from the original on 2016-04-04. Retrieved 2016-02-20.
- ^ Nayar, K. G; Panchanathan, D; McKinley, G. H; Lienhard, J. H (November 2014). «Surface tension of seawater» (PDF). J. Phys. Chem. Ref. Data. 43 (4): 43103. Bibcode:2014JPCRD..43d3103N. doi:10.1063/1.4899037. hdl:1721.1/96884. Archived from the original on 2022-09-22. Retrieved 2018-04-20.
- ^ Millero, Frank J; Feistel, Rainer; Wright, Daniel G; McDougall, Trevor J (January 2008). «The composition of Standard Seawater and the definition of the Reference-Composition Salinity Scale». Deep-Sea Research Part I. 55 (1): 50. Bibcode:2008DSRI…55…50M. doi:10.1016/j.dsr.2007.10.001.
- ^ Guideline on the Surface Tension of Seawater (PDF) (Technical report). International Association for the Properties of Water and Steam. October 2019. IAPWS G14-19. Archived (PDF) from the original on 2020-03-26. Retrieved 2020-03-26.
External links[edit]
- «Why is surface tension parallel to the interface?». Physics Stack Exchange. Retrieved 2021-03-19.
- Berry, M V (1971-03-01). «The molecular mechanism of surface tension». Physics Education. 6 (2): 79–84. doi:10.1088/0031-9120/6/2/001. ISSN 0031-9120.
- Marchand, Antonin; Weijs, Joost H.; Snoeijer, Jacco H.; Andreotti, Bruno (2011-09-26). «Why is surface tension a force parallel to the interface?». American Journal of Physics. 79 (10): 999–1008. doi:10.1119/1.3619866. ISSN 0002-9505. arXiv: https://arxiv.org/abs/1211.3854
- On surface tension and interesting real-world cases
- Surface Tensions of Various Liquids
- Calculation of temperature-dependent surface tensions for some common components
- Surface tension calculator for aqueous solutions containing the ions H+, NH+
4, Na+, K+, Mg2+, Ca2+, SO2−
4, NO−
3, Cl−, CO2−
3, Br− and OH−. - T. Proctor Hall (1893) New methods of measuring surface tension in liquids, Philosophical Magazine (series 5, 36: 385–415), link from Biodiversity Heritage Library.
- The Bubble Wall[permanent dead link] (Audio slideshow from the National High Magnetic Field Laboratory explaining cohesion, surface tension and hydrogen bonds)
- C. Pfister: Interface Free Energy. Scholarpedia 2010 (from first principles of statistical mechanics)
- Surface and Interfacial Tension
- «Molten salts mixture surface tension». The Journal of Chemical Thermodynamics. 3 (2): 259–265. March 1971. doi:10.1016/S0021-9614(71)80111-8.



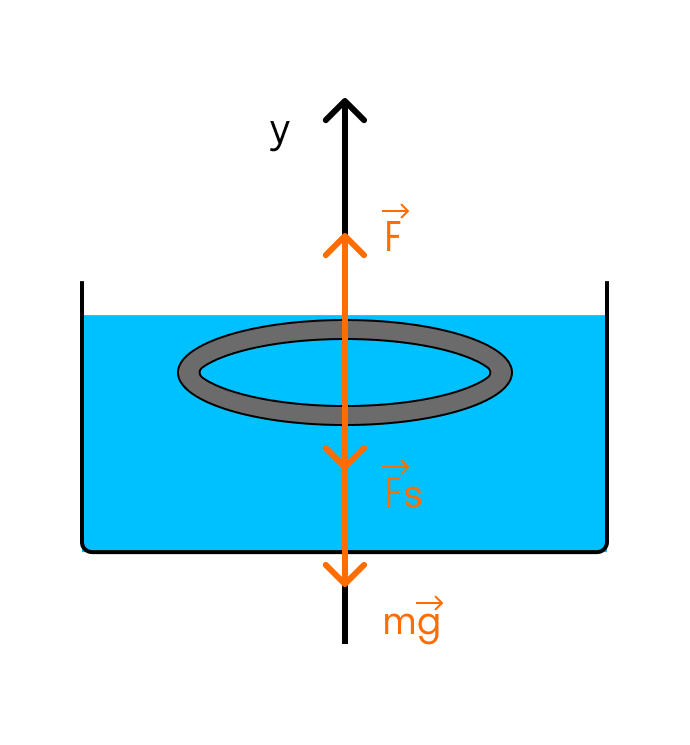
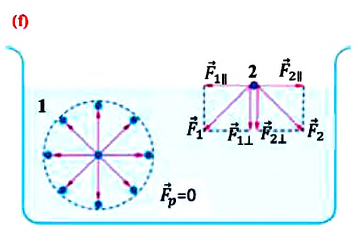
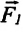


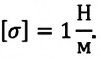
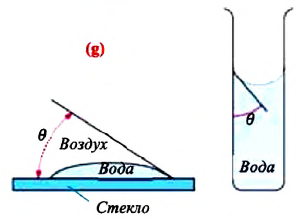
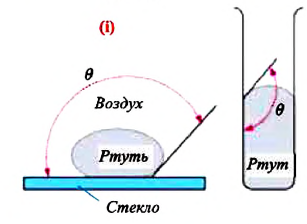
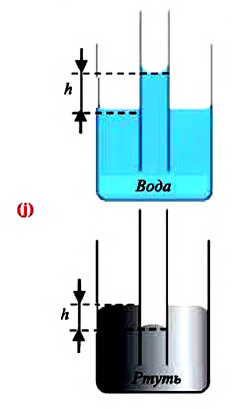
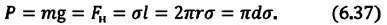
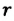 — радиус капилляра,
— радиус капилляра, 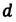 — диаметр капилляра.
— диаметр капилляра.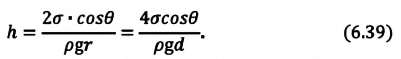
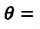
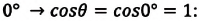

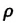 — плотность жидкости, поднимающейся в капилляре. Высота подъема жидкости в капилляре зависит от рода жидкости и обратно пропорциональна радиусу капилляра.
— плотность жидкости, поднимающейся в капилляре. Высота подъема жидкости в капилляре зависит от рода жидкости и обратно пропорциональна радиусу капилляра.
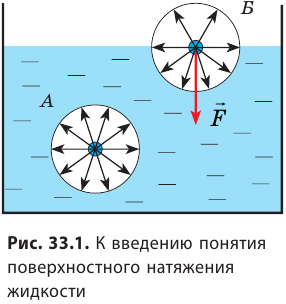
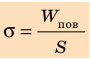
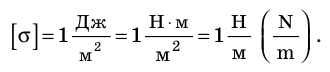
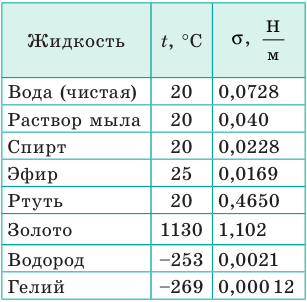
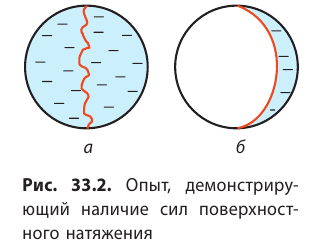
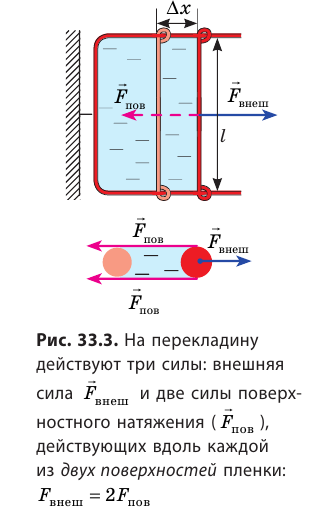
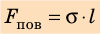
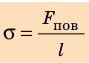



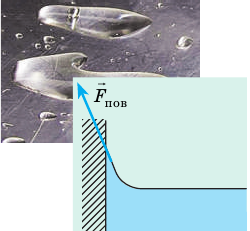
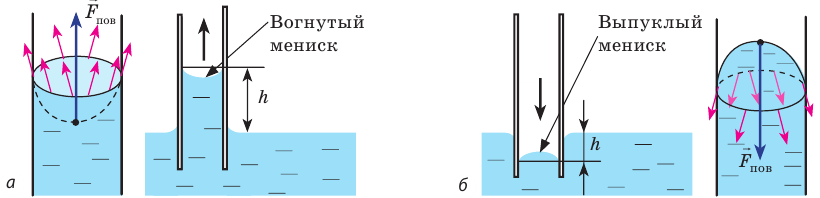
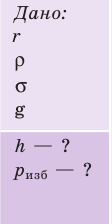
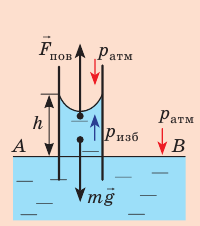
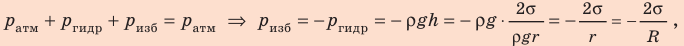
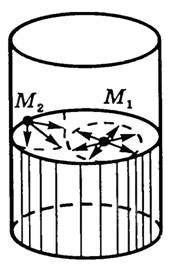
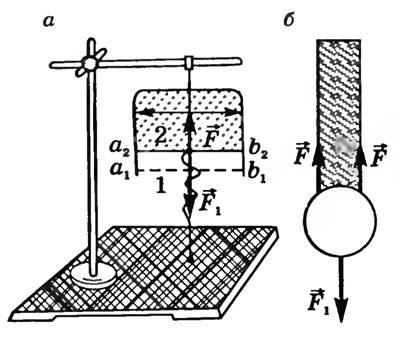













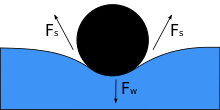


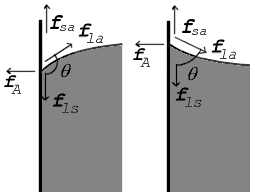































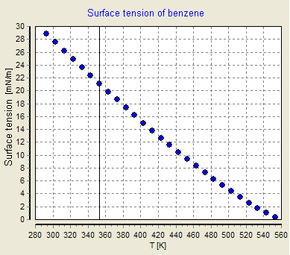






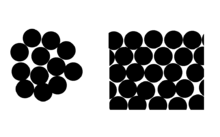
![{displaystyle gamma _{text{w}}=235.8left(1-{frac {T}{T_{text{C}}}}right)^{1.256}left[1-0.625left(1-{frac {T}{T_{text{C}}}}right)right]~{text{mN/m}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b65193820b2a29652f19d30a1adecdf0c13c8ea)
