Содержание книги
Предыдующая страница
§16. Превращение энергии в электрических и магнитных явлениях
16.7 Изменение энергии конденсатора при изменении его емкости.
Энергия конденсатора зависит от его емкости. Емкость конденсатора можно изменять, когда он заряжен — при этом будет изменяться его энергия. При рассмотрении этих процессов можно выделить два принципиально различных случая: первый — изменение емкости происходит при неизменных зарядах на обкладках; второй – емкость конденсатора изменяется при постоянном напряжении между обкладками (в этом случае конденсатор подключен к источнику постоянной ЭДС).
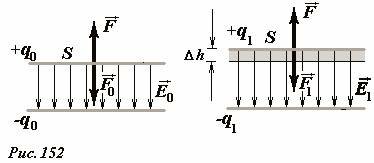
Рассмотрим теперь превращения энергии при изменении емкости плоского конденсатора, образованного двумя параллельными одинаковыми платинами площади S. Размеры пластин будем считать значительно превышающими расстояние между ними, что позволяет пренебречь краевыми эффектами, то есть считать электрическое поле (~vec E) однородным (Рис. 152). Пусть конденсатор заряжен, так что заряды каждой пластины одинаковы по модулю и равны q и противоположны по знаку, поверхностная плотность заряда на каждой пластине равна (~sigma = frac{q}{S}). Напряженность поля между пластинами в этом случае равна
(~E = frac{sigma}{varepsilon_0} = frac{q}{varepsilon_0 S}) , (1)
причем заряды каждой пластины создают поле, напряженность которого в два раза меньше напряженности суммарного поля (1); разность потенциалов между пластинами равна
(~Delta varphi = U = Eh = frac{qh}{varepsilon_0 S}) . (2)
Так заряды пластин разноименные, то пластины будут притягиваться друг к другу с некоторой силой F. Сила, действующая на одну пластину, равна произведению ее заряда на напряженность поля, создаваемого зарядом второй пластины,
(~F = q frac{E}{2} = frac{q^2}{2 varepsilon_0 S}) . (3)
Этой формуле можно придать иной вид, если выразить силу через напряженность электрического поля с помощью формулы (1)
(~F = frac{q^2}{2 varepsilon_0 S} = frac{varepsilon_0 E^2}{2} S) . (4)
Важно отметить, что давление электрического поля на проводящую платину в точности равно объемной плотности энергии поля
(~p = frac{F}{S} = frac{varepsilon_0 E^2}{2} = w) . (5)
Чтобы изменить (для определенности увеличить см. Рис. 152) расстояние между пластинами, к ним необходимо приложить внешнюю силу F0, превышающую по модулю силе электрического притяжения. При перемещении пластины (увеличении расстояния) на величину Δh эта внешняя сила совершит положительную работу.
Если пластины конденсатора изолированы, то электрический заряд и, как следствие, напряженность поля и сила притяжения не зависят от расстояния между пластинами. Поэтому работа внешней силы по перемещению пластины на расстояние Δh будет минимальна, когда эта сила равна силе притяжения между пластинами, при этом
(~A = F_0 Delta h = frac{varepsilon_0 E^2}{2} S Delta h) . (6)
Благодаря этой работе возрастает энергия электрического поля – при неизменной напряженности и плотности энергии возрастает объем, занятый полем ((Delta V = S Delta h)), что выражается формулой
(~A = Delta W = w Delta V) . (7)
При увеличении расстояния между пластинами емкость конденсатора изменяется (уменьшается). Изменение энергии конденсатора можно также рассчитать, с помощью формулы для его энергии, причем следует выразить энергию через не изменяющийся в данном случае заряд конденсатора, то есть
(~Delta W = W_1 — W_0 = frac{q^2}{2 C_1} — frac{q^2}{2 C_0} = frac{q^2}{2} left(frac{h_1}{varepsilon_0 S} — frac{h_0}{varepsilon_0 S}right) = frac{q^2 Delta h}{2 varepsilon_0 S}) . (8)
Эта формула равносильна полученным выше выражениям для изменения энергии. Таким образом, в рассмотренном процессе превращения энергии понятны: работа внешней силы увеличивает энергию электрического поля конденсатора.
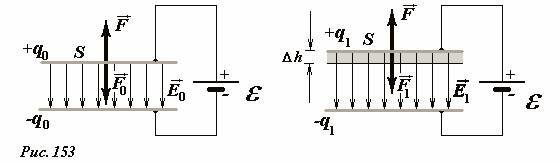
Рассмотрим теперь этот же процесс при условии, что обкладки конденсатора подключены к источнику постоянной ЭДС (Рис. 153). В этом случае при изменении расстояния между пластинами, остается неизменным напряжение U = ε между ними.
В этом случае разноименно заряженные пластины также притягиваются, поэтому для увеличения расстояния между ними внешняя сила также совершает положительную работу, однако при этом энергия конденсатора уменьшается, а не растет! Действительно, при постоянном напряжении между пластинами, изменение энергии конденсатора рассчитывается по формуле
(~Delta W_C = W_1 — W_0 = frac{C_1 U^2}{2} — frac{C_0 U^2}{2} = frac{U^2}{2} left(frac{varepsilon_0 S}{h_1} — frac{varepsilon_0 S}{h_0}right) = frac{varepsilon_0 S U^2}{2} left(frac{1}{h_1} — frac{1}{h_0}right)) . (9)
Так как h1 > h0 , то C1 < C0 и ΔWC < 0.
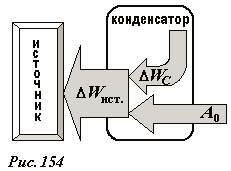
Но и в этом случае нарушения закона сохранения энергии нет, переданная системе энергия (равная совершенной работе) не «теряется» — конденсатор не является замкнутой системой, он же подключен к источнику ЭДС. При увеличении расстояния между пластинами емкость конденсатора уменьшается, поэтому уменьшается заряд на пластинах, которому некуда деться, кроме как вернуться назад, в источник. Их возращению препятствуют сторонние силы (вспомните – сторонние силы источника стремятся «вытолкнуть заряды из источника), поэтому при возвращении зарядов энергия источника повышается. Таким образом, при раздвигании пластин конденсатора происходит подзарядка источника, а энергия, переданная посредством совершенной работы, переходит в энергию источника. Кроме того, энергия поля в конденсаторе также уменьшается, поэтому эта «потеря» энергии также переходит в источник. Иными словами, при перемещении пластины внешняя сила не только совершает работу по подзарядке источника, но и «заставляет» электрическое поле вернуть часть своей энергии. Схематически потоки энергии в этом процессе показаны на Рис. 154.
Подтвердим проведенные рассуждения расчетами энергетического баланса и покажем, что он точно выполняется. Силу притяжения между пластинами (4) выразим через постоянное напряжение между пластинами
(~F = frac{varepsilon_0 E^2}{2} S = frac{varepsilon_0}{2} left(frac{U}{h}right)^2 S = frac{varepsilon_0 U^2 S}{2 h^2}) . (10)
В данном случае эта сила зависит от расстояния между пластинами. Поэтому для расчета работы необходимо разбить процесс движения пластины на малые участки и затем просуммировать работы на этих участках. Чтобы избежать этой громоздкой математической процедуры, будем считать, что смещение Δh мало настолько, что можно пренебречь изменением силы притяжения. В этом приближении работа внешней силы будет равна
(~delta A_0 = F Delta h = frac{varepsilon_0 U^2 S}{2 h^2_0} Delta h) . (11)
Преобразуем также выражение для изменения энергии конденсатора с учетом малости смещения. Запишем (h_1 = h_0 + Delta h) и подставим в формулу (9)
(~Delta W_C = W_1 — W_0 = frac{varepsilon_0 S U^2}{2} left(frac{1}{h_0 + Delta h} — frac{1}{h_0}right) = -frac{varepsilon_0 S U^2}{2} frac{Delta h}{h_0(h_0 + Delta h)} approx -frac{varepsilon_0 S U^2}{2} frac{Delta h}{h^2_0}) . (12)
Наконец, найдем работу по зарядке источника, которая равна произведению «вернувшегося» заряда на ЭДС источника (которая равна напряжению конденсатора):
(~Delta W_{ist} = U(q_0 — q_1) = U(C_0 U — C_1 U) = U^2 left(frac{varepsilon_0 S}{h_0} — frac{varepsilon_0 S}{h_0 + Delta h}right) = varepsilon_0 S U^2 left(frac{1}{h_0} — frac{1}{h_0 + Delta h}right) approx frac{varepsilon_0 S U^2 Delta h}{h^2_0}) .
Итак, проведенный расчет полностью подтверждает сделанные ранее заключения: увеличение энергии источника (что равносильно — работа по его подзарядке) равно сумме работы внешней силы и уменьшения энергии поля конденсатора
(~Delta W_{ist} = delta A_0 + (-Delta W_C)) .
Задание для самостоятельной работы.
- Докажите, что в рассмотренном процессе энергетический баланс выполняется при любом (не малом) смещении пластины.
Признавая, что «аналогии ничего не доказывают, но много объясняют», рассмотрим гидростатическую аналогию преобразования энергии при изменении «емкости» сосуда. Как мы указывали, аналогом электрического заряда может служить объем жидкости, налитой в сосуд, аналогом изменения потенциала – изменение уровня жидкости, тогда аналогом электроемкости вертикального сосуда служит площадь его дна. Таким образом, изменению емкости должно соответствовать изменение площади поперечного сечения сосуда. Представим себе сосуд в форме параллелепипеда (аквариума), одна из стенок которого может двигаться – при ее смещении изменяется площадь сосуда, то есть изменяется его «емкость». При уменьшении площади сосуда уменьшается «емкость». В рассмотренных электростатических примерах – уменьшению емкости конденсатора соответствует увеличению расстояния между его пластинами.
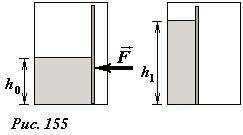
Пусть теперь в нашем сосуде находится некоторый объем жидкости, уровень которой равен h0 (Рис. 155 ). Чтобы сместить подвижную стенку, к ней необходимо приложить некоторую внешнюю силу F. Если объем жидкости в сосуде сохраняется, то при смещении стенки ее уровень повышается, следовательно, увеличивается ее энергия. Понятно, что увеличение потенциальной энергии жидкости равно работе внешней силы.
Сравните: при неизменном объеме жидкости (электрическом заряде) уменьшение площади сосуда (емкости конденсатора) под действием внешней силы приводит к возрастанию уровня жидкости (разности потенциалов) и гидростатической энергии жидкости (электростатической энергии поля).
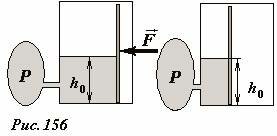
Если конденсатор подключен к источнику постоянной ЭДС, то его напряжение поддерживается постоянным. В гидростатической аналогии необходимо в этом случае говорить о постоянной высоте уровня жидкости в сосуде. В качестве устройства, поддерживающего постоянный уровень можно предложить, например, резиновый сосуд («грушу»), жидкость в которой поддерживается при постоянном давлении. Если теперь наш сосуд «переменной емкости» подключить к источнику постоянного давления (резиновой груше), то получим аналог конденсатора, подключенного к источнику постоянной ЭДС (Рис.156) При смещении подвижной стенки в этом случае внешняя сила также совершает положительную работу, но потенциальная энергия жидкости в сосуде уменьшается, так как уменьшается ее объем при неизменной высоте уровня. Под действием этой внешней силы часть жидкости из сосуда заталкивается в резиновую грушу, при этом энергия последней возрастает. Увеличение ее энергии равно сумме работы внешней силы и уменьшения потенциальной энергии жидкости в сосуде.
Сравниваем: при постоянном уровне жидкости в сосуде (напряжении конденсатора) уменьшение площади дна (емкости конденсатора) под действием внешней силы приводит к возвращению части жидкости (электрического заряда) в резиновый сосуд, поддерживаемый при постоянном давлении (источник постоянной ЭДС). При этом увеличение энергии жидкости в резиновом сосуде постоянного давления (источника ЭДС) равно сумме работы внешней силы и уменьшения потенциальной энергии жидкости в сосуде (энергии конденсатора).
Задание для самостоятельной работы.
- Докажите, что в рассмотренных гидростатических аналогиях энергетический баланс выполняется точно.
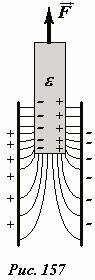
Электроемкость конденсатора зависит также от диэлектрической проницаемости вещества, находящегося между обкладками. Поэтому емкость конденсатора можно изменять, меняя вещество, находящееся между обкладками. Пусть, например, между обкладками плоского конденсатора находится диэлектрическая пластинка. Если конденсатор заряжен, то для извлечения пластинки необходимо приложить к ней внешнюю силу и совершить положительную работу. Механизм возникновения силы, действующей на пластинку со стороны электрического поля, проиллюстрирован на Рис. 157. При ее смещении изначально однородное распределение зарядов на обкладках конденсатора и поляризационных зарядов на пластинке искажается. Как следствие этого перераспределения зарядов искажается и электрическое поле, поэтому возникаю силы, стремящиеся втянуть пластинку внутрь конденсатора.
Расчет этих сил сложен, но энергетические характеристики происходящих процессов могут быть найдены без особого труда. С формальной точки зрения, не важно чем вызваны изменения емкости конденсатора, поэтому можно воспользоваться всеми рассуждениями и выводами предыдущего раздела, как для случая изолированного конденсатора (при сохранении заряда), так для конденсатора подключенного к источнику постоянной ЭДС.
Чрезвычайно интересными и практически важными являются энергетические характеристики процессов поляризации диэлектриков, однако их расчет представляет собой весьма сложную задачу. Для решения возникающих здесь проблем требует привлечения сведения о строении вещества. Некоторые из этих вопросов мы рассмотрим в следующем году после ознакомления с основами теории строения вещества.
Следующая страница
Способ, как увеличить емкость конденсатора при подключении

Такая проблема может также возникнуть, если, например, нужного номинала нет в продаже, то есть для нестандартных подключений, например, в радиотехнических опытах.
Электрическая емкость
При соединении приборов для конденсации заряда, как правило, техника интересует электрическая емкость, которая получится в итоге.
Электроемкость показывает способность двухполюсника накапливать в себе заряд и измеряется в фарадах. Может показаться, что чем выше это значение, тем лучше, но на практике не существует возможности создать все возможные на свете емкости, более того, часто это и не нужно, так как во всех приборах, использующихся повседневно, применяются стандартные приборы для конденсации.
Можно соединить несколько приборов для конденсации в цепь, создав одну конденсирующую емкость, при этом значение характерной величины будет зависеть от типа подключения, и для его расчета есть давно известные формулы.
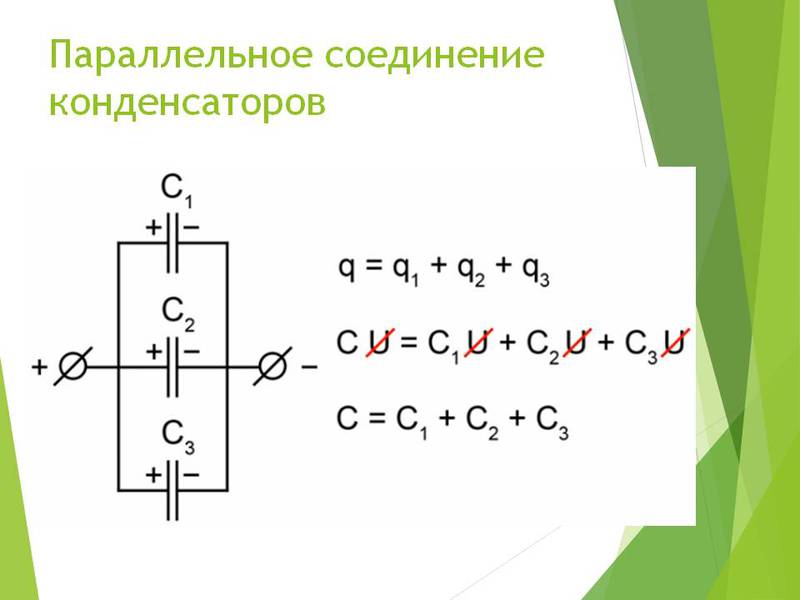
Параллельное соединение
Существует два типа подключения приборов в цепь: последовательное и параллельное. Каждый из них обладает своими свойствами, но, как правило, используется параллельное соединение конденсаторов.
Параллельное соединение обладает такими свойствами:
- Емкость составного двухполюсника увеличивается по сравнению с каждым отдельным прибором.
- Напряжение в сети не изменяется.
Соединить конденсаторы для увеличения емкости, как показывают свойства, лучше этим способом. Для этого нужно соединить выводы с каждого двухполюсника по группам: у каждого из них два вывода. Нужно создать две группы: в одну соединить все конденсаторы с одного вывода, а во вторую с оставшегося.

Например, если имеются номинальные значения 50мкф, 100мкф и 150мкф, то при последовательном подключении общее значение в цепи будет 300мкф.
В жизни это подключение используют довольно часто, например, если при расчетах оказалось, что требуется такой двухполюсник, которого в продаже точно не найти. С помощью этого способа можно варьировать емкость конденсатора так, как это потребуется, при этом не изменяя напряжение в сети.
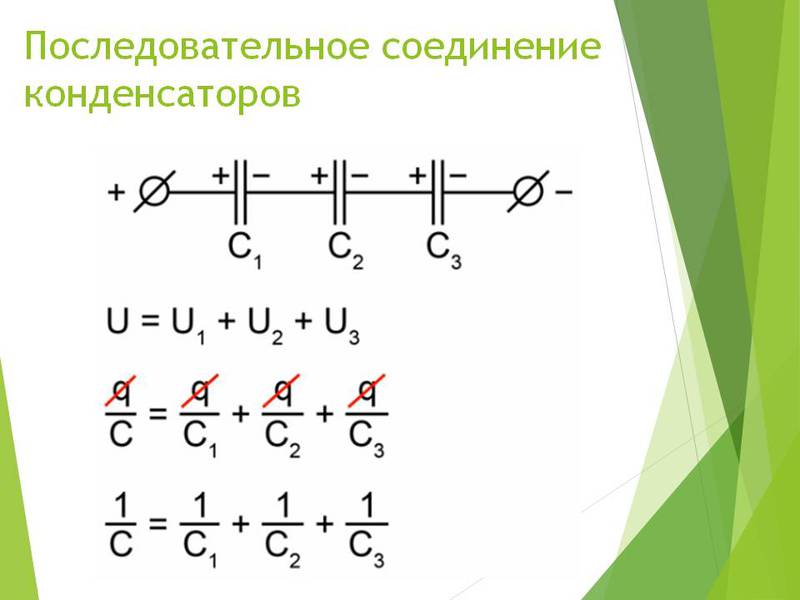
Последовательное включение конденсаторов
Свойства последовательного включения конденсаторов:
- Емкость последовательно соединенных приборов для конденсации заряда в отличие от емкости параллельно соединенных конденсаторов уменьшается.
- Напряжение на приборах растет.
Для такого подключения нужно просто соединять выводы двухполюсников один с другим, образуя цепочку: вывод первого будет соединен с выводом второго, оставшийся вывод второго с выводом третьего и так далее.
Формула подключения: 1/(1/С1+1/С2+…+1/СN), где N — это количество приборов в соединении.
Например, есть три конденсатора по 100мкф. 1/100+1/100+1/100=0,03мкф. 1/0,03=33мкф.
Заряды распределятся с чередующимся знаком, а емкостное значение будет ограничено только им же для самого слабого звена в цепи. Как только он получит свой заряд, передача тока в цепи прекратится.
Для чего тогда нужен подобный способ подключения? Такая цепь более устойчива и может выдержать большее напряжение при подключении в схему при меньшем емкостном номинале конденсатора. Однако в продаже имеются приборы, которые и без того обладают нужными свойствами, поэтому-то такое подключение в жизни практически не используется, а если используется, то для специфических задач.
Смешанный способ
Сочетает в себе параллельное и последовательное подключения.
При этом для участков с последовательным соединением характерны свойства последовательного соединения, а для участков с параллельным — свойства параллельного.
Оно используется, когда ни электроемкость, ни номинальное напряжение приборов, имеющихся в продаже, не подходят для задачи. Обычно такая проблема возникает в радиотехнике.
Чтобы определить общее значение электроемкости, нужно будет сначала определить это же значение для параллельно соединенных двухполюсников, а потом для их последовательного соединения.
Сравнение различных вариантов
| Емкость | Напряжение | |
| Параллельное | Увеличивается | Не изменяется |
| Последовательное | Уменьшается | Увеличивается |
| Смешанное | Изменяется | Увеличивается |
Для выбора соединения можно воспользоваться такой таблицей. Слева тип соединения приборов, сверху свойства прибора для конденсации заряда.
Если требуется увеличить емкость, то нужно использовать параллельное соединение, а если увеличить напряжение — то последовательное. Если же требуется и то, и то, то нужно будет рассчитывать смешанное подключение конденсаторов в цепь.
Источник
Изменение ёмкости керамических конденсаторов от температуры и напряжения, или как ваш конденсатор на 4,7мкФ превращается в 0,33мкФ
Вступление: я был озадачен.
Несколько лет назад, после более чем 25 лет работы с этими вещами, я узнал кое-что новое о керамических конденсаторах. Работая над драйвером светодиодной лампы я обнаружил, что постоянная времени RC-цепочки в моей схеме не сильно смахивает на расчётную.
Предположив, что на плату были впаяны не те компоненты, я измерил сопротивление двух резисторов составлявших делитель напряжения — они были весьма точны. Тогда был выпаян конденсатор — он так же был великолепен. Просто чтобы убедиться, я взял новые резисторы и конденсатор, измерил их, и впаял обратно. После этого я включил схему, проверил основные показатели, и ожидал увидеть что моя проблема с RC-цепочкой решена… Если бы.
Я проверял схему в её естественной среде: в корпусе, который в свою очередь сам по себе был зачехлён чтобы имитировать кожух потолочного светильника. Температура компонентов в некоторых местах достигала более чем 100ºC. Для уверенности, и чтобы освежить память я перечитал даташит на используемые конденсаторы. Так началось моё переосмысление керамических конденсаторов.
Справочная информация об основных типах керамических конденсаторов.
Для тех кто этого не помнит (как практически все), в таблице 1 указана маркировка основных типов конденсаторов и её значение. Эта таблица описывает конденсаторы второго и третьего класса. Не вдаваясь глубоко в подробности, конденсаторы первого класса обычно сделаны на диэлектрике типа C0G (NP0).
Таблица 1.
| Нижняя рабочая температура | Верхняя рабочая температура | Изменение ёмкости в диапазоне (макс.) | |||
|---|---|---|---|---|---|
| Символ | Температура (ºC) | Символ | Температура (ºC) | Символ | Изменение (%) |
| Z | +10 | 2 | +45 | A | ±1.0 |
| Y | -30 | 4 | +65 | B | ±1.5 |
| X | -55 | 5 | +85 | C | ±2.2 |
| – | – | 6 | +105 | D | ±3.3 |
| – | – | 7 | +125 | E | ±4.7 |
| – | – | 8 | +150 | F | ±7.5 |
| – | – | 9 | +200 | P | ±10 |
| – | – | – | – | R | ±15 |
| – | – | – | – | S | ±22 |
| – | – | – | – | T | +22, -33 |
| – | – | – | – | U | +22, -56 |
| – | – | – | – | V | +22, -82 |
Из описанных выше на моём жизненном пути чаще всего мне попадались конденсаторы типа X5R, X7R и Y5V. Я никогда не использовал конденсаторы типа Y5V из-за их экстремально высокой чувствительности к внешним воздействиям.
Когда производитель конденсаторов разрабатывает новый продукт, он подбирает диэлектрик так, чтобы ёмкость конденсатора изменялась не более определённых пределов в определённом температурном диапазоне. Конденсаторы X7R которые я использую не должны изменять свою ёмкость более чем на ±15% (третий символ) при изменении температуры от -55ºC (первый символ) до +125ºC (второй символ). Так что, либо мне попалась плохая партия, либо что-то ещё происходит в моей схеме.
Не все X7R созданы одинаковыми.
Так как изменение постоянной времени моей RC-цепочки было куда больше, чем это могло быть объяснено температурным коэффициентом ёмкости, мне пришлось копать глубже. Глядя на то, насколько уплыла ёмкость моего конденсатора от приложенного к нему напряжения я был очень удивлён. Результат был очень далёк от того номинала, который был впаян. Я брал конденсатор на 16В для работы в цепи 12В. Даташит говорил, что мои 4,7мкФ превращаются в 1,5мкФ в таких условиях. Это объясняло мою проблему.
Даташит также говорил, что если только увеличить типоразмер с 0805 до 1206, то результирующая ёмкость в тех же условиях будет уже 3,4мкФ! Этот момент требовал более пристального изучения.
Я нашёл, что сайты Murata® и TDK® имеют классные инструменты для построения графиков изменения ёмкости конденсаторов в зависимости от различных условий. Я прогнал через них керамические конденсаторы на 4,7мкФ для разных типоразмеров и номинальных напряжений. На рисунке 1 показаны графики построенные Murata. Были взяты конденсаторы X5R и X7R типоразмеров от 0603 до 1812 на напряжение от 6,3 до 25В.
Рисунок 1. Изменение ёмкости в зависимости от приложенного напряжения для выбранных конденсаторов.
Обратите внимание, что во-первых, при увеличении типоразмера уменьшается изменение ёмкости в зависимости от приложенного напряжения, и наоборот.
Второй интересный момент состоит в том, что в отличии от типа диэлектрика и типоразмера, номинальное напряжение похоже ни на что не влияет. Я ожидал бы, что конденсатор на 25В под напряжением 12В меньше изменит свою ёмкость, чем конденсатор на 16В под тем же напряжением. Глядя на график для X5R типоразмера 1206 мы видим, что конденсатор на 6,3В на самом деле ведёт себя лучше, чем его родня на большее номинальное напряжение.
Если взять более широкий ряд конденсаторов, то мы увидим, что это поведение характерно для всех керамических конденсаторов в целом.
Третье наблюдение состоит в том, что X7R при том же типоразмере имеет меньшую чувствительность к изменениям напряжения, чем X5R. Не знаю, насколько универсально это правило, но в моём случае это так.
Используя данные графиков, составим таблицу 2, показывающую насколько уменьшится ёмкость конденсаторов X7R при 12В.
Таблица 2. Уменьшение ёмкости конденсаторов X7R разных типоразмеров при напряжении 12В.
| Типоразмер | Ёмкость, мкФ | % от номинала |
|---|---|---|
| 0805 | 1,53 | 32,6 |
| 1206 | 3,43 | 73,0 |
| 1210 | 4,16 | 88,5 |
| 1812 | 4,18 | 88,9 |
| Номинал | 4,7 | 100 |
Мы видим устойчивое улучшение ситуации по мере роста размера корпуса пока мы не достигнем типоразмера 1210. Дальнейшее увеличение корпуса уже не имеет смысла.
В моём случае я выбрал наименьший возможный типоразмер компонентов, поскольку этот параметр был критичен для моего проекта. В своём невежестве я полагал что любой конденсатор X7R будет так же хорошо работать, как другой с тем же диэлектриком — и был неправ. Чтобы RC-цепочка заработала правильно я должен был взять конденсатор того же номинала, но в большем корпусе.
Выбор правильного конденсатора
Я очень не хотел использовать конденсатор типоразмера 1210. К счастью, я имел возможность увеличить сопротивление резисторов в пять раз, уменьшив при этом ёмкость до 1мкФ. Графики на рисунке 2 показывают поведение различных X7R конденсаторов 1мкФ на 16В в сравнении с их собратьями X7R 4,7мкФ на 16В.
Рисунок 2. Поведение различных конденсаторов на 1мкФ и 4,7мкФ.
Конденсатор 0603 1мкФ ведёт себя так же, как 0805 4,7мкФ. Вместе взятые 0805 и 1206 на 1мкФ чувствуют себя лучше, чем 4,7мкФ типоразмера 1210. Используя конденсатор 1мкФ в корпусе 0805 я мог сохранить требования к размерам компонентов, получив при этом в рабочем режиме 85% от исходной ёмкости, а не 30%, как было ранее.
Но это ещё не всё. Я был изрядно озадачен, ибо считал что все конденсаторы X7R должны иметь сходные коэффициенты изменения ёмкости от напряжения, поскольку все выполены на одном и том же диэлектрике — а именно X7R. Я связался с коллегой — специалистом по керамическим конденсаторам 1 . Он пояснил, что есть много материалов, которые квалифицируются как «X7R». На самом деле, любой материал который позволяет компоненту функционировать в температурном диапазоне от -55ºC до +125ºC с изменением характеристик не более чем на ±15% можно назвать «X7R». Так же он сказал, что нет каких-либо спецификаций на коэффициент изменения ёмкости от напряжения ни для X7R, ни для каких-либо других типов.
Это очень важный момент, и я его повторю. Производитель может называть конденсатор X7R (или X5R, или еще как-нибудь) до тех пор, пока он соответствует допускам по температурному коэффициенту ёмкости. Вне зависимости от того, насколько плох его коэффициент по напряжению.
Для инженера-разработчика этот факт только освежает старую шутку — «любой опытный инженер знает: читай даташит!»
Производители выпускают всё более миниатюрные компоненты, и вынуждены искать компромиссные материалы. Для того чтобы обеспечить необходимые ёмкостно-габаритные показатели, им приходится ухудшать коэффициенты по напряжению. Конечно, более авторитетные производители делают все возможное, чтобы свести к минимуму неблагоприятные последствия этого компромисса.
А как насчёт типа Y5V, который я сразу отбросил? Для контрольного в голову, давайте рассмотрим обычный конденсатор Y5V. Я не буду выделять какого-то конкретного производителя этих конденсаторов — все примерно одинаковы. Выберем 4,7мкФ на 6,3В в корпусе 0603, и посмотрим его параметры при температуре +85ºC и напряжении 5В. Типовая ёмкость на 92,3% ниже номинала, или 0,33мкФ. Это так. Приложив 5В к этому конденсатору мы получаем падение ёмкости в 14 раз по сравнению с номиналом.
При температуре +85ºC и напряжении 0В ёмкость уменьшается на 68,14%, с 4,7мкФ до 1,5мкФ. Можно предположить, что приложив 5В мы получим дальнейшее уменьшение ёмкости — от 0,33мкФ до 0,11мкФ. К счастью, эти эффекты не объединяются. Уменьшение ёмкости под напряжением 5В при комнатной температуре куда хуже, чем при +85ºC.
Для ясности, в данном случае при напряжении 0В ёмкость падает от 4,7мкФ до 1,5мкФ при +85ºC, в то время как при напряжении 5В ёмкость конденсатора увеличивается от 0,33мкФ при комнатной температуре, до 0,39мкФ при +85ºC. Это должно убедить вас действительно тщательно проверять все спецификации тех компонентов, которые вы используете.
Вывод
В результате этого урока я уже не просто указываю типы X7R или X5R коллегам или поставщикам. Вместо этого я указываю конкретные партии конкретных поставщиков, которые я сам проверил. Я также предупреждаю клиентов о том, чтобы они перепроверяли спецификации при рассмотрении альтернативных поставщиков для производства, чтобы гарантировать что они не столкнутся с этими проблемами.
Главный вывод из всей этой истории, как вы наверное догадались, это: «читайте даташиты!». Всегда. Без исключений. Запросите дополнительные данные, если даташит не содержит достаточной информации. Помните, что обозначения керамических конденсаторов X7V, Y5V и т.д. совершенно ничего не говорят о их коэффициентах по напряжению. Инженеры должны перепроверять данные чтобы знать, реально знать о том, как используемые конденсаторы будут вести себя в реальных условиях. В общем, имейте в виду, в нашей безумной гонке за меньшими и меньшими габаритами это становится всё более важным моментом каждый день.
Об авторе
Марк Фортунато провёл большую часть жизни пытаясь сделать так, чтобы эти противные электроны оказались в нужное время в нужном месте. Он работал над различными вещами — от систем распознавания речи и микроволновой аппаратуры, до светодиодных ламп (тех, которые регулируются правильно, заметьте!). Он провёл последние 16 лет помогая клиентам приручить их аналоговые схемы. Г-н Фортунато сейчас является ведущим специалистом подразделения коммуникационных и автомобильных решений Maxim Integrated. Когда он не пасёт электроны, Марк любит тренировать молодёжь, читать публицистику, смотреть как его младший сын играет в лакросс, а старший сын играет музыку. В целом, он стремится жить в гармонии. Марк очень сожалеет, что больше не встретится с Джимом Уильямсом или Бобом Пизом.
Сноски
1 Автор хотел бы поблагодарить Криса Буркетта, инженера по применению из TDK за его объяснения «что здесь, чёрт возьми, происходит».
Murata является зарегистрированной торговой маркой компании Murata Manufacturing Co., Ltd.
Источник
в условии
в решении
в тексте к заданию
в атрибутах
Категория:
Атрибут:
Всего: 70 1–20 | 21–40 | 41–60 | 61–70
Добавить в вариант
Между пластинами заряженного плоского конденсатора поместили диэлектрик с диэлектрической проницаемостью так, что он полностью заполнил объем между пластинами. Как изменились емкость конденсатора, заряд на пластинах и напряжение между ними, если конденсатор подключен к источнику?
ФИЗИЧЕСКАЯ ХАРАКТЕРИСТИКА
А) Заряд на пластинах
Б) Напряжение между пластинами
В) Емкость конденсатора
ЕЕ ИЗМЕНЕНИЕ
1) Уменьшится в раз
2) Останется неизменной
3) Увеличится в раз
К каждой позиции первого столбца подберите соответствующую позицию второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
Конденсатор подключён к источнику с постоянным напряжением U = 10 В, C = 10 мкФ. Какой станет энергия конденсатора, если расстояние между обкладками заполнить диэлектриком с диэлектрической проницаемостью = 2? Ответ запишите в миллиджоулях.
Обкладки плоского воздушного конденсатора изготовлены из двух тонких квадратных металлических пластин со стороной a (на рисунке показан вид сбоку). Расстояние между обкладками d << a. Этот конденсатор подключён к источнику постоянного напряжения U с пренебрежимо малым внутренним сопротивлением.
Через пространство между обкладками начинают медленно протаскивать с постоянной скоростью V квадратную пластину со стороной a и толщиной d, сделанную из однородного непроводящего материала с диэлектрической
проницаемостью В некоторый момент всё пространство между обкладками конденсатора оказывается заполненным диэлектриком. Затем пластину продолжают двигать в том же направлении с той же скоростью до тех пор, пока она не покинет пространство между обкладками.
Опираясь на законы физики, изобразите график зависимости силы электрического тока I, протекающего через источник напряжения, от времени t. Искажениями электрического поля вблизи краёв обкладок и пластины можно пренебречь. Отсчёт времени начинается в момент, когда правый край пластины находится на уровне левых краёв обкладок конденсатора, а заканчивается, когда пластина оказывается полностью вынутой из конденсатора с противоположной стороны. Объясните построение графика, указав явления и закономерности, которые Вы при этом использовали. На осях координат обозначьте физические величины в «особых» точках графика (максимумы, минимумы, разрывы, точки излома графика), если они есть.
Пластины плоского конденсатора, подключённого к батарее, сделаны из металлических листов в виде квадрата со стороной а. Квадратные пластины заменили на круглые диаметром а. При этом расстояние между пластинами увеличили, а батарею оставили прежней. Как в результате изменятся следующие физические величины: электрическая ёмкость конденсатора, модуль напряжённости электрического поля между пластинами конденсатора, заряд конденсатора?
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
A) Электрическая ёмкость конденсатора
Б) Модуль напряжённости электрического поля между пластинами конденсатора
B) Заряд конденсатора
ИХ ИЗМЕНЕНИЕ
1) Увеличится
2) Уменьшится
3) Не изменится
Плоский воздушный конденсатор подключён к аккумулятору. Не отключая конденсатор от аккумулятора, уменьшили расстояние между пластинами конденсатора. Как изменятся при этом ёмкость конденсатора и величина заряда на его обкладках?
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Ёмкость
конденсатора |
Величина заряда
конденсатора |
Плоский воздушный конденсатор подключён к аккумулятору. Не отключая конденсатор от аккумулятора, вставили диэлектрик между пластинами конденсатора. Как изменятся при этом ёмкость конденсатора и величина заряда на его обкладках?
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Ёмкость
конденсатора |
Величина заряда
конденсатора |
Источник: ЕГЭ по физике 11.06.2021. Основная волна. Москва
Конденсатор подключён к источнику тока последовательно с резистором R = 20 кОм (см. рис.). В момент времени t = 0 ключ замыкают. В этот момент конденсатор полностью разряжен. Результаты измерений силы тока в цепи представлены в таблице.
| t, с | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| I, мкА | 300 | 110 | 40 | 15 | 5 | 2 | 1 |
Внутренним сопротивлением источника и сопротивлением проводов пренебречь. Выберите все верные утверждения о процессах, наблюдаемых в опыте.
1) В момент времени t = 3 с напряжение на резисторе равно 0,6 В.
2) Через 6 с после замыкания ключа конденсатор полностью зарядился.
3) ЭДС источника тока составляет 6 В.
4) В момент времени t = 3 с напряжение на конденсаторе равно 5,7 В.
5) Ток через резистор в процессе наблюдения увеличивается.
Источник: ЕГЭ — 2015. Досрочная волна.
Конденсатор подключен к источнику тока последовательно с резистором R = 20 кОм (см. рис.). В момент времени t = 0 ключ замыкают. В этот момент конденсатор полностью разряжен. Результаты измерений силы тока в цепи, выполненных с точностью ±1 мкА, представлены в таблице
| t, с | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| I, мкА | 300 | 110 | 40 | 15 | 5 | 2 | 1 |
Выберите все верные утверждения о процессах, наблюдаемых в опыте.
1) Ток через резистор в процессе наблюдения уменьшается.
2) Через 3 с после замыкания ключа конденсатор полностью зарядился.
3) ЭДС источника тока составляет 4 В.
4) В момент времени t = 3 с напряжение на резисторе равно 0,3 В.
5) В момент времени t = 3 с напряжение на конденсаторе равно 5,1 В.
Источник: РЕШУ ЕГЭ
Плоский конденсатор с воздушным зазором между обкладками подключён к источнику постоянного напряжения. Как изменятся величина заряда конденсатора и разность потенциалов между его обкладками при увеличении зазора между ними?
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Величина заряда
конденсатора |
Разность потенциалов между обкладками конденсатора |
Источник: ЕГЭ — 2015. Досрочная волна.
Плоский воздушный конденсатор ёмкостью С0, подключённый к источнику постоянного напряжения, состоит из двух металлических пластин, находящихся на расстоянии d0 друг от друга. Расстояние между пластинами меняется со временем так, как показано на графике.
Выберите все верные утверждения, соответствующих описанию опыта.
1) В момент времени t4 ёмкость конденсатора увеличилась в 5 раз по сравнению с первоначальной (при t = 0).
2) В интервале времени от t1 до t4 заряд конденсатора возрастает.
3) В интервале времени от t1 до t4 энергия конденсатора равномерно уменьшается.
4) В промежутке времени от t1 до t4 напряжённость электрического поля между пластинами конденсатора остаётся постоянной.
5) В промежутке времени от t1 до t4 напряжённость электрического поля между пластинами конденсатора убывает.
Источник: Демонстрационная версия ЕГЭ—2020 по физике.
В колебательном контуре, состоящем из двух параллельно соединенных конденсаторов и подключенной к ним катушки индуктивности, происходят свободные электромагнитные колебания. В момент, когда конденсаторы разряжены, один из них отсоединяют. Как после этого изменятся следующие физические величины: запасенная в контуре энергия, частота свободных электромагнитных колебаний, амплитуда напряжения между пластинами второго конденсатора?
Для каждой величины определите соотвествующий характер изменения. Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
А) Запасенная в контуре энергия
Б) Частота свободных электромагнитных колебаний
В) Амплитуда напряжения между пластинами второго конденсатора
ИХ ИЗМЕНЕНИЕ
1) Увеличится
2) Уменьшится
3) Не изменится
К источнику тока с ЭДС 2 В подключён конденсатор ёмкостью 1 мкФ. Какую работу совершил источник тока при зарядке конденсатора? (Ответ дайте в микроджоулях.)
Плоский воздушный конденсатор с диэлектриком между пластинами подключён к аккумулятору. Не отключая конденсатор от аккумулятора, диэлектрик удаляют из конденсатора. Как изменятся при этом ёмкость конденсатора и разность потенциалов между его обкладками?
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины.
Цифры в ответе могут повторяться.
| Ёмкость конденсатора | Разность потенциалов между обкладками конденсатора |
Конденсатор колебательного контура длительное время подключён к источнику постоянного напряжения (см. рис.). В момент t = 0 переключатель К переводят из положения 1 в положение 2. На графиках А и Б представлены изменения физических величин, характеризующих колебания в контуре после этого. T – период электромагнитных колебаний.
Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
ГРАФИКИ
А)
Б)
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
1) заряд правой обкладки конденсатора
2) заряд левой обкладки конденсатора
3) энергия электрического поля конденсатора
4) модуль напряжения на конденсаторе
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
Источник: ЕГЭ по физике. Вариант 114
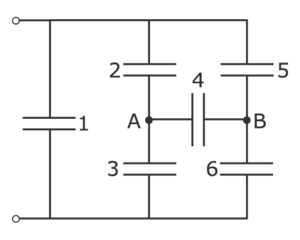
В электрической цепи, схема которой изображена на рисунке, ёмкости конденсаторов равны C1 = 1 мкФ, C2 = 2 мкФ, C3 = 3 мкФ, C4 = 4 мкФ, C5 = 5 мкФ, и все они первоначально не заряжены. Какой заряд установится на конденсаторе C5 после подключения к этой цепи источника с напряжением U = 12 В?
В электрической цепи, схема которой изображена на рисунке, ёмкости конденсаторов равны C1 = 1 мкФ, C2 = 2 мкФ, C3 = 3 мкФ, C4 = 4 мкФ, C5 = 5 мкФ, и все они первоначально не заряжены. Какой заряд установится на конденсаторе C5 после подключения к этой цепи источника с напряжением U = 10 В?
К источнику тока с ЭДС 2 В подключен конденсатор емкостью 1 мкФ. Какое тепло выделится в цепи в процессе зарядки конденсатора? (Ответ дайте в микроджоулях.) Эффектами излучения пренебречь.
Плоский конденсатор заполнен непроводящим веществом с диэлектрической проницаемостью, равной 3, и подключён к источнику постоянного напряжения. Это вещество удаляют из конденсатора и взамен помещают между пластинами другой изолирующий материал с диэлектрической проницаемостью, равной 5. Как меняются в результате замены диэлектрика электрическая ёмкость конденсатора и заряд на его пластинах? Для каждой величины определите соответствующий характер её изменения:
1) увеличивается;
2) уменьшается;
3) не изменяется.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Электрическая ёмкость конденсатора | Заряд на пластинах конденсатора |
Всего: 70 1–20 | 21–40 | 41–60 | 61–70