Коррекция ошибок ecc - Исправление ошибок и поиск оптимальных решений проблем

«Interleaver» redirects here. For the fiber-optic device, see optical interleaver.

In computing, telecommunication, information theory, and coding theory, forward error correction (FEC) or channel coding^[1]^[2]^[3] is a technique used for controlling errors in data transmission over unreliable or noisy communication channels.

The central idea is that the sender encodes the message in a redundant way, most often by using an error correction code or error correcting code, (ECC).^[4]^[5] The redundancy allows the receiver not only to detect errors that may occur anywhere in the message, but often to correct a limited number of errors. Therefore a reverse channel to request re-transmission may not be needed. The cost is a fixed, higher forward channel bandwidth.

The American mathematician Richard Hamming pioneered this field in the 1940s and invented the first error-correcting code in 1950: the Hamming (7,4) code.^[5]

FEC can be applied in situations where re-transmissions are costly or impossible, such as one-way communication links or when transmitting to multiple receivers in multicast.
Long-latency connections also benefit; in the case of a satellite orbiting Uranus, retransmission due to errors can create a delay of five hours. FEC is widely used in modems and in cellular networks, as well.

FEC processing in a receiver may be applied to a digital bit stream or in the demodulation of a digitally modulated carrier. For the latter, FEC is an integral part of the initial analog-to-digital conversion in the receiver. The Viterbi decoder implements a soft-decision algorithm to demodulate digital data from an analog signal corrupted by noise. Many FEC decoders can also generate a bit-error rate (BER) signal which can be used as feedback to fine-tune the analog receiving electronics.

FEC information is added to mass storage (magnetic, optical and solid state/flash based) devices to enable recovery of corrupted data, and is used as ECC computer memory on systems that require special provisions for reliability.

The maximum proportion of errors or missing bits that can be corrected is determined by the design of the ECC, so different forward error correcting codes are suitable for different conditions. In general, a stronger code induces more redundancy that needs to be transmitted using the available bandwidth, which reduces the effective bit-rate while improving the received effective signal-to-noise ratio. The noisy-channel coding theorem of Claude Shannon can be used to compute the maximum achievable communication bandwidth for a given maximum acceptable error probability. This establishes bounds on the theoretical maximum information transfer rate of a channel with some given base noise level. However, the proof is not constructive, and hence gives no insight of how to build a capacity achieving code. After years of research, some advanced FEC systems like polar code^[3] come very close to the theoretical maximum given by the Shannon channel capacity under the hypothesis of an infinite length frame.

How it works[edit]

ECC is accomplished by adding redundancy to the transmitted information using an algorithm. A redundant bit may be a complex function of many original information bits. The original information may or may not appear literally in the encoded output; codes that include the unmodified input in the output are systematic, while those that do not are non-systematic.

A simplistic example of ECC is to transmit each data bit 3 times, which is known as a (3,1) repetition code. Through a noisy channel, a receiver might see 8 versions of the output, see table below.

Triplet received	Interpreted as
000	0 (error-free)
001	0
010	0
100	0
111	1 (error-free)
110	1
101	1
011	1

This allows an error in any one of the three samples to be corrected by «majority vote», or «democratic voting». The correcting ability of this ECC is:

Up to 1 bit of triplet in error, or
up to 2 bits of triplet omitted (cases not shown in table).

Though simple to implement and widely used, this triple modular redundancy is a relatively inefficient ECC. Better ECC codes typically examine the last several tens or even the last several hundreds of previously received bits to determine how to decode the current small handful of bits (typically in groups of 2 to 8 bits).

Averaging noise to reduce errors[edit]

ECC could be said to work by «averaging noise»; since each data bit affects many transmitted symbols, the corruption of some symbols by noise usually allows the original user data to be extracted from the other, uncorrupted received symbols that also depend on the same user data.

Because of this «risk-pooling» effect, digital communication systems that use ECC tend to work well above a certain minimum signal-to-noise ratio and not at all below it.
This all-or-nothing tendency – the cliff effect – becomes more pronounced as stronger codes are used that more closely approach the theoretical Shannon limit.
Interleaving ECC coded data can reduce the all or nothing properties of transmitted ECC codes when the channel errors tend to occur in bursts. However, this method has limits; it is best used on narrowband data.

Most telecommunication systems use a fixed channel code designed to tolerate the expected worst-case bit error rate, and then fail to work at all if the bit error rate is ever worse.
However, some systems adapt to the given channel error conditions: some instances of hybrid automatic repeat-request use a fixed ECC method as long as the ECC can handle the error rate, then switch to ARQ when the error rate gets too high;
adaptive modulation and coding uses a variety of ECC rates, adding more error-correction bits per packet when there are higher error rates in the channel, or taking them out when they are not needed.

Types of ECC[edit]

A block code (specifically a Hamming code) where redundant bits are added as a block to the end of the initial message

A continuous code convolutional code where redundant bits are added continuously into the structure of the code word

The two main categories of ECC codes are block codes and convolutional codes.

Block codes work on fixed-size blocks (packets) of bits or symbols of predetermined size. Practical block codes can generally be hard-decoded in polynomial time to their block length.
Convolutional codes work on bit or symbol streams of arbitrary length. They are most often soft decoded with the Viterbi algorithm, though other algorithms are sometimes used. Viterbi decoding allows asymptotically optimal decoding efficiency with increasing constraint length of the convolutional code, but at the expense of exponentially increasing complexity. A convolutional code that is terminated is also a ‘block code’ in that it encodes a block of input data, but the block size of a convolutional code is generally arbitrary, while block codes have a fixed size dictated by their algebraic characteristics. Types of termination for convolutional codes include «tail-biting» and «bit-flushing».

There are many types of block codes; Reed–Solomon coding is noteworthy for its widespread use in compact discs, DVDs, and hard disk drives. Other examples of classical block codes include Golay, BCH, Multidimensional parity, and Hamming codes.

Hamming ECC is commonly used to correct NAND flash memory errors.^[6]
This provides single-bit error correction and 2-bit error detection.
Hamming codes are only suitable for more reliable single-level cell (SLC) NAND.
Denser multi-level cell (MLC) NAND may use multi-bit correcting ECC such as BCH or Reed–Solomon.^[7]^[8] NOR Flash typically does not use any error correction.^[7]

Classical block codes are usually decoded using hard-decision algorithms,^[9] which means that for every input and output signal a hard decision is made whether it corresponds to a one or a zero bit. In contrast, convolutional codes are typically decoded using soft-decision algorithms like the Viterbi, MAP or BCJR algorithms, which process (discretized) analog signals, and which allow for much higher error-correction performance than hard-decision decoding.

Nearly all classical block codes apply the algebraic properties of finite fields. Hence classical block codes are often referred to as algebraic codes.

In contrast to classical block codes that often specify an error-detecting or error-correcting ability, many modern block codes such as LDPC codes lack such guarantees. Instead, modern codes are evaluated in terms of their bit error rates.

Most forward error correction codes correct only bit-flips, but not bit-insertions or bit-deletions.
In this setting, the Hamming distance is the appropriate way to measure the bit error rate.
A few forward error correction codes are designed to correct bit-insertions and bit-deletions, such as Marker Codes and Watermark Codes.
The Levenshtein distance is a more appropriate way to measure the bit error rate when using such codes.
^[10]

Code-rate and the tradeoff between reliability and data rate[edit]

The fundamental principle of ECC is to add redundant bits in order to help the decoder to find out the true message that was encoded by the transmitter. The code-rate of a given ECC system is defined as the ratio between the number of information bits and the total number of bits (i.e., information plus redundancy bits) in a given communication package. The code-rate is hence a real number. A low code-rate close to zero implies a strong code that uses many redundant bits to achieve a good performance, while a large code-rate close to 1 implies a weak code.

The redundant bits that protect the information have to be transferred using the same communication resources that they are trying to protect. This causes a fundamental tradeoff between reliability and data rate.^[11] In one extreme, a strong code (with low code-rate) can induce an important increase in the receiver SNR (signal-to-noise-ratio) decreasing the bit error rate, at the cost of reducing the effective data rate. On the other extreme, not using any ECC (i.e., a code-rate equal to 1) uses the full channel for information transfer purposes, at the cost of leaving the bits without any additional protection.

One interesting question is the following: how efficient in terms of information transfer can an ECC be that has a negligible decoding error rate? This question was answered by Claude Shannon with his second theorem, which says that the channel capacity is the maximum bit rate achievable by any ECC whose error rate tends to zero:^[12] His proof relies on Gaussian random coding, which is not suitable to real-world applications. The upper bound given by Shannon’s work inspired a long journey in designing ECCs that can come close to the ultimate performance boundary. Various codes today can attain almost the Shannon limit. However, capacity achieving ECCs are usually extremely complex to implement.

The most popular ECCs have a trade-off between performance and computational complexity. Usually, their parameters give a range of possible code rates, which can be optimized depending on the scenario. Usually, this optimization is done in order to achieve a low decoding error probability while minimizing the impact to the data rate. Another criterion for optimizing the code rate is to balance low error rate and retransmissions number in order to the energy cost of the communication.^[13]

Concatenated ECC codes for improved performance[edit]

Classical (algebraic) block codes and convolutional codes are frequently combined in concatenated coding schemes in which a short constraint-length Viterbi-decoded convolutional code does most of the work and a block code (usually Reed–Solomon) with larger symbol size and block length «mops up» any errors made by the convolutional decoder. Single pass decoding with this family of error correction codes can yield very low error rates, but for long range transmission conditions (like deep space) iterative decoding is recommended.

Concatenated codes have been standard practice in satellite and deep space communications since Voyager 2 first used the technique in its 1986 encounter with Uranus. The Galileo craft used iterative concatenated codes to compensate for the very high error rate conditions caused by having a failed antenna.

Low-density parity-check (LDPC)[edit]

Low-density parity-check (LDPC) codes are a class of highly efficient linear block
codes made from many single parity check (SPC) codes. They can provide performance very close to the channel capacity (the theoretical maximum) using an iterated soft-decision decoding approach, at linear time complexity in terms of their block length. Practical implementations rely heavily on decoding the constituent SPC codes in parallel.

LDPC codes were first introduced by Robert G. Gallager in his PhD thesis in 1960,
but due to the computational effort in implementing encoder and decoder and the introduction of Reed–Solomon codes,
they were mostly ignored until the 1990s.

LDPC codes are now used in many recent high-speed communication standards, such as DVB-S2 (Digital Video Broadcasting – Satellite – Second Generation), WiMAX (IEEE 802.16e standard for microwave communications), High-Speed Wireless LAN (IEEE 802.11n),^[14] 10GBase-T Ethernet (802.3an) and G.hn/G.9960 (ITU-T Standard for networking over power lines, phone lines and coaxial cable). Other LDPC codes are standardized for wireless communication standards within 3GPP MBMS (see fountain codes).

Turbo codes[edit]

Turbo coding is an iterated soft-decoding scheme that combines two or more relatively simple convolutional codes and an interleaver to produce a block code that can perform to within a fraction of a decibel of the Shannon limit. Predating LDPC codes in terms of practical application, they now provide similar performance.

One of the earliest commercial applications of turbo coding was the CDMA2000 1x (TIA IS-2000) digital cellular technology developed by Qualcomm and sold by Verizon Wireless, Sprint, and other carriers. It is also used for the evolution of CDMA2000 1x specifically for Internet access, 1xEV-DO (TIA IS-856). Like 1x, EV-DO was developed by Qualcomm, and is sold by Verizon Wireless, Sprint, and other carriers (Verizon’s marketing name for 1xEV-DO is Broadband Access, Sprint’s consumer and business marketing names for 1xEV-DO are Power Vision and Mobile Broadband, respectively).

Local decoding and testing of codes[edit]

Sometimes it is only necessary to decode single bits of the message, or to check whether a given signal is a codeword, and do so without looking at the entire signal. This can make sense in a streaming setting, where codewords are too large to be classically decoded fast enough and where only a few bits of the message are of interest for now. Also such codes have become an important tool in computational complexity theory, e.g., for the design of probabilistically checkable proofs.

Locally decodable codes are error-correcting codes for which single bits of the message can be probabilistically recovered by only looking at a small (say constant) number of positions of a codeword, even after the codeword has been corrupted at some constant fraction of positions. Locally testable codes are error-correcting codes for which it can be checked probabilistically whether a signal is close to a codeword by only looking at a small number of positions of the signal.

Interleaving[edit]

«Interleaver» redirects here. For the fiber-optic device, see optical interleaver.

A short illustration of interleaving idea

Interleaving is frequently used in digital communication and storage systems to improve the performance of forward error correcting codes. Many communication channels are not memoryless: errors typically occur in bursts rather than independently. If the number of errors within a code word exceeds the error-correcting code’s capability, it fails to recover the original code word. Interleaving alleviates this problem by shuffling source symbols across several code words, thereby creating a more uniform distribution of errors.^[15] Therefore, interleaving is widely used for burst error-correction.

The analysis of modern iterated codes, like turbo codes and LDPC codes, typically assumes an independent distribution of errors.^[16] Systems using LDPC codes therefore typically employ additional interleaving across the symbols within a code word.^[17]

For turbo codes, an interleaver is an integral component and its proper design is crucial for good performance.^[15]^[18] The iterative decoding algorithm works best when there are not short cycles in the factor graph that represents the decoder; the interleaver is chosen to avoid short cycles.

Interleaver designs include:

rectangular (or uniform) interleavers (similar to the method using skip factors described above)
convolutional interleavers
random interleavers (where the interleaver is a known random permutation)
S-random interleaver (where the interleaver is a known random permutation with the constraint that no input symbols within distance S appear within a distance of S in the output).^[19]
a contention-free quadratic permutation polynomial (QPP).^[20] An example of use is in the 3GPP Long Term Evolution mobile telecommunication standard.^[21]

In multi-carrier communication systems, interleaving across carriers may be employed to provide frequency diversity, e.g., to mitigate frequency-selective fading or narrowband interference.^[22]

Example[edit]

Transmission without interleaving:

Error-free message:                                 aaaabbbbccccddddeeeeffffgggg
Transmission with a burst error:                    aaaabbbbccc____deeeeffffgggg

Here, each group of the same letter represents a 4-bit one-bit error-correcting codeword. The codeword cccc is altered in one bit and can be corrected, but the codeword dddd is altered in three bits, so either it cannot be decoded at all or it might be decoded incorrectly.

With interleaving:

Error-free code words:                              aaaabbbbccccddddeeeeffffgggg
Interleaved:                                        abcdefgabcdefgabcdefgabcdefg
Transmission with a burst error:                    abcdefgabcd____bcdefgabcdefg
Received code words after deinterleaving:           aa_abbbbccccdddde_eef_ffg_gg

In each of the codewords «aaaa», «eeee», «ffff», and «gggg», only one bit is altered, so one-bit error-correcting code will decode everything correctly.

Transmission without interleaving:

Original transmitted sentence:                      ThisIsAnExampleOfInterleaving
Received sentence with a burst error:               ThisIs______pleOfInterleaving

The term «AnExample» ends up mostly unintelligible and difficult to correct.

With interleaving:

Transmitted sentence:                               ThisIsAnExampleOfInterleaving...
Error-free transmission:                            TIEpfeaghsxlIrv.iAaenli.snmOten.
Received sentence with a burst error:               TIEpfe______Irv.iAaenli.snmOten.
Received sentence after deinterleaving:             T_isI_AnE_amp_eOfInterle_vin_...

No word is completely lost and the missing letters can be recovered with minimal guesswork.

Disadvantages of interleaving[edit]

Use of interleaving techniques increases total delay. This is because the entire interleaved block must be received before the packets can be decoded.^[23] Also interleavers hide the structure of errors; without an interleaver, more advanced decoding algorithms can take advantage of the error structure and achieve more reliable communication than a simpler decoder combined with an interleaver^{[citation needed]}. An example of such an algorithm is based on neural network^[24] structures.

Software for error-correcting codes[edit]

Simulating the behaviour of error-correcting codes (ECCs) in software is a common practice to design, validate and improve ECCs. The upcoming wireless 5G standard raises a new range of applications for the software ECCs: the Cloud Radio Access Networks (C-RAN) in a Software-defined radio (SDR) context. The idea is to directly use software ECCs in the communications. For instance in the 5G, the software ECCs could be located in the cloud and the antennas connected to this computing resources: improving this way the flexibility of the communication network and eventually increasing the energy efficiency of the system.

In this context, there are various available Open-source software listed below (non exhaustive).

AFF3CT(A Fast Forward Error Correction Toolbox): a full communication chain in C++ (many supported codes like Turbo, LDPC, Polar codes, etc.), very fast and specialized on channel coding (can be used as a program for simulations or as a library for the SDR).
IT++: a C++ library of classes and functions for linear algebra, numerical optimization, signal processing, communications, and statistics.
OpenAir: implementation (in C) of the 3GPP specifications concerning the Evolved Packet Core Networks.

List of error-correcting codes[edit]

Distance	Code
2 (single-error detecting)	Parity
3 (single-error correcting)	Triple modular redundancy
3 (single-error correcting)	perfect Hamming such as Hamming(7,4)
4 (SECDED)	Extended Hamming
5 (double-error correcting)
6 (double-error correct-/triple error detect)	Nordstrom-Robinson code
7 (three-error correcting)	perfect binary Golay code
8 (TECFED)	extended binary Golay code

AN codes
BCH code, which can be designed to correct any arbitrary number of errors per code block.
Barker code used for radar, telemetry, ultra sound, Wifi, DSSS mobile phone networks, GPS etc.
Berger code
Constant-weight code
Convolutional code
Expander codes
Group codes
Golay codes, of which the Binary Golay code is of practical interest
Goppa code, used in the McEliece cryptosystem
Hadamard code
Hagelbarger code
Hamming code
Latin square based code for non-white noise (prevalent for example in broadband over powerlines)
Lexicographic code
Linear Network Coding, a type of erasure correcting code across networks instead of point-to-point links
Long code
Low-density parity-check code, also known as Gallager code, as the archetype for sparse graph codes
LT code, which is a near-optimal rateless erasure correcting code (Fountain code)
m of n codes
Nordstrom-Robinson code, used in Geometry and Group Theory^[25]
Online code, a near-optimal rateless erasure correcting code
Polar code (coding theory)
Raptor code, a near-optimal rateless erasure correcting code
Reed–Solomon error correction
Reed–Muller code
Repeat-accumulate code
Repetition codes, such as Triple modular redundancy
Spinal code, a rateless, nonlinear code based on pseudo-random hash functions^[26]
Tornado code, a near-optimal erasure correcting code, and the precursor to Fountain codes
Turbo code
Walsh–Hadamard code
Cyclic redundancy checks (CRCs) can correct 1-bit errors for messages at most $2^{n-1}-1$ bits long for optimal generator polynomials of degree , see Mathematics of cyclic redundancy checks#Bitfilters

References[edit]

^ Charles Wang; Dean Sklar; Diana Johnson (Winter 2001–2002). «Forward Error-Correction Coding». Crosslink. The Aerospace Corporation. 3 (1). Archived from the original on 14 March 2012. Retrieved 5 March 2006.
^ Charles Wang; Dean Sklar; Diana Johnson (Winter 2001–2002). «Forward Error-Correction Coding». Crosslink. The Aerospace Corporation. 3 (1). Archived from the original on 14 March 2012. Retrieved 5 March 2006. How Forward Error-Correcting Codes Work]
^ ^a ^b Maunder, Robert (2016). «Overview of Channel Coding».
^ Glover, Neal; Dudley, Trent (1990). Practical Error Correction Design For Engineers (Revision 1.1, 2nd ed.). CO, USA: Cirrus Logic. ISBN 0-927239-00-0.
^ ^a ^b Hamming, Richard Wesley (April 1950). «Error Detecting and Error Correcting Codes». Bell System Technical Journal. USA: AT&T. 29 (2): 147–160. doi:10.1002/j.1538-7305.1950.tb00463.x. S2CID 61141773.
^ «Hamming codes for NAND flash memory devices» Archived 21 August 2016 at the Wayback Machine. EE Times-Asia. Apparently based on «Micron Technical Note TN-29-08: Hamming Codes for NAND Flash Memory Devices». 2005. Both say: «The Hamming algorithm is an industry-accepted method for error detection and correction in many SLC NAND flash-based applications.»
^ ^a ^b «What Types of ECC Should Be Used on Flash Memory?» (Application note). Spansion. 2011. Both Reed–Solomon algorithm and BCH algorithm are common ECC choices for MLC NAND flash. … Hamming based block codes are the most commonly used ECC for SLC…. both Reed–Solomon and BCH are able to handle multiple errors and are widely used on MLC flash.
^ Jim Cooke (August 2007). «The Inconvenient Truths of NAND Flash Memory» (PDF). p. 28. For SLC, a code with a correction threshold of 1 is sufficient. t=4 required … for MLC.
^ Baldi, M.; Chiaraluce, F. (2008). «A Simple Scheme for Belief Propagation Decoding of BCH and RS Codes in Multimedia Transmissions». International Journal of Digital Multimedia Broadcasting. 2008: 1–12. doi:10.1155/2008/957846.
^ Shah, Gaurav; Molina, Andres; Blaze, Matt (2006). «Keyboards and covert channels». USENIX. Retrieved 20 December 2018.
^ Tse, David; Viswanath, Pramod (2005), Fundamentals of Wireless Communication, Cambridge University Press, UK
^ Shannon, C. E. (1948). «A mathematical theory of communication» (PDF). Bell System Technical Journal. 27 (3–4): 379–423 & 623–656. doi:10.1002/j.1538-7305.1948.tb01338.x. hdl:11858/00-001M-0000-002C-4314-2.
^ Rosas, F.; Brante, G.; Souza, R. D.; Oberli, C. (2014). «Optimizing the code rate for achieving energy-efficient wireless communications». Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC). pp. 775–780. doi:10.1109/WCNC.2014.6952166. ISBN 978-1-4799-3083-8.
^ IEEE Standard, section 20.3.11.6 «802.11n-2009» Archived 3 February 2013 at the Wayback Machine, IEEE, 29 October 2009, accessed 21 March 2011.
^ ^a ^b Vucetic, B.; Yuan, J. (2000). Turbo codes: principles and applications. Springer Verlag. ISBN 978-0-7923-7868-6.
^ Luby, Michael; Mitzenmacher, M.; Shokrollahi, A.; Spielman, D.; Stemann, V. (1997). «Practical Loss-Resilient Codes». Proc. 29th Annual Association for Computing Machinery (ACM) Symposium on Theory of Computation.
^ «Digital Video Broadcast (DVB); Second generation framing structure, channel coding and modulation systems for Broadcasting, Interactive Services, News Gathering and other satellite broadband applications (DVB-S2)». En 302 307. ETSI (V1.2.1). April 2009.
^ Andrews, K. S.; Divsalar, D.; Dolinar, S.; Hamkins, J.; Jones, C. R.; Pollara, F. (November 2007). «The Development of Turbo and LDPC Codes for Deep-Space Applications». Proceedings of the IEEE. 95 (11): 2142–2156. doi:10.1109/JPROC.2007.905132. S2CID 9289140.
^ Dolinar, S.; Divsalar, D. (15 August 1995). «Weight Distributions for Turbo Codes Using Random and Nonrandom Permutations». TDA Progress Report. 122: 42–122. Bibcode:1995TDAPR.122…56D. CiteSeerX 10.1.1.105.6640.
^ Takeshita, Oscar (2006). «Permutation Polynomial Interleavers: An Algebraic-Geometric Perspective». IEEE Transactions on Information Theory. 53 (6): 2116–2132. arXiv:cs/0601048. Bibcode:2006cs……..1048T. doi:10.1109/TIT.2007.896870. S2CID 660.
^ 3GPP TS 36.212, version 8.8.0, page 14
^ «Digital Video Broadcast (DVB); Frame structure, channel coding and modulation for a second generation digital terrestrial television broadcasting system (DVB-T2)». En 302 755. ETSI (V1.1.1). September 2009.
^ Techie (3 June 2010). «Explaining Interleaving». W3 Techie Blog. Retrieved 3 June 2010.
^ Krastanov, Stefan; Jiang, Liang (8 September 2017). «Deep Neural Network Probabilistic Decoder for Stabilizer Codes». Scientific Reports. 7 (1): 11003. arXiv:1705.09334. Bibcode:2017NatSR…711003K. doi:10.1038/s41598-017-11266-1. PMC 5591216. PMID 28887480.
^ Nordstrom, A.W.; Robinson, J.P. (1967), «An optimum nonlinear code», Information and Control, 11 (5–6): 613–616, doi:10.1016/S0019-9958(67)90835-2
^ Perry, Jonathan; Balakrishnan, Hari; Shah, Devavrat (2011). «Rateless Spinal Codes». Proceedings of the 10th ACM Workshop on Hot Topics in Networks. pp. 1–6. doi:10.1145/2070562.2070568. hdl:1721.1/79676. ISBN 9781450310598.

External links[edit]

Morelos-Zaragoza, Robert (2004). «The Correcting Codes (ECC) Page». Retrieved 5 March 2006.
lpdec: library for LP decoding and related things (Python)

Источник

«Interleaver» redirects here. For the fiber-optic device, see optical interleaver.

The American mathematician Richard Hamming pioneered this field in the 1940s and invented the first error-correcting code in 1950: the Hamming (7,4) code.^[5]

How it works[edit]

A simplistic example of ECC is to transmit each data bit 3 times, which is known as a (3,1) repetition code. Through a noisy channel, a receiver might see 8 versions of the output, see table below.

Triplet received	Interpreted as
000	0 (error-free)
001	0
010	0
100	0
111	1 (error-free)
110	1
101	1
011	1

This allows an error in any one of the three samples to be corrected by «majority vote», or «democratic voting». The correcting ability of this ECC is:

Up to 1 bit of triplet in error, or
up to 2 bits of triplet omitted (cases not shown in table).

Averaging noise to reduce errors[edit]

Because of this «risk-pooling» effect, digital communication systems that use ECC tend to work well above a certain minimum signal-to-noise ratio and not at all below it.
This all-or-nothing tendency – the cliff effect – becomes more pronounced as stronger codes are used that more closely approach the theoretical Shannon limit.
Interleaving ECC coded data can reduce the all or nothing properties of transmitted ECC codes when the channel errors tend to occur in bursts. However, this method has limits; it is best used on narrowband data.

Types of ECC[edit]

A block code (specifically a Hamming code) where redundant bits are added as a block to the end of the initial message

A continuous code convolutional code where redundant bits are added continuously into the structure of the code word

The two main categories of ECC codes are block codes and convolutional codes.

Block codes work on fixed-size blocks (packets) of bits or symbols of predetermined size. Practical block codes can generally be hard-decoded in polynomial time to their block length.
Convolutional codes work on bit or symbol streams of arbitrary length. They are most often soft decoded with the Viterbi algorithm, though other algorithms are sometimes used. Viterbi decoding allows asymptotically optimal decoding efficiency with increasing constraint length of the convolutional code, but at the expense of exponentially increasing complexity. A convolutional code that is terminated is also a ‘block code’ in that it encodes a block of input data, but the block size of a convolutional code is generally arbitrary, while block codes have a fixed size dictated by their algebraic characteristics. Types of termination for convolutional codes include «tail-biting» and «bit-flushing».

Nearly all classical block codes apply the algebraic properties of finite fields. Hence classical block codes are often referred to as algebraic codes.

Code-rate and the tradeoff between reliability and data rate[edit]

Concatenated ECC codes for improved performance[edit]

Low-density parity-check (LDPC)[edit]

Turbo codes[edit]

Local decoding and testing of codes[edit]

Interleaving[edit]

«Interleaver» redirects here. For the fiber-optic device, see optical interleaver.

A short illustration of interleaving idea

Interleaver designs include:

rectangular (or uniform) interleavers (similar to the method using skip factors described above)
convolutional interleavers
random interleavers (where the interleaver is a known random permutation)
S-random interleaver (where the interleaver is a known random permutation with the constraint that no input symbols within distance S appear within a distance of S in the output).^[19]
a contention-free quadratic permutation polynomial (QPP).^[20] An example of use is in the 3GPP Long Term Evolution mobile telecommunication standard.^[21]

In multi-carrier communication systems, interleaving across carriers may be employed to provide frequency diversity, e.g., to mitigate frequency-selective fading or narrowband interference.^[22]

Example[edit]

Transmission without interleaving:

Error-free message:                                 aaaabbbbccccddddeeeeffffgggg
Transmission with a burst error:                    aaaabbbbccc____deeeeffffgggg

With interleaving:

Error-free code words:                              aaaabbbbccccddddeeeeffffgggg
Interleaved:                                        abcdefgabcdefgabcdefgabcdefg
Transmission with a burst error:                    abcdefgabcd____bcdefgabcdefg
Received code words after deinterleaving:           aa_abbbbccccdddde_eef_ffg_gg

In each of the codewords «aaaa», «eeee», «ffff», and «gggg», only one bit is altered, so one-bit error-correcting code will decode everything correctly.

Transmission without interleaving:

Original transmitted sentence:                      ThisIsAnExampleOfInterleaving
Received sentence with a burst error:               ThisIs______pleOfInterleaving

The term «AnExample» ends up mostly unintelligible and difficult to correct.

With interleaving:

Transmitted sentence:                               ThisIsAnExampleOfInterleaving...
Error-free transmission:                            TIEpfeaghsxlIrv.iAaenli.snmOten.
Received sentence with a burst error:               TIEpfe______Irv.iAaenli.snmOten.
Received sentence after deinterleaving:             T_isI_AnE_amp_eOfInterle_vin_...

No word is completely lost and the missing letters can be recovered with minimal guesswork.

Disadvantages of interleaving[edit]

Software for error-correcting codes[edit]

In this context, there are various available Open-source software listed below (non exhaustive).

AFF3CT(A Fast Forward Error Correction Toolbox): a full communication chain in C++ (many supported codes like Turbo, LDPC, Polar codes, etc.), very fast and specialized on channel coding (can be used as a program for simulations or as a library for the SDR).
IT++: a C++ library of classes and functions for linear algebra, numerical optimization, signal processing, communications, and statistics.
OpenAir: implementation (in C) of the 3GPP specifications concerning the Evolved Packet Core Networks.

List of error-correcting codes[edit]

Distance	Code
2 (single-error detecting)	Parity
3 (single-error correcting)	Triple modular redundancy
3 (single-error correcting)	perfect Hamming such as Hamming(7,4)
4 (SECDED)	Extended Hamming
5 (double-error correcting)
6 (double-error correct-/triple error detect)	Nordstrom-Robinson code
7 (three-error correcting)	perfect binary Golay code
8 (TECFED)	extended binary Golay code

AN codes
BCH code, which can be designed to correct any arbitrary number of errors per code block.
Barker code used for radar, telemetry, ultra sound, Wifi, DSSS mobile phone networks, GPS etc.
Berger code
Constant-weight code
Convolutional code
Expander codes
Group codes
Golay codes, of which the Binary Golay code is of practical interest
Goppa code, used in the McEliece cryptosystem
Hadamard code
Hagelbarger code
Hamming code
Latin square based code for non-white noise (prevalent for example in broadband over powerlines)
Lexicographic code
Linear Network Coding, a type of erasure correcting code across networks instead of point-to-point links
Long code
Low-density parity-check code, also known as Gallager code, as the archetype for sparse graph codes
LT code, which is a near-optimal rateless erasure correcting code (Fountain code)
m of n codes
Nordstrom-Robinson code, used in Geometry and Group Theory^[25]
Online code, a near-optimal rateless erasure correcting code
Polar code (coding theory)
Raptor code, a near-optimal rateless erasure correcting code
Reed–Solomon error correction
Reed–Muller code
Repeat-accumulate code
Repetition codes, such as Triple modular redundancy
Spinal code, a rateless, nonlinear code based on pseudo-random hash functions^[26]
Tornado code, a near-optimal erasure correcting code, and the precursor to Fountain codes
Turbo code
Walsh–Hadamard code
Cyclic redundancy checks (CRCs) can correct 1-bit errors for messages at most $2^{n-1}-1$ bits long for optimal generator polynomials of degree , see Mathematics of cyclic redundancy checks#Bitfilters

References[edit]

^ Charles Wang; Dean Sklar; Diana Johnson (Winter 2001–2002). «Forward Error-Correction Coding». Crosslink. The Aerospace Corporation. 3 (1). Archived from the original on 14 March 2012. Retrieved 5 March 2006.
^ Charles Wang; Dean Sklar; Diana Johnson (Winter 2001–2002). «Forward Error-Correction Coding». Crosslink. The Aerospace Corporation. 3 (1). Archived from the original on 14 March 2012. Retrieved 5 March 2006. How Forward Error-Correcting Codes Work]
^ ^a ^b Maunder, Robert (2016). «Overview of Channel Coding».
^ Glover, Neal; Dudley, Trent (1990). Practical Error Correction Design For Engineers (Revision 1.1, 2nd ed.). CO, USA: Cirrus Logic. ISBN 0-927239-00-0.
^ ^a ^b Hamming, Richard Wesley (April 1950). «Error Detecting and Error Correcting Codes». Bell System Technical Journal. USA: AT&T. 29 (2): 147–160. doi:10.1002/j.1538-7305.1950.tb00463.x. S2CID 61141773.
^ «Hamming codes for NAND flash memory devices» Archived 21 August 2016 at the Wayback Machine. EE Times-Asia. Apparently based on «Micron Technical Note TN-29-08: Hamming Codes for NAND Flash Memory Devices». 2005. Both say: «The Hamming algorithm is an industry-accepted method for error detection and correction in many SLC NAND flash-based applications.»
^ ^a ^b «What Types of ECC Should Be Used on Flash Memory?» (Application note). Spansion. 2011. Both Reed–Solomon algorithm and BCH algorithm are common ECC choices for MLC NAND flash. … Hamming based block codes are the most commonly used ECC for SLC…. both Reed–Solomon and BCH are able to handle multiple errors and are widely used on MLC flash.
^ Jim Cooke (August 2007). «The Inconvenient Truths of NAND Flash Memory» (PDF). p. 28. For SLC, a code with a correction threshold of 1 is sufficient. t=4 required … for MLC.
^ Baldi, M.; Chiaraluce, F. (2008). «A Simple Scheme for Belief Propagation Decoding of BCH and RS Codes in Multimedia Transmissions». International Journal of Digital Multimedia Broadcasting. 2008: 1–12. doi:10.1155/2008/957846.
^ Shah, Gaurav; Molina, Andres; Blaze, Matt (2006). «Keyboards and covert channels». USENIX. Retrieved 20 December 2018.
^ Tse, David; Viswanath, Pramod (2005), Fundamentals of Wireless Communication, Cambridge University Press, UK
^ Shannon, C. E. (1948). «A mathematical theory of communication» (PDF). Bell System Technical Journal. 27 (3–4): 379–423 & 623–656. doi:10.1002/j.1538-7305.1948.tb01338.x. hdl:11858/00-001M-0000-002C-4314-2.
^ Rosas, F.; Brante, G.; Souza, R. D.; Oberli, C. (2014). «Optimizing the code rate for achieving energy-efficient wireless communications». Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC). pp. 775–780. doi:10.1109/WCNC.2014.6952166. ISBN 978-1-4799-3083-8.
^ IEEE Standard, section 20.3.11.6 «802.11n-2009» Archived 3 February 2013 at the Wayback Machine, IEEE, 29 October 2009, accessed 21 March 2011.
^ ^a ^b Vucetic, B.; Yuan, J. (2000). Turbo codes: principles and applications. Springer Verlag. ISBN 978-0-7923-7868-6.
^ Luby, Michael; Mitzenmacher, M.; Shokrollahi, A.; Spielman, D.; Stemann, V. (1997). «Practical Loss-Resilient Codes». Proc. 29th Annual Association for Computing Machinery (ACM) Symposium on Theory of Computation.
^ «Digital Video Broadcast (DVB); Second generation framing structure, channel coding and modulation systems for Broadcasting, Interactive Services, News Gathering and other satellite broadband applications (DVB-S2)». En 302 307. ETSI (V1.2.1). April 2009.
^ Andrews, K. S.; Divsalar, D.; Dolinar, S.; Hamkins, J.; Jones, C. R.; Pollara, F. (November 2007). «The Development of Turbo and LDPC Codes for Deep-Space Applications». Proceedings of the IEEE. 95 (11): 2142–2156. doi:10.1109/JPROC.2007.905132. S2CID 9289140.
^ Dolinar, S.; Divsalar, D. (15 August 1995). «Weight Distributions for Turbo Codes Using Random and Nonrandom Permutations». TDA Progress Report. 122: 42–122. Bibcode:1995TDAPR.122…56D. CiteSeerX 10.1.1.105.6640.
^ Takeshita, Oscar (2006). «Permutation Polynomial Interleavers: An Algebraic-Geometric Perspective». IEEE Transactions on Information Theory. 53 (6): 2116–2132. arXiv:cs/0601048. Bibcode:2006cs……..1048T. doi:10.1109/TIT.2007.896870. S2CID 660.
^ 3GPP TS 36.212, version 8.8.0, page 14
^ «Digital Video Broadcast (DVB); Frame structure, channel coding and modulation for a second generation digital terrestrial television broadcasting system (DVB-T2)». En 302 755. ETSI (V1.1.1). September 2009.
^ Techie (3 June 2010). «Explaining Interleaving». W3 Techie Blog. Retrieved 3 June 2010.
^ Krastanov, Stefan; Jiang, Liang (8 September 2017). «Deep Neural Network Probabilistic Decoder for Stabilizer Codes». Scientific Reports. 7 (1): 11003. arXiv:1705.09334. Bibcode:2017NatSR…711003K. doi:10.1038/s41598-017-11266-1. PMC 5591216. PMID 28887480.
^ Nordstrom, A.W.; Robinson, J.P. (1967), «An optimum nonlinear code», Information and Control, 11 (5–6): 613–616, doi:10.1016/S0019-9958(67)90835-2
^ Perry, Jonathan; Balakrishnan, Hari; Shah, Devavrat (2011). «Rateless Spinal Codes». Proceedings of the 10th ACM Workshop on Hot Topics in Networks. pp. 1–6. doi:10.1145/2070562.2070568. hdl:1721.1/79676. ISBN 9781450310598.

External links[edit]

Morelos-Zaragoza, Robert (2004). «The Correcting Codes (ECC) Page». Retrieved 5 March 2006.
lpdec: library for LP decoding and related things (Python)

Источник

Вступление

На сегодняшний день на просторах Рунета можно встретить открытые темы на форумах с вопросами – стоит ли брать рабочую станцию с ECC-памятью или можно обойтись обычной? В данных ветках можно прочесть множество противоречивых утверждений, и часть из них говорит о том, что коррекция ошибок сильно замедляет память, а следовательно и ЦП. Но мало кто это проверял на деле на современных процессорах.

Сегодня мы разберемся в этом вопросе и сравним производительность серверного процессора с обоими типами памяти. Но для начала небольшой экскурс.

Коррекция ошибок

Для чего необходима коррекция? И почему в работе памяти возникают ошибки? Перед ответом на эти вопросы следует разделить ошибки на два типа:

Аппаратные ошибки;
Случайные ошибки.

Причиной появления аппаратных ошибок является дефектная микросхема DRAM, а случайные ошибки возникают под воздействием излучения, альфа-частиц, элементарных частиц и прочего. Соответственно, первые в принципе неисправимы – если чип дефектный, то поможет только его замена; а вот вторые могут быть исправлены.

Почему же так необходима коррекция ошибок в рабочих станциях и серверах? Однобитовая ошибка в 64-битном слове меняет содержимое ячейки памяти, а в конечном итоге на жесткий диск может быть записано другое число, другие данные, при этом компьютер не зафиксирует эту подмену. А изменение бита в оперативной памяти может вызвать сбой программы, что для рабочей станции и сервера недопустимо.

рекомендации

3060 дешевле 30тр в Ситилинке

3080 дешевле 70 тр — цены снова пошли вниз

3070 Gigabyte дешевле 50 тр

Выбираем игровой ноут: на что смотреть, на чем сэкономить

3070 Gainward Phantom дешевле 50 тр

MSI 3060 Ti Ventus OC за 40 тр

RTX 3070 Ti за 55 тр в Ситилинке

5 видов 4090 в Ситилинке по норм ценам

-19% на 13900KF — цены рухнули

13700K дешевле 40 тр в Регарде

Ищем PHP-программиста для апгрейда конфы

-17% на RTX 4070 Ti в Ситилинке

3070 Gigabyte Gaming за 50 тр с началом

13600K дешевле 30 тр в Регарде

3070 дешевле 50 тр в Ситилинке

MSI 3050 за 25 тр в Ситилинке

3060 Gigabyte Gaming за 30 тр с началом

12900K за 40тр с началом в Ситилинке

3060 Ti Gigabyte за 40тр в Регарде

Для обнаружения изменения битов памяти можно использовать метод подсчета контрольной суммы, но он позволяет лишь обнаруживать ошибки без их исправления.

В свое время было предложено много различных способов решения данной проблемы, но на сегодняшний день наибольшее распространение получил метод коррекции ошибок или ECC (Error-Correcting Code). Данный метод позволяет автоматически исправлять однобитовые ошибки в 64-битном слове – SEC (Single Error Correction) и детектировать двухбитовые – DED (Double Error Detection).

Физическая реализация ECC заключается в размещении дополнительной микросхемы памяти на модуле ОЗУ – соответственно, при одностороннем дизайне модуля памяти вместо восьми чипов располагается девять, а при двустороннем вместо шестнадцати – восемнадцать. Таким образом, ширина модуля становится не 64 бита, а 72 бита.

Метод коррекции ошибок работает следующим образом: при записи 64 бит данных в ячейку памяти происходит подсчет контрольной суммы, составляющей 8 бит. Когда процессор обращается к этим данным и производит считывание, проводится повторный подсчет контрольной суммы и сравнение с исходной. Если суммы не совпадают – произошла ошибка. Если она однобитовая, то неправильный бит исправляется автоматически, если двухбитовая – детектируется и сообщается ОС.

Финансовая сторона

Прежде чем приступить к тестированию, необходимо затронуть финансовый вопрос.

Стоимость обычного модуля памяти DDR3-1600 с напряжением 1.35 В и объемом 8 Гбайт составляет около 3600 рублей, а с коррекцией ошибок – 4800 рублей. На первый взгляд ECC-память выходит на 30-35% дороже, что, в целом, не позволяет их сравнивать в силу существенно большей стоимости последней. Но почему же тогда такой вопрос возникает при сборке рабочей станции? Все просто – необходимо смотреть на данный вопрос шире, а именно – смотреть на общую стоимость рабочей станции.

Ценник однопроцессорной станции на базе четырехъядерного восьмипоточного Xeon (настольные процессоры серий i5 и i7 не поддерживают ECC-память) с 32 Гбайтами памяти, материнской платы с чипсетом C222/С224/С226 (десктопные наборы логики Z87/Z97 и другие также не поддерживают память с коррекцией ошибок) будет превышать 70 000 рублей (при условии, что устанавливаются серверные SSD с повышенным ресурсом). А если включить в эту стоимость и дискретную видеокарту, и прочие сопутствующие компоненты, например, ИБП, то ценник из пятизначного превратится в шестиизначный, перевалив планку в 100 000 рублей.

Покупка 32 Гбайт памяти с коррекцией ошибок потребует дополнительных 4-6 тысяч рублей, что по отношению к общей стоимости рабочей станции не превышает 5%, то есть не является критичным. Также переход от десктопного к серверному железу предоставит и другие преимущества, например: интегрированные графические карты P4600 в процессорах Intel Xeon E3-1200 третьего поколения получили оптимизированные драйверы, которые должны повышать производительность в профессиональных приложениях, например, в CAD; поддержка технологии Intel VT-d, которая позволяет пробрасывать устройства в виртуальную среду, например, видеокарты; прочие серверные технологии – Intel AMT или IPMI, WatchDog и другие, которые также могут оказаться полезными.

Таким образом, хоть и сама ECC-память стоит заметно дороже обычной, в общей стоимости рабочей станции данная статья затрат является несущественной, и переплата не превышает 5%.

Тестовый стенд

Для данного обзора использовалась следующая конфигурация:

Материнская плата: Supermicro X10SAE (Intel C226, LGA 1150);
Процессор: Xeon E3-1245V3 (Turbo Boost – off, EIST – off, HT – on);
Оперативная память:

2x Kingston DDR3-1600 ECC 8 Гбайт (KVR16LE11/8 CL11, 1.35 В);
2x Kingston DDR3-1600 8 Гбайт (KVR16LN11/8 CL11, 1.35 В);

ОС: Windows 8.1 Pro 64-bit.

Методика тестирования

В рамках тестирования были произведены замеры производительности как при одноканальном режиме работы ИКП, так и при двухканальном. Суммарный объем ОЗУ составил 8 (один модуль) и 16 Гбайт (два модуля) соответственно.

Программное обеспечение:

3DMark 2006 1.2;
7Zip 9.20;
AIDA64 Extreme 5.20.3400;
Cinebench R15;
CrystalMark 2004R3;
Fritz 4.20;
LinX 0.6.5;
wPrime 2.10.

Результаты тестирования

Тест памяти

Перед тем, как приступить к тестированию, проведем замер пропускной способности памяти и латентности.

При изучении результатов можно заключить, что производительность ECC- и non-ECC- памяти находится на одном и том же уровне в рамках погрешности.

Если в предыдущем тесте от замера к замеру выигрывал то один, то другой тип памяти, то при замере латентности ECC-память постоянно показывает большие задержки. Но разница несущественна – всего лишь 1 нс.

Таким образом, замер ПС и латентности памяти не показал особых различий между ECC- и non-ECC-памятью. Посмотрим, повторится ли это в последующих тестах.

3DMark

Тестовый пакет 3DMark содержит подтесты как для процессора, так и для графической карты. Здесь и кроется самое интересное – давно известно, что встроенному видеоядру не хватает существующей ПСП в 25.6 Гбайт/с, поэтому именно в графических подтестах можно выявить негативное влияние коррекции ошибок, если оно вообще есть,…

… но разницы нет – что ECC, что non-ECC. Ни процессор, ни интегрированное ядро никак не реагируют на замену обычной памяти на DDR с коррекцией ошибок – результаты одинаковы в рамках погрешности. Среднеарифметическая разница составила 0.02% в пользу ECC-памяти для одноканального режима и 1.6% для двухканального режима.

При этом нельзя сказать, что встроенная видеокарта P4600 не зависит от скорости ОЗУ – при одноканальном доступе общий результат почти на 30% ниже, чем при двухканальном. Другими словами, скорость ОЗУ критична для графического ядра, но сами по себе «ECC-версии» не влияют ни на скорость ОЗУ, ни на видеокарту.

7Zip

Архиваторы, как известно, чувствительны к памяти, поэтому, возможно, здесь получится зафиксировать влияние типа памяти на производительность.

Ситуация с архивацией неоднозначная: с одной стороны – в одноканальном режиме (как при распаковке, так и при сжатии) ECC-память уверенно оказывается медленнее на 2%; с другой – в двухканальном режиме при сжатии ECC-память уверенно быстрее, а при распаковке – медленнее, а среднее арифметическое – быстрее на 0.65%.

Скорее всего, причина в следующем – пропускной способности памяти при одноканальном доступе процессору явно недостаточно, и поэтому чуть большая латентность ECC-памяти сказывается на производительности; а при двухканальном доступе ПСП полностью покрывает нужды CPU и поэтому чуть большая латентность памяти с коррекцией ошибок не сказывается на производительности. В любом случае зафиксировать существенного влияния на скорость архивации не получилось.

Cinebench

Тестовый пакет Cinebench содержит подтест как процессора, так и видеокарты.

Но ни первый, ни вторая никак не отреагировали на ECC-память.

Зато налицо явная зависимость видеокарты от ПСП – при одноканальном доступе результат в OpenGL оказался на 25% ниже, чем при двухканальном. Вспоминая результаты 3DMark и смотря на нынешние, можно заключить, что производительность интегрированной видеокарты хоть и зависит от ПСП, но ECC-память не оказывает на нее негативного влияния.

Источник

Всем привет! Тема сегодняшней публикации — поддержка ECC оперативной памяти: что это такое, как работает данная функция, зависит ли от процессора ее использование на ПК.

Что такое ЕСС память

Аббревиатура происходит от английского названия error correcting code memory, то есть память с коррекцией ошибок кода. Такая ОЗУ распознает и устраняет спонтанно возникающие изменения в битах памяти, которых быть не должно.

Как правило, такая память может исправить изменения в одном бите одного машинного слова. При его чтении будет опознано то же значение, что и было записано, несмотря на возникающие «глюки».

Обычная память, то есть non-ECC, этого делать не умеет.

Этот тип памяти используется в компьютерах, для которых важна бесперебойная работа, включая крупные серверные станции. Для использования такого режима необходима поддержка контроллером ОЗУ – как встраиваемого в чипсет, так и реализованном на кристалле вместе с ядрами.

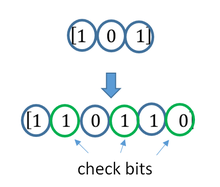
Базовый алгоритм, который используется чаще всего, основан на коде Хемминга – самоконтролирующемся двоичном коде, названном в честь предложившего такую систему американского математика.

Существуют алгоритмы, способные исправлять более одной ошибки, но используются они реже. С технологической точки зрения такая система предполагает использование модулей ОЗУ, в которых на каждые 8 микросхем памяти приходится один компонент, хранящий ЕСС-коды (то есть 8 бит на каждые 64 бита).

Причины появления ошибок в ОЗУ

Главная проблема для любого электронного устройства – невидимые космические лучи, от которых земная атмосфера не защищает должным образом. Элементарные частицы, которые пребывают в этом потоке, способны влиять на работу электроники.Под их воздействием физические свойства оперативки могут меняться, что уже ведет к размагничиванию. При смене данных, из единицы (заряженное состояние) на ноль (разряженное) уже появляется искажение.

А так как любой компьютер на самом «глубинном» уровне проводит все вычисления с помощью двоичных кодов, нарушения свойств электронных компонентов и провоцируют ошибки в работе.

Характерно, что чем выше от уровня моря, тем меньше плотность воздуха и соответственно, интенсивнее космическое излучение. Компьютерные системы, которые работают на большой высоте, требуют более эффективной защиты. Советую также почитать «Что такое ОЗУ в компьютере: из чего состоит и для чего служит?»(уже на сайте).

Стоит ли использовать ЕСС память

Объективных причин для использования такой ОЗУ на домашнем ПК нет.

Несмотря на то, что земной диск медленно дрейфует по Космическому океану, покоясь на спинах трех китов, вероятность искажения данных под воздействием вредоносных лучей, на самом-то деле крайне мала. При этом самое страшное, что может случиться при таких неполадках – вылет операционной системы в синий экран.

Впрочем, это может быть действительно страшно – например, в случае, если вы в течение пары часов монтировали видеоролик, забывая сохраняться в процессе, или же у вас последний и решительный бой, от которого зависит судьба клана, в какой-нибудь ММОРПГ.

Такая память работает медленнее обычной – в среднем, на 2-3%, так как для проверки контрольных сумм необходим один дополнительный такт контроллера. Такой режим работы требует больше логических ресурсов.

Как уже сказано выше, в основном такая память почти всегда регистровая (Registered), то есть имеет дополнительный регистр для считывания и хранения двоичных кодов. Существуют модули ECC памяти без регистров (UDIMM), которые можно использовать в домашних ПК.

Однако учтите, что такое удовольствие обойдется дороже, так как цена на такие модули ОЗУ обычно выше. Кроме того, требуется наличие материнской платы, чипсета и процессора (к слову, такие модели есть и у Intel, и у AMD), поддерживающих ЕСС память. Стоят они внезапно тоже, как правило, дороже.

И если вы решили проапгрейдить комп для использования ЕСС памяти, проверьте спецификации упомянутых выше компонентов. Если в описании написано что нет поддержки такого режима, деталь придется менять на более подходящую, что значит дополнительные расходы.

Не исключено, что придется менять и мать, и «камень», и планки оперативки. При сборке нового компьютера несколько проще: можно сразу купить соответствующие компоненты. Однако, на мой взгляд, это уже лишнее – страховка от мнимых сбоев не стоит потери быстродействия.

Также советую на эту тему ознакомиться с публикациями «Влияние тактовой частоты оперативной памяти в компьютере»(уже на блоге) и «Тайминги и частота оперативной памяти: кто важнее и влиятельней?». Буду признателен всем, кто расшарит эту статью в социальных сетях. До завтра!

С уважением, автор блога Андрей Андреев.

Источник

ECC, от английского error-correcting code, переводиться на русский язык, как код коррекции ошибок. Встроенная в контроллёры флешек технология, обнаружения и исправления ошибок при передаче данных. ECC способна справиться только с несущественными проблемами, в тяжелых случаях флешка заблокируется на запись данных.

ЗАЧЕМ ЭТО НАДО

Если в эпоху качественных SLC и MLC микросхем флэш-памяти, не было особого смысла обращать внимание на этот механизм исправления ошибок. То сейчас когда в подавляющем количестве флешек, установлена или банально TLC-память или какая-нибудь MLC DownGrade, не стоит пренебрегать настройками ECC-механизма.

Данная технология позволяет продлить жизнь флешки до следующих затыков с ней, ведь не хочется, каждый месяц заново перепрошивать свою флешку.

Еще одной положительной чертой, является вероятность достижения максимального возможного объёма флэш-диска. Он может быть даже выше, чем изначально имел носитель, особенно у флешек с отбракованными микросхемами.

НЕДОСТАТКИ

Чем выше вы установите значение ECC-параметра, тем большую нагрузку он создаст на контроллёр флешки. А это в свою очередь, может негативно сказаться на её производительность, т.е. скорость работы. Также из заметных недостатков, высокой нагрузки, это больший разогрев флешки.

РЕКОМЕНДУЕМЫЕ ЗНАЧЕНИЯ ПАРАМЕТРА ECC

В большинстве утилитах, используется не применяемые в флэш-листах значения (например: 7b/512B и 72b/1K), а суммы определенных параметров. Как правило, в диапазоне равеном от 0 до 15, в некоторых производственных программах, ввиду поддержки крайне некачественной памяти, от 0 до 20. Для посетителей проекта USBDev.ru, я составил следующую таблицу.

ECC Value
MEMORY TYPE:	ECC:
SLC	1
MLC 32nm, 35nm, 42nm, 50nm, …	3-4
MLC 24nm, 25nm, 26nm, 32nm	4-8
MLC 21nm, 20nm, 19nm, …	8-12
TLC 27nm, 32nm, 43nm, …	8
TLC 24nm, 21nm, 19nm, …	12-15

В некоторых утилитах, используется другая система координат, к примеру производственный комплекс Dyna для контроллёров SMI. На этот случай, чуть ниже можно обнаружить ссылку на особености настроек у конкретных производителей.

Немного поясню, как следует использовать таблицу данную выше. Так вот, если ваша флешка добротная (хорошо зарекомендовавший себя бренд), то выбирайте минимальное значение из неё. Для подарочных и поддельных флешек, настоятельно советую использовать максимальное значение параметра ECC, для своего типа памяти.

РЕАЛИЗАЦИЯ В ПРОИЗВОДСТВЕННЫХ УТИЛИТАХ

Далеко не во всех утилит, имеется возможность ручной корректировки ECC-опции. Можно сказать что ECC, это такая фитча Sorting-составляющей производственных утилит. Попробую кратко выразить это в таблице, для основных производителей USB-контроллёров.

ECC Compatible Software
Company:	Tools:
ALCOR	AlcorMP_UFD FC MpTool AAMP
CHIPSBANK	Chipsbank UMPTool CBM2093 UMPTool CBM2098 UMPTool umptool209X V68 Building Tools
INNOSTOR	Innostor MPTool Innostor 917 LFA MP Tool
PHISON	UPTool UP19_CTool UP21_CTool UP23_CTool
SILICON GO	KingStore Manufacture Tool SiliconGo MPTools SiliconGo MPTool2
SKYMEDI	SK6221 MPTool
SMI	Dyna Mass Storage Production Tool

СТАТЬИ НА ТЕМУ ECC-КОРРЕКЦИИ

ECC значения для контроллёров Alcor с DownGrade памятью	2015
Настройка ECC у контроллёров Silicon Motion (SMI)	2015

Для ваших вопросов, на проекте USBDev существует форум – FORUM.

Источник

ECC (англ. error-correcting
code,
код коррекции ошибок) — данные,
присоединяемые к каждому передаваемому
сигналу, позволяющие принимающей стороне
определить факт сбоя и (в некоторых
случаях) исправить несущественную
ошибку. Принцип основан на коде
Хэмминга.

ECC используется
в устройствах хранения данных,(в том
числе и для оперативной памяти).

Циклический
избыточный код (англ. Cyclic
redundancy check, CRC^[1]) —
алгоритм нахождения контрольной
суммы,
предназначенный для проверки целостности
данных^[2].
CRC является практическим
приложением помехоустойчивого
кодирования,
основанном на определенных математических
свойствах циклического
кода.

Контро́льная
су́мма —
некоторое значение, рассчитанное по
набору данных путём применения
определённого алгоритма и используемое
для проверки целостности данных при их
передаче или хранении. Также контрольные
суммы могут использоваться для быстрого
сравнения двух наборов данных на
неэквивалентность: с большой вероятностью
различные наборы данных будут иметь
неравные контрольные суммы. Это может
быть использовано, например, для
детектирования компьютерных
вирусов.
Несмотря на своё название, контрольная
сумма не обязательно вычисляется путем
суммирования.

Первые
попытки создания кодов с избыточной
информацией начались задолго до появления
современных ПК. К примеру, ещё в
шестидесятых годах прошлого века Ридом
и Соломоном была разработана эффективная
методика кодирования — Код
Рида-Соломона.
Использование её в те времена не
представлялось возможным, так как
произвести операцию декодирования за разумное
время первыми
алгоритмами не удавалось. Точку в этом
вопросе поставила фундаментальная
работа Берлекампа, опубликованная в
1968 году.Эта
методика,
на практическое применение которой
указал через год Мэсси, и по сей день
используется в цифровых устройствах,
обеспечивающих прием RS-кодированных
данных. Более того: данная система
позволяет не только определять позиции,
но и исправлять неверные кодовые символы
(чаще всего октеты).

Но
далеко не везде от кода требуется
коррекция ошибок. Многие современные
каналы связи обладают приемлемыми
характеристиками, и зачастую достаточно
лишь проверить, успешно ли прошла
передача или возникли какие-нибудь сложности;
структура же ошибок и конкретные позиции
неверных символов совершенно не
интересуют принимающую сторону. И в
этих условиях очень удачным решением
оказались алгоритмы, использующие
контрольные суммы. CRC как нельзя лучше
подходит для подобных задач: невысокие
затраты ресурсов, простота реализации
и уже сформированный математический
аппарат из теории линейных циклических
кодов обеспечили ей огромную популярность.

Источник

How it works[edit]

Averaging noise to reduce errors[edit]

Types of ECC[edit]

Code-rate and the tradeoff between reliability and data rate[edit]

Concatenated ECC codes for improved performance[edit]

Low-density parity-check (LDPC)[edit]

Turbo codes[edit]

Local decoding and testing of codes[edit]

Interleaving[edit]

Example[edit]

Disadvantages of interleaving[edit]

Software for error-correcting codes[edit]

List of error-correcting codes[edit]

See also[edit]

References[edit]

Further reading[edit]

External links[edit]

How it works[edit]

Averaging noise to reduce errors[edit]

Types of ECC[edit]

Code-rate and the tradeoff between reliability and data rate[edit]

Concatenated ECC codes for improved performance[edit]

Low-density parity-check (LDPC)[edit]

Turbo codes[edit]

Local decoding and testing of codes[edit]

Interleaving[edit]

Example[edit]

Disadvantages of interleaving[edit]

Software for error-correcting codes[edit]

List of error-correcting codes[edit]

See also[edit]

References[edit]

Further reading[edit]

External links[edit]

Оглавление

Вступление

Коррекция ошибок

Финансовая сторона

Тестовый стенд

Методика тестирования

Результаты тестирования

Тест памяти

3DMark

7Zip

Cinebench

Что такое ЕСС память

Причины появления ошибок в ОЗУ

Стоит ли использовать ЕСС память

Читайте также: