Что такое корреляция и что означает коррелировать — простыми словами о сложном
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Когда некоторые люди слышат слово «корреляция», то зачастую просто впадают в ступор. Оно и понятно: жуткий термин из мира высшей математики и статистики.
Сразу представляются унылые графики, многоэтажные формулы, при взгляде на которые хочется забиться в угол и плакать. На самом деле все гораздо проще.
Потратив несколько минут на прочтение этой статьи, вы узнаете, что такое корреляция и как ее использовать в повседневной жизни.
Определение корелляции — что это
Простыми словами корреляция – это взаимосвязь двух или нескольких случайных параметров. Когда одна величина растет или уменьшается, другая тоже изменяется.
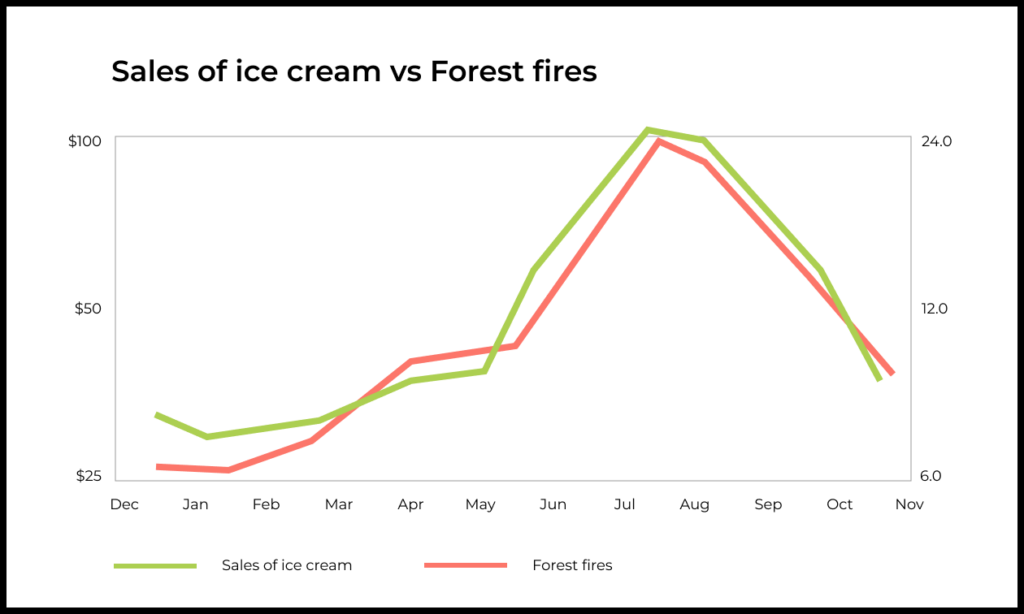
Объясним на примере: существует корреляция между температурой воздуха и потреблением мороженого. Чем жарче погода, тем больше холодного лакомства покупают люди. И наоборот.
Такие закономерности устанавливаются путем исследования больших объемов статистических данных. Собираем информацию о потреблении мороженого за несколько лет и сведения о колебаниях температуры за тот же период. А дальше сопоставляем и ищем зависимость.
Коррелировать – это значит быть взаимосвязанным с чем-то. Существует положительная и отрицательная корреляции.
При положительной чем больше один параметр, тем больше и другой. Например, чем масштабнее траты фермера на удобрения, тем обильнее урожай. При обратной корреляции рост одной величины сопровождается уменьшением другой. Чем выше здание, тем хуже оно противостоит землетрясениям.
Корреляция — это взаимосвязь без гарантий
Рассмотрим пример прямой корреляции: чем выше уровень благосостояния человека, тем больше его продолжительность жизни. Обеспеченные люди питаются качественной пищей и своевременно получают врачебную помощь. В отличие от бедняков.
Однако нельзя с уверенностью сказать, что определенный олигарх проживет дольше вот этого нищего.
Это лишь статистическая вероятность, которая может не сработать для одного конкретного случая. Этим корреляция отличается от линейной зависимости, где исход известен со 100-процентной вероятностью.
Но если мы возьмем выборку из сотни тысяч богачей и такого же числа малоимущих, сравним их продолжительность жизни, то общая тенденция будет верна.
Коэффициент корреляции
Это число, которое обозначается как «r». Оно находится в промежутке от -1 до 1. Отражает силу и полюс взаимосвязи величин. Посмотрим на примере:
| Значение коэффициента | Какая корреляция? | О чем это говорит? |
|---|---|---|
| r=1 | Сильная положительная корреляция | Люди, которые едят чернику, обладают острым зрением. Ешьте чернику! |
| r меньше 0,5 | Слабая положительная корреляция | Некоторые люди, которые любят чернику, обладают острым зрением. Но это не точно. Короче, ничего не пока понятно. Но лучше есть чернику на всякий случай. |
| r=0 | Корреляция отсутствует | Черника и зрение никак не связаны. |
| r меньше -0,5 | Слабая отрицательная корреляция | Бывают случаи ухудшения зрения из-за черники. Не стоит рисковать. |
| r=-1 | Сильная отрицательная корреляция | Практически все, кто ел чернику, ослепли. Берегитесь черники! |
Величина коэффициента корреляции рассчитывается по формуле:
Если внезапно потемнело в глазах и возникло непреодолимое желание закрыть статью (синдром гуманитария), то есть вариант попроще. Microsoft Exel все выполнит сам при помощи функции «КОРРЕЛ». Делается это так:
Судя по расчетам, рост человека практически никак не влияет на уровень зарплаты.
Реальные причины корреляции и возможные гипотезы
Курс доллара и стоимость нефти отрицательно коррелируют. Можем выдвинуть гипотезу: повышение цен на черное золото вызывает падение стоимости американской валюты. Но почему так происходит? Откуда взялась связь между этими явлениями?
Определение причины корреляции – это очень сложная задача. Переплетаются тысячи различных факторов, часть из которых скрыта.
Возможно, дело в том, что США – крупнейший потребитель нефти в мире. Каждый день они импортируют около 7,2 миллиона баррелей. Снижение цены на черное золото – хорошо для американской экономики, ведь позволяет тратить меньше денег. Следовательно, доллар растет.
Корреляция предоставляет возможность сделать вывод из статистических данных.
Например, мы выяснили, что существует отрицательная взаимосвязь между доходом персонала и его эффективностью в работе. Наша гипотеза: «Лентяи и бездельники получают больше, чем ответственные сотрудники». Тогда мы пересмотрим систему мотивации и избавимся от бесполезных людей.
Гипотеза – это лишь статистический вывод, предположение. Она вполне может оказаться ошибочной.
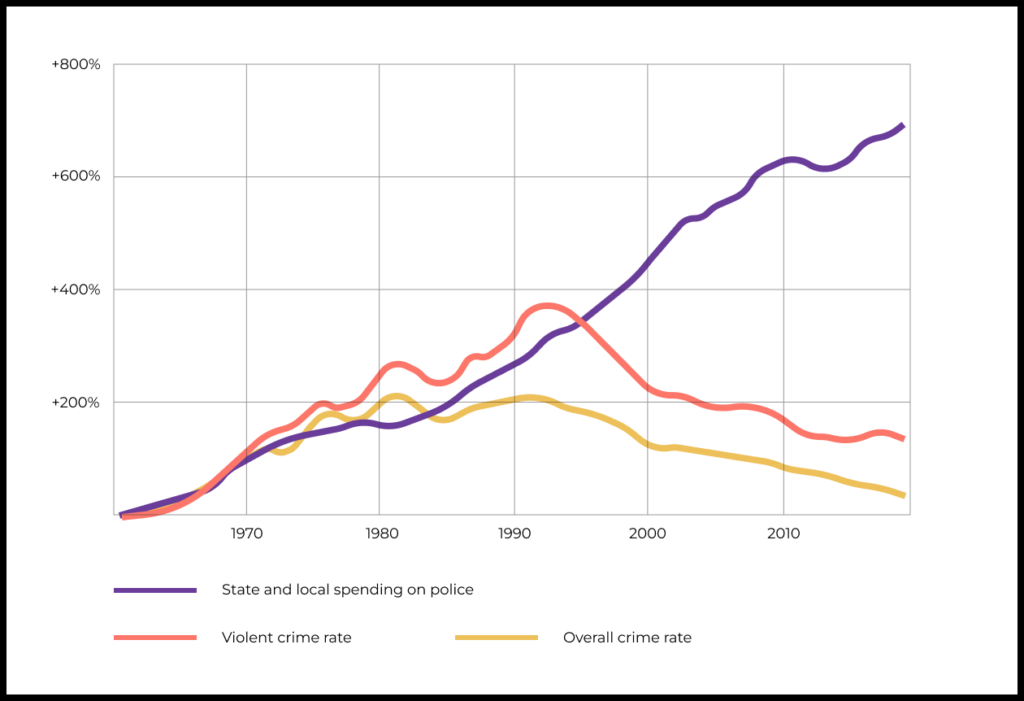
Согласно статистике, чем больше пожарных участвует в тушении огня, тем существенней размер ущерба. Какую гипотезу можем сделать отсюда? Пожарные приносят вред, давайте сократим их! Но если разобраться, то настоящая причина повреждения – это огонь. А увеличение числа лиц, задействованных в его тушении, – следствие масштаба пожара.
Наша вселенная бесконечна, а значит всегда можно найти несколько переменных, которые будут коррелировать между собой, несмотря на полное отсутствие причинно-следственных связей. Даже самое буйное воображение не сможет объяснить, что объединяет сыр и одеяло-убийцу:
Более подробно на эту тему смотрите в видео:
Как при помощи корреляции люди становятся богаче
Главное правило любого инвестора: не класть все яйца в одну корзину. Вложения рекомендуется диверсифицировать (что это?) – распределять. Поэтому люди покупают акции не одной компании, а десятка разных, формируя инвестиционные портфели. Если котировки какой-то фирмы упадут, то оставшиеся девять смогут отыграть падение или хотя бы уменьшить убытки.
Но это в теории, а на практике все портит корреляция. Проблема в том, что стоимости акций разных компаний внутри отрасли или даже всей страны могут сильно коррелировать. Проблемы огромной корпорации провоцируют панику на рынке, снижают стоимость иных активов, на первый взгляд не связанных между собой. В 2008 году случился крах Lehman Brothers, который вызвал цепную реакцию и обвал на мировых рынках.
Поэтому при инвестировании нужно стараться выбирать направления, которые не связаны между собой (r стремится к 0).
Например, пара «золото – облигации США» = -0,13. Если собрать портфель из совершенно независимых частей, риски финансовых потерь сократятся.
Территориальное приближение активов друг к другу усиливает корреляцию. Значит, нужно рассматривать варианты в разных точках мира, максимально удаленных друг от друга.
В жизни этот принцип тоже действует. Если ваши навыки и знания позволяют трудиться программистом, таксистом, сантехником и журналистом – вы хорошо защищены от риска безработицы.
Памятка
- Корреляция – это соотношение, взаимозависимость нескольких переменных.
- Связь бывает положительной и отрицательной.
- Коэффициент корреляции определяет степень взаимозависимости одной переменной от другой.
- На основании корреляции люди выдвигают гипотезы (часто ошибочные).
- Истинная причина корреляции порою скрыта под множеством факторов и внешних сил.
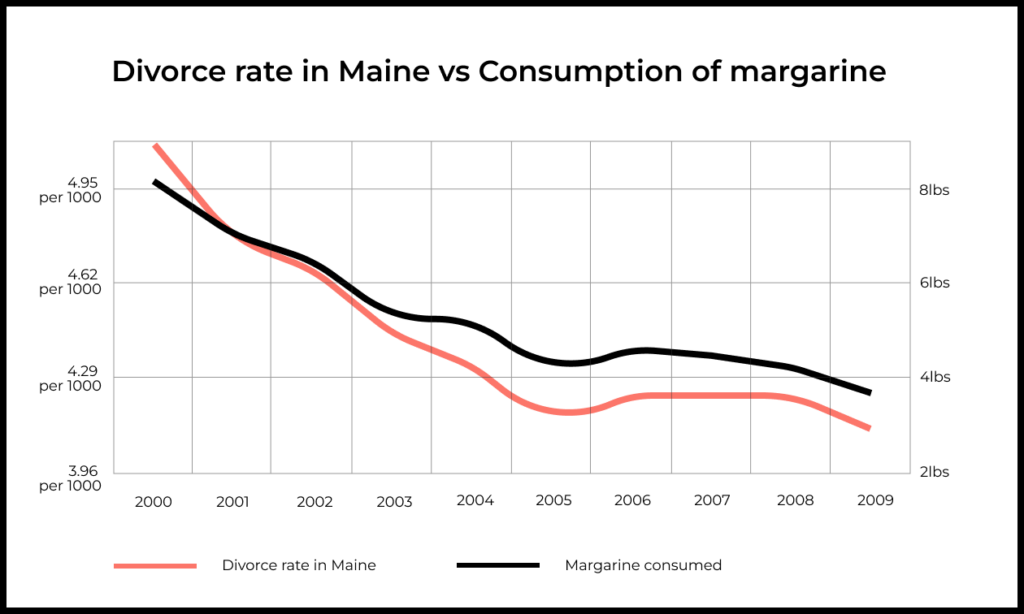
- Бывает ложная корреляционная зависимость.
- Раскладывая яйца по корзинам, помните о том, что они не должны коррелироваться друг с другом.
This article is about correlation and dependence in statistical data. For other uses, see Correlation (disambiguation).
Several sets of (x, y) points, with the Pearson correlation coefficient of x and y for each set. The correlation reflects the noisiness and direction of a linear relationship (top row), but not the slope of that relationship (middle), nor many aspects of nonlinear relationships (bottom). N.B.: the figure in the center has a slope of 0 but in that case, the correlation coefficient is undefined because the variance of Y is zero.
In statistics, correlation or dependence is any statistical relationship, whether causal or not, between two random variables or bivariate data. Although in the broadest sense, «correlation» may indicate any type of association, in statistics it usually refers to the degree to which a pair of variables are linearly related.
Familiar examples of dependent phenomena include the correlation between the height of parents and their offspring, and the correlation between the price of a good and the quantity the consumers are willing to purchase, as it is depicted in the so-called demand curve.
Correlations are useful because they can indicate a predictive relationship that can be exploited in practice. For example, an electrical utility may produce less power on a mild day based on the correlation between electricity demand and weather. In this example, there is a causal relationship, because extreme weather causes people to use more electricity for heating or cooling. However, in general, the presence of a correlation is not sufficient to infer the presence of a causal relationship (i.e., correlation does not imply causation).
Formally, random variables are dependent if they do not satisfy a mathematical property of probabilistic independence. In informal parlance, correlation is synonymous with dependence. However, when used in a technical sense, correlation refers to any of several specific types of mathematical operations between the tested variables and their respective expected values. Essentially, correlation is the measure of how two or more variables are related to one another. There are several correlation coefficients, often denoted 

Pearson’s product-moment coefficient[edit]
Example scatterplots of various datasets with various correlation coefficients.
The most familiar measure of dependence between two quantities is the Pearson product-moment correlation coefficient (PPMCC), or «Pearson’s correlation coefficient», commonly called simply «the correlation coefficient». It is obtained by taking the ratio of the covariance of the two variables in question of our numerical dataset, normalized to the square root of their variances. Mathematically, one simply divides the covariance of the two variables by the product of their standard deviations. Karl Pearson developed the coefficient from a similar but slightly different idea by Francis Galton.[4]
A Pearson product-moment correlation coefficient attempts to establish a line of best fit through a dataset of two variables by essentially laying out the expected values and the resulting Pearson’s correlation coefficient indicates how far away the actual dataset is from the expected values. Depending on the sign of our Pearson’s correlation coefficient, we can end up with either a negative or positive correlation if there is any sort of relationship between the variables of our data set.
The population correlation coefficient 






where 


Correlation and independence[edit]
It is a corollary of the Cauchy–Schwarz inequality that the absolute value of the Pearson correlation coefficient is not bigger than 1. Therefore, the value of a correlation coefficient ranges between −1 and +1. The correlation coefficient is +1 in the case of a perfect direct (increasing) linear relationship (correlation), −1 in the case of a perfect inverse (decreasing) linear relationship (anti-correlation),[5] and some value in the open interval 
If the variables are independent, Pearson’s correlation coefficient is 0, but the converse is not true because the correlation coefficient detects only linear dependencies between two variables.
For example, suppose the random variable 







Even though uncorrelated data does not necessarily imply independence, one can check if random variables are independent if their mutual information is 0.
Sample correlation coefficient[edit]
Given a series of 





where 







Equivalent expressions for 
where 



If 


Example[edit]
Consider the joint probability distribution of X and Y given in the table below.
-
y
x
−1 0 1 0 0 1/3 0 1 1/3 0 1/3
For this joint distribution, the marginal distributions are:
This yields the following expectations and variances:
Therefore:
Rank correlation coefficients[edit]
Rank correlation coefficients, such as Spearman’s rank correlation coefficient and Kendall’s rank correlation coefficient (τ) measure the extent to which, as one variable increases, the other variable tends to increase, without requiring that increase to be represented by a linear relationship. If, as the one variable increases, the other decreases, the rank correlation coefficients will be negative. It is common to regard these rank correlation coefficients as alternatives to Pearson’s coefficient, used either to reduce the amount of calculation or to make the coefficient less sensitive to non-normality in distributions. However, this view has little mathematical basis, as rank correlation coefficients measure a different type of relationship than the Pearson product-moment correlation coefficient, and are best seen as measures of a different type of association, rather than as an alternative measure of the population correlation coefficient.[7][8]
To illustrate the nature of rank correlation, and its difference from linear correlation, consider the following four pairs of numbers 
- (0, 1), (10, 100), (101, 500), (102, 2000).
As we go from each pair to the next pair 





Other measures of dependence among random variables[edit]
The information given by a correlation coefficient is not enough to define the dependence structure between random variables.[9] The correlation coefficient completely defines the dependence structure only in very particular cases, for example when the distribution is a multivariate normal distribution. (See diagram above.) In the case of elliptical distributions it characterizes the (hyper-)ellipses of equal density; however, it does not completely characterize the dependence structure (for example, a multivariate t-distribution’s degrees of freedom determine the level of tail dependence).
Distance correlation[10][11] was introduced to address the deficiency of Pearson’s correlation that it can be zero for dependent random variables; zero distance correlation implies independence.
The Randomized Dependence Coefficient[12] is a computationally efficient, copula-based measure of dependence between multivariate random variables. RDC is invariant with respect to non-linear scalings of random variables, is capable of discovering a wide range of functional association patterns and takes value zero at independence.
For two binary variables, the odds ratio measures their dependence, and takes range non-negative numbers, possibly infinity: ![{displaystyle [0,+infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f32245981f739c86ea8f68ce89b1ad6807428d35)
![[-1, 1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)
The correlation ratio, entropy-based mutual information, total correlation, dual total correlation and polychoric correlation are all also capable of detecting more general dependencies, as is consideration of the copula between them, while the coefficient of determination generalizes the correlation coefficient to multiple regression.
Sensitivity to the data distribution[edit]
The degree of dependence between variables X and Y does not depend on the scale on which the variables are expressed. That is, if we are analyzing the relationship between X and Y, most correlation measures are unaffected by transforming X to a + bX and Y to c + dY, where a, b, c, and d are constants (b and d being positive). This is true of some correlation statistics as well as their population analogues. Some correlation statistics, such as the rank correlation coefficient, are also invariant to monotone transformations of the marginal distributions of X and/or Y.
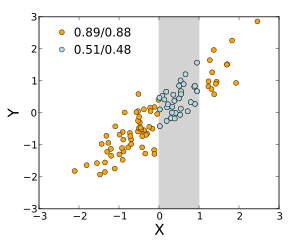
Pearson/Spearman correlation coefficients between X and Y are shown when the two variables’ ranges are unrestricted, and when the range of X is restricted to the interval (0,1).
Most correlation measures are sensitive to the manner in which X and Y are sampled. Dependencies tend to be stronger if viewed over a wider range of values. Thus, if we consider the correlation coefficient between the heights of fathers and their sons over all adult males, and compare it to the same correlation coefficient calculated when the fathers are selected to be between 165 cm and 170 cm in height, the correlation will be weaker in the latter case. Several techniques have been developed that attempt to correct for range restriction in one or both variables, and are commonly used in meta-analysis; the most common are Thorndike’s case II and case III equations.[13]
Various correlation measures in use may be undefined for certain joint distributions of X and Y. For example, the Pearson correlation coefficient is defined in terms of moments, and hence will be undefined if the moments are undefined. Measures of dependence based on quantiles are always defined. Sample-based statistics intended to estimate population measures of dependence may or may not have desirable statistical properties such as being unbiased, or asymptotically consistent, based on the spatial structure of the population from which the data were sampled.
Sensitivity to the data distribution can be used to an advantage. For example, scaled correlation is designed to use the sensitivity to the range in order to pick out correlations between fast components of time series.[14] By reducing the range of values in a controlled manner, the correlations on long time scale are filtered out and only the correlations on short time scales are revealed.
Correlation matrices[edit]
The correlation matrix of 




Thus the diagonal entries are all identically one. If the measures of correlation used are product-moment coefficients, the correlation matrix is the same as the covariance matrix of the standardized random variables 



The correlation matrix is symmetric because the correlation between 



A correlation matrix appears, for example, in one formula for the coefficient of multiple determination, a measure of goodness of fit in multiple regression.
In statistical modelling, correlation matrices representing the relationships between variables are categorized into different correlation structures, which are distinguished by factors such as the number of parameters required to estimate them. For example, in an exchangeable correlation matrix, all pairs of variables are modeled as having the same correlation, so all non-diagonal elements of the matrix are equal to each other. On the other hand, an autoregressive matrix is often used when variables represent a time series, since correlations are likely to be greater when measurements are closer in time. Other examples include independent, unstructured, M-dependent, and Toeplitz.
In exploratory data analysis, the iconography of correlations consists in replacing a correlation matrix by a diagram where the “remarkable” correlations are represented by a solid line (positive correlation), or a dotted line (negative correlation).
Nearest valid correlation matrix[edit]
In some applications (e.g., building data models from only partially observed data) one wants to find the «nearest» correlation matrix to an «approximate» correlation matrix (e.g., a matrix which typically lacks semi-definite positiveness due to the way it has been computed).
In 2002, Higham[15] formalized the notion of nearness using the Frobenius norm and provided a method for computing the nearest correlation matrix using the Dykstra’s projection algorithm, of which an implementation is available as an online Web API.[16]
This sparked interest in the subject, with new theoretical (e.g., computing the nearest correlation matrix with factor structure[17]) and numerical (e.g. usage the Newton’s method for computing the nearest correlation matrix[18]) results obtained in the subsequent years.
Uncorrelatedness and independence of stochastic processes[edit]
Similarly for two stochastic processes 

Common misconceptions[edit]
Correlation and causality[edit]
The conventional dictum that «correlation does not imply causation» means that correlation cannot be used by itself to infer a causal relationship between the variables.[20] This dictum should not be taken to mean that correlations cannot indicate the potential existence of causal relations. However, the causes underlying the correlation, if any, may be indirect and unknown, and high correlations also overlap with identity relations (tautologies), where no causal process exists. Consequently, a correlation between two variables is not a sufficient condition to establish a causal relationship (in either direction).
A correlation between age and height in children is fairly causally transparent, but a correlation between mood and health in people is less so. Does improved mood lead to improved health, or does good health lead to good mood, or both? Or does some other factor underlie both? In other words, a correlation can be taken as evidence for a possible causal relationship, but cannot indicate what the causal relationship, if any, might be.
Simple linear correlations[edit]
The Pearson correlation coefficient indicates the strength of a linear relationship between two variables, but its value generally does not completely characterize their relationship.[21] In particular, if the conditional mean of 




The adjacent image shows scatter plots of Anscombe’s quartet, a set of four different pairs of variables created by Francis Anscombe.[22] The four 
These examples indicate that the correlation coefficient, as a summary statistic, cannot replace visual examination of the data. The examples are sometimes said to demonstrate that the Pearson correlation assumes that the data follow a normal distribution, but this is only partially correct.[4] The Pearson correlation can be accurately calculated for any distribution that has a finite covariance matrix, which includes most distributions encountered in practice. However, the Pearson correlation coefficient (taken together with the sample mean and variance) is only a sufficient statistic if the data is drawn from a multivariate normal distribution. As a result, the Pearson correlation coefficient fully characterizes the relationship between variables if and only if the data are drawn from a multivariate normal distribution.
Bivariate normal distribution[edit]
If a pair 









where 







The empirical correlation 


where 

See also[edit]
- Autocorrelation
- Canonical correlation
- Coefficient of determination
- Cointegration
- Concordance correlation coefficient
- Cophenetic correlation
- Correlation function
- Correlation gap
- Covariance
- Covariance and correlation
- Cross-correlation
- Ecological correlation
- Fraction of variance unexplained
- Genetic correlation
- Goodman and Kruskal’s lambda
- Iconography of correlations
- Illusory correlation
- Interclass correlation
- Intraclass correlation
- Lift (data mining)
- Mean dependence
- Modifiable areal unit problem
- Multiple correlation
- Point-biserial correlation coefficient
- Quadrant count ratio
- Spurious correlation
- Statistical arbitrage
- Subindependence
References[edit]
- ^ Croxton, Frederick Emory; Cowden, Dudley Johnstone; Klein, Sidney (1968) Applied General Statistics, Pitman. ISBN 9780273403159 (page 625)
- ^ Dietrich, Cornelius Frank (1991) Uncertainty, Calibration and Probability: The Statistics of Scientific and Industrial Measurement 2nd Edition, A. Higler. ISBN 9780750300605 (Page 331)
- ^ Aitken, Alexander Craig (1957) Statistical Mathematics 8th Edition. Oliver & Boyd. ISBN 9780050013007 (Page 95)
- ^ a b Rodgers, J. L.; Nicewander, W. A. (1988). «Thirteen ways to look at the correlation coefficient». The American Statistician. 42 (1): 59–66. doi:10.1080/00031305.1988.10475524. JSTOR 2685263.
- ^ Dowdy, S. and Wearden, S. (1983). «Statistics for Research», Wiley. ISBN 0-471-08602-9 pp 230
- ^ Francis, DP; Coats AJ; Gibson D (1999). «How high can a correlation coefficient be?». Int J Cardiol. 69 (2): 185–199. doi:10.1016/S0167-5273(99)00028-5. PMID 10549842.
- ^ a b Yule, G.U and Kendall, M.G. (1950), «An Introduction to the Theory of Statistics», 14th Edition (5th Impression 1968). Charles Griffin & Co. pp 258–270
- ^ Kendall, M. G. (1955) «Rank Correlation Methods», Charles Griffin & Co.
- ^ Mahdavi Damghani B. (2013). «The Non-Misleading Value of Inferred Correlation: An Introduction to the Cointelation Model». Wilmott Magazine. 2013 (67): 50–61. doi:10.1002/wilm.10252.
- ^ Székely, G. J. Rizzo; Bakirov, N. K. (2007). «Measuring and testing independence by correlation of distances». Annals of Statistics. 35 (6): 2769–2794. arXiv:0803.4101. doi:10.1214/009053607000000505. S2CID 5661488.
- ^ Székely, G. J.; Rizzo, M. L. (2009). «Brownian distance covariance». Annals of Applied Statistics. 3 (4): 1233–1303. arXiv:1010.0297. doi:10.1214/09-AOAS312. PMC 2889501. PMID 20574547.
- ^ Lopez-Paz D. and Hennig P. and Schölkopf B. (2013). «The Randomized Dependence Coefficient», «Conference on Neural Information Processing Systems» Reprint
- ^ Thorndike, Robert Ladd (1947). Research problems and techniques (Report No. 3). Washington DC: US Govt. print. off.
- ^ Nikolić, D; Muresan, RC; Feng, W; Singer, W (2012). «Scaled correlation analysis: a better way to compute a cross-correlogram». European Journal of Neuroscience. 35 (5): 1–21. doi:10.1111/j.1460-9568.2011.07987.x. PMID 22324876. S2CID 4694570.
- ^ Higham, Nicholas J. (2002). «Computing the nearest correlation matrix—a problem from finance». IMA Journal of Numerical Analysis. 22 (3): 329–343. CiteSeerX 10.1.1.661.2180. doi:10.1093/imanum/22.3.329.
- ^ «Portfolio Optimizer». portfoliooptimizer.io/. Retrieved 2021-01-30.
- ^ Borsdorf, Rudiger; Higham, Nicholas J.; Raydan, Marcos (2010). «Computing a Nearest Correlation Matrix with Factor Structure» (PDF). SIAM J. Matrix Anal. Appl. 31 (5): 2603–2622. doi:10.1137/090776718.
- ^ Qi, HOUDUO; Sun, DEFENG (2006). «A quadratically convergent Newton method for computing the nearest correlation matrix». SIAM J. Matrix Anal. Appl. 28 (2): 360–385. doi:10.1137/050624509.
- ^ Park, Kun Il (2018). Fundamentals of Probability and Stochastic Processes with Applications to Communications. Springer. ISBN 978-3-319-68074-3.
- ^ Aldrich, John (1995). «Correlations Genuine and Spurious in Pearson and Yule». Statistical Science. 10 (4): 364–376. doi:10.1214/ss/1177009870. JSTOR 2246135.
- ^ Mahdavi Damghani, Babak (2012). «The Misleading Value of Measured Correlation». Wilmott Magazine. 2012 (1): 64–73. doi:10.1002/wilm.10167. S2CID 154550363.
- ^ Anscombe, Francis J. (1973). «Graphs in statistical analysis». The American Statistician. 27 (1): 17–21. doi:10.2307/2682899. JSTOR 2682899.
- ^ Taraldsen, Gunnar (2021). «The Confidence Density for Correlation». Sankhya A. doi:10.1007/s13171-021-00267-y. ISSN 0976-8378. S2CID 244594067.
- ^ Taraldsen, Gunnar (2020). «Confidence in Correlation». doi:10.13140/RG.2.2.23673.49769.
Further reading[edit]
- Cohen, J.; Cohen P.; West, S.G. & Aiken, L.S. (2002). Applied multiple regression/correlation analysis for the behavioral sciences (3rd ed.). Psychology Press. ISBN 978-0-8058-2223-6.
- «Correlation (in statistics)», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Oestreicher, J. & D. R. (February 26, 2015). Plague of Equals: A science thriller of international disease, politics and drug discovery. California: Omega Cat Press. p. 408. ISBN 978-0963175540.
External links[edit]
- MathWorld page on the (cross-)correlation coefficient/s of a sample
- Compute significance between two correlations, for the comparison of two correlation values.
- «A MATLAB Toolbox for computing Weighted Correlation Coefficients». Archived from the original on 24 April 2021.
- Proof that the Sample Bivariate Correlation has limits plus or minus 1
- Interactive Flash simulation on the correlation of two normally distributed variables by Juha Puranen.
- Correlation analysis. Biomedical Statistics
- R-Psychologist Correlation visualization of correlation between two numeric variables
This article is about correlation and dependence in statistical data. For other uses, see Correlation (disambiguation).
Several sets of (x, y) points, with the Pearson correlation coefficient of x and y for each set. The correlation reflects the noisiness and direction of a linear relationship (top row), but not the slope of that relationship (middle), nor many aspects of nonlinear relationships (bottom). N.B.: the figure in the center has a slope of 0 but in that case, the correlation coefficient is undefined because the variance of Y is zero.
In statistics, correlation or dependence is any statistical relationship, whether causal or not, between two random variables or bivariate data. Although in the broadest sense, «correlation» may indicate any type of association, in statistics it usually refers to the degree to which a pair of variables are linearly related.
Familiar examples of dependent phenomena include the correlation between the height of parents and their offspring, and the correlation between the price of a good and the quantity the consumers are willing to purchase, as it is depicted in the so-called demand curve.
Correlations are useful because they can indicate a predictive relationship that can be exploited in practice. For example, an electrical utility may produce less power on a mild day based on the correlation between electricity demand and weather. In this example, there is a causal relationship, because extreme weather causes people to use more electricity for heating or cooling. However, in general, the presence of a correlation is not sufficient to infer the presence of a causal relationship (i.e., correlation does not imply causation).
Formally, random variables are dependent if they do not satisfy a mathematical property of probabilistic independence. In informal parlance, correlation is synonymous with dependence. However, when used in a technical sense, correlation refers to any of several specific types of mathematical operations between the tested variables and their respective expected values. Essentially, correlation is the measure of how two or more variables are related to one another. There are several correlation coefficients, often denoted 

Pearson’s product-moment coefficient[edit]
Example scatterplots of various datasets with various correlation coefficients.
The most familiar measure of dependence between two quantities is the Pearson product-moment correlation coefficient (PPMCC), or «Pearson’s correlation coefficient», commonly called simply «the correlation coefficient». It is obtained by taking the ratio of the covariance of the two variables in question of our numerical dataset, normalized to the square root of their variances. Mathematically, one simply divides the covariance of the two variables by the product of their standard deviations. Karl Pearson developed the coefficient from a similar but slightly different idea by Francis Galton.[4]
A Pearson product-moment correlation coefficient attempts to establish a line of best fit through a dataset of two variables by essentially laying out the expected values and the resulting Pearson’s correlation coefficient indicates how far away the actual dataset is from the expected values. Depending on the sign of our Pearson’s correlation coefficient, we can end up with either a negative or positive correlation if there is any sort of relationship between the variables of our data set.
The population correlation coefficient 






where 


Correlation and independence[edit]
It is a corollary of the Cauchy–Schwarz inequality that the absolute value of the Pearson correlation coefficient is not bigger than 1. Therefore, the value of a correlation coefficient ranges between −1 and +1. The correlation coefficient is +1 in the case of a perfect direct (increasing) linear relationship (correlation), −1 in the case of a perfect inverse (decreasing) linear relationship (anti-correlation),[5] and some value in the open interval 
If the variables are independent, Pearson’s correlation coefficient is 0, but the converse is not true because the correlation coefficient detects only linear dependencies between two variables.
For example, suppose the random variable 







Even though uncorrelated data does not necessarily imply independence, one can check if random variables are independent if their mutual information is 0.
Sample correlation coefficient[edit]
Given a series of 





where 







Equivalent expressions for 
where 



If 


Example[edit]
Consider the joint probability distribution of X and Y given in the table below.
-
y
x
−1 0 1 0 0 1/3 0 1 1/3 0 1/3
For this joint distribution, the marginal distributions are:
This yields the following expectations and variances:
Therefore:
Rank correlation coefficients[edit]
Rank correlation coefficients, such as Spearman’s rank correlation coefficient and Kendall’s rank correlation coefficient (τ) measure the extent to which, as one variable increases, the other variable tends to increase, without requiring that increase to be represented by a linear relationship. If, as the one variable increases, the other decreases, the rank correlation coefficients will be negative. It is common to regard these rank correlation coefficients as alternatives to Pearson’s coefficient, used either to reduce the amount of calculation or to make the coefficient less sensitive to non-normality in distributions. However, this view has little mathematical basis, as rank correlation coefficients measure a different type of relationship than the Pearson product-moment correlation coefficient, and are best seen as measures of a different type of association, rather than as an alternative measure of the population correlation coefficient.[7][8]
To illustrate the nature of rank correlation, and its difference from linear correlation, consider the following four pairs of numbers 
- (0, 1), (10, 100), (101, 500), (102, 2000).
As we go from each pair to the next pair 





Other measures of dependence among random variables[edit]
The information given by a correlation coefficient is not enough to define the dependence structure between random variables.[9] The correlation coefficient completely defines the dependence structure only in very particular cases, for example when the distribution is a multivariate normal distribution. (See diagram above.) In the case of elliptical distributions it characterizes the (hyper-)ellipses of equal density; however, it does not completely characterize the dependence structure (for example, a multivariate t-distribution’s degrees of freedom determine the level of tail dependence).
Distance correlation[10][11] was introduced to address the deficiency of Pearson’s correlation that it can be zero for dependent random variables; zero distance correlation implies independence.
The Randomized Dependence Coefficient[12] is a computationally efficient, copula-based measure of dependence between multivariate random variables. RDC is invariant with respect to non-linear scalings of random variables, is capable of discovering a wide range of functional association patterns and takes value zero at independence.
For two binary variables, the odds ratio measures their dependence, and takes range non-negative numbers, possibly infinity: ![{displaystyle [0,+infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f32245981f739c86ea8f68ce89b1ad6807428d35)
![[-1, 1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)
The correlation ratio, entropy-based mutual information, total correlation, dual total correlation and polychoric correlation are all also capable of detecting more general dependencies, as is consideration of the copula between them, while the coefficient of determination generalizes the correlation coefficient to multiple regression.
Sensitivity to the data distribution[edit]
The degree of dependence between variables X and Y does not depend on the scale on which the variables are expressed. That is, if we are analyzing the relationship between X and Y, most correlation measures are unaffected by transforming X to a + bX and Y to c + dY, where a, b, c, and d are constants (b and d being positive). This is true of some correlation statistics as well as their population analogues. Some correlation statistics, such as the rank correlation coefficient, are also invariant to monotone transformations of the marginal distributions of X and/or Y.
Pearson/Spearman correlation coefficients between X and Y are shown when the two variables’ ranges are unrestricted, and when the range of X is restricted to the interval (0,1).
Most correlation measures are sensitive to the manner in which X and Y are sampled. Dependencies tend to be stronger if viewed over a wider range of values. Thus, if we consider the correlation coefficient between the heights of fathers and their sons over all adult males, and compare it to the same correlation coefficient calculated when the fathers are selected to be between 165 cm and 170 cm in height, the correlation will be weaker in the latter case. Several techniques have been developed that attempt to correct for range restriction in one or both variables, and are commonly used in meta-analysis; the most common are Thorndike’s case II and case III equations.[13]
Various correlation measures in use may be undefined for certain joint distributions of X and Y. For example, the Pearson correlation coefficient is defined in terms of moments, and hence will be undefined if the moments are undefined. Measures of dependence based on quantiles are always defined. Sample-based statistics intended to estimate population measures of dependence may or may not have desirable statistical properties such as being unbiased, or asymptotically consistent, based on the spatial structure of the population from which the data were sampled.
Sensitivity to the data distribution can be used to an advantage. For example, scaled correlation is designed to use the sensitivity to the range in order to pick out correlations between fast components of time series.[14] By reducing the range of values in a controlled manner, the correlations on long time scale are filtered out and only the correlations on short time scales are revealed.
Correlation matrices[edit]
The correlation matrix of 




Thus the diagonal entries are all identically one. If the measures of correlation used are product-moment coefficients, the correlation matrix is the same as the covariance matrix of the standardized random variables 



The correlation matrix is symmetric because the correlation between 



A correlation matrix appears, for example, in one formula for the coefficient of multiple determination, a measure of goodness of fit in multiple regression.
In statistical modelling, correlation matrices representing the relationships between variables are categorized into different correlation structures, which are distinguished by factors such as the number of parameters required to estimate them. For example, in an exchangeable correlation matrix, all pairs of variables are modeled as having the same correlation, so all non-diagonal elements of the matrix are equal to each other. On the other hand, an autoregressive matrix is often used when variables represent a time series, since correlations are likely to be greater when measurements are closer in time. Other examples include independent, unstructured, M-dependent, and Toeplitz.
In exploratory data analysis, the iconography of correlations consists in replacing a correlation matrix by a diagram where the “remarkable” correlations are represented by a solid line (positive correlation), or a dotted line (negative correlation).
Nearest valid correlation matrix[edit]
In some applications (e.g., building data models from only partially observed data) one wants to find the «nearest» correlation matrix to an «approximate» correlation matrix (e.g., a matrix which typically lacks semi-definite positiveness due to the way it has been computed).
In 2002, Higham[15] formalized the notion of nearness using the Frobenius norm and provided a method for computing the nearest correlation matrix using the Dykstra’s projection algorithm, of which an implementation is available as an online Web API.[16]
This sparked interest in the subject, with new theoretical (e.g., computing the nearest correlation matrix with factor structure[17]) and numerical (e.g. usage the Newton’s method for computing the nearest correlation matrix[18]) results obtained in the subsequent years.
Uncorrelatedness and independence of stochastic processes[edit]
Similarly for two stochastic processes 

Common misconceptions[edit]
Correlation and causality[edit]
The conventional dictum that «correlation does not imply causation» means that correlation cannot be used by itself to infer a causal relationship between the variables.[20] This dictum should not be taken to mean that correlations cannot indicate the potential existence of causal relations. However, the causes underlying the correlation, if any, may be indirect and unknown, and high correlations also overlap with identity relations (tautologies), where no causal process exists. Consequently, a correlation between two variables is not a sufficient condition to establish a causal relationship (in either direction).
A correlation between age and height in children is fairly causally transparent, but a correlation between mood and health in people is less so. Does improved mood lead to improved health, or does good health lead to good mood, or both? Or does some other factor underlie both? In other words, a correlation can be taken as evidence for a possible causal relationship, but cannot indicate what the causal relationship, if any, might be.
Simple linear correlations[edit]
The Pearson correlation coefficient indicates the strength of a linear relationship between two variables, but its value generally does not completely characterize their relationship.[21] In particular, if the conditional mean of 




The adjacent image shows scatter plots of Anscombe’s quartet, a set of four different pairs of variables created by Francis Anscombe.[22] The four 
These examples indicate that the correlation coefficient, as a summary statistic, cannot replace visual examination of the data. The examples are sometimes said to demonstrate that the Pearson correlation assumes that the data follow a normal distribution, but this is only partially correct.[4] The Pearson correlation can be accurately calculated for any distribution that has a finite covariance matrix, which includes most distributions encountered in practice. However, the Pearson correlation coefficient (taken together with the sample mean and variance) is only a sufficient statistic if the data is drawn from a multivariate normal distribution. As a result, the Pearson correlation coefficient fully characterizes the relationship between variables if and only if the data are drawn from a multivariate normal distribution.
Bivariate normal distribution[edit]
If a pair 









where 







The empirical correlation 


where 

See also[edit]
- Autocorrelation
- Canonical correlation
- Coefficient of determination
- Cointegration
- Concordance correlation coefficient
- Cophenetic correlation
- Correlation function
- Correlation gap
- Covariance
- Covariance and correlation
- Cross-correlation
- Ecological correlation
- Fraction of variance unexplained
- Genetic correlation
- Goodman and Kruskal’s lambda
- Iconography of correlations
- Illusory correlation
- Interclass correlation
- Intraclass correlation
- Lift (data mining)
- Mean dependence
- Modifiable areal unit problem
- Multiple correlation
- Point-biserial correlation coefficient
- Quadrant count ratio
- Spurious correlation
- Statistical arbitrage
- Subindependence
References[edit]
- ^ Croxton, Frederick Emory; Cowden, Dudley Johnstone; Klein, Sidney (1968) Applied General Statistics, Pitman. ISBN 9780273403159 (page 625)
- ^ Dietrich, Cornelius Frank (1991) Uncertainty, Calibration and Probability: The Statistics of Scientific and Industrial Measurement 2nd Edition, A. Higler. ISBN 9780750300605 (Page 331)
- ^ Aitken, Alexander Craig (1957) Statistical Mathematics 8th Edition. Oliver & Boyd. ISBN 9780050013007 (Page 95)
- ^ a b Rodgers, J. L.; Nicewander, W. A. (1988). «Thirteen ways to look at the correlation coefficient». The American Statistician. 42 (1): 59–66. doi:10.1080/00031305.1988.10475524. JSTOR 2685263.
- ^ Dowdy, S. and Wearden, S. (1983). «Statistics for Research», Wiley. ISBN 0-471-08602-9 pp 230
- ^ Francis, DP; Coats AJ; Gibson D (1999). «How high can a correlation coefficient be?». Int J Cardiol. 69 (2): 185–199. doi:10.1016/S0167-5273(99)00028-5. PMID 10549842.
- ^ a b Yule, G.U and Kendall, M.G. (1950), «An Introduction to the Theory of Statistics», 14th Edition (5th Impression 1968). Charles Griffin & Co. pp 258–270
- ^ Kendall, M. G. (1955) «Rank Correlation Methods», Charles Griffin & Co.
- ^ Mahdavi Damghani B. (2013). «The Non-Misleading Value of Inferred Correlation: An Introduction to the Cointelation Model». Wilmott Magazine. 2013 (67): 50–61. doi:10.1002/wilm.10252.
- ^ Székely, G. J. Rizzo; Bakirov, N. K. (2007). «Measuring and testing independence by correlation of distances». Annals of Statistics. 35 (6): 2769–2794. arXiv:0803.4101. doi:10.1214/009053607000000505. S2CID 5661488.
- ^ Székely, G. J.; Rizzo, M. L. (2009). «Brownian distance covariance». Annals of Applied Statistics. 3 (4): 1233–1303. arXiv:1010.0297. doi:10.1214/09-AOAS312. PMC 2889501. PMID 20574547.
- ^ Lopez-Paz D. and Hennig P. and Schölkopf B. (2013). «The Randomized Dependence Coefficient», «Conference on Neural Information Processing Systems» Reprint
- ^ Thorndike, Robert Ladd (1947). Research problems and techniques (Report No. 3). Washington DC: US Govt. print. off.
- ^ Nikolić, D; Muresan, RC; Feng, W; Singer, W (2012). «Scaled correlation analysis: a better way to compute a cross-correlogram». European Journal of Neuroscience. 35 (5): 1–21. doi:10.1111/j.1460-9568.2011.07987.x. PMID 22324876. S2CID 4694570.
- ^ Higham, Nicholas J. (2002). «Computing the nearest correlation matrix—a problem from finance». IMA Journal of Numerical Analysis. 22 (3): 329–343. CiteSeerX 10.1.1.661.2180. doi:10.1093/imanum/22.3.329.
- ^ «Portfolio Optimizer». portfoliooptimizer.io/. Retrieved 2021-01-30.
- ^ Borsdorf, Rudiger; Higham, Nicholas J.; Raydan, Marcos (2010). «Computing a Nearest Correlation Matrix with Factor Structure» (PDF). SIAM J. Matrix Anal. Appl. 31 (5): 2603–2622. doi:10.1137/090776718.
- ^ Qi, HOUDUO; Sun, DEFENG (2006). «A quadratically convergent Newton method for computing the nearest correlation matrix». SIAM J. Matrix Anal. Appl. 28 (2): 360–385. doi:10.1137/050624509.
- ^ Park, Kun Il (2018). Fundamentals of Probability and Stochastic Processes with Applications to Communications. Springer. ISBN 978-3-319-68074-3.
- ^ Aldrich, John (1995). «Correlations Genuine and Spurious in Pearson and Yule». Statistical Science. 10 (4): 364–376. doi:10.1214/ss/1177009870. JSTOR 2246135.
- ^ Mahdavi Damghani, Babak (2012). «The Misleading Value of Measured Correlation». Wilmott Magazine. 2012 (1): 64–73. doi:10.1002/wilm.10167. S2CID 154550363.
- ^ Anscombe, Francis J. (1973). «Graphs in statistical analysis». The American Statistician. 27 (1): 17–21. doi:10.2307/2682899. JSTOR 2682899.
- ^ Taraldsen, Gunnar (2021). «The Confidence Density for Correlation». Sankhya A. doi:10.1007/s13171-021-00267-y. ISSN 0976-8378. S2CID 244594067.
- ^ Taraldsen, Gunnar (2020). «Confidence in Correlation». doi:10.13140/RG.2.2.23673.49769.
Further reading[edit]
- Cohen, J.; Cohen P.; West, S.G. & Aiken, L.S. (2002). Applied multiple regression/correlation analysis for the behavioral sciences (3rd ed.). Psychology Press. ISBN 978-0-8058-2223-6.
- «Correlation (in statistics)», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Oestreicher, J. & D. R. (February 26, 2015). Plague of Equals: A science thriller of international disease, politics and drug discovery. California: Omega Cat Press. p. 408. ISBN 978-0963175540.
External links[edit]
- MathWorld page on the (cross-)correlation coefficient/s of a sample
- Compute significance between two correlations, for the comparison of two correlation values.
- «A MATLAB Toolbox for computing Weighted Correlation Coefficients». Archived from the original on 24 April 2021.
- Proof that the Sample Bivariate Correlation has limits plus or minus 1
- Interactive Flash simulation on the correlation of two normally distributed variables by Juha Puranen.
- Correlation analysis. Biomedical Statistics
- R-Psychologist Correlation visualization of correlation between two numeric variables
Если вы где-то читаете фразу вида «оказалось, что у данных событий корреляция вот такая вот», то примерно в 99,99% случаев, если прямо не оговорено иного, речь идёт о коэффициенте корреляции Пирсона. «Дефолт-корреляция» — это он.
Причём пользуются им далеко не только безграмотные журналисты, но и в целом довольно грамотные учёные. Что, на мой взгляд, весьма странно, ибо область его осмысленного применения сильно уже, чем область его фактического использования.
По этой причине мне хотелось бы рассказать, какими способами при помощи «дефолт-корреляции» можно сделать множество совершенно неправильных, однако весьма наукообразных и кажущихся весьма правдоподобными выводов.
Но для начала о том…
Что такое «коэффициент корреляции Пирсона»?
Вполне понятно, что для несведущих это — особая научная магия, однако довольно обидно, что для многих сведущих дела обстоят аналогично. «Я же биолог, а не математик — зачем мне лезть в эти тонкости?» — обычное дело.
Положим, у нас есть некие два предполагаемых процесса, для каждого из которых мы замеряем какой-то параметр, обычно называемый в данном случае «величиной». В результате у нас появляется набор пар чисел.
Предполагая заодно, что эти процессы не только существуют, но и как-то связаны, мы предполагаем же, что эта связь должна численно проявиться в сделанных нами измерениях. То есть из полученных пар чисел мы каким-то образом можем получить сведения о наличии или отсутствии связи.
Однако связи бывают разной степени жёсткости, поэтому желательно получать не бинарное «да» или «нет», а что-то типа непрерывной по пространству состояний оценки «силы связи».
И вот, встречайте, коэффициент корреляции Пирсона.
Я понимаю, что на этом месте очень многие испугались, что и дальше всё будет столь же непонятным. Какие-то страшные буковки в страшных комбинациях, всё такое.
Признаться, я тоже не особо-то люблю математический вариант записи. Мне «программистский» кажется гораздо более понятным. Поэтому я попытаюсь следовать именно ему.
Есть такое понятие «математическое ожидание величины», для краткости называемое «матожиданием». В простейшем случае его смысл крайне прост: это среднее арифметическое от всех полученных значений.
Получили мы какой-то набор измерений, представленный тут в виде списка
Потом мы просуммировали их все, поделили на количество чисел в этом списке — и вот оно, среднее арифметическое.
Далее мы найдём для каждого числа из списка его отклонение от матожидания.
…и получим, таким образом, список отклонений. Список отклонений каждого из значений от среднего арифметического по всему этому списку.
То же самое можно проделать и с другим списком, в котором находятся измерения второго параметра, измеренного одновременно с первым.
Например, мы у каждого пациента в палате померили температуру. И, кроме того, зафиксировали, сколько таблеток аспирина он сегодня принял. И теперь по вышеуказанной процедуре построим список отклонений температуры каждого пациента от средней температуры пациентов и соответствующий ему список отклонений количества принятых пациентом таблеток аспирина от среднего принятого их количества.
Да, тут уже и так есть суровые подозрения о множестве натяжек, но мы всё-таки не остановимся и предположим, что если температура как-то связана с приёмом аспирина, то должны быть связаны между собой и эти самые отклонения.
Например, если приём аспирина приводит к росту температуры, то мы будем видеть следующее.
Если пациент выпил больше таблеток, чем другие, то его температура отклоняется от средней в бо́льшую сторону.
Если пациент выпил меньше таблеток, чем другие, то его температура отклоняется от средней в меньшую сторону.
То есть оба отклонения — в одну и ту же сторону.
Если мы перемножим попарно все отклонения, то все произведения будут положительными.
И наоборот: если приём аспирина понижает температуру, то все произведения отклонений будут отрицательными.
Иными словами, у нас получилась некая величина, которая обладает чудесным свойством: для прямой связи явлений она положительная, а для обратной — отрицательная.
Однако что с ней будет, если явления не связаны?
Навскидку, с ней будет — «когда как».
Но ведь если явления действительно не связаны, то на большом количестве измерений приблизительно в равной мере должны быть распределены оба варианта: положительное произведение отклонений и отрицательное. Если их просуммировать, то, видимо, получится что-то около нуля. Причём, тем ближе к нулю, чем больше было измерений.
Собственно, вышевведённая функция «матожидание» именно это и делает: суммирует. Потом, правда, ещё делит на количество измерений, но для обнаруженного свойства это не так важно: ведь деление на положительное число не меняет знак результата и не может превратить ноль в не ноль или наоборот.
Поэтому вот он, критерий: ковариация.
Или, если расположить все формулы рядом…
Да, так несколько длиннее, чем в оригинальном определении, но зато и лучше понятно, что происходит.
Теперь, в общем, остался последний момент. Ковариация, увы, может иметь произвольную величину, а потому, для того, чтобы сделать по ней вывод о связи между списками, надо ещё знать максимальное её значение именно для этих величин.
Однако, по счастью, оное можно вычислить в общем виде.
Для этого введём ещё одну интересную величину — выведенную из списка квадратов отклонений от среднего.
Это, как можно видеть, корень из матожидания квадратов отклонений от среднего. Оно так и называется «среднеквадратическое отклонение».
Так вот, можно показать, что ковариация по своей абсолютной величине не превышает произведения среднеквадратических отклонений по этим двум спискам.
Ну а так как среднеквадратическое отклонение по построению всегда положительно, то можно заключить, что
или
В общем, если за меру взаимосвязи взять такую «нормированную величину», то она получится очень удобной и очень универсальной: будет показывать, связаны ли величины между собой, давая для прямой связи единицу, для обратной — минус единицу, а для несвязанных величин — ноль…
…думали они.
Но ага, щаз.
Всё очень удобно и универсально, однако в вышеприведённых рассуждениях есть изрядное количество изъянов, которые — ввиду очевидного удобства и универсальности полученной «меры взаимосвязей» — очень удобно игнорировать, и от этого иметь универсальный способ для поточной генерации совершенно неверных, но зато наукообразных выводов.
Впрочем, надо отметить, что процесса «нормировки» это не касается — со знаменателем всё зашибись, а способ стрельбы себе в ногу кроется в числителе. Да и в самом подходе в целом.
Поэтому, хотя для проформы я тут и привёл полное рассуждение, вскрываемые далее явления вызваны ковариацией и именно на способ её вычисления следует обратить особое внимание.
Выстрел номер один: Ньютон всё наврал
Предположим, некий физик усомнился в законе всемирного тяготения. И решил — в полном соответствии с научным методом — проверить, что тела и правда притягиваются по определённому закону.
Для этого он заказал себе очень точные приборы и сделал экспериментальную установку, в центре которой размещено массивное тело, на любом расстоянии от которого можно размещать другие тела и замерять воздействующую на них силу.
Со всей тщательностью физик измерил силу, действующее на тело, отнесённое от центра на самые разные расстояния. Запротоколировал данные. А потом посчитал корреляцию между координатой изображённого тут зелёным тела и действующей на него силой.
Хм. Ньютон вроде бы утверждал, что сила тяготения однозначно связана с расстоянием между центрами объектов. Почему же мы тут получаем не единицу, а что-то меньшее? Ну ладно, это, быть может, погрешность измерений. Всё равно ведь понятно, что определённо между расстоянием по оси икс и действующей силой есть заметная обратная связь.
На беду, у этого физика были свои личные подозрения об устройстве мира. «Вдруг», — думал он — «миру не всё равно, с какой стороны расположено тело?». Надо попробовать размещать тела не только справа, но и слева.
Правда, прибор для измерения силы умел измерять только её абсолютную величину, но ничего страшного: ведь если есть взаимосвязь между двумя величинами, то между величиной и модулем второй тоже должна быть взаимосвязь.
Поэтому физик провёл второй эксперимент: помещая теперь тело не только справа, но иногда и слева от центра.
В результате, его подозрения оправдались: теперь корреляция координаты с абсолютной величиной силы уже не просто отличалась от единицы или минус единицы…
Она стала нулевой.
Что же тут произошло?
Сейчас, подождите, сначала мы посмотрим на ещё один способ стрельбы в собственные конечности.
Выстрел номер два: хаос энергоснабжения
Однажды физик обнаружил у себя дома удивительный артефакт: электрическую розетку.
Про розетки он слышал, что в них есть электрический ток, которым как раз и питаются электроприборы. А у тока есть напряжение. Которое, вроде бы, в розетках переменное. Так вот, интересно, связано ли это переменное напряжение со временем? Или же, напротив, оно там совершенно хаотичное и меняется как попало?
Для ответа на этот вопрос физик собрал хитрую схему из компьютера и вольтметра, которая через равные промежутки времени измеряет напряжение в сети.
Если связь есть, — рассуждал физик, — то я её таким образом обнаружу. И он был прав: таким образом её действительно можно обнаружить. Причём для этого даже не обязательно быть физиком.
Но на беду и этот физик тоже решил не доверяться интуиции, а вычислить связь автоматически. Для этого он посчитал корреляцию измеренных напряжений с теми моментами времени, когда они были измерены.
Как вы думаете, что в результате получил физик?
Не спешите с ответом…
Не спешите…
Wait…
Wait…
Here it comes…
Физик получил случайную величину от минус до плюс единицы.
В зависимости от того, как встали звёзды, физик мог «выяснить», что напряжение связано со временем прямой или обратной связью, или же, что оно со временем вообще не связано.
Но как?! Как совершенно логичный математический коэффициент может привести к столь абсурдному результату?
Сбитый прицел номер один
Чтобы понять, откуда в мире берётся такая фигня, мы временно, для простоты забудем про знаменатель.
Расположенная в числителе ковариация — это среднее арифметическое произведений отклонений.
Отклонений от чего?
От среднего.
Когда первый физик меряет силу, в зависимости от координаты, слева и справа в симметричных точках у него получаются одинаковые силы. Они отклонены от средней силы совершенно идентично, какой бы эта сила ни была.
Средняя же координата — 0. Отклонения от неё в симметричных точках равны по абсолютной величине, но противоположны по знаку.
Пусть в точке 1 отклонение силы от среднего равно dF1. Тогда в точке −1 будет такое же отклонение dF1. Но вот отклонения в координатах будут уже 1 и −1. Если мы перемножим отклонения, то получим…
| Координата | dx | dF | dx*dF |
|---|---|---|---|
| 1 | 1 | dF1 | dF1 |
| −1 | −1 | dF1 | −dF1 |
С точки зрения ковариации, эти симметричные значения просто взаимно уничтожаются.
Поскольку же физик приблизительно равномерно измерял силы слева и справа, то в среднем все измерения взаимно уничтожились.
Вот как выглядит график произведений отклонений, в зависимости от координаты.
Если случайным образом набрать с него точек, то сумма значений в них будет приблизительно равна нулю. И, следовательно, будет равна нулю ковариация.
И чем больше точек мы возьмём, тем она ближе к нулю. Что наверняка будет убеждать физика, что тут нет никакой ошибки или случайности: чем больше измерений он производит, тем более очевидно, что корреляция — нулевая.
И это при том, что наличие связи между координатой и действующей силой видно невооружённым глазом.
Быть может, ошибка была в том, что физик измерял абсолютную величину силы? Быть может, стоило ему измерить силу с учётом направления, всё получилось бы правильно?
О да, в этом случае корреляция была бы не нулевой, а ранее упомянутыми −0,68. Ведь в этом случае произведения симметричных отклонений не уничтожали бы друг друга.
Только это всё равно был бы ошибочный результат. Просто вывод, сделанный по нему, случайно совпал бы с правильным.
Ведь предположим, что Ньютон действительно наврал, и тела, расположенные справа, притягиваются, но вот расположенные слева — отталкиваются. В этом случае, напротив, игнорирование направления силы дало бы ненулевую корреляцию, а вот его учёт — нулевую.
И в одном из двух вариантов по-прежнему можно было бы сделать вывод об отсутствии взаимосвязи при реальном её наличии.
Причём с правильным совпадал бы вывод, сделанный по тому методу, по которому в другом случае получался бы вывод, не совпадающий с правильным.
Таким образом, в рамках данного метода в обязательном порядке надо сделать выбор между вариантами, заранее зная правильный ответ, — иначе можно выбрать тот вариант, который приводит к ошибке.
То есть это сам метод ошибочен. С его помощью невозможно сделать правильный вывод, не зная его заранее.
Сбитый прицел номер два
Аналогичная история происходит и со вторым физиком: он измеряет процесс, в котором взаимно уничтожаются произведения отклонений от среднего, хотя сам процесс при этом вполне закономерен.
Я для примера взял колебания вокруг нуля, однако это только для наглядности: коэффициент корреляции зависит не от величины, а от её отклонения от среднего, поэтому «без разницы», где расположено это среднее.
Здесь мы тоже наблюдаем симметрию. И эта симметрия с неизбежностью приводит к тому, что на некотором отрезке — кратном двойному периоду колебаний — сумма произведений отклонений взаимно уничтожается. И фактически на корреляцию будет оказывать влияние только тот «хвостик», который останется после последнего обнуления.
Вот как для данного фрагмента будет вести себя корреляция — в зависимости от того момента, когда физик остановил измерения.
Поскольку момент начала и конца измерений зависит только от стечения обстоятельств, физик в реальности высчитывает случайное число, а вовсе не «надёжный показатель связи между явлениями».
Правда, тут выручает то, что одна из величин — время — неограниченно растёт с ростом количества измерений, а вторая величина — напряжение — ограничена определённым диапазоном. В результате, расположенное в знаменателе среднеквадратическое отклонение времени увеличивается до сколь угодно большой величины быстрее, а потому корреляция стремится к нулю с увеличением отрезка времени, на котором проводятся измерения.
Это позволяет уверенно «доказывать» независимость абсолютно любой ограниченной диапазоном величины от времени, а не просто диагностировать наличие или отсутствие связи, в зависимости от того, как звёзды встали.
Хотя, конечно, и тут есть шанс выбрать периодичность замеров, слегка некратную периодичности колебаний, и снова тщательно вычислить случайное число. Например, напряжение в сети колеблется со слегка плавающей частотой: 50 раз в секунду. Поэтому проведение измерений с интуитивно напрашивающейся частотой раз в секунду — серьёзная заявка на успех.
В общем, если физику повезёт, и он замерит много периодов колебаний, не попав при этом в нужную «слегка некратность», он обнаружит на них близкую к нулю корреляцию. После чего сделает ошибочный вывод, что связи между временем и напряжением нет.
Если не повезёт, то результат вообще будет случайным числом, и тут уже, разумеется, никакой ошибки не будет.
Шутка.
В любом случае, вывод ошибочен. Даже если он случайно совпадёт с правильным — ведь ошибочен сам метод его получения.
Но иллюзия о научном обнаружении наличия или отсутствия связи в обоих случаях вполне может сохраниться.
Hold your fire №1 and №2
Первые два примера демонстрируют штуку, которую надо помнить в обязательном порядке: введённая нами «мера взаимосвязи» не универсальна. Сделанные при её построении рассуждения относились только к линейным зависимостям одной величины от другой.
Грубо говоря, это работает только тогда, когда предполагается зависимость…
Если же зависимость иная, то, вообще говоря, коэффициент корреляции может оказаться произвольным.
Да-да, не нулевым, а произвольным.
Ведь даже при очень хорошем случае — при убывании одной величины при возрастании другой — первый физик уже получил странный результат. Ещё до того, как он начал пробовать помещать тело не только справа, но и слева, при наличии совершенно однозначной и непериодической зависимости, полученный им коэффициент корреляции уже заметно отличался от −1.
И дело тут не в погрешности измерений. Дело в том, что даже зависимость
достаточно нелинейна для коэффициента корреляции. Уже на ней результат опасно близок к «хм, возможно, на силу влияет что-то ещё». Да, это, конечно, не −0,1, но всё-таки −0,68 — это и не чистая минус единица. Всё выглядит так, будто бы тут не совсем детерминированная связь.
Так какие же заключения можно сделать, вычислив коэффициент корреляции?
Если она нулевая, значит ли это, что величины не связаны?
Два примера показывают, что нет, нельзя.
А если она ненулевая, значит ли это, что зависимость есть?
Второй пример показывает, что и это тоже совершенно не обязательно: ведь вполне возможно и даже весьма вероятно на, например, периодическом процессе получить случайное число, довольно существенно отличающееся от нуля.
Иными словами, исследователь откуда-то должен знать заранее, что тут либо линейная зависимость, либо вообще никакой, чтобы сделать более-менее правильный вывод.
Но откуда он может это знать до исследований? Только из других исследований. Где анализ делался другими методами. Например, основывался на вдумчивом разглядывании графиков или распределений, формированием на их основе гипотезы о функции, связывающей две величины, и последующей экспериментальной проверке того, что эта функция и правда именно такая, поскольку с её помощью удаётся предсказать значение второй величины, зная первую.
Но если это всё уже проделано, то зачем ему вообще считать корреляцию? У него же уже есть более надёжные результаты.
Может быть, коэффициент корреляции можно использовать как первое приближение? Как оценку связи навскидку?
Хороша же такая оценка, которая при весьма вероятных закономерностях даёт случайное число, и приводит, таким образом, к совершенно разным выводам — в зависимости от расположения звёзд.
То есть в сухом остатке оказывается, что единственное, что можно сделать при помощи корреляции — это вывод об отсутствии одной и той же линейной на всём отрезке взаимосвязи между величинами.
Именно об отсутствии — ведь даже о наличии такой взаимосвязи вывод сделать нельзя (см. «случайное число»).
И именно что линейной на всём отрезке, поскольку при фрагментарно линейной вполне возможно взаимное уничтожение произведений отклонений.
Причём натолкнуться на такое может совсем даже не только усомнившийся в законе всемирного тяготения физик. Ровно так же хлебнуть полную чашу горя может медик, решивший выяснить связь температуры тела пациента с самочувствием пациента. При нормальной температуре — 36,6 °C — самочувствие, видимо, наилучшее. При повышении температуры оно ухудшается. Однако и при понижении температуры оно тоже ухудшается…
Чувствуете схожесть ситуации с экспериментами первого физика? О да, и с корреляцией будет тоже: при симметричности оценок слева и справа от нормальной температуры корреляция окажется близкой к нулю. Из чего медик сможет заключить, что связи между температурой и самочувствием нет.
И ровно то же самое будет с лекарством, у которого есть оптимальная доза приёма: при этой дозе результаты будут наилучшими, но вот при меньшей и при большей они будут хуже, что тоже приведёт к чисто техническому занулению коэффициента корреляции.
И вы думаете, на этом проблемы с коэффициентом кончились?
Ага. Щаз.
Выстрел номер три: неубедительный экстрасенс
Однажды к группе заинтересованных в изучении паранормальных явлений пришёл человек, обладающий удивительной способностью — он абсолютно безошибочно умел угадывать выпавшее на кубиках.
Правда, по воле паранормальных сил эта способность у него была выражена в весьма странной форме: если кто-то собирался бросить четыре кубика, то Космос тут же шептал экстрасенсу сумму выпавшего на них в тридцатой степени. Увы, экстрасенс был безграмотен (он просто слушал голос Космоса), а потому извлекать корень тридцатой степени не умел.
Впрочем, паранормологи этого делать тоже не умели: ни извлекать корень тридцатой степени, ни возводить в тридцатую степень. Однако они предположили, что его предсказания всё равно должны коррелировать с суммой выпавшего на кубиках (которую они считать всё-таки умели) — ведь между числом и его тридцатой степенью имеется однозначная математическая связь.
Не поленившись, паранормологи провели 10 000 испытаний. Не было никаких сомнений в том, что такого вполне достаточно для исключения любых случайностей.
Но результат их разочаровал: предсказания экстрасенса имели корреляцию с суммой выпавшего на кубиках всего 0,2. Такой вшивой корреляции явно недостаточно, чтобы подтвердить экстрасенсорные способности. 0,5 ещё куда ни шло, но вот 0,2…
В результате экстрасенс был изгнан и высмеян.
Сбитый прицел номер три
Я специально придумал этот пример, чтобы развеять сомнения, будто бы «дефолт-корреляция» может не срабатывать только при попытках измерять связь времени и состояния, но вот для неких случайных событий она всегда подходит.
О нет. И данные паранормологи тому примером.
На самом деле они прогнали экстрасенса, который совершенно правильно угадал в 100% случаев. Да-да, он ни разу не ошибся.
Однако проведи они даже миллион испытаний, всё равно корреляция была бы всё столь же низкой. Ибо я не зря сказал о том, что корреляция более-менее корректно отображает только линейную связь между величинами.
Здесь же наблюдался аналог того, что произошло с первым физиком, только в гипертрофированной форме: корреляция была не просто несколько подозрительной, а существенно ниже порогового уровня достоверности.
Случайно угадать все сто тысяч раз тридцатую степень суммы выпавшего на четырёх кубиках столь нереально, что такое вряд ли можно рассматривать всерьёз, но корреляция при этом утверждает, что экстрасенс как бы не угадывал.
Как бы утверждает.
Hold your fire №3
На самом же деле, совершенно не зря в справочниках пишут, что всё это осмыслено только при гауссовом распределении случайных величин. И зря так многие это либо не читают, либо игнорируют в своей практической деятельности.
«Гауссово» распределение подразумевает концентрацию основной массы результатов измерений вокруг некоторой величины (того самого «матожидания» или «среднего»). Причём чем дальше от неё случай, тем меньше раз мы его должны встречать.
Имеющаяся же в формуле корреляции σ — среднеквадратическое отклонение — характеризует в этом случае «ширину» данного колокола.
Негауссовость одного или обоих распределений — залог получения очень низкой корреляции даже при очевидной прямой взаимосвязи величин.
В данном случае сумма выпавшего на четырёх кубиках имела распределение, близкое к гауссову, но вот возведение результата в тридцатую степень убило даже намёк на гауссовость, что не замедлило сказаться на результате.
И не помогли даже 10 000 испытаний.
В реальных же исследованиях испытаний вполне может быть штук 100, например. И негауссовость распределения там может быть существенно менее экстремальной, но всё равно пагубно сказаться на результатах.
Выстрел номер четыре: убедительный экстрасенс
К тем же самым паранормологам через некоторое время пришёл ещё один посетитель. Он тоже имел паранормальную связь с кубиками, но его метод был проще: он бросал один кубик, а потом предлагал экспериментатору бросить второй. Благодаря тому, что в его руках была заключена особая магия, первый бросок кубика мистическим образом влиял на всю ситуацию в целом.
О нет, выпавшее на втором кубике он не брался предсказать, однако утверждал, что первый бросок окажет очень сильное влияние на второй бросок, суть коего влияния он, впрочем, не брался объяснить. Но предлагал просто взять и посчитать корреляцию выпавшего на первом кубике с суммой выпавшего на двух кубиках.
Первые сто испытаний повергли паранормологов в шок и трепет: корреляция действительно оказывалась весьма нехилой: 0,75.
Правда, они всё-таки усомнились, не было ли тут простого везения. Однако, проделав привычные для них 10 000 испытаний, они с удивлением отметили, что корреляция упала, но не так, чтобы очень сильно. Всё-таки 0,7 — это весьма неплохо. Согласно всем справочникам, это уже тянет на термин «высокая корреляция».
Определённо у этого экстрасенса был талант — оставалось только понять, каким способом из его предсказаний можно извлекать сведения о том, что выпадет на втором кубике…
Сбитый прицел номер четыре
…и правильный ответ: никаким. Нет никакого способа предсказать, что именно там выпадет. И даже, внезапно, нет никакого способа предсказать сумму.
Да-да, корреляция — высокая, однако всё, что можно сказать про сумму, это то, что она будет лежать на отрезке от выпавшего на первом кубике плюс один до выпавшего на первом кубике плюс шесть. Что было вполне понятно и безо всяких экстрасенсов.
Но никаких случайных совпадений — корреляция, правда, получится примерно вот такая.
Hold your fire №4
Разумеется, выпавшее на первом кубике влияет на сумму, поскольку оно входит туда как слагаемое. Однако корреляция показала всего лишь линейную связь первого со вторым. Выпавшего на первом кубике и случайной величины, полученной прибавлением к уже выпавшему второй случайной величины.
Но сколь же легко очароваться большим значением коэффициента и сделать вывод, который вовсе из него не следует: первый кубик как-то влияет на второй. Или даже, наоборот: ещё не брошенный второй кубик как-то влияет на первый.
Или хотя бы, что из результата броска первого кубика можно узнать что-то ещё, кроме и так очевидного.
Ах, сколько же раз такого рода эксперименты приводят к восторженным публикациям — причём не только в обычной прессе, но даже и во вполне научной.
Временами ничто не отделяет добросовестного биолога от того, чтобы путём сотен замеров открыть удивительный факт: все муравьи планеты строят муравейники, длина окружности основания которых примерно втрое больше диаметра этого основания.
Кажется, будто бы выполнение некого «научного» ритуала обязательно должно давать правильные результаты, даже если при этом не понимать сути этого ритуала, оправдывая фразами вида «я же паранормолог, а не математик».
Математика как бы работает сама. Ведь она же математика. Математика не обманывает.
И да, математика не обманывает — обманывают её трактовки.
Выстрел номер пять: хороший способ вызвать дождь
Как-то раз антрополог наблюдал за обычным городским жителем (конечно же, с его, этого жителя, согласия). И через некоторое время он заметил удивительную закономерность: если этот житель брал с собой зонт, то в этот день шёл дождь.
Конечно, так случалось не каждый раз: иногда объект наблюдения брал зонт, но дождь не шёл, иногда не брал, но дождь всё равно шёл, — однако слишком часто наличие зонта с наличием дождя и отсутствие зонта с отсутствием дождя случались одновременно.
Антрополог, как настоящий учёный, конечно, не доверился таким «навскидочным» оценкам, а вместо этого стал каждый день тщательно протоколировать свои наблюдения.
Через год он приписал событиям «взят зонт» и «был дождь» число 1, событиям «не взял зонт» и «не было дождя» число 0, и посчитал корреляцию по своим протоколам.
Корреляция была очень высокой: 0,95. Эти два события однозначно были связаны.
Гордый собой антрополог написал статью «Как вызывать дождь», в которой убедительно — по трём с половиной сотням наблюдений — доказывал, что именно вот этот житель управляет дождями по месту своего проживания. При помощи ношения зонта.
К сожалению, эту статью отказались печатать, ссылаясь на то, что как-то это всё неубедительно звучит.
Подумав некоторое время, антрополог пришёл к мысли, что наверно всё наоборот: это дождь управляет взятием зонта этим жителем. Просто данный гражданин способен видеть будущий дождь своим внутренним зрением. И, увидев будущий дождь, берёт с собой зонт — даже если на улице сейчас пока ещё нет никакого дождя. Если, конечно, не забыл с утра внутренним зрением посмотреть в будущее.
Ведь однозначно, столь высокая корреляция не может быть результатом случайности.
К сожалению, эту статью в журнал тоже не взяли, поскольку тамошние скептики не поверили в реальности внутреннего футуристического зрения, несмотря на столь яркие доказательства существования оного.
Однако антрополог не отчаялся. Подумав ещё, он сделал финальный вывод: существует мистическая незримая сила, которая вызывает дожди и одновременно с тем побуждает отдельных граждан брать с собой зонт. Поиском этой силы срочно следует заняться, поскольку она перевернёт все представления о мироздании.
В этот раз Фортуна улыбнулась антропологу: под это дело был создан специальный институт и много лет всевозможные учёные мужи пытались найти эту силу, под чутким руководством данного антрополога, которого хоть и не сделали директором, но всё-таки сделали замом. Вот так добро победило зло.
Сбитый прицел номер пять
Если коэффициент корреляции показал реальную связь одной величины с другой (а не случайное число, как это было со вторым физиком), это всё равно никак не доказывает, что одно явление вызывается другим. Даже если этим способом с самого начала хотели доказать наличие таковой связи, что многим почему-то кажется гарантией верности выводов.
Вполне может быть так, что первое явление не вызывается вторым, и при этом даже второе явление не вызывается первым.
В этих случаях говорят: «может быть, что есть некое третье явление, вызывающее оба два», — но и это в ряде случаев скорее вводит в заблуждение, нежели помогает. Ведь правда может быть такое явление, но на этом всё равно возможные варианты не кончаются.
И уж, тем более, никто не гарантирует, что именно то «третье явление», которое предположил кто-то там, и есть то самое искомое.
Улыбнувшаяся антропологу Фортуна, в это время со спины показывала человечеству средний палец, ибо не было никакой внешней мистической силы. Гражданин просто утром смотрел прогноз погоды, и, если там обещался дождь, брал с собой зонт.
Может показаться, что, ну ладно, пусть не мистическая сила, но всё-таки третье явление, вызывающее первые два, тут есть.
Предположим, есть. Но какое?
Прогноз погоды вызывает дождь?
Или ещё не случившийся дождь вызывает прогноз?
Ну Ok, не сам дождь, а атмосферное давление, скорость и направление ветра, наличие водоёмов и т. п. вызывают и дождь, и прогноз?
Однако мы могли бы убедиться, что, вообще говоря, данного жителя побуждают взять зонт сами опубликованные прогнозы, а вовсе не физические явления. Для этого надо было бы просто попросить тот источник, в котором он эти прогнозы читает, некоторое время публиковать неправильные прогнозы. И тем самым воочию узреть, что зонт берётся, если в прогнозе написано, что будет дождь, а вовсе не если какие-то физические параметры указывают на его высокую вероятность.
То есть некого одного «третьего явления», вызывающие первые два, не существует. Вместо этого есть целый набор явлений, состоящих друг с другом в весьма непростых отношениях.
Долгое время некая служба делала прогнозы, ориентируясь на ряд параметров. Их метод правда работал, поэтому их прогнозам начали доверять. Настолько, что некоторые даже стали игнорировать положение вещей, опираясь только на сказанное этой службой. И теперь слова этой службы побуждают этих людей брать зонт. И они достаточно долгое время брали бы его, даже если бы данные метеорологи поголовно сошли бы с ума и начали бы строить прогнозы на основе рисунка кофейной гущи.
Хотя в прошлом связь между явлениями через общую «третью силу» была, сейчас её уже нет. Но по инерции всё продолжает работать.
Выстрел номер шесть — прибытие автобуса
Один психолог наблюдал за ещё одним гражданином. И выяснил, что каждый раз, когда тот гражданин приходит на остановку, не позже, чем через пять минут, к ней приезжает автобус. Причём всё время один и тот же.
Естественно, предположение о том, что приход на остановку именно этого человека вызывает приезд этого автобуса, психолог сразу же отверг, как слишком абсурдное.
Но его заинтересовало, может ли быть верно обратное: что приезд этого автобуса вызывает приход этого человека на остановку? Это выглядело очень правдоподобным.
С согласия этого человека психолог начал за ним наблюдать. Оказалось, что этот человек каждый будний день встаёт в одно и то же время, за полчаса собирается и завтракает, а потом идёт на остановку.
Все введённые психологом способы измерить корреляцию данных событий указывали на одно и то же: связь тут очень жёсткая. Совершенно точно приезд этого автобуса вызывает приход человека на остановку. Точнее, не сам приезд, а знание о приезде.
Именно под приезд данного автобуса (время прибытия которого этот человек, видимо, вычислил на стихийной серии экспериментов) данный человек подстроил свой распорядок дня, учтя, разумеется, время на «успеть собраться».
Это вам не дождь, вызывающий зонт, тут всё тип-топ. Вон, даже читатели этой статьи сейчас думают: «А здесь-то что не так с выводами?!»
Сбитый прицел номер шесть
А с выводами здесь тоже не так всё.
Все способы подсчёта корреляции действительно могут показать однозначную линейную взаимосвязь. Совершенно честно. Без ошибок. И даже другие, не дефолтные, коэффициенты корреляции её покажут. И всё может казаться вообще очевидным. Но и в этом случае вполне возможны неверные выводы.
Дело в том, что описанный гражданин не вычислял время прибытия автобуса. И никогда не видел расписания. И не подстраивал под него свой график.
Он по городскому навигатору узнал время поездки от дома до работы, а потом поставил будильник на красивое круглое число, позволяющее ему успевать на работу. Ну, на девять утра, например.
Полчаса ему хватало на сборы, после этого он выходил на улицу, и — ну надо же — именно в это время приходил данный автобус. Да, вот так вот удачно совпало расписание.
Впрочем, там, в этом расписании, автобусы вообще ходили раз в пять минут, поэтому не совпасть оно просто не могло: округления времени будильника до красивого числа с запасом хватало на покрытие даже максимального ожидания — пяти минут. Приходи этот автобус на две минуты раньше, ну так этот человек ездил бы на следующем. И точно так же каждый раз успевал бы вовремя.
Да, можно понатягивать сову на глобус и выстроить какую-то отмазку про «третье явление». Ну, там, «третьим явлением в данном случае оказывается всё человеческое общество, где людей на работу развозит общественный транспорт, а потому какие-то работники автобусного парка составили правильное расписание с достаточно частым движением автобусов и так далее». Однако всё это совершенно не помогает понять то самое, что хотел понять психолог: почему этот человек так делает? Что его побуждает поступать именно так? Какая сила?
И в данном случае реальной «силой» оказалось «я попробовал почти наугад, оно сработало, поэтому я и дальше так делал».
Сравните это с нарисованной психологом картиной, согласно которой этот человек, как стихийный, но добросовестный исследователь, вычислял расписание автобуса, рассчитывал свои действия, составлял план… в общем, явно был кем-то не тем, кем оказался на самом деле.
И вся эта стройная теория отлично подтверждалась всеми возможными корреляциями и даже, вроде бы, правдоподобными рассуждениями.
Возможно даже, услышав о реальном положении вещей непосредственно от самого наблюдаемого, психолог всё равно решил бы сохранить свой вариант описания, добавив модификацию «он всё равно планирует, только подсознательно». И даже, не исключено, построил бы целую теорию подсознательного планирования, столь же хорошо подкреплённую высокими корреляциями, как и его первоначальный вывод.
Hold your fire №5 and №6
Мораль последних двух историй в том, что никакой статистический показатель сам по себе не может подтвердить нравящуюся вам теорию. Теории подтверждаются только совокупностью показателей в рамках правильно построенной серии экспериментов.
Серии, а не одного эксперимента — пусть даже с большим числом данных.
Какими бы ни оказались все подсчитанные вами статистические показатели, они лишь дают вам некоторую почву для размышлений и предположений. Для гипотез, а не для «теорий», о которых многие любят на первом же этапе заявлять.
Первый эксперимент — первый. По его результатам вам надо сформулировать гипотезу и в следующих экспериментах проверять, правда ли она даёт сбывающиеся прогнозы.
Намеренное в первом эксперименте — это ведь данные, на которых строится гипотеза. На этих данных нельзя проверить, правда ли гипотеза работает: ведь именно на них вы её построили — ясен пень, на них она будет работать. Так будет с любой гипотезой — даже с неверной.
При сбывшихся же прогнозах на новых экспериментах уже правда появится «статистическое доказательство»: ведь предположенная вами зависимость одной величины от другой правда позволяет делать прогнозы на тех данных, которые мы на момент её введения в качестве гипотезы ещё не получили. Вот это доказывает реальность связи, а не просто высокая корреляция.
Более того, мало повторить тот же эксперимент и убедиться, что и второй раз сработало. Сработало или нет, но надо всё это проверить и в других условиях тоже. Ведь реальная теория не может описывать один частный случай — она должна распространяться на довольно обширную область возможных вариантов.
Но и на этом всё не кончается: даже если эта гипотеза правда даёт сбывающиеся прогнозы на широкой области, всё равно на следующих экспериментах надо ещё проверить, что все альтернативные гипотезы на них не срабатывают. В ином случае окажется, что вы доказали не верность именно вашей гипотезы, а лишь верность довольно обширного множества гипотез, включая вашу.
Заметьте, в пунктах пять и шесть исследователи имели дело именно с таким случаем: полученные ими данные укладывались в несколько совершенно разных гипотез. И для окончательного вывода исследователям следовало экспериментально доказать, что в других случаях одна из гипотез срабатывает, а все остальные — нет. И именно по этой причине она стала бы наиболее вероятным объяснением наблюдаемого и заслужила бы звания «теории». А без этого она не «теория», но «одна из возможных гипотез».
Hold your fire now
Собственно, можно догадаться, какие эмоции я испытываю, читая очередную статью, где исследователи замерили две величины, посчитали корреляцию между ними и уже называют это «открытием» и «построением новой теории». О нет, на данном этапе вы ещё не сделали открытие. Вы получили какой-то намёк и первую порцию данных, которые потом, если вы не бросите это занятие и будете ставить корректные серии экспериментов с корректным же анализом результатов, возможно, приведут к открытию.
Увы, сейчас вся мировая наука медленно, но верно, движется в направлении безудержной генерации «теорий» на ровном месте, что в основном провоцируется специфическим подходом к оценке работы учёного.
Считается, что учёный отчитывается за свою работу строго публикациями в журналах. И что эти публикации должны следовать с определённой плотностью, иначе а-я-яй, плохо работал. При этом журналы имеют тенденцию публиковать те работы, где заявлено о «прорывах», «успехах» и «новых теориях», а вовсе не о «проверили — не работает»
И даже статьи, где измерено что-то полезное, зачастую получают низкий приоритет, если в них не содержится заявлений или хотя бы намёков на тему «мы с первой попытки поняли, как всё устроено».
Естественно, в данном эволюционном процессе преимущество получает стратегия высасывания «открытий» из пальца. Что фактически приводит к отсеву добросовестных учёных в пользу недобросовестных, а также склоняет всех учёных к подтасовке результатов исследований и фабрикации недостоверных выводов.
Метод незатейлив: взяли как можно больше данных, посчитали попарные корреляции всего со всем, нашли ту, которая — пусть даже случайно — «высокая», приписали к ней тот вариант объяснения, который первым пришёл в голову или просто понравился, и вот уже публикация об «открытии».
Даже странно, что всё ещё так мало статей, создаваемых на основании данных с сайта «Ложные корреляции». Давно уже пора построить стройную теорию о том, почему количество выпущенных за год фильмов с Николасом Кейджем так тесно связано с количеством утонувших в этом году в бассейне.
Тут, вон, не только корреляция 66%, но и даже сходство в графиках видно невооружённым глазом.
Кто-то обязательно должен объяснить всё это.
И тем более, объяснить, почему количество потребляемого на душу населения маргарина на 99,26% коррелирует с интенсивностью разводов в Майне.

Затем каждую из величин Σfxyax перемножаем на условные отклонения ряда у для данной строки (ay) и результаты записываем в графу 17. Суммируя полученные произведения, получаем величину Σ(Σfxyax)ay=417.
Теперь в нашем распоряжении имеются все необходимые величины для вычисления r по формуле:
Величина полученного коэффициента корреляции говорит об умеренной тесноте связи исследованных признаков, а знак свидетельствует о прямом характере этой связи.
Иногда при наличии линейной связи можно, используя коэффициент корреляции, оценить влияние признака-фактора на результативный признак. Для этого применяется квадрат коэффициента корреляции, называемый коэффициентом детерминации (r2). Если выразить коэффициент детерминации в процентах, то он покажет долю влияния данного факториального признака на результативный. Например, коэффициент корреляции между ростом и весом детей равен +0,75, тогда коэффициент детерминации будет: rxy2=0,752=0,56. Если принять все факторы, влияющие на вес тела, за 100%, то на долю роста приходится 56%.
Поскольку коэффициент корреляции в клинических исследованиях рассчитывается обычно для ограниченного числа наблюдений, нередко возникает вопрос о надежности полученного коэффициента. С этой целью определяют сред-
нюю ошибку коэффициента корреляции. При достаточно большом числе на-
блюдений (больше 100) средняя ошибка коэффициента корреляции (тr) вычисляется по формуле:
|
1− r |
2 |
|||
|
mr |
= |
xy |
(1.37) |
|
|
n |
||||
где n — число парных наблюдений.
В том случае, если число наблюдений меньше 100, но больше 30, точнее определять среднюю ошибку коэффициента корреляции, пользуясь формулой:
|
1− r 2 |
|||
|
mr = |
xy |
(1.38) |
|
|
n −1 |
|||
66

С достаточной для медицинских исследований надежностью о наличии той или иной степени связи можно утверждать только тогда, когда величина коэффициента корреляции превышает или равняется величине трех своих ошибок (rxy>=3mr). Обычно это отношение коэффициента корреляции (rху) к его средней ошибке (тr) обозначают буквой t и называют критерием достоверности:
|
tr |
= |
rxy |
(1.39) |
|
|
mr |
||||
Если tr >= 3, то коэффициент корреляции достоверен. В рассмотренном выше примере число наблюдений 142, а коэффициент корреляции 0,68. Тогда
|
mr |
= |
1− rxy2 |
1−(0,68)2 |
||
|
n |
= |
142 |
= 0,045 |
||
|
r |
|||||
|
tr = |
= |
0,68 |
=15 , |
||
|
mr |
0,045 |
||||
т. е. коэффициент корреляции вполне достоверен.
В случае малой выборки (число наблюдений меньше 30) для оценки достоверности коэффициента корреляции, т. е. для определения соответствия коэффициента корреляции, вычисленного по выборочным данным, действительным размерам связи в генеральной совокупности, средняя ошибка коэффициента корреляции (тr) определяется по формуле:
|
1− r 2 |
|||
|
mr = |
xy |
(1.40) |
|
|
n − 2 |
|||
Значения критерия tr оцениваются по таблице t Стьюдента при числе степеней свободы v = п — 2. Если величина tr больше табличного значения t05, то коэффициент корреляции признается надежным с доверительной вероятностью больше 95%. Например, имеется коэффициент корреляции, равный +0,72 при числе наблюдений 28. Тогда
mr = 1−(0,72)2 = ±0,019 28 −2
tr = 0,0190,72 = 35,9
Полученное значение tr = 35,9 значительно больше табличного t01 = 2,779, следовательно, полученному коэффициенту корреляции можно доверять с высокой степенью вероятности (>99%).
В медицинской практике нередко возникает необходимость сравнить между собой два выборочных коэффициента корреляции и определить, существенна ли разница между ними. Ввиду того, что распределение коэффициента корреляции отличается от нормального, для оценки значимости различия между двумя коэффициентами корреляции рекомендуется использовать величину Z,
67

предложенную Р. Фишером. Величины Z, соответствующие различным значениям коэффициента корреляции, представлены в табл. 1.38.
Например, при исследовании тесноты связи между ростом и весом девочек и мальчиков было установлено, что у мальчиков коэффициент корреляции равен 0,5, а у девочек — 0,7. При этом обследовано 20 мальчиков и 30 девочек. Можно ли считать, что у девочек сильнее выражена связь между ростом и весом, чем у мальчиков? Для решения этого вопроса переведем значение наших коэффициентов корреляции (r) в величины Z. Находим по таблице, что r = 0,5 соответствует Z = 0,5493, а для r = 0,7 соответствует Z = 0,8673. Ошибка разности вычисляется по формуле:
|
mz |
= |
n1 |
1 |
+ |
1 |
= |
1 |
+ |
1 |
= 0,10 = 0,316 |
|
−3 |
n2 −3 |
20 −3 |
30 −3 |
Вычисляем критерий значимости различий:
|
tz |
= |
z1 − z2 |
= |
0,8673 −0,5493 |
= |
0,3188 |
=1,005 |
|
|
mz |
0,316 |
0,316 |
||||||
Разность признается значимой, если tz ≥ 3. В нашем примере tz < 3; следовательно, на основании полученных коэффициентов корреляции нельзя делать вывод о более выраженной связи между ростом и весом у девочек.
Таблица 1.38 — Таблица величин Z
|
r |
0,00 |
0,01 |
0,02 |
0,03 |
0,04 |
0,05 |
0,06 |
0,07 |
0,08 |
0,09 |
|
0,90 |
1,4722 |
1,5275 |
1,5890 |
1,6584 |
1,7380 |
1,8318 |
1,9459 |
2,0923 |
2,2976 |
2,6467 |
|
0,80 |
1,0986 |
1,1270 |
1,1568 |
1,1881 |
1,2212 |
1,2562 |
1,2933 |
1,3101 |
1,3758 |
1,4219 |
|
0,70 |
0,8673 |
0,8872 |
0,9076 |
0,9287 |
0,9505 |
0,9730 |
0,9962 |
1,0203 |
1,0454 |
1,0714 |
|
0,60 |
0,6931 |
0,7089 |
0,7250 |
0,7414 |
0,7582 |
0,7753 |
0,7623 |
0,8107 |
0,8291 |
0,8480 |
|
0,50 |
0,5493 |
0,5627 |
0,5763 |
0,5901 |
0,6042 |
0,6184 |
0,6328 |
0,6475 |
0,6625 |
0,6777 |
|
0,40 |
0,4236 |
0,4356 |
0,4477 |
0,4599 |
0,4722 |
0,4847 |
0,4973 |
0,5101 |
0,5230 |
0,5361 |
|
0,30 |
0,3045 |
0,3205 |
0,3316 |
0,3428 |
0,3541 |
0,3654 |
0,3769 |
0,3884 |
0,4001 |
0,4118 |
|
0,20 |
0,2027 |
0,2132 |
0,2237 |
0,2342 |
0,2448 |
0,2554 |
0,2661 |
0,2769 |
0,2877 |
0,2986 |
|
0,10 |
0,1003 |
0,1104 |
0,1205 |
0,1307 |
0,1409 |
0,1511 |
0,1614 |
0,1717 |
0,1820 |
0,1923 |
|
0,00 |
0,0000 |
0,0100 |
0,0200 |
0,0300 |
0,0400 |
0,0501 |
0,0600 |
0,0701 |
0,0802 |
0,0902 |
1.8.5 Определение тесноты связи между качественными признаками
При изучении зависимости качественных признаков используется коэффициент сопряженности. Для определения тесноты связи в случае альтернативной изменчивости двух сопоставляемых признаков имеющиеся данные сводятся в четырехпольную таблицу, и коэффициент сопряженности вычисляется по формуле:
|
C1 = |
ad −bc |
(1.41) |
|
(a +c)(b + d)(a +b)(c + d) |
68

Если ранее по данным этой таблицы был вычислен критерий χ2, то коэффициент сопряженности вычисляется по формуле:
|
C1 = |
χ2 |
= |
χ2 |
(1.42) |
|
a +b +c + d |
n |
Например, требуется установить, имеется ли связь между степенью тяжести ревматизма и эффективностью тонзиллэктомии (табл. 1.39).
Таблица 1.39 — Эффективность тонзиллэктомии в зависимости от симптоматики ревматизма
|
Симптоматика ревматизма |
Результат лечения |
Итого |
|||
|
успешное |
неэффективное |
||||
|
Больные, имевшие изменения со |
9 |
26 |
|||
|
cтороны сердца и суставов. |
|||||
|
Больные, имевшие изменения |
8 |
16 |
|||
|
только со cтороны сердца . . |
|||||
|
Всего |
25 |
17 |
42 |
||
Коэффициент сопряженности изменяется в пределах от +1 до -1 и оценивается аналогично коэффициенту корреляции.
При сопоставлении качественных признаков, имеющих три и больше групп, для определения тесноты связи, пользуются коэффициентом средней квадратичной сопряженности Пирсона:
и коэффициентом взаимной сопряженности Чупрова:
|
K = |
φ2 |
(1.44) |
|
(k1 −1) (k2 −1) |
где k1 — число групп по столбцам;
k2 — число групп по строкам таблицы;
ϕ2 + 1 — равно о сумме отношений квадратов частот каждой клетки таблицы к произведению итогов строк и соответствующих итогов столбцов
|
2 |
||||||||
|
ϕ2 |
+ 1 = |
∑ |
mxy |
(1.45) |
||||
|
m |
m |
|||||||
|
x |
||||||||
|
y |
Пример. Вычислим коэффициент средней квадратической сопряженности Пирсона между гистологической структурой и типом роста опухоли по данным таблицы 1.40.
Находим значение ϕ2 + 1:
69

|
φ |
2 |
+1 |
= |
∑ |
mxy2 |
= |
112 |
+ |
62 |
+ |
22 |
+ |
2 |
2 |
+ |
32 |
+ |
10 |
2 |
+ |
12 |
+ |
12 |
+ |
32 |
+ |
|||||||||||||||||||||||||||||||||||
|
mx |
my |
20 |
21 |
33 21 |
14 |
21 |
6 |
21 |
20 |
15 |
33 |
15 |
14 15 |
6 |
15 |
20 |
12 |
||||||||||||||||||||||||||||||||||||||||||||
|
+ |
52 |
+ |
32 |
+ |
12 |
+ |
12 |
+ |
72 |
+ |
32 |
+ |
12 |
+ |
52 |
+ |
2 |
2 |
+ |
4 |
2 |
+ |
22 |
=1,47 |
|||||||||||||||||||||||||||||||||||||
|
33 12 |
14 12 |
6 12 |
20 12 |
33 11 |
14 11 |
33 6 |
14 6 |
20 |
8 |
33 |
6 |
6 8 |
|||||||||||||||||||||||||||||||||||||||||||||||||
Отсюда находим ϕ2 =1,47 – 1 = 0,47.
Коэффициент средней квадратичной сопряженности Пирсона:
C1 = 
Коэффициент взаимной сопряженности Чупрова равняется
|
K = |
0,47 |
= |
0,47 |
= |
0,47 |
= 0,12 = 0,348 |
|
(4 |
−1) (6 −1) |
3 5 |
15 |
Полученный коэффициент К также свидетельствует о наличии связи между рассматриваемыми признаками.
Таблица 1.40 — Зависимость между гистологической структурой опухоли и типом ее роста
|
Гистологическая |
Тип роста опухоли (х) |
Итого |
|||
|
структура (у) |
экзофит- |
язвенно- |
диффузно- |
переход- |
(my) |
|
ный |
инфиль- |
инфильтра- |
ный |
||
|
тративный |
тивный |
||||
|
Аденокарцинома |
11(mxy) |
6 |
2 |
2 |
21 |
|
Cr. simplex……… |
3 |
10 |
1 |
1 |
15 |
|
Солидный рак…… |
3 |
5 |
3 |
1 |
12 |
|
Слизистый……… |
1 |
7 |
3 |
─ |
11 |
|
Фиброзный рак… |
─ |
1 |
5 |
─ |
6 |
|
Смешанные формы |
2 |
4 |
─ |
2 |
8 |
|
Всего (mx)……… |
20 |
33 |
14 |
6 |
73 |
При применении коэффициента сопряженности С1 следует учитывать, что он всегда меньше 1 и теоретическая его величина зависит от числа строк и столбцов таблицы. Поэтому вычисление коэффициента С1 правомочно только тогда, когда каждый из сопоставляемых признаков имеет не менее 5 градаций (таблица 5×5 групп). Коэффициент Чупрова, который всегда меньше коэффициента С1 не имеет этого ограничения.
Достоверность выборочного коэффициента взаимной сопряженности оценивается с помощью критерия χ2. Полученная величина χ2=nϕ2 сопоставляется с табличными значениями χ2 при числе степеней свободы v=(k —1)(k2-1) и р = 0,05.
70
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В работе над продуктом часто можно услышать такую логику рассуждений от продакт-менеджера или продуктового аналитика: «Я проанализировал данные и увидел, что пользователи, которые делают Х, с большей вероятностью покупают премиум-версию или становятся успешными». На основе этого инсайта они решают инвестировать время и силы в то, чтобы большая доля пользователей делала X.
Проблема в том, что в этом случае корреляция выдается за причинно-следственную связь. Может быть, там и есть зависимость между переменными, а может быть, это частный случай корреляции, когда рост одной метрики сопровождается ростом другой.
В этом материале разберемся, почему легко упустить разницу между корреляцией и причинно-следственной связью, как доказать наличие причинно-следственной связи и почему это важно при работе над продуктом.
На первый взгляд, выражение «корреляция не означает причинно-следственную связь» не требует дополнительных разъяснений: звучит как прописная истина. Но снова и снова люди с разным уровнем опыта приравнивают эти понятия. Иногда умышленно, а иногда по невнимательности.
Корреляция и причинно-следственная связь
Корреляция — это взаимосвязь между двумя переменными, при которой изменение одной из них сопровождается изменением в другой. Здесь важно подчеркнуть слово «сопровождается», поскольку при корреляции эти изменения могут происходить без прямого влияния одной переменной на другую.
В ситуации же, когда такое прямое влияние доказано — можно говорить о причинно-следственной связи.
Пример корреляции может звучать так:
Рост потребления мороженого сопровождается ростом числа лесных пожаров.
Другой пример:
Cнижение потребления маргарина сопровождается снижением количества разводов.
Отличие корреляции от причинно-следственной связи
У корреляции может быть несколько причин. Например, на две переменные влияет некий третий фактор, как в случае с ростом продаж мороженого и лесными пожарами. Этот фактор — теплое время года и высокая интенсивность солнечного излучения.
В случае с корреляцией не всегда можно идентифицировать другие факторы, которые влияют на обе переменные, а иногда их может не быть вовсе. В таком случае уместно говорить о случайности. Одновременное снижение числа разводов и потребления маргарина — пример такой ложной корреляции (spurious correlation).
В чем отличие корреляции от причинно-следственной связи?
Причинно-следственная связь всегда подразумевает наличие корреляции. Корреляция не обязательно означает наличие причинно-следственной связи. Корреляция может быть случайной, но причинно-следственная связь по определению не может быть случайностью.
Если корреляция есть, то для доказательства причинно-следственной связи должны соблюдаться еще два условия:
- Отсутствие сторонних факторов, которые влияют на обе переменные;
- Прямая временная последовательность между изменением первого и второго показателя, между событием A и событием B.
Хотя разница между корреляцией и причинно-следственной связью кажется очевидной, на практике принять одно за другое очень просто.
Примеры корреляций, которые ошибочно принимают за причинно следственную связь
Рассмотрим типовые ситуации из жизни, когда наличие корреляции приводит к ложному выводу о наличии причинно-следственной связи в бытовых ситуациях.
В своей книге «Thinking, Fast and Slow» Daniel Kahneman (Даниэль Канеман) описывает случай на лекции для израильских летчиков. Один из инструкторов настаивал, что курсанты лучше справляются с задачей после того, как он жестко критикует их за ошибки. Канеман предложил провести эксперимент, в ходе которого эти курсанты должны были не глядя дважды бросить монетку в нарисованную на полу мишень. Опыт показал: те, у кого первый бросок был ближе к цели, во второй раз бросали не так точно. И наоборот.
Таким экспериментом Канеман продемонстрировал феномен регрессии к среднему. Когда летчик очень плохо или очень хорошо исполнил упражнение, то часто для него это было отклонением от среднего значения. Поэтому с высокой вероятностью его следующее исполнение будет ближе к среднему, то есть лучше или хуже предыдущего.
Получается, что не критика помогала курсантам показывать лучшие результаты после провального опыта, а регрессия к среднему. Инструктор ошибочно принял корреляцию между критикой и улучшением результатов курсантов после нее за причинно-следственную связь.
Некоторые широко известные убеждения тоже являются корреляцией, которая маскируется под причинно-следственную связь.
Например, идея о том, что занятия музыкой в дошкольном возрасте улучшают когнитивные способности, память и внимание ребенка. Хотя корреляция между этими факторами действительно может быть, говорить о прямой причинно-следственной связи нельзя, так как на результат может влиять масса факторов.
Может быть, занятия музыкой для ребенка требуют от семьи дополнительных финансовых ресурсов. То есть, если семья может направить деньги не только на базовые потребности, но и на дополнительное образование, с высокой вероятностью ребенок имеет доступ к лучшему питанию, лучшему основному образованию и другим благам, которые могут позитивно отражаться на интеллекте ребенка.
Еще один пример.
В одном из материалов Washington Post пришла к выводу, что рост затрат на полицию в США не привел к сокращению преступности. Автор через кажущееся отсутствие прямой корреляции пытается опровергнуть причинно-следственную связь между событиями: увеличение бюджета полиции не приводит к пропорциональному сокращению уровня преступности.
Но говорить о том, что здесь обязательно должна быть причинно-следственная связь, нельзя. Например, именно рост преступности может быть драйвером расходов на полицию, а не наоборот. Без тщательного исследования мы не можем утверждать ни того, ни другого.
Корреляция в бизнесе
В 2013 году eBay тратил десятки миллионов долларов на поисковую рекламу по брендовым запросам “eBay”. В компании были уверены, что рост продаж обусловлен именно покупным трафиком. Но исследование показало, что реклама оказалась направлена как раз на ту аудиторию, которая в любом случае совершила бы покупку на eBay.
В данном случае именно намерение пользователей совершить покупку приводило и к показу рекламы, и к продажам на площадке. В eBay же думали, что именно реклама выступала причиной, а продажи — ее следствием.
→ Кейс eBay иллюстрирует проблему инкрементальности — то есть ситуации, когда рекламной кампании в одном канале атрибутируются целевые действия, которые произошли бы и без нее.
↓ Подробнее о влиянии моделей атрибуции и инкрементальности на расчет ROI в маркетинге и о том, как установить причинно-следственную связь между каналом и целевыми действиями в продукте, мы подробно рассказывали в подготовленной вместе с Захаром Сташевским серии материалов.
Корреляцию часто ошибочно принимают за причинно-следственную связь при анализе успеха чужих продуктов со стороны. «Продукт А выстрелил и нашел product/market fit, благодаря фиче X. Мы можем повторить успех, добавив ту же фичу в нашем продукте и на нашем локальном рынке».
Допустим, что продукт А действительно стал успешным после того, как внедрил определенную фичу. Но нельзя назвать причиной сам факт добавления фичи. Причина зачастую более комплексна и опирается на массу факторов. Но главное, что для определенного сегмента пользователей продукт решает некоторую задачу эффективнее всех доступных альтернатив.
Например, WeChat Pay набрал популярность как платежный инструмент в Китае не потому, что они соединили мессенджер и платежный инструмент. Дело в том, что этот инструмент стал намного более эффективной альтернативой наличным деньгам, поэтому его добавочная ценность оказалась столь высока, а продукт — столь успешным.
На этом фоне становится понятно, почему Facebook Messenger так тяжело давались попытки запустить свой платежный сервис. Просто прикрутить функциональность к мессенджеру недостаточно, потому что на рынке США гораздо сильнее развиты платежные инструменты, а значит, добавочная ценность решения от Facebook для клиента менее ощутима или не ощутима вовсе.
Корреляция в работе над продуктом
Работа над продуктом подразумевает постоянные вопросы о причинах тех или иных изменений в метриках. И зачастую велик соблазн объяснить их через что-то, что мы сделали осознанно и недавно. Однако важно помнить, что продукт и пользователи не существуют в вакууме.
Пример с притоком пользователей в продукт
Вы фиксируете приток пользователей за последнюю неделю, а перед этим вы добавили в продукт новую большую фичу. Кажется, что продуктовое изменение привело к росту.
Однако позже выясняется, что приток пользователей в ваш продукт стал следствием того, что ваш прямой конкурент резко ограничил возможности базового тарифа. Ваш отдел маркетинга заметил это и стал активно использовать этот аргумент в разных каналах коммуникации. Отсюда — приток новых пользователей.
Между добавлением новой фичи и приростом пользовательской базы действительно была корреляция. Но, как мы выяснили, причина этого роста скрывалась в другом.
Пример с монетизацией мобильной игры
Работая над мобильной игрой, вы заметили, что пользователи, которые подключают соцсети, делают больше покупок. На этом этапе может возникнуть соблазн предположить наличие между событиями причинно-следственную связь и решить, что увеличение конверсии игроков в подключение соцсетей пропорционально увеличит выручку с таких пользователей. Если это правда так, то у вас есть множество гипотез, как повлиять на этот параметр.
Однако на деле в такой ситуации вполне может быть еще один или несколько факторов, которые одинаково влияют и на первое, и на второе явление. Скрытым от глаз фактором может быть то, что пользователи, которые и активно подключают соцсети, и чаще делают покупки, просто изначально сильнее мотивированы и больше заинтересованы в игре. То есть это не подключение соцсетей влияет на их поведение, а изначальная предрасположенность к игре.
Если это так, то на практике активное навязывание пользователям возможности подключиться к соцсети в действительности не даст никакого результата. С другой стороны, сразу решить, что такое навязывание не даст никаких изменений, тоже нельзя. Чтобы выяснить это, нужно провести эксперимент.
Как эксперименты помогают доказать причинно-следственную связь
Суеверия, псевдонаучные дисциплины и архаичные методы лечения появились во многом благодаря путанице между корреляцией и причинно-следственной связью. Так появились ритуалы, которые призывают дождь, и жертвоприношения, которые гарантируют удачную охоту и богатые урожаи.
Примерно такой подход прослеживается в древней и средневековой медицине. Например, эффективным способом поправить здоровье больного считалось кровопускание. Если пациент после этой процедуры выживает, то успех приписывается именно ей. Если нет, то значит, болезнь была слишком сильной.
То есть в этом случае корреляция между процедурой и выздоровлением не только ложная, но и избирательная.
Мы не случайно упомянули архаичные методы лечения, потому что именно развитие медицины дало дорогу появлению эффективных методов доказательства причинно-следственной связи.
Одним из важнейших этапов на пути развития доказательной медицины стало проведение в середине XX века первого рандомизированного контролируемого испытания (randomized controlled trial). Его суть заключается в том, чтобы взять две группы людей — тестовую и контрольную, — и одной вручить лекарство, а другой плацебо. Отсутствие различий в других переменных позволяет сделать вывод о влиянии лишь одного конкретного фактора.
В интернете практика подобных испытаний получит название A/B-тестов.
A/B-тестирование для проверки наличия причинно-следственной связи
Вы наблюдаете корреляцию между событиями X и Y. Но для принятия решения вам нужно понять, есть ли между ними причинно-следственная связь.
Для ответа на этот вопрос надо провести эксперимент.
Например, когда одна группа пользователей получает фичу, а другая нет. Все остальные условия для них идентичны. По итогам теста собираются и анализируются данные. На их основе вы можете понять, оказала ли фича влияние на интересующую нас метрику.
Хотя порядок действий и звучит просто, на деле проведение A/B-тестов требует внимания ко множеству деталей и дисциплины. В частности, вам нужно быть очень аккуратными, чтобы не спутать случайное изменение в значение целевой метрики с влиянием тестируемого изменения. Для этого используется понятие статистической значимости — подробнее об этом читайте здесь.
Понимание корреляции и причинно-следственной связи уберегает от ошибок и помогает глубже видеть продукт
В работе над продуктом легко принять корреляцию за причинно-следственную связь. Допускают такую ошибку в разных случаях: либо человек не знает про эту разницу, либо — что чаще — знает в теории, но не всегда может заметить на практике, либо умышленно хочет выдать одно за другое, чтобы добиться желаемого.
Путанице между корреляцией и причинно-следственной связью способствуют различные когнитивные искажения, например confirmation bias или иллюзия контроля. Confirmation bias заставляет нас отметать те факторы, которые не укладываются в желаемую картину происходящего. Иллюзия контроля создает впечатление, что мы знаем о продукте все и понимаем, что и отчего напрямую зависит.
Понимать разницу между корреляцией и причинно-следственной связью важно, чтобы не прийти к ошибочным решениям или не потратить время и ресурсы без какого-либо результата.
Проверка гипотез через эксперименты, дотошное выяснение причин тех или иных наблюдаемых изменений не только помогает ответить на один конкретный вопрос (например, почему падает конверсия в покупку), но и позволяет глубже понять продукт. Такое понимание помогает находить новые инсайты и увеличивать ценность продукта для пользователей.



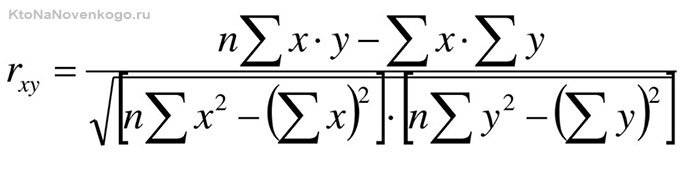
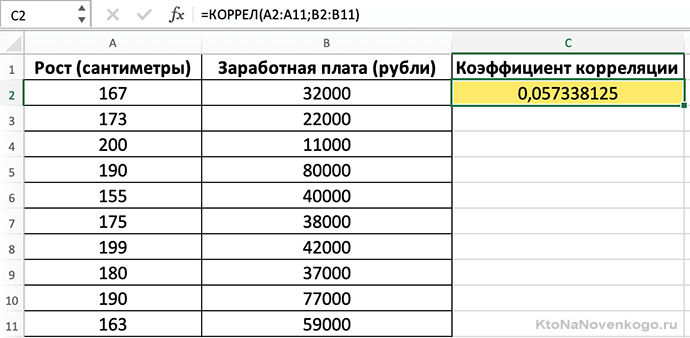

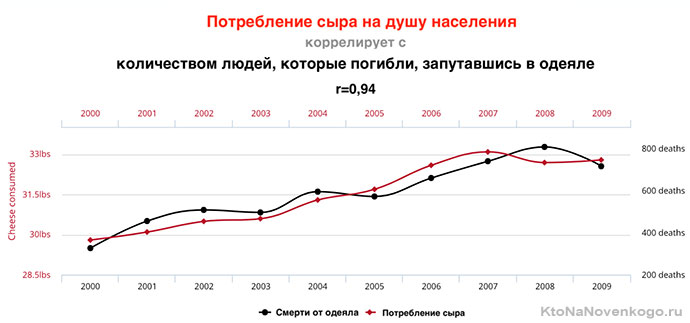


![{displaystyle rho _{X,Y}=operatorname {corr} (X,Y)={operatorname {cov} (X,Y) over sigma _{X}sigma _{Y}}={operatorname {E} [(X-mu _{X})(Y-mu _{Y})] over sigma _{X}sigma _{Y}},quad {text{if}} sigma _{X}sigma _{Y}>0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b551ad29592ae746bf05fe397fbdc56201f483a5)



![{displaystyle {begin{aligned}r_{xy}&={frac {sum x_{i}y_{i}-n{bar {x}}{bar {y}}}{ns'_{x}s'_{y}}}\[5pt]&={frac {nsum x_{i}y_{i}-sum x_{i}sum y_{i}}{{sqrt {nsum x_{i}^{2}-(sum x_{i})^{2}}}~{sqrt {nsum y_{i}^{2}-(sum y_{i})^{2}}}}}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6da33b8144a5e67959969ef2c4830ece1938bbb2)







![{displaystyle {begin{aligned}rho _{X,Y}&={frac {1}{sigma _{X}sigma _{Y}}}mathrm {E} [(X-mu _{X})(Y-mu _{Y})]\[5pt]&={frac {1}{sigma _{X}sigma _{Y}}}sum _{x,y}{(x-mu _{X})(y-mu _{Y})mathrm {P} (X=x,Y=y)}\[5pt]&=left(1-{frac {2}{3}}right)(-1-0){frac {1}{3}}+left(0-{frac {2}{3}}right)(0-0){frac {1}{3}}+left(1-{frac {2}{3}}right)(1-0){frac {1}{3}}=0.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/75bf2b7806338758b4c55d7b4f18a5071b8e919b)