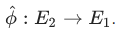Постквантовая криптография — часть криптографии, которая остаётся актуальной и при появлении квантовых компьютеров и квантовых атак. Так как по скорости вычисления традиционных криптографических алгоритмов квантовые компьютеры значительно превосходят классические компьютерные архитектуры, современные криптографические системы становятся потенциально уязвимыми для криптографических атак. Большинство традиционных криптосистем опирается на проблемы факторизации целых чисел или задачи дискретного логарифмирования, которые будут легко разрешимы на достаточно больших квантовых компьютерах, использующих алгоритм Шора[1][2]. Многие криптографы в настоящее время ведут разработку алгоритмов, независимых от квантовых вычислений, то есть устойчивых к квантовым атакам.
Существуют классические криптосистемы, которые опираются на вычислительно сложные задачи и имеют ряд существенных отличий от указанных выше систем, из-за чего их гораздо сложнее решить. Эти системы независимы от квантовых вычислений, и, следовательно, их считают квантово-устойчивыми (quantum-resistant), или «постквантовыми» криптосистемами.
Постквантовая криптография в свою очередь отличается от квантовой криптографии, которая занимается методами защиты коммуникаций, основанных на принципах квантовой физики.
Алгоритмы
Постквантовые криптографические конструкции способны спасти криптографический мир от квантовых атак. Хотя квантовый компьютер и уничтожит большинство традиционных алгоритмов (RSA, DSA, ECDSA), но сверхбыстрыми вычислениями не получится полностью избавиться от криптографии, так как постквантовая криптография, в основном, сосредоточена на пяти различных подходах, решающих проблему квантовых атак[2][3].
Криптография, основанная на хеш-функциях
Классическим примером является подпись Меркла с открытым ключом на основе хеш-дерева. Ральф Чарльз Меркл предложил этот алгоритм цифровой подписи в 1979 году как интересную альтернативу цифровым подписям RSA и DSA. Основной недостаток схемы Меркла состоит в том, что для любого открытого ключа на основе хеш-функции существует ограничение на количество подписей, которые могут быть получены из соответствующего набора закрытых ключей. Этот факт и снижал уровень интереса к подписям такого типа, пока не появилась потребность в криптографии, устойчивой к воздействию квантовых компьютеров.
Криптография, основанная на кодах исправления ошибок
Является одним из наиболее перспективных кандидатов на пост-квантовые криптосистемы. Классическим примером является схемы шифрования McEliece и Niederreiter.
Криптография, основанная на решётках
Классическим примером схем шифрования являются Ring-Learning with Errors[4][5][6][7] или более старые NTRU, GGH и криптосистема Миччанчо.
Криптография, основанная на многомерных квадратичных системах
Одной из самых интересных схем является подпись с открытым ключом Жака Патарина HFE, предложенная им в 1996 году как обобщение предложений Matsumoto и Imai[2].
Шифрование с секретным ключом
Ярким примером является шифр Rijndael, предложенный в 1998 году, впоследствии переименованный в AES (Advanced Encryption Standard).
Шифрование с использованием суперсингулярной изогении
Это аналог протокола Диффи-Хеллмана, основанный на блуждании в суперсингулярном изогенном графе, позволяющий двум и более сторонам получить общий секретный ключ, используя незащищённый от прослушивания канал связи[8].
Примеры криптографических атак на RSA[2]
В 1978 году документ, опубликованный разработчиками криптографического алгоритма с открытым ключом RSA (аббревиатура от фамилий Rivest, Shamir и Adleman), упоминал новый алгоритм Ричарда Шреппеля[en] «linear sieve», который факторизовал любой RSA модуль [math]displaystyle{ n }[/math] длины [math]displaystyle{ [ log_2 n ] + 1 }[/math] бит, используя [math]displaystyle{ 2^{(1+o(1))(log_2 n)^{1/2}(log_2log_2 n)^{1/2}} }[/math] простых операций. Таким образом, для того чтобы этот алгоритм требовал по меньшей мере [math]displaystyle{ 2^b }[/math] простых операций, необходимо выбирать [math]displaystyle{ n }[/math] длины по крайней мере не меньше чем [math]displaystyle{ (0,5 + o(1))b^2/{log_2 b} }[/math] бит. Так как [math]displaystyle{ 0{,}5 + o(1) }[/math] означает, что что-то сходится к [math]displaystyle{ 0{,}5 }[/math] при [math]displaystyle{ bto infty }[/math], то для выяснения правильного размера [math]displaystyle{ n }[/math] при конечном [math]displaystyle{ b }[/math] требуется более тщательный анализ скорости «linear sieve».
В 1988 году Джон Поллард[en] предложил новый алгоритм факторизации, который называется Общий метод решета числового поля. Этот алгоритм факторизовал RSA-модуль [math]displaystyle{ n }[/math] размерности [math]displaystyle{ log_2 n }[/math] бит, используя [math]displaystyle{ 2^{(1,9dotso+o(1))(log_2 n)^{1/3}(log_2log_2 n)^{2/3}} }[/math] простых операций. Таким образом, требуется выбирать [math]displaystyle{ n }[/math] длины не меньше чем [math]displaystyle{ (0,016dotso + o(1))b^3/(log_2 b)^2 }[/math] бит, чтобы алгоритму потребовалось как минимум [math]displaystyle{ 2^b }[/math] простых операций.
С 2008 года самые быстрые алгоритмы факторизации для классических компьютерных архитектур используют по меньшей мере [math]displaystyle{ 2^{(const + o(1))(log_2 n)^{1/3}(log_2log_2 n)^{2/3}} }[/math] простых операций. Были некоторые улучшения в значениях [math]displaystyle{ const }[/math] и в деталях [math]displaystyle{ o(1) }[/math], но не трудно догадаться, что [math]displaystyle{ 1/3 }[/math] оптимально, и что выбор модуля [math]displaystyle{ n }[/math] длиной примерно равной [math]displaystyle{ b^3 }[/math] бит, позволит сопротивляться всем возможным атакам на классических компьютерах.
В 1994 году Питер Шор предложил алгоритм, который факторизовал любой RSA-модуль [math]displaystyle{ n }[/math] размерности [math]displaystyle{ b=log_2 n }[/math] бит, используя [math]displaystyle{ b^{2+o(1)} }[/math] (точнее [math]displaystyle{ b^2 cdot log(b) cdot log(log(b)) }[/math]) кубитовых операций на квантовом компьютере размера порядка [math]displaystyle{ 2cdot b^{1+o(1)} }[/math] кубит (и небольшого количества вспомогательных вычислений на классическом компьютере). Пользуясь алгоритмом Шора, необходимо по крайней мере выбирать модуль [math]displaystyle{ n }[/math] битовым размером не меньше чем [math]displaystyle{ 2^{(0,5+o(1))b} }[/math] бит, что является слишком большим числом для любого интересующего нас [math]displaystyle{ b }[/math][9].
Практические применения криптографических конструкций[2]
Примеров алгоритмов, устойчивых к квантовым атакам, крайне мало. Но несмотря на больший уровень криптографической устойчивости, постквантовые алгоритмы неспособны вытеснить современные криптосистемы (RSA, DSA, ECDSA и др.).
Рассмотрим нападения на криптосистему с открытым ключом, а именно на алгоритм шифрования McEliece, который использует двоичные коды Гоппы. Первоначально Роберт Мак-Элис[en] представил документы, в которых коды длиной [math]displaystyle{ n }[/math] взламываются за [math]displaystyle{ 2^{(0,5+o(1))n/{log_2n}} }[/math] простых операций. Таким образом, требуется выбирать [math]displaystyle{ n }[/math] не меньше чем [math]displaystyle{ (2+o(1))blog_2b }[/math] бит, чтобы алгоритму потребовалось как минимум [math]displaystyle{ 2^b }[/math] простых операций. Несколько последующих работ сократили количество операций атаки до [math]displaystyle{ n^{log_2n} = 2^{(log_2n)^2} }[/math], но [math]displaystyle{ (log_2n)^2 }[/math] значительно меньше [math]displaystyle{ 0{,}5n/{log_2n} }[/math], если [math]displaystyle{ n }[/math] большое. Поэтому улучшенные атаки до сих пор используют [math]displaystyle{ 2^{(0,5+o(1))n/{log_2n}} }[/math] простых операций. Что касается квантовых компьютеров, то их использование приведёт лишь к уменьшению константы [math]displaystyle{ 0,5 }[/math], что совсем незначительно сократит количество операций, необходимых для взлома этого алгоритма.
Если система шифрования McEliece так хорошо защищена, то почему она не приходит на смену RSA? Всё дело в эффективности — в частности, в размере ключа. Открытый ключ McEliece использует примерно [math]displaystyle{ {n^2}/4 }[/math] ≈ [math]displaystyle{ {b^2}(log_2b)^2 }[/math] бит, в то время как открытому ключу RSA достаточно около [math]displaystyle{ (0{,}016dots)b^3/(log_2b)^2 }[/math] бит. Если [math]displaystyle{ bto infty }[/math], то [math]displaystyle{ b^{2+o(1)} }[/math] бит для McEliece, будет меньше [math]displaystyle{ b^{3+o(1)} }[/math] бит для RSA, но реальные уровни безопасности, такие как [math]displaystyle{ b = 128 }[/math], позволяют RSA иметь открытый ключ в несколько тысяч бит, в то время как для McEliece размер ключа приближается к миллиону бит.
Конференция PQCrypto
С 2006 года проводится серия конференций, посвящённых постквантовой криптографии.
- PQCrypto 2006. Лёвенский католический университет, Бельгия, с 23 по 26 мая[10]
- PQCrypto 2008. Университет Цинциннати, США, с 17 по 19 октября[11]
- PQCrypto 2010. Дармштадт, Германия, с 25 по 28 мая[12]
- PQCrypto 2011. Тайбэй, Тайвань, с 29 ноября по 2 декабря[13]
- PQCrypto 2013. Лимож, Франция, с 4 по 7 июня[14]
- PQCrypto 2014. Университет Ватерлоо, Канада, с 1 по 3 октября[15]
- PQCrypto 2016. Предварительный план: Фукуока, Япония, февраль 2016
См. также
- Криптография на решётках
- Алгоритм Шора
Примечания
- ↑ Peter Shor (1995-08-30), Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer, arΧiv:quant-ph/9508027.
- ↑ 2,0 2,1 2,2 2,3 2,4 Daniel J. Bernstein. Introduction to post-quantum cryptography (неопр.) // (Introductory chapter to book «Post-quantum cryptography»). — 2009.
- ↑ Q&A With Post-Quantum Computing Cryptography Researcher Jintai Ding, IEEE Spectrum (1 ноября 2008). Архивировано 8 октября 2015 года. Дата обращения 26 ноября 2014.
- ↑ рус. обучение с ошибками
- ↑ Peikert, Chris Lattice Cryptography for the Internet. IACR (2014). Дата обращения: 10 мая 2014. Архивировано 12 мая 2014 года.
- ↑ Guneysu, Tim Practical Lattice-Based Cryptography: A Signature Scheme for Embedded Systems. INRIA (2012). Дата обращения: 12 мая 2014. Архивировано 18 мая 2014 года.
- ↑ Zhang, jiang Authenticated Key Exchange from Ideal Lattices. iacr.org. IACR (2014). Дата обращения: 7 сентября 2014. Архивировано 7 сентября 2014 года.
- ↑ Протокол Диффи-Хеллмана с использованием суперсингулярной изогении.
- ↑ http://crypto.rsuh.ru/papers/bogdanov-kizhvatov-quantum.pdf Архивная копия от 15 декабря 2017 на Wayback Machine стр 9
- ↑ официальный сайт PQCrypto 2006. Дата обращения: 19 ноября 2014. Архивировано 26 октября 2014 года.
- ↑ официальный сайт PQCrypto 2008 (недоступная ссылка). Дата обращения: 19 ноября 2014. Архивировано 19 октября 2014 года.
- ↑ официальный сайт PQCrypto 2010. Дата обращения: 19 ноября 2014. Архивировано 9 октября 2014 года.
- ↑ официальный сайт PQCrypto 2011. Дата обращения: 19 ноября 2014. Архивировано 27 декабря 2014 года.
- ↑ официальный сайт PQCrypto 2013. Дата обращения: 19 ноября 2014. Архивировано 23 декабря 2014 года.
- ↑ официальный сайт PQCrypto 2014 (недоступная ссылка). Дата обращения: 19 ноября 2014. Архивировано 26 октября 2014 года.
Ссылки
- PQCrypto, the post-quantum cryptography conference
- Post-Quantum Cryptography (неопр.). — Springer, 2008. — С. 245. — ISBN 978-3-540-88701-0.
- ETSI Квантовая безопасность (англ.)
- NIST’s Постквантовый криптопроект (англ.)
- PQCrypto Использование и развертывание (англ.)
In cryptography, post-quantum cryptography (PQC) (sometimes referred to as quantum-proof, quantum-safe or quantum-resistant) refers to cryptographic algorithms (usually public-key algorithms) that are thought to be secure against a cryptanalytic attack by a quantum computer. The problem with currently popular algorithms is that their security relies on one of three hard mathematical problems: the integer factorization problem, the discrete logarithm problem or the elliptic-curve discrete logarithm problem. All of these problems could be easily solved on a sufficiently powerful quantum computer running Shor’s algorithm.[1][2]
Even though current quantum computers lack processing power to break any real cryptographic algorithm,[3] many cryptographers are designing new algorithms to prepare for a time when quantum computing becomes a threat. This work has gained greater attention from academics and industry through the PQCrypto conference series since 2006 and more recently by several workshops on Quantum Safe Cryptography hosted by the European Telecommunications Standards Institute (ETSI) and the Institute for Quantum Computing.[4][5][6]
In contrast to the threat quantum computing poses to current public-key algorithms, most current symmetric cryptographic algorithms and hash functions are considered to be relatively secure against attacks by quantum computers.[2][7] While the quantum Grover’s algorithm does speed up attacks against symmetric ciphers, doubling the key size can effectively block these attacks.[8] Thus post-quantum symmetric cryptography does not need to differ significantly from current symmetric cryptography.
Algorithms[edit]
Currently post-quantum cryptography research is mostly focused on six different approaches:[2][5]
Lattice-based cryptography[edit]
This approach includes cryptographic systems such as learning with errors, ring learning with errors (ring-LWE),[9][10][11] the ring learning with errors key exchange and the ring learning with errors signature, the older NTRU or GGH encryption schemes, and the newer NTRU signature and BLISS signatures.[12] Some of these schemes like NTRU encryption have been studied for many years without anyone finding a feasible attack. Others like the ring-LWE algorithms have proofs that their security reduces to a worst-case problem.[13] The Post Quantum Cryptography Study Group sponsored by the European Commission suggested that the Stehle–Steinfeld variant of NTRU be studied for standardization rather than the NTRU algorithm.[14][15] At that time, NTRU was still patented. Studies have indicated that NTRU may have more secure properties than other lattice based algorithms.[16]
Multivariate cryptography[edit]
This includes cryptographic systems such as the Rainbow (Unbalanced Oil and Vinegar) scheme which is based on the difficulty of solving systems of multivariate equations. Various attempts to build secure multivariate equation encryption schemes have failed. However, multivariate signature schemes like Rainbow could provide the basis for a quantum secure digital signature.[17] There is a patent on the Rainbow Signature Scheme.
Hash-based cryptography[edit]
This includes cryptographic systems such as Lamport signatures, the Merkle signature scheme, the XMSS,[18] the SPHINCS,[19] and the WOTS schemes. Hash based digital signatures were invented in the late 1970s by Ralph Merkle and have been studied ever since as an interesting alternative to number-theoretic digital signatures like RSA and DSA. Their primary drawback is that for any hash-based public key, there is a limit on the number of signatures that can be signed using the corresponding set of private keys. This fact had reduced interest in these signatures until interest was revived due to the desire for cryptography that was resistant to attack by quantum computers. There appear to be no patents on the Merkle signature scheme[citation needed] and there exist many non-patented hash functions that could be used with these schemes. The stateful hash-based signature scheme XMSS developed by a team of researchers under the direction of Johannes Buchmann is described in RFC 8391.[20]
Note that all the above schemes are one-time or bounded-time signatures, Moni Naor and Moti Yung invented UOWHF hashing in 1989 and designed a signature based on hashing (the Naor-Yung scheme)[21] which can be unlimited-time in use (the first such signature that does not require trapdoor properties).
Code-based cryptography[edit]
This includes cryptographic systems which rely on error-correcting codes, such as the McEliece and Niederreiter encryption algorithms and the related Courtois, Finiasz and Sendrier Signature scheme. The original McEliece signature using random Goppa codes has withstood scrutiny for over 40 years. However, many variants of the McEliece scheme, which seek to introduce more structure into the code used in order to reduce the size of the keys, have been shown to be insecure.[22] The Post Quantum Cryptography Study Group sponsored by the European Commission has recommended the McEliece public key encryption system as a candidate for long term protection against attacks by quantum computers.[14]
Supersingular elliptic curve isogeny cryptography[edit]
This cryptographic system relies on the properties of supersingular elliptic curves and supersingular isogeny graphs to create a Diffie-Hellman replacement with forward secrecy.[23] This cryptographic system uses the well studied mathematics of supersingular elliptic curves to create a Diffie-Hellman like key exchange that can serve as a straightforward quantum computing resistant replacement for the Diffie-Hellman and elliptic curve Diffie–Hellman key exchange methods that are in widespread use today. Because it works much like existing Diffie–Hellman implementations, it offers forward secrecy which is viewed as important both to prevent mass surveillance by governments but also to protect against the compromise of long term keys through failures.[24] In 2012, researchers Sun, Tian and Wang of the Chinese State Key Lab for Integrated Service Networks and Xidian University, extended the work of De Feo, Jao, and Plut to create quantum secure digital signatures based on supersingular elliptic curve isogenies.[25] There are no patents covering this cryptographic system.
Symmetric key quantum resistance[edit]
Provided one uses sufficiently large key sizes, the symmetric key cryptographic systems like AES and SNOW 3G are already resistant to attack by a quantum computer.[26] Further, key management systems and protocols that use symmetric key cryptography instead of public key cryptography like Kerberos and the 3GPP Mobile Network Authentication Structure are also inherently secure against attack by a quantum computer. Given its widespread deployment in the world already, some researchers recommend expanded use of Kerberos-like symmetric key management as an efficient way to get post quantum cryptography today.[27]
Security reductions[edit]
In cryptography research, it is desirable to prove the equivalence of a cryptographic algorithm and a known hard mathematical problem. These proofs are often called «security reductions», and are used to demonstrate the difficulty of cracking the encryption algorithm. In other words, the security of a given cryptographic algorithm is reduced to the security of a known hard problem. Researchers are actively looking for security reductions in the prospects for post quantum cryptography. Current results are given here:
Lattice-based cryptography – Ring-LWE Signature[edit]
In some versions of Ring-LWE there is a security reduction to the shortest-vector problem (SVP) in a lattice as a lower bound on the security. The SVP is known to be NP-hard.[28] Specific ring-LWE systems that have provable security reductions include a variant of Lyubashevsky’s ring-LWE signatures defined in a paper by Güneysu, Lyubashevsky, and Pöppelmann.[10] The GLYPH signature scheme is a variant of the Güneysu, Lyubashevsky, and Pöppelmann (GLP) signature which takes into account research results that have come after the publication of the GLP signature in 2012. Another Ring-LWE signature is Ring-TESLA.[29] There also exists a «derandomized variant» of LWE, called Learning with Rounding (LWR), which yields » improved speedup (by eliminating sampling small errors from a Gaussian-like distribution with deterministic errors) and bandwidth.»[30] While LWE utilizes the addition of a small error to conceal the lower bits, LWR utilizes rounding for the same purpose.
Lattice-based cryptography – NTRU, BLISS[edit]
The security of the NTRU encryption scheme and the BLISS[12] signature is believed to be related to, but not provably reducible to, the Closest Vector Problem (CVP) in a Lattice. The CVP is known to be NP-hard. The Post Quantum Cryptography Study Group sponsored by the European Commission suggested that the Stehle–Steinfeld variant of NTRU which does have a security reduction be studied for long term use instead of the original NTRU algorithm.[14]
Multivariate cryptography – Unbalanced Oil and Vinegar[edit]
Unbalanced Oil and Vinegar signature schemes are asymmetric cryptographic primitives based on multivariate polynomials over a finite field 
Hash-based cryptography – Merkle signature scheme[edit]
In 2005, Luis Garcia proved that there was a security reduction of Merkle Hash Tree signatures to the security of the underlying hash function. Garcia showed in his paper that if computationally one-way hash functions exist then the Merkle Hash Tree signature is provably secure.[32]
Therefore, if one used a hash function with a provable reduction of security to a known hard problem one would have a provable security reduction of the Merkle tree signature to that known hard problem.[33]
The Post Quantum Cryptography Study Group sponsored by the European Commission has recommended use of Merkle signature scheme for long term security protection against quantum computers.[14]
Code-based cryptography – McEliece[edit]
The McEliece Encryption System has a security reduction to the Syndrome Decoding Problem (SDP). The SDP is known to be NP-hard[34] The Post Quantum Cryptography Study Group sponsored by the European Commission has recommended the use of this cryptography for long term protection against attack by a quantum computer.[14]
Code-based cryptography – RLCE[edit]
In 2016, Wang proposed a random linear code encryption scheme RLCE[35] which is based on McEliece schemes. RLCE scheme can be constructed using any linear code such as Reed-Solomon code by inserting random columns in the underlying linear code generator matrix.
Supersingular elliptic curve isogeny cryptography[edit]
Security is related to the problem of constructing an isogeny between two supersingular curves with the same number of points. The most recent investigation of the difficulty of this problem is by Delfs and Galbraith indicates that this problem is as hard as the inventors of the key exchange suggest that it is.[36] There is no security reduction to a known NP-hard problem.
Comparison[edit]
One common characteristic of many post-quantum cryptography algorithms is that they require larger key sizes than commonly used «pre-quantum» public key algorithms. There are often tradeoffs to be made in key size, computational efficiency and ciphertext or signature size. The table lists some values for different schemes at a 128 bit post-quantum security level.
| Algorithm | Type | Public Key | Private Key | Signature |
|---|---|---|---|---|
| NTRU Encrypt[37] | Lattice | 766.25 B | 842.875 B | |
| Streamlined NTRU Prime[citation needed] | Lattice | 154 B | ||
| Rainbow[38] | Multivariate | 124 KB | 95 KB | |
| SPHINCS[19] | Hash Signature | 1 KB | 1 KB | 41 KB |
| SPHINCS+[39] | Hash Signature | 32 B | 64 B | 8 KB |
| BLISS-II | Lattice | 7 KB | 2 KB | 5 KB |
| GLP-Variant GLYPH Signature[10][40] | Ring-LWE | 2 KB | 0.4 KB | 1.8 KB |
| NewHope[41] | Ring-LWE | 2 KB | 2 KB | |
| Goppa-based McEliece[14] | Code-based | 1 MB | 11.5 KB | |
| Random Linear Code based encryption[42] | RLCE | 115 KB | 3 KB | |
| Quasi-cyclic MDPC-based McEliece[43] | Code-based | 1,232 B | 2,464 B | |
| SIDH[44] | Isogeny | 564 B | 48 B | |
| SIDH (compressed keys)[45] | Isogeny | 330 B | 48 B | |
| 3072-bit Discrete Log | not PQC | 384 B | 32 B | 96 B |
| 256-bit Elliptic Curve | not PQC | 32 B | 32 B | 65 B |
A practical consideration on a choice among post-quantum cryptographic algorithms is the effort required to send public keys over the internet. From this point of view, the Ring-LWE, NTRU, and SIDH algorithms provide key sizes conveniently under 1KB, hash-signature public keys come in under 5KB, and MDPC-based McEliece takes about 1KB. On the other hand, Rainbow schemes require about 125KB and Goppa-based McEliece requires a nearly 1MB key.
Lattice-based cryptography – LWE key exchange and Ring-LWE key exchange[edit]
The fundamental idea of using LWE and Ring LWE for key exchange was proposed and filed at the University of Cincinnati in 2011 by Jintai Ding. The basic idea comes from the associativity of matrix multiplications, and the errors are used to provide the security. The paper[46] appeared in 2012 after a provisional patent application was filed in 2012.
In 2014, Peikert[47] presented a key transport scheme following the same basic idea of Ding’s, where the new idea of sending additional 1 bit signal for rounding in Ding’s construction is also utilized. For somewhat greater than 128 bits of security, Singh presents a set of parameters which have 6956-bit public keys for the Peikert’s scheme.[48] The corresponding private key would be roughly 14,000 bits.
In 2015, an authenticated key exchange with provable forward security following the same basic idea of Ding’s was presented at Eurocrypt 2015,[49] which is an extension of the HMQV[50] construction in Crypto2005. The parameters for different security levels from 80 bits to 350 bits, along with the corresponding key sizes are provided in the paper.[49]
Lattice-based cryptography – NTRU encryption[edit]
For 128 bits of security in NTRU, Hirschhorn, Hoffstein, Howgrave-Graham and Whyte, recommend using a public key represented as a degree 613 polynomial with coefficients 
Multivariate cryptography – Rainbow signature[edit]
For 128 bits of security and the smallest signature size in a Rainbow multivariate quadratic equation signature scheme, Petzoldt, Bulygin and Buchmann, recommend using equations in 
Hash-based cryptography – Merkle signature scheme[edit]
In order to get 128 bits of security for hash based signatures to sign 1 million messages using the fractal Merkle tree method of Naor Shenhav and Wool the public and private key sizes are roughly 36,000 bits in length.[51]
Code-based cryptography – McEliece[edit]
For 128 bits of security in a McEliece scheme, The European Commissions Post Quantum Cryptography Study group recommends using a binary Goppa code of length at least 







The group is also investigating the use of Quasi-cyclic MDPC codes of length at least 





Barreto et al. recommend using a binary Goppa code of length at least 







Supersingular elliptic curve isogeny cryptography[edit]
For 128 bits of security in the supersingular isogeny Diffie-Hellman (SIDH) method, De Feo, Jao and Plut recommend using a supersingular curve modulo a 768-bit prime. If one uses elliptic curve point compression the public key will need to be no more than 8×768 or 6144 bits in length.[53] A March 2016 paper by authors Azarderakhsh, Jao, Kalach, Koziel, and Leonardi showed how to cut the number of bits transmitted in half, which was further improved by authors Costello, Jao, Longa, Naehrig, Renes and Urbanik resulting in a compressed-key version of the SIDH protocol with public keys only 2640 bits in size.[45] This makes the number of bits transmitted roughly equivalent to the non-quantum secure RSA and Diffie-Hellman at the same classical security level.[54]
Symmetric–key-based cryptography[edit]
As a general rule, for 128 bits of security in a symmetric-key-based system, one can safely use key sizes of 256 bits. The best quantum attack against generic symmetric-key systems is an application of Grover’s algorithm, which requires work proportional to the square root of the size of the key space. To transmit an encrypted key to a device that possesses the symmetric key necessary to decrypt that key requires roughly 256 bits as well. It is clear that symmetric-key systems offer the smallest key sizes for post-quantum cryptography.
Forward secrecy[edit]
A public-key system demonstrates a property referred to as perfect forward secrecy when it generates random public keys per session for the purposes of key agreement. This means that the compromise of one message cannot lead to the compromise of others, and also that there is not a single secret value which can lead to the compromise of multiple messages. Security experts recommend using cryptographic algorithms that support forward secrecy over those that do not.[55] The reason for this is that forward secrecy can protect against the compromise of long term private keys associated with public/private key pairs. This is viewed as a means of preventing mass surveillance by intelligence agencies.
Both the Ring-LWE key exchange and supersingular isogeny Diffie-Hellman (SIDH) key exchange can support forward secrecy in one exchange with the other party. Both the Ring-LWE and SIDH can also be used without forward secrecy by creating a variant of the classic ElGamal encryption variant of Diffie-Hellman.
The other algorithms in this article, such as NTRU, do not support forward secrecy as is.
Any authenticated public key encryption system can be used to build a key exchange with forward secrecy.[56]
Open Quantum Safe project[edit]
Open Quantum Safe (OQS) project was started in late 2016 and has the goal of developing and prototyping quantum-resistant cryptography.[57][58] It aims to integrate current post-quantum schemes in one library: liboqs.[59] liboqs is an open source C library for quantum-resistant cryptographic algorithms. It initially focuses on key exchange algorithms. It provides a common API suitable for post-quantum key exchange algorithms, and will collect together various implementations. liboqs will also include a test harness and benchmarking routines to compare performance of post-quantum implementations. Furthermore, OQS also provides integration of liboqs into OpenSSL.[60]
As of April 2017, the following key exchange algorithms are supported:[57]
| Algorithm | Type |
|---|---|
| BCNS15[61] | Ring learning with errors key exchange |
| NewHope[62][41] | Ring learning with errors key exchange |
| Frodo[63] | Learning with errors |
| NTRU[64] | Lattice-based cryptography |
| SIDH[65][66] | Supersingular isogeny key exchange |
| McBits[67] | Error-correcting codes |
Implementation[edit]
One of the main challenges in post-quantum cryptography is considered to be the implementation of potentially quantum safe algorithms into existing systems. There are tests done, for example by Microsoft Research implementing PICNIC in a PKI using Hardware security modules.[68] Test implementations for Google’s NewHope algorithm have also been done by HSM vendors.
Other notable implementations include:
- bouncycastle[69]
- liboqs[70]
See also[edit]
- NIST Post-Quantum Cryptography Standardization
- Quantum cryptography – cryptography based on quantum mechanics
- Crypto-shredding — Deleting encryption keys
References[edit]
- ^ Peter W. Shor (1997). «Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer». SIAM Journal on Computing. 26 (5): 1484–1509. arXiv:quant-ph/9508027. Bibcode:1995quant.ph..8027S. doi:10.1137/S0097539795293172. S2CID 2337707.
- ^ a b c Daniel J. Bernstein (2009). «Introduction to post-quantum cryptography» (PDF). Post-Quantum Cryptography.
- ^ «New qubit control bodes well for future of quantum computing». phys.org.
- ^ «Cryptographers Take On Quantum Computers». IEEE Spectrum. 2009-01-01.
- ^ a b «Q&A With Post-Quantum Computing Cryptography Researcher Jintai Ding». IEEE Spectrum. 2008-11-01.
- ^ «ETSI Quantum Safe Cryptography Workshop». ETSI Quantum Safe Cryptography Workshop. ETSI. October 2014. Archived from the original on 17 August 2016. Retrieved 24 February 2015.
- ^ Daniel J. Bernstein (2009-05-17). «Cost analysis of hash collisions: Will quantum computers make SHARCS obsolete?» (PDF).
- ^ Daniel J. Bernstein (2010-03-03). «Grover vs. McEliece» (PDF).
- ^ Peikert, Chris (2014). «Lattice Cryptography for the Internet» (PDF). IACR. Archived from the original on 12 May 2014. Retrieved 10 May 2014.
{{cite web}}: CS1 maint: bot: original URL status unknown (link) - ^ a b c Güneysu, Tim; Lyubashevsky, Vadim; Pöppelmann, Thomas (2012). «Practical Lattice-Based Cryptography: A Signature Scheme for Embedded Systems» (PDF). INRIA. Retrieved 12 May 2014.
- ^ Zhang, jiang (2014). «Authenticated Key Exchange from Ideal Lattices» (PDF). iacr.org. IACR. Archived from the original on 7 September 2014. Retrieved 7 September 2014.
{{cite web}}: CS1 maint: bot: original URL status unknown (link) - ^ a b Ducas, Léo; Durmus, Alain; Lepoint, Tancrède; Lyubashevsky, Vadim (2013). «Lattice Signatures and Bimodal Gaussians». Retrieved 2015-04-18.
- ^ Lyubashevsky, Vadim; Peikert; Regev (2013). «On Ideal Lattices and Learning with Errors Over Rings» (PDF). IACR. Archived from the original on 31 January 2014. Retrieved 14 May 2013.
{{cite web}}: CS1 maint: bot: original URL status unknown (link) - ^ a b c d e f g Augot, Daniel (7 September 2015). «Initial recommendations of long-term secure post-quantum systems» (PDF). PQCRYPTO. Retrieved 13 September 2015.
- ^ Stehlé, Damien; Steinfeld, Ron (2013-01-01). «Making NTRUEncrypt and NTRUSign as Secure as Standard Worst-Case Problems over Ideal Lattices». Cryptology ePrint Archive.
- ^ Easttom, Chuck (2019-02-01). «An Analysis of Leading Lattice-Based Asymmetric Cryptographic Primitives». An Analysis of Leading Lattice-Based Asymmetric Cryptographic Primitivess. pp. 0811–0818. doi:10.1109/CCWC.2019.8666459. ISBN 978-1-7281-0554-3. S2CID 77376310.
- ^ Ding, Jintai; Schmidt (7 June 2005). «Rainbow, a New Multivariable Polynomial Signature Scheme». In Ioannidis, John (ed.). Third International Conference, ACNS 2005, New York, NY, USA, June 7–10, 2005. Proceedings. Lecture Notes in Computer Science. Vol. 3531. pp. 64–175. doi:10.1007/11496137_12. ISBN 978-3-540-26223-7.
- ^ Buchmann, Johannes; Dahmen, Erik; Hülsing, Andreas (2011). «XMSS — A Practical Forward Secure Signature Scheme Based on Minimal Security Assumptions». Post-Quantum Cryptography. PQCrypto 2011. Lecture Notes in Computer Science. Vol. 7071. pp. 117–129. CiteSeerX 10.1.1.400.6086. doi:10.1007/978-3-642-25405-5_8. ISSN 0302-9743.
- ^ a b Bernstein, Daniel J.; Hopwood, Daira; Hülsing, Andreas; Lange, Tanja; Niederhagen, Ruben; Papachristodoulou, Louiza; Schneider, Michael; Schwabe, Peter; Wilcox-O’Hearn, Zooko (2015). Oswald, Elisabeth; Fischlin, Marc (eds.). SPHINCS: practical stateless hash-based signatures. Lecture Notes in Computer Science. Vol. 9056. Springer Berlin Heidelberg. pp. 368–397. CiteSeerX 10.1.1.690.6403. doi:10.1007/978-3-662-46800-5_15. ISBN 9783662467992.
- ^ Huelsing, A.; Butin, D.; Gazdag, S.; Rijneveld, J.; Mohaisen, A. (2018). «RFC 8391 — XMSS: eXtended Merkle Signature Scheme». tools.ietf.org. doi:10.17487/RFC8391.
- ^ Moni Naor, Moti Yung: Universal One-Way Hash Functions and their Cryptographic Applications .STOC 1989: 33-43
- ^ Overbeck, Raphael; Sendrier (2009). Bernstein, Daniel (ed.). Code-based cryptography. Post-Quantum Cryptography. pp. 95–145. doi:10.1007/978-3-540-88702-7_4. ISBN 978-3-540-88701-0.
- ^ De Feo, Luca; Jao; Plut (2011). «Towards quantum-resistant cryptosystems from supersingular elliptic curve isogenies» (PDF). PQCrypto 2011. Retrieved 14 May 2014.
- ^ Higgins, Peter (2013). «Pushing for Perfect Forward Secrecy, an Important Web Privacy Protection». Electronic Frontier Foundation. Retrieved 15 May 2014.
- ^ Sun, Xi; Tian; Wang (19–21 Sep 2012). Browse Conference Publications > Intelligent Networking and Co … Help Working with Abstracts Toward Quantum-Resistant Strong Designated Verifier Signature from Isogenies. Intelligent Networking and Collaborative Systems (INCoS), 2012 4th International Conference on. pp. 292–296. doi:10.1109/iNCoS.2012.70. ISBN 978-1-4673-2281-2. S2CID 18204496.
- ^ Perlner, Ray; Cooper (2009). «Quantum Resistant Public Key Cryptography: A Survey». NIST. Retrieved 23 Apr 2015.
- ^ Campagna, Matt; Hardjono; Pintsov; Romansky; Yu (2013). «Kerberos Revisited Quantum-Safe Authentication» (PDF). ETSI.
- ^ Lyubashevsky, Vadim; Peikert; Regev (25 June 2013). «On Ideal Lattices and Learning with Errors Over Rings» (PDF). Springer. Retrieved 19 June 2014.
- ^ Akleylek, Sedat; Bindel, Nina; Buchmann, Johannes; Krämer, Juliane; Marson, Giorgia Azzurra (2016). «An Efficient Lattice-Based Signature Scheme with Provably Secure Instantiation». Cryptology ePrint Archive.
- ^ Nejatollahi, Hamid; Dutt, Nikil; Ray, Sandip; Regazzoni, Francesco; Banerjee, Indranil; Cammarota, Rosario (2019-02-27). «Post-Quantum Lattice-Based Cryptography Implementations: A Survey». ACM Computing Surveys. 51 (6): 1–41. doi:10.1145/3292548. ISSN 0360-0300. S2CID 59337649.
- ^ Bulygin, Stanislav; Petzoldt; Buchmann (2010). «Towards Provable Security of the Unbalanced Oil and Vinegar Signature Scheme under Direct Attacks». Progress in Cryptology – INDOCRYPT 2010. Lecture Notes in Computer Science. Vol. 6498. pp. 17–32. CiteSeerX 10.1.1.294.3105. doi:10.1007/978-3-642-17401-8_3. ISBN 978-3-642-17400-1.
- ^ Pereira, Geovandro; Puodzius, Cassius; Barreto, Paulo (2016). «Shorter hash-based signatures». Journal of Systems and Software. 116: 95–100. doi:10.1016/j.jss.2015.07.007.
- ^ Garcia, Luis. «On the security and the efficiency of the Merkle signature scheme» (PDF). Cryptology ePrint Archive. IACR. Retrieved 19 June 2013.
- ^ Blaum, Mario; Farrell; Tilborg (31 May 2002). Information, Coding and Mathematics. Springer. ISBN 978-1-4757-3585-7.
- ^ Wang, Yongge (2016). «Quantum resistant random linear code based public key encryption scheme RLCE». Proceedings of Information Theory (ISIT). IEEE ISIT: 2519–2523. arXiv:1512.08454. Bibcode:2015arXiv151208454W.
- ^ Delfs, Christina; Galbraith (2013). «Computing isogenies between supersingular elliptic curves over F_p». arXiv:1310.7789 [math.NT].
- ^ a b Hirschborrn, P; Hoffstein; Howgrave-Graham; Whyte. «Choosing NTRUEncrypt Parameters in Light of Combined Lattice Reduction and MITM Approaches» (PDF). NTRU. Archived from the original (PDF) on 30 January 2013. Retrieved 12 May 2014.
- ^ a b Petzoldt, Albrecht; Bulygin; Buchmann (2010). «Selecting Parameters for the Rainbow Signature Scheme – Extended Version -» (PDF). Archived from the original on 4 March 2016. Retrieved 12 May 2014.
{{cite web}}: CS1 maint: bot: original URL status unknown (link) - ^ «SPHINCS+: Submission to the NIST post-quantum project» (PDF).
- ^ Chopra, Arjun (2017). «GLYPH: A New Insantiation of the GLP Digital Signature Scheme». Cryptology ePrint Archive.
- ^ a b Alkim, Erdem; Ducas, Léo; Pöppelmann, Thomas; Schwabe, Peter (2015). «Post-quantum key exchange — a new hope» (PDF). Cryptology ePrint Archive, Report 2015/1092. Retrieved 1 September 2017.
- ^ Wang, Yongge (2017). «Revised Quantum Resistant Public Key Encryption Scheme RLCE and IND-CCA2 Security for McEliece Schemes». Cryptology ePrint Archive.
- ^ Misoczki, R.; Tillich, J. P.; Sendrier, N.; Barreto, P. S. L. M. (2013). MDPC-McEliece: New McEliece variants from Moderate Density Parity-Check codes. 2013 IEEE International Symposium on Information Theory. pp. 2069–2073. CiteSeerX 10.1.1.259.9109. doi:10.1109/ISIT.2013.6620590. ISBN 978-1-4799-0446-4. S2CID 9485532.
- ^ Costello, Craig; Longa, Patrick; Naehrig, Michael (2016). «Efficient algorithms for supersingular isogeny Diffie-Hellman» (PDF). Advances in Cryptology.
- ^ a b Costello, Craig; Jao; Longa; Naehrig; Renes; Urbanik. «Efficient Compression of SIDH public keys». Retrieved 8 October 2016.
- ^ Lin, Jintai Ding, Xiang Xie, Xiaodong (2012-01-01). «A Simple Provably Secure Key Exchange Scheme Based on the Learning with Errors Problem». Cryptology ePrint Archive.
- ^ Peikert, Chris (2014-01-01). «Lattice Cryptography for the Internet». Cryptology ePrint Archive.
- ^ Singh, Vikram (2015). «A Practical Key Exchange for the Internet using Lattice Cryptography». Retrieved 2015-04-18.
- ^ a b Zhang, Jiang; Zhang, Zhenfeng; Ding, Jintai; Snook, Michael; Dagdelen, Özgür (2015-04-26). «Authenticated Key Exchange from Ideal Lattices». In Oswald, Elisabeth; Fischlin, Marc (eds.). Advances in Cryptology — EUROCRYPT 2015. Lecture Notes in Computer Science. Springer Berlin Heidelberg. pp. 719–751. CiteSeerX 10.1.1.649.1864. doi:10.1007/978-3-662-46803-6_24. ISBN 978-3-662-46802-9.
- ^ Krawczyk, Hugo (2005-08-14). «HMQV: A High-Performance Secure Diffie-Hellman Protocol». In Shoup, Victor (ed.). Advances in Cryptology – CRYPTO 2005. Lecture Notes in Computer Science. Vol. 3621. Springer. pp. 546–566. doi:10.1007/11535218_33. ISBN 978-3-540-28114-6.
- ^ Naor, Dalit; Shenhav; Wool (2006). «One-Time Signatures Revisited: Practical Fast Signatures Using Fractal Merkle Tree Traversal» (PDF). IEEE. Retrieved 13 May 2014.
- ^ Barreto, Paulo S. L. M.; Biasi, Felipe Piazza; Dahab, Ricardo; López-Hernández, Julio César; Morais, Eduardo M. de; Oliveira, Ana D. Salina de; Pereira, Geovandro C. C. F.; Ricardini, Jefferson E. (2014). Koç, Çetin Kaya (ed.). A Panorama of Post-quantum Cryptography. Springer International Publishing. pp. 387–439. doi:10.1007/978-3-319-10683-0_16. ISBN 978-3-319-10682-3.
- ^ De Feo, Luca; Jao; Plut (2011). «Towards Quantum-Resistant Cryptosystems From Supersingular Elliptic Curve Isogenies» (PDF). Archived from the original on 11 February 2014. Retrieved 12 May 2014.
{{cite web}}: CS1 maint: bot: original URL status unknown (link) - ^ «Cryptology ePrint Archive: Report 2016/229». eprint.iacr.org. Retrieved 2016-03-02.
- ^ Ristic, Ivan (2013-06-25). «Deploying Forward Secrecy». SSL Labs. Retrieved 14 June 2014.
- ^ «Does NTRU provide Perfect Forward Secrecy?». crypto.stackexchange.com.
- ^ a b «Open Quantum Safe». openquantumsafe.org.
- ^ Stebila, Douglas; Mosca, Michele. «Post-Quantum Key Exchange for the Internet and the Open Quantum Safe Project». Cryptology ePrint Archive, Report 2016/1017, 2016. Retrieved 9 April 2017.
- ^ «liboqs: C library for quantum-resistant cryptographic algorithms». 26 November 2017 – via GitHub.
- ^ «openssl: Fork of OpenSSL that includes quantum-resistant algorithms and ciphersuites based on liboqs». 9 November 2017 – via GitHub.
- ^ Stebila, Douglas (26 Mar 2018). «liboqs nist-branch algorithm datasheet: kem_newhopenist». GitHub. Retrieved 27 September 2018.
- ^ «Lattice Cryptography Library». Microsoft Research. 19 Apr 2016. Retrieved 27 September 2018.
- ^ Bos, Joppe; Costello, Craig; Ducas, Léo; Mironov, Ilya; Naehrig, Michael; Nikolaenko, Valeria; Raghunathan, Ananth; Stebila, Douglas (2016-01-01). «Frodo: Take off the ring! Practical, Quantum-Secure Key Exchange from LWE». Cryptology ePrint Archive.
- ^ «NTRUOpenSourceProject/NTRUEncrypt». GitHub. Retrieved 2017-04-10.
- ^ «SIDH Library — Microsoft Research». Microsoft Research. Retrieved 2017-04-10.
- ^ Feo, Luca De; Jao, David; Plût, Jérôme (2011-01-01). «Towards quantum-resistant cryptosystems from supersingular elliptic curve isogenies». Archived from the original on 2014-05-03.
- ^ Bernstein, Daniel J.; Chou, Tung; Schwabe, Peter (2015-01-01). «McBits: fast constant-time code-based cryptography». Cryptology ePrint Archive.
- ^ «Microsoft/Picnic» (PDF). GitHub. Retrieved 2018-06-27.
- ^ «Bouncy Castle Betas».
- ^ «Open Quantum Safe».
Further reading[edit]
- Post-Quantum Cryptography. Springer. 2008. p. 245. ISBN 978-3-540-88701-0.
- Isogenies in a Quantum World
- On Ideal Lattices and Learning With Errors Over Rings
- Kerberos Revisited: Quantum-Safe Authentication
- The picnic signature scheme
External links[edit]
- PQCrypto, the post-quantum cryptography conference
- ETSI Quantum Secure Standards Effort
- NIST’s Post-Quantum crypto Project
- PQCrypto Usage & Deployment
In cryptography, post-quantum cryptography (PQC) (sometimes referred to as quantum-proof, quantum-safe or quantum-resistant) refers to cryptographic algorithms (usually public-key algorithms) that are thought to be secure against a cryptanalytic attack by a quantum computer. The problem with currently popular algorithms is that their security relies on one of three hard mathematical problems: the integer factorization problem, the discrete logarithm problem or the elliptic-curve discrete logarithm problem. All of these problems could be easily solved on a sufficiently powerful quantum computer running Shor’s algorithm.[1][2]
Even though current quantum computers lack processing power to break any real cryptographic algorithm,[3] many cryptographers are designing new algorithms to prepare for a time when quantum computing becomes a threat. This work has gained greater attention from academics and industry through the PQCrypto conference series since 2006 and more recently by several workshops on Quantum Safe Cryptography hosted by the European Telecommunications Standards Institute (ETSI) and the Institute for Quantum Computing.[4][5][6]
In contrast to the threat quantum computing poses to current public-key algorithms, most current symmetric cryptographic algorithms and hash functions are considered to be relatively secure against attacks by quantum computers.[2][7] While the quantum Grover’s algorithm does speed up attacks against symmetric ciphers, doubling the key size can effectively block these attacks.[8] Thus post-quantum symmetric cryptography does not need to differ significantly from current symmetric cryptography.
Algorithms[edit]
Currently post-quantum cryptography research is mostly focused on six different approaches:[2][5]
Lattice-based cryptography[edit]
This approach includes cryptographic systems such as learning with errors, ring learning with errors (ring-LWE),[9][10][11] the ring learning with errors key exchange and the ring learning with errors signature, the older NTRU or GGH encryption schemes, and the newer NTRU signature and BLISS signatures.[12] Some of these schemes like NTRU encryption have been studied for many years without anyone finding a feasible attack. Others like the ring-LWE algorithms have proofs that their security reduces to a worst-case problem.[13] The Post Quantum Cryptography Study Group sponsored by the European Commission suggested that the Stehle–Steinfeld variant of NTRU be studied for standardization rather than the NTRU algorithm.[14][15] At that time, NTRU was still patented. Studies have indicated that NTRU may have more secure properties than other lattice based algorithms.[16]
Multivariate cryptography[edit]
This includes cryptographic systems such as the Rainbow (Unbalanced Oil and Vinegar) scheme which is based on the difficulty of solving systems of multivariate equations. Various attempts to build secure multivariate equation encryption schemes have failed. However, multivariate signature schemes like Rainbow could provide the basis for a quantum secure digital signature.[17] There is a patent on the Rainbow Signature Scheme.
Hash-based cryptography[edit]
This includes cryptographic systems such as Lamport signatures, the Merkle signature scheme, the XMSS,[18] the SPHINCS,[19] and the WOTS schemes. Hash based digital signatures were invented in the late 1970s by Ralph Merkle and have been studied ever since as an interesting alternative to number-theoretic digital signatures like RSA and DSA. Their primary drawback is that for any hash-based public key, there is a limit on the number of signatures that can be signed using the corresponding set of private keys. This fact had reduced interest in these signatures until interest was revived due to the desire for cryptography that was resistant to attack by quantum computers. There appear to be no patents on the Merkle signature scheme[citation needed] and there exist many non-patented hash functions that could be used with these schemes. The stateful hash-based signature scheme XMSS developed by a team of researchers under the direction of Johannes Buchmann is described in RFC 8391.[20]
Note that all the above schemes are one-time or bounded-time signatures, Moni Naor and Moti Yung invented UOWHF hashing in 1989 and designed a signature based on hashing (the Naor-Yung scheme)[21] which can be unlimited-time in use (the first such signature that does not require trapdoor properties).
Code-based cryptography[edit]
This includes cryptographic systems which rely on error-correcting codes, such as the McEliece and Niederreiter encryption algorithms and the related Courtois, Finiasz and Sendrier Signature scheme. The original McEliece signature using random Goppa codes has withstood scrutiny for over 40 years. However, many variants of the McEliece scheme, which seek to introduce more structure into the code used in order to reduce the size of the keys, have been shown to be insecure.[22] The Post Quantum Cryptography Study Group sponsored by the European Commission has recommended the McEliece public key encryption system as a candidate for long term protection against attacks by quantum computers.[14]
Supersingular elliptic curve isogeny cryptography[edit]
This cryptographic system relies on the properties of supersingular elliptic curves and supersingular isogeny graphs to create a Diffie-Hellman replacement with forward secrecy.[23] This cryptographic system uses the well studied mathematics of supersingular elliptic curves to create a Diffie-Hellman like key exchange that can serve as a straightforward quantum computing resistant replacement for the Diffie-Hellman and elliptic curve Diffie–Hellman key exchange methods that are in widespread use today. Because it works much like existing Diffie–Hellman implementations, it offers forward secrecy which is viewed as important both to prevent mass surveillance by governments but also to protect against the compromise of long term keys through failures.[24] In 2012, researchers Sun, Tian and Wang of the Chinese State Key Lab for Integrated Service Networks and Xidian University, extended the work of De Feo, Jao, and Plut to create quantum secure digital signatures based on supersingular elliptic curve isogenies.[25] There are no patents covering this cryptographic system.
Symmetric key quantum resistance[edit]
Provided one uses sufficiently large key sizes, the symmetric key cryptographic systems like AES and SNOW 3G are already resistant to attack by a quantum computer.[26] Further, key management systems and protocols that use symmetric key cryptography instead of public key cryptography like Kerberos and the 3GPP Mobile Network Authentication Structure are also inherently secure against attack by a quantum computer. Given its widespread deployment in the world already, some researchers recommend expanded use of Kerberos-like symmetric key management as an efficient way to get post quantum cryptography today.[27]
Security reductions[edit]
In cryptography research, it is desirable to prove the equivalence of a cryptographic algorithm and a known hard mathematical problem. These proofs are often called «security reductions», and are used to demonstrate the difficulty of cracking the encryption algorithm. In other words, the security of a given cryptographic algorithm is reduced to the security of a known hard problem. Researchers are actively looking for security reductions in the prospects for post quantum cryptography. Current results are given here:
Lattice-based cryptography – Ring-LWE Signature[edit]
In some versions of Ring-LWE there is a security reduction to the shortest-vector problem (SVP) in a lattice as a lower bound on the security. The SVP is known to be NP-hard.[28] Specific ring-LWE systems that have provable security reductions include a variant of Lyubashevsky’s ring-LWE signatures defined in a paper by Güneysu, Lyubashevsky, and Pöppelmann.[10] The GLYPH signature scheme is a variant of the Güneysu, Lyubashevsky, and Pöppelmann (GLP) signature which takes into account research results that have come after the publication of the GLP signature in 2012. Another Ring-LWE signature is Ring-TESLA.[29] There also exists a «derandomized variant» of LWE, called Learning with Rounding (LWR), which yields » improved speedup (by eliminating sampling small errors from a Gaussian-like distribution with deterministic errors) and bandwidth.»[30] While LWE utilizes the addition of a small error to conceal the lower bits, LWR utilizes rounding for the same purpose.
Lattice-based cryptography – NTRU, BLISS[edit]
The security of the NTRU encryption scheme and the BLISS[12] signature is believed to be related to, but not provably reducible to, the Closest Vector Problem (CVP) in a Lattice. The CVP is known to be NP-hard. The Post Quantum Cryptography Study Group sponsored by the European Commission suggested that the Stehle–Steinfeld variant of NTRU which does have a security reduction be studied for long term use instead of the original NTRU algorithm.[14]
Multivariate cryptography – Unbalanced Oil and Vinegar[edit]
Unbalanced Oil and Vinegar signature schemes are asymmetric cryptographic primitives based on multivariate polynomials over a finite field 
Hash-based cryptography – Merkle signature scheme[edit]
In 2005, Luis Garcia proved that there was a security reduction of Merkle Hash Tree signatures to the security of the underlying hash function. Garcia showed in his paper that if computationally one-way hash functions exist then the Merkle Hash Tree signature is provably secure.[32]
Therefore, if one used a hash function with a provable reduction of security to a known hard problem one would have a provable security reduction of the Merkle tree signature to that known hard problem.[33]
The Post Quantum Cryptography Study Group sponsored by the European Commission has recommended use of Merkle signature scheme for long term security protection against quantum computers.[14]
Code-based cryptography – McEliece[edit]
The McEliece Encryption System has a security reduction to the Syndrome Decoding Problem (SDP). The SDP is known to be NP-hard[34] The Post Quantum Cryptography Study Group sponsored by the European Commission has recommended the use of this cryptography for long term protection against attack by a quantum computer.[14]
Code-based cryptography – RLCE[edit]
In 2016, Wang proposed a random linear code encryption scheme RLCE[35] which is based on McEliece schemes. RLCE scheme can be constructed using any linear code such as Reed-Solomon code by inserting random columns in the underlying linear code generator matrix.
Supersingular elliptic curve isogeny cryptography[edit]
Security is related to the problem of constructing an isogeny between two supersingular curves with the same number of points. The most recent investigation of the difficulty of this problem is by Delfs and Galbraith indicates that this problem is as hard as the inventors of the key exchange suggest that it is.[36] There is no security reduction to a known NP-hard problem.
Comparison[edit]
One common characteristic of many post-quantum cryptography algorithms is that they require larger key sizes than commonly used «pre-quantum» public key algorithms. There are often tradeoffs to be made in key size, computational efficiency and ciphertext or signature size. The table lists some values for different schemes at a 128 bit post-quantum security level.
| Algorithm | Type | Public Key | Private Key | Signature |
|---|---|---|---|---|
| NTRU Encrypt[37] | Lattice | 766.25 B | 842.875 B | |
| Streamlined NTRU Prime[citation needed] | Lattice | 154 B | ||
| Rainbow[38] | Multivariate | 124 KB | 95 KB | |
| SPHINCS[19] | Hash Signature | 1 KB | 1 KB | 41 KB |
| SPHINCS+[39] | Hash Signature | 32 B | 64 B | 8 KB |
| BLISS-II | Lattice | 7 KB | 2 KB | 5 KB |
| GLP-Variant GLYPH Signature[10][40] | Ring-LWE | 2 KB | 0.4 KB | 1.8 KB |
| NewHope[41] | Ring-LWE | 2 KB | 2 KB | |
| Goppa-based McEliece[14] | Code-based | 1 MB | 11.5 KB | |
| Random Linear Code based encryption[42] | RLCE | 115 KB | 3 KB | |
| Quasi-cyclic MDPC-based McEliece[43] | Code-based | 1,232 B | 2,464 B | |
| SIDH[44] | Isogeny | 564 B | 48 B | |
| SIDH (compressed keys)[45] | Isogeny | 330 B | 48 B | |
| 3072-bit Discrete Log | not PQC | 384 B | 32 B | 96 B |
| 256-bit Elliptic Curve | not PQC | 32 B | 32 B | 65 B |
A practical consideration on a choice among post-quantum cryptographic algorithms is the effort required to send public keys over the internet. From this point of view, the Ring-LWE, NTRU, and SIDH algorithms provide key sizes conveniently under 1KB, hash-signature public keys come in under 5KB, and MDPC-based McEliece takes about 1KB. On the other hand, Rainbow schemes require about 125KB and Goppa-based McEliece requires a nearly 1MB key.
Lattice-based cryptography – LWE key exchange and Ring-LWE key exchange[edit]
The fundamental idea of using LWE and Ring LWE for key exchange was proposed and filed at the University of Cincinnati in 2011 by Jintai Ding. The basic idea comes from the associativity of matrix multiplications, and the errors are used to provide the security. The paper[46] appeared in 2012 after a provisional patent application was filed in 2012.
In 2014, Peikert[47] presented a key transport scheme following the same basic idea of Ding’s, where the new idea of sending additional 1 bit signal for rounding in Ding’s construction is also utilized. For somewhat greater than 128 bits of security, Singh presents a set of parameters which have 6956-bit public keys for the Peikert’s scheme.[48] The corresponding private key would be roughly 14,000 bits.
In 2015, an authenticated key exchange with provable forward security following the same basic idea of Ding’s was presented at Eurocrypt 2015,[49] which is an extension of the HMQV[50] construction in Crypto2005. The parameters for different security levels from 80 bits to 350 bits, along with the corresponding key sizes are provided in the paper.[49]
Lattice-based cryptography – NTRU encryption[edit]
For 128 bits of security in NTRU, Hirschhorn, Hoffstein, Howgrave-Graham and Whyte, recommend using a public key represented as a degree 613 polynomial with coefficients 
Multivariate cryptography – Rainbow signature[edit]
For 128 bits of security and the smallest signature size in a Rainbow multivariate quadratic equation signature scheme, Petzoldt, Bulygin and Buchmann, recommend using equations in 
Hash-based cryptography – Merkle signature scheme[edit]
In order to get 128 bits of security for hash based signatures to sign 1 million messages using the fractal Merkle tree method of Naor Shenhav and Wool the public and private key sizes are roughly 36,000 bits in length.[51]
Code-based cryptography – McEliece[edit]
For 128 bits of security in a McEliece scheme, The European Commissions Post Quantum Cryptography Study group recommends using a binary Goppa code of length at least 







The group is also investigating the use of Quasi-cyclic MDPC codes of length at least 





Barreto et al. recommend using a binary Goppa code of length at least 







Supersingular elliptic curve isogeny cryptography[edit]
For 128 bits of security in the supersingular isogeny Diffie-Hellman (SIDH) method, De Feo, Jao and Plut recommend using a supersingular curve modulo a 768-bit prime. If one uses elliptic curve point compression the public key will need to be no more than 8×768 or 6144 bits in length.[53] A March 2016 paper by authors Azarderakhsh, Jao, Kalach, Koziel, and Leonardi showed how to cut the number of bits transmitted in half, which was further improved by authors Costello, Jao, Longa, Naehrig, Renes and Urbanik resulting in a compressed-key version of the SIDH protocol with public keys only 2640 bits in size.[45] This makes the number of bits transmitted roughly equivalent to the non-quantum secure RSA and Diffie-Hellman at the same classical security level.[54]
Symmetric–key-based cryptography[edit]
As a general rule, for 128 bits of security in a symmetric-key-based system, one can safely use key sizes of 256 bits. The best quantum attack against generic symmetric-key systems is an application of Grover’s algorithm, which requires work proportional to the square root of the size of the key space. To transmit an encrypted key to a device that possesses the symmetric key necessary to decrypt that key requires roughly 256 bits as well. It is clear that symmetric-key systems offer the smallest key sizes for post-quantum cryptography.
Forward secrecy[edit]
A public-key system demonstrates a property referred to as perfect forward secrecy when it generates random public keys per session for the purposes of key agreement. This means that the compromise of one message cannot lead to the compromise of others, and also that there is not a single secret value which can lead to the compromise of multiple messages. Security experts recommend using cryptographic algorithms that support forward secrecy over those that do not.[55] The reason for this is that forward secrecy can protect against the compromise of long term private keys associated with public/private key pairs. This is viewed as a means of preventing mass surveillance by intelligence agencies.
Both the Ring-LWE key exchange and supersingular isogeny Diffie-Hellman (SIDH) key exchange can support forward secrecy in one exchange with the other party. Both the Ring-LWE and SIDH can also be used without forward secrecy by creating a variant of the classic ElGamal encryption variant of Diffie-Hellman.
The other algorithms in this article, such as NTRU, do not support forward secrecy as is.
Any authenticated public key encryption system can be used to build a key exchange with forward secrecy.[56]
Open Quantum Safe project[edit]
Open Quantum Safe (OQS) project was started in late 2016 and has the goal of developing and prototyping quantum-resistant cryptography.[57][58] It aims to integrate current post-quantum schemes in one library: liboqs.[59] liboqs is an open source C library for quantum-resistant cryptographic algorithms. It initially focuses on key exchange algorithms. It provides a common API suitable for post-quantum key exchange algorithms, and will collect together various implementations. liboqs will also include a test harness and benchmarking routines to compare performance of post-quantum implementations. Furthermore, OQS also provides integration of liboqs into OpenSSL.[60]
As of April 2017, the following key exchange algorithms are supported:[57]
| Algorithm | Type |
|---|---|
| BCNS15[61] | Ring learning with errors key exchange |
| NewHope[62][41] | Ring learning with errors key exchange |
| Frodo[63] | Learning with errors |
| NTRU[64] | Lattice-based cryptography |
| SIDH[65][66] | Supersingular isogeny key exchange |
| McBits[67] | Error-correcting codes |
Implementation[edit]
One of the main challenges in post-quantum cryptography is considered to be the implementation of potentially quantum safe algorithms into existing systems. There are tests done, for example by Microsoft Research implementing PICNIC in a PKI using Hardware security modules.[68] Test implementations for Google’s NewHope algorithm have also been done by HSM vendors.
Other notable implementations include:
- bouncycastle[69]
- liboqs[70]
See also[edit]
- NIST Post-Quantum Cryptography Standardization
- Quantum cryptography – cryptography based on quantum mechanics
- Crypto-shredding — Deleting encryption keys
References[edit]
- ^ Peter W. Shor (1997). «Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer». SIAM Journal on Computing. 26 (5): 1484–1509. arXiv:quant-ph/9508027. Bibcode:1995quant.ph..8027S. doi:10.1137/S0097539795293172. S2CID 2337707.
- ^ a b c Daniel J. Bernstein (2009). «Introduction to post-quantum cryptography» (PDF). Post-Quantum Cryptography.
- ^ «New qubit control bodes well for future of quantum computing». phys.org.
- ^ «Cryptographers Take On Quantum Computers». IEEE Spectrum. 2009-01-01.
- ^ a b «Q&A With Post-Quantum Computing Cryptography Researcher Jintai Ding». IEEE Spectrum. 2008-11-01.
- ^ «ETSI Quantum Safe Cryptography Workshop». ETSI Quantum Safe Cryptography Workshop. ETSI. October 2014. Archived from the original on 17 August 2016. Retrieved 24 February 2015.
- ^ Daniel J. Bernstein (2009-05-17). «Cost analysis of hash collisions: Will quantum computers make SHARCS obsolete?» (PDF).
- ^ Daniel J. Bernstein (2010-03-03). «Grover vs. McEliece» (PDF).
- ^ Peikert, Chris (2014). «Lattice Cryptography for the Internet» (PDF). IACR. Archived from the original on 12 May 2014. Retrieved 10 May 2014.
{{cite web}}: CS1 maint: bot: original URL status unknown (link) - ^ a b c Güneysu, Tim; Lyubashevsky, Vadim; Pöppelmann, Thomas (2012). «Practical Lattice-Based Cryptography: A Signature Scheme for Embedded Systems» (PDF). INRIA. Retrieved 12 May 2014.
- ^ Zhang, jiang (2014). «Authenticated Key Exchange from Ideal Lattices» (PDF). iacr.org. IACR. Archived from the original on 7 September 2014. Retrieved 7 September 2014.
{{cite web}}: CS1 maint: bot: original URL status unknown (link) - ^ a b Ducas, Léo; Durmus, Alain; Lepoint, Tancrède; Lyubashevsky, Vadim (2013). «Lattice Signatures and Bimodal Gaussians». Retrieved 2015-04-18.
- ^ Lyubashevsky, Vadim; Peikert; Regev (2013). «On Ideal Lattices and Learning with Errors Over Rings» (PDF). IACR. Archived from the original on 31 January 2014. Retrieved 14 May 2013.
{{cite web}}: CS1 maint: bot: original URL status unknown (link) - ^ a b c d e f g Augot, Daniel (7 September 2015). «Initial recommendations of long-term secure post-quantum systems» (PDF). PQCRYPTO. Retrieved 13 September 2015.
- ^ Stehlé, Damien; Steinfeld, Ron (2013-01-01). «Making NTRUEncrypt and NTRUSign as Secure as Standard Worst-Case Problems over Ideal Lattices». Cryptology ePrint Archive.
- ^ Easttom, Chuck (2019-02-01). «An Analysis of Leading Lattice-Based Asymmetric Cryptographic Primitives». An Analysis of Leading Lattice-Based Asymmetric Cryptographic Primitivess. pp. 0811–0818. doi:10.1109/CCWC.2019.8666459. ISBN 978-1-7281-0554-3. S2CID 77376310.
- ^ Ding, Jintai; Schmidt (7 June 2005). «Rainbow, a New Multivariable Polynomial Signature Scheme». In Ioannidis, John (ed.). Third International Conference, ACNS 2005, New York, NY, USA, June 7–10, 2005. Proceedings. Lecture Notes in Computer Science. Vol. 3531. pp. 64–175. doi:10.1007/11496137_12. ISBN 978-3-540-26223-7.
- ^ Buchmann, Johannes; Dahmen, Erik; Hülsing, Andreas (2011). «XMSS — A Practical Forward Secure Signature Scheme Based on Minimal Security Assumptions». Post-Quantum Cryptography. PQCrypto 2011. Lecture Notes in Computer Science. Vol. 7071. pp. 117–129. CiteSeerX 10.1.1.400.6086. doi:10.1007/978-3-642-25405-5_8. ISSN 0302-9743.
- ^ a b Bernstein, Daniel J.; Hopwood, Daira; Hülsing, Andreas; Lange, Tanja; Niederhagen, Ruben; Papachristodoulou, Louiza; Schneider, Michael; Schwabe, Peter; Wilcox-O’Hearn, Zooko (2015). Oswald, Elisabeth; Fischlin, Marc (eds.). SPHINCS: practical stateless hash-based signatures. Lecture Notes in Computer Science. Vol. 9056. Springer Berlin Heidelberg. pp. 368–397. CiteSeerX 10.1.1.690.6403. doi:10.1007/978-3-662-46800-5_15. ISBN 9783662467992.
- ^ Huelsing, A.; Butin, D.; Gazdag, S.; Rijneveld, J.; Mohaisen, A. (2018). «RFC 8391 — XMSS: eXtended Merkle Signature Scheme». tools.ietf.org. doi:10.17487/RFC8391.
- ^ Moni Naor, Moti Yung: Universal One-Way Hash Functions and their Cryptographic Applications .STOC 1989: 33-43
- ^ Overbeck, Raphael; Sendrier (2009). Bernstein, Daniel (ed.). Code-based cryptography. Post-Quantum Cryptography. pp. 95–145. doi:10.1007/978-3-540-88702-7_4. ISBN 978-3-540-88701-0.
- ^ De Feo, Luca; Jao; Plut (2011). «Towards quantum-resistant cryptosystems from supersingular elliptic curve isogenies» (PDF). PQCrypto 2011. Retrieved 14 May 2014.
- ^ Higgins, Peter (2013). «Pushing for Perfect Forward Secrecy, an Important Web Privacy Protection». Electronic Frontier Foundation. Retrieved 15 May 2014.
- ^ Sun, Xi; Tian; Wang (19–21 Sep 2012). Browse Conference Publications > Intelligent Networking and Co … Help Working with Abstracts Toward Quantum-Resistant Strong Designated Verifier Signature from Isogenies. Intelligent Networking and Collaborative Systems (INCoS), 2012 4th International Conference on. pp. 292–296. doi:10.1109/iNCoS.2012.70. ISBN 978-1-4673-2281-2. S2CID 18204496.
- ^ Perlner, Ray; Cooper (2009). «Quantum Resistant Public Key Cryptography: A Survey». NIST. Retrieved 23 Apr 2015.
- ^ Campagna, Matt; Hardjono; Pintsov; Romansky; Yu (2013). «Kerberos Revisited Quantum-Safe Authentication» (PDF). ETSI.
- ^ Lyubashevsky, Vadim; Peikert; Regev (25 June 2013). «On Ideal Lattices and Learning with Errors Over Rings» (PDF). Springer. Retrieved 19 June 2014.
- ^ Akleylek, Sedat; Bindel, Nina; Buchmann, Johannes; Krämer, Juliane; Marson, Giorgia Azzurra (2016). «An Efficient Lattice-Based Signature Scheme with Provably Secure Instantiation». Cryptology ePrint Archive.
- ^ Nejatollahi, Hamid; Dutt, Nikil; Ray, Sandip; Regazzoni, Francesco; Banerjee, Indranil; Cammarota, Rosario (2019-02-27). «Post-Quantum Lattice-Based Cryptography Implementations: A Survey». ACM Computing Surveys. 51 (6): 1–41. doi:10.1145/3292548. ISSN 0360-0300. S2CID 59337649.
- ^ Bulygin, Stanislav; Petzoldt; Buchmann (2010). «Towards Provable Security of the Unbalanced Oil and Vinegar Signature Scheme under Direct Attacks». Progress in Cryptology – INDOCRYPT 2010. Lecture Notes in Computer Science. Vol. 6498. pp. 17–32. CiteSeerX 10.1.1.294.3105. doi:10.1007/978-3-642-17401-8_3. ISBN 978-3-642-17400-1.
- ^ Pereira, Geovandro; Puodzius, Cassius; Barreto, Paulo (2016). «Shorter hash-based signatures». Journal of Systems and Software. 116: 95–100. doi:10.1016/j.jss.2015.07.007.
- ^ Garcia, Luis. «On the security and the efficiency of the Merkle signature scheme» (PDF). Cryptology ePrint Archive. IACR. Retrieved 19 June 2013.
- ^ Blaum, Mario; Farrell; Tilborg (31 May 2002). Information, Coding and Mathematics. Springer. ISBN 978-1-4757-3585-7.
- ^ Wang, Yongge (2016). «Quantum resistant random linear code based public key encryption scheme RLCE». Proceedings of Information Theory (ISIT). IEEE ISIT: 2519–2523. arXiv:1512.08454. Bibcode:2015arXiv151208454W.
- ^ Delfs, Christina; Galbraith (2013). «Computing isogenies between supersingular elliptic curves over F_p». arXiv:1310.7789 [math.NT].
- ^ a b Hirschborrn, P; Hoffstein; Howgrave-Graham; Whyte. «Choosing NTRUEncrypt Parameters in Light of Combined Lattice Reduction and MITM Approaches» (PDF). NTRU. Archived from the original (PDF) on 30 January 2013. Retrieved 12 May 2014.
- ^ a b Petzoldt, Albrecht; Bulygin; Buchmann (2010). «Selecting Parameters for the Rainbow Signature Scheme – Extended Version -» (PDF). Archived from the original on 4 March 2016. Retrieved 12 May 2014.
{{cite web}}: CS1 maint: bot: original URL status unknown (link) - ^ «SPHINCS+: Submission to the NIST post-quantum project» (PDF).
- ^ Chopra, Arjun (2017). «GLYPH: A New Insantiation of the GLP Digital Signature Scheme». Cryptology ePrint Archive.
- ^ a b Alkim, Erdem; Ducas, Léo; Pöppelmann, Thomas; Schwabe, Peter (2015). «Post-quantum key exchange — a new hope» (PDF). Cryptology ePrint Archive, Report 2015/1092. Retrieved 1 September 2017.
- ^ Wang, Yongge (2017). «Revised Quantum Resistant Public Key Encryption Scheme RLCE and IND-CCA2 Security for McEliece Schemes». Cryptology ePrint Archive.
- ^ Misoczki, R.; Tillich, J. P.; Sendrier, N.; Barreto, P. S. L. M. (2013). MDPC-McEliece: New McEliece variants from Moderate Density Parity-Check codes. 2013 IEEE International Symposium on Information Theory. pp. 2069–2073. CiteSeerX 10.1.1.259.9109. doi:10.1109/ISIT.2013.6620590. ISBN 978-1-4799-0446-4. S2CID 9485532.
- ^ Costello, Craig; Longa, Patrick; Naehrig, Michael (2016). «Efficient algorithms for supersingular isogeny Diffie-Hellman» (PDF). Advances in Cryptology.
- ^ a b Costello, Craig; Jao; Longa; Naehrig; Renes; Urbanik. «Efficient Compression of SIDH public keys». Retrieved 8 October 2016.
- ^ Lin, Jintai Ding, Xiang Xie, Xiaodong (2012-01-01). «A Simple Provably Secure Key Exchange Scheme Based on the Learning with Errors Problem». Cryptology ePrint Archive.
- ^ Peikert, Chris (2014-01-01). «Lattice Cryptography for the Internet». Cryptology ePrint Archive.
- ^ Singh, Vikram (2015). «A Practical Key Exchange for the Internet using Lattice Cryptography». Retrieved 2015-04-18.
- ^ a b Zhang, Jiang; Zhang, Zhenfeng; Ding, Jintai; Snook, Michael; Dagdelen, Özgür (2015-04-26). «Authenticated Key Exchange from Ideal Lattices». In Oswald, Elisabeth; Fischlin, Marc (eds.). Advances in Cryptology — EUROCRYPT 2015. Lecture Notes in Computer Science. Springer Berlin Heidelberg. pp. 719–751. CiteSeerX 10.1.1.649.1864. doi:10.1007/978-3-662-46803-6_24. ISBN 978-3-662-46802-9.
- ^ Krawczyk, Hugo (2005-08-14). «HMQV: A High-Performance Secure Diffie-Hellman Protocol». In Shoup, Victor (ed.). Advances in Cryptology – CRYPTO 2005. Lecture Notes in Computer Science. Vol. 3621. Springer. pp. 546–566. doi:10.1007/11535218_33. ISBN 978-3-540-28114-6.
- ^ Naor, Dalit; Shenhav; Wool (2006). «One-Time Signatures Revisited: Practical Fast Signatures Using Fractal Merkle Tree Traversal» (PDF). IEEE. Retrieved 13 May 2014.
- ^ Barreto, Paulo S. L. M.; Biasi, Felipe Piazza; Dahab, Ricardo; López-Hernández, Julio César; Morais, Eduardo M. de; Oliveira, Ana D. Salina de; Pereira, Geovandro C. C. F.; Ricardini, Jefferson E. (2014). Koç, Çetin Kaya (ed.). A Panorama of Post-quantum Cryptography. Springer International Publishing. pp. 387–439. doi:10.1007/978-3-319-10683-0_16. ISBN 978-3-319-10682-3.
- ^ De Feo, Luca; Jao; Plut (2011). «Towards Quantum-Resistant Cryptosystems From Supersingular Elliptic Curve Isogenies» (PDF). Archived from the original on 11 February 2014. Retrieved 12 May 2014.
{{cite web}}: CS1 maint: bot: original URL status unknown (link) - ^ «Cryptology ePrint Archive: Report 2016/229». eprint.iacr.org. Retrieved 2016-03-02.
- ^ Ristic, Ivan (2013-06-25). «Deploying Forward Secrecy». SSL Labs. Retrieved 14 June 2014.
- ^ «Does NTRU provide Perfect Forward Secrecy?». crypto.stackexchange.com.
- ^ a b «Open Quantum Safe». openquantumsafe.org.
- ^ Stebila, Douglas; Mosca, Michele. «Post-Quantum Key Exchange for the Internet and the Open Quantum Safe Project». Cryptology ePrint Archive, Report 2016/1017, 2016. Retrieved 9 April 2017.
- ^ «liboqs: C library for quantum-resistant cryptographic algorithms». 26 November 2017 – via GitHub.
- ^ «openssl: Fork of OpenSSL that includes quantum-resistant algorithms and ciphersuites based on liboqs». 9 November 2017 – via GitHub.
- ^ Stebila, Douglas (26 Mar 2018). «liboqs nist-branch algorithm datasheet: kem_newhopenist». GitHub. Retrieved 27 September 2018.
- ^ «Lattice Cryptography Library». Microsoft Research. 19 Apr 2016. Retrieved 27 September 2018.
- ^ Bos, Joppe; Costello, Craig; Ducas, Léo; Mironov, Ilya; Naehrig, Michael; Nikolaenko, Valeria; Raghunathan, Ananth; Stebila, Douglas (2016-01-01). «Frodo: Take off the ring! Practical, Quantum-Secure Key Exchange from LWE». Cryptology ePrint Archive.
- ^ «NTRUOpenSourceProject/NTRUEncrypt». GitHub. Retrieved 2017-04-10.
- ^ «SIDH Library — Microsoft Research». Microsoft Research. Retrieved 2017-04-10.
- ^ Feo, Luca De; Jao, David; Plût, Jérôme (2011-01-01). «Towards quantum-resistant cryptosystems from supersingular elliptic curve isogenies». Archived from the original on 2014-05-03.
- ^ Bernstein, Daniel J.; Chou, Tung; Schwabe, Peter (2015-01-01). «McBits: fast constant-time code-based cryptography». Cryptology ePrint Archive.
- ^ «Microsoft/Picnic» (PDF). GitHub. Retrieved 2018-06-27.
- ^ «Bouncy Castle Betas».
- ^ «Open Quantum Safe».
Further reading[edit]
- Post-Quantum Cryptography. Springer. 2008. p. 245. ISBN 978-3-540-88701-0.
- Isogenies in a Quantum World
- On Ideal Lattices and Learning With Errors Over Rings
- Kerberos Revisited: Quantum-Safe Authentication
- The picnic signature scheme
External links[edit]
- PQCrypto, the post-quantum cryptography conference
- ETSI Quantum Secure Standards Effort
- NIST’s Post-Quantum crypto Project
- PQCrypto Usage & Deployment
Привет, Вы узнаете про постквантовая криптография, Разберем основные ее виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое
постквантовая криптография, криптография , настоятельно рекомендую прочитать все из категории Криптография и криптоанализ, Стеганография и Стегоанализ.
постквантовая
криптография — часть криптографии, которая остается актуальной и при появлении квантовых компьютеров и квантовых атак. Так как по скорости вычисления традиционных криптографических алгоритмов квантовые компьютеры значительно превосходят классические компьютерные архитектуры, современные криптографические системы становятся потенциально уязвимыми для криптографических атак. Большинство традиционных криптосистем опирается на проблемы факторизации целых чисел или задачи дискретного логарифмирования, которые будут легко разрешимы на достаточно больших квантовых компьютерах, использующих алгоритм Шора. Многие криптографы в настоящее время ведут разработку алгоритмов, независимых от квантовых вычислений, то есть устойчивых к квантовым атакам.
Существуют классические криптосистемы, которые опираются на вычислительно сложные задачи и имеют ряд существенных отличий от систем указанных выше, из-за чего их гораздо сложнее решить. Эти системы независимы от квантовых вычислений, и, следовательно, их считают квантово-устойчивыми (quantum-resistant), или «постквантовыми» криптосистемами.
Постквантовая криптография в свою очередь отличается от квантовой криптографии, которая занимается методами защиты коммуникаций, основанных на принципах квантовой физики.
1. Основы криптографии ( повторение)
Что такое криптография и для чего она вообще нужна? Скажем, Алиса и Боб хотят обменяться сообщением, да так, чтобы его содержание оставалось в секрете. Очевидно, что у каждой из сторон должен быть свой ключ. И на этом этапе можно выделить два подвида криптосистем.
К первому из них относятся симметричные криптосистемы. Здесь один ключ может быть легко вычислен из другого, а зачастую они и вовсе совпадают. Значимыми плюсами таких криптосистем являются простота реализации и высокая скорость работы за счет использования более простых операций. Однако, если один из ключей будет скомпрометирован, всякая попытка защитить секретную информацию потеряет свой смысл.
Такая проблема изящно решается в асимметричных криптосистемах с помощью специальных алгоритмов. Однако тут мы сталкиваемся с трудоемкостью операций, что может быть неэффективно для большого объема данных. В таких криптосистемах нужно очень постараться, чтобы из одного ключа вычислить другой, и, пока чей-то компьютер не обладает огромной мощью темной стороны, можно быть относительно спокойными за секретность защищаемых данных.
Интересная многоходовочка… Ну а как она реализуется, спросит пытливый %username%? Все дело в так называемых односторонних функциях. Пусть есть функция y=f(x). По известному аргументу x вычислить значение функции y проще, чем захватить Вестерос с тремя драконами и армией безупречных. Однако вычисление аргумента x по известному значению функции y является довольно-таки трудоемкой задачей.
Наиболее известными кандидатами в односторонние функции являются задача факторизации числа, которая состоит в разложении числа на простые множители, и задача дискретного логарифмирования, которая заключается в поиске неизвестного k по известным значениям y и g, которые удовлетворяют: y=gk. Первая, например, применяется в широко известной криптосистеме RSA, а вторую можно встретить в схеме установления ключа Диффи-Хэллмана.
Однако с учетом стремительного, как полет дракона, роста производительности вычислительных устройств, возникает необходимость в увеличении длины ключа, ну а это может стать критическим фактором для устройств с ограниченной мощностью…Эх, было бы так здорово, появись такая структура, которая бы позволила сократить размер ключа при таком же уровне стойкости… И, к счастью, она существует! Название сему чуду – эллиптическая кривая.
2 Введение в постквантовую криптографию и закат RSA
RSA, эллиптические кривые, квантовый компьютер, изогении… На первый взгляд, эти слова напоминают какие-то заклинания, но все куда проще сложнее, чем кажется!
Необходимость перехода к криптографии, устойчивой к атаке на квантовом компьютере, уже официально анонсирована NIST и NSA, из чего вывод довольно-таки простой: пора вылезать из зоны комфорта!
А значит, стоит отходить от старой доброй RSA и даже, вероятно, от полюбившихся многим эллиптических кривых и узнавать новые, не менее интересные примитивы, способные обезопасить конфиденциальную информацию.
Чтобы разобраться в тонкостях криптографии на эллиптических кривых, проследить новомодные веяния постквантовой криптографии и даже прикоснуться к ней с помощью библиотеки Microsoft SIDH, добро пожаловать под кат, %username%!
3. Введение в использование эллиптических кривых
Эллиптическая кривая — над полем — неособая кубическая кривая на проективной плоскости над
(алгебраическим замыканием поля
), задаваемая уравнением 3-й степени с коэффициентами из поля
и «точкой на бесконечности».
. Неособой ее называют, потому что ко всем ее точкам можно однозначно провести касательную. Ну раз это кривая кубическая, то и задаваться она должна уравнением третьей степени, которое в обобщенной форме Вейерштрасса выглядит следующим образом:
y2+a1xy+a3y=x3+a2x2+a4x+a6
Однако на практике такую форму кривой можно встретить нечасто. Различают формы Лежандра, Монтгомери, Гессе и т.д. Использование той или иной формы может увеличить эффективность операций над точками эллиптической кривой. Например, в форме Монтгомери есть возможность выполнять умножение точки на число за фиксированное время благодаря алгоритму лестницы Монтгомери.
Наверняка многие сталкивались с формой Вейерштрасса, ее называют канонической для полей с характеристикой charK≠2,3:
E(K):y2=x3+ax+b
Важной характеристикой эллиптической кривой является ее дискриминант, который для формы Вейерштрасса вычисляется так:Δ=4a3+27b2.
Дискриминант не должен быть равен нулю, иначе кривая уже не будет эллиптической, так как будут существовать точки перегиба, как на кривой y2=x3−3x+2 на рисунке справа.
Наверняка многим знакомо изображение эллиптической кривой, которое можно увидеть на рисунке слева. Здесь кривая вида y2=x3−3x+5 задана над полем рациональных чисел.
Однако, при использовании рациональных чисел возникает сложность с их округлением, и, как следствие, с неоднозначностью операций зашифрования и расшифрования. Поэтому в криптографии эллиптические кривые задаются над конечным полем, где координаты точек – это элементы поля. График кривой, конечно, потеряет свою былую привлекательность, плавные линии заменятся на точки, но мы же любим эллиптические кривые далеко не за это!
Нельзя не упомянуть еще одну характеристику эллиптических кривых, которая (СПОЙЛЕР!) еще одарит читателей своим присутствием в статье. Речь идет о j−инварианте, постоянной величине. Его вычисление для эллиптической кривой в форме Вейерштрасса тоже не обладает устрашающим воздействием на организм:j=17284a34a3+27b2
Свойства группы
Важным моментом в криптографии на эллиптических кривых является то, что точки эллиптической кривой с абстрактной бесконечно удаленной точкой образуют абелеву группу. Возьмем в качестве групповой операции сложение, тогда группа — это такая алгебраическая структура, которая обладает следующими свойствами:
- Замкнутость означает, что результат сложения элементов группы тоже является элементом группы. Переведем в термины эллиптической кривой: при сложении точек эллиптической кривой получается точка, принадлежащая этой же кривой.
Как видно из рисунков сверху, геометрический смысл сложения точек на эллиптической кривой состоит в следующем: необходимо провести секущую через складываемые точки и отразить точку пересечения этой прямой с эллиптической кривой относительно оси Ox.
- Ассоциативность означает независимость результата сложения от изменения порядка действия.
- В группе должен существовать нейтральный элемент. Результат сложения любого элемента группы g и нейтрального будет равен тому же элементу.В эллиптических кривых роль нейтрального элемента играет бесконечно удаленная точка: P∞:P∞+P=P+P∞=P
- К каждому элементу должен существовать обратный к нему (относительно основной операции). При сложении элемента группы и обратного к нему получаем нейтральный элемент.
- Свойство коммутативности нам знакомо еще из школьной математики: от перестановки слагаемых сумма не меняется. Именно данное свойство и делает группу абелевой.
Пара слов о стойкости
Теперь поговорим немного о стойкости криптосистем, основанных на задаче дискретного логарифмирования. Пусть G – конечная циклическая группа, то есть, каждый ее элемент представим в виде степени одного-единственного элемента — образующей g: =G={1,g2,g3,…,gq−1}.
В зависимости от выбора группы G существуют различные методы решения задачи дискретного логарифмирования. Так, для решения задачи дискретного логарифмирования в конечном поле, на общее несчастье существуют не только универсальные алгоритмы (метод Полига-Хеллмана, ρ-метод Полларда и др.), которые имеют экспоненциальную сложность, но и специальные, имеющие субэкспоненциальную сложность (метод базы разложения, метод решета числового поля).
Если же в качестве образующей группы G взять точку эллиптической кривой, то криптожуликам придется довольствоваться лишь универсальными алгоритмами . Об этом говорит сайт https://intellect.icu . Поэтому криптография на эллиптических кривых «балует» пользователей меньшей длиной ключа.
Однако не все эллиптические кривые способны обеспечить высокий уровень стойкости в криптографических протоколах. Первую опасность представляют суперсингулярные кривые . Их преимущество состоит в легкости вычисления числа точек, в отличие от несуперсингулярных кривых. Есть немало факторов, по которым можно отличить суперсингулярную кривую от несуперсингулярной, однако в данной статье не будем заострять на этом внимание.
Данные кривые уязвимы к MOV атаке, которая позволяет сводить вычисление задачи дискретного логарифмирования в группе точек эллиптической кривой над полем Fq к задаче дискретного логарифмирования в конечном поле Fqk. Учитывая, что длина ключа в криптографии на эллиптических кривых меньше, и что для суперсингулярных кривых значение k не является большим, реализация данной атаки проходит крайне успешно для злоумышленника.
Ну так в чем же проблема? Используем подходящие эллиптические кривые и радуемся жизни! Но не тут-то было…
4 Алгоритмы постквантовой криптографии
Постквантовые криптографические конструкции способны спасти криптографический мир от квантовых атак. Хотя квантовый компьютер и уничтожит большинство традиционных алгоритмов (RSA, DSA, ECDSA), но сверхбыстрыми вычислениями не получится полностью избавиться от криптографии, так как постквантовая криптография, в основном, сосредоточена на пяти различных подходах, решающих проблему квантовых атак.
Криптография, основанная на хеш-функциях
Классическим примером является подпись Меркла с открытым ключом на основе хеш-дерева, Ральф Чарльз Меркл предложил этот алгоритм цифровой подписи в 1979 году, как интересную альтернативу цифровым подписям RSA и DSA. Основной недостаток схемы Меркла состоит в том, что для любого открытого ключа на основе хеш-функции существует ограничение на количество подписей, которые могут быть получены из соответствующего набора закрытых ключей. Этот факт и снижал уровень интереса к подписям такого типа, пока не появилась потребность в криптографии, устойчивой к воздействию квантовых компьютеров.
Криптография, основанная на кодах исправления ошибок
Является одним из наиболее перспективных кандидатов на пост-квантовые криптосистемы. Классическим примером является схемы шифрования McEliece и Niederreiter.
Криптография, основанная на решетках
Классическим примером схем шифрования являются Ring-Learning with Errors или более старые NTRU и GGH .
Криптография, основанная на многомерных квадратичных системах
Одной из самых интересных схем является подпись с открытым ключом Жака Патарина HFE, предложенная им в 1996 году, как обобщение предложений Matsumoto и Imai.
Шифрование с секретным ключом
Ярким примером является шифр Rijndael, предложенный в 1998 году, впоследствии переименованный в AES (Advanced Encryption Standard).
Шифрование с использованием суперсингулярной изогении
Это аналог протокола Диффи-Хеллмана, основанный на блуждании в суперсингулярном изогенном графе, позволяющий двум и более сторонам получить общий секретный ключ, используя незащищенный от прослушивания канал связи.
5 Примеры криптографических атак на RSA
В 1978 году документ, опубликованный разработчиками криптографического алгоритма с открытым ключом RSA (аббревиатура от фамилий Rivest, Shamir и Adleman), упоминал новый алгоритм Ричарда Шреппеля «linear sieve», который факторизовал любой RSA модуль } длины
бит, используя
простых операций. Таким образом, для того чтобы этот алгоритм требовал по меньшей мере
простых операций, необходимо выбирать
по крайней мере не меньше чем
бит. Так как
означает, что что-то сходится к {displaystyle 0,5}
при
, то для выяснения правильного размера {displaystyle n}
при конечном {displaystyle b}
требуется более тщательный анализ скорости «linear sieve».
В 1988 году Джон Поллард ] предложил новый алгоритм факторизации, который называется Общий метод решета числового поля. Этот алгоритм факторизовал RSA-модуль размерности
бит, используя
простых операций. Таким образом, требуется выбирать
не меньше чем
бит, чтобы алгоритму потребовалось как минимум
простых операций.
С 2008 года самые быстрые алгоритмы факторизации для классических компьютерных архитектур используют по меньшей мере простых операций. Были некоторые улучшения в значениях
и в деталях
, но не трудно догадаться, что {displaystyle 1/3}
оптимально, и что выбор модуля
длиной примерно равной
бит, позволит сопротивляться всем возможным атакам на классических компьютерах.
В 1994 году Питер Шор предложил алгоритм, который факторизовал любой RSA-модуль размерности
(точнее
) кубитовых операций на квантовом компьютере размера порядка
кубит (и небольшого количества вспомогательных вычислений на классическом компьютере). Пользуясь алгоритмом Шора, необходимо по крайней мере выбирать модуль {displaystyle n}
битовым размером не меньше чем
бит, что является слишком большим числом для любого интересующего нас {displaystyle b}
.
6 Практические применения криптографических конструкций
Примеров алгоритмов, устойчивых к квантовым атакам, крайне мало. Но несмотря на больший уровень криптографической устойчивости, постквантовые алгоритмы неспособны вытеснить современные криптосистемы (RSA, DSA, ECDSA и др.).
Рассмотрим нападения на криптосистему с открытым ключом, а именно на алгоритм шифрования McEliece, который использует двоичные коды Гоппы[en]. Первоначально Роберт Мак-Элис ] представил документы, в которых коды длиной {displaystyle n} взламываются за
простых операций. Таким образом, требуется выбирать
не меньше чем
бит, чтобы алгоритму потребовалось как минимум
простых операций. Несколько последующих работ сократили количество операций атаки до
, но
значительно меньше
, если {displaystyle n}
большое. Поэтому улучшенные атаки до сих пор используют
простых операций. Что касается квантовых компьютеров, то их использование приведет лишь к уменьшению константы {displaystyle 0,5}
, что совсем незначительно сократит количество операций, необходимых для взлома этого алгоритма.
Если система шифрования McEliece так хорошо защищена, то почему она не приходит на смену RSA? Все дело в эффективности — в частности, в размере ключа. Открытый ключ McEliece использует примерно ≈
бит, в то время как открытому ключу RSA достаточно около
бит. Если
бит для McEliece, будет меньше
бит для RSA, но реальные уровни безопасности, такие как
, позволяют RSA иметь открытый ключ в несколько тысяч бит, в то время как для McEliece размер ключа приближается к миллиону бит.
7 Квантовая угроза
В последнее время широкую популярность получают квантовые вычисления. Если в классическом компьютере наименьшая единица информации представляется битом, который может принимать значение либо 0, либо 1 в одно время, то в квантовом эту роль выполняют кубиты. Их особенность состоит в том, что кубит может находиться и в состоянии 0, и в состоянии 1 одновременно. Это и дает квантовым компьютерам их превосходящую вычислительную мощь. Например, если мы рассматриваем четыре бита информации, то из всевозможных 16 состояний мы можем выбрать лишь одно в один момент времени. 4 кубита же могут находиться в 16 состояниях одновременно, то есть в суперпозиции, и данная зависимость растет экспоненциально с каждым новым кубитом.
Если в классическом компьютере логические элементы получают на вход биты информации, а на выходе выдают однозначно определенный результат, то в квантовом компьютере в качестве логического элемента берется так называемый квантовый гейт (quantim gate), который манипулирует значением целой суперпозиции.
Важное явление, свойственное кубитам, – это запутанность. Например, имеем два запутанных кубита. Измерение состояния одного из них поможет узнать информацию о состоянии его пары без необходимости какой-либо проверки.
Следует отметить, что квантовый компьютер — это не замена привычным нам классическим, так как они быстрее лишь в выполнении вычислительных операций, где необходимо использовать всевозможные суперпозиции. Так что для просмотра видео с котиками использовать такую машину совсем нецелесообразно.
С одной стороны, появление квантового компьютера — это круто. Серьезно. Во многих сферах науки такая машина принесет немало пользы (например, при моделировании), однако для криптографии такой значимый прорыв будет критичен. А все потому, что в 1994 году Питер Шор предложил квантовый алгоритм, который позволяет разложить число не за стотыщмильонов лет, а за вполне обозримое время.
7.1 Об алгоритме Шора
Модификация данного алгоритма позволяет решить и задачу дискретного логарифмирования. Обобщенно метод Шора состоит в сведении сложновычислимой на классическом компьютере задачи к вычислению порядка некой функции. Если рассматривать разложение числа на множители, или задачу факторизации, то в качестве той самой функции берется f(x)=ax(modN), где N− число, которое раскладывается, а a−специально подобранное значение, взаимно простое с N.Далее по ходу алгоритма находится период функции w, который удовлетворяет соотношению:f(x+w)=f(x) и, как следствие, выполняется aw=1(modN). По найденном периоду вычислить собственный делитель числа N можно с помощью алгоритма Евклида: gcd(aw2,N).
Для того, чтобы решить задачу дискретного логарифмирования, то есть, найти такое k по данным y=gk, необходимо вычислить порядок другой функции, а именно: f(x1,x2)=gx1yx2, где g− образующая группы c числом элементов, равным q. Период функции представляется парой чисел (w1,w2): f(w1+x1,w2+x2)=f(x1,x2). Тогда решение задачи дискретного логарифмирования будет иметь вид: k=−w1w2(modq).
Таким образом, в методе Шора можно выделить квантовую и классическую часть, причем задача квантовой части алгоритма состоит в отыскании периода функции с использованием метода суперпозиции.
Неудивительно, что существование подобных алгоритмов и тенденция к разработке квантовых компьютеров подтолкнули специальные организации к размышлениям. Агентством национальной безопасности США, например, еще в 2015 году был анонсирован план перехода к алгоритмам, устойчивым к атаке на квантовом компьютере. А в 2016 году NIST США официально объявил о о запуске конкурса заявок на разработку алгоритмов постквантовой криптографии.
Постквантовая криптография не ограничивается одним примитивом, на самом деле, на данный момент рассматриваются несколько кандидатов. В их число могут, например, входить быстрые криптографические протоколы на решетках, схемы на хэш-функциях (например, подпись Меркла) и криптосистемы, основанные на некоммутативной алгебре (например, на группе кос). Свой выбор мы остановили на альтернативе, тесно связанной с эллиптическими кривыми (ведь мы их так любим!), а именно, с изогениями.
7.2 изогения – рациональное отображение и его использование в криптографии
Начнем с понятия: изогения – это рациональное отображение, переводящее точки одной эллиптической кривой в точки изогенной кривой, оставляя неподвижной бесконечно удаленную точку. Пусть имеем две изогенные эллиптические кривые E1 и E2. Изогенными они называются, если они заданы над одним полем и имеют одинаковое число точек.
Так вот, изогения — это, по сути, небольшой ВЖУХ, который берет точку кривой E1 на вход, а на выходе выдает точку кривой E2. Ядром изогении называется множество точек на кривой E1, которые переходят в бесконечно удаленную точку кривой E2.
Для каждой изогении существует единственная дуальная изогения, выполняющая обратное преобразование. То есть, если изогения имеет следующий вид: 
Если перемножить изогению и дуальную к ней, получим точку кривой E2, умноженную на целое число l, которую называют степенью изогении. Изогении простых степеней могут задавать перестановки на множестве j−инвариантов изогенных кривых. А последовательное наложение графов изогенных эллиптических кривых позволяет получить просто космически красивую звезду изогенных кривых, как на рисунке ниже.
Возможность применения изогений для построения криптосистем была предложена сравнительно недавно. В 2003 году автором E. Teske была опубликована работа, где изогении использовались в схеме с возможностью депонирования ключей. В 2006 году А. Г. Ростовцевым и А. Столбуновым схема шифрования Эль-Гамаля была адаптирована под изогении эллиптических кривых. В том же 2006 году для построения хэш-функций было предложено использовать графы изогенных суперсингулярных кривых. Важным и, можно сказать, переломным моментом в исследовании изогений является работа, опубликованная в 2010 году, где предлагается квантовый алгоритм, решающий задачу нахождения изогений несуперсингулярных кривых за субэкспоненциальное время. С этого момента исследования стали больше ориентированы на суперсингулярные кривые. Так, в сети уже можно найти схемы шифрования с открытым ключом, доказательства с нулевым разглашением, схему неоспоримой подписи и подписи вслепую.
7.3. Microsoft SIDH
Компания Microsoft тоже не осталась в стороне и в 2016 году выпустила библиотеку SIDH(Supersingular Isogeny Key Exchange) с открытым исходным кодом. Одним из преимуществ данной библиотеки является возможность использования эллиптических кривых в форме Монтгомери, которые защищают от атак по времени.
SIDH реализована на языке C и поддерживает использование Microsoft Visual Studio на OC Windows и LNU GCC и clang на OC Linux. В библиотеке представлена реализация базовых арифметических функций с возможностью поддержки различных платформ, включая x64, x86 и ARM. Большим плюсом к производительности является оптимизированная реализация операций на эллиптических кривых.
В библиотеке реализован протокол разделения ключа Диффи-Хеллмана на изогениях суперсингулярных кривых.
Эта схема была предложена авторами Jao и DeFeo. Упрощенно ее можно описать следующим образом. В качестве параметров криптосистемы используется общеизвестная суперсингулярная кривая E0 и зафиксированные на ней точки PA,QA,PB,QB. Для удобства за ходом протокола можно следить на рисунке ниже.
Пусть Алиса хочет разделить с Бобом не жизнь, а закрытый ключ. Для этого она генерирует случайные числа mA,nA и строит изогению ϕA:E0→EA, где ядро задается как .
Боб выполняет те же действия, но только строит уже изогению , где в качестве ядра выбирается .
Изогении ϕA и ϕB являются секретными и кому попало не передаются. Однако, и Боб, и Алиса могут без каких-либо последствий разделить точки на своих изогенных кривых, к тому же, переданы могут быть и сами кривые. Так и происходит на самом деле. Данный этап обозначен на рисунке пунктирной линией. Алиса передает Бобу точки ϕA(PB) и ϕA(QB), и саму кривую EA. Боб делает тоже самое: передает Алисе точки ϕB(PA) и ϕB(QA и кривую EB.
А это вообще законно?! Можешь быть спокоен, %username%, зная обе изогенные кривые, злоумышленник не сможет вычислить саму изогению.
Итак, Алиса и Боб обменялись данными, теперь подходим к завершающему и невероятно красивому этапу, а именно, к получению общего ключа. Зная образы точек PA и QA на кривой EB и случайные числа mB и nB, Боб сможет легко построить изогению ϕA′, а Алиса, обладающая тем же объемом информации, сможет построить изогению ϕB′. Изящное решение заключается в том, что изогении ϕA′ и ϕB′ приведут наших собеседников к кривой EAB, и в качестве ключа может быть взят ее j−инвариант.
Microsoft существенно упростила жизнь реализацией базовых функций, которые освобождают от кодинга вышеописанных шагов алгоритма. Перед тем, как реализовать схему разделения ключа, необходимо инициализировать структуру, в которой содержатся параметры криптосистемы:
CurveIsogeny = SIDH_curve_allocate(CurveIsogenyData);
if (CurveIsogeny == NULL) {
Status = CRYPTO_ERROR_NO_MEMORY;
goto cleanup;
}
Status = SIDH_curve_initialize(CurveIsogeny, &random_bytes_test, CurveIsogenyData);
if (Status != CRYPTO_SUCCESS) {
goto cleanup;
}
Сама структура:
typedef struct
{
CurveIsogeny_ID CurveIsogeny;
unsigned int pwordbits;
unsigned int owordbits;
unsigned int pbits;
uint64_t prime[MAXWORDS_FIELD];
uint64_t A[MAXWORDS_FIELD];
uint64_t C[MAXWORDS_FIELD];
unsigned int oAbits;
uint64_t Aorder[MAXWORDS_ORDER];
unsigned int oBbits;
unsigned int eB;
uint64_t Border[MAXWORDS_ORDER];
uint64_t PA[2*MAXWORDS_FIELD];
uint64_t PB[2*MAXWORDS_FIELD];
unsigned int BigMont_A24;
uint64_t BigMont_order[BIGMONT_MAXWORDS_ORDER];
uint64_t Montgomery_R2[MAXWORDS_FIELD];
uint64_t Montgomery_pp[MAXWORDS_FIELD];
uint64_t Montgomery_one[MAXWORDS_FIELD];
} CurveIsogenyStaticData;
Чтобы Алисе и Бобу обменяться ключами, достаточно вызвать пару функций, которые не обязывают знать того, что же творится «под капотом». Генерация ключей происходит с помощью функций:
Status = KeyGeneration_A(PrivateKeyA,PublicKeyA, CurveIsogeny);
и
Status = KeyGeneration_B(PrivateKeyB,PublicKeyAB CurveIsogeny);
Алиса и Боб обмениваются вычисленными открытыми ключами и находят общий ключ:
Status = SecretAgreement_A(PrivateKeyA, PublicKeyB, SharedSecretA, false, CurveIsogeny);
и
Status = SecretAgreement_B(PrivateKeyB, PublicKeyA, SharedSecretB, false, CurveIsogeny);
Среди функций в библиотеке можно выделить и базовые арифметические, которые помогут в реализации своих протоколов. Это, например, j_inv, вычисляющая j-инвариант эллиптической кривой, inv_3_way, находящая значение мультипликативно обратного, удвоение точки и сложение точек – xDBLADD, утроение точки – xTPL и т.д. С полным описанием вы можете ознакомиться в публикации.
Выводы
Безусловно, пока сложно судить о необходимости постквантовой криптографии, когда мощного квантового компьютера, по сути, и нет… Однако суета в NSA и NIST не могут не наводить на подозрения. О реальных мотивах такой спешки нам остается только догадываться. В любом случае, никогда не помешает перестраховаться и начать изучение нового и интересного направления в криптографии, тем более, если это вполне осуществимо на практике.
См. также
- Криптография на решетках
- Алгоритм Шора
Надеюсь, эта статья об постквантовая криптография, была вам интересна и не так слона для восприятия как могло показаться, удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое постквантовая криптография, криптография
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Криптография и криптоанализ, Стеганография и Стегоанализ
О том, что такое постквантовая криптография, от каких киберугроз она может защитить и почему о ней все чаще говорят в мире
Об авторе: Антон Гугля, руководитель QApp — компании-разработчика отечественных решений кибербезопасности на основе постквантовых алгоритмов шифрования.
Развитие квантовых вычислений создает беспрецедентную угрозу для современных методов защиты данных. Государственная, профессиональная и коммерческая тайны, финансовые и персональные данные — все это в два счета перестанет быть конфиденциальным, как только злоумышленник получит доступ к мощным квантовым компьютерам. Однако на помощь классической криптографии приходит новая — постквантовая. Что такое постквантовые алгоритмы и почему готовиться к новому типу кибератак надо уже сейчас.
Зачем требуется шифрование
О какой бы криптографии ни заходила речь, окружающие зачастую считают, что это их мало касается. Крупный бизнес — да, а вот нас с вами — едва ли. Конечно, это не так. Покупки в интернет-магазинах, переписки в мессенджерах и социальных сетях, интернет-серфинг по пути на работу — все эти активности неразрывно связаны с шифрованием данных. Простой пример — защищенное соединение https, которое преобразует передаваемые в сети данные в зашифрованный формат и не дает посторонним прямой доступ к конфиденциальной информации.
Современная классическая криптография может быть симметричной и асимметричной. В симметричной для шифровки и расшифровки сообщения используется всего один ключ: отправитель делится им с получателем, и тот успешно применяет его для чтения зашифрованных данных. Однако если ключ кто-то перехватит, вся эффективность защиты сводится к нулю. В асимметричной криптографии присутствуют уже два ключа: открытый и закрытый.
Первый необходим, чтобы зашифровать данные, второй — чтобы расшифровать. Несмотря на то, что оба ключа связаны между собой математической функцией, без закрытого ключа доступ к данным не получить: ни привычные нам персональные компьютеры, ни суперкомпьютеры справиться с этой задачей не смогут из-за недостатка вычислительных мощностей.

Квантовая угроза
Между тем возможность взломать асимметричный шифр существует: алгоритм, способный справиться с этой задачей, еще в 1994 году разработал ученый Питер Шор. Реализовать этот алгоритм позволяет квантовый компьютер. В отличие от обычных устройств, работающих на основе полупроводниковых технологий, мощность квантовых растет экспоненциально. Поэтому их возможности значительно превосходят любые инструменты, которые сегодня используют хакеры.
Современные квантовые компьютеры пока не обладают мощностью достаточной для взлома систем на основе асимметричного шифрования. Но с начала 2000-х такие технологические гиганты, как IBM, Google, Intel ведут разработки по развитию квантовых вычислений, что приближает нас к кибератакам нового типа. По мнению большинства экспертов, первые случаи подобных атак могут быть зафиксированы до 2030 года. Впрочем, аналитики McKinsey предостерегают, что финансовый и государственный секторы, а также страховая индустрия могут столкнуться с ними уже в ближайшие два года.
Это подводит нас к понятию квантовой угрозы — риска, что злоумышленники могут уже сегодня сохранять конфиденциальные данные, зашифрованные асимметричной криптографией, чтобы дешифровать их в будущем при первой появившейся возможности. Неважно каким образом хакеры получат доступ к квантовым устройствам — будет ли это социальный инжиниринг, облачная платформа квантовых вычислений или трудоустройство в компанию-разработчика квантовых компьютеров. Важно лишь то, что все накопленные данные, актуальные на тот момент, будут расшифрованы и приведут к колоссальным потерям. Поэтому защищать их необходимо уже сегодня.
К таким данным с длинным жизненным циклом относятся в том числе персональные данные клиентов банков и других финансовых организаций, медицинских учреждений и мобильных операторов, а также информация, представляющая коммерческую и государственную тайны.

Постквантовое шифрование
В ответ на квантовую угрозу специалисты по информационной безопасности стали разрабатывать новые методы защиты. Самым оптимальным по стоимости и скорости интеграции стали решения на основе постквантовых алгоритмов. Такие алгоритмы строятся на сложных математических задачах, при решении которых квантовые компьютеры не получают вычислительного преимущества. Стойкость постквантового шифрования гарантируется математическими доказательствами секретности каждого из алгоритмов — все они проверяются мировым научным математическим сообществом.
В частности, это алгоритмы, основанные на линейных кодах, теории решеток и хеш-функциях. Первый тип (code-based) основан на гипотезе, что декодировать случайный линейный код очень сложно. Первый алгоритм такого типа появился еще в 1978 году — это была система McEliece, одна из первых систем с открытым ключом. В тот момент об атаках с использованием квантового компьютера не было и речи, однако после появления алгоритма Шора, способного легко взломать используемое повсеместно шифрование, криптографы-исследователи вновь заинтересовались алгоритмом McEliece.
Другой тип схем постквантовой криптографии — алгоритмы на основе теории решеток. Такие схемы хорошо изучены и легко применимы на практике, в частности, их использует IBM в своих приложениях безопасности.
В постквантовом шифровании применяется и один из самых популярных криптографических инструментов — хеш-функция. Хеширование — это преобразование произвольного объема данных в уникальный набор символов фиксированной длины, расшифровать который очень сложно. А постквантовые алгоритмы с использованием хеш-функции делают декодирование сообщения невозможным, во всяком случае, всеми известными методами. Хеш-функция может лежать в основе электронной подписи, в частности, эта модель сейчас прорабатывается в России.

Пора применять
Над интеграцией и пилотированием криптографических алгоритмов в свои продукты уже работают такие гиганты рынка, как Microsoft, Google, Verizon, Thales, Toshiba, Amazon, Cloudflare.
Так, весной 2022 года IBM представила новое поколение мейнфреймов (универсальных высокопроизводительных серверов) z16, которые используют для защиты данных постквантовую криптографию. z16 оснащен ускорителем на базе искусственного интеллекта, что позволяет быстро обрабатывать огромные объемы информации. Это критично, в частности, для финансовых компаний и медицинских организаций, то есть тех, чьи данные обладают долгим циклом жизни. Именно поэтому для их защиты IBM применяет продукты в области постквантового шифрования, построенные на теории решеток.
В то же время южнокорейский мобильный оператор LG Uplus (принадлежит LG Group) выпустил коммерческий сервис для проводной и беспроводной связи, устойчивый к атакам с помощью квантового компьютера. А уже осенью LG Electronics объявила, что будет использовать этот метод защиты для ряда задач, в том числе в технологии V2X (vehicle to everything) — обмена данными между автомобилями и объектами дорожной инфраструктуры.
В октябре 2022 года компания Cloudflare объявила о запуске поддержки постквантовой криптографии для всех веб-сайтов и API, обслуживаемых через ее сеть. По сути это делает доступным квантовое шифрование для 19% мировых веб-ресурсов. Это наглядно демонстрирует, насколько критично к квантовой угрозе относится одна из крупнейших сетевых инфраструктур.
В России работа по пилотированию постквантовых продуктов также идет полным ходом: в июне 2022 года отечественные специалисты подтвердили совместимость постквантового шифрования с российскими процессорами Baikal-M, в октябре — с процессорами «Эльбрус». Первой в стране финансовой организацией, пилотировавшей постквантовые алгоритмы, стал Газпромбанк — в 2022 году он обеспечил квантово-устойчивую защиту host-to-host соединения при проведении финансовых поручений.

Финальный штрих
На сегодняшний день постквантовая криптография находится на стадии стандартизации. В США этот процесс курирует Национальный институт стандартов и технологий (NIST). На конкурсной основе эксперты выбирают наиболее квантово-устойчивые алгоритмы, которые лягут в основу стандартов постквантового шифрования. В 2022 году институт выбрал четыре алгоритма — они станут частью постквантового криптографического стандарта, окончательная доработка которого ожидается примерно через два года. В то же время Белый дом обязал госструктуры уже к маю 2023 года совершить всецелую подготовку к переходу на постквантовые алгоритмы.
В России разработкой стандартов постквантовых алгоритмов занялись в 2019 году под руководством Технического комитета 26, куда входят представители государственных и коммерческих организаций. Ожидается, что отечественные стандарты будут утверждены к 2024–2025 году. Рынок вступил в фазу активного формирования, а значит уже в ближайшие один-два года число пилотных проектов мирового уровня вырастет в разы.
То, как могут повлиять на технологии криптографии и всей отрасли, базирующейся на их использовании, те новые возможности, которые могут открыться благодаря доступности квантовых вычислений, рассматривает Игорь Голдовский, директор Департамента инноваций, главный архитектор АО НСПК. Как и в своих предыдущих материалах, он выступает в качестве независимого эксперта в области платежных технологий, с чьим богатым опытом и всесторонней профессиональной экспертизой в области электронных платежей мы продолжаем знакомить наших читателей.
Предыдущие материалы: 1, 2.
Сегодня в СМИ, в том числе в профессиональных изданиях, периодически появляются материалы, посвященные вопросам создания и применения квантовых компьютеров. Все сходятся в том, что сегодняшние квантовые компьютеры, имеющие память в диапазоне от 50 до 100 кубитов, оказать заметного влияния на нашу повседневную жизнь не могут. Нужны машины, обладающие хотя бы несколькими тысячами кубитов памяти и работающие с невысокой вероятностью ошибки — не выше 0,5% на один кубит.
Никто не знает точного времени появления квантовых компьютеров с такими параметрами. Некоторые авторитетные эксперты утверждают, что это может случиться уже в 20-е годы нашего столетия. Другие специалисты говорят о том, что на достижение такого результата могут уйти десятилетия.
Не существует и ясного понимания спектра задач, которые могут успешно решаться с использованием квантовых компьютеров и непосильны для обычных компьютеров. На сегодняшний день можно уверенно говорить о следующих задачах, при решении которых преимущества квантовых компьютеров очевидны:
- задачи факторизации целых чисел и логарифмирования в конечном поле (о них будет сказано ниже), при решении которых квантовые компьютеры дают экспоненциальное ускорение в сравнении с классическими компьютерами. Решение этих задач лежит в основе практически всех применяемых алгоритмов асимметричного шифрования;
- задачи полного перебора: квантовый компьютер позволяет получить здесь квадратичное ускорение, что, например, потребует увеличения размера ключей в симметричных алгоритмах шифрования;
- задачи моделирования физических и химических систем. Грубо говоря, квантовый вероятностный характер вычислений позволяет параллельно моделировать различные состояния подобных систем.
Цель настоящей статьи — проанализировать угрозы для используемых сегодня криптографических схем от ожидаемого в недалеком будущем появления квантовых компьютеров производительностью в несколько тысяч кубитов, а также рассказать о новых перспективных криптографических методах для минимизации влияния квантовых технологий на криптостойкость средств защиты информации.
Что можно и что нельзя взломать с помощью квантовых вычислений?
Как будет рассказано ниже, для квантовых компьютеров были придуманы алгоритмы (алгоритмы Шора и Гровера (Shor Grover)), оказывающие существенное влияние на криптостойкость сегодняшних криптографических алгоритмов [Circuit for Shor’s algorithm using 2n+3 qubits. Stephane Beauregard, 2003; Shor’s discrete logarithm quantum algorithm for elliptic curves. John Proos, Christof Zalka, 2008]. В частности, наиболее широко используемые на практике алгоритмы асимметричного шифрования RSA, DSA, ECDSA, EdDSA, EC-SDSA перестают быть криптостойкими и взламываются (находится секретный ключ) за полиномиальное от размера публичного ключа время. Это утверждение верно для любых алгоритмов асимметричного шифрования, криптостойкость которых базируется на трудоемкости решения математических задач факторизации (разложения числа на простые сомножители) и дискретного логарифмирования в конечном поле или на множестве точек эллиптической кривой. Другими словами, все массово используемые алгоритмы асимметричного шифрования требуется менять на алгоритмы, криптостойкость которых базируется на трудоемкости решения неких иных математических задач!
Последствия от появления квантовых компьютеров для алгоритмов симметричного шифрования и хэш-функций не столь катастрофичны. Например, ниже будет показано, что криптостойкость любого симметричного алгоритма шифрования при использовании квантового компьютера эквивалентна криптостойкости того же алгоритма при использовании классического компьютера, но с увеличенной в два раза длиной ключа шифрования. Другими словами, в случае симметричных алгоритмов шифрования можно просто удвоить длину ключа, чтобы добиться прежней криптостойкости, не меняя при этом криптографического алгоритма.
Конечно, увеличение длины ключа приведет к увеличению времени шифрования. Но это естественное развитие событий: растет производительность компьютеров и их количество, а значит, растут вычислительные ресурсы для проведения атак. Чтобы от них защититься, нужно увеличивать размер симметричного ключа. Факт грядущего появления квантовых компьютеров лишь скачкообразно ускоряет этот процесс.
В то же время существуют алгоритмы шифрования, которые «ломаются» с помощью квантовых алгоритмов за полиномиальное время. В качестве примера можно привести варианты алгоритма DES: 2K-DES (выполняет 64 раунда шифрования 96 битным ключом, который представляется в виде двух 48 битных половинок, поочередно используемых в раундах алгоритма) и 4K-DES (то же количество раундов выполняется с уже 192 битным ключом, который представляется в виде четырех поочередно используемых 48 битных частей). С помощью квантового алгоритма Саймона (Simon) ключи этих алгоритмов находятся за полиномиальное время.
Следует отметить, что эти алгоритмы относительно просто вскрываются и с помощью классических компьютеров с использованием так называемой сдвиговой атаки, изобретенной Алексом Бирюковым (Alex Biryukov) и Дэвидом Вагнером (David Wagner). Для вскрытия 2K-DES с помощью этой атаки требуется всего 232 известных открытых текстов и 233 операций шифрования. Однако тот же алгоритм Саймона позволяет вскрыть российский алгоритм шифрования, определенный в стандарте ГОСТ Р28147–89, используя 2114.8 квантовых запросов, что в 213.2 раз быстрее, чем вскрытие этого алгоритма шифрования с помощью алгоритма Гровера (квантового перебора ключей).
Еще меньшее влияние появление квантовых компьютеров окажет на стойкость хэш-функций (под стойкостью в данном случае понимается трудоемкость решения задачи поиска коллизии хэш-функции). Асимптотически потребуется увеличить длину значения хэш-функции в полтора раза. Например, вместо функции SHA-256 потребуется применять функцию SHA-384.
Что делать?
Как мы видим, последствия от появления квантовых компьютеров значительные, а поскольку криптография сегодня используется массово (достаточно в качестве примера привести протокол TLS, практически постоянно используемый пользователями интернета), то готовиться к их появлению нужно уже сегодня. Именно так рассудил Национальный институт по стандартизации США (NIST), который еще в 2016 году запустил проект PQC (Post-Quantum Cryptography) Standardization.
У проекта PQC (Post-Quantum Cryptography) Standardization три задачи:
- Заменить схемы создания цифровой подписи, определенные в стандарте FIPS 186–4 (RSA, DSA, ECDSA)
- Заменить протокол шифрования данных при передаче ключей, определенный в SP 800–56B и основанный на использовании RSA
- Заменить протокол согласования ключей, определенный в SP 800–56A, в основе которого лежит алгоритм Диффи- Хеллмана (Diffie- Hellman).
В конце 2016 года NIST выпустил сообщение (Federal Notice) о сборе предложений по решению перечисленных задач до конца 2017 г. В 2018 г. NIST приступил к анализу полученных многочисленных предложений и планирует до конца 2023 г. завершить выбор алгоритмов, решающих поставленные задачи. При этом допускается выбор нескольких победителей. Из сообщения NIST: We may not be able to select one single winner for each function (signature, encryption, key agreement).

NIST также внимательно изучает процесс миграции со старых алгоритмов на новые. Речь идет о работе в т. н. гибридной моде, когда какие-то пользователи пока поддерживают только старые алгоритмы. Предполагается, что наряду с поддержкой новых алгоритмов пользователи должны будут в течение какого-то времени поддерживать и старые алгоритмы. Такие продвинутые пользователи будут генерировать подпись документа с использованием старого и нового алгоритмов, и продвинутым пользователем подпись будет признаваться при наличии двух подписей сообщения и только когда обе подписи верны.
NIST предполагает, что миграция на постквантовые криптографические алгоритмы начнется в 2030 году. До этого времени ожидается использование в основном сегодняшних стандартов FIPS.
Состояние дел с построением квантовых компьютеров
Как следует из сказанного выше, виновником будущего переполоха в криптографии могут стать квантовые компьютеры. Причем не просто квантовые компьютеры, а, как будет показано ниже, компьютеры, способные поддержать несколько тысяч надежно функционирующих кубитов. Каково же положение дел с построением таких компьютеров в наши дни?
Сегодняшними мировыми лидерами в построении универсальных квантовых компьютеров являются компании Google, IBM и Intel. В марте 2018 года компания Google объявила, что ей удалось построить 72 кубитный квантовый процессор Bristlecone, имеющий низкую вероятность ошибок в вычислениях: вероятность ошибки в 2 кубитном логическом элементе процессора Bristlecone составляет 0,6%, что чуть выше уже упоминавшегося нами значения (0,5%), установленного в техническом задании на разработку. Компания не раскрыла подробных характеристик своего устройства, однако утверждает, что оно позволяет достичь «квантового превосходства».
Чуть раньше, в ноябре 2017 года, компания IBM сообщила о создании и успешном испытании процессора с 50 кубитами, а в январе 2018 г. исполнительный директор компании Intel Брайан Кржанич (Brian Krzanich) сообщил о создании сверхпроводящего квантового чипа под кодовым названием «Tangle Lake», обладающего 49 кубитами.
Несколько отдельно от лидеров стоит канадская компания D-Wave Systems со своими адиабатическими компьютерами, которая заявляет о создании различных вариантов квантового компьютера: от 16 кубитного до 2000 кубитного. Компьютеры D-Wave пригодны для решения лишь узкого класса задач (например, задачи поиска глобального минимума функции). Некоторые исследователи высказывали сомнения в том, что в компьютерах компании действительно достигается существенное «квантовое ускорение». В декабре 2015 г. специалисты компании Google подтвердили, что, согласно их исследованию, компьютер D-Wave использует квантовые эффекты. При этом в «1000 кубитном» компьютере кубиты в действительности организованы в кластеры по 8 кубитов каждый. Тем не менее это позволило добиться быстродействия в 100 млн раз больше (по сравнению с обычным компьютером) в одном из алгоритмов (алгоритме поиска глобального минимума функции).
Процессор «Везувий» фирмы D-Wave на 512 кубит в обвязке охлаждения
Компьютеры D-Wave предлагаются на рынке по ценам 10–15 млн долл. США и уже приобретались компаниями Google, Lockheed Martin, Temporal Defense Systems, а также агентством NASA и Лос- Аламосской национальной лабораторией.
Как следует из короткого обзора по состоянию дел с разработкой универсальных квантовых компьютеров, их сегодняшние возможности на два порядка ниже того, что требуется для взлома криптографических алгоритмов. Построить квантовый компьютер, поддерживающий большое количество кубитов, совсем непросто, поскольку роль кубитов выполняется сверхминиатюрными хрупкими по своей природе квантовыми системами размера электрона или фотона, которые требуется поддерживать в стабильном состоянии в течение достаточно долгого времени (хотя бы в течение нескольких секунд). Кроме того, такие квантовые системы подвержены многочисленным внешним воздействиям (в первую очередь электромагнитным воздействиям), которые приводят к появлению ошибок вычислений. Теоретически такие ошибки, если их не очень много, можно исправлять, используя дополнительные кубиты, предназначенные для исправления ошибок с помощью специальных помехоустойчивых квантовых кодов. На практике же получается, что для обеспечения надежных квантовых вычислений количество таких дополнительных кубитов, предназначенных для исправления ошибок, сравнимо с количеством полезных кубитов, применяемых для квантовых вычислений.
В настоящее время для создания кубитов и, следовательно, построения квантовых компьютеров применяются всего два подхода (раньше их было существенно больше: от использования ядерного магнитного резонанса и поляризованных фотонов до применения квантовых точек — электронов, захваченных группой атомов): это ионные ловушки и сверхпроводящие нанокольца. Ионные ловушки представляют собой одномерный кристалл, состоящий из ионов, находящихся в электромагнитном поле. Ионы в кристалле взаимодействуют друг с другом, обмениваясь колебательными возбуждениями. Изменение состояния кубита в соответствии с заданным алгоритмом происходит за счет воздействия поляризованного лазерного пучка на один или группу ионов.
Сверхпроводящие нанокольца, расположенные в магнитном поле при температуре, близкой к абсолютному нулю, поддерживают ток, текущий в кольце в противоположных направлениях. Тем самым моделируется кубит, способный одновременно находиться в двух состояниях.
Как уже отмечалось, точное время появления квантовых компьютеров, реально представляющих угрозу современной криптографии, сегодня спрогнозировать невозможно — на это может потребоваться от нескольких лет до десятилетий. История показывает, что на начальном этапе развития новой технологии часто возникают прорывные идеи, значительно сокращающие сроки ее внедрения.
Алгоритм Шора
В 1995 году исследователь компании AT&T Питер Шор (Peter Shor) опубликовал статью Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer («Алгоритм полиномиальной сложности для разложения числа на простые множители и дискретного логарифмирования на квантовом компьютере»). Алгоритм Шора является квантовым алгоритмом (предназначен для исполнения на квантовом компьютере) и позволяет добиться экспоненциального ускорения при решении математических задач факторизации, дискретного логарифмирования в конечном поле (DLP) и дискретного логарифмирования на множестве точек эллиптической кривой (ECDLP). Эти задачи при определенных практически важных значениях параметров невозможно за обозримое время решить на классическом компьютере, но их решение возможно на квантовом компьютере. Это, в свою очередь, означает, что с появлением квантового компьютера будет возможно взломать такие широко используемые на практике алгоритмы асимметричного шифрования, как RSA, Diffie–Hellman, DSA, ECDSA, EC-SDSA, EdDSA, криптостойкость которых базируется на сложности решения перечисленных выше математических задач. Другими словами, статью Шора можно было бы назвать Breaking All Public- Key Crypto on a Quantum Computer («Компрометация всей асимметричной криптографии на квантовом компьютере»). Алгоритм Шора был назван известным специалистом в теории сложности Скотом Ааронсоном (Scott Joel Aaronson) одним из главных научных достижений конца ХХ века.
Отметим, что лучший классический алгоритм факторизации числа N требует времени, экспоненциально зависящего от n, где n = log N. В то же время алгоритм Шора на квантовом компьютере требует полиномиального времени от n, а именно O(n2log2n(log2log2n)) операций. На практике это означает экспоненциальное ускорение решения проблемы факторизации: на квантовом компьютере для компрометации схемы RSA вместо тысяч лет потребуется несколько часов, дней, недель, месяцев.
В работе [1] показано, что для факторизации числа длиной n бит достаточно иметь квантовый компьютер, использующий 2n+3 кубитов, содержащий O(n3log2n) элементарных гейтов глубиной O(n3). Для взлома алгоритма RSA с модулем открытого ключа 2048 битов требуется квантовый компьютер, содержащий 4099 кубитов.
Проблема дискретного логарифмирования DLP состоит в следующем: по произвольным заданным значениям y, g и простого p требуется найти значение x такое, что y = gx (mod p). Решение задачи DLP на классическом компьютере требует экспоненциально большого от p количества времени (операций), в то время как алгоритм Шора поиска периода функции позволяет решить задачу за полиномиальное время.
И снова сложность задачи нахождения значения x равна O(n2log2n(log2log2n)) , где n –длина в битах числа p. Следовательно, решение проблемы DLP на квантовом компьютере при использовании алгоритма Шора имеет полиномиальную сложность.
Аналогичным образом полиномиальная сложность задачи дискретного логарифмирования ECDLP (Elliptic Curve Discrete Logarithm Problem) на точках эллиптической кривой. Задача требует решения уравнения Y = xP относительно х при заданных точках кривой P и Y.
В работе [2] показано, что для решения проблемы ECDLP для кривой n битов существует алгоритм с разделением регистров, требующий поддержки
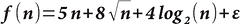
кубитов, где ε — константа, приблизительно равная 10. Отсюда для наиболее актуальных значений n получаем f(256) = 1500 кубитов, f(512) = 2800 кубитов.
Алгоритм Гровера
Вслед за алгоритмом Шора, обеспечивающим экспоненциальное ускорение решения задач факторизации и логарифмирования, для квантовых компьютеров был придуман алгоритм Гровера, который обеспечивает квадратичное ускорение решения задачи поиска по неструктурированной БД. Этот алгоритм был впервые опубликован в 1996 году. Предположим, что некоторая величина x принимает n различных значений. Пусть на m значениях х функция f(x) принимает значение 1, а на остальных (n-m) значениях х выполняется равенство f(x) = 0. Задача состоит в поиске любого значения x, при котором f(x) = 1. Можно показать, что на обычном классическом компьютере для решения задачи потребуется
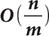
операций. В то же время при использовании алгоритма Гровера на квантовом компьютере для решения задачи потребуется
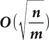
операций, т. е. наблюдается квадратичное ускорение решения задачи, хотя и не такое значительное, как при использовании алгоритма Шора для решения задачи факторизации на квантовом компьютере.
Посмотрим, какие последствия на стойкость криптографических алгоритмов оказывает алгоритм Гровера. Рассмотрим функцию f(x), которая принимает значение 1 тогда и только тогда, когда x равно неизвестному значению секретного ключа K, при котором выполняется равенство E(K, P) = C для некоторых известных значений шифруемого текста P и соответствующего ему шифротекста C и некоторой известной функции шифрования E(). На практике это означает, что для поиска 128 битного ключа AES на квантовом компьютере требуется время, пропорциональное 264, а не 2128, как на классическом компьютере. Потребуется также достаточно большое количество шифруемых текстов, чтобы гарантировать уникальность ключа. Трудоемкость 264 операций существенно меньше 2128, что означает, что найти ключ на квантовом компьютере значительно проще, чем на классическом.
Однако существует простое решение для восстановления криптостойкости алгоритма AES при использовании квантового компьютера. Чтобы обеспечить криптостойкость, получаемую на классическом компьютере при применении 128 битового ключа, на квантовом компьютере нужно использовать 256 битный ключ! Алгоритм Гровера уменьшит сложность решения задачи поиска ключа «всего» до
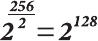
операций шифрования.
Алгоритм Гровера также позволяет более эффективным образом искать прообразы значений хэш-функции Hash(). Определим задачу поиска прообраза значения h хэш-функции Hash() через следующую функцию f(): «f(x) = 1 тогда и только тогда, когда Hash(x) = h, в противном случае f(x) = 0». Алгоритм Гровера на квантовом компьютере позволит найти прообраз значения h n-битовой хэш-функции за
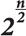
операций. Как и в случае с шифрованием, чтобы обеспечить безопасность 2n на квантовом компьютере, нужно использовать хэш-функции с удвоенной длиной их значений. Для поиска прообраза хэш-функции размером 2n бит на квантовом компьютере с помощью алгоритма Гровера потребуется порядка 2n операций вычисления значения хэша.
Отметим, что квантовые вычисления позволяют также находить коллизии хэш-функции за время, пропорциональное
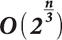
, вместо
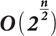
при использовании классической атаки birthday attack. Отсюда можно заключить, что квантовые компьютеры могут превосходить классические и при решении задачи поиска коллизий для хэш-функций. Однако алгоритм поиска коллизий, требующий времени, пропорционального
, также требует для своей работы памяти, пропорциональной
.
Можно показать, что при использовании такого объема памяти на классическом компьютере можно распараллелить вычисления, и поиск коллизии в этом случае займет время, пропорциональное
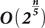
, что значительно меньше времени
, требуемого для решения задачи на квантовом компьютере.
Из сказанного выше следует вывод: применение квантового компьютера делает полностью бесполезным все сегодня массово используемые алгоритмы асимметричного шифрования, основанные на сложности решения задачи факторизации, DLP и ECDLP.
В то же время существует простая возможность обеспечить требуемую криптостойкость симметричных алгоритмов шифрования, просто удваивая размер используемых в них ключей.
Постквантовая криптография
В качестве ответа на вызовы квантовых вычислений была разработана целая серия новых криптографических алгоритмов, не подверженных атакам с использованием квантовых вычислений. Ниже приведены некоторые из них:
- система Мак-Элиса (code-based algorithm). Используется двоичный код Гоппы, исправляющий большое число ошибок и для которого существует эффективный алгоритм декодирования. Если код выбирается из достаточно большого класса кодов, то угадать, какой именно код был выбран, практически невозможно. Порождающая матрица кода Гоппы преобразуется до такой степени, что получившаяся в результате матрица выглядит случайной. Таким образом, криптоаналитик должен решить общую задачу декодирования линейных кодов, т. е. задачу поиска ближайшего кодового слова к произвольному слову, которая является NP-полной задачей;
- алгоритмы на решетках (lattice-based algorithms). Базируются на решении следующих NP-трудных задач: 1) определения короткого базиса по длинному базису (Short Basis Problem) решетки (специальной математической структуры) или 2) поиска точки решетки, заданной длинным базисом, ближайшей к произвольной точке n-мерного пространства (Closest Vector Problem, или CVP). Наиболее популярны в криптографии на решетках вариации задачи CVP;
- алгоритмы на базе систем квадратичных уравнений (multivariate algorithm). Задача нахождения решения квадратичной системы линейных уравнений со многими неизвестными (multivariate quadratics, или MQ) является NP-трудной, и это является основой для построения криптографических алгоритмов;
- алгоритмы на основе хэш-функций (hash-based algorithm). В отличие от остальных рассмотренных здесь схем постквантовой криптографии криптография на основе хэш-функций базируется на безопасности криптографических хэш-функций (трудоемкости задачи поиска прообраза), а не на решении трудных математических проблем типа факторизации и логарифмирования в конечном поле. Как было показано ранее, квантовый компьютер обеспечивает всего лишь квадратичное ускорение в решении задачи нахождения прообраза для хэш-функции, а потому криптографические алгоритмы на основе хэш-функций могут с успехом использоваться и в постквантовой криптографии. Сами по себе криптографические алгоритмы на основе хэш-функций достаточно сложные. Примером алгоритма этого класса является алгоритм формирования одноразовой подписи, предложенный Винтерницем (Winternitz) в 1979 году (WOTS, или Winternitz One-Time Signature).
- Протокол Диффи-Хеллмана с использованием суперсингулярной изогении (Supersingular isogeny Diffie-Hellman key exchange, SIDH). Основан на сложности решения следующей задачи. Даны две изогенные эллиптические кривые E1 и E2 с различными j–инвариантами (известная характеристика эллиптической кривой). Требуется найти изогению (специальное рациональное преобразование) между кривыми E1 и E2.
С подробным описанием алгоритмов постквантовой криптографии можно ознакомиться во 2 и 3 номерах журнала «Платежные Технологии».