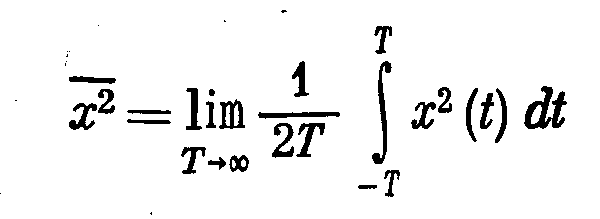Критерий минимума среднеквадратичной ошибки

При использовании
критерия минимума СКО, взвешивающие коэффициенты ячеек  эквалайзера подстраиваются
так, чтобы минимизировать средний квадрат ошибки

,                      (10.2.24)

где  — информационный символ,
переданный на -ом
сигнальном интервале, a  — оценка этого символа на выходе
эквалайзера, определяемая (10.2.1). Если информационные символы  комплексные, то
показатель качества при СКО критерия, обозначаемый , определяется так

.                        (10.2.25)

С другой стороны, когда
информационные символы вещественные, показатель качества просто равен квадрату
вещественной величины . В любом случае,  является квадратичнйй
функцией коэффициентов эквалайзера . При дальнейшем обсуждении мы
рассмотрим минимизацию комплексной формы, даваемой (10.2.25).

Эквалайзер неограниченной
длины. Сначала
определим взвешивающие коэффициенты ячеек, которые минимизируют , когда эквалайзер
имеет неограниченное число ячеек. В этом случае, оценка  определяется так

                       (10.2.26)

Подстановка (10.2.26) в
выражение для ,
определяемая (10.2.25), и расширение результата приводит к квадратичной функции
от коэффициентов .
Эту функцию можно легко минимизировать по  посредством решения системы
(неограниченной) линейных уравнений для . Альтернативно, систему линейных
уравнений можно получить путём использования принципа ортогональности при
среднеквадратичном оценивании. Это значит, мы выбираем коэффициенты  такие, что ошибка  ортогональна
сигнальной

последовательности  для . То есть

                         (10.2.27)

Подстановка  в (10.2.27) даёт

или, что эквивалентно,

.                      (10.2.28)

Чтобы вычислить моменты в
(10.2.28), мы используем выражение для  даваемое (10.1.16). Таким образом,
получим

             (10.2.29)

и

                     (10.2.30)

Теперь, если подставим
(10.2.29) и (10.2.30) в (10.2.28) и возьмём -преобразование от обеих частей
результирующего уравнения, мы находим

.                       (10.2.31)

Следовательно,
передаточная функция эквалайзера, основанного на критерии минимума СКО, равна

.                     (10.2.32)

Если обеляющий фильтр
включён в ,
мы получаем эквивалентный эквалайзер с передаточной функцией

.                      (10.2.33)

Видим, что единственная
разница между этим выражением для  и тем, которое базируется на критерии
пикового искажения — это спектральная плотность шума , которая появилась в (10.2.33),
Если  очень
мало по сравнению с сигналом, коэффициенты, которые минимизируют пиковые
искажения  приближённо
равны коэффициентам, которые минимизируют по СКО показатель качества . Это значит, что в
пределе, когда ,
два критерия дают одинаковое решение для взвешивающих коэффициентов. Следовательно,
когда , минимизация
СКО ведёт к полному исключению МСИ. С другой стороны, это не так, когда . В общем, когда , оба критерия дают
остаточное МСИ и аддитивный шум на выходе эквалайзера.

Меру остаточного МСИ и
аддитивного шума на выходе эквалайзера можно получить расчётом минимальной
величины ,
обозначаемую ,
когда передаточная функция

эквалайзера определена
(10.2.32). Поскольку  и поскольку  с учётом условия
ортогональности (10.2.27), следует

.                    (10.2.34)

Эта частная форма для  не очень
информативна. Больше понимания зависимости качества эквалайзера от канальных
характеристик можно получить, если суммы в (10.2.34) преобразовать в частотную
область. Это можно выполнить, заметив, что сумма в (10.2.34) является свёрткой  и , вычисленной при
нулевом сдвиге. Так, если через  обозначить свёртку этих
последовательностей, то сумма в (10.2.34) просто равна . Поскольку — преобразование
последовательности  равно

,                      (10.2.35)

 то слагаемое  равно

.                      (10.2.36)

Контурный интеграл в
(10.2.36) можно преобразовать в эквивалентный линейный интеграл путём замены
переменной .
В результате этой замены получаем

.                     (10.2.37)

Наконец, подставив (10.2.37)
в сумму (10.2.34), получаем желательное выражение для минимума СКО в виде

                       (10.2.38)

В отсутствие МСИ  и, следовательно,

.                       (10.2.39)

Видим, что . Далее,
соотношение между выходным (нормированного по энергии сигнала) ОСШ  и  выглядит так

.                                                  

Более
существенно то, что соотношение  и  также имеет силу, когда имеется
остаточная МСИ в дополнении к шуму на выходе эквалайзера.

Эквалайзер ограниченной длины. Теперь
вернём наше внимание к случаю, когда длительность импульсной характеристики
трансверсального эквалайзера простирается на ограниченном временном интервале,
т.е. эквалайзер имеет конечную память или ограниченную длину. Выход эквалайзера
на -м сигнальном
интервале равен

СКО эквалайзера с  ячейками, обозначаемый , равен

Минимизация  по взвешивающим
коэффициентам ячеек  или, что эквивалентно, требуя, чтобы
ошибка  была
бы ортогональна сигнальным отсчётам , , приводит к следующей системе
уравнений:

где

Удобно
выразить систему линейных уравнений в матричной форме, т.е.

где  означает вектор столбец  взвешивающих
значений кодовых ячеек, означает  матрицу ковариаций Эрмита с
элементами ;
а  мерный
вектор столбец с элементами . Решение (10.2.46) можно записать в
виде

Таким образом, решение для  включает в себя
обращение матрицы . Оптимальные взвешивающие
коэффициенты ячеек, даваемые (10.2.47), минимизируют показатель качества , что приводит к
минимальной величине

где  определяет  транспонированный вектор
столбец .
 можно
использовать в (10.2.40) для вычисления ОСШ линейного эквивалента с  коэффициентами
ячеек.

In statistics and signal processing, a minimum mean square error (MMSE) estimator is an estimation method which minimizes the mean square error (MSE), which is a common measure of estimator quality, of the fitted values of a dependent variable. In the Bayesian setting, the term MMSE more specifically refers to estimation with quadratic loss function. In such case, the MMSE estimator is given by the posterior mean of the parameter to be estimated. Since the posterior mean is cumbersome to calculate, the form of the MMSE estimator is usually constrained to be within a certain class of functions. Linear MMSE estimators are a popular choice since they are easy to use, easy to calculate, and very versatile. It has given rise to many popular estimators such as the Wiener–Kolmogorov filter and Kalman filter.

Motivation[edit]

The term MMSE more specifically refers to estimation in a Bayesian setting with quadratic cost function. The basic idea behind the Bayesian approach to estimation stems from practical situations where we often have some prior information about the parameter to be estimated. For instance, we may have prior information about the range that the parameter can assume; or we may have an old estimate of the parameter that we want to modify when a new observation is made available; or the statistics of an actual random signal such as speech. This is in contrast to the non-Bayesian approach like minimum-variance unbiased estimator (MVUE) where absolutely nothing is assumed to be known about the parameter in advance and which does not account for such situations. In the Bayesian approach, such prior information is captured by the prior probability density function of the parameters; and based directly on Bayes theorem, it allows us to make better posterior estimates as more observations become available. Thus unlike non-Bayesian approach where parameters of interest are assumed to be deterministic, but unknown constants, the Bayesian estimator seeks to estimate a parameter that is itself a random variable. Furthermore, Bayesian estimation can also deal with situations where the sequence of observations are not necessarily independent. Thus Bayesian estimation provides yet another alternative to the MVUE. This is useful when the MVUE does not exist or cannot be found.

Definition[edit]

Let be a hidden random vector variable, and let be a known random vector variable (the measurement or observation), both of them not necessarily of the same dimension. An estimator of is any function of the measurement . The estimation error vector is given by and its mean squared error (MSE) is given by the trace of error covariance matrix

where the expectation is taken over conditioned on . When is a scalar variable, the MSE expression simplifies to . Note that MSE can equivalently be defined in other ways, since

The MMSE estimator is then defined as the estimator achieving minimal MSE:

Properties[edit]

• When the means and variances are finite, the MMSE estimator is uniquely defined^[1] and is given by:

In other words, the MMSE estimator is the conditional expectation of given the known observed value of the measurements. Also, since is the posterior mean, the error covariance matrix is equal to the posterior covariance matrix,

.

• The MMSE estimator is unbiased (under the regularity assumptions mentioned above):

• The MMSE estimator is asymptotically unbiased and it converges in distribution to the normal distribution:

where is the Fisher information of . Thus, the MMSE estimator is asymptotically efficient.

for all in closed, linear subspace of the measurements. For random vectors, since the MSE for estimation of a random vector is the sum of the MSEs of the coordinates, finding the MMSE estimator of a random vector decomposes into finding the MMSE estimators of the coordinates of X separately:

for all i and j. More succinctly put, the cross-correlation between the minimum estimation error and the estimator should be zero,

Linear MMSE estimator[edit]

In many cases, it is not possible to determine the analytical expression of the MMSE estimator. Two basic numerical approaches to obtain the MMSE estimate depends on either finding the conditional expectation or finding the minima of MSE. Direct numerical evaluation of the conditional expectation is computationally expensive since it often requires multidimensional integration usually done via Monte Carlo methods. Another computational approach is to directly seek the minima of the MSE using techniques such as the stochastic gradient descent methods ; but this method still requires the evaluation of expectation. While these numerical methods have been fruitful, a closed form expression for the MMSE estimator is nevertheless possible if we are willing to make some compromises.

One possibility is to abandon the full optimality requirements and seek a technique minimizing the MSE within a particular class of estimators, such as the class of linear estimators. Thus, we postulate that the conditional expectation of given is a simple linear function of , , where the measurement is a random vector, is a matrix and is a vector. This can be seen as the first order Taylor approximation of . The linear MMSE estimator is the estimator achieving minimum MSE among all estimators of such form. That is, it solves the following the optimization problem:

One advantage of such linear MMSE estimator is that it is not necessary to explicitly calculate the posterior probability density function of . Such linear estimator only depends on the first two moments of and . So although it may be convenient to assume that and are jointly Gaussian, it is not necessary to make this assumption, so long as the assumed distribution has well defined first and second moments. The form of the linear estimator does not depend on the type of the assumed underlying distribution.

The expression for optimal and is given by:

where , the is cross-covariance matrix between and , the is auto-covariance matrix of .

Thus, the expression for linear MMSE estimator, its mean, and its auto-covariance is given by

where the is cross-covariance matrix between and .

Lastly, the error covariance and minimum mean square error achievable by such estimator is

Univariate case[edit]

For the special case when both and are scalars, the above relations simplify to

where is the Pearson’s correlation coefficient between and .

The above two equations allows us to interpret the correlation coefficient either as normalized slope of linear regression

or as square root of the ratio of two variances

.

When , we have and . In this case, no new information is gleaned from the measurement which can decrease the uncertainty in . On the other hand, when , we have and . Here is completely determined by , as given by the equation of straight line.

Computation[edit]

Standard method like Gauss elimination can be used to solve the matrix equation for . A more numerically stable method is provided by QR decomposition method. Since the matrix is a symmetric positive definite matrix, can be solved twice as fast with the Cholesky decomposition, while for large sparse systems conjugate gradient method is more effective. Levinson recursion is a fast method when is also a Toeplitz matrix. This can happen when is a wide sense stationary process. In such stationary cases, these estimators are also referred to as Wiener–Kolmogorov filters.

Linear MMSE estimator for linear observation process[edit]

Let us further model the underlying process of observation as a linear process: , where is a known matrix and is random noise vector with the mean and cross-covariance . Here the required mean and the covariance matrices will be

Thus the expression for the linear MMSE estimator matrix further modifies to

Putting everything into the expression for , we get

Lastly, the error covariance is

The significant difference between the estimation problem treated above and those of least squares and Gauss–Markov estimate is that the number of observations m, (i.e. the dimension of ) need not be at least as large as the number of unknowns, n, (i.e. the dimension of ). The estimate for the linear observation process exists so long as the m-by-m matrix exists; this is the case for any m if, for instance, is positive definite. Physically the reason for this property is that since is now a random variable, it is possible to form a meaningful estimate (namely its mean) even with no measurements. Every new measurement simply provides additional information which may modify our original estimate. Another feature of this estimate is that for m < n, there need be no measurement error. Thus, we may have , because as long as is positive definite, the estimate still exists. Lastly, this technique can handle cases where the noise is correlated.

Alternative form[edit]

An alternative form of expression can be obtained by using the matrix identity

which can be established by post-multiplying by and pre-multiplying by to obtain

and

Since can now be written in terms of as , we get a simplified expression for as

In this form the above expression can be easily compared with weighed least square and Gauss–Markov estimate. In particular, when , corresponding to infinite variance of the apriori information concerning , the result is identical to the weighed linear least square estimate with as the weight matrix. Moreover, if the components of are uncorrelated and have equal variance such that where is an identity matrix, then is identical to the ordinary least square estimate.

Sequential linear MMSE estimation[edit]

In many real-time applications, observational data is not available in a single batch. Instead the observations are made in a sequence. One possible approach is to use the sequential observations to update an old estimate as additional data becomes available, leading to finer estimates. One crucial difference between batch estimation and sequential estimation is that sequential estimation requires an additional Markov assumption.

In the Bayesian framework, such recursive estimation is easily facilitated using Bayes’ rule. Given observations, , Bayes’ rule gives us the posterior density of as

The is called the posterior density, is called the likelihood function, and is the prior density of k-th time step. Note that the prior density for k-th time step is the posterior density of (k-1)-th time step. This structure allows us to formulate a recursive approach to estimation. Here we have assumed the conditional independence of from previous observations given as

This is the Markov assumption.

The MMSE estimate given the th observation is then the mean of the posterior density . Here, we have implicitly assumed that the statistical properties of does not change with time. In other words, is stationary.

In the context of linear MMSE estimator, the formula for the estimate will have the same form as before. However, the mean and covariance matrices of and will need to be replaced by those of the prior density and likelihood , respectively.

The mean and covariance matrix of the prior density is given by the previous MMSE estimate, , and the error covariance matrix,

respectively, as per by the property of MMSE estimators.

Similarly, for the linear observation process, the mean and covariance matrix of the likelihood is given by and

.

The difference between the predicted value of , as given by , and the observed value of gives the prediction error , which is also referred to as innovation. It is more convenient to represent the linear MMSE in terms of the prediction error, whose mean and covariance are and

.

Hence, in the estimate update formula, we should replace and by and , respectively. Also, we should replace and by and . Lastly, we replace by

Thus, we have the new estimate as

and the new error covariance as

From the point of view of linear algebra, for sequential estimation, if we have an estimate based on measurements generating space , then after receiving another set of measurements, we should subtract out from these measurements that part that could be anticipated from the result of the first measurements. In other words, the updating must be based on that part of the new data which is orthogonal to the old data.

The repeated use of the above two equations as more observations become available lead to recursive estimation techniques. The expressions can be more compactly written as

The matrix is often referred to as the Kalman gain factor. The alternative formulation of the above algorithm will give

The repetition of these three steps as more data becomes available leads to an iterative estimation algorithm. The generalization of this idea to non-stationary cases gives rise to the Kalman filter. The three update steps outlined above indeed form the update step of the Kalman filter.

Special case: scalar observations[edit]

As an important special case, an easy to use recursive expression can be derived when at each k-th time instant the underlying linear observation process yields a scalar such that , where is n-by-1 known column vector whose values can change with time, is n-by-1 random column vector to be estimated, and is scalar noise term with variance . After (k+1)-th observation, the direct use of above recursive equations give the expression for the estimate as:

where is the new scalar observation and the gain factor is n-by-1 column vector given by

The is n-by-n error covariance matrix given by

Here, no matrix inversion is required. Also, the gain factor, , depends on our confidence in the new data sample, as measured by the noise variance, versus that in the previous data. The initial values of and are taken to be the mean and covariance of the aprior probability density function of .

Alternative approaches: This important special case has also given rise to many other iterative methods (or adaptive filters), such as the least mean squares filter and recursive least squares filter, that directly solves the original MSE optimization problem using stochastic gradient descents. However, since the estimation error cannot be directly observed, these methods try to minimize the mean squared prediction error . For instance, in the case of scalar observations, we have the gradient Thus, the update equation for the least mean square filter is given by

where is the scalar step size and the expectation is approximated by the instantaneous value . As we can see, these methods bypass the need for covariance matrices.

Examples[edit]

Example 1[edit]

We shall take a linear prediction problem as an example. Let a linear combination of observed scalar random variables and be used to estimate another future scalar random variable such that . If the random variables are real Gaussian random variables with zero mean and its covariance matrix given by

then our task is to find the coefficients such that it will yield an optimal linear estimate .

In terms of the terminology developed in the previous sections, for this problem we have the observation vector , the estimator matrix as a row vector, and the estimated variable as a scalar quantity. The autocorrelation matrix is defined as

The cross correlation matrix is defined as

We now solve the equation by inverting and pre-multiplying to get

So we have and
as the optimal coefficients for . Computing the minimum
mean square error then gives .^[2] Note that it is not necessary to obtain an explicit matrix inverse of to compute the value of . The matrix equation can be solved by well known methods such as Gauss elimination method. A shorter, non-numerical example can be found in orthogonality principle.

Example 2[edit]

Consider a vector formed by taking observations of a fixed but unknown scalar parameter disturbed by white Gaussian noise. We can describe the process by a linear equation , where . Depending on context it will be clear if represents a scalar or a vector. Suppose that we know to be the range within which the value of is going to fall in. We can model our uncertainty of by an aprior uniform distribution over an interval , and thus will have variance of . Let the noise vector be normally distributed as where is an identity matrix. Also and are independent and . It is easy to see that

Thus, the linear MMSE estimator is given by

We can simplify the expression by using the alternative form for as

where for we have

Similarly, the variance of the estimator is

Thus the MMSE of this linear estimator is

For very large , we see that the MMSE estimator of a scalar with uniform aprior distribution can be approximated by the arithmetic average of all the observed data

while the variance will be unaffected by data and the LMMSE of the estimate will tend to zero.

However, the estimator is suboptimal since it is constrained to be linear. Had the random variable also been Gaussian, then the estimator would have been optimal. Notice, that the form of the estimator will remain unchanged, regardless of the apriori distribution of , so long as the mean and variance of these distributions are the same.

Example 3[edit]

Consider a variation of the above example: Two candidates are standing for an election. Let the fraction of votes that a candidate will receive on an election day be Thus the fraction of votes the other candidate will receive will be We shall take as a random variable with a uniform prior distribution over so that its mean is and variance is A few weeks before the election, two independent public opinion polls were conducted by two different pollsters. The first poll revealed that the candidate is likely to get fraction of votes. Since some error is always present due to finite sampling and the particular polling methodology adopted, the first pollster declares their estimate to have an error with zero mean and variance Similarly, the second pollster declares their estimate to be with an error with zero mean and variance Note that except for the mean and variance of the error, the error distribution is unspecified. How should the two polls be combined to obtain the voting prediction for the given candidate?

As with previous example, we have

Here, both the . Thus, we can obtain the LMMSE estimate as the linear combination of and as

where the weights are given by

Here, since the denominator term is constant, the poll with lower error is given higher weight in order to predict the election outcome. Lastly, the variance of is given by

which makes smaller than Thus, the LMMSE is given by

In general, if we have pollsters, then where the weight for i-th pollster is given by and the LMMSE is given by

Example 4[edit]

Suppose that a musician is playing an instrument and that the sound is received by two microphones, each of them located at two different places. Let the attenuation of sound due to distance at each microphone be and , which are assumed to be known constants. Similarly, let the noise at each microphone be and , each with zero mean and variances and respectively. Let denote the sound produced by the musician, which is a random variable with zero mean and variance How should the recorded music from these two microphones be combined, after being synced with each other?

We can model the sound received by each microphone as

Here both the . Thus, we can combine the two sounds as

where the i-th weight is given as

See also[edit]

• Bayesian estimator
• Mean squared error
• Least squares
• Minimum-variance unbiased estimator (MVUE)
• Orthogonality principle
• Wiener filter
• Kalman filter
• Linear prediction
• Zero-forcing equalizer

Notes[edit]

Further reading[edit]

In statistics and signal processing, a minimum mean square error (MMSE) estimator is an estimation method which minimizes the mean square error (MSE), which is a common measure of estimator quality, of the fitted values of a dependent variable. In the Bayesian setting, the term MMSE more specifically refers to estimation with quadratic loss function. In such case, the MMSE estimator is given by the posterior mean of the parameter to be estimated. Since the posterior mean is cumbersome to calculate, the form of the MMSE estimator is usually constrained to be within a certain class of functions. Linear MMSE estimators are a popular choice since they are easy to use, easy to calculate, and very versatile. It has given rise to many popular estimators such as the Wiener–Kolmogorov filter and Kalman filter.

Motivation[edit]

The term MMSE more specifically refers to estimation in a Bayesian setting with quadratic cost function. The basic idea behind the Bayesian approach to estimation stems from practical situations where we often have some prior information about the parameter to be estimated. For instance, we may have prior information about the range that the parameter can assume; or we may have an old estimate of the parameter that we want to modify when a new observation is made available; or the statistics of an actual random signal such as speech. This is in contrast to the non-Bayesian approach like minimum-variance unbiased estimator (MVUE) where absolutely nothing is assumed to be known about the parameter in advance and which does not account for such situations. In the Bayesian approach, such prior information is captured by the prior probability density function of the parameters; and based directly on Bayes theorem, it allows us to make better posterior estimates as more observations become available. Thus unlike non-Bayesian approach where parameters of interest are assumed to be deterministic, but unknown constants, the Bayesian estimator seeks to estimate a parameter that is itself a random variable. Furthermore, Bayesian estimation can also deal with situations where the sequence of observations are not necessarily independent. Thus Bayesian estimation provides yet another alternative to the MVUE. This is useful when the MVUE does not exist or cannot be found.

Definition[edit]

Let be a hidden random vector variable, and let be a known random vector variable (the measurement or observation), both of them not necessarily of the same dimension. An estimator of is any function of the measurement . The estimation error vector is given by and its mean squared error (MSE) is given by the trace of error covariance matrix

where the expectation is taken over conditioned on . When is a scalar variable, the MSE expression simplifies to . Note that MSE can equivalently be defined in other ways, since

The MMSE estimator is then defined as the estimator achieving minimal MSE:

Properties[edit]

• When the means and variances are finite, the MMSE estimator is uniquely defined^[1] and is given by:

In other words, the MMSE estimator is the conditional expectation of given the known observed value of the measurements. Also, since is the posterior mean, the error covariance matrix is equal to the posterior covariance matrix,

.

• The MMSE estimator is unbiased (under the regularity assumptions mentioned above):

• The MMSE estimator is asymptotically unbiased and it converges in distribution to the normal distribution:

where is the Fisher information of . Thus, the MMSE estimator is asymptotically efficient.

for all in closed, linear subspace of the measurements. For random vectors, since the MSE for estimation of a random vector is the sum of the MSEs of the coordinates, finding the MMSE estimator of a random vector decomposes into finding the MMSE estimators of the coordinates of X separately:

for all i and j. More succinctly put, the cross-correlation between the minimum estimation error and the estimator should be zero,

Linear MMSE estimator[edit]

In many cases, it is not possible to determine the analytical expression of the MMSE estimator. Two basic numerical approaches to obtain the MMSE estimate depends on either finding the conditional expectation or finding the minima of MSE. Direct numerical evaluation of the conditional expectation is computationally expensive since it often requires multidimensional integration usually done via Monte Carlo methods. Another computational approach is to directly seek the minima of the MSE using techniques such as the stochastic gradient descent methods ; but this method still requires the evaluation of expectation. While these numerical methods have been fruitful, a closed form expression for the MMSE estimator is nevertheless possible if we are willing to make some compromises.

One possibility is to abandon the full optimality requirements and seek a technique minimizing the MSE within a particular class of estimators, such as the class of linear estimators. Thus, we postulate that the conditional expectation of given is a simple linear function of , , where the measurement is a random vector, is a matrix and is a vector. This can be seen as the first order Taylor approximation of . The linear MMSE estimator is the estimator achieving minimum MSE among all estimators of such form. That is, it solves the following the optimization problem:

One advantage of such linear MMSE estimator is that it is not necessary to explicitly calculate the posterior probability density function of . Such linear estimator only depends on the first two moments of and . So although it may be convenient to assume that and are jointly Gaussian, it is not necessary to make this assumption, so long as the assumed distribution has well defined first and second moments. The form of the linear estimator does not depend on the type of the assumed underlying distribution.

The expression for optimal and is given by:

where , the is cross-covariance matrix between and , the is auto-covariance matrix of .

Thus, the expression for linear MMSE estimator, its mean, and its auto-covariance is given by

where the is cross-covariance matrix between and .

Lastly, the error covariance and minimum mean square error achievable by such estimator is

Univariate case[edit]

For the special case when both and are scalars, the above relations simplify to

where is the Pearson’s correlation coefficient between and .

The above two equations allows us to interpret the correlation coefficient either as normalized slope of linear regression

or as square root of the ratio of two variances

.

When , we have and . In this case, no new information is gleaned from the measurement which can decrease the uncertainty in . On the other hand, when , we have and . Here is completely determined by , as given by the equation of straight line.

Computation[edit]

Standard method like Gauss elimination can be used to solve the matrix equation for . A more numerically stable method is provided by QR decomposition method. Since the matrix is a symmetric positive definite matrix, can be solved twice as fast with the Cholesky decomposition, while for large sparse systems conjugate gradient method is more effective. Levinson recursion is a fast method when is also a Toeplitz matrix. This can happen when is a wide sense stationary process. In such stationary cases, these estimators are also referred to as Wiener–Kolmogorov filters.

Linear MMSE estimator for linear observation process[edit]

Let us further model the underlying process of observation as a linear process: , where is a known matrix and is random noise vector with the mean and cross-covariance . Here the required mean and the covariance matrices will be

Thus the expression for the linear MMSE estimator matrix further modifies to

Putting everything into the expression for , we get

Lastly, the error covariance is

The significant difference between the estimation problem treated above and those of least squares and Gauss–Markov estimate is that the number of observations m, (i.e. the dimension of ) need not be at least as large as the number of unknowns, n, (i.e. the dimension of ). The estimate for the linear observation process exists so long as the m-by-m matrix exists; this is the case for any m if, for instance, is positive definite. Physically the reason for this property is that since is now a random variable, it is possible to form a meaningful estimate (namely its mean) even with no measurements. Every new measurement simply provides additional information which may modify our original estimate. Another feature of this estimate is that for m < n, there need be no measurement error. Thus, we may have , because as long as is positive definite, the estimate still exists. Lastly, this technique can handle cases where the noise is correlated.

Alternative form[edit]

An alternative form of expression can be obtained by using the matrix identity

which can be established by post-multiplying by and pre-multiplying by to obtain

and

Since can now be written in terms of as , we get a simplified expression for as

In this form the above expression can be easily compared with weighed least square and Gauss–Markov estimate. In particular, when , corresponding to infinite variance of the apriori information concerning , the result is identical to the weighed linear least square estimate with as the weight matrix. Moreover, if the components of are uncorrelated and have equal variance such that where is an identity matrix, then is identical to the ordinary least square estimate.

Sequential linear MMSE estimation[edit]

In many real-time applications, observational data is not available in a single batch. Instead the observations are made in a sequence. One possible approach is to use the sequential observations to update an old estimate as additional data becomes available, leading to finer estimates. One crucial difference between batch estimation and sequential estimation is that sequential estimation requires an additional Markov assumption.

In the Bayesian framework, such recursive estimation is easily facilitated using Bayes’ rule. Given observations, , Bayes’ rule gives us the posterior density of as

The is called the posterior density, is called the likelihood function, and is the prior density of k-th time step. Note that the prior density for k-th time step is the posterior density of (k-1)-th time step. This structure allows us to formulate a recursive approach to estimation. Here we have assumed the conditional independence of from previous observations given as

This is the Markov assumption.

The MMSE estimate given the th observation is then the mean of the posterior density . Here, we have implicitly assumed that the statistical properties of does not change with time. In other words, is stationary.

In the context of linear MMSE estimator, the formula for the estimate will have the same form as before. However, the mean and covariance matrices of and will need to be replaced by those of the prior density and likelihood , respectively.

The mean and covariance matrix of the prior density is given by the previous MMSE estimate, , and the error covariance matrix,

respectively, as per by the property of MMSE estimators.

Similarly, for the linear observation process, the mean and covariance matrix of the likelihood is given by and

.

The difference between the predicted value of , as given by , and the observed value of gives the prediction error , which is also referred to as innovation. It is more convenient to represent the linear MMSE in terms of the prediction error, whose mean and covariance are and

.

Hence, in the estimate update formula, we should replace and by and , respectively. Also, we should replace and by and . Lastly, we replace by

Thus, we have the new estimate as

and the new error covariance as

From the point of view of linear algebra, for sequential estimation, if we have an estimate based on measurements generating space , then after receiving another set of measurements, we should subtract out from these measurements that part that could be anticipated from the result of the first measurements. In other words, the updating must be based on that part of the new data which is orthogonal to the old data.

The repeated use of the above two equations as more observations become available lead to recursive estimation techniques. The expressions can be more compactly written as

The matrix is often referred to as the Kalman gain factor. The alternative formulation of the above algorithm will give

The repetition of these three steps as more data becomes available leads to an iterative estimation algorithm. The generalization of this idea to non-stationary cases gives rise to the Kalman filter. The three update steps outlined above indeed form the update step of the Kalman filter.

Special case: scalar observations[edit]

As an important special case, an easy to use recursive expression can be derived when at each k-th time instant the underlying linear observation process yields a scalar such that , where is n-by-1 known column vector whose values can change with time, is n-by-1 random column vector to be estimated, and is scalar noise term with variance . After (k+1)-th observation, the direct use of above recursive equations give the expression for the estimate as:

where is the new scalar observation and the gain factor is n-by-1 column vector given by

The is n-by-n error covariance matrix given by

Here, no matrix inversion is required. Also, the gain factor, , depends on our confidence in the new data sample, as measured by the noise variance, versus that in the previous data. The initial values of and are taken to be the mean and covariance of the aprior probability density function of .

Alternative approaches: This important special case has also given rise to many other iterative methods (or adaptive filters), such as the least mean squares filter and recursive least squares filter, that directly solves the original MSE optimization problem using stochastic gradient descents. However, since the estimation error cannot be directly observed, these methods try to minimize the mean squared prediction error . For instance, in the case of scalar observations, we have the gradient Thus, the update equation for the least mean square filter is given by

where is the scalar step size and the expectation is approximated by the instantaneous value . As we can see, these methods bypass the need for covariance matrices.

Examples[edit]

Example 1[edit]

We shall take a linear prediction problem as an example. Let a linear combination of observed scalar random variables and be used to estimate another future scalar random variable such that . If the random variables are real Gaussian random variables with zero mean and its covariance matrix given by

then our task is to find the coefficients such that it will yield an optimal linear estimate .

In terms of the terminology developed in the previous sections, for this problem we have the observation vector , the estimator matrix as a row vector, and the estimated variable as a scalar quantity. The autocorrelation matrix is defined as

The cross correlation matrix is defined as

We now solve the equation by inverting and pre-multiplying to get

So we have and
as the optimal coefficients for . Computing the minimum
mean square error then gives .^[2] Note that it is not necessary to obtain an explicit matrix inverse of to compute the value of . The matrix equation can be solved by well known methods such as Gauss elimination method. A shorter, non-numerical example can be found in orthogonality principle.

Example 2[edit]

Consider a vector formed by taking observations of a fixed but unknown scalar parameter disturbed by white Gaussian noise. We can describe the process by a linear equation , where . Depending on context it will be clear if represents a scalar or a vector. Suppose that we know to be the range within which the value of is going to fall in. We can model our uncertainty of by an aprior uniform distribution over an interval , and thus will have variance of . Let the noise vector be normally distributed as where is an identity matrix. Also and are independent and . It is easy to see that

Thus, the linear MMSE estimator is given by

We can simplify the expression by using the alternative form for as

where for we have

Similarly, the variance of the estimator is

Thus the MMSE of this linear estimator is

For very large , we see that the MMSE estimator of a scalar with uniform aprior distribution can be approximated by the arithmetic average of all the observed data

while the variance will be unaffected by data and the LMMSE of the estimate will tend to zero.

However, the estimator is suboptimal since it is constrained to be linear. Had the random variable also been Gaussian, then the estimator would have been optimal. Notice, that the form of the estimator will remain unchanged, regardless of the apriori distribution of , so long as the mean and variance of these distributions are the same.

Example 3[edit]

Consider a variation of the above example: Two candidates are standing for an election. Let the fraction of votes that a candidate will receive on an election day be Thus the fraction of votes the other candidate will receive will be We shall take as a random variable with a uniform prior distribution over so that its mean is and variance is A few weeks before the election, two independent public opinion polls were conducted by two different pollsters. The first poll revealed that the candidate is likely to get fraction of votes. Since some error is always present due to finite sampling and the particular polling methodology adopted, the first pollster declares their estimate to have an error with zero mean and variance Similarly, the second pollster declares their estimate to be with an error with zero mean and variance Note that except for the mean and variance of the error, the error distribution is unspecified. How should the two polls be combined to obtain the voting prediction for the given candidate?

As with previous example, we have

Here, both the . Thus, we can obtain the LMMSE estimate as the linear combination of and as

where the weights are given by

Here, since the denominator term is constant, the poll with lower error is given higher weight in order to predict the election outcome. Lastly, the variance of is given by

which makes smaller than Thus, the LMMSE is given by

In general, if we have pollsters, then where the weight for i-th pollster is given by and the LMMSE is given by

Example 4[edit]

Suppose that a musician is playing an instrument and that the sound is received by two microphones, each of them located at two different places. Let the attenuation of sound due to distance at each microphone be and , which are assumed to be known constants. Similarly, let the noise at each microphone be and , each with zero mean and variances and respectively. Let denote the sound produced by the musician, which is a random variable with zero mean and variance How should the recorded music from these two microphones be combined, after being synced with each other?

We can model the sound received by each microphone as

Here both the . Thus, we can combine the two sounds as

where the i-th weight is given as

See also[edit]

• Bayesian estimator
• Mean squared error
• Least squares
• Minimum-variance unbiased estimator (MVUE)
• Orthogonality principle
• Wiener filter
• Kalman filter
• Linear prediction
• Zero-forcing equalizer

Notes[edit]

Further reading[edit]

Спектральная плотность вычисляется по известной корреляционной функции при помощи формул.

Вопросы
самоконтроля:

1. Дайте
   определение спектральной плотности.

2. Какой
   функцией является спектральная
   плотность.

3. Как
   вычисляется спектральная плотность
   по известной корреляционной функции.

Лекция 59

Цель
лекции: ознакомиться
с расчетами по минимуму среднеквадратичной
ошибки случайной величины.

Задачи лекции:

1. Расчет
   по минимуму среднеквадратичной ошибки
   случайной величины.

2. Критерий
   минимума среднеквадратичной ошибки
   при одновременном действии полезного
   сигнала и помехи.

Желаемый
результат:

Студенты
должны знать:

1. Расчет
   по минимуму среднеквадратичной ошибки
   случайной величины.

2. Критерий
   минимума среднеквадратичной ошибки
   при одновременном действии полезного
   сигнала и помехи.

Учебный материал Расчеты по минимуму среднеквадратичной ошибки

Если
на автоматическую систему действуют
одновременно полезный сигнал и помеха,
то возникает задача оптимального расчета
системы с тем, чтобы получить наименьшую
результирующую ошибку. С точки зрения
наилучшего воспроизведения полезного
сигнала система должна иметь возможно
большую полосу пропускания, а с точки
зрения наилучшего подавления помехи
система, наоборот, должна иметь возможно
меньшую полосу пропускания. Критерием
получения оптимального решения здесь
будет минимальное значение результирующей
ошибки системы, определяемой полезным
сигналом и помехой.

Для случайных
величин наиболее просто определить
среднеквадратичную ошибку, поэтому ее
и используют для оценки точности
автоматической системы.

Рассмотрим
расчет системы по критерию
минимума среднеквадратич­ной ошибки
при одновременном действии полезного
сигнала и помехи.

Согласно
этому критерию, нежелательность ошибки
пропорциональна квадрату ее величины.
Такая постановка является часто логичной,
но она не может, конечно, претендовать
на полную универсальность. В некоторых
случаях например при стрельбе по
какой-либо цели, все ошибки, большие
некоторого значения, являются одинаково
нежелательными. Однако средний квадрат
ошибки системы регулирования

практически
во всех случаях является наиболее просто
вычисляемой вели­чиной, что и определило
использование этого критерия.

Возможны
несколько формулировок задачи. Наиболее
просто задача может быть сформулирована
так. Если имеется какая-то система
автомати­ческого регулирования
заданной структуры, то необходимо так
выбрать параметры этой системы, чтобы
получить минимум среднеквадратичной
ошибки при заданных статистических
характеристиках полезного сигнала и
помехи.

Эта
задача решается следующим образом. По
спектральной плотности ошибки путем
ее интегрирования находится дисперсия.
Дисперсия полу­чается зависящей от
вероятностных характеристик полезного
сигнала, помехи и параметров системы.
Затем ищутся условия, которые должны
быть наложены на параметры системы,
чтобы получить минимум дисперсии. При
достаточно простом выражении для
дисперсии это может быть определено
непосредственным дифференцированием
и приравниванием нулю частных производных.

В
более сложных случаях приходится искать
минимум дисперсии путем числового
задания интересующих параметров и
построения соответствующих графиков,
а также расчетом на ЭВМ.

Нахождение
оптимальной передаточной функции еще
не означает, что реальная автоматическая
система может быть выполнена оптимальной,
так как реализация ее может быть сопряжена
с большими трудностями. Оптимальную
передаточную функцию, за исключением
простейших слу­чаев, следует считать
идеальной функцией, к которой по
возможности надо стремиться при
выполнении реальной автоматической
системы.

Вопросы
самоконтроля:

1. Какую
   величину используют для оценки точности
   автоматической системы со случайными
   сигналами.

2. Дайте
   определение критерию
   минимума среднеквадратичной ошибки
   при одновременном действии полезного
   сигнала и помехи.

3. Как
   определяется минимум
   дисперсии.

Соседние файлы в папке лекции

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Критерий — минимум — среднеквадратичная ошибка

Cтраница 1

Критерий минимума среднеквадратичной ошибки используется для решения более сложных задач по сравнению с задачей определения оптимальных параметров при известной структуре системы.
 [1]

Идея приближения по критерию минимума среднеквадратичной ошибки, как уже указывалось, не единственна.
 [2]

Тх корректирующего устройства по критерию минимума среднеквадратичной ошибки, если полезный сигнал и помеха независимы и приложены к одной точке системы.
 [3]

Первое из этих условий удовлетворялось и при синтезе по критерию минимума среднеквадратичной ошибки.
 [4]

Адекватность полученной модели и необходимость ее коррекции оценивают чаще всего по критерию минимума среднеквадратичной ошибки. Этот метод наиболее целесообразен.
 [5]

Причем объем вычислений может быть значительно уменьшен за счет незначительного ухудшения качества, фильтрации по критерию минимума среднеквадратичной ошибки.
 [6]

В большинстве практически встречающихся случаев представляется возможным, хотя бы в первом приближении, рассматривать процессы изменения технологических величин или других производственных показателей как стационарные случайные функции с нормальным распределением. Поэтому обычно критерий минимума среднеквадратичной ошибки является наиболее приемлемым в качестве критерия наилучшего предсказания в большинстве рассматриваемых задач управления.
 [7]

Кроме того, по критерию минимума среднеквадратичной ошибки определяются оптимальная структура и передаточная функция замкнутой системы, обеспечивающие минимальную величину погрешности.
 [8]

Анализ и синтез нелинейных систем с неизвестной структурой предлагается проводить с помощью многопеременных прямоугольных функций. Практически реализуемый алгоритм с применением этих функций получен на основе критерия минимума среднеквадратичной ошибки. Алгоритм применим при входных стационарных сигналах с произвольной плотностью распределения вероятностей.
 [9]

Задача заключается в оценке значений, к-рые реализация рассматриваемого процесса ( или нек-рых его параметров, таких, как ср. Здесь в большинстве случаев определяется инвариантный во времени линейный реализуемый фильтр, оптимизирующий оценку по критерию минимума среднеквадратичной ошибки. Возможны и часто желательны др. критерии, но указанный критерий отличается математич. Для решения задач такого рода часто применяется теория Винера — Колмогорова. В этой теории предполагается, что сигнал S ( t) характеризуется только статистич. Мешающий шум N ( t) представляет также чисто случайный процесс, комбинируется с сигналом аддитивно и может быть с ним связан статистически. Далее предполагается, что накопление и обработка данных совершаются только над прошлым процессов на входе, к-рые считаются стационарными в широком смысле и имеющими положительно определенные ковариант-ные ф-ции. Кроме того, в большинстве случаев реализуются оптимальные линейные фильтры, к-рые не только реализуемы, но также и инвариантны во времени. При этих условиях импульсная переходная ф-ция линейного фильтра определяется из интегр.
 [10]

Задача заключается в оценке значений, к-рые реализация рассматриваемого процесса ( или нек-рых его параметров, таких, как ср. Здесь в большинство случаев определяется инвариантный во времени линейный реализуемый фильтр, оптимизирующий оценку по критерию минимума среднеквадратичной ошибки. Возможны и часто желательны др. критерии, но указанный критерий отличается математич. Для решения задач такого рода часто применяется теория Винера — Колмогорова. В этой теории предполагается, что сигнал S ( t) характеризуется только статпстич. Мешающий шум N ( t) представляет также чисто случайный процесс, комбинируется с сигналом аддитивно и может быть с ним связан статистически. Далее предполагается, что накопление и обработка данных совершаются только над прошлым процессов па входе, к-рые считаются стационарными в широком смысле и имеющими положительно определенные ковариант-ные ф-ции. Кроме того, в большинстве случаев реализуются оптимальные линейные фильтры, к-рые не только реализуемы, но также и инвариантны во времени. При этих условиях импульсная переходная ф-ция линейного фильтра определяется из интегр.
 [11]

После определения среднеквадратичной ошибки необходимо обеспечить минимальное значение ее. Наиболее просто задача решается путем минимизации среднеквадратичной ошибки по тому или иному параметру системы при заданных воздействиях. В качестве параметров, которые желательно сделать оптимальными на основе критерия минимума среднеквадратичной ошибки, могут рассматриваться различные постоянные, имеющие большое значение для определения динамических свойств системы.
 [12]

Страницы:  

   1

    Анализ систем на основе критерия минимума среднеквадратичной ошибки [c.189]

    Если ковариационные функции процессов Х( ) и У(/) известны точно, то можно воспользоваться винеровским критерием минимума среднеквадратичной ошибки Этот критерий утверждает, что функция /г(и) должна быть выбрана так, чтобы минимизировать среднеквадратичную ошибку шумовой компоненты, т е [c.190]

    Синтез следящих систем. Одно из первых инженерных применений анализа на основе критерия минимума среднеквадратичной ошибки было сделано при синтезировании следящих систем для зенитных орудий и в радиолокационных следящих системах [5] Например, от радиолокационной следящей системы требуется, чтобы она следила за самолетом несмотря на возмущения отра- [c.189]

    Другое применение критерий минимума среднеквадратичной ошибки находит в задаче об идентификации системы В этом случае в распоряжении имеются входной сигнал и соответствующий ему выходной сигнал от некоторой системы, требуется вывести линейное приближение к этой системе для дальнейшего его использования при управлении или моделировании Предположим, например, что система представляет собой черный ящик (рис 5 7). Если вход является реализацией случайного процесса Х 1), то выход можно рассматривать как реализацию случайного процесса У(0< где [c.190]

    Оптимальное в любом смысле корреляционное окно, например (7 2 3), будет зависеть от неизвестного спектра Гхх(/). Этот недостаток свойствен не только спектральному анализу Вообще говоря, справедливо правило, согласно которому наилучший план действий должен опираться на некоторые представления об истинном положении вещей Следовательно, очень валено проводить четкое различие между планированием спектрального анализа до сбора данных и самим анализом данных, после того как они собраны Мы хотели бы использовать критерии минимума среднеквадратичной ошибки или какой-нибудь аналогичный критерий до проведения спектрального анализа, чтобы решить, например, какой длины нужно взять запись Но после того как данные собраны, могло бы оказаться, что наши представления относительно Гхх (/) были абсолютно неправильны [c.26]

    Если плотность вероятности ге ([х у) симметрична относительно среднего значения гпг [х у и унимодальна (т. е. монотонно невозрастающая функция [х — /П] [х у ), то байесовская оценка (5.18) совпадает с оценкой по критерию максимума апостериорной плотности вероятности. В этом случае функция С (х) не должна быть обязательно выпуклой, а лишь монотонно неубывающей функцией х (см. приложение С). Так как нормальная плотность вероятности унимодальна, то всегда, когда плотность вероятности ге ([х I у) нормальна, оценка по максимуму апостериорной плотности вероятности совпадает с широким классом байесовских оценок, который включает оценки по минимуму среднеквадратичной ошибки (или минимуму дисперсии). [c.158]