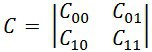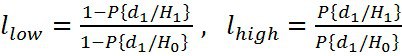Критерий минимума суммы условных вероятностей ошибок

Научная библиотека популярных научных изданий

Макеты страниц

Статистические критерии различения детерминированных сигналов. Для того чтобы задача поиска, или синтеза, оптимальных правил различения сигналов обрела математическую содержательность, необходимо прежде всего задаться некоторым формальным показателем (критерием) качества различения, т. е. количественной мерой, суммирующей ущерб, наносимый ошибочными решениями.

Введение такого показателя не является плодом каких-либо формально-теоретических выкладок: при решении вопроса

об адекватности того или иного критерий реальной ситуации исследователь или проектировщик, учтя все специфические стороны последней, во многом опирается на здравый смысл и техническую интуицию. Избранный на этом этапе критерий в дальнейшем воспринимается как аксиома.

В тех задачах, которые удается свести к проверке простых гипотез, продуктивным оказывается критерий минимума среднего риска, называемый также критерием Байеса. Для того чтобы наиболее наглядно ввести связанную с ним систему понятий и терминов, обратимся к конкретному примеру различения М детерминированных сигналов , на фоне помех с полностью заданным статистическим описанием, т. е. с точно известной ПВ любой размерности или точно известным функционалом ПВ. В рамках такой модели различения ПВ любой размерности или функционал ПВ наблюдаемого колебания при условии, что в входит сигнал с номером — некоторая вполне определенная функция, вид которой зависит лишь от номера . При этом имеется М классов, содержащих по одному распределению, т. е. различение сигналов состоит в проверке простых гипотез.

Предположим, что известна вероятность присутствия в сигнала . Эту вероятность называют априорной (доопытной), поскольку она отражает сведения, которыми располагает наблюдатель, еще не имея в распоряжении реализации и показывает, насколько часто при длительной эксплуатации изучаемой системы можно ожидать появления в . Для систем М-ичной цифровой связи, например, вероятность , характеризует среднюю частоту, с которой посылается в канал. Очевидно, вероятность можно назвать и априорной вероятностью истинности записав . Ясно также, что подчинены условию нормировки , ибо события составляют полную группу несовместных событий.

Предположим, что — условная вероятность перепутывания сигнала с , т. е. принятия решения [о присутствии в ] при условии, что истинна [в содержится ]. Следовательно, множество вероятностей при составляет набор условных вероятностен всех ошибочных решений.

Эти вероятности для любого фиксированного способа различения сигналов можно вычислить, так как помехи считаются полностью статистически заданными (см. далее).

Введем неотрицательных величин ПЛ, каждая из которых характеризует риск (потери, ущерб) от перепутывания -го сигнала с . При этом правильные решения считаются не наносящими ущерба, так что . Для наглядности можно считать некими денежными штрафами, уплачиваемыми за ошибки.

В каждой отдельной попытке различения сигналов итог (решение) оказывается случайным событием, а поэтому случайным будет и значение риска. Очевидно, безусловную вероятность того, что риск окажется равным , по теореме умножения вероятностей можно найти как , поэтому математическое ожидание риска или средний риск

Критерий Байеса, или минимального среднего риска, предписывает добиваться минимума (2.1). Различитель, оптимальный по этому критерию (байесовский различите , при длительной эксплуатации будет наиболее «экономичным» из всех, поскольку сумма штрафов за ошибки у него окажется наименьшей.

Хотя задание рисков (часто и априорных вероятностей ) достаточно произвольно, практическая ценность критерия Байеса чрезвычайно велика, так как он, обобщая ряд других критериев, позволяет получить универсальный ответ на вопрос о наилучшей стратегии различения сигналов. Предположим, например, что, не имея объективных данных для назначения всех рисков, разработчик стремится лишь к тому, чтобы различитель как можно реже ошибался, т. е. чтобы полная вероятность ошибки

была минимальной. Нетрудно видеть, что такой критерий качества, называемый критерием идеального наблюдателя или критерием Котельникова, можно рассматривать как частный случай байесовского, положив в (2.1) , , где П — произвольная неотрицательная константа. При этом и минимизация среднего риска равносильна минимизации (2.2).

Представим теперь, что затруднение вызывает задание не только рисков, но и априорных вероятностей. Подобная картина типична, например, для радиолокационного обнаружения. Тогда определить полную вероятность ошибки нельзя, но можно предложить вполне удовлетворительный критерий качества — критерий минимума суммы условных вероятностей ошибок

Легко убедиться, что это частный случай байесовского критерия, в котором . Действительно, после этих подстановок (2.1) примет вид , указывающий на идентичность задач минимизации .

В частном случае рассматриваемая задача переходит в обнаружение детерминированного сигнала на фоне помех с известным статистическим этом условные вероятности и на статистическом языке называют вероятностями ошибок первого и второго рода. Согласно терминологии, принятой в радиоэлектронике, эти же величины именуют более выразительно — вероятности ложной тревоги и (сигнала), понимая под ложной тревогой факт решения об обнаружении сигнала при условии, что он в наблюдаемом колебании не содержится, а под пропуском — объявление о том, что сигнала в нет при условии, что в действительности он в присутствует. Далее для вероятностей ложной тревоги и пропуска будут использованы обозначения и . Средний риск при обнаружении где и — риски, связанные с ложной тревогой и пропуском; — априорная вероятность отсутствия в . Соотношения (2.2) и (2.3) в этом случае можно представить в виде

Помимо введенных общих критериев, не связанных с какими-либо допущениями относительно числа М проверяемых гипотез, при обнаружении часто применяют критерий Неймана — Пирсона, предписывающий добиваться минимума вероятности пропуска при ограничении сверху на вероятность ложной тревоги .

В математической дисциплине, называемой нелинейным программированием и занимающейся вопросами отыскания условных (в заданных областях аргументов) экстремумов функций многих переменных, доказывается известная теорема Куна—Таккера, согласно которой минимизация при равносильна безусловной минимизации целевой функции , где неопределенный коэффициент Лагранжа. Положив и приведя (2.1) к виду , нетрудно убедиться в возможности интерпретации и этого критерия как частного случая байесовского.

Правила оптимального различения обнаружения. Попытаемся выяснить, какой стратегии должен придерживаться байесовский различитель М детерминированных сигналов. При этом в свете ранее изложенного сразу будут установлены и стратегии функционирования различителен, оптимальных по критериям минимума и , а также обнаружителя Неймана — Пирсона.

Предположим, что из наблюдаемой реализации доступны лишь дискретных отсчетов , составляющих вектор наблюдения . Обобщение на случай непрерывного наблюдения в дальнейшем не составит труда. Пусть — условная ПВ вектора при условии, что верна гипотеза т. е. что в содержится . Так как помехи полностью статистически заданы, то — некая конкретная функция, удовлетворяющая условиям где, как и далее, отсутствие пределов интеграла соответствует интегрированию по всей области задания функции.

Любая нерандомизированная (не включающая преднамеренно введенных действий со случайным исходом типа бросания жребия) процедура различения М сигналов может интерпретироваться следующим образом. Допустим, что -мерное пространство векторов разбито на М (соответственно числу различаемых сигналов) непересекающихся областей решения :

Тогда принятие решения различителем сводится к указанию номера области, в которую попал вектор наблюдения . Если , то принимается решение о присутствии в сигнала . Возможность такой «геометризации» различения сводит поиски оптимальной стратегии различителя к отысканию наилучшего разбиения на области решений.

В случае обнаружения число областей решения также равно двум: , причем область называют допустимой (при принимают решение об истинности ), а область -критической (при гипотезу отклоняют и принимают решение ).

Для того чтобы найти оптимальное правило разбиения, подставим в (2.1) выражения для условных вероятностей ошибок , вытекающие из определения

областей .Тогда

Очевидно, «назначение» конкретной конфигурации областей решения сводится к тому, чтобы, перебрав все векторы , расписать их по М областям, включив каждый в одну и только одну область . При этом, как следует из последней формулы, каждый вектор войдет в одно и только одно слагаемое суммы по , отвечающее той области, за которой он закреплен. Поэтому минимума можно добиться, если охватить областью именно те векторы , для которых подынтегральное выражение в интеграле минимально. Следовательно, разбиением на области , минимизирующим , будет такое, при котором в включаются векторы (и только они), удовлетворяющие системе неравенств

Если перейти к случаю непрерывного наблюдения (к пространствам бесконечной размерности), то ПВ в (2.4) превратятся в функционалы ПВ , т. е. область принятия решения определится системой М неравенств

Таким образом, байесовский различитель, наблюдая реализацию , должен установить номер для которого совместно выполнены неравенства (2.5), и принять решение о наличии в сигнала с номером . Представим это правило в виде, который и далее будет использоваться для записи алгоритмов различения сигналов:

где символ указывает на решение, принимаемое при одновременном выполнении всех неравенств в (2.6). Отметим, что величину

называют условным или апостериорным [вычисленным для данной конкретной наблюдаемой реализации ] средним риском. Поэтому выражение (2.6) подразумевает вычисление для анализируемой реализации значений условного среднего риска , и принятие решения о наличии в сигнала с тем номером , для которого значение минимально.

Рассмотрим важнейшие частные случаи. Для идеального наблюдателя, минимизирующего (2.2), следует положить . Тогда выражение (2.6) примет вид

На основании формулы полной вероятности

согласно (2.7), получим

Так как, по теореме умножения вероятностей, , то соотношение (2.8) может быть переписано как

Величина определяет апостериорную (обратную, послсопытную) вероятность гипотезы т. е. вероятность наличия -гo сигнала в с учетом всех сведений, которые можно извлечь из наблюдаемой реализации . Следовательно, идеальный наблюдатель принимает решение в пользу сигнала, имеющего наибольшую апостериорную вероятность, т. е. действует по правилу максимума апостериорной вероятности (МАВ).

Если данные об априорных вероятностях ненадежны и проектировщик предпочел критерий минимума суммы условных вероятностей ошибок (2.3), то соответствующее оптимальное правило различения можно получить из (2.8) при :

Функционал ПВ — условной ПВ, определенной при условии истинности гипотезы [присутствия в ], — рассматриваемый как функция номера гипотезы при фиксированной реализации , называют функцией (функционалом) правдоподобия (ФП). Таким образом, стратегия различителя, минимизирующего (2.3), сводится к использованию правила максимума правдоподобия (МП), т. е. к подстановке принятой реализации в выражение для ФП, известное в силу детерминированности сигналов и статистической определенности помех, и подбору , максимизирующего ФП.

В случае обнаружения детерминированного сигнала выражение (2.6) можно переписать так:

где расстановка символов и показывает, вьшолнение какого из неравенств влечет за собой принятие соответствующего решения. Правило (2.11) традиционно представляют в виде

называя отношение двух значений ФП отношением (коэффициентом) правдоподобия (ОП). Как видно, байесовский обнаружитель детерминированного сигнала должен для полученной реализации вычислить ОП и сравнить его с порогом , зависящим от рисков и априорных вероятностей отсутствия и наличия сигнала.

Если разработчик обнаружителя ориентируется на критерий идеального наблюдателя, то в выражении (2.12) следует положить , что превратит его в правило МАВ, сделав пороговый уровень равным . Аналогично, принятие за основу критерия минимума придаст (2.12) вид правила МП, для которого .

Наконец, стратегию обнаружителя,оптимального по Нейману — Пирсону, также можно описать соотношением (2.12), если значение выбрать из условия поддержания вероятности ложной тревоги не выше заданного уровня.

Как видно, обнаружители, оптимальные по любому из рассмотренных критериев, должны выполнять одни и те же действия: вычислять ОП и сравнивать его с порогом. От конкретного критерия зависит лишь значение порога, и поэтому обнаружитель, наилучший по одному критерию, трансформируется в оптимальный по другому простым изменением порога

Завершим параграф одним существенным для дальнейшего рассуждением. Хотя выражения (2.6) — (2.12) однозначно определяют последовательность действий оптимальных различителен, соображения практического плана нередко толкают на путь таких модификаций этих правил, реальное воплощение которых (аппаратурное или программное) оказалось бы наиболее простым. В основе подобных модификаций лежит переход от величин, фигурирующих в (2.6) — (2.12), к так называемым статистикам — величинам, заменяющим ФП, ОП и т. п. без потери оптимальности соответствующего правила. Так, достаточными статистиками при различении сигналов по правилу МАВ будут величины , по правилу МП — , при и , где — любая монотонно изменяющаяся функция. Действительно, если, например, функция монотонно возрастает, то система неравенств

равносильна системе неравенств в (2.10), поэтому правило

есть просто эквивалентная запись правила МП (2.10).

1

Оглавление

  • Предисловие
  • ВВЕДЕНИЕ
  • ЧАСТЬ 1. ВВЕДЕНИЕ В СТАТИСТИЧЕСКУЮ ТЕОРИЮ РАДИОТЕХНИЧЕСКИХ СИСТЕМ
  • ГЛАВА 1. ПЕРЕНОСЧИКИ ИНФОРМАЦИИ И ПОМЕХИ В РАДИОТЕХНИЧЕСКИХ СИСТЕМАХ
  • §1.2. ПОЛЯ, СИГНАЛЫ, ПОМЕХИ. ПРЕДМЕТ СТАТИСТИЧЕСКОЙ ТЕОРИИ РТС
  • § 1.3. ПРЕДСТАВЛЕНИЕ СИГНАЛОВ И ПОМЕХ
  • § 1.4. НОРМАЛЬНЫЙ ВЕКТОР И НОРМАЛЬНЫЙ СЛУЧАЙНЫЙ ПРОЦЕСС. БЕЛЫЙ ШУМ
  • ГЛАВА 2. ОСНОВЫ ТЕОРИИ ОБНАРУЖЕНИЯ И РАЗЛИЧЕНИЯ СИГНАЛОВ
  • § 2.1. СОДЕРЖАНИЕ И КЛАССИФИКАЦИЯ ЗАДАЧ ОБНАРУЖЕНИЯ И РАЗЛИЧЕНИЯ СИГНАЛОВ
  • § 2.2. РАЗЛИЧЕНИЕ ДЕТЕРМИНИРОВАННЫХ СИГНАЛОВ
  • § 2.3. РАЗЛИЧЕНИЕ СИГНАЛОВ СО СЛУЧАЙНЫМИ ПАРАМЕТРАМИ
  • § 2.4. ФУНКЦИЯ И ОТНОШЕНИЕ ПРАВДОПОДОБИЯ ПРИ РАЗЛИЧЕНИИ СИГНАЛОВ НА ФОНЕ АДДИТИВНОГО НОРМАЛЬНОГО ШУМА
  • ГЛАВА 3. АЛГОРИТМЫ И УСТРОЙСТВА ОПТИМАЛЬНОГО ОБНАРУЖЕНИЯ И РАЗЛИЧЕНИЯ СИГНАЛОВ
  • § 3.1. ОБНАРУЖЕНИЕ ДЕТЕРМИНИРОВАННОГО СИГНАЛА
  • § 3.2. ОБНАРУЖЕНИЕ СИГНАЛА СО СЛУЧАЙНОЙ НАЧАЛЬНОЙ ФАЗОЙ
  • § 3.3. ОБНАРУЖЕНИЕ СИГНАЛА СО СЛУЧАЙНЫМИ АМПЛИТУДОЙ И НАЧАЛЬНОЙ ФАЗОЙ
  • § 3.4. ОБНАРУЖЕНИЕ ПАКЕТОВ ИМПУЛЬСОВ
  • § 3.5. ОБНАРУЖЕНИЕ СЛУЧАЙНЫХ СИГНАЛОВ
  • §3.6. СТРУКТУРЫ И ПОКАЗАТЕЛИ РАЗЛИЧИТЕЛЕЙ ДЕТЕРМИНИРОВАННЫХ СИГНАЛОВ
  • §3.7. РАЗЛИЧЕНИЕ СИГНАЛОВ СО СЛУЧАЙНЫМИ НАЧАЛЬНЫМИ ФАЗАМИ
  • §3.8. ОПТИМАЛЬНЫЙ ПРИЕМ СИГНАЛОВ НА ФОНЕ НЕБЕЛОГО ШУМА
  • ГЛАВА 4. ОСНОВЫ ТЕОРИИ ИЗМЕРЕНИЯ ПАРАМЕТРОВ СИГНАЛОВ РАДИОТЕХНИЧЕСКИХ СИСТЕМ
  • § 4.1. СОДЕРЖАНИЕ И КЛАССИФИКАЦИЯ ЗАДАЧ ИЗМЕРЕНИЯ ПАРАМЕТРОВ СИГНАЛОВ
  • § 4.2. БАЙЕСОВСКИЕ ОЦЕНКИ СЛУЧАЙНЫХ ПАРАМЕТРОВ СИГНАЛОВ
  • § 4.3. КРИТЕРИИ ОЦЕНКИ НЕСЛУЧАЙНЫХ ПАРАМЕТРОВ СИГНАЛОВ. ГРАНИЦА КРАМЕРА—РАО
  • § 4.4. ОЦЕНКИ ПО МАКСИМУМУ ПРАВДОПОДОБИЯ
  • § 4.5. ОЦЕНКИ ПО МАКСИМУМУ ПРАВДОПОДОБИЯ ПРИ НАЛИЧИИ У СИГНАЛА НЕИНФОРМАЦИОННЫХ ПАРАМЕТРОВ
  • § 4.6. ОЦЕНКА ПАРАМЕТРОВ СИГНАЛА НА ФОНЕ АДДИТИВНОГО НОРМАЛЬНОГО ШУМА
  • § 4.7. ВЫЧИСЛЕНИЕ ДИСПЕРСИЙ ОЦЕНОК. ФУНКЦИИ НЕОПРЕДЕЛЕННОСТИ
  • § 4.8. АНОМАЛЬНЫЕ ОШИБКИ И ПОРОГОВЫЕ ЭФФЕКТЫ ПРИ ОЦЕНКЕ ПАРАМЕТРОВ СИГНАЛОВ
  • § 4.9. ЭЛЕМЕНТЫ ТЕОРИИ ФИЛЬТРАЦИИ ПАРАМЕТРОВ СИГНАЛОВ
  • ГЛАВА 5. ПРИМЕРЫ РЕАЛИЗАЦИИ И РАСЧЕТА ТОЧНОСТИ АЛГОРИТМОВ ОЦЕНКИ ПАРАМЕТРОВ СИГНАЛОВ
  • § 5.1. ОЦЕНКА ВСЕХ НЕИЗВЕСТНЫХ ПАРАМЕТРОВ СИГНАЛОВ
  • §5.2. ОЦЕНКИ ПАРАМЕТРОВ СИГНАЛА СО СЛУЧАЙНОЙ ФАЗОЙ
  • ГЛАВА 6. РАЗРЕШЕНИЕ СИГНАЛОВ. СЛОЖНЫЕ СИГНАЛЫ
  • § 6.1. ПОНЯТИЕ О РАЗРЕШЕНИИ И РАЗРЕШАЮЩЕЙ СПОСОБНОСТИ
  • § 6.2. ФУНКЦИЯ НЕОПРЕДЕЛЕННОСТИ В ТЕОРИИ РАЗРЕШЕНИЯ
  • § 6.3. РАЗРЕШЕНИЕ ПО ВРЕМЕНИ ЗАПАЗДЫВАНИЯ. ПРОСТЫЕ И СЛОЖНЫЕ СИГНАЛЫ
  • § 6.4. ВИДЫ СЛОЖНЫХ СИГНАЛОВ
  • § 6.5. РАЗРЕШЕНИЕ ПО ВРЕМЕНИ ЗАПАЗДЫВАНИЯ И ЧАСТОТЕ. ЧАСТОТНО-ВРЕМЕННАЯ ФУНКЦИЯ НЕОПРЕДЕЛЕННОСТИ СИГНАЛА
  • ЧАСТЬ 2. РАДИО ЛОКАЦИОННЫЕ И РАДИО НАВИГАЦИОННЫЕ СИСТЕМЫ
  • ГЛАВА 7. ОСНОВНЫЕ ПРИНЦИПЫ ПОСТРОЕНИЯ РАДИОЛОКАЦИОННЫХ И РАДИОНАВИГАЦИОННЫХ СИСТЕМ
  • § 7.2. РАДИОТЕХНИЧЕСКИЕ МЕТОДЫ ИЗМЕРЕНИЯ КООРДИНАТ И ИХ ПРОИЗВОДНЫХ
  • § 7.3. КЛАССИФИКАЦИЯ РАДИОЛОКАЦИОННЫХ И РАДИОНАВИГАЦИОННЫХ СИСТЕМ, ИХ ТАКТИЧЕСКИЕ И ТЕХНИЧЕСКИЕ ХАРАКТЕРИСТИКИ
  • § 7.4. ПОСТРОЕНИЕ И ОСНОВНЫЕ ХАРАКТЕРИСТИКИ РЛС КРУГОВОГО ОБЗОРА
  • ГЛАВА 8. ФИЗИЧЕСКИЕ ОСНОВЫ РАДИОЛОКАЦИОННОГО ОБНАРУЖЕНИЯ ОБЪЕКТОВ
  • § 8.1. РАДИОЛОКАЦИОННЫЕ ЦЕЛИ И ФОРМИРОВАНИЕ ОТРАЖЕННЫХ СИГНАЛОВ
  • § 8.2. ЭФФЕКТИВНАЯ ПЛОЩАДЬ РАССЕЯНИЯ ПРОСТЕЙШИХ ОБЪЕКТОВ
  • § 8.3. ЭФФЕКТИВНАЯ ПЛОЩАДЬ РАССЕЯНИЯ ГРУППОВЫХ И РАСПРЕДЕЛЕННЫХ ОБЪЕКТОВ
  • § 8.4. СТАТИСТИЧЕСКИЕ СВОЙСТВА ЭПР ЦЕЛЕЙ И ОТРАЖЕННЫХ СИГНАЛОВ
  • ГЛАВА 9. ДАЛЬНОСТЬ ДЕЙСТВИЯ РАДИОСИСТЕМ
  • § 9.1. ДАЛЬНОСТЬ ДЕЙСТВИЯ РАДИОЛИНИЙ
  • § 9.2. ОБОБЩЕННОЕ УРАВНЕНИЕ ДАЛЬНОСТИ РАДИОЛОКАЦИОННОГО НАБЛЮДЕНИЯ В СВОБОДНОМ ПРОСТРАНСТВЕ
  • § 9.3. ВЛИЯНИЕ ОТРАЖЕНИЯ РАДИОВОЛН ОТ ЗЕМНОЙ ПОВЕРХНОСТИ НА ДАЛЬНОСТЬ ДЕЙСТВИЯ РЛС
  • § 9.4. ВЛИЯНИЕ УСЛОВИЙ РАСПРОСТРАНЕНИЯ РАДИОВОЛН НА ДАЛЬНОСТЬ ДЕЙСТВИЯ РАДИОЛОКАЦИОННЫХ И РАДИОНАВИГАЦИОННЫХ СИСТЕМ
  • ГЛАВА 10. ТОЧНОСТЬ РАДИОТЕХНИЧЕСКИХ МЕТОДОВ МЕСТООПРЕДЕЛЕНИЯ
  • § 10.1. ПОГРЕШНОСТИ ИЗМЕРЕНИЯ РАДИОНАВИГАЦИОННОГО ПАРАМЕТРА
  • § 10.2. ПОГРЕШНОСТИ ОПРЕДЕЛЕНИЯ ЛИНИЙ ПОЛОЖЕНИЯ РАДИОНАВИГАЦИОННЫХ СИСТЕМ
  • § 10.3. ПОГРЕШНОСТИ ОПРЕДЕЛЕНИЯ КООРДИНАТ ОБЪЕКТА ПОЗИЦИОННЫМ МЕТОДОМ
  • § 10.4. РАБОЧИЕ ЗОНЫ РАДИОНАВИГАЦИОННЫХ СИСТЕМ
  • § 10.5. ВЛИЯНИЕ ГЕОМЕТРИЧЕСКОГО ФАКТОРА РАДИОНАВИГАЦИОННОЙ СИСТЕМЫ И УСЛОВИЙ РАСПРОСТРАНЕНИЯ РАДИОВОЛН НА ТОЧНОСТЬ ОПРЕДЕЛЕНИЯ МЕСТОПОЛОЖЕНИЯ ОБЪЕКТА
  • ГЛАВА 11 ПОИСК СИГНАЛОВ В РАДИОЛОКАЦИОННЫХ И РАДИОНАВИГАЦИОННЫХ СИСТЕМАХ
  • § 11.1. ПОИСК СИГНАЛОВ ПО УГЛОВЫМ КООРДИНАТАМ, ДАЛЬНОСТИ И СКОРОСТИ
  • § 11.2. МЕТОДЫ ПОСЛЕДОВАТЕЛЬНОГО ОБЗОРА ПРОСТРАНСТВА
  • § 11.3. МНОГОКАНАЛЬНЫЙ И УПРАВЛЯЕМЫЙ ОБЗОР ПРОСТРАНСТВА
  • § 11.4. ОСОБЕННОСТИ ПОИСКА СИГНАЛОВ В РАДИОНАВИГАЦИОННЫХ СИСТЕМАХ
  • ГЛАВА 12. ВЫДЕЛЕНИЕ СИГНАЛОВ ДВИЖУЩИХСЯ ЦЕЛЕЙ НА ФОНЕ ПАССИВНЫХ ПОМЕХ
  • § 12.1. МЕТОДЫ ЗАЩИТЫ ОТ ПАССИВНЫХ ПОМЕХ
  • § 12.2. СЕЛЕКЦИИ ДВИЖУЩИХСЯ ЦЕЛЕЙ НА ОСНОВЕ ЭФФЕКТА ДОПЛЕРА
  • § 12.3. АНАЛОГОВАЯ И ЦИФРОВАЯ ФИЛЬТРАЦИИ В СИСТЕМАХ СЕЛЕКЦИИ ДВИЖУЩИХСЯ ЦЕЛЕЙ
  • § 12.4. ЭФФЕКТИВНОСТЬ СИСТЕМЫ СЕЛЕКЦИИ ДВИЖУЩИХСЯ ЦЕЛЕЙ И ЕЕ ЗАВИСИМОСТЬ ОТ ПАРАМЕТРОВ РАДИОЛОКАЦИОННОЙ СТАНЦИИ
  • § 12.5. МЕТОДЫ ПОВЫШЕНИЯ ЭФФЕКТИВНОСТИ СИСТЕМ СЕЛЕКЦИИ ДВИЖУЩИХСЯ ЦЕЛЕЙ
  • ГЛАВА 13. ФАЗОВЫЕ И ИМПУЛЬСНО-ФАЗОВЫЕ РАДИОНАВИГАЦИОННЫЕ СИСТЕМЫ
  • § 13.1. ОСОБЕННОСТИ ФАЗОВЫХ РАДИОНАВИГАЦИОННЫХ СИСТЕМ. ФАЗОВЫЙ МЕТОД ИЗМЕРЕНИЯ ДАЛЬНОСТИ
  • § 13.2. МНОГОЧАСТОТНЫЕ ФАЗОВЫЕ РАДИОНАВИГАЦИОННЫЕ СИСТЕМЫ
  • § 13.3. УСТРАНЕНИЕ МНОГОЗНАЧНОСТИ ИЗМЕРЕНИЙ В МНОГОЧАСТОТНЫХ ФАЗОВЫХ РАДИОНАВИГАЦИОННЫХ СИСТЕМАХ
  • § 13.4. ПОСТРОЕНИЕ ПРИЕМОИНДИКАТОРОВ МНОГОЧАСТОТНЫХ ФАЗОВЫХ РАДИОНАВИГАЦИОННЫХ СИСТЕМ
  • § 13.5. ИМПУЛЬСНО-ФАЗОВЫЕ РАДИОНАВИГАЦИОННЫЕ СИСТЕМЫ
  • § 13.6. УСТРАНЕНИЕ МНОГОЗНАЧНОСТИ ИЗМЕРЕНИЙ В ИМПУЛЬСНО-ФАЗОВЫХ РАДИОНАВИГАЦИОННЫХ СИСТЕМАХ
  • § 13.7. ПОСТРОЕНИЕ ЦИФРОВЫХ ПРИЕМОИНДИКАТОРОВ ИМПУЛЬСНО-ФАЗОВЫХ РАДИОНАВИГАЦИОННЫХ СИСТЕМ
  • ГЛАВА 14 СПУТНИКОВЫЕ РАДИОНАВИГАЦИОННЫЕ СИСТЕМЫ
  • § 14.1. СПУТНИКОВЫЕ РАДИОНАВИГАЦИОННЫЕ СИСТЕМЫ ПЕРВОГО ПОКОЛЕНИЯ
  • § 14.2. СПУТНИКОВЫЕ РАДИОНАВИГАЦИОННЫЕ СИСТЕМЫ ВТОРОГО ПОКОЛЕНИЯ
  • § 14.3. ПРИНЦИПЫ ПОСТРОЕНИЯ АППАРАТУРЫ ПОТРЕБИТЕЛЕЙ СПУТНИКОВЫХ РАДИОНАВИГАЦИОННЫХ СИСТЕМ ВТОРОГО ПОКОЛЕНИЯ
  • ГЛАВА 15. ИЗМЕРЕНИЕ ВРЕМЕНИ ЗАПАЗДЫВАНИЯ СИГНАЛОВ В РАДИОНАВИГАЦИОННЫХ СИСТЕМАХ
  • § 15.2. ПРИНЦИПЫ ПОСТРОЕНИЯ СЛЕДЯЩИХ ИЗМЕРИТЕЛЕЙ
  • § 15.3. РАСЧЕТ ДИСПЕРСИИ ОЦЕНКИ ВРЕМЕНИ ЗАПАЗДЫВАНИЯ В СЛЕДЯЩИХ ИЗМЕРИТЕЛЯХ ПРИ ДЕЙСТВИИ ФЛУКТУАЦИОННЫХ ПОМЕХ
  • § 15.4. КАЧЕСТВЕННЫЕ ПОКАЗАТЕЛИ ВРЕМЕННЫХ ДИСКРИМИНАТОРОВ ПРИ ИСПОЛЬЗОВАНИИ ПРОСТЫХ СИГНАЛОВ
  • § 15.5. ОСОБЕННОСТИ ПОСТРОЕНИЯ ВРЕМЕННЫХ ДИСКРИМИНАТОРОВ ПРИ ИСПОЛЬЗОВАНИИ СЛОЖНЫХ СИГНАЛОВ
  • ГЛАВА 16 ЧАСТОТНЫЕ ДАЛЬНОМЕРНЫЕ СИСТЕМЫ
  • § 16.1. ЧАСТОТНЫЙ МЕТОД ИЗМЕРЕНИЯ ДАЛЬНОСТИ
  • § 16.2. СОВМЕСТНОЕ ИЗМЕРЕНИЕ ДАЛЬНОСТИ И СКОРОСТИ ОБЪЕКТА ЧАСТОТНЫМ МЕТОДОМ
  • § 16.3. ИЗМЕРЕНИЕ ДАЛЬНОСТИ МНОГИХ ОБЪЕКТОВ
  • § 16.4. ОСОБЕННОСТИ ПРИМЕНЕНИЯ ЧАСТОТНОГО МЕТОДА В РАДИОВЫСОТОМЕРАХ
  • ГЛАВА 17. РАДИОТЕХНИЧЕСКИЕ СИСТЕМЫ ИЗМЕРЕНИЯ СКОРОСТИ
  • § 17.1. ДОПЛЕРОВСКИЙ МЕТОД ИЗМЕРЕНИЯ ПУТЕВОЙ СКОРОСТИ И УГЛА СНОСА
  • § 17.2. ИЗМЕРЕНИЕ ПУТЕВОЙ СКОРОСТИ И УГЛА СНОСА МНОГОЛУЧЕВЫМИ СИСТЕМАМИ
  • § 17.3. ПОСТРОЕНИЕ ДОПЛЕРОВСКИХ ИЗМЕРИТЕЛЕЙ ВЕКТОРА СКОРОСТИ
  • § 17.4. КОРРЕЛЯЦИОННЫЙ МЕТОД ИЗМЕРЕНИЯ ПУТЕВОЙ СКОРОСТИ И УГЛА СНОСА
  • § 17.5. ИЗМЕРИТЕЛЬ СКОРОСТИ В СОСТАВЕ НАВИГАЦИОННОГО КОМПЛЕКСА
  • ГЛАВА 18. МЕТОДЫ И УСТРОЙСТВА ИЗМЕРЕНИЯ УГЛОВЫХ КООРДИНАТ
  • § 18.1. МЕТОДЫ ИЗМЕРЕНИЯ УГЛОВЫХ КООРДИНАТ
  • § 18.2. ТОЧНОСТЬ И РАЗРЕШАЮЩАЯ СПОСОБНОСТЬ РАДИОСИСТЕМ ПРИ ПРОСТРАНСТВЕННО-ВРЕМЕННОЙ ОБРАБОТКЕ
  • § 18.3. РЛС БОКОВОГО ОБЗОРА С СИНТЕЗИРОВАНИЕМ АПЕРТУРЫ
  • § 18.4. СЛЕДЯЩИЕ ИЗМЕРИТЕЛИ НАПРАВЛЕНИЯ
  • § 18.5. ОДНОКАНАЛЬНЫЕ СЛЕДЯЩИЕ ИЗМЕРИТЕЛИ НАПРАВЛЕНИЯ С КОНИЧЕСКИМ СКАНИРОВАНИЕМ
  • § 18.6. МОНОИМПУЛЬСНЫЕ ИЗМЕРИТЕЛИ УГЛОВЫХ КООРДИНАТ
  • § 18.7. ПРЕОБРАЗОВАНИЕ УГЛОВЫХ КООРДИНАТ В ЦИФРОВОЙ КОД
  • ГЛАВА 19. ОПТИЧЕСКАЯ ЛОКАЦИЯ
  • § 19.1. ФИЗИЧЕСКИЕ ОСНОВЫ ОПТИЧЕСКОЙ ЛОКАЦИИ
  • § 19.2. ОПТИМАЛЬНЫЕ МЕТОДЫ ОБРАБОТКИ СИГНАЛОВ В ОПТИЧЕСКИХ ЛОКАЦИОННЫХ СИСТЕМАХ
  • ГЛАВА 20. РАДИОТЕПЛОЛОКАЦИЯ
  • § 20.1. ФИЗИЧЕСКИЕ ОСНОВЫ ПАССИВНОЙ РАДИОЛОКАЦИИ
  • § 20.2. ОБНАРУЖЕНИЕ РАДИОТЕПЛОВЫХ СИГНАЛОВ. СТРУКТУРНЫЕ СХЕМЫ РАДИОМЕТРОВ
  • § 20.3. ИЗМЕРЕНИЕ КООРДИНАТ ОБЪЕКТОВ С ПОМОЩЬЮ РАДИОТЕПЛОЛОКАТОРОВ
  • ГЛАВА 21 СИСТЕМЫ РАДИОПРОТИВОДЕЙСТВИЯ. ЗАЩИТА ОТ АКТИВНЫХ ПОМЕХ
  • § 21.1. МЕТОДЫ РАДИОПРОТИВОДЕЙСТВИЯ. ОСНОВНЫЕ ВИДЫ АКТИВНЫХ ПОМЕХ
  • § 21.2. СИСТЕМЫ РАДИОТЕХНИЧЕСКОЙ РАЗВЕДКИ
  • § 21.3. МЕТОДЫ ЗАЩИТЫ ОТ АКТИВНЫХ ПОМЕХ
  • ГЛАВА 22. МЕТОДЫ ОЦЕНИВАНИЯ ПАРАМЕТРОВ ДВИЖЕНИЯ ОБЪЕКТОВ И КОМПЛЕКСИРОВАНИЕ СИСТЕМ
  • § 22.2. МЕТОДЫ ОЦЕНИВАНИЯ ПАРАМЕТРОВ ДВИЖЕНИЯ ОБЪЕКТОВ
  • § 22.3. КОМПЛЕКСНЫЕ РАДИОТЕХНИЧЕСКИЕ СИСТЕМЫ
  • § 22.4. НАВИГАЦИОННЫЕ КОМПЛЕКСЫ САМОЛЕТОВ И СУДОВ
  • ЗАКЛЮЧЕНИЕ
  • Список литературы
Источник

ВВЕДЕНИЕ

Радиотехнические системы
относятся к классу информационно-управляющих технических систем, осуществляющих
извлечение, передачу или разрушение информации с помощью радиоволн.

 Отличительный признак радиосистемы – наличие радиоканала (одного
или нескольких), состоящего из источника радиоволн, являющихся носителем информации,
среды, в которой распространяются радиоволны, и приемника, извлекающего
информацию путем соответствующей обработки радиоволн, достигающих его антенны.
Радиоволны, несущие ту или иную информацию, называются радиосигналом. Таким
образом, характерным признаком радиосистемы является использование радиосигнала
в качестве носителя информации.

Назначение информации – один
из признаков классификации радиосистем. По этому признаку радиосистемы можно
подразделить на системы передачи, извлечения и разрушения информации  (радиопротиводействия), а также системы
радиоуправления.

К системам
извлечения информации относятся радиолокационные и радионавигационные
системы, системы радиоастрономии, радионаблюдения поверхности Земли или других
планет, ради о разведки радиотехнических средств противника.

Системы
разрушения информации (радиопротиводействия) предназначены для создания условий, в которых
работа радиосистем противника становится невозможной.

Системы
радиоуправления служат для управления работой различных объектов с помощью радиосигналов.

По виду применяемых сигналов различают непрерывные,
импульсные и цифровые радиосистемы. В непрерывных системах информация
отображается изменением параметров (амплитуды, частоты, фазы) непрерывного,
обычно гармонического, сигнала. В импульсных системах сигнал представляет собой
последовательность радиоимпульсов, в которой информацию могут нести как
изменяющиеся параметры отдельных импульсов (амплитуда, частота, фаза, длительность),
так и всей последовательности (число импульсов в последовательности, интервал
между ними).

В цифровых системах
передаваемый сигнал предварительно квантуется по времени и уровню. Каждому
уровню соответствует кодовая группа импульсов, которые и модулируют несущее
колебание. Цифровые системы — легко сопрягаются с ЭВМ, осуществляющими
обработку и запоминание информации, воспроизводимой затем устройством отображения.

Для создания радиосистем
различных назначений используется практически весь диапазон радиоволн от мириаметровых
(l= 10 –: 100 км) до миллиметровых (l =1 –: 10 мм); лазерные системы, тесно
примыкающие по принципу действия и назначению к радиотехническим, работают в
инфракрасном и видимом диапазонах электромагнитных волн. Таким образом,
применяется почти весь спектр электромагнитных колебаний.

 Следует подчеркнуть, что использование того или иного диапазона
радиочастот для систем различных назначений регламентировано международной комиссией
распределения радиочастот (МКРР), так же как и ширина спектра частот,
отводимого системе того или иного типа. Эти ограничения влияют на выбор вида
радиосигнала и построение радиосистемы, и в конечном счете сказываются на ее
тактико-технических характеристиках.

При создании системы стремятся получить наилучшие характеристики для
определенных условий ее работы.

Лекция 1

ВВЕДЕНИЕ В СТАТИСТИЧЕСКУЮ ТЕОРИЮ
РАДИОТЕХНИЧЕСКИХ СИГНАЛОВ

Физические
явления, колебания, процессы, осуществляющие перенос информации, называют сигналами, и так как в радиотехнике сообщения
передаются посредством радиоволн, т. е. электромагнитного поля, то за ним и
следовало бы закрепить наименование «сигнал».
Поскольку поле математически описывается скалярной (напряженностью) или векторной
(при учете поляризационных эффектов) функцией времени и пространственных
координат, сигнал в РТС является пространственно-временным, задаваемым
зависимостью S (t, г), в которой г – радиус-вектор рассматриваемой точки
трехмерного пространства.

Сигналы можно разделить на детерминированные[M2] и случайные[M3].

Случайные процессы
подчиняются статистическим закономерностям, для их описания вводят
характеристики случайных процессов.

1.    
Закон
распределения вероятностей

Вероятность того, что
величина x(t1) при
измерении попадет в интервал (a,b),
где p(x1,t1)
– дифференциальный закон распределения случайной величины х.

2.     Среднее
значение  (математическое ожидание)

3. Среднеквадратичное
значение

3.    
Корреляционная
функция

Помехи, упоминавшиеся ранее,
есть не что иное, как некоторое вредное поле х (t, г), взаимодействующее с
сигналом S (t, г), продуктом чего оказывается
результирующее поле у (t, г) = F[S(t, г), х (t,r)], где F[.,.] – оператор,
описывающий закон комбинирования сигнала и помехи (S (t, г) и х (t, г) могут складываться,
скалярно или векторно перемножаться и т. д.). Наблюдатель, т. е. приемная сторона, воспринимает именно
результирующее поле у (t, г).

В силу своей
недетерминированности, непредсказуемости помеха разрушает однозначную связь
поля, наблюдаемого в данной области пространства, с переносимым им сообщением,
так что у приемной стороны могут возникать сомнения в достоверности получаемых
ею сведений.

Статистическая теория РТС как раз и призвана
вооружить специалиста умением строить систему так, чтобы, используя имеющиеся
средства, максимизировать помехоустойчивость РТС, в наибольшей степени защитить
обрабатываемую информацию от искажающего влияния помех.

Таким образом ,под сигналом
далее будем понимать функцию времени, в которую тем или иным способом «вложено»
передаваемое сообщение. Приемной стороне (наблюдателю) сигнал доступен лишь в
смеси с помехой, т. е. в виде колебания (1.1).

y(t)=F[
S(t), x (t) ]                                         (1.1)

Важнейшая задача теории –
научить наблюдателя оптимально, т. е. с
наивысшей достоверностью, извлекать информацию, вложенную в сигнал, содержащийся
в у(t).

Под извлечением информации
понимают такие процедуры, как обнаружение, оценка параметров, фильтрация
и т. д., однако все они в конечном счете сводятся к различению сигналов, т. е. к установлению того, какой из
возможных сигналов присутствует в у (t).

Выполнив различение, наблюдатель, осведомленный
заранее об алгоритме «вложения» сообщения в сигнал, т. е. о законе соответствия
сигналов сообщениям, узнает и само сообщение.

2.ОСНОВЫ ТЕОРИИ ОБНАРУЖЕНИЯ
И РАЗЛИЧЕНИЯ

СИГНАЛОВ.

Несмотря на многообразие  целевых назначений, видов и принципов работы
современных радиоэлектронных систем , можно выделить целый ряд операций,
поддающихся унифицированию и в достаточной мере абстрактному исследованию, не
опирающемуся на специфику той или иной системы, продуктивному для многих
конкретных приложений. К числу таких операций процедуры обнаружения и
различения сигналов.

Под обнаружением сигнала в
радиоэлектронике понимают анализ принятого колебания у (t), завершающийся вынесением
решения о наличии или отсутствии в нем некоторой полезной составляющей, которую
и называют сигналом.

Различение М сигналов определяют как анализ принятого колебания у (t), заканчивающийся принятием решения о том, какой именно из М сигналов,
принадлежащих указанному заранее множеству S= {S0 (t), S1, (t), …, SM-1, (t)}, присутствует в у(t).

Нетрудно видеть, что
обнаружение сигнала есть частный случай различения двух сигналов, один из
которых равен нулю на всем интервале наблюдения. Характерными практическими примерами
выполнения указанных действий являются обнаружение отраженных от целей сигналов
в радионавигации, гидролокации, обнаружение сигналов опорных маяков в
радионавигации, различение М передаваемых
посылок в системах цифровой связи и т. д.

Вероятностный характер наблюдаемого колебания у(t) приводит к тому, что любой
различитель или обнаружитель, сколь бы тщательно он ни был спроектирован, не
застрахован от ошибок. Таким образом, любой различитель[M4][1]
время от времени выносит решения, не соответствующие действительности, считая,
что в наблюдаемом колебании присутствует k-й сигнал, тогда как в
действительности в у (t) содержится i-й
сигнал. Разрабатывая тот или иной различитель, следует стремиться так выбрать
стратегию его работы, чтобы вредные последствия, связанные с указанными
ошибками, были минимальными.

Теория проверки гипотез служит методологическим
базисом всех исследований по обнаружению и
различению сигналов.

 Незначительно адаптируя язык теории статистических решений к
форме, более привычной для радиоспециалистов, можно так сформулировать задачу
проверки М гипотез. Пусть наблюдаемое
колебание у (t) является реализацией случайного процесса, который имеет распределение
W(t) т. е. n-мерную ПВ W(у) [либо функционал ПВ W(у(t))], принадлежащее
одному из М непересекающихся классов W (Wi∩Wk=Ø, i≠k, i; k=0, 1,
…, М – 1). Необходимо, пронаблюдав реализацию у (t), решить, какому из классов принадлежит Wy,.
Предположение о том, что Wy Є Wi, называют гипотезой Н1: Wy Є Wi.

Решения, являющиеся
результатом проверки гипотез, будем далее обозначать Н1, где i Є (0, 1,
…, М- 1) – номер гипотезы, истинность
которой декларируется принятым решением.

Частный случай М=2 называют двухальтернативным или проверкой гипотезы Н0 относительно альтернативы Н1. Если М>2, то проверку гипотез называют
мyогоальтернанивной.. Параллели между проверкой
гипотез и различением сигналов в радиотехнике
очевидны, если учесть, что, согласно (1.1), анализируемое различителем колебание
у(t) является результатом взаимодействия присутствующего в нем сигнала S (t) с мешающим
случайным процессом (помехой, шумом) х (t): у (t) = F [S(t), х (t)]. Гипотезы Нi , в
терминах различения сигналов трактуются как предположения о наличии i-го (и только i-го) сигнала в у (t) . При этом решения Hi, одно из которых служит итогом процедуры различения, есть утверждения
о том, что в принятом колебании содержится именно i-й сигнал. В частном случае
обнаружения гипотезы Н0 и Н1, выражают предположения об отсутствии
и наличии сигнала в у (t);
соответственно решения H0  и H1, означают утверждение, что сигнала в у (t) нет или сигнал в у (t) есть.

Лекция 2

2.1 Статистические критерии
различения и обнаружения сигналов.

Для того чтобы
задача поиска, или синтеза, оптимальных правил различения
сигналов обрела математическую содержательность, необходимо прежде всего
задаться некоторым формальным показателем (критерием)
качества различения, т. е. количественной мерой, суммирующей ущерб,
наносимый ошибочными решениями.

В тех задачах, которые
удается свести к проверке простых гипотез, продуктивным оказывается критерий минимума среднего риска, называемый также критерием Байеса. Для
того чтобы наиболее наглядно ввести связанную с ним систему понятий и терминов,
обратимся к конкретному примеру различения М
детерминироваиных сигналов S0 (t), S1 (t), …, SM-1, (t) на фоне помех с
полностью заданным статистическим описанием, т. е. с точно известной ПВ любой
размерности n или с точно известным
функционалом ПВ. В рамках такой модели различения ПВ любой размерности или
функционал ПВ наблюдаемого колебания у (t)
при условии, что в у (t) входит
сигнал с номером i, – некоторая вполне определенная функция, вид
которой зависит лишь от номера i. При этом имеется М классов, содержащих по одному распределению, т. е. различение
сигналов состоит в проверке простых гипотез.

Предположим, что известна
вероятность рi присутствия в у(t) сигнала Si,(t). Эту вероятность называют априорной (доопытной), поскольку она отражает сведения, которыми
располагает наблюдатель, еще не имея в распоряжении реализации у (t), и показывает, насколько
часто при длительной эксплуатации изучаемой системы можно ожидать появления Si (t) в у(t). Для систем М-ичной цифровой связи,
например, вероятность рi характеризует среднюю частоту, с которой Si (t) посылается в канал. Очевидно, вероятность рi можно назвать и априорной вероятностью
истинности Нi, записав рi = Р (Нi). Ясно также, что рi  подчинены
условию нормировки

∑ рi = 1, ибо события H0, H1,…, HM-1 составляют полную группу несовместных событий.

Предположим, что рi = Р (Hk/Hi) – условная вероятность перепутывания i-го
сигнала с k-м, т. е. принятия решения Hk
[о присутствии Sk(t) в у
(t) ] при условии, что истинна Нi.[в у (t)
содержится Si (t) ]. Следовательно,
множество вероятностей рik при i≠k составляет набор условных вероятностей всех
ошибочных решений. Эти вероятности для любого фиксированного способа
различения сигналов можно вычислить, так как помехи считаются полностью
статистически заданными .

Введем М2 неотрицательных величин Пik,
каждая из которых характеризует риск (потери, ущерб) от перепутывания i-го
сигнала с k-м. При этом правильные решения считаются не
наносящими ущерба, так что Пii = 0.

В каждой отдельной попытке
различения сигналов итог (решение) оказывается случайным событием, а поэтому
случайным будет и значение риска. Очевидно, безусловную вероятность того, что
риск окажется равным Пik, по теореме умножения
вероятностей можно найти как Р (Нi)
*Р (Hk/ Нi)
=рi*рik-поэтому
математическое ожидание риска или средний риск

П = ∑Пik piр ik.                                                                 (2.1.1)

Критерий Байеса,
или минимального среднего риска, предписывает добиваться минимума (2.1.1).
Различитель, оптимальный по этому критерию (байесовский различитель), при длительной эксплуатации будет наиболее «эконо- мичным»
из всех, поскольку сумма штрафов за ошибки у него окажется наименьшей.

Хотя задание рисков Пik (часто
и априорных вероятностей р,) достаточно произвольно, практическая ценность
критерия Байеса чрезвычайно велика, так как он, обобщая ряд других критериев,
позволяет получить универсальный ответ на вопрос о наилучшей стратегии
различения сигналов. Предположим, например, что, не имея объективных данных для
назначения всех рисков, разработчик стремится лишь к тому, чтобы различитель
как можно реже ошибался, т. e. чтобы полная вероятность
ошибки


 была минимальной. Нетрудно видеть, что такой
критерий качества, называемый критерием
идеального наблюдателя или критерием Котельникова, можно рассматривать как частный случай
байесовского, положив в (2.1.1) Пik= П, i≠k, где
П – произвольная неотрицательная константа. При этом П=ПРош, и минимизация
среднего риска равносильна минимизации (2.1.2).


Представим теперь, что
затруднение вызывает задание не только рисков, но и априорных вероятностей.
Подобная картина типична, например, для радиолокационного обнаружения. Тогда
определить полную вероятность ошибки нельзя, но можно предложить вполне
удовлетворительный критерий качества – критерий
минимума суммы условных вероятностей ошибок

В частном
случае М=2, S0(t)=0 рассматриваемая задача
переходит в обнаружение детерминированного сигнала S1 (t) на фоне помех с известным
статистическим описанием. При этом условные вероятности р01 = Р(H1 / Н0) и р10=Р(H0/Н1) на статистическом языке
называют вероятностями ошибок первого и второго рода. Согласно
терминологии, принятой в радиоэлектронике, эти же величины именуют более
выразительно – вероятности ложной
тревоги и пропуска (сигнала),
понимая под ложной тревогой факт решения H1, об обнаружении сигнала при
условии, что он в наблюдаемом колебании у
(t) не содержится, а под пропуском – объявление H0 о том, что сигнала в у (t) нет
при условии, что в действительности он в у
(t) присутствует. Далее для вероятностей ложной тревоги и пропуска будут
использованы обозначения рлт=р01
и р по=р10. Средний
риск при обнаружении П=рлтр0П01 +рпс
(1 – р0) П10, где П01, и П10 – риски,
связан- ные с ложной тревогой и пропуском; р0
– априорная вероятность отсутствия S1 (t) в у (t). Соотношения (2.1.2) и (2. 1.3) в
этом случае можно представить в виде,

Pош=pлтpО +pпс (1 – p0) и Pошусл = pлт +pпс.

Помимо введенных общих
критериев, не связанных с какими-либо допущениями относительно числа М проверяемых гипотез, при обнаружении
часто применяют критeрий Неймана – Пирсона, предписывающий добиваться минимума
вероятности пропуска рgc при ограничении сверху на
вероятность ложной тревоги.


Правила оптимального различения и обнаружения. Попытаемся выяснить,
какой стратегии должен придерживаться байесовский различитель М детерминированных сигналов.

Любая нерандомизированная
(не включающая преднамеренно введенных действий со случайным исходом типа
бросания жребия) процедура различения М сигналов
может интерпретироваться следующим образом. Допустим, что n-мерное пространство векторов Еn разбито на М (соответственно числу различаемых
сигналов) непересекающихся областей решения G0,G1,…, GM-1

Тогда принятие решения
различителем сводится к указанию номера области, в которую попал вектор
наблюдения у. Если у ÎG k то принимается решение Нk о присутствии в у (t) сигнала Sk (t). Возможность такой «геометризации» различения сводит поиски оптимальной
стратегии различителя к отысканию наилучшего разбиения Еn на области решений.


Для того чтобы найти
оптимальное правило разбиения, подставкм в (2.1) выражения для условных
вероятностей ошибок рik= ∫P(у / Нi)dу,
вытекающие из определения областей G0,G1,…, GM-1 Тогда

Очевидно, «назначение»
конкретной конфигурации областей решения сводится к тому, чтобы, перебрав все
векторы у, расписать их по М областям, включив каждый в одну и
только одну область Gk,. При этом, как следует из последней
формулы, каждый вектор войдет в одно и только одно слагаемое суммы по k,
отвечающее той области, за которой он закреплен. Поэтому минимума можно
добиться, если охватить областью Gk, именно те векторы у, для которых подынтегральное
выражение в k-м интеграле минимально. Следовательно, разбиением Еn на области минимизируюшим П,
будет такое, при котором в Gk включаются векторы у (и только они), удовлетворяющие
системе М неравенств


 

Если перейти к случаю
непрерывного наблюдения (к пространствам бесконечной размерности), то n-мерные
ПВ в (2.1.4) превратятся в функционалы ПВ F(у(t)/Нi),
т. е. область принятия решения Hk определится
системой М неравенств

 


 


Таким
образом, байесовский- различитель, наблюдая реализацию у(t), должен установить номер k, для
которого совместно выполнены неравенства (2.1.5), н принять решение Hk o наличии в у (t) сигнала
с номером k. Представим это правило в виде, который и далее
будет использоваться для записи алгоритмов различения сигналов:

где символ Нk указывает на решение, принимаемое при одновременном
выполнении всех неравенств в (1.2.6), Отметим, что величину

—        
апостериорный  условный (вычисляемый для данной реализации y(t)) средний
риск.

Поэтому выражение (2.1.6)
подразумевает вычисление для анализируемой реализации у(t) М значений условного среднего риска П =[у (t),i],
i= 0, 1, …, М – 1, и принятие решения о наличии в у
(t) сигнала с тем номером k, для которого значение П [у (t), i] минимально.


Рассмотрим важнейшие
частные случаи. Для идеального наблюдателя, минимизирующего (1.2.2),
следует положить Пik = П, i≠k.
Тогда выражение (2.1.6) примет вид


На основании формулы
полной вероятности

 согласно
(2.7), получим


Так как, по теореме
умножения вероятностей,

, то соотношение (2.1. 8)
может быть переписано как

Величина Р(Нi/у(t)) определяет апостериорную (обратную, послеопытную) вероятность гипотезы Нi, т. е, вероятность наличия i-го сигнала в у (t) с учетом всех сведений,
которые можно извлечь из наблюдаемой реализации у(t). Следовательно,
идеальный наблюдатель принимает решение в пользу сигнала, имеющего наибольшую
апостериорную вероятность, т. е. действует по правилу максимума апостериорной вероятности (МАВ).

Если данные об априорных
вероятностях ненадежны и проектировщик предпочел критерий минимума суммы условных
вероятностей ошибок (2.1,3), то соответствующее оптимальное правило различения
можно получить из (2.1.8) при рi=1/М,i=0, 1, …, М – 1:

W(y(t)/Hk)≥W(y(t)/Hi),  i=0,1,2,…,M-1.

Функционал ПВ W(y(t)/Hi) – условной ПВ, определенной при условии истинности гипотезы Нi [присутствия
Si(t) в у (t) ], – рассматриваемый как функция номера гипотезы i при
фиксированной реализации у (t),
называют функцией (функционалом) правдоподобия (ФП). Таким образом, стратегия
различителя, минимизирующего (2.1.3), сводится к использованию
правила максимума правдоподобия (МП),
т. е. к подстановке принятой реализации
у(t) в выражение для ФП, известное в силу детерминированности сигналов и
статистической определенности помех, и подбору i, максимизирующего ФП.

В
случае обнаружения детерминированного сигнала (М=2, S0(t)=0) выражение (2.1.6) можно переписать так:

 


где расстановка
символов H0 и H1, показывает, выполнение какого из неравенств влечет
за собой принятие соответствующего решения. Правило (2.1.10)
традиционно представляют в виде

называя отношение l двух значений ФП отношением (коэффициентом) правдоподобия (ОП). Как видно, байесовский
обнаружитель детерминированного сигнала должен для полученной реализации у(t) вычислить ОП l и сравнить —

его с порогом lп,   зависящим от рисков и
априорных вероятностей отсутствия и наличия сигнала.

Если разработчик
обнаружителя ориентируется на критерий идеального наблюдателя, то в выражении
(2.1.11) следует положить П01, =П10,
что превратит его в правило МАВ, сделав пороговый уровень равным р0=/(1
– р0). Аналогично, принятие за основу критерия минимума Рошусл= =рлт+рпс(П01=П10,
р0=1/2) придаст (2.1.11) вид правила МП, для которого l,=1. Наконец, стратегию
обнаружителя,

оптимального
по Нейману – Пирсону, также можно описать соотношением (2.1.11), если значение lп  выбрать из условия
поддержания вероятности ложной тревоги не выше заданного уровня.

Как видно, обнаружители,
оптимальные по любому из рассмотренных критериев, должны выполнять одни и те же
действия: вычислять ОП и сравнивать его с порогом. От конкретного критерия
зависит лишь значение порога, и поэтому обнаружитель, наилучший по одному
критерию, трансформируется в оптимальный по другому простым изменением порога lп,

2.2 Различение
сигналов cо случайными параметрами

Далеко не всегда наблюдатель
столь подробно априори осведомлен о различаемых сигналах, как это полагалось.
Чаще ему заранее не известны не только номер присутствующего в анализируемой реализации сигнала, но и
значения каких-либо параметров (амплитуды, частоты, фазы и др.) каждого из М возможных сигналов. Сами сигналы при
этом уже не являются детерминированными,

поскольку
параметры их не заданы; соответствующую задачу различения называют различением сигналов с неизвестными параметрами.

Знание априорной ПВ W (Θi)
случайных параметров различаемых сигналов позволяет трансформировать сложные гипотезы в простые, открывая
тем самым путь к   использованию
байесовского подхода и критериев.


Детерминированные сигналы. При различении М детерминированных сигналов на фоне аддитивного шума гипотеза Нi означает, что у(t)=х(t)+ Si(t), т. е. х(t)=у(t) – Si(t). Поэтому из выражения для
ФП получаем

где
обозначением Wn(.)
подчеркнуто, что у(t) – Si(t) подставляют в функционал
ПВ помехи х(t)=n(t).

Последняя запись позволяет
дать наглядную интерпретацию правила МП (2.1.9) для данной реализации у(t) принимают решение о
присутствии в ней того из М сигналов,
который наименее уклоняется от у(t). При этом мерой уклонения
является энергия разности у(t) и Si(t).

Для дальнейшего использования
ФП удобно представить в форме, следующей из (2.2.1) после раскрытия скобок под
интегралом:


где Еi=∫Si2 (t)dt  – энергия i-го сигнала; zi=∫ у(t)Si(t)dt – корреляционный интеграл (или просто корреляция) принятой реализации и i-го cигнала;

су=сехр [– 1/N0
∫ у2(t)dt] –
коэффициент, зависящий от у(t), но
не от i, и потому не влияющий на
решения, принимаемые согласно выводам 2.1 по результатам сравнения
значений соответствующих функций i (условного среднего риска,
апостериорной вероятности, ФП), вычисленных для конкретной наблюдаемой реализации
у(t).

Смысл корреляционного
интеграла очевиден: если у(t) и Si(t) согласно современным
концепциям теории сигналов, рассматривать как векторы в бесконечномерном
евклидовом пространстве, то zi, окажется
их скалярным произведением, т. е. величиной, характеризующей близость, сходство
у(t) и  Si(t). Отсюда вытекает следующая
физическая трактовка правила МП применительно к различению М детерминированных сигналов равной энергии (Еi = Е, i=0, 1, …, М
– 1): принимают решение о наличии в у(t) того сигнала, который имеет
наибольшее сходство с у(t).

В
частном случае обнаружения детерминированного сигнала М=2, S0(t)=0, z0=0, Е0=0 и, согласно (2.2.1), W(y(t)/H0)=cy. Соответственно  zi=∫ у(t)S1(t)dt,   

Е1= ∫ Si2(t)dt  и  W(y(t)/H1)=cyexp((2z-E)/N0)


Подставив эти выражения в (2.2.1),
для ОП получим

где индекс 1 у z  и Е опущен, так как ненулевой сигнал единственный и может быть обозначен
как S(t).

2.3 Сигналы со случайными
параметрами.


В соответствии с
выводами  2.2 ФП при различении сигналов
со случайными параметрами, априорные распределения которых заданы, может быть
получена усреднением ФП, построенной для детерминированных сигналов. При конкретных
значениях неизвестных параметров i-го сигнала последний становится детерминированным и, согласно (2.2.1),

где
Е1= ∫ Si2(t,θi)dt  – энергия i-го
сигнала с фиксированным и равным θi, значением вектора
неизвестных параметров zi=∫ у(t)S1(t)dt – корреляция y(t) с 

сигналом,
имеющим фиксированное и равное θi , значение вектора
неизвестных параметров. Приходим к выражению для ФП


В частном случае обнаружения ненулевого сигнала, повторив в
приложении к рассуждения, приведенные в конце предыдущего пункта, придем к
выражению для ОП


Где z(θ)- корреляция y(t) с обнаруживаемым сигналом S(t, θ ) =S 1 (t, θ1 ) при фиксированном и равном θ ,
значение вектора  его неизвестных
параметров.

Изложенные принципы
обнаружения и различения сигналов в следующей главе будут конкретизированы
применительно к различным моделям сигналов.

Источник

Для
учета разных последствий ошибок передачи
различных сообщений следует обобщить
критерий Котельникова, минимизируя
сумму условных вероятностей
в
его выражении (6.1) с заранее назначенными
весами (ценой, платой)Li,j.
Средневзвешенная сумма условных
вероятностей
при передаче сообщенияbi
(обычно называемая условным риском)
имеет вид

,

а сам критерий
требует

,
(6.7)

где
R
– средний риск.

При
использовании этого критерия оптимальной
считается решающая схема, обеспечивающая
наименьшее значение среднего риска
(6.7).

Из критерия
минимального среднего риска, как наиболее
общего, вытекают оба вышерассмотренных
критерия:

  1. критерий
    Котельникова при Li,i
    = 0 и Li,j
    = const
    (i
    ≠     j
    ),

  2. критерий
    максимального правдоподобия при
    Li,i
    = 0 и
    .

Практическое
использование критерия минимального
среднего риска затруднено необходимостью
знать вероятности передачи сообщений
и
сложностью объективного определения
весовых коэффициентовLi,j.

6.2.4. Критерий Неймана-Пирсона

Критерий
Неймана-Пирсона применяется в двоичных
системах в ситуациях, когда невозможно
определить априорные вероятности
отдельных сообщений, а последствия
ошибок разного рода неодинаковы. Такая
ситуация типична для радиолокации, где
осуществляется зондирование пространства
узким радиолучом и прием отраженного
от цели сигнала. При этом имеют место
две ситуации: 1) наличие цели – колебание
на входе приемника содержит сигнал в
аддитивной смеси с помехой (с неизвестной
априорной вероятностью P(b1)),
2) отсутствие цели – на входе приемника
действует одна помеха (с вероятностью
P(b0)
= 1 –
P(b1)).
Задача приема – обнаружение сигнала
на фоне помех. При ее реализации возможны
два вида ошибок:

  1. пропуск
    цели     (цель
    есть, но отраженный сигнал не обнаружен)
    с условной вероятностью ;

  2. ложная
    тревога
    (цель отсутствует, но принято решение
    о наличии отраженного сигнала) с условной
    вероятностью .

Очевидно, что
последствия этих ошибок сильно
различаются.

В
таком случае целесообразно стремиться
к уменьшению условной вероятности
ошибки, вызывающей особо тяжелые
последствия (пропуск цели), что можно
сделать только за счет увеличения
вероятности ошибки другого вида (ложной
тревоги). Ясно, что это можно делать до
определенной степени, т. к. слишком
большая вероятность ложной тревоги
приведет к ощутимым экономическим
потерям и к подрыву доверия к системе
в целом. Разумный выход – зафиксировать
вероятность ложной тревоги на выбранном
уровне ε

,
(6.8)

и затем минимизировать
вероятность пропуска цели

.
(6.9)

Минимизация
(6.9) при заданной величине (6.8) достигается,
если решение о наличии цели принимается
при выполнении неравенства

,

где λ(ε) – пороговый
уровень, определяемый заданной
вероятностью ложной тревоги.

Контрольные вопросы

  1. Сформулируйте
    задачу оптимального приема дискретных
    сообщений.

  2. Дайте геометрическую
    трактовку задаче оптимального приема
    дискретных сообщений.

  3. Что
    называют правилом решения (решающей
    схемой) демодулятора?

  4. Что
    такое идеальный (оптимальный) приемник
    дискретных сообщений?

  5. Что понимают под
    потенциальной помехоустойчивостью
    приема дискретных сообщений?

  6. В чем суть теории
    потенциальной помехоустойчивости?
    Когда и кем были заложены ее основы?

  7. Какой
    смысл вкладывают в понятие критерия
    качества приема дискретных сообщений?
    Перечислите известные Вам критерии.

  8. В
    чем суть критерия идеального наблюдателя
    (критерия Котельникова)?

  9. Укажите особенности
    критерия Котельникова.

  10. Что представляет
    собой критерий максимального
    правдоподобия? Как он соотносится с
    критерием Котельникова?

  11. Расскажите о
    критерии минимального среднего риска.
    В чем его общность?

  12. При
    каких условиях критерий минимального
    среднего риска совпадает с критерием
    Котельникова?

  13. При
    каких условиях критерий минимального
    среднего риска совпадает с критерием
    максимального правдоподобия?

  14. В
    чем сущность критерия Неймана-Пирсона?
    В каких случаях целесообразно его
    использование?

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Аннотация

В статье рассмотрены основы статистической обработки сигналов и методы их оптимальной обработки* на фоне шума.

Оптимальная обработка

*Под оптимальной обработкой в радиолокации понимают такую операцию над входной реализацией**, приводящей к повышению вероятности правильно обнаружения полезного сигнала, как правило, известной формы, при условии наличия во входной реализации шума в виде случайного процесса с известным или неизвестным законом распределения.

**Процесс наблюдаемый на входе приёмника. Строго говоря, назвать его «Входной сигнал» нельзя, так как в теории связи «Шум» и «Сигнал» — антонимы.

Введение

Основной задачей радиотехники является приём, передача и обработка информации с использованием в качестве переносчика – радиосигнала. Главное требование, предъявляемое к радиотехническим системам – получение своевременной и достоверной информации от источника к потребителю. Однако этому мешает физика принципов работы приёмопередающих устройств и среды распространения сигнала, суть которой заключается во флюктуации физических параметров системы и случайным значением принимаемого сигнала, имеющего шумовую составляющую, также относящуюся к стохастическим процессам.

На текущий момент, самый эффективный способ различения полезных сигналов на фоне шумов и помех является оптимальная обработка, реализуемая, как правило, сравнением принимаемой входной реализации с априорно известной формой полезного сигнала. При этом шумы, которые по своей природе процесс слабокоррелированный, вносят меньший вклад в величину, показывающую степень этого сравнения и называющуюся коэффициентом корреляции. Таким образом, любая задача обнаружения сводится к проверке минимум двух гипотез. В общем случае задача обнаружения состоит из двух гипотез: H_0 – сигнал отсутствует на входе приёмного устройства, H_1 – сигнал присутствует на входе приёмного устройства. Различные алгоритмы обнаружения обеспечивают различную вероятность правильного обнаружения P{d_1/H_1} при различных прочих статистических параметрах. Для сравнения эффективности алгоритмов обнаружения существуют критерии, а так как обрабатываются вероятностные величины, то характер этих критериев статистический. Иными словами критерий можно определить как мерило сравнения.

Статистические критерии обнаружения

Большая часть алгоритмов обнаружения радиолокационных целей включают в себя следующие этапы:

  1. Прием входной реализации
  2. Формирование порога на основе априорной или апостериорной информации.
  3. Оптимальная фильтрация входной реализации
  4. Принятие решения о наличии сигнала/цели

При этом очередность приёма входной реализации и формирования порога зависит непосредственно от типа алгоритма. Алгоритмы, формирующие порог на основе апостериорной информации о принятой входной реализации называют адаптивными [1]. Критерий выбирается эмпирически исходя из типа задачи. Например: при выборе места работы обычно рассматривают два критерия:

  • Максимума отношения заработанных денег к затраченной силе.
  • Максимума удовольствия, получаемого от работы.

К сожалению, современные реалии ставят в приоритет такого специалиста, навыки которого позволяли бы как можно быстрее выпустить продукцию и максимизировать прибыль компании. И зачастую второй критерий либо отбрасывается, либо при анализе ситуации ему присваивается низкий приоритет. Показатель, в данном случае, определяющий приоритет критериев, называется его мощностью.

В математической статистике мощность критерия определяется, как вероятность не совершить ошибку второго рода при принятии решения. В нашем случае ошибка второго рода — это не устроится на оптимальную для себя работу, в общем же случае это ложное принятие за истину события соответствующего гипотезе H_0.

Разумеется, универсальных критериев не существует. Так, например, критерий, имеющий наибольшую мощность, в решении одной задачи, в решении другой может оказаться наихудшим по этому показателю.

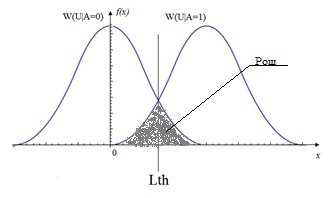
Критерий минимального среднего риска (критерий Байеса)


Рис.1 График распределения условной плотности вероятности наличия W(U|A=1) и отсутствия W(U|A=0) с вероятностями ошибок

Пусть A = 1 соответствует наличию сигнала s(t), а A = 0 – его отсутствию. Множество решений d вырождается в два: d_0 →A=1 and d_1→A=0.
При решении задачи бинарного обнаружения задача эквивалентна проверке гипотезы H_1 о том, что А = 1, при альтернативной гипотезе H_0 о том, что А = 0, а функция потерь переходит в квадратную матрицу:

Таким образом, условный риск при A = 0 равен r_0= C_00 P{d_0/H_0 }+ C_01 P{d_1/H_0 }=C_00 (1-P{d_1/H_0 })+ C_01 P{d_1/H_0 }, а при A = 1 равен r_1= C_10 P{d_0/H_1 }+ C_11 P{d_1/H_1}=C_10 (1-P{d_1/H_1} )+C_11 P{d_1/H_1}, где P{d_1/H_1} – вероятность правильного обнаружения, а P{d_1/H_0 } – вероятность ложной тревоги.

Средний риск определяется как r ̅=qr_0+pr_1, где q – априорная вероятность отсутствия сигнала, а p – априорная вероятность присутствия сигнала и определяет средние потери при ложной тревоге и пропуске цели [2]. Например: при использовании такого критерия для выставления порога срабатывания пожарной сигнализации, стоимость риска при ложной тревоге – вызов пожарной службы, а при пропуске – стоимость вещей в сгоревшей квартире или офисе.

На рис.1 проиллюстрированы графики распределения плотности вероятности при наличии и отсутствии сигнала, также выделены зоны, площадь которых численно равна вероятностям ошибок при принятии решения. Ввиду стохастической природы явлений рассматриваемых в данном примере, распределения имеют ненулевую дисперсию. Согласно критерию минимального среднего риска лучшим алгоритмом обнаружения сигнала будет тот, у которого величина r ̅ будет минимальна [2].

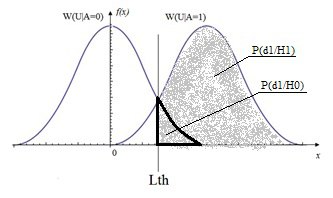
Критерий максимума апостериорной вероятности (максимального правдоподобия)

Этот критерий получается из критерия минимального среднего риска при условии, что потери при совершении ошибки обратно пропорциональны вероятности их совершения C_01=1/P{d_0}, C_10=1/P{d_1}. При этом порог оптимального обнаружителя выставляется таким образом, чтобы минимизировать сумму вероятностей ошибок P_ош=P{d_0/H_1 }+P{d_1/H_0 } (см рис.2).


Рис.2 График распределения условной плотности вероятности наличия W(U|A=1) и отсутствия W(U|A=0) с вероятностью ошибки

Двухпороговый критерий Вальда

В случаях, когда большую роль играет время наблюдения за процессом, например при наличии нескольких каналов и одного обнаружителя или круговом обзоре РЛС, применяют критерий последовательной проверки гипотез Вальда также известный под названием двухпороговый.


Рис.3 График распределения условной плотности вероятности наличия W(U|A=1) и отсутствия W(U|A=0) с вероятностью правильного обнаружения и вероятностью ложной тревоги

По этому критерию область определения вероятности делится на три подобласти, разделяемыми двумя порогами, определяемыми вероятностями правильного обнаружения и ложной тревоги (см.рис 3):
Критерий Вальда является оптимальным в смысле минимизации среднего времени наблюдения по большому количеству экспериментов [4]. Так как наиболее предпочтительным для радиолокации является сокращение длительности процедуры обнаружения, современные реалии ведут к всё более активному использованию этого критерия [5].

Критерий Неймана-Пирсона

Большим минусом критериев Байесовского класса является необходимость априорного знания элементов матрицы потерь. Например: при пропуске вражеского бомбардировщика на союзную территорию стоимость рисков не поддается исчислению.

В критерии Неймана-Пирсона фиксируется время обнаружения. Оптимальным будет алгоритм с максимальной вероятностью правильного обнаружения P{d_1/H_1 }, при условии, что вероятность ложной тревоги P{d_1/H_0 } не превышает заданной величины [6].

В виду того, что критерий Неймана-Пирсона не требует знания априорных вероятностей ситуаций A = 1 и A = 0, в радиолокации его используют одним из основных [5].

Заключение

При разработке обнаружителей очень важно осознанно выбирать критерий оптимальности, ведь, как уже упоминалось ранее, каждый критерий имеет максимальную мощность в какой-либо определенной ситуации и применение иных может привести к нежелательным последствиям.

Список использованных источников:

[1] Bulyakulov R.R. The adaptive threshold device // Processing of the 2014 IEEE North West Russia Section Young Researches in Electrical and Electronic Engineering Conference. P.165.
doi: 10.1109/EIConRusNW.2016.7448237
[2] Бакулев, П.А. Радиолокационные системы. Учебник для ВУЗов / П.А. Бакулев; М.: Радиотехника, 2004. – 46 с.
[3] Юревич, Е.И. Теория автоматического управления / Е.И. Юревич; М.: Энергия, 1969
[4] Богатырев, А.А. Стандартизация статистических методов управления качеством / А. А. Богатырев, Ю. Д. Филиппов; М.: Изд-во стандартов, 1989. – 42 с.
[5] Храменков, А.С. Сопоставительный анализ радиолокационных обнаружителей, основанных на критерии неймана-пирсона и последовательном критерии отношения вероятностей /А.С. Храменков, С.Н. Ярмолик // доклады БГУИР №6(76) Минск, 2013.
[6] Васильев, К.К. Методы обработки сигналов: Учебное пособие / К.К. Васильев; Ульяновск, 2001.

Источник

Понравилась статья? Поделить с друзьями:

Читайте также:

  • Критерий минимума среднеквадратичной ошибки
  • Критерий минимума полной вероятности ошибки
  • Критерии эффективности совещания ошибки совещания
  • Критерием истины являются знания исправить ошибку
  • Крита рендеринг анимации не удался неизвестная ошибка

    • 0 0 голоса
    Рейтинг статьи
    Подписаться
    Уведомить о
    guest

    0 комментариев
    Старые
    Новые Популярные
    Межтекстовые Отзывы
    Посмотреть все комментарии