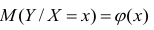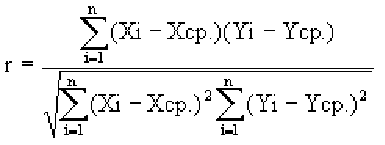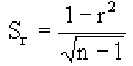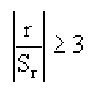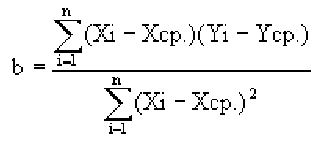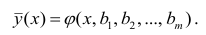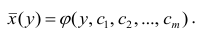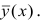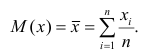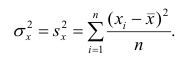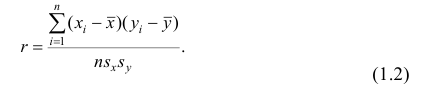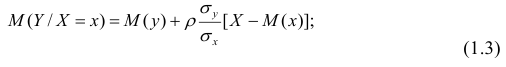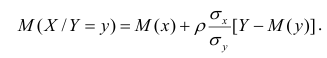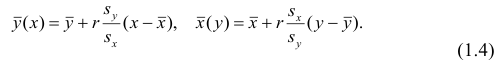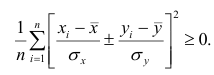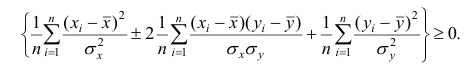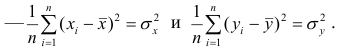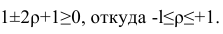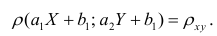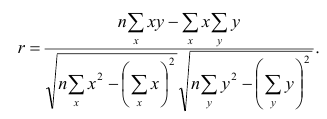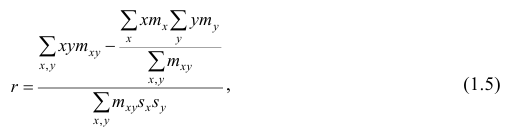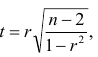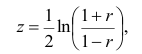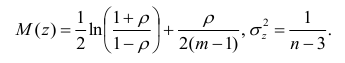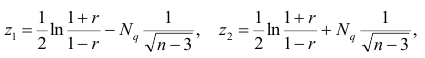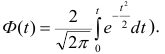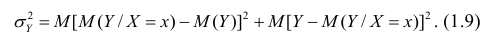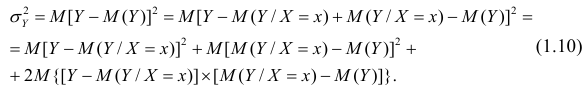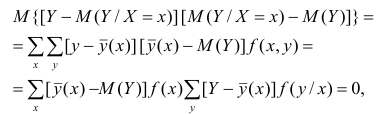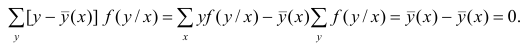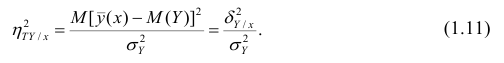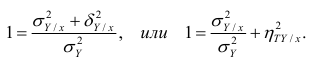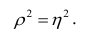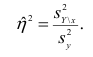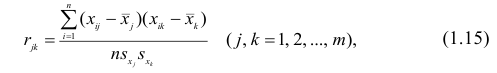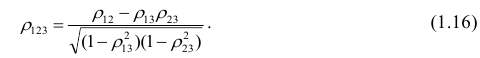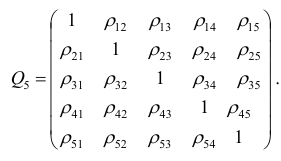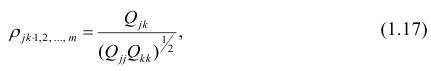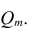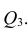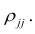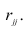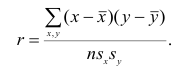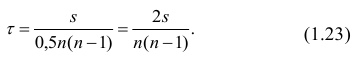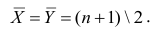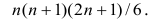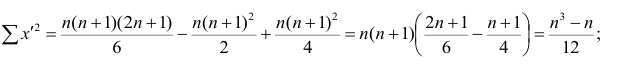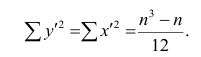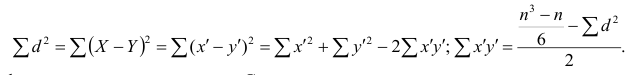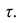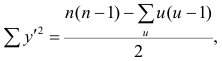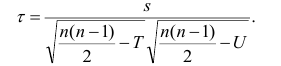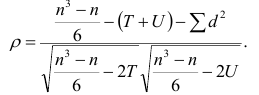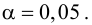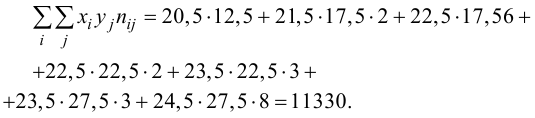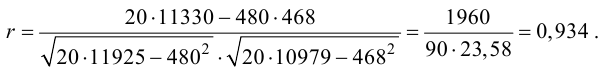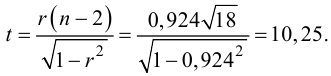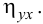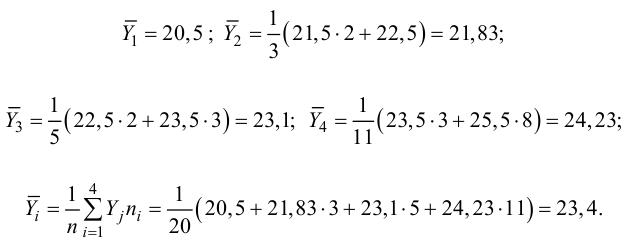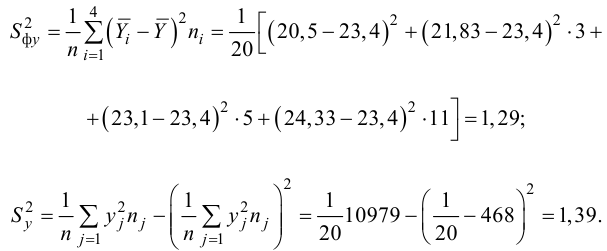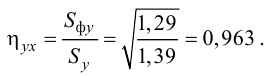Частные коэффициенты регрессии
Ошибки относительно линейной регрессии
Соотношения между дисперсиями, регрессиями и корреляциями различных порядков
Приближенные частные линейные регрессии
Частные коэффициенты регрессии
8. Обобщим теперь соотношения линейной регрессии на случай p величин. Для p совместно нормальных величин xi с нулевым средним и дисперсиями математическое ожидание величины x1 при условии, что x2, …, xp фиксированы, как видно из выражения в экспоненте распределения, равно
. (17)
Коэффициент регрессии x1 по xj при фиксированных остальных p-2 величинах будем обозначать или, короче
, где q символизирует совокупность величин, отличных от указанных первичными индексами, а индекс у q служит для различения этих совокупностей. Коэффициенты
называются частными коэффициентами регрессии.
Следовательно, мы имеем
. (18)
Сравнивая (18) с (17), получаем для многомерного нормального случая

Аналогично, коэффициент регрессии xj по x1 при фиксированных остальных переменных есть

Таким образом, поскольку C1j=Cj1, то из (6), (19) и (20) получаем

— очевидное обобщение соотношения (17). Соотношения (19) и (20) показывают, что коэффициент не симметричен относительно x1 и xj, как и следовало ожидать от коэ ффициента зависимости. Подобно(5) и (6), (19) и (20) являются определениями частных коэффициентов регрессии в общем случае.
Ошибки относительно линейной регрессии
9. Назовем ошибкой (эту величину часто называют «остатком» (residual) но мы будем проводить различие между ошибками (errors) относительно линейных регрессий в генеральной совокупности и остатками, возникающими при подгонке регрессий к выборочным данным) порядка (p-1) величину
.
Ее среднее равно нулю, а дисперсия равна
.
так что является дисперсией ошибки величины x1 относительно регрессии. Из (18) немедленно получаем


Если брать математическое ожидание в два этапа, фиксируя вначале x2, …, xp, то условное математическое ожидание от второго члена в (23) будет равно, согласно (18), нулю. Таким образом,

Дисперсия ошибки (24) не зависит от фиксируемых значений x3, …, xp, если только от них не зависят коэффициенты .
В этом случае условное распределение величины x1 называется гомоскедастическим (homoscedastic) (или гетероскедастическим (heteroscedastic) в противном случае). Это постоянство дисперсии ошибок делает интерпретацию регрессий и корреляций более простой.
Например, в нормальном случае условные дисперсии и ковариации, полученные при фиксировании множества величин, не зависят от значений, в которых последние фиксированы (см. (14)).
В других случаях при интерпретациях мы должны надлежащим образом учитывать обнаруженную гетероскедастичность, тогда, возможно, частные коэффициенты регрессии лучше всего рассматривать как показатели зависимости, усредненные по всевозможным значениям фиксированных величин.
Соотношения между дисперсиями, регрессиями и корреляциями различных порядков
Если даны p величин, то мы можем изучать корреляцию между любыми двумя из них, когда среди оставшихся зафиксированы значения произвольного подмножества величин. Аналогично, можно интересоваться регрессией произвольной величины относительно любого подмножества из оставшихся величин. С возрастанием p число всевозможных коэффициентов становится очень большим.
Если некоторый коэффициент содержит k вторичных индексов, то говорят, что он имеет порядок k. Так, порядок p12.34 равен 2, порядок p12.3 — единице, порядок p12 — нулю, тогда как β12.678 имеет порядок 3, а — порядок 4. В наших нынешних обозначениях коэффициенты линейной регрессии β1 и β2 должны быть записаны в виде β12 и β21 соответственно. Они имеют порядок нуль, как и обычная дисперсия σ2.
В 4 и 7 мы уже видели, как любой коэффициент корреляции первого порядка может быть выражен через коэффициенты нулевого порядка. Теперь будут получены более общие результаты такого сорта для коэффициентов всех типов.
11. Из (24) и (19) имеем

откуда
.
Пользуясь символом q, введенным в 8, получаем
, (26)
и аналогично, если 1 заменить любым другим индексом.
Точно таким же путем можно получить более общий результат

который сводится к (26) при l=m. Соотношение (27) применимо в случае, когда вторичные индексы одной величины включают в себя первичные индексы другой.
Если, с другой стороны, оба множества вторичных индексов не содержат l и m, то обозначим через r общее множество вторичных индексов. Ковариация двух ошибок xl.r, xm.r связана с их корреляцией и дисперсиями соотношениями:

что согласуется с уже найденным соотношением (21). Присоединяя множество индексов r к обеим величинам xl, xm, мы попросту должны сделать то же самое со всеми их коэффициентами.
12. Теперь можно использовать (26) для получения соотношения между дисперсиями ошибок различных порядков. Обозначая |D| корреляционный определитель всех величин, кроме x2. Тогда, имеем из (26)
(где индекс q-2 обозначает множество q без x2) и
,
откуда
. (29)
По определению |D|=C22, а согласно обобщенной теореме Якоби об определителях
, (30)
так как D11 является дополнительным минором для в C. Таким образом, используя (30), получаем из (29)

или, учитывая (6), находим
. (32)
Соотношение (32) является обобщением двумерного результата, который может быть представлен в виде
.
13. Соотношение (32) дает нам возможность выразить дисперсию ошибки порядка (p-1) через дисперсию ошибки и коэффициент корреляции порядка (p-2). Если мы теперь вновь воспользуемся (32) для того, чтобы выразить , то тем же путем найдем, что
.
Применяя последовательно (32) и записывая более полно индексы, получаем
. (33)
В (33), очевидно, не играет роли порядок вторичных индексов у σ1.23…p; мы их можем переставить так, как пожелаем. Например, для простоты в силу (26) можно написать
. (34)
В (34) индексы, отличные от 1, допускают перестановку. Соотношение (34) позволяет нам выразить дисперсию ошибки порядка s через дисперсию ошибки нулевого порядка и s коэффициентов корреляции, порядок которых принимает значения от нуля до (s-1).
14. Перейдем теперь к коэффициентам регрессии. Перепишем (15) для ковариации между x1 и x2 при фиксированном xp:
.
Присоединяя повсюду индексы 3, …, (p-1), имеем
. (35)
Используя определение (28) коэффициента регрессии как отношения ковариации к дисперсии, т.е.
,
и обозначим через r множество 3, …, (p-1), находим из (35)
,
или
. (36)
Если в (36) положить x1≡x2, то получим
, (37)
другую форму соотношения (32). Таким образом, из (36) и (37) имеем
. (38)
Это и есть требуемая формула для выражения коэффициента регрессии через некоторые коэффициенты следующего более низкого порядка. Повторно применяя (38), найдем представление любого коэффициента регрессии в терминах коэффициентов нулевого порядка.
Наконец, используя (21), из (38) получаем соотношение
, (39)
обобщающее (5) путем присоединения множества индексов r.
Приближенные частные линейные регрессии
15. В нашем изложении, начиная с 8, мы занимались точно линейными регрессионными зависимостями типа (18). Рассмотрим теперь вопрос подгонки регрессионных соотношений этого типа к наблюденным совокупностям, регрессии которых почти никогда не бывают точно линейными.
С помощью тех же рассуждений мы приходим к методу наименьших квадратов. Мы выбираем поэтому так, чтобы минимизировать сумму квадратов уклонений n наблюдений от подгоняемой регрессии:

где «иксы» измеряются от своих средних значений и предполагается n>p. Решение имеет вид
, (41)
где матрица X составлена из наблюдений над p-1 величинами x2, …, xp, а x1 — вектор наблюдений величины x1. Соотношение (41) можно переписать в виде
, (42)
где Vp-1 — матрица рассеяния для x2, …, xp, а M — вектор ковариаций между x1 и xj (j=2, …, p). Таким образом,
. (43)
Поскольку |Vp-1| есть минор V11 матрицы рассеяния V всех p величин, то (Vp-1)jl представляет собой дополнительный минор для
в V, так что сумма в правой части (43) является алгебраическим дополнением для (-σ1j) в V. Поэтому (43) представляется в виде
. (44)
Соотношение (44) совпадает с (19). Таким образом, мы приходим к заключению, что аппроксимация по методу наименьших квадратов дает те же коэффициенты регрессии, что и в случае точной линейной регрессии.
Из этого следует, что все результаты данной главы остаются в силе, когда для наблюденных совокупностей мы подгоняем регрессии по методу наименьших квадратов.
Связанные определения:
Выборочный коэффициент корреляции
Корреляционный анализ
Корреляция
Коэффициент корреляции
Линейная регрессия
Логистическая регрессия
Матрица плана
Метод наименьших квадратов
Независимый признак
Некоррелированный
Общая линейная модель
Регрессия
В начало
Содержание портала
Частные коэффициенты корреляции для
модели множественной регрессии с тремя
и более факторными переменными позволяют
определить степень зависимости между
результативной переменной и одной из
факторных переменных при постоянстве
остальных факторных переменных,
включённых в модель.
Для модели множественной регрессии с
тремя факторными переменными рассчитываются
частные коэффициенты, как первого, так
и второго порядка.
Общий вид модели трёхфакторной регрессии:
yi=β0+β1x1i+β2x2i+β3x3i+εi,
где yi
– результативная переменная,
x1i– первая факторная переменная;
x2i– второй факторная переменная;
x3i– третья факторная переменная;
β0,β1,β2,β3– неизвестные коэффициенты
модели регрессии;
εi– случайная ошибка модели
регрессии.
Частные коэффициенты корреляции первого
порядка для модели трёхфакторной
регрессии строятся точно так же, как и
для модели двухфакторной регрессии.
Частные коэффициенты корреляции второго
порядка для модели трёхфакторной
регрессии строятся следующим образом.
Частный коэффициент
корреляции между результативной
переменной у
и факторной переменной х1
при постоянстве факторных переменных
х2 и х3:
Частный коэффициент
корреляции между результативной
переменной у
и факторной переменной х2
при постоянстве факторных переменных
х1
и х3:
Частный коэффициент
корреляции между результативной
переменной у
и факторной переменной х3
при постоянстве факторных переменных
х1
и х1:
Частные коэффициенты корреляции второго
порядка построены с использованием
частных коэффициентов корреляции
первого порядка.
Следовательно, частный
коэффициент корреляции порядка t
может быть построен через частный
коэффициент корреляции (t-1)
порядка. Формулы, построенные через
указанную взаимосвязь, называются
рекуррентными.
При анализе модели
множественной регрессии с n
факторными переменными, частный
коэффициент корреляции (n-1)
порядка рассчитывается по общей формуле:
Частные коэффициенты корреляции,
вычисленные по рекуррентным формулам,
изменяются в пределах от минус единицы
до плюс единицы.
32. Построение частных коэффициентов корреляции для модели множественной регрессии через показатель остаточной дисперсии и коэффициент множественной детерминации
Помимо рекуррентных формул, которые
используются для построения частных
коэффициентов корреляции для моделей
множественной регрессии, возможно также
построение этих показателей с помощью
показателя остаточной дисперсии.
В случае линейной модели парной регрессии
показатель остаточной дисперсии
определяется по формуле:
где
– это оценка модели парной
регрессии с независимой переменной х1.
Если в линейную модель
парной регрессии включить новую
независимую переменную х2,
то можно вычислить показатель остаточной
дисперсии для линейной модели регрессии
с двумя независимыми переменными:
где
– это оценка модели регрессии
с двумя независимыми переменными х1
и х2.
Вне зависимости от качества построенной
линейной модели двухфакторной регрессии
будет справедливо неравенство вида:
Тогда величину
можно охарактеризовать как
долю сокращения остаточной дисперсии
за счёт включения в модель регрессии
новой независимой переменной х2.
Чем больше величина данного показателя,
тем сильнее дополнительная переменная
х2
влияет на результативную переменную у
и на качество модели регрессии в целом.
Для линейной модели
двухфакторной регрессии частный
коэффициент корреляции между независимой
переменной х2
и результативной переменной у
при постоянном значении независимой
переменной х1
через показатель остаточной дисперсии
определяется по формуле:
Для модели множественной
регрессии с n независимыми переменными
частный коэффициент корреляции (n-1)
порядка независимой переменной х1
и результативной переменной у
при постоянном значении остальных
независимых переменных, включённых в
модель, определяется по формуле:
Показатель остаточной дисперсии
результативной переменной и коэффициент
множественной детерминации связаны
отношением:
Если в формуле частного
коэффициента корреляции выразить
остаточную дисперсию результативной
переменной с помощью коэффициента
множественной детерминации, то для
модели множественной регрессии с n
независимыми переменными частный
коэффициент корреляции в общем виде
можно определить по формуле:
Частные коэффициенты корреляции,
вычисленные через показатель остаточной
дисперсии или коэффициент множественной
детерминации, изменяются в пределах от
нуля до единицы.
Частный коэффициент корреляции для
модели множественной регрессии в общем
случае характеризует степень зависимости
между результативной переменной и одной
из факторных переменных при постоянном
значении остальных независимых
переменных, включённых в модель регрессии.
Содержание:
Корреляционный анализ:
Связи между различными явлениями в природе сложны и многообразны, однако их можно определённым образом классифицировать. В технике и естествознании часто речь идёт о функциональной зависимости между переменными x и у, когда каждому возможному значению х поставлено в однозначное соответствие определённое значение у. Это может быть, например, зависимость между давлением и объёмом газа (закон Бойля—Мариотта).
В реальном мире многие явления природы происходят в обстановке действия многочисленных факторов, влияния каждого из которых ничтожно, а число их велико. В этом случае связь теряет свою однозначность и изучаемая физическая система переходит не в определённое состояние, а в одно из возможных для неё состояний. Здесь речь может идти лишь о так называемой статистической связи. Статистическая связь состоит в том, что одна случайная переменная реагирует на изменение другой изменением своего закона распределения. Следовательно, для изучения статистической зависимости нужно знать аналитический вид двумерного распределения. Однако нахождение аналитического вида двумерного распределения по выборке ограниченного объёма, во-первых, громоздко, во-вторых, может привести к значительным ошибкам. Поэтому на практике при исследовании зависимостей между случайными переменными X и У обычно ограничиваются изучением зависимости между одной из них и условным математическим ожиданием другой, т.е.
Вопрос о том, что принять за зависимую переменную, а что — за независимую, следует решать применительно к каждому конкретному случаю.
Знание статистической зависимости между случайными переменными имеет большое практическое значение: с её помощью можно прогнозировать значение зависимой случайной переменной в предположении, что независимая переменная примет определенное значение. Однако, поскольку понятие статистической зависимости относится к осредненным условиям, прогнозы не могут быть безошибочными. Применяя некоторые вероятностные методы, как будет показано далее, можно вычислить вероятность того, что ошибка прогноза не выйдет за определенные границы.
Введение в корреляционный анализ
Связь, которая существует между случайными величинами разной природы, например, между величиной X и величиной Y, не обязательно является следствием прямой зависимости одной величины от другой (так называемая функциональная связь).
В некоторых случаях обе величины зависят от целой совокупности разных факторов, общих для обеих величин, в результате чего и формируется связанные друг с другом закономерности. Когда связь между случайными величинами обнаружена с помощью статистики, мы не можем утверждать, что обнаружили причину происходящего изменения параметров, скорее мы лишь увидели два взаимосвязанных следствия.
Например, дети, которые чаще смотрят по телевизору американские боевики, меньше читают. Дети, которые больше читают, лучше учатся. Не так-то просто решить, где тут причины, а где следствия, но это и не является задачей статистики.
Статистика может лишь, выдвинув гипотезу о наличии связи, подкрепить ее цифрами. Если связь действительно имеется, говорят, что между двумя случайными величинами есть корреляция. Если увеличение одной случайной величины связано с увеличением второй случайной величины, корреляция называется прямой.
Например, количество прочитанных страниц за год и средний балл (успеваемость). Если, напротив рост одной величины связано с уменьшением другой, говорят об обратной корреляции. Например, количество боевиков и количество прочитанных страниц. Взаимная связь двух случайных величин называется корреляцией, корреляционный анализ позволяет определить наличие такой связи, оценить, насколько тесна и существенна эта связь. Все это выражается количественно.
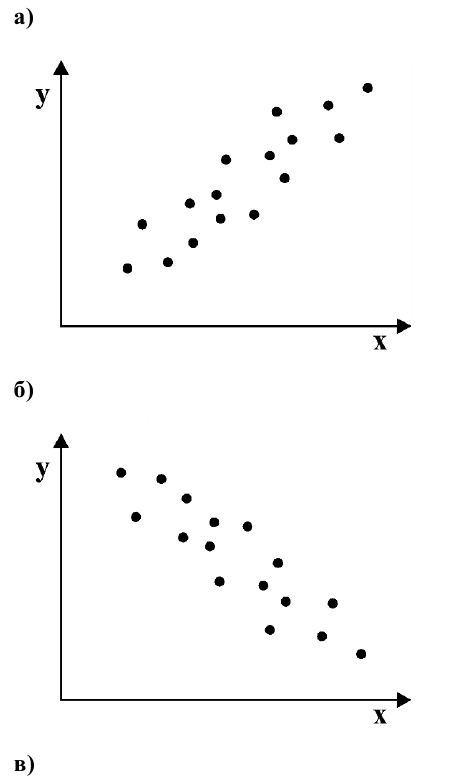
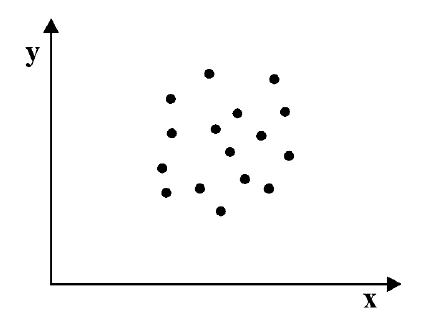
Как определить, есть ли корреляция между величинами? В большинстве случаев, это можно увидеть на обычном графике. Например, по каждому ребенку из нашей выборки можно определить величину 
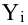
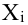
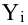
Если график имеет вид а), то это говорит о наличии прямой корреляции, в случае, если он имеет вид б) — корреляция обратная. Отсутствие корреляции тоже можно приблизительно определить по виду графика — это случай в).
С помощью коэффициента корреляции можно посчитать насколько тесная связь существует между величинами.
Пусть, существует корреляция между ценой и спросом на товар. Количество купленных единиц товара в зависимости от цены у разных продавцов показано в таблице: 
Коэффициент r мы считаем в Excel, с помощью функции 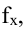
Надо отметить, что чем ближе к 0 коэффициент корреляции, тем слабее связь между величинами. Наиболее тесная связь при прямой корреляции соответствует коэффициенту r, близкому к +1. В нашем случае, корреляция обратная, но тоже очень тесная, и коэффициент близок к -1.
Что можно сказать о случайных величинах, у которых коэффициент имеет промежуточное значение? Например, если бы мы получили r = 0,65. В этом случае, статистика позволяет сказать, что две случайные величины частично связаны друг с другом. Скажем на 65% влияние на количество покупок оказывала цена, а на 35% — другие обстоятельства. И еще одно важное обстоятельство надо упомянуть.
Поскольку мы говорим о случайных величинах, всегда существует вероятность, что замеченная нами связь — случайное обстоятельство. Причем вероятность найти связь там, где ее нет, особенно велика тогда, когда точек в выборке мало, а при оценке Вы не построили график, а просто посчитали значение коэффициента корреляции на компьютере. Так, если мы оставим всего две разные точки в любой произвольной выборке, коэффициент корреляции будет равен или +1 или -1. Из школьного курса геометрии мы знаем, что через две точки можно всегда провести прямую линию. Для оценки статистической достоверности факта обнаруженной Вами связи полезно использовать так называемую корреляционную поправку:
Связь нельзя считать случайной, если:
В то время как задача корреляционного анализа — установить, являются ли данные случайные величины взаимосвязанными, цель регрессионного анализа — описать эту связь аналитической зависимостью, т.е. с помощью уравнения. Мы рассмотрим самый несложный случай, когда связь между точками на графике может быть представлена прямой линией. Уравнение этой прямой линии 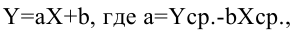
Зная уравнение прямой, мы можем находить значение функции по значению аргумента в тех точках, где значение X известно, a Y — нет. Эти оценки бывают очень нужны, но они должны использоваться осторожно, особенно, если связь между величинами не слишком тесная. Отметим также, что из сопоставления формул для b и r видно, что коэффициент не дает значение наклона прямой, а лишь показывает сам факт наличия связи.
Определение формы связи. Понятие регрессии
Определить форму связи — значит выявить механизм получения зависимой случайной переменной. При изучении статистических зависимостей форму связи можно характеризовать функцией регрессии (линейной, квадратной, показательной и т.д.).
Условное математическое ожидание 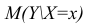
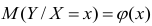
функцией регрессии случайной переменной Y относительно X (или функцией регрессии Y по X). Точно так же условное математическое ожидание
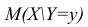
На примере, дискретного распределения найдём функцию регрессии.
Функция регрессии имеет важное значение при статистическом анализе зависимостей между переменными и может быть использована для прогнозирования одной из случайных переменных, если известно значение другой случайной переменной. Точность такого прогноза определяется дисперсией условного распределения.
Несмотря на важность понятия функции регрессии, возможности её практического применения весьма ограничены. Для оценки функции регрессии необходимо знать аналитический вид двумерного распределения (X, Y). Только в этом случае можно точно определить вид функции регрессии, а затем оценить параметры двумерного распределения. Однако для подобной оценки мы чаще всего располагаем лишь выборкой ограниченного объема, по которой нужно найти вид двумерного распределения (X, Y), а затем вид функции регрессии. Это может привести к значительным ошибкам, так как одну и ту же совокупность точек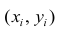
Кривой регрессии Y по X (или Y на А) называют условное среднее значение случайной переменной У, рассматриваемое как функция определенного класса, параметры которой находят методом наименьших квадратов по наблюдённым значениям двумерной случайной величины (х, у), т.е.
Аналогично определяется кривая регрессии X по Y (X на Y):
Кривую регрессии называют также эмпирическим уравнением регрессии или просто уравнением регрессии. Уравнение регрессии является оценкой соответствующей функции регрессии.
Возникает вопрос: почему для определения кривой регрессии
используют именно условное среднее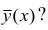
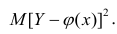
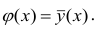
Если рассеивание вычисляется относительно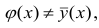
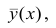
Основные положения корреляционного анализа
Статистические связи между переменными можно изучать методом корреляционного и регрессионного анализа. С помощью этих методов решают разные задачи; требования, предъявляемые к исследуемым переменным, в каждом методе различны.
Основная задача корреляционного анализа — выявление связи между случайными переменными путём точечной и интервальной оценки парных коэффициентов корреляции, вычисления и проверки значимости множественных коэффициентов корреляции и детерминации, оценки частных коэффициентов корреляции. Корреляционный анализ позволяет также оценить функцию регрессии одной случайной переменной на другую.
Предпосылки корреляционного анализа следующие:
- 1) переменные величины должны быть случайными;
- 2) случайные величины должны иметь совместное нормальное распределение.
Рассмотрим простейший случай корреляционного анализа — двумерную модель. Введём основные понятия и опишем принцип проведения корреляционного анализа. Пусть X и Y — случайные переменные, имеющие совместное нормальное распределение. В этом случае связь между X и Y можно описать коэффициентом корреляции p;. Этот коэффициент определяется как ковариация между X и Y, отнесённая к их среднеквадратическим отклонениям:
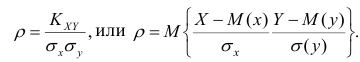
Оценкой коэффициента корреляции является выборочный коэффициент корреляции r. Для его нахождения необходимо знать оценки следующих параметров: 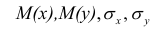
математического ожидания является среднее арифметическое, т.е.
Оценкой дисперсии служит выборочная дисперсия, т.е.
Тогда выборочный коэффициент корреляции
Коэффициент р называют также парным коэффициентом корреляции, а r— выборочным парным коэффициентом корреляции.
При совместном нормальном законе распределения случайных величин X и Y, используя рассмотренные выше параметры распределения и коэффициент корреляции, можно получить выражение для условного математического ожидания, т. е, записать выражение для функции регрессии одной случайной величины на другую. Так, функция регрессии Y на X имеет вид:
функция регрессии X на Y — следующий вид:
Выражения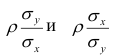
Подставив в (1.3) соответствующие оценки параметров, получим уравнения регрессии, график которых — прямая линия, проходящая через точку 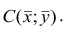
Таким образом, в корреляционном анализе на основе оценок параметров двумерной нормальной совокупности получаем оценки тесноты связи между случайными переменными и можем оценить регрессию одной переменной на другую. Особенностью корреляционного анализа является строго линейная зависимость между переменными. Это обусловливается исходными предпосылками. На практике корреляционный анализ можно применять для обработки наблюдений, сделанных на предприятиях при нормальных условиях работы, если случайные изменения свойства сырья или других факторов вызывают случайные изменения свойств продукции.
Свойства коэффициента корреляции
Коэффициент корреляции является одним из самых распространенных способов измерения связи между случайными переменными. Рассмотрим некоторые свойства этого коэффициента.
Теорема 1. Коэффициент корреляции принимает значения на интервале (-1, +1).
Доказательство. Докажем справедливость утверждения для случая дискретных переменных. Запишем явно неотрицательное выражение:
Возведём выражение под знаком суммы в квадрат:
Первое и третье из слагаемых равны единице, поскольку из определения дисперсии следует, что
Таким образом, окончательно получаем
Если коэффициент корреляции положителен, то связь между переменными также положительна и значения переменных увеличиваются или уменьшаются одновременно. Если коэффициент корреляции имеет отрицательное значение, то при увеличении одной переменной уменьшается другая.
Приведём следующее важное свойство коэффициента корреляции: коэффициент корреляции не зависит от выбора начала отсчёта и единицы измерения, т. е. от любых постоянных 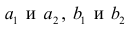
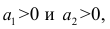
Таким образом, переменные X и У можно уменьшать или увеличивать в а раз, а также вычитать или прибавлять к значениям X и У одно и то же число b. В результате величина коэффициента корреляции не изменится.
Если коэффициент корреляции 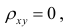
Выборочный коэффициент корреляции вычисляют по формуле (1.2). Имеется несколько модификаций этой формулы, которые удобно использовать при той или иной форме представления исходной информации. Так, при малом числе наблюдений выборочный коэффициент корреляции удобно вычислять по формуле
Если информация имеет вид корреляционной таблицы (см. п 1.5), то удобно пользоваться формулой
где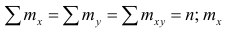
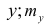
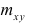
Из формулы (1.2) очевидно, что 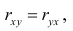
Поле корреляции. Вычисление оценок параметров двумерной модели
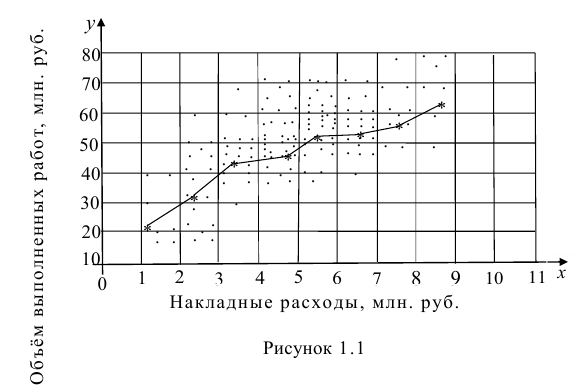
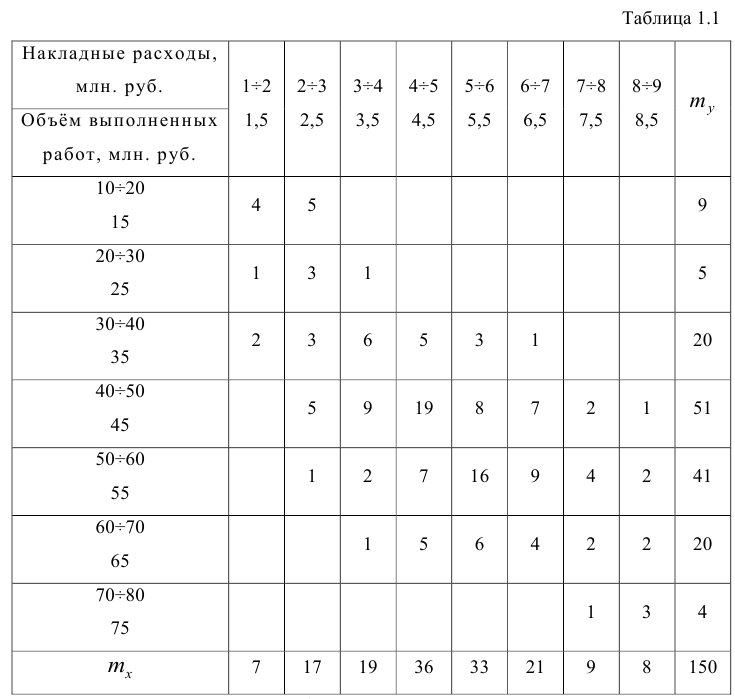
На практике для вычисления оценок параметров двумерной модели удобно использовать корреляционную таблицу и поле корреляции. Пусть, например, изучается зависимость между объёмом выполненных работ (у) и накладными расходами (x). Имеем выборку из генеральной совокупности, состоящую из 150 пар переменных 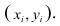
Пару случайных чисел 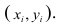
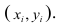
По осям координат откладывают или дискретные значения переменных, или интервалы их изменения. Для интервального ряда наносят координатную сетку. Каждую пару переменных из данной выборки изображают в виде точки с соответствующими координатами для дискретного ряда или в виде точки в соответствующей клетке для интервального ряда. Такое изображение корреляционной зависимости называют полем корреляции. На рис. 1.1 изображено поле корреляции для выборки, состоящей из 150 пар переменных (ряд интервальный).
Если вычислить средние значения у в каждом интервале изменения х [обозначим их 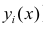
Корреляционную таблицу, как и поле корреляции, строят по
сгруппированному ряду (дискретному или интервальному). Табл. 1.1 построена на основе интервального ряда. В первой строке и первом столбце таблицы помещают интервалы изменения х и у и значения середин интервалов. Так, например, 1,5 — середина интервала изменения *=1-2,15— середина интервала изменения у= 10-20. В ячейки, образованные пересечением строк и столбцов, заносят частоты попадания пар значений (л у) в соответствующие интервалы по х и у. Например, частота 4 означает, что в интервал изменения у от 10 до 20 попало 4 пары наблюдавшихся значений. Эти частоты обозначают 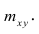
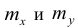
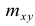
Как будет показано в дальнейшем, корреляционно таблицей удобно пользоваться при вычислении коэффициентов корреляций и параметров уравнений регрессии.
Корреляционная таблица построена на основе интервального ряда, поэтому для оценок параметров воспользуемся формулами гл. 1 для вычисления средней арифметической и дисперсии. Имеем:
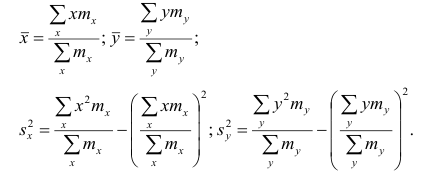
Проверка гипотезы о значимости коэффициента корреляции
На практике коэффициент корреляции р обычно неизвестен. По результатам выборки может быть найдена его точечная оценка — выборочный коэффициент корреляции r.
Равенство нулю выборочного коэффициента корреляции ещё не свидетельствует о равенстве нулю самого коэффициента корреляции, а следовательно, о некоррелированности случайных величин X и Y. Чтобы выяснить, находятся ли случайные величины в корреляционной зависимости, нужно проверить значимость выборочного коэффициента корреляции г, т.е. установить, достаточна ли его величина для обоснованного вывода о наличии корреляционной связи. Для этого проверяют нулевую гипотезу 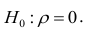
которая имеет распределение Стьюдента с k=n-2
степенями свободы. Для проверки нулевой гипотезы по уровню значимости а и числу степеней свободы к находят по таблицам распределения Стьюдента (t-распределение; см. табл. 1 приложения) критическое значение 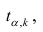
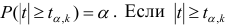
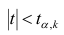
В случае значимого выборочного коэффициента, корреляции есть смысл построить доверительный интервал для коэффициента корреляций р. Однако для этого нужно знать закон распределения выборочного коэффициента корреляции r.
Плотность вероятности выборочного коэффициента корреляции имеет сложный вид, поэтому прибегают к специально подобранным функциям от выборочного коэффициента корреляции, которые сводятся к хорошо изученным распределениям, например нормальному или Стьюдента. Чаще всего для подбора функции применяют преобразование Фишера. Вычисляют статистику:
где r=thz — гиперболический тангенс от z.
Распределение статистики z хорошо аппроксимируется нормальным распределением с параметрами
В этом, случае доверительный интервал для римеетвид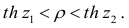
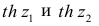
где 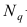
Если коэффициент корреляции значим, то коэффициенты регрессии также значимо отличаются от нуля, а интервальные оценки для них можно получить по следующим формулам:
где 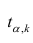
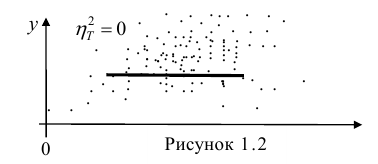
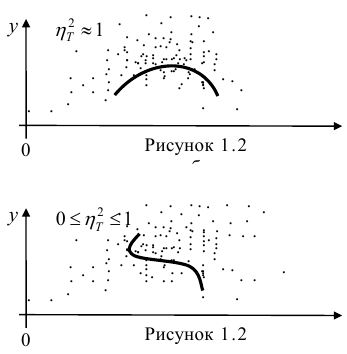
Корреляционное отношение
На практике часто предпосылки корреляционного анализа нарушаются: один из признаков оказывается величиной не случайной, или признаки не имеют совместного нормального распределения. Однако статистическая зависимость между ними существует. Для изучения связи между признаками в этом случае существует общий показатель зависимости признаков, основанный на показателе изменчивости — общей (или полной) дисперсии.
Полной называется дисперсия признака относительно его математического ожидания. Так, для признака Y это 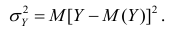
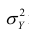
Очевидно, чем меньше влияние прочих факторов, тем теснее связь, тем более приближается она к функциональной. Представим 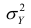
Первое слагаемое обозначим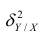
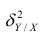
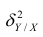
Покажем, что 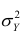
Для простоты полагаем распределение дискретным. Имеем
так как при любом х справедливо равенство
Третье слагаемое в равенстве (1.10) равно нулю, поэтому равенство (1.9) справедливо. Поскольку второе слагаемое в равенстве (1.9) оценивает влияние признака X на Y, то его можно использовать для оценки тесноты связи между X и Y. Тесноту связи удобно оценивать в единицах общей дисперсии 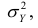
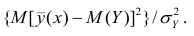
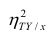
Разделив обе части равенства (1.9) на 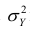
Из последней формулы имеем
Поскольку 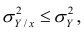
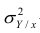
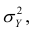
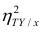
Все сделанные выводы справедливы и для 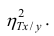
следует, что 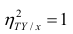
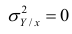
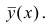
Далее, из равенства (1.12) следует, что 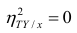
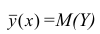
Аналогичными свойствами обладает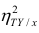
Часто используют величину
Считают, что она не может быть отрицательной. Значения величины 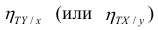
Значения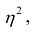
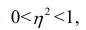
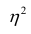
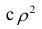
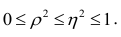
Разность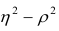
При вычислении 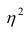
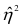
Понятие о многомерном корреляционном анализе
Частный коэффициент корреляции. Основные понятия корреляционного анализа, введенные для двумерной модели, можно распространить на многомерный случай. Задачи и предпосылки корреляционного анализа были сформулированы в п. 1.3. Однако если при изучении взаимосвязи переменных по двумерной модели мы ограничивались рассмотрением парных коэффициентов корреляции, то для многомерной модели этого недостаточно. Многообразие связей между переменными находит отражение в частных и множественных коэффициентах корреляции.
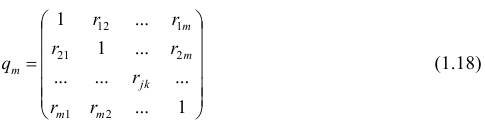
Пусть имеется многомерная нормальная совокупность с m признаками 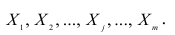
можно описать корреляционной матрицей. Под корреляционной матрицей будем понимать, матрицу, составленную из парных коэффициентов корреляции (вычисляются по формуле (1,1)):
где 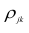
Оценкой парного коэффициента корреляции является выборочный парный коэффициент корреляции, определяемый по формуле (1.2), однако для m признаков формула (9.2) принимает вид
где 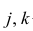
Как и в двумерном случае, для оценки коэффициента корреляции необходимо оценить математические ожидания и дисперсии. В многомерном корреляционном анализе имеем т математических ожиданий и m дисперсий, а также m(m—1)/2 парных коэффициентов корреляции. Таким образом, нужно произвести оценку 2m+m(m—1)/2 параметров.
В случае многомерной корреляции зависимости между признаками более многообразны и сложны, чем в двумерном случае. Одной корреляционной матрицей нельзя полностью описать зависимости между признаками. Введём понятие частного коэффициента корреляции l-го порядка.
Пусть исходная совокупность состоит из т признаков. Можно изучать зависимости между двумя из них при фиксированном значении l признаков из m-2 оставшихся. Рассмотрим, например, систему из 5 признаков. Изучим зависимости между 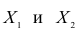
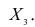
Рассмотрим более подробно структуру частных коэффициентов корреляции на примере системы из трёх признаков 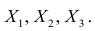
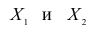
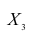
корреляции и имеет вид
Частный коэффициент корреляции, так же как и парный коэффициент корреляции, изменяется от —1 до +1, В общем виде, когда система состоит из m признаков, частный коэффициент корреляции l-го порядка может быть найден из корреляционной матрицы. Если 1=m—2, то рассматривается матрица порядка m, при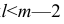
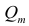
корреляции. Например, корреляционная матрица системы из пяти признаков имеет вид
Для определения частного коэффициента корреляции второго порядка, например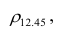
вычеркнув из исходной матрицы 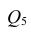
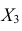
В общем виде формулу частного коэффициента корреляции l-го порядка (1=m—2) можно записать в виде
где 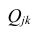
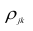
матрицы 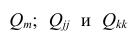
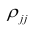
Очевидно, что выражение (1.16) является частым случаем выражения (1.17), в чём легко убедиться, рассмотрев корреляционную матрицу
Оценкой частного коэффициента корреляции l-го порядка является выборочный частный коэффициент корреляции l-го порядка. Он вычисляется на основе корреляционной матрицы, составленной из выборочных парных коэффициентов корреляции:
Формула выборочного частного коэффициента корреляции имеет вид
где 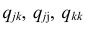
Частный коэффициент корреляции l-го порядка, вызволенный на основе п наблюдений над признаками, имеет такое же распределение, что и парный коэффициент корреляции, вычисленный 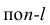
Множественный коэффициент корреляции
Часто представляет интерес оценить связь одного из признаков со всеми остальными. Это можно сделать с помощью множественного, или совокупного, коэффициента корреляции
где 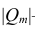
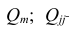
дополнение к элементу
Квадрат коэффициента множественной корреляции 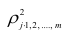
множественным коэффициентом детерминации. Коэффициенты множественной корреляции и детерминации — величины положительные, принимающие значения в интервале
коэффициентов являются выборочные множественные коэффициенты корреляции и детерминации, которые обозначают соответственно 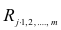
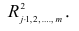
где 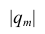
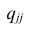
Многомерный корреляционный анализ позволяет получить оценку функции регрессии — уравнение регрессии. Коэффициенты в уравнении регрессии можно найти непосредственно через выборочные парные коэффициенты корреляции или воспользоваться методом многомерной регрессии, который мы рассмотрим в вопросе 2.7. В этом случае все предпосылки регрессионного анализа оказываются выполненными и, кроме того, связь между переменными строго линейна.
Ранговая корреляция
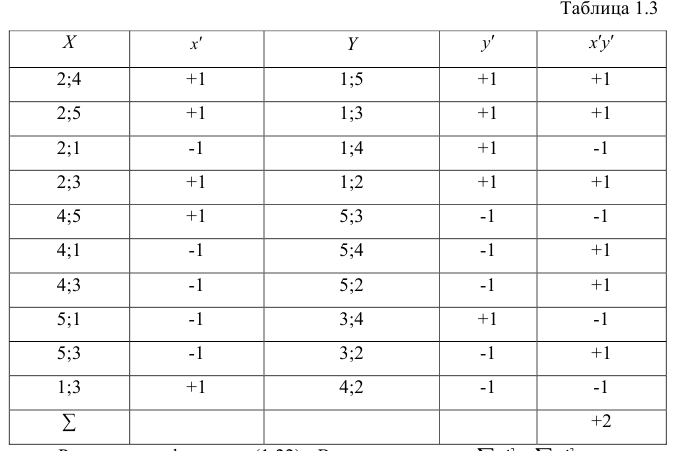
В некоторых случаях встречаются признаки, не поддающиеся количественной оценке (назовём такие признаки объектами). Попытаемся, например, оценить соотношение между математическими и музыкальными способностями группы учащихся. «Уровень способностей» является переменной величиной в том смысле; что он варьирует от одного индивидуума к другому. Его можно измерить, если выставлять каждому индивидууму отметки. Однако этот способ лишен объективности, так как разные экзаменаторы могут выставить одному и тому же учащемуся разные отметки. Элемент субъективизма можно исключить, если учащиеся будут ранжированы. Расположим учащихся по порядку, в соответствии со степенью способностей и присвоим каждому из них порядковый номер, который назовем рангом. Корреляция между рангами более точно отражает соотношение между способностями учащихся, чем корреляция между отметками.
Тесноту связи между рангами измеряют так же, как и между признаками. Рассмотрим уже известную формулу коэффициента корреляции
Пусть 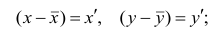
что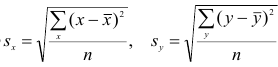
В зависимости от того, что принять за меру различия между величинами 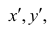
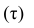
Введём следующую меру различия между объектами: будем считать 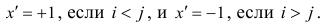
Рассмотрим отдельно каждую из них. В последовательности X первой паре элементов —2; 4 припишем значение +1, так как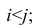
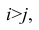
Рассмотрим формулу ( 1 .22). В нашем случае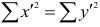
количеству пар, участвовавших в переборе. Каждая пара встречается только один раз, поэтому их общее количество равно числу сочетаний из n по 2, т.е.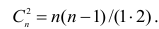
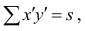
Теперь рассмотрим другую меру различия между объектами. Если обозначить через 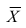
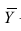
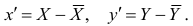
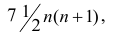
Тогда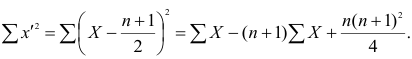
чисел натурального ряда равна
Тогда
Введём новую величину d, равную разности между рангами: d=X—Y, и определим через неё величину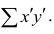
Коэффициент корреляции рангов Спирмэна
У коэффициентов 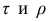
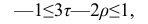
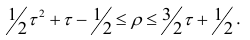
При вычислении коэффициента корреляций рангов Кэнделла для подсчёта s можно использовать следующий приём: одну из последовательностей упорядочивают так, чтобы её элементы были числами натурального ряда; соответственно изменяют и другую последовательность. Тогда сумму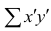
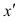
Если нельзя установить ранговое различие нескольких объектов, говорят, что такие объекты являются связанными. В этом случае объектам приписывается средний ранг. Например, если связанными являются объекты 4 и 5, то им приписывают ранг 4.5; если связанными являются объекты 1, 2, 3, 4 и 5, то их средний ранг (1+2+3+4+5)/5=3. Сумма рангов связанных объектов должна быть равна сумме рангов при ранжировании без связей. Формулы коэффициентов корреляции для 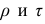
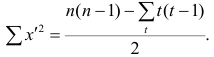
где t и u—число связанных пар в последовательностях.
Обозначая 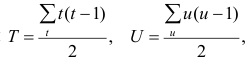
Аналогично находим выражение для р. Только в этом случае
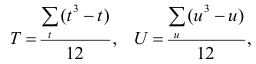
последовательностях, а
Если имеется несколько последовательностей, то возникает необходимость определить общую меру согласованности между ними. Такой мерой является коэффициент копкордации.
Пусть ь — число последовательностей, т — количество рангов в каждой последовательности. Тогда коэффициент конкордации
где d — фактически встречающееся отклонение от среднего значения суммы рангов одного объекта.
Коэффициент корреляции рангов может быть использован для быстрого оценивания взаимосвязи между признаками, не имеющими нормального распределения, и полезен в тех случаях, когда признаки поддаются ранжированию, но не могут быть точно измерены.
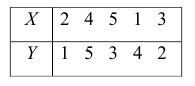
Пример:
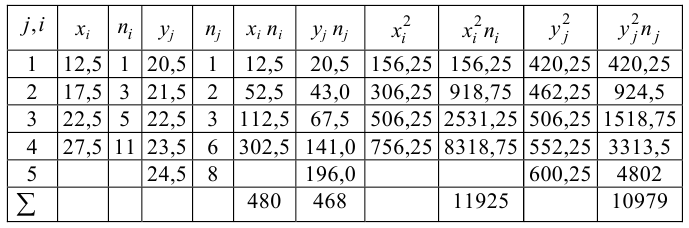
Для данных табл. 13 найти выборочный коэффициент корреляции, проверить его значимость на уровне
Решение. Для вычислений составим таблицу. Находим суммы
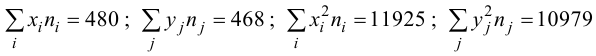
Подставляя полученные значения сумм в (8), найдем выборочный коэффициент корреляции
Проверим значимость 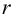
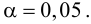
По таблице распределения П6 Стьюдента 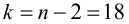
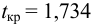
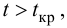
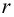
Пример:
Для данных табл. 13 найти корреляционное отношение
Для вычисления эмпирического корреляционного отношения найдем групповые средние
Тогда
Вычисляем корреляционное отношение
- Статистические решающие функции
- Случайные процессы
- Выборочный метод
- Статистическая проверка гипотез
- Доверительный интервал для математического ожидания
- Доверительный интервал для дисперсии
- Проверка статистических гипотез
- Регрессионный анализ