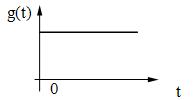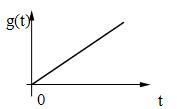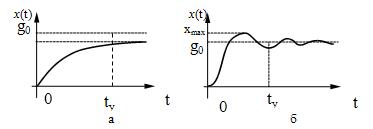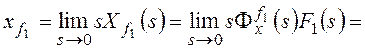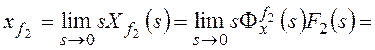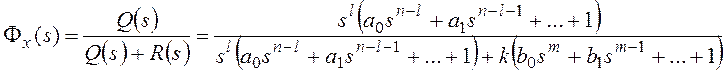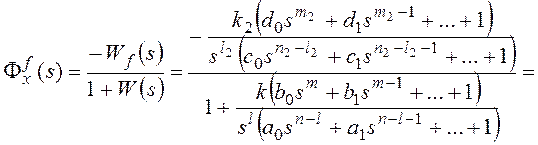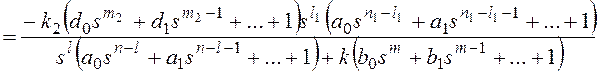Точность систем управления является
важнейшим показателем их качества. Чем выше точность, тем выше качество
системы. Однако предъявление повышенных требований к точности вызывает
неоправданное удорожание системы, усложняет ее конструкцию. Недостаточная
точность может привести к несоответствию характеристик системы условиям
функционирования и необходимости ее повторной разработки. Поэтому на этапе
проектирования системы должно быть проведено тщательное обоснование требуемых
показателей точности.
В этом разделе рассматриваются методы
определения ошибок, возникающих при работе систем управления с детерминированными
входными воздействиями. Вначале анализируются ошибки систем в переходном
режиме. Затем особое внимание уделено простым способам расчета ошибок систем в
установившемся режиме. Будет показано, что все системы управления можно разделить
по величине установившихся ошибок на системы без памяти, так называемые статические
системы, и системы, обладающие памятью, – астатические
системы управления.
Типовые
входные воздействия
Для оценки качества работы систем
управления рассматривают их поведение при некоторых типовых воздействиях.
Обычно такими воздействиями служат следующие три основные вида функций:
а) ступенчатое воздействие: g(t) = 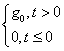
;
б) линейное воздействие: g(t) = t , t > 0
; ;
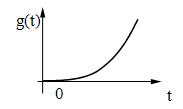
в) квадратичное воздействие:
/2 , t > 0 ;
g(p) = .
В
некоторых случаях рассматривают обобщенное полиномиальное воздействие:
, t > 0.
Ступенчатое воздействие является одним
из простейших, но именно с его помощью определяется ряд важных свойств систем
управления, связанных с видом переходного процесса. Линейное и квадратичное
воздействия часто бывают связаны с задачами слежения за координатами
движущегося объекта. Тогда линейное воздействие соответствует движению объекта
с постоянной скоростью; квадратичное — движению объекта с постоянным ускорением.
Переходные процессы при типовых
воздействиях можно построить следующим образом. Пусть задана передаточная
функция замкнутой системы управления W(p). Тогда
x(p)
= W(p) g(p),
где g(p) – изображение соответствующего воздействия.
Например, если , то
и для g(t) = g0
получим .
С помощью вычетов или по таблицам
находим обратное преобразование Лапласа и получаем вид переходного процесса x(t)
для заданного входного воздействия:
,
где Res
x(p)
– вычет функции x(p)
в точке a.
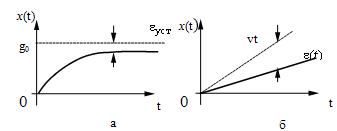
Обычно реакция системы на ступенчатое
воздействие имеет вид, показанный на рис. 21,а или рис. 21,б.
Рис.
21.
Переходный процесс,
как правило, характеризуют двумя параметрами – длительностью переходного
процесса (временем установления) и величиной перерегулирования.
Под временем установления tу
понимают временной интервал, по истечении которого отклонение |x(t) — xуст
| выходного процесса от установившегося значения xуст не
превышает определенную величину, например, 0,1gо. Время
установления является важным параметром САУ, позволяющим оценить ее быстродействие.
Величину tу можно оценить приближенно по амплитудно-частотной
характеристике системы. При заданной частоте среза . Для оценки качества системы
используется также величина перерегулирования, определяемая соотношением .
В зависимости от
характера собственных колебаний системы переходный процесс в ней может быть
колебательным, как это показано на рис. 21, б, или плавным гладким, называемым
апериодическим (рис. 21,а). Если корни характеристического уравнения системы
действительны, то переходный процесс в ней апериодический. В случае
комплексных корней характеристического уравнения собственные колебания
устойчивой системы управления являются затухающими гармоническими и переходный
процесс в системе имеет колебательный характер.
При малом запасе устойчивости САУ ее
собственные колебания затухают медленно, и перерегулирование в переходном режиме
получается значительным. Как следствие, величина перерегулирования может
служить мерой запаса устойчивости системы. Для многих систем запас
устойчивости считается достаточным, если величина перерегулирования .
Установившийся
режим
При проектировании систем управления
часто требуется оценить ошибку слежения в установившемся режиме . В зависимости от
вида воздействия и свойств системы эта ошибка может быть нулевой, постоянной
или бесконечно большой величиной.
Очень важно, что величина
установившейся ошибки может быть легко найдена с помощью теоремы о предельном
значении оригинала: .
При использовании этой теоремы нужно
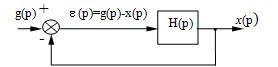
выразить величину ошибки e (p) через g(p). Для этого рассмотрим
структурную схему замкнутой системы управления (рис. 22).
Рис.
22
Очевидно, e (p) = g(p) — x(p)
= g(p) — H(p)e(p). Отсюда или e (p) = He(p)g(p)
, где He(p) = называется передаточной функцией
системы управления от входного воздействия g(p) к ошибке слежения e(p).
Таким образом, величину установившейся ошибки можно найти с помощью следующего
соотношения:
,
где He(p) = 1/(1+H(p));
g(p) — изображение типового входного воздействия.
Пример 1. Рассмотрим
систему управления, в составе которой нет интеграторов, например,
.
Найдем величину установившейся
ошибки при ступенчатом входном воздействии g(t) = g0, t ³ 0.
В этом случае
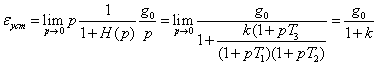
Предположим теперь, что входное
воздействие изменяется линейно t или
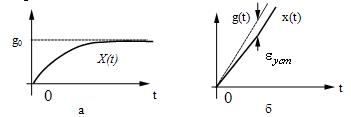
.
Тогда . Соответствующие входные воздействия и
переходные процессы можно представить графиками на рис. 23,а и б.
Рис.
23
Пример 2. Рассмотрим
теперь систему, содержащую один интегратор. Типичным примером может быть
система сервопривода (рис. 6) с .
Для ступенчатого воздействия g(t) = g0
или g(p) = получим
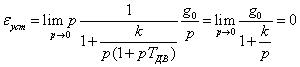
При линейном входном воздействии
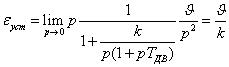
Такие процессы можно проиллюстрировать
соответствующими кривыми на рис.24, а и б.
Рис.
24
Пример 3.
Рассмотрим систему с двумя интеграторами. Пусть, например, . При ступенчатом
воздействии 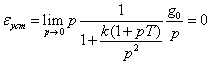
При линейном 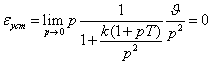
Наконец, если входное воздействие
квадратичное g(t) = at2/2 (g(p) = a/p3),
то
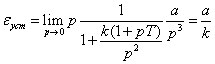
Таким образом, в системе с двумя
интеграторами может осуществляться слежение за квадратичным входным
воздействием при конечной величине установившейся ошибки. Например, можно
следить за координатами объекта, движущегося с постоянным ускорением.
Статические
и астатические системы управления
Анализ рассмотренных примеров
показывает, что системы управления, содержащие интегрирующие звенья, выгодно
отличаются от систем без интеграторов. По этому признаку все системы делятся на
статические системы, не содержащие интегрирующих звеньев, и астатические
системы, которые содержат интеграторы. Системы с одним интегратором называются
системами с астатизмом первого порядка. Системы с двумя интеграторами –
системами с астатизмом второго порядка и т.д.
Для статических систем даже при
неизменяющемся воздействии g(t) = g0 установившаяся ошибка имеет
конечную величину g(t) = g0 . В системах с астатизмом первого
порядка при ступенчатом воздействии установившаяся ошибка равна нулю, но при линейно
изменяющемся воздействии . Наконец, в системах с астатизмом
второго порядка ненулевая установившаяся ошибка появляется только при
квадратичных входных воздействиях g(t) = at2 /2 и
составляет величину eуст =
a/k.
Какие же физические причины лежат в
основе таких свойств астатических систем управления?
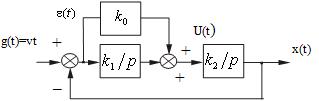
Рассмотрим систему управления с
астатизмом второго порядка (рис. 25)
Рис.
25
Пусть входной сигнал системы управления
изменяется линейно:
t. Как было
установлено, в такой системе установившаяся ошибка равна нулю, т.е. e
(t) =0. Каким же образом система работает при нулевом сигнале ошибки? Если x(t)
= t , то на
входе второго интегратора должен быть сигнал . Действительно, при нулевом
рассогласовании e (t) =0 в системе с интеграторами
возможно существование ненулевого выходного сигнала первого интегратора . Первый интегратор
после окончания переходного процесса «запоминает» скорость изменения входного
воздействия и в дальнейшем работа системы управления осуществляется по
«памяти». Таким образом, физическим объяснением такого значительного различия
статических и астатических систем является наличие памяти у астатических систем
управления.
*
* *
Итак, существуют простые возможности
определения важнейшего показателя систем управления – величины их динамических
ошибок. Детальный анализ переходных процессов в системах управления обычно
выполняют с помощью моделирования на ПЭВМ. Вместе с тем величины
установившихся ошибок легко находятся аналитически. При этом астатические
системы управления, т.е. системы с интеграторами, имеют существенно лучшие
показатели качества по сравнению со статическими системами.
Точность системы автоматического управления Статическая ошибка системы
В системах
автоматического управления часто
приходится решать задачу стабилизации
управляемой величины. Точность поддержания
требуемого значения управляемой величины
в такой системе можно оценить как разницу
между заданным значением управляемой
величины и её установившимся значением
в системе после окончания переходного
процесса:
.
Эта величина
получила название статической ошибки
системы. При вычислении статической
ошибки предполагается, что система
находится в статике и все сигналы в ней
имеют постоянные величины. Статическая
ошибка используется для оценки точности
установления в системе заданной
постоянной выходной величины после
окончания переходного процесса.
Используя
передаточную функцию замкнутой системы
по ошибке, для изображения ошибки в
системе можно записать
,
гдепередаточная
функция замкнутой системы по ошибке,изображение
задающего воздействия.
Для статики,
когда все сигналы в системе неизменны,
выражение для ошибки можно перенести
в область оригиналов
.
Поскольку
,
гдеW(p)
– передаточная функция разомкнутой
системы, то статическую ошибку системы
можно вычислить, зная передаточную
функцию разомкнутой системы:
,
где.
Вместо
абсолютного значения статической ошибки
часто используют относительную
статическую ошибку
.
Если система
статическая (т.е. не содержит интегрирующих
звеньев), то передаточную функцию
разомкнутой системы можно представить
в следующем нормированном виде:
,
гдеK– коэффициент
усиления системы,A*(p),B*(p)
– нормированные полиномыA(p)
иB(p).
При этоми
.
Тогдаи статическая ошибка в статической
системе
.
Статическая
ошибка в статической системе уменьшается
с увеличением коэффициента усиления
системы. Статическая система всегда
будет иметь некоторую ошибку. Физический
смысл такой ошибки заключается в
необходимости некоторого рассогласования
между задающей и выходной величинами
системы для получения сигнала управления.
Если в системе
управления имеются интегрирующие
звенья, то система будет астатической.
Для астатической системы первого порядка
(содержащей одно интегрирующее звено)
передаточная функция разомкнутой
системы
и передаточная функция замкнутой системы
по ошибке
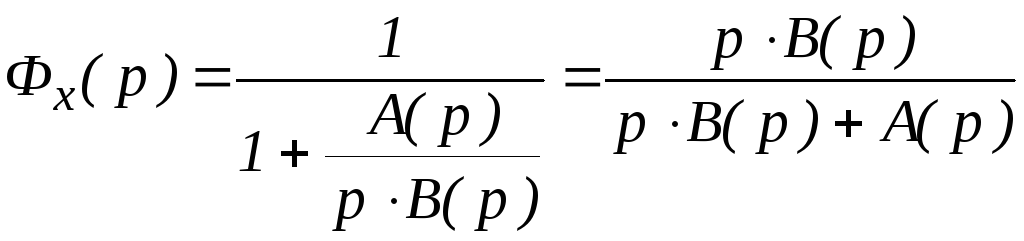
В этом случае всегда
и, следовательно, статическая ошибка
астатической системы будет равна нулю.
Таким образом, статическая ошибка в
астатической системе в принципе
отсутствует, что обуславливает более
высокую точность астатических систем,
по сравнению со статическими системами.
В астатической системе автоматического
управления установившееся значение
управляемой величины равно заданному
значению этой величины.
Вынужденная ошибка системы
Процесс в
системе складывается из свободного
процесса и вынужденного процесса:
.
Для
устойчивой системы свободный процесс
по истечении времениtпзатухает и в системе устанавливается
вынужденный процесс
Точность
поддержания заданного значения
управляемой величины в вынужденном
режиме характеризуется вынужденной
ошибкой системы
.
Вынужденная
ошибка хорошо характеризует работу
системы автоматического управления в
том случае, когда изменения управляющего
воздействия происходят существенно
медленнее собственных переходных
процессов в системе и последними можно
пренебречь.
Рассмотрим
вычисление вынужденной ошибки системы
автоматического управления. Изображение
для вынужденной ошибки
.
В общем случае
является дробно-рациональной функцией
отpи ее можно разложить
в ряд Тейлора по степенямрвблизи, тогда
и
выражение для вынужденной ошибки системы
примет вид
где
постоянные
коэффициенты.
Для полученного
изображения вынужденной ошибки на
основе свойств преобразования Лапласа
легко находится выражение для оригинала
ошибки
где
,
,
…коэффициенты
ошибок, полученные выше (C0– коэффициент статической ошибки,C1
– коэффициент скоростной ошибки и
т. д.).
Коэффициенты
ошибки могут быть также получены делением
числителя передаточной функции на ее
знаменатель. Полученное выражение для
вынужденной ошибки позволяет оценить
точность системы автоматического
управления в установившемся режиме.
Вынужденная ошибка, например, хорошо
характеризует точность работы следящих
систем автоматического управления.
Соседние файлы в папке ТАУ
- #
- #
- #
Лекция 17. Расчет установившейся ошибки в системах управления.
Структурные признаки астатизма
Установившейся (статической) ошибкой называют
постоянное значение сигнала ошибки x(t)=g(t)-y(t),
которое она приобретает по окончании переходного процесса: , рисунок 116.
Очевидно, установившаяся ошибка зависит от законов
изменения и численных характеристик входных сигналов системы. Поэтому при ее
определении принято рассматривать так называемые типовые входные сигналы,
законы изменения которых составляют степенной ряд относительно времени.
Например, для задающего воздействия:
,
,

далее.
При наличии нескольких воздействий на линейную систему
для определения xуст используется
принцип суперпозиции – реакция линейной системы на совокупность входных
сигналов совпадает с алгебраической суммой ее реакций на каждый из сигналов в
отдельности:
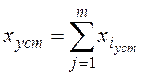
каждое слагаемое, или составляющая сигнала ошибки, определяется
для i-го входного сигнала при условии, что остальные
тождественно равны нулю. Такой подход полностью соответствует определению
передаточной функции и позволяет выполнять расчет установившейся ошибки на
основе структурной схемы системы.
Рассмотрим порядок расчета установившейся ошибки на
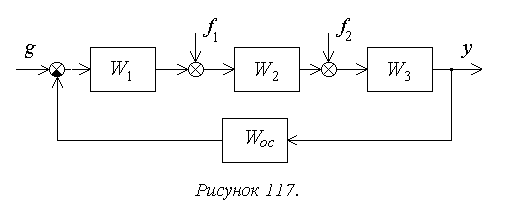
следующем достаточно общем примере (рисунок 117).
В соответствии с принципом суперпозиции установившаяся
ошибка будет определяться здесь в виде суммы трех составляющих .
Изображение по Лапласу ошибки от задающего воздействия
получают через передаточную функцию замкнутой системы по ошибке при известном изображении задающего
воздействия G(s):
, где
F(s) – основная передаточная функция замкнутой системы.
Для структурной схемы на рисунке 117
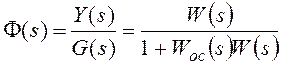
— передаточная функция
разомкнутой системы, или прямой цепи системы, для рассматриваемого примера.
Непосредственно для расчета
установившегося значения ошибки от задающего воздействия используют теорему о
конечном значении для преобразования Лапласа:
В результате:
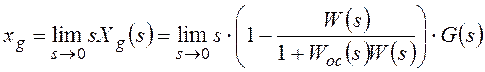
Изображение по Лапласу ошибки от возмущающего
воздействия получают через передаточную функцию замкнутой системы по ошибке от
возмущения при известном изображении возмущающего
воздействия F(s):
, где
Ff(s) –передаточная функция замкнутой системы по
возмущающему воздействию,
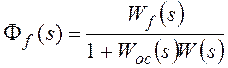
Wf(s)
– передаточная функция разомкнутой системы по возмущению (передаточная функция
участка прямой цепи системы от точки приложения возмущающего воздействия до
выхода системы).
Для структурной схемы на рисунке 8 необходимо
учитывать два возмущающих воздействия, приложенные в различные точки системы.
Для f1:
,
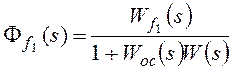
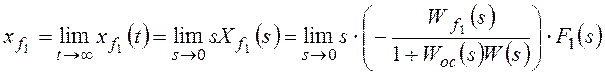
Для f2:
,
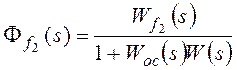
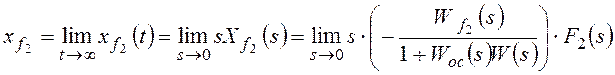
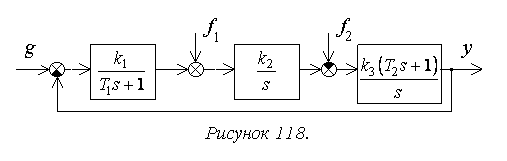
Расчет упрощается для
системы с единичной отрицательной обратной связью (рисунок 118):
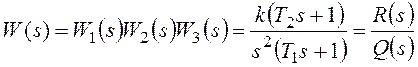
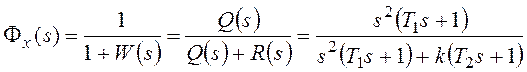
разомкнутой системы.
Найдем установившуюся ошибку
для некоторых типовых вариантов задающего воздействия.
При получим:
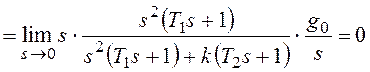
При получим:
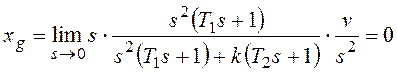
При 
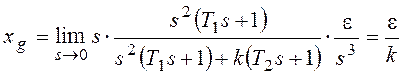
Если установившаяся ошибка
тождественно равна нулю при каком-либо типовом варианте входного сигнала,
независимо от его численных характеристик, систему называют астатической по
рассматриваемому входному сигналу.
Количество типовых вариантов
входного сигнала – членов степенного ряда, при которых установившаяся ошибка
тождественно равна нулю, определяет порядок астатизма.
Рассматриваемая система
обладает свойством астатизма второго порядка по задающему воздействию.
Рассмотрим установившуюся
ошибку от возмущения f1:
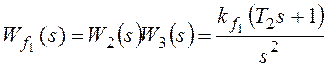
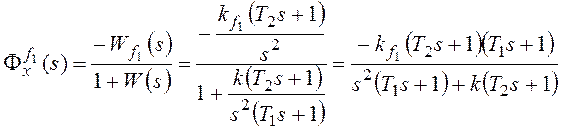
–
коэффициент передачи разомкнутой системы по возмущению f1.
При получим:
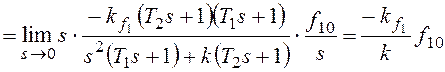
При получим:
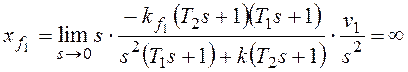
При 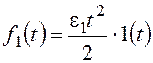
тот же результат.
Отметим, что по возмущению f1 рассматриваемая система
не является астатической. Кроме того, она не в состоянии отработать два последних
варианта входного сигнала.
Рассмотрим установившуюся
ошибку от возмущения f2:
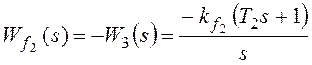
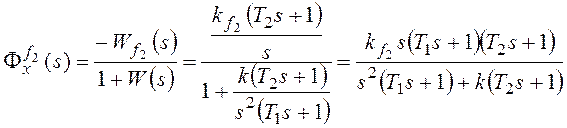
–
коэффициент передачи разомкнутой системы по возмущению f2.
При получим:
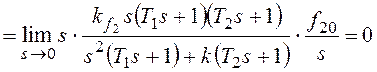
При получим:
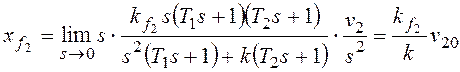
При 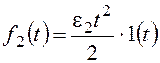
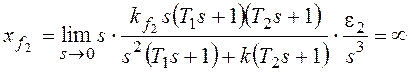
По возмущению f2 рассматриваемая система имеет
астатизм первого порядка. Она не в состоянии отработать возмущающее
воздействие, изменяющееся во времени с постоянным ускорением.
Подведем некоторые итоги:
1. Наличие и глубина
свойства астатизма зависят от точки приложения входного сигнала.
2. Постоянные времени
звеньев системы не влияют на ее точность.
3. Увеличение значения
коэффициента передачи разомкнутой системы приводит к снижению величины
установившейся ошибки.
Для систем с единичной
отрицательной обратной связью существуют достаточно простые структурные
признаки астатизма.
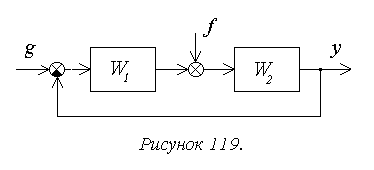
Рассмотрим структуру,
показанную на рисунке 119.
В общем случае передаточная
функция разомкнутой системы может быть представлена в следующей форме:
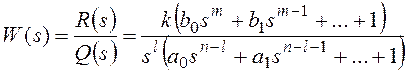
Тогда получим:
и для общего вида задающего воздействия 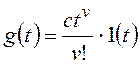
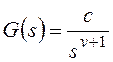
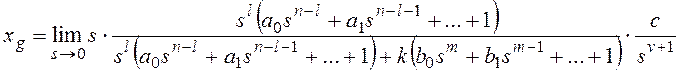
Результат нахождения этого
предела зависит от соотношения показателей степени:
— при l>v установившаяся
ошибка равна нулю независимо от остальных параметров, то есть имеет место
астатизм;
— при l=v получаем
константу;
— при l<v установившаяся
ошибка стремится к бесконечности, то есть система не в состоянии отработать
входной сигнал.
Учитывая, что минимальное
значение v нулевое,
получаем условие астатизма по задающему воздействию: l>0.
Таким образом, структурный
признак астатизма по задающему воздействию в системе с единичной отрицательной
обратной связью состоит в наличии нулевых корней в знаменателе передаточной
функции разомкнутой системы, или интегрирующих звеньев в прямой цепи системы.
Нетрудно также убедиться,
что положительное значение l совпадает
с порядком астатизма.
Для получения признака
астатизма по возмущающему воздействию представим передаточные функции на
рисунке 10 в форме:
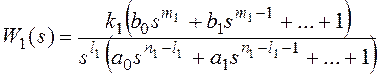
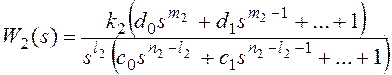
k1k2=k, m1+m2=m,
n1+n2=n,
причем и
.
Тогда получим:
и для общего вида возмущающего воздействия 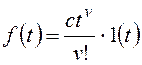
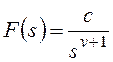
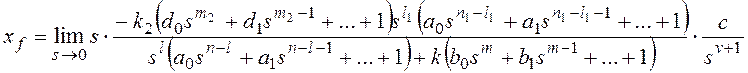
Все вышеприведенные выводы
можно повторить для показателя степени l1.
Таким образом, структурный
признак астатизма по возмущающему воздействию в системе с единичной
отрицательной обратной связью состоит в наличии нулевых корней в знаменателе
передаточной функции участка системы до точки приложения воздействия, или
интегрирующих звеньев на том же участке.
The deviation of the output of control system from desired response during steady state is known as steady state error. It is represented as $e_{ss}$. We can find steady state error using the final value theorem as follows.
$$e_{ss}=lim_{t to infty}e(t)=lim_{s to 0}sE(s)$$
Where,
E(s) is the Laplace transform of the error signal, $e(t)$
Let us discuss how to find steady state errors for unity feedback and non-unity feedback control systems one by one.
Steady State Errors for Unity Feedback Systems
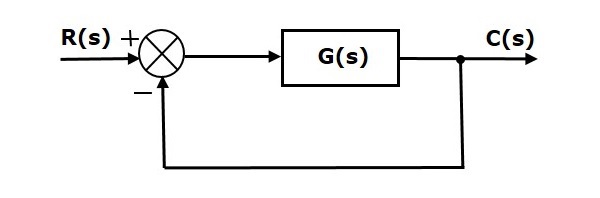
Consider the following block diagram of closed loop control system, which is having unity negative feedback.
Where,
- R(s) is the Laplace transform of the reference Input signal $r(t)$
- C(s) is the Laplace transform of the output signal $c(t)$
We know the transfer function of the unity negative feedback closed loop control system as
$$frac{C(s)}{R(s)}=frac{G(s)}{1+G(s)}$$
$$Rightarrow C(s)=frac{R(s)G(s)}{1+G(s)}$$
The output of the summing point is —
$$E(s)=R(s)-C(s)$$
Substitute $C(s)$ value in the above equation.
$$E(s)=R(s)-frac{R(s)G(s)}{1+G(s)}$$
$$Rightarrow E(s)=frac{R(s)+R(s)G(s)-R(s)G(s)}{1+G(s)}$$
$$Rightarrow E(s)=frac{R(s)}{1+G(s)}$$
Substitute $E(s)$ value in the steady state error formula
$$e_{ss}=lim_{s to 0} frac{sR(s)}{1+G(s)}$$
The following table shows the steady state errors and the error constants for standard input signals like unit step, unit ramp & unit parabolic signals.
| Input signal | Steady state error $e_{ss}$ | Error constant |
|---|---|---|
|
unit step signal |
$frac{1}{1+k_p}$ |
$K_p=lim_{s to 0}G(s)$ |
|
unit ramp signal |
$frac{1}{K_v}$ |
$K_v=lim_{s to 0}sG(s)$ |
|
unit parabolic signal |
$frac{1}{K_a}$ |
$K_a=lim_{s to 0}s^2G(s)$ |
Where, $K_p$, $K_v$ and $K_a$ are position error constant, velocity error constant and acceleration error constant respectively.
Note − If any of the above input signals has the amplitude other than unity, then multiply corresponding steady state error with that amplitude.
Note − We can’t define the steady state error for the unit impulse signal because, it exists only at origin. So, we can’t compare the impulse response with the unit impulse input as t denotes infinity.
Example
Let us find the steady state error for an input signal $r(t)=left( 5+2t+frac{t^2}{2} right )u(t)$ of unity negative
feedback control system with $G(s)=frac{5(s+4)}{s^2(s+1)(s+20)}$
The given input signal is a combination of three signals step, ramp and parabolic. The following table shows the error constants and steady state error values for these three signals.
| Input signal | Error constant | Steady state error |
|---|---|---|
|
$r_1(t)=5u(t)$ |
$K_p=lim_{s to 0}G(s)=infty$ |
$e_{ss1}=frac{5}{1+k_p}=0$ |
|
$r_2(t)=2tu(t)$ |
$K_v=lim_{s to 0}sG(s)=infty$ |
$e_{ss2}=frac{2}{K_v}=0$ |
|
$r_3(t)=frac{t^2}{2}u(t)$ |
$K_a=lim_{s to 0}s^2G(s)=1$ |
$e_{ss3}=frac{1}{k_a}=1$ |
We will get the overall steady state error, by adding the above three steady state errors.
$$e_{ss}=e_{ss1}+e_{ss2}+e_{ss3}$$
$$Rightarrow e_{ss}=0+0+1=1$$
Therefore, we got the steady state error $e_{ss}$ as 1 for this example.
Steady State Errors for Non-Unity Feedback Systems
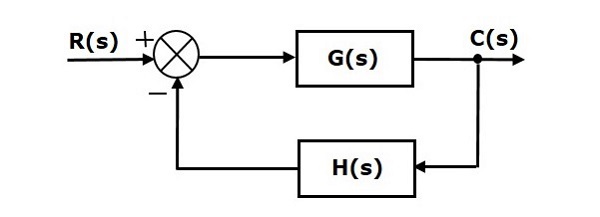
Consider the following block diagram of closed loop control system, which is having nonunity negative feedback.
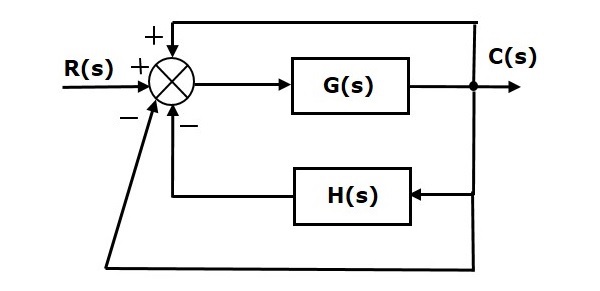
We can find the steady state errors only for the unity feedback systems. So, we have to convert the non-unity feedback system into unity feedback system. For this, include one unity positive feedback path and one unity negative feedback path in the above block diagram. The new block diagram looks like as shown below.
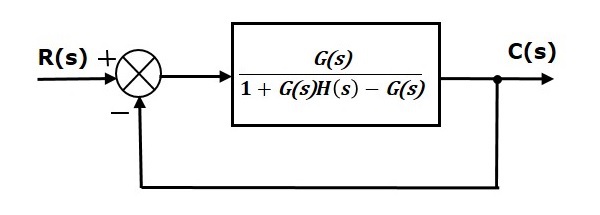
Simplify the above block diagram by keeping the unity negative feedback as it is. The following is the simplified block diagram.
This block diagram resembles the block diagram of the unity negative feedback closed loop control system. Here, the single block is having the transfer function $frac{G(s)}{1+G(s)H(s)-G(s)}$ instead of $G(s)$. You can now calculate the steady state errors by using steady state error formula given for the unity negative feedback systems.
Note − It is meaningless to find the steady state errors for unstable closed loop systems. So, we have to calculate the steady state errors only for closed loop stable systems. This means we need to check whether the control system is stable or not before finding the steady state errors. In the next chapter, we will discuss the concepts-related stability.
The deviation of the output of control system from desired response during steady state is known as steady state error. It is represented as $e_{ss}$. We can find steady state error using the final value theorem as follows.
$$e_{ss}=lim_{t to infty}e(t)=lim_{s to 0}sE(s)$$
Where,
E(s) is the Laplace transform of the error signal, $e(t)$
Let us discuss how to find steady state errors for unity feedback and non-unity feedback control systems one by one.
Steady State Errors for Unity Feedback Systems
Consider the following block diagram of closed loop control system, which is having unity negative feedback.
Where,
- R(s) is the Laplace transform of the reference Input signal $r(t)$
- C(s) is the Laplace transform of the output signal $c(t)$
We know the transfer function of the unity negative feedback closed loop control system as
$$frac{C(s)}{R(s)}=frac{G(s)}{1+G(s)}$$
$$Rightarrow C(s)=frac{R(s)G(s)}{1+G(s)}$$
The output of the summing point is —
$$E(s)=R(s)-C(s)$$
Substitute $C(s)$ value in the above equation.
$$E(s)=R(s)-frac{R(s)G(s)}{1+G(s)}$$
$$Rightarrow E(s)=frac{R(s)+R(s)G(s)-R(s)G(s)}{1+G(s)}$$
$$Rightarrow E(s)=frac{R(s)}{1+G(s)}$$
Substitute $E(s)$ value in the steady state error formula
$$e_{ss}=lim_{s to 0} frac{sR(s)}{1+G(s)}$$
The following table shows the steady state errors and the error constants for standard input signals like unit step, unit ramp & unit parabolic signals.
| Input signal | Steady state error $e_{ss}$ | Error constant |
|---|---|---|
|
unit step signal |
$frac{1}{1+k_p}$ |
$K_p=lim_{s to 0}G(s)$ |
|
unit ramp signal |
$frac{1}{K_v}$ |
$K_v=lim_{s to 0}sG(s)$ |
|
unit parabolic signal |
$frac{1}{K_a}$ |
$K_a=lim_{s to 0}s^2G(s)$ |
Where, $K_p$, $K_v$ and $K_a$ are position error constant, velocity error constant and acceleration error constant respectively.
Note − If any of the above input signals has the amplitude other than unity, then multiply corresponding steady state error with that amplitude.
Note − We can’t define the steady state error for the unit impulse signal because, it exists only at origin. So, we can’t compare the impulse response with the unit impulse input as t denotes infinity.
Example
Let us find the steady state error for an input signal $r(t)=left( 5+2t+frac{t^2}{2} right )u(t)$ of unity negative
feedback control system with $G(s)=frac{5(s+4)}{s^2(s+1)(s+20)}$
The given input signal is a combination of three signals step, ramp and parabolic. The following table shows the error constants and steady state error values for these three signals.
| Input signal | Error constant | Steady state error |
|---|---|---|
|
$r_1(t)=5u(t)$ |
$K_p=lim_{s to 0}G(s)=infty$ |
$e_{ss1}=frac{5}{1+k_p}=0$ |
|
$r_2(t)=2tu(t)$ |
$K_v=lim_{s to 0}sG(s)=infty$ |
$e_{ss2}=frac{2}{K_v}=0$ |
|
$r_3(t)=frac{t^2}{2}u(t)$ |
$K_a=lim_{s to 0}s^2G(s)=1$ |
$e_{ss3}=frac{1}{k_a}=1$ |
We will get the overall steady state error, by adding the above three steady state errors.
$$e_{ss}=e_{ss1}+e_{ss2}+e_{ss3}$$
$$Rightarrow e_{ss}=0+0+1=1$$
Therefore, we got the steady state error $e_{ss}$ as 1 for this example.
Steady State Errors for Non-Unity Feedback Systems
Consider the following block diagram of closed loop control system, which is having nonunity negative feedback.
We can find the steady state errors only for the unity feedback systems. So, we have to convert the non-unity feedback system into unity feedback system. For this, include one unity positive feedback path and one unity negative feedback path in the above block diagram. The new block diagram looks like as shown below.
Simplify the above block diagram by keeping the unity negative feedback as it is. The following is the simplified block diagram.
This block diagram resembles the block diagram of the unity negative feedback closed loop control system. Here, the single block is having the transfer function $frac{G(s)}{1+G(s)H(s)-G(s)}$ instead of $G(s)$. You can now calculate the steady state errors by using steady state error formula given for the unity negative feedback systems.
Note − It is meaningless to find the steady state errors for unstable closed loop systems. So, we have to calculate the steady state errors only for closed loop stable systems. This means we need to check whether the control system is stable or not before finding the steady state errors. In the next chapter, we will discuss the concepts-related stability.