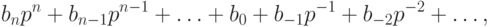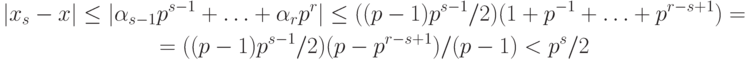Ошибки округления при вычислениях на компьютере - Исправление ошибок и поиск оптимальных решений проблем

Ошибки округления

Даже
если предположить, что исходная информация
не содержит никаких ошибок и все
вычислительные процессы конечны и не
приводят к ошибкам ограничения, то все
равно в этом случае присутствует третий
тип ошибок – ошибки округления.
Предположим, что вычисления производятся
на машине, в которой каждое число
представляется 5-ю значащими цифрами,
и что необходимо сложить два числа
9.2654 и 7.1625, причем эти два числа являются
точными. Сумма их равна 16.4279, она содержит
6 значащих цифр и не помещается в разрядной
сетке нашей гипотетической машины.
Поэтому 6-значный результат будет
округлен
до 16.428, и при этом возникает ошибка
округления.
Так как компьютеры всегда работают с
конечным числом значащих цифр, то
потребность в округлении возникает
довольно часто.

Вопросы
округления относятся только к
действительным числам. При выполнении
операций с целыми числами потребность
в округлении не возникает. Сумма, разность
и произведение целых чисел сами являются
целыми числами; если результат слишком
велик, то это свидетельствует об ошибке
в программе. Частное от деления двух
целых чисел не всегда является целым
числом, но при делении целых чисел
дробная часть отбрасывается.

Абсолютная и относительная погрешности

Допустим,
что точная ширина стола – А=384 мм, а мы,
измерив ее, получили а=381 мм. Модуль
разности между точным значением
измеряемой величины и ее приближенным
значением называется абсолютной
погрешностью
.
В данном примере абсолютная погрешность
3 мм. Но на практике мы никогда не знаем
точного значения измеряемой величины,
поэтому не можем точно знать абсолютную
погрешность.

Но
обычно мы знаем точность измерительных
приборов, опыт наблюдателя, производящего
измерения и т.д. Это дает возможность
составить представление об абсолютной
погрешности измерения. Если, например,
мы рулеткой измеряем длину комнаты, то
нам нетрудно учесть метры и сантиметры,
но вряд ли мы сможем учесть миллиметры.
Да в этом и нет надобности. Поэтому мы
сознательно допускаем ошибку в пределах
1 см. абсолютная погрешность длины
комнаты меньше 1 см. Измеряя длину
какого-либо отрезка миллиметровой
линейкой, мы имеем право утверждать,
что погрешность измерения не превышает
1 мм.

Абсолютная
погрешность _а
приближенного числа а дает возможность
установить границы, в которых лежит
точное число А:

Абсолютная
погрешность не является достаточным
показателем качества измерения и не
характеризует точность вычислений или
измерений. Если известно, что, измерив
некоторую длину, мы получили абсолютную
погрешность в 1 см, то никаких заключений
о том, хорошо или плохо мы измеряли,
сделать нельзя. Если мы измеряли длину
карандаша в 15 см и ошиблись на 1 см, наше
измерение никуда не годится. Если же мы
измеряли 20-метровый коридор и ошиблись
всего на 1 см, то наше измерение – образец
точности. Важна
не только сама абсолютная погрешность,
но и та доля, которую она составляет от
измеренной величины.
В первом примере абс. погрешность 1 см
составляет 1/15 долю измеряемой величины
или 7%, во втором – 1/2000 или 0.05%. Второе
измерение значительно лучше.

Относительной
погрешностью называют отношение
абсолютной погрешности к абсолютному
значению приближенной величины:

В
отличие от абсолютной погрешности,
которая обычно есть величина размерная,
относительная погрешность всегда есть
величина безразмерная. Обычно ее выражают
в %.

Пример

При измерении
длины в 5 см допущена абсолютная
погрешность в 0.1 см. Какова относительная
погрешность? (Ответ 2%)

При
подсчете числа жителей города, которое
оказалось равным 2000000,
допущена
погрешность 100 человек. Какова относительная
погрешность? (Ответ
0.005%)

Результат
всякого измерения выражается числом,
лишь приблизительно характеризующим
измеряемую величину. Поэтому при
вычислениях мы имеем дело с приближенными
числами. При записи приближенных чисел
принимается, что последняя цифра справа
характеризует величину абсолютной
погрешности.

Например,
если записано 12.45, то это не значит, что
величина, характеризуемая этим числом,
не содержит тысячных долей. Можно
утверждать, что тысячные доли при
измерении не учитывались, следовательно,
абсолютная погрешность меньше половины
единицы последнего разряда:
.
Аналогично, относительно приближенного
числа 1.283, можно сказать, что абсолютная
погрешность меньше 0.0005:.

Приближенные
числа принято записывать так, чтобы
абсолютная погрешность не превышала
единицы последнего десятичного разряда.
Или, иначе говоря, абсолютная
погрешность приближенного числа
характеризуется числом десятичных
знаков после запятой.

Как же
быть, если при тщательном измерении
какой-нибудь величины получится, что
она содержит целую единицу, 2 десятых,
5 сотых, не содержит тысячных, а
десятитысячные не поддаются учету? Если
записать 1.25, то в этой записи тысячные
не учтены, тогда как на самом деле мы
уверены, что их нет. В таком случае
принято ставить на их месте 0, – надо
писать 1.250. Таким образом, числа 1.25 и
1.250 обозначают не одно и то же. Первое –
содержит тысячные; мы только не знаем,
сколько именно. Второе – тысячных не
содержит, о десятитысячных ничего
сказать нельзя.

Сложнее
приходится при записи больших приближенных
чисел. Пусть число жителей деревни равно
2000 человек, а в городе приблизительно
457000
жителей. Причем относительно города в
тысячах мы уверены, но допускаем
погрешность в сотнях и десятках. В первом
случае нули в конце числа указывают на
отсутствие сотен, десятков и единиц,
такие нули мы назовем значащими;
во втором случае нули указывают на наше
незнание числа сотен, десятков и единиц.
Такие нули мы назовем незначащими.
При записи приближенного числа,
содержащего нули надо дополнительно
оговаривать их значимость. Обычно нули
– незначащие. Иногда на незначимость
нулей можно указывать, записывая число
в экспоненциальном виде (457*10³).

Сравним
точность двух приближенных чисел 1362.3
и 2.37. В первом абсолютная погрешность
не превосходит 0.1, во втором – 0.01. Поэтому
второе число выглядит более точным, чем
первое.

Подсчитаем
относительную погрешность. Для первого
числа
;
для второго.
Второе число значительно (почти в 100
раз) менее точно, чем первое. Получается
это потому, что в первом числе дано 5
верных (значащих) цифр, тогда как во
втором – только 3.

Все
цифры приближенного числа, в которых
мы уверены, будем называть верными
(значащими) цифрами. Нули сразу справа
после запятой не бывают значащими, они
лишь указывают на порядок стоящих правее
значащих цифр. Нули в крайних правых
позициях числа могут быть как значащими,
так и не значащими. Например, каждое из
следующих чисел имеет 3 значащие цифры:
283*10⁵,
200*10²,
22.5, 0.0811, 2.10, 0.0000458.

Пример

Сколько
значащих (верных) цифр в следующих
числах:

0.75
(2), 12.050 (5), 1875*10⁵
(4), 0.06*10⁹
(1)

Оценить
относительную погрешность следующих
приближенных чисел:

0.989
(0.1%),

нули
значащие: 21000 (0.005%),

0.000
024
(4%),

0.05 (20%)

Нетрудно
заметить, что для примерной оценки
относительной погрешности числа
достаточно подсчитать количество
значащих цифр. Для числа, имеющего только
одну значащую цифру относительная
погрешность около 10%;

с
2-мя значащими цифрами – 1%;

с
3-мя значащими цифрами – 0.1%;

с
4-мя значащими цифрами – 0.01% и т.д.

При
вычислениях с приближенными числами
нас будет интересовать вопрос: как,
исходя из данных приближенных чисел,
получить ответ с нужной относительной
погрешностью.

Часто
при этом все исходные данные приходится
брать с одной и той же погрешностью,
именно с погрешностью наименее точного
из данных чисел. Поэтому часто приходится
более точное число заменять менее точным
– округлять.

округление
до десятых 27.136 
27.1,

округление
до целых 32.8 
33.

Правило
округления: Если крайняя левая из
отбрасываемых при округлении цифр
меньше 5, то последнюю сохраняемую цифру
не изменяют; если крайняя левая из
отбрасываемых цифр больше 5 или если
она равна 5, то последнюю сохраняемую
цифру увеличивают на 1.

Пример

округлить
до десятых 17.96 (18.0)

округлить
до сотых 14.127 (14.13)

округлить,
сохранив 3 верные цифры: 83.501 (83.5), 728.21
(728), 0.0168835 (0.01688).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Материал из MachineLearning.

Перейти к: навигация, поиск

Содержание

1 Введение
- 1.1 Постановка вопроса. Виды погрешностей
2 Виды мер точности
3 Предельные погрешности
4 Погрешности округлений при представлении чисел в компьютере
5 Погрешности арифметических операций
6 Погрешности вычисления функций
7 Числовые примеры
8 Список литературы
9 См. также

Введение

Постановка вопроса. Виды погрешностей

Процесс исследования исходного объекта методом математического моделирования и вычислительного эксперимента неизбежно носит приближенный характер, так как на каждом этапе вносятся погрешности. Построение математической модели связано с упрощением исходного явления, недостаточно точным заданием коэффициентов уравнения и других входных данных. По отношению к численному методу, реализующему данную математическую модель, указанные погрешности являются неустранимыми, поскольку они неизбежны в рамках данной модели.

При переходе от математической модели к численному методу возникают погрешности, называемые погрешностями метода. Они связаны с тем, что всякий численный метод воспроизводит исходную математическую модель приближенно. Наиболее типичными погрешностями метода являются погрешность дискретизации и погрешность округления.
При построении численного метода в качестве аналога исходной математической задачи обычно рассматривается её дискретная модель. Разность решений дискретизированной задачи и исходной называется погрешностью дискретизации. Обычно дискретная модель зависит от некоторого параметра (или их множества) дискретизации, при стремлении которого к нулю должна стремиться к нулю и погрешность дискретизации.
Дискретная модель представляет собой систему большого числа алгебраических уравнений. Для её решения используется тот или иной численный алгоритм. Входные данные этой системы, а именно коэффициенты и правые части, задаются в ЭВМ не точно, а с округлением. В процессе работы алгоритма погрешности округления обычно накапливаются, и в результате, решение, полученное на ЭВМ, будет отличаться от точного решения дискретизированной задачи. Результирующая погрешность называется погрешностью округления (вычислительной погрешностью). Величина этой погрешности определяется двумя факторами: точностью представления вещественных чисел в ЭВМ и чувствительностью данного алгоритма к погрешностям округления.

Итак, следует различать погрешности модели, дискретизации и округления. В вопросе преобладания какой-либо погрешности ответ неоднозначен. В общем случае нужно стремиться, чтобы все погрешности имели один и тот же порядок. Например, нецелесообразно пользоваться разностными схемами, имеющими точность 10⁻⁶, если коэффициенты исходных уравнений задаются с точностью 10⁻².

Виды мер точности

Мерой точности вычислений являются абсолютные и относительные погрешности. Абсолютная погрешность определяется формулой

где tilde a – приближение к точному значению .
Относительная погрешность определяется формулой

$delta(tilde a)=frac{|tilde a-a|}{a}.$

Относительная погрешность часто выражается в процентах. Абсолютная и относительная погрешности тесно связаны с понятием верных значащих цифр. Значащими цифрами числа называют все цифры в его записи, начиная с первой ненулевой цифры слева. Например, число 0,000129 имеет три значащих цифры. Значащая цифра называется верной, если абсолютная погрешность числа не превышает половины веса разряда, соответствующего этой цифре. Например, , абсолютная погрешность . Записывая число в виде

имеем , следовательно, число имеет две верных значащих цифр (9 и 3).

В общем случае абсолютная погрешность должна удовлетворять следующему неравенству:

$Delta(tilde a)<0,5cdot10^{m-n+1} ,$

где — порядок (вес) старшей цифры, — количество верных значащих цифр.
В рассматриваемом примере $Delta(tilde a)le0,5cdot10^{3-2+1}le0,5cdot10^2=50$ .

Относительная погрешность связана с количеством верных цифр приближенного числа соотношением:

$delta(tilde a)lefrac{Delta(tilde a)}{alpha_m}10^mlefrac{10^{m-n+1}}{alpha_m10^m}lefrac{1}{alpha_m10^{n-1}},$

где alpha_m — старшая значащая цифра числа.

Для двоичного представления чисел имеем $delta(tilde a)le2^{-n}$ .

Тот факт, что число tilde a является приближенным значением числа с абсолютной погрешностью , записывают в виде

причем числа tilde a и записываются с одинаковым количеством знаков после запятой, например, или $a=2,347pm2cdot10^{-3}$ .

Запись вида

означает, что число tilde a является приближенным значение числа с относительной погрешностью .

Так как точное решение задачи как правило неизвестно, то погрешности приходится оценивать через исходные данные и особенности алгоритма. Если оценка может быть вычислена до решения задачи, то она называется априорной. Если оценка вычисляется после получения приближенного решения задачи, то она называется апостериорной.

Очень часто степень точности решения задачи характеризуется некоторыми косвенными вспомогательными величинами. Например точность решения системы алгебраических уравнений

AX=F

характеризуется невязкой

где tilde X — приближенное решение системы.
Причём невязка достаточно сложным образом связана с погрешностью решения , причём если невязка мала, то погрешность может быть значительной.

Предельные погрешности

Пусть искомая величина является функцией параметров — приближенное значение . Тогда предельной абсолютной погрешностью называется величина

$D(a^*) = suplimits_{(t_1, ldots ,t_n) in Omega } left|{a(t_1, ldots ,t_n) - a^*}right| ,$

Предельной относительной погрешностью называется величина .

Пусть $left|{t_j - t_j^*}right| le Delta (t_j^* ), qquad j = 1 div n$ — приближенное значение . Предполагаем, что — непрерывно дифференцируемая функция своих аргументов. Тогда, по формуле Лагранжа,

$a(t_1, ldots ,t_n) - a^* = sumlimits_{j = 1}^n gamma_j (alpha )(t_j - t_j^*),$

где $gamma_j (alpha ) = a^{prime}_{t_j}(t_1^* + alpha (t_1 - t_1^*), ldots ,t_n^* + alpha (t_n - t_n^*)), qquad 0 le alpha le 1$ .

Отсюда

$left|{a(t_1, ldots ,t_n) - a^*}right| le D_1 (a^*) = sumlimits_{j = 1}^n b_j Delta (t_j^*),$

где $b_j = suplimits_Omega left|{a^{prime}_{t_j}(t_1, ldots ,t_n)}right|$ .

Можно показать, что при малых $rho = sqrt{{(Delta (t_1^* ))}^2 + ldots + {(Delta (t_n^* ))}^2 }$ эта оценка не может быть существенно улучшена. На практике иногда пользуются грубой (линейной) оценкой

$left|{a(t_1, ldots ,t_n) - a^*}right| le D_2 (a^*),$

где $D_2 (a^*) = sumlimits_{j = 1} left|{gamma_j (0)}right| Delta (t^*)$ .

Несложно показать, что:

— предельная погрешность суммы или разности равна сумме предельных погрешностей.
$delta (t_1^* cdots t_m^* cdot d_1^{* - 1} cdots d_m^{* - 1} ) = delta (t_1^* ) + ldots + delta (t_m^*) + delta (d_1^*) + ldots + delta (d_n^*)$ — предельная относительная погрешность произведения или частного приближенного равна сумме предельных относительных погрешностей.

Погрешности округлений при представлении чисел в компьютере

Одним из основных источников вычислительных погрешностей является приближенное представление чисел в компьютере, обусловленное конечностью разрядной сетки (см. Международный стандарт представления чисел с плавающей точкой в ЭВМ). Число , не представимое в компьютере, подвергается округлению, т. е. заменяется близким числом tilde a , представимым в компьютере точно.
Найдем границу относительной погрешности представления числа с плавающей точкой. Допустим, что применяется простейшее округление – отбрасывание всех разрядов числа, выходящих за пределы разрядной сетки. Система счисления – двоичная. Пусть надо записать число, представляющее бесконечную двоичную дробь

$a=underbrace{pm2^p}_{order}underbrace{left(frac{a_1}{2}+frac{a_2}{2^2}+dots+frac{a_t}{2^t}+frac{a_{t+1}}{2^{t+1}}+dotsright)}_{mantissa},$

где $a_j={0\1$ , — цифры мантиссы.
Пусть под запись мантиссы отводится t двоичных разрядов. Отбрасывая лишние разряды, получим округлённое число

$tilde a=pm2^pleft(frac{a_1}{2}+frac{a_2}{2^2}+dots+frac{a_t}{2^t}right).$

Абсолютная погрешность округления в этом случае равна

$a-tilde a=pm2^pleft(frac{a_{t+1}}{2^{t+1}}+frac{a_{t+2}}{2^{t+2}}+dotsright).$

Наибольшая погрешность будет в случае $a_{t+1}=1, qquad a_{t+2}=1,$ , тогда

$|a-tilde a|lepm2^pfrac{1}{2^{t+1}}underbrace{left(1+frac{1}{2}+frac{1}{2^2}+dotsright)}_{=2}=2^{p-t}.$

Т.к. , где — мантисса числа , то всегда a_1=1 . Тогда $|a|ge2^pcdot2^{-1}=2^{p-1}$ и относительная погрешность равна $frac{|a-tilde a|}{|a|}le2^{-t+1}$ . Практически применяют более точные методы округления и погрешность представления чисел равна

( 1 )

$frac{|a-tilde a|}{|a|}le2^{-t},$

т.е. точность представления чисел определяется разрядностью мантиссы .
Тогда приближенно представленное в компьютере число можно записать в виде , где $|epsilon|le2^{-t}$ – «машинный эпсилон» – относительная погрешность представления чисел.

Погрешности арифметических операций

При вычислениях с плавающей точкой операция округления может потребоваться после выполнения любой из арифметических операций. Так умножение или деление двух чисел сводится к умножению или делению мантисс. Так как в общем случае количество разрядов мантисс произведений и частных больше допустимой разрядности мантиссы, то требуется округление мантиссы результатов. При сложении или вычитании чисел с плавающей точкой операнды должны быть предварительно приведены к одному порядку, что осуществляется сдвигом вправо мантиссы числа, имеющего меньший порядок, и увеличением в соответствующее число раз порядка этого числа. Сдвиг мантиссы вправо может привести к потере младших разрядов мантиссы, т.е. появляется погрешность округления.

Округленное в системе с плавающей точкой число, соответствующее точному числу , обозначается через fl(x) (от англ. floating – плавающий). Выполнение каждой арифметической операции вносит относительную погрешность, не большую, чем погрешность представления чисел с плавающей точкой (1). Верна следующая запись:

где box — любая из арифметических операций, $|epsilon|le2^{-t}$ .

Рассмотрим трансформированные погрешности арифметических операций. Арифметические операции проводятся над приближенными числами, ошибка арифметических операций не учитывается (эту ошибку легко учесть, прибавив ошибку округления соответствующей операции к вычисленной ошибке).

Рассмотрим сложение и вычитание приближенных чисел. Абсолютная погрешность алгебраической суммы нескольких приближенных чисел равна сумме абсолютных погрешностей слагаемых.

Если сумма точных чисел равна

сумма приближенных чисел равна

где — абсолютные погрешности представления чисел.

Тогда абсолютная погрешность суммы равна

Относительная погрешность суммы нескольких чисел равна

( 2 )

$delta(S)=frac{Delta(S)}{S}=frac{a_1}{S}left(frac{Delta(a_1)}{a_1}right)+frac{a_2}{S}left(frac{Delta(a_2)}{a_2}right)+dots=frac{a_1delta(a_1)+a_2delta(a_2)+dots}{S},$

где — относительные погрешности представления чисел.

Из (2) следует, что относительная погрешность суммы нескольких чисел одного и того же знака заключена между наименьшей и наибольшей из относительных погрешностей слагаемых:

При сложении чисел разного знака или вычитании чисел одного знака относительная погрешность может быть очень большой (если числа близки между собой). Так как даже при малых величина может быть очень малой. Поэтому вычислительные алгоритмы необходимо строить таким образом, чтобы избегать вычитания близких чисел.

Необходимо отметить, что погрешности вычислений зависят от порядка вычислений. Далее будет рассмотрен пример сложения трех чисел.

( 3 )

tilde S=(tilde S_1+x_3)(1+delta_2)=(x_1+x_2)(1+delta_1)(1+delta_2)+x_3(1+delta_2).

При другой последовательности действий погрешность будет другой:

tilde S=(x_3+x_2)(1+delta_1)(1+delta_2)+x_1(1+delta_2).

Из (3) видно, что результат выполнения некоторого алгоритма, искаженный погрешностями округлений, совпадает с результатом выполнения того же алгоритма, но с неточными исходными данными. Т.е. можно применять обратный анализ: свести влияние погрешностей округления к возмущению исходных данных. Тогда вместо (3) будет следующая запись:

где

При умножении и делении приближенных чисел складываются и вычитаются их относительные погрешности.

tilde S=a_1cdot a_2(1+delta(a_1))(1+delta(a_2))

≅

с точностью величин второго порядка малости относительно delta .

Тогда .

Если $S=frac{a_1}{a_2}$ , то $Delta(S)=frac{a_1(1+delta_1)}{a_2(1+delta_2)}-frac{a_1}{a_2}=frac{a_1(delta_1-delta_2)}{a_2(1+delta_2)}approx frac{a_1}{a_2}(delta_1-delta_2), qquad delta(S)$ ≅

При большом числе n арифметических операций можно пользоваться приближенной статистической оценкой погрешности арифметических операций, учитывающей частичную компенсацию погрешностей разных знаков:

$delta_Sigma approx delta_{fl} quad sqrt{n},$

где – суммарная погрешность, $|delta_{fl}|leepsilon$ – погрешность выполнения операций с плавающей точкой, epsilon – погрешность представления чисел с плавающей точкой.

Погрешности вычисления функций

Рассмотрим трансформированную погрешность вычисления значений функций.

Абсолютная трансформированная погрешность дифференцируемой функции y=f(x) , вызываемая достаточно малой погрешностью аргумента , оценивается величиной .

Если f(x)>0 , то $delta(y)=frac{|f'(x)|}{f(x)}Delta(x)=left|(ln(f(x)))'right|cdotDelta(x)$ .

Абсолютная погрешность дифференцируемой функции многих аргументов , вызываемая достаточно малыми погрешностями аргументов оценивается величиной:

$Delta(y)=sumlimits_{i=1}^nleft|frac{partial f}{partial x_i}right|Delta(x_i)$

Если , то $delta(y)=sumlimits_{i=1}^nfrac{1}{f}cdotleft|frac{partial f}{partial x_i}right|cdotDelta(x_i)=sumlimits_{i=1}^{n}left|frac{partial l_n(f)}{partial x_i}right|Delta(x_i)$ .

Практически важно определить допустимую погрешность аргументов и допустимую погрешность функции (обратная задача). Эта задача имеет однозначное решение только для функций одной переменной y=f(x) , если f(x) дифференцируема и :

$Delta(x)=frac{1}{|f'(x)|}Delta(y)$

Для функций многих переменных задача не имеет однозначного решения, необходимо ввести дополнительные ограничения. Например, если функция наиболее критична к погрешности , то:

$Delta(x_i)=frac{Delta(y)}{left|frac{partial f}{partial x_i}right|}qquad$

(погрешностью других аргументов пренебрегаем).

Если вклад погрешностей всех аргументов примерно одинаков, то применяют принцип равных влияний:

$Delta(x_i)=frac{Delta(y)}{nleft|frac{partial f}{partial x_i}right|},qquad i=overline{1,n}.$

Числовые примеры

Специфику машинных вычислений можно пояснить на нескольких элементарных примерах.

ПРИМЕР 1. Вычислить все корни уравнения

$x^4 - 4x^3 + 8x^2 - 16x + 15.underbrace{99999999}_8 = {(x - 2)}^4 - 10^{- 8} = 0.$

Точное решение задачи легко найти:

$(x - 2)^2 = pm 10^{- 4},$

$x_1= 2,01; x_2= 1,99; x_{3,4}= 2 pm 0,01i.$

Если компьютер работает при $delta _M > 10^{ - 8}$ , то свободный член в исходном уравнении будет округлен до 16,0 и, с точки зрения представления чисел с плавающей точкой, будет решаться уравнение , т.е. $x_{1,2,3,4} = 2$ , что, очевидно, неверно. В данном случае малые погрешности в задании свободного члена $approx10^{-8}$ привели, независимо от метода решения, к погрешности в решении $approx10^{-2}$ .

ПРИМЕР 2. Решается задача Коши для обыкновенного дифференциального уравнения 2-го порядка:

u''(t) = u(t), qquad u(0) = 1, qquad u'(0) = - 1.

Общее решение имеет вид:

$u(t) = 0,5[u(0) + u'(0)]e^t + 0,5[u(0) - u'(0)]e^{- t}.$

При заданных начальных данных точное решение задачи: $u(x) = e^{-t}$ , однако малая погрешность delta в их задании приведет к появлению члена , который при больших значениях аргумента может существенно исказить решение.

ПРИМЕР 3. Пусть необходимо найти решение обыкновенного дифференциального уравнения:

$stackrel{cdot}{u} = 10u,qquad u = u(t),\ u(t_0) = u_0,qquad t in [0,1].$

Его решение: $u(t) = u_0e^{10(t - t_0 )}$ , однако значение u(t_0) известно лишь приближенно: , и на самом деле $u^*(t) = u_0^*e^{10(t - t_0)}$ .

Соответственно, разность u* - u будет:

$u^* - u = (u_0^* - u_0)e^{10(t - t_0)}.$

Предположим, что необходимо гарантировать некоторую заданную точность вычислений всюду на отрезке . Тогда должно выполняться условие:

$|{u^*(t) - u(t)}| le varepsilon.$

Очевидно, что:

$maxlimits_{t in [0,1]} |{u^*(t) - u(t)}| = |{u*(1) - u(1)}| = |{u_0^* - u_0}|e^{10(1 - t_0)}.$

Отсюда можно получить требования к точности задания начальных данных $delta: qquad|u_0^* - u_0| < delta, qquad delta le varepsilon e^{ - 10}$ при t_0= 0 .

Таким образом, требование к заданию точности начальных данных оказываются в $e^{10}$ раз выше необходимой точности результата решения задачи. Это требование, скорее всего, окажется нереальным.

Решение оказывается очень чувствительным к заданию начальных данных. Такого рода задачи называются плохо обусловленными.

ПРИМЕР 4. Решением системы линейных алгебраических уравнений (СЛАУ):

$left{ begin{array}{l} u + 10v = 11, \ 100u + 1001v = 1101; \ end{array} right.$

является пара чисел .

Изменив правую часть системы на 0,01 , получим возмущенную систему:

$left{ begin{array}{l} u + 10v = 11.01, \ 100u + 1001v = 1101; \ end{array} right.$

с решением , сильно отличающимся от решения невозмущенной системы. Эта система также плохо обусловлена.

ПРИМЕР 5. Рассмотрим методический пример вычислений на модельном компьютере, обеспечивающем точность . Проанализируем причину происхождения ошибки, например, при вычитании двух чисел, взятых с точностью до третьей цифры после десятичной точки , разность которых составляет .

В памяти машины эти же числа представляются в виде:

u_M = u(1 + delta_M^u), quad v_M = v(1 + delta_M^v)

, причем

Тогда:

u_M - u approx udelta_M^u, quad v_M - v approx vdelta_M^v.

Относительная ошибка при вычислении разности будет равна:

$delta = frac{(u_M - v_M) - (u - v)}{(u - v)} = frac{(u_M - u) - (v_M - v)}{(u - v)} = frac{delta_M^u - delta_M^v}{(u - v)}.$

Очевидно, что $delta = left|{frac{delta_M^u - delta_M^v}{Delta }} right| le frac{2delta_M}{0,001} approx 2000delta_M = 1$ , т.е. все значащие цифры могут оказаться неверными.

ПРИМЕР 6. Рассмотрим рекуррентное соотношение $u_{i+1} = qu_i, quad i ge 0, quad u_0 = a,quad q > 0, quad u_i > 0.$

Пусть при выполнении реальных вычислений с конечной длиной мантиссы на -м шаге возникла погрешность округления, и вычисления проводятся с возмущенным значением , тогда вместо $u_{i+1}$ получим $u_{i + 1}^M = q(u_i + delta_i) = u_{i + 1} + qdelta_i$ , т.е. $delta_{i + 1} = qdelta_i,quad i = 0,1,ldots$ .

Следовательно, если |q| > 1 , то в процессе вычислений погрешность, связанная с возникшей ошибкой округления, будет возрастать (алгоритм неустойчив). В случае погрешность не возрастает и численный алгоритм устойчив.

Список литературы

А.А.Самарский, А.В.Гулин. Численные методы. Москва «Наука», 1989.
http://www.mgopu.ru/PVU/2.1/nummethods/Chapter1.htm
http://www.intuit.ru/department/calculate/calcmathbase/1/4.html

См. также

Практикум ММП ВМК, 4й курс, осень 2008

Источник

Проблемы округления в EXCEL

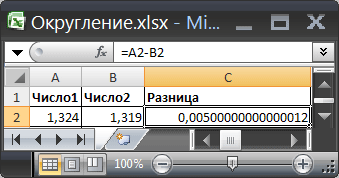
Причиной того, что результат вычисления вышеуказанной формулы равен не 0,005, а 0,00500000000000012 в том, что EXCEL хранит и проводит вычисления с числами на основе стандарта IEEE 754 (стандарта двоичной арифметики с плавающей запятой). Этот стандарт предписывает хранить числа с плавающей запятой в двоичном формате. Это означает, что перед тем как значение будет использовано в вычислениях, его необходимо конвертировать в десятичный формат. Проблема в том, что не все числа могут быть абсолютно точно представлены в двоичном формате с плавающей запятой. Например, 0,1 не может быть представлено в виде конечного дробного двоичного числа, т.к. 0,1 соответствует 0,0001100110011 с периодом 0011. Т.к. EXCEL оперирует с точностью до 15 значащих цифр, то округление неизбежно. Хотя точность округления из-за конвертации из двоичного формата примерно 2,8Е-17, но как показывает практика, вполне можно получить вместо 0,005 число 0,00500000000000012, а это в некоторых случаях далеко не одно и тоже.

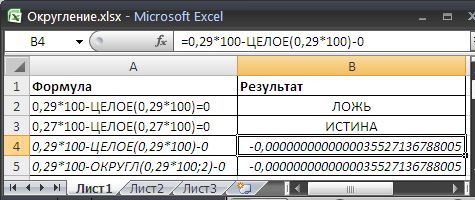
Приведем еще один пример: =0,29*100-ЦЕЛОЕ(0,29*100)=0

Результат равен ЛОЖЬ, а не ИСТИНА, не как следовало ожидать. Обратите внимание, что формула =0,27*100-ЦЕЛОЕ(0,27*100)=0 возвращает правильный результат (ИСТИНА).

Если переписать формулу в другом виде =0,29*100-ЦЕЛОЕ(0,29*100)-0 , то результат будет -3,5527136788005E-15, что и указывает на источник ошибки (значение, хотя и мало, но совсем не равно 0).

Источник ошибки Представим ситуацию, когда, например, в Условном форматировании , задано правило форматирования для результатов вычислений. Если значение ячейки равно 0, то, результат должен быть выделен красным фоном. В случае формулы =0,27*100-ЦЕЛОЕ(0,27*100) , этого не произойдет, т.к. 0 не равен числу -3,5527136788005E-15 (см. выше).

В итоге легко получить неправильный результат работы Условного форматирования : пользователь может при просмотре таблицы с результатами вычислений легко пропустить нулевое значение.

Вывод : при сравнении результатов вычисления формул с константами никогда не полагайтесь на встроенную в EXCEL точность вычисления .

Лучше использовать следующий подход – задавайте точность округления самостоятельно, прямо в формуле. Для нашего случая это будет выглядеть так: =0,29*100-ЦЕЛОЕ(0,29*100)<0,001

Результат будет всегда ИСТИНА, даже если указать фантастическую точность =0,29*100-ЦЕЛОЕ(0,29*100)<1E-204

Другой подход – использовать явное округление =ЦЕЛОЕ(0,29*100)

Напоследок покажем, что коммутативный закон сложения (сумма не меняется от перестановки её слагаемых) в EXCEL работает не всегда (см. Файл примера ).

вернет результат =0, а не -3,55Е-15. А ведь мы просто переставили 0 из формулы =0,29*100-ЦЕЛОЕ(0,29*100)-0

=0,29*100-0,29-0 (результат -3,5527136788005E-15) =1*(0,5-0,4-0,1) (результат -2,77555756156289E-17)

Весьма вероятно, что таких арифметических операций в природе существует множество.

Ошибки Excel при округлении и введении данных в ячейки

Excel старается облегчить наш труд разными подсказками и авто-подстановками. Если все это выполняется вместе с нашими ожиданиями мы в восторге от этой программы. Но если авто-подстановка является ошибочной мы просто выходим из себя.

Например, ошибки при округлении дробных чисел и т.п. Давайте разберемся почему часто возникают ошибки при скруглениях чисел? Ведь данная операция играет очень важную роль в процессе формирования цен и расчетов. Поэтому лучше как можно раньше разобраться в данной особенности программы.

Ошибки при округлении дробных чисел

Как правильно округлить и суммировать числа в Excel?

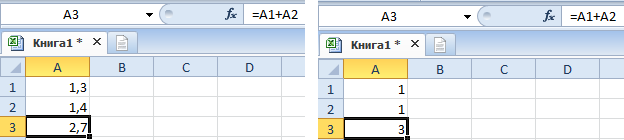
Для наглядного примера выявления подобного рода ошибок ведите дробные числа 1,3 и 1,4 так как показано на рисунке, а под ними формулу для суммирования и вычисления результата.

Дальше нужно выделить все числа и формулу, чтобы уменьшить разрядность для округления.

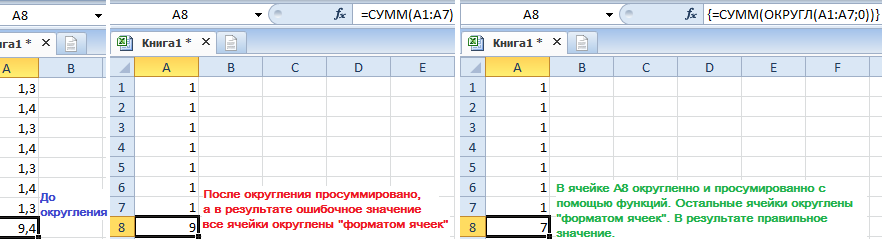
Как видите, в результате получаем абсурд: 1+1=3. Никакие форматы здесь не помогут. Решить данный вопрос поможет только функция «ОКРУГЛ». Запишите формулу с функцией так: =ОКРУГЛ(A1;0)+ОКРУГЛ(A2;0)

Как правильно округлить и суммировать числа в столбце таблицы Excel? Если этих чисел будет целый столбец, то для быстрого получения точных расчетов следует использовать массив функций. Для этого мы введем такую формулу: =СУММ(ОКРУГЛ(A1:A7;0)). После ввода массива функций следует нажимать не «Enter», а комбинацию клавиш Ctrl+Shifi+Enter. В результате Excel сам подставит фигурные скобки «» – это значит, что функция выполняется в массиве. Результат вычисления массива функций на картинке:

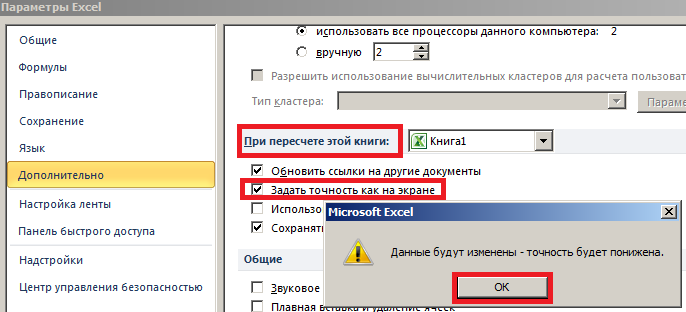
Можно пойти еще более рискованным путем, но его применять крайне не рекомендуется! Можно заставить Excel изменять содержимое ячейки в зависимости от ее формата. Для этого следует зайти «Файл»-«Параметры»-«Дополнительно» и в разделе «При пересчете этой книги:» указать «задать точность как на экране». Появиться предупреждение: «Данные будут изменены — точность будет понижена!»

Внимание. Работая в таком режиме, изменив один раз количество разрядов, уже нельзя вернуть исходные данные обратно. Это путь только в одну сторону. Поэтому лучше его не использовать. А массив функций прекрасно и безопасно справляется с данной задачей.

Здесь мы забегаем вперед, но иногда без этого сложно объяснить решение важных задач.

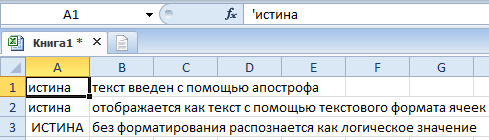
Пишем в Excel слово ИСТИНА или ЛОЖЬ как текст

Вначале вписать форматирующий символ.
Изменить формат ячейки на текстовый.

В ячейке А1 реализуем первый способ, а в А2 – второй.

Задание 1. В ячейку А1 введите слово с форматирующим символом так: «’истина». Обязательно следует поставить в начале слова символ апострофа «’», который можно ввести с английской раскладки клавиатуры (в русской раскладке символа апострофа нет). Тогда Excel скроет первый символ и будет воспринимать слова «истина» как текст, а не логический тип данных.

Задание 2. Перейдите на ячейку А2 и вызовите диалоговое окно «Формат ячеек». Например, с помощью комбинации клавиш CTRL+1 или контекстным меню правой кнопкой мышки. На вкладке «Число» в списке числовых форматов выберите «текстовый» и нажмите ОК. После чего введите в ячейку А2 слово «истина».

Задание 3. Для сравнения напишите тоже слово в ячейке А3 без апострофа и изменений форматов.

Как видите, апостроф виден только в строке формул.

Примечание. В ячейках А1 и А2 символы текста не были сменены на большие, а значит не была выполнена авто-подстановка, потому что слово воспринято программой как текст.

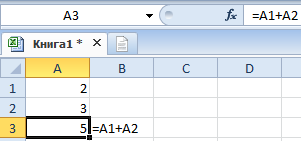
Отображение формул

Заполните данными ячейки, так как показано ниже на рисунке:

Обычно комбинация символов набранных в B3 должна быть воспринята как формула и автоматически выполнен расчет. Но что если нам нужно записать текст именно таким способом и мы не желаем вычислять результат? Решить данную задачу можно аналогичным способом из примера описанного выше.

Excel для бухгалтера: исправление ошибки округления

Видно, что общий итог по налогу (значение в ячейке G7) и стоимости товаров (Н7) отличаются на копейку от суммы по строкам (G4:G6 и Н4:Н6, соответственно). Это ошибка является следствием округления. Дело в том, что значения только отображаются в формате с двумя десятичными знаками. Фактические значения в этих ячейках содержат больше десятичных знаков (рис. 2). Excel суммирует не отображаемые значения, а фактические.

Рис. 2. Тот же счет-фактура с большим числом знаков после запятой

Чтобы значение в ячейке G7 равнялось сумме отображаемых значений в ячейках G4:G6, можно применить формулу массива, проводящую округление значений до двух десятичных знаков перед суммированием: (рис. 3). [1]

Рис. 3. «Правильное» суммирование с использованием формулы массива

Чуть подробнее, как работает эта формула. Excel формирует виртуальный массив (в памяти компьютера), состоящий из трех элементов: ОКРУГЛ(G4;2), ОКРУГЛ(G5;2), ОКРУГЛ(G6;2), то есть значений в ячейках G4:G6, округленных до двух десятичных знаков, а затем суммирует эти три элемента. Вуаля!

Ошибки округления можно также исключить, применив функцию ОКРУГЛ в каждой из ячеек диапазона G4:G6. Этот прием не требует применения формулы массива, однако требует многократного использования функции ОКРУГЛ. Вам судить, что проще!

[1] Идея подсмотрена в книге Джона Уокенбаха «MS Excel 2007. Библия пользователя». Если вы не использовали ранее формулы массива, рекомендую начать с заметки Excel. Введение в формулы массива .

50 комментариев для “Excel для бухгалтера: исправление ошибки округления”

Для полноты картины можно упомянуть еще об одном варианте, в параметрах Excel указать «точность как на экране» (Файл-Параметры-Дополнительно-При пересчете этой книги: задать точность как на экране)

Спасибо за статью. «соответсвенно» лучше исправить

а как быть, если в документе производится большое количество вычислений, и числа «завязаны» друг за друга. использование формул ОКРУГЛ и т.п. немного неудобно.
как можно отключить округление отображаемого числа? как сделать, чтобы ексель показывал то что есть? пример — число 12345.6789, с точностью после запятой 2, он не округлял 12345.68, а отображал 12345.67, но значение оставалось 12345.6789?

Александр, если Вы хотите, чтобы Excel отражал с точностью до двух знаков после запятой, а хранил число с максимальной точностью, просто задайте форматирование «два знака после запятой», и никакие дополнительные формулы не потребуются. Но… именно против этого и направлена статья, так как в бухгалтерских расчетах не допускается расхождение между суммой и слагаемыми…

Источник

Аннотация: Позиционные системы счисления, ошибки округления,
наилучшее округление, преимущества сокращенных систем счисления,
фиксированная и плавающая запятая, машинный нуль, точность
представления чисел, обоснование вероятностных свойств ошибок
округления, особенность операций сложения и вычитания, двоичная
система счисления не является лучшей, ошибки округления иногда
помогают

Известно, что при решении задач на компьютере неизбежно возникают
ошибки округления. Они крайне малы, но при решении больших задач их
появляется очень много. Поэтому в совокупности они могут оказывать
значительное влияние на точность получаемых результатов. Тем не менее,
в курсах вычислительной математики ошибкам округления уделяется
неоправданно мало внимания. Возможно, именно поэтому вокруг ошибок
округления возникает немало необоснованных мнений и даже мифов.

Например, в одном из них утверждается, что при решении задач на
вычислительных системах параллельной архитектуры влияние ошибок
округления уменьшается и это уменьшение тем значительнее, чем больше
параллелизм. В обоснование этого тезиса даже приводится вроде бы
вполне разумный довод. Он сводится к тому, что на параллельных
системах в каждый момент времени выполняются независимые операции. А
поскольку независимые операции порождают не связанные между собой
ошибки округления, то и совокупное влияние ошибок на весь
вычислительный процесс становится меньше. Но как было показано в
«Математически эквивалентные преобразования»
, при заданном способе
округления и фиксированном множестве операций ошибки округления
зависят только от графа алгоритма, а совсем не
от того, на какой вычислительной системе, последовательной или
параллельной, реализуется сам алгоритм.

Широко распространен миф, согласно которому ошибки округления можно
считать случайными величинами. Но, естественно, возникает вопрос,
почему они случайные и что это означает? Имеются немало и других
необоснованных постулатов. Чтобы они не становились руководством к
действию, познакомимся с ошибками округления поближе.

Общий эффект от решения задачи и даже возможность ее решения во
многом определяется тем, как в действительности выполняются операции
над числами. А это в свою очередь зависит от принятой системы записи
чисел или, как говорят, системы счисления. Наиболее совершенным
принципом записи является тот, на котором основана общепринятая
десятичная система. Создание вычислительной техники не связано с
какими-либо принципиально другими системами счисления. Запись чисел, с
которыми оперирует компьютер, основана на той же идее, что и
десятичная система. В математическом плане изменения невелики и
заключаются в следующем.

Зафиксируем некоторое целое положительное число р >1 и целые числа $alpha_0,alpha_1,ldots,alpha_{p-1}$ . Пусть любое неотрицательное число x может быть
представлено в виде ряда

$b_np^n+b_{n-1}p^{n-1}+ldots+b_0+b_{-1}p^{-1}+b_{-2}p^{-2}+ldots,$

где каждый из коэффициентов 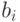b_i может принимать одно из значений $alpha_0,alpha_1,ldots,alpha_{p-1}$ . Перечислив подряд все коэффициенты и приписав слева знак
числа, получаем похожую на десятичную запись

$x=pm b_n b_{n-1}ldots b_0,b_{-1}b_{-2}ldots$

Такие формы записи чисел называются позиционными системами
счисления. Их название связано с тем, что роль, которую играет каждое
число 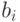b_i в записи, зависит от занимаемой им позиции. Отсчет позиции
определяется положением запятой или, что то же самое, положением
коэффициента b_0 .

В литературе, связанной с вычислительной математикой, слово
«позиция» чаще всего заменяется словом «разряд».
Нумерация разрядов устанавливается в убывающем порядке подряд слева
направо, причем первый разряд слева от запятой имеет нулевой номер.
Различаются разряды числа до запятой и разряды после запятой. Число p
называется основанием системы счисления, числа $alpha_0,alpha_1,ldots,alpha_{p-1}$ — базисными. Если используется система счисления с основанием p, то
правую часть представления числа x называют p -ичной дробью. Дробь
называется бесконечной, если в ее записи имеется бесконечно много
ненулевых коэффициентов, и конечной в противном случае. Обычно в
записи дроби опускаются все первые и последние нулевые коэффициенты.
Опускается и запятая, если все коэффициенты после нее являются
нулевыми.

Выбор базисных чисел $alpha_0,alpha_1,ldots,alpha_{p-1}$ определяется в основном
требованиями удобства работы с вещественными числами в данной системе
счисления. Не видно каких-либо особых преимуществ, которое дало бы
использование базисных чисел, превосходящих по модулю основание
системы счисления. Поэтому будем считать, что для всех . В вычислительной технике чаще всего используются системы
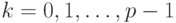
счисления с базисными числами 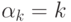. В дальнейшем, если не сделано
каких-либо оговорок, выполнение этого условия предполагается.

Арифметические операции над числами, заданными в любой позиционной
системе счисления, реализуются по таким же правилам, что и в
десятичной системе. При этом используются таблицы сложения и умножения
не десятичной системы, а системы с основанием p.
Позиционные системы счисления широко используются для
представления чисел в вычислительной технике. Наиболее часто
применяется простейшая из них — двоичная система счисления.
Использование именно позиционных систем объясняется возможностью
реализации в них достаточно простых алгоритмов выполнения
арифметических операций над числами.

Никакие технические средства не позволяют выполнять операции над
числами, заданными бесконечными дробями. Поэтому замена любого числа
конечной дробью является необходимой операцией. Округлением числа x до s разрядов в заданной системе счисления называется операция замены
этого числа таким числом 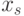x_s , все младшие разряды которого в той же
системе счисления, начиная с s -1-го, являются нулевыми.
Разность x_s-x называется ошибкой округления.

Заметим, что в данном определении ничего не говорится ни о способе
выполнения операции округления, ни о том, насколько округленное число
близко к округляемому. Это не случайно. В практике конструирования
компьютеров операции округления реализуются самыми различными
способами. Единственное, что их объединяет, — это малость в том или
ином смысле ошибок округления, по крайней мере, для большинства
чисел.

Один из простейших способов округления заключается в следующем.
Пусть задана p -ичная дробь 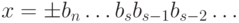$x=pm b_nldots b_s b_{s-1} b_{s-2}ldots$ . В качестве
результата выполнения операции округления числа x до s разрядов
берется число . Основное достоинство данного способа
округления — простота реализации. Однако сразу же видны и некоторые
недостатки.

Предположим, что в качестве базисных берутся числа .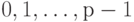
Тогда для ошибки округления справедливо соотношение .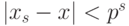
Равенство достигается только в одном случае, когда число
представлено бесконечной дробью и во всех его младших разрядах,
начиная с s -1-го, стоят числа p -1.
Уже сравнение с общепринятым «школьным» правилом округления в десятичной системе
показывает, что в рассмотренном способе оценка ошибки вдвое больше. Но
более важным является то, что независимо от своей величины ошибка
округления всегда имеет вполне определенный знак, противоположный
знаку округляемого числа. Это явление нежелательно, так как оно
приводит к более быстрому накоплению ошибок округления.

Хотя описанный способ округления чисел и не является лучшим, тем не
менее именно с ним тесно связаны все другие способы округления. В
самом деле, как бы ни выполнялась операция округления, ее результатом
будет число, все младшие разряды которого, начиная с s -1-го, являются
нулевыми. Следовательно, операцию округления всегда можно трактовать
как отбрасывание всех разрядов, начиная с s -1-го, и последующее
добавление или вычитание некоторого числа, кратного 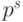p^s . Для того чтобы
ошибка округления была малой, необходимо и достаточно, чтобы было
малым именно это число.

Числа, имеющие нулевые младшие разряды, начиная с s -1-го, образуют
на вещественной оси равномерную сетку с шагом 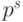p^s . Среди этих чисел
есть число 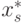x^*_s , наиболее близкое к x.
Ясно, что .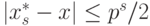
Наилучшее приближение 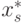x^*_s к x будет единственным, если имеет место
строгое неравенство, и таких приближений будет два, если имеет место
равенство. Замена числа x числом 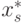x^*_s является операцией округления до s разрядов, причем лучшей во многих отношениях. Однако по сравнению с
описанной ранее операцией она имеет два существенных недостатка. Во-первых,
для ее реализации необходимо всегда дополнительно осуществлять
проверку, какой из двух кандидатов должен быть взят в качестве
округленного числа 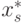x^*_s . После этой проверки примерно в половине
случаев нужно дополнительно выполнить еще одну операцию сложения
чисел. Так как округление осуществляется после каждой арифметической
операции, реализация наилучшего по точности округления приводит к
замедлению работы арифметических устройств компьютера. Кроме этого,
есть некоторая неоднозначность в выполнении данного варианта операции
округления, когда имеется два наилучших приближения 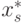x^*_s к числу x.
Хотя такая неоднозначность встречается относительно редко, она совсем
не безобидна, как будет показано в дальнейшем.

Естественным является желание объединить достоинства обоих способов
округления. Покажем, как этого можно добиться путем использования
специальных систем счисления.

До сих пор предполагалось, что в качестве базисных чисел p -ичной
системы счисления используются числа 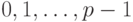. При этом
оказалось, что лучший по точности способ округления не является самым
простым в реализации и приводит к замедлению выполнения арифметических
операций. Рассмотрим теперь p -ичные позиционные системы счисления с
другими наборами базисных чисел. Пусть основание p системы счисления
является нечетным и в качестве базисных выбраны числа 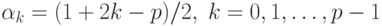. Такая система называется сокращенной.

В этом случае для всех k из заданного диапазона выполняется
неравенство 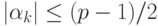. Допустим, что перед округлением до s -го
разряда округляемое число было представлено p -ичной дробью до r -го
разряда, где r — целое число и r < s.
Снова рассмотрим число 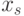x_s Однако теперь, принимая во внимание неравенства , получаем, что

$begin{gathered} |x_s-x|le |alpha_{s-1}p^{s-1}+ldots+alpha_r p^r|le((p-1)p^{s-1}/2)(1+p^{-1}+ldots+p^{r-s+1})= \ =((p-1)p^{s-1}/2)(p-p^{r-s+1})/(p-1)<p^s/2 end{gathered}$

Из этих соотношений вытекает несколько интересных выводов. Главный
из них состоит в том, что в любой сокращенной системе счисления
простое отбрасывание всех младших разрядов, начиная с s -1-го, дает
правильно округленное число. В таких системах нет необходимости
задавать отдельно знак числа, так как он совпадает со знаком старшего
разряда. В любой сокращенной системе не возникает никакой
неоднозначности при правильном округлении, о чем говорилось ранее.
Можно также показать, что x_s>x , если первый из ненулевых отброшенных
разрядов отрицательный, и x_s<x , если он положительный. Число p^s/2 не
может быть представлено конечной дробью и т.д.

Среди сокращенных позиционных систем счисления простейшей является троичная система. Как уже отмечалось, в современной вычислительной
технике наиболее широко используется двоичная система. С точки зрения
округления чисел этот выбор не является лучшим. Но если троичная
система счисления так хороша, то почему же нет большого числа
построенных на ней компьютеров?

Рядовой пользователь не видит систему счисления, лежащую в основе
работы компьютера, поскольку он отгорожен от нее языком
программирования. С точки зрения пользователя троичная система хороша
только тем, что позволяет без каких-либо дополнительных усилий
получать более точные результаты. Безусловно, это очень важно. Однако
достижение лучшей точности очень редко становится приоритетным
условием для конструкторов компьютеров. Поэтому в первую очередь на
выбор системы счисления влияют другие факторы. Это и трудности
построения большого числа базисных элементов, имеющих 3 устойчивых
состояния, и традиции конструирования элементной базы, и конкуренция в
среде производителей компьютеров, и многое другое.

Тем не менее, совсем не очевидно, на каких принципах и с какой
целевой функцией будут строиться компьютеры в будущем. И вполне
возможно, что троичная система счисления еще окажется востребованной.
Тем более что успешный опыт создания компьютера на такой системе
имеется. Это машина «Сетунь». Она была разработана в
вычислительном центре Московского университета в конце 50-х годов
прошлого столетия. Ее главным конструктором является к.т.н.
Н.П.Брусенцов, программное обеспечение выполнялось под руководством
проф. Е.А.Жоголева.

Запоминание цифровой информации во всех компьютерах основано на
использовании достаточно простых однотипных элементов. Каждый из таких
элементов представляет некоторое физическое устройство, имеющее p
устойчивых состояний, где p >1. При этом само устройство допускает
возможность перевода любого своего состояния в любое другое. Эти
элементы называются базисными и служат для моделирования одного
числового разряда p -ичной системы счисления.

Компьютер не может содержать бесконечно много базисных элементов.
Поэтому он всегда имеет возможность оперировать лишь с конечным числом
конечных р -ичных дробей. Это важный вывод, из которого вытекают все
основные особенности компьютерной арифметики.

Источник