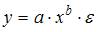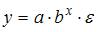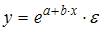Спецификация
эконометрической модели, реально
отражающей действительность, тонкая и
сложная задача. Модель – это всегда –
упрощенное, схематичное описание
реальности, которая намного порядков
сложнее любой модели. Не существует
простых моделей, которые могут адекватно
отразить сущность реальных детерминант
из интересующего нас множества.
Цель построения
модели –достижение такой её простой
формулировки, которая не противоречит
лежащей в её основе сложной реальности.
Хотя простая форма модели определенно
лучше для работы, существенные расхождения
модели с реальностью могут иметь
следствием серьезные ошибки в заключениях
о поведении изучаемого объекта.
Важный аспект
спецификации модели – выбор функциональной
формы, соединяющей зависимую и независимые
переменные. Если принять за основу для
модели функциональную форму существенно
отличающуюся от истинной, то любые
заключения по оцениваемой модели будут
иметь сомнительную ценность. Другая
важная часть спецификации модели состоит
в предположении о статистических
свойствах в терминах ошибок уравнения
регрессии. (об этом мы уже так же говорили).
Мы всегда начинаем анализ (построение
модели) в предположении, что эти ошибки
имеют постоянную вариацию, некоррелированны
друг с другом. Если эти предположения
верны, то мы используя МНК и подходящую
для нашей задачи процедуру оценивания,
делаем и заключения об изучаемом
процессе. Однако, если эти предположения
серьезно нарушаются, то заключения наши
так же будут расходиться с реальностью.
Обсудим одну
специфическую форму ошибочной спецификации
модели и прольем свет на возможные
последствия этого явления. При формулировке
регрессионной модели исследователь
обычно делает попытку соотнести зависимую
переменную интересующую его со всеми
важными детерминантами. Отсюда, если
как подходящая форма, принята линейная
модель, то мы желаем включить в число
независимых переменных все величины,
которые могут заметно воздействовать
на зависимую переменную.
В
формулировке регрессионной модели
неявно предполагается, что набор
независимых переменных содержит все
величины, существенно влияющие на
поведение зависимой переменной. Ясно,
что в любой практической проблеме будут
другие факторы, которые так же влияют
на зависимые переменные. Совместное
влияние этих факторов и отражено в
термине ошибки
.
Однако, потенциально очень важным
является допущение, что в перечне
независимых переменных нет пропущенных
из числа тех, что существенно влияют на
зависимую переменную.
Исключая очень
специальный (и редкий) случай, когда
пропущенные переменные некоррелируют
с независимыми переменными, включенными
в регрессионную модель, очень важные
последствия может иметь следующий из
этого тип ошибочной спецификации. В
частности оценки МНК будут смещенными
и обычные заключения, которые мы
производим из доверительных интервалов
или проверок гипотез могут быть весьма
ошибочными.
Для иллюстрации
этого частного типа ошибочной спецификации
обсудим пример из параграфа 3.2. Заключение,
которое мы сделали в результате анализа
задачи, состоит в том, что для заданного
числа кредитных учреждений увеличение
на один процент годовой ставки по
депозитам ведет к ожидаемому увеличению
на 0.237 процентов в годовом доходе этих
учреждений.
Теперь
предположим, что нас интересует только
эффект влияния процентной ставки по
депозитам на годовой доход кредитных
учреждений. Один из подходов к этой
проблеме может состоять в том, что мы
оценим регрессионное уравнение с двумя
переменными, где зависимая переменная
– как и прежде — годовой доход кредитных
учреждений, а независимая – процентная
ставка по депозитам. Мы используем тот
же набор значений за 25 лет. Результатом
анализа будет модель:
.
Значение стандартной ошибки для
коэффициента регрессии составило
0,0356. ЗначениеR2
для этой модели заметно уменьшилось и
составило 0,59. Однако здесь есть и более
серьезные последствия. Полученная
модель предполагает, что однопроцентное
увеличение по долларовым депозитам
ведет к ожидаемому снижению на 0,169
процента годового дохода. Более того,
сравнение коэффициента оценки с оценкой
стандартной ошибки показывает, что нуль
гипотеза о нелинейной связи между этими
переменными отклоняется в пользу
альтернативной, состоящей в том, что
увеличение процента по депозитам ведет
к ожидаемому снижению годового дохода.
Но такое заключение, несомненно, не
соответствует нашему интуитивному
пониманию проблемы, состоящему в том,
что, при прочих равных, мы можем ожидать,
что рост ставок депозитов повлечет за
собой увеличение годового дохода
кредитной организации. Однако за 25
летний период, для которого мы оценивали
модель условие «при прочих равных» не
выполнялось. В частности, другая
потенциально важная переменная – число
кредитных учреждений – заметно изменялась
в течение этого периода. Когда эта важная
переменная была включена в регрессионный
анализ, мы пришли к противоположному
заключению. Выяснилось, как мы и
предполагали, что связь между прибылью
и процентом по депозиту – положительная,
если число кредитных учреждений
принимается в расчет.
Этот пример очень
хорошо иллюстрирует обсуждаемую
ситуацию. Если важная объясняющая
переменная не была включена в регрессионную
модель, любые заключения об эффекте
других независимых переменных могут
быть абсолютно ложными. В этом частном
случае мы видим, что добавление необходимой
переменной, может изменить связь от
существенной негативной на существенную
позитивную.
Дальнейшее
осмысление может быть достигнуто
проверкой исходных данных. Во второй
части периода годовой доход уменьшался,
а ставки депозитов росли, что предполагает
негативную связь между переменными.
Однако дальнейший взгляд в данные
обнаруживает рост числа кредитных
учреждений в этот период. Мы предполагали
возможность того, что этот фактор может
быть причиной уменьшения годового
дохода. Разумный путь выхода из запутанной
ситуации — разделение эффекта двух
независимых переменных на зависимую
переменную в модели с совместным их
влиянием в регрессионном уравнении.
Этот пример иллюстрирует важность
использования множественной регрессии
вместо парной в случае, когда изучаемое
явление существенно детерминирует
несколько независимых переменных.
-
Фиктивные
переменные в моделях множественной
регрессии
Как
известно, одним из условий, лежащих в
основе стандартных регрессионных
моделей, является то, что переменные
должны быть непрерывного типа. Значительная
часть переменных в социально-экономических
исследованиях таковыми не является.
Так, например, среди переменных, имеющих
значительное влияние на величину
заработной платы, мы анализируем пол,
образование, профессию и ряд других
переменных дискретного типа. Обойти
это препятствие в регрессионной модели
позволяет введение двоичных или, как
еще называют, фиктивных (dummy) переменных.
При введении таких переменных в модель
мы преобразуем их в атрибутивные и
присваиваем значение единицы в случае
наличия признака и нуля – при его
отсутствии.
Поясним
наш подход на следующем простом примере.
Пусть yi
– заработная плата
i-го работника
(или функция от заработной платы), xi
– пол работника. Предположим, что
заработная плата распределена согласно
нормальному закону с дисперсией 2
и средней 0
в случае если работник — женщина, и 1,
если работник — мужчина. Эта ситуация
описывается регрессионной моделью, в
которой зависимая переменная – заработная
плата (Y), а пол работника (X) – объясняющая
переменная.
(3.13),
где
,
если работник мужчина,
,
в других случаях,
– случайная
переменная, удовлетворяющая основным
условиям классической нормальной
регрессионной модели.
Средняя
оценка y
корреспондирует
с двумя оценками x
так, что:
e(yx=0)
=,
e(yx=1)
=+.
Отсюда
=0
и +=
1 или
=1-0.
Это
означает, что свободный член модели –
мера средней заработной платы при
условии, что работник – женщина, а
коэффициент
– разница между заработной платой
мужчины и женщины.
Коэффициенты
регрессионного уравнения (3.13) оцениваются
методом наименьших квадратов. Напомним:
,.
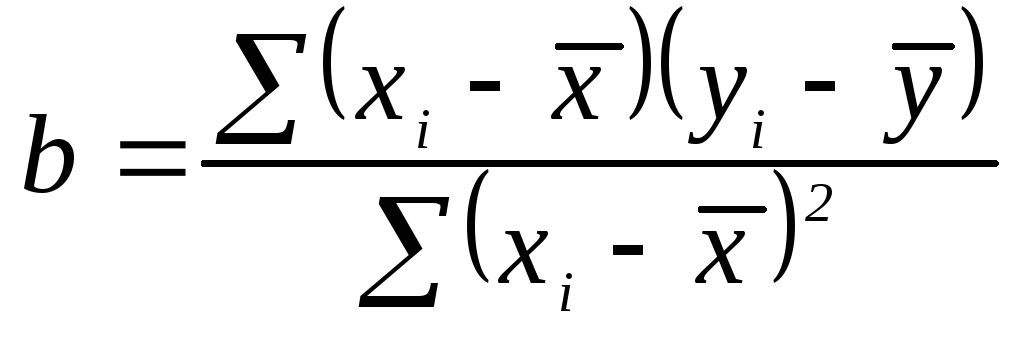
Пусть
— число мужчин в выборке,
—
число женщин.
—
средняя заработная плата мужчин,
—
средняя заработная плата женщин.
Тогда
Следовательно,
и
,
и
.
То
есть оценка МНК коэффициентов регрессии
равна разности между выборочной средней
заработной платой мужчин и женщин, а
свободный член, полученный МНК равен
средней заработной плате женщин. Проверка
гипотезы о равенстве 
эквивалентна t-статистике о равенстве
двух средних.
Если
нам необходимо ввести в уравнение в
качестве объясняющей переменной
полихотомические характеристики такие,
например, как образование, профессия и
так далее, то необходимо каждую из
категорий преобразовать в двоичную
переменную. Например, если шкала видов
образования работника имеет следующие
характеристики: высшее, среднее и
неполное среднее, то необходимые для
модели двоичные переменные будут иметь
вид xi1=1,
если работник имеет высшее образование,
и равна 0 во всех других случаях, xi2=1,
если работник имеет среднее образование,
и равна 0 во всех других случаях, xi3=1,
если у работника неполное среднее
образование, равна 0 во всех других
случаях.
Обозначим
среднюю заработную плату работников с
различным типом образования 1,
2,
3
соответственно. Подходящее регрессионное
уравнение может быть записано так:
yi=1+2xi2+3xi3+i,
(3.14)
где
Y—
заработная плата.
Заметим,
что когда xi2=0,
xi3
должен быть равен 1 и наоборот. Средняя
оценка yi
корреспондирует с различными оценками
регрессора как
e(yi
xi2=1,
xi3=0)
= 1+2,
e(yi
xi2=0,
xi3=1)
= 1+3,
e(yi
xi2=0,
xi3=0)
= 1.
Из этого следует,
что
1=1,
2=2-1,
3=3-1.
Такой результат
аналогичен полученному для дихотомической
переменной в уравнении (3.13). Модели,
описанные в уравнениях (3.13) и (3.14),
аналогичны моделям дисперсионного
анализа, но более компактны и легки в
интерпретации.
Модели
довольно просто расширить на случай
нескольких качественных объясняющих
переменных. Для пояснения воспользуемся
предыдущими переменными, описанными в
уравнениях (3.13) и (3.14). Предположим, что
заработная плата работника зависит не
только от его пола, но и от того какое
он имеет образование. Мы вновь допускаем,
что заработная плата – нормально
распределенная величина с дисперсией
2
и наблюдения независимы. Пусть:
11
– средняя
заработная плата в случае, если работник
– мужчина с высшим образованием;
10
– средняя
заработная плата в случае, если работник
– женщина с высшим образованием;
21
– средняя
заработная плата в случае, если работник
– мужчина со средним образованием;
20
– средняя
заработная плата в случае, если работник
– женщина со средним образованием;
31
– средняя
заработная плата в случае, если работник
– мужчина с неполным средним образованием;
30
– средняя
заработная плата в случае, если работник
– женщина с неполным средним образованием.
Регрессионная
модель формулируется так:
yi=1+2xi2+3xi3+zi+i,
(3.15)
где
yi,
xi2,
xi3
– определены
как в уравнениях (3.13) и (3.14), а zi=1,
если работник мужчина, zi=0,
если – женщина. Заметим вновь, что когда
xi2=0,
то xi3=1
и наоборот. Средние оценки yi,
корреспондирующие с различными оценками
регрессора, следующие:
e(yi
xi2=1,
xi3=0,
zi=1)
= 1+2+,
e(yi
xi2=1,
xi3=0,
zi=1)
= 1+3+,
e(yi
xi2=1,
xi3=0,
zi=1)
= 1+,
e(yi
xi2=1,
xi3=0,
zi=0)
= 1+2,
e(yi
xi2=1,
xi3=0,
zi=0)
= 1+3,
e(yi
xi2=1,
xi3=0,
zi=0)
= 1.
Вследствие чего:
1=
10,
2=
20-10
= 21-11,
3=
30-10
= 31-11,
=
11-10
= 21-20
= 31-30.
Это
значит, что 1
– мера средней заработной платы, если
работник – женщина с высшим образованием,
2
– разница между средними заработками
в случае, если работник имеет высшее
или среднее образование независимо от
пола, 3
– разница между средней заработной
платой в случае, если работник имеет
неполное среднее образование и если
работник с высшим образованием независимо
от пола,
– разница между средними заработками
в зависимости от того мужчина это или
женщина.
Увеличение
числа объясняющих переменных не меняет
принципа интерпретации результатов
регрессионных моделей с двоичными
переменными. Необходимо лишь строго
соблюдать ряд правил. Так, мы не можем
представить трихотомическую переменную
тремя двоичными переменными, необходимо
использовать две переменные, иначе мы
пропустим константу в регрессионном
уравнении. Например, если мы запишем
уравнение (3.14) в виде:
yi=1+2xi2+3xi3+4xi4+i,
где
xi4=1,
если работник имеет высшее образование,
а xi4=0
во всех других случаях, то решение для
b1,
b2,
b3,
b4
будут
неопределенными. Причина этого в том,
что xi4=1-xi2—xi3
и система
нормальных уравнений не будет независима.
Таким образом, когда объясняющие
характеристики предполагают классификацию
по G типам,
мы используем (G-1)
двоичных переменных для их представления.
Следующее
обстоятельство связано с интерпретацией
эффекта двоичных переменных в
полулогарифмических уравнениях. Это
уравнения, зависимая переменная в
которых представлена в логарифмической
форме. Как правило, при оценке заработной
платы мы исходим из того, что она
подчиняются логарифмически-нормальному
распределению, поэтому во всех уравнениях
мы используем значение логарифма
заработной платы. Общая форма уравнения
может быть записана в следующем виде:
,
(3.16)
где
xi
– представляет непрерывные (количественные)
переменные, а Dj
представляет двоичные переменные.
Коэффициенты количественных переменных:
(3.17)
Следовательно,
i,
умноженное на сто, показывает на сколько
процентов изменяется y
при малых изменениях в x,
то есть интерпретируется как коэффициент
эластичности.
Поскольку
двоичные переменные входят в уравнение
в дихотомической форме, то производная
от зависимой переменной по отношению
к двоичной переменной не существует.
Подходящую интерпретацию коэффициента
двоичных переменных можно продемонстрировать
путем трансформации регрессионного
уравнения. Предположим для простоты,
что в уравнении одна двоичная переменная.
Уравнение запишется так:
,
где
g – относительный эффект присутствия
фактора, представленного двоичной
переменной. Тогда g=(y1—y0)/y0,
где y1
и y0
– оценки зависимой переменной, когда
двоичная переменная равна 1 или 0
соответственно. Отсюда коэффициент при
двоичной переменной =Ln(1+g).
Относительный эффект на y:
g=exp()-1,
а процентный эффект: 100g=100(exp()-1).
Для малых g
приблизительно равно g.
Когда g
положительно,
меньше, чем g,
а когда
отрицательно, то
алгебраически меньше, чем g,
но больше по абсолютной величине.
Модель множественной
регрессии может включать в себя и
переменные, называемые “интерактивными
терминами”. В предыдущем примере мы
обсуждали зависимость заработной платы
от пола и образования работника. Мы
условно предполагали, что средняя
заработная плата зависела от уровня
образования работника и его пола и что
разница между средней заработной платой
мужчин и женщин – одинакова для всех
уровней образования. Предположим, что
мы не уверены в правильности такого
допущения. Тогда регрессионная модель
(3.15) может быть модифицирована так:
(3.18),
где
все переменные определены как в (3.14).
Среднее значение 
,
корреспондирующее с различными значениями
регрессора есть:
Это
означает, что мы можем определить
регрессионные коэффициенты в терминах
средней заработной платы следующим
образом:
1=10
2=20—10
3=30—10
=11—10
2=(31—30)
–(11—0)
3=(21—20)
–(11—0)
Различия
в средней заработной плате для мужчин
и женщин, имеющих различный уровень
образования составит:
-
Высшее образование
11—10=
Среднее образование
21—20=+3
Не
имеет среднего образования31—30=+2
В эконометрических
моделях не так часты ситуации, когда к
качестве объясняющих переменных
выступают только фиктивные или только
количественные переменные. Чаще в модели
присутствуют и те, и другие переменные.
Традиционный пример – функция потребления,
оцениваемая из данных, которые включают
различные периоды времени, например,
военное и мирное время. В этой модели
предполагается, что среднее потребление
зависит от дохода и от того какой период
мы рассматриваем: войну или мир. Простой
путь представления такой модели есть:
где
С представляет потребление, Y – доход,
а Z – фиктивная переменная, такая, что
Zt
= 1, если период войны,
Zt=
0, в другом случае.
Тогда мы имеем:
—
война,
—
мир.
Таким
образом, мы фактически постулируем, что
в военное время пересечение (свободный
член модели) функции потребления
изменяется от 
до
.
Графическая иллюстрация этого дана на
рисунке 9
П
Военное
время
Мирное
время
отребление
Доходы
Рис. 9
Если
представить свободный член модели как
прожиточный минимум, то эта модель
показывает, как прожиточный минимум
изменяется в период войны. Существенность
этих изменений можно проверить, выдвигая
гипотезу:
H0:
=0
H1:
0.
Эффект войны можно
учесть в функции потребления различно,
например, если мы постулируем, что
военные условия влияют на наклон линии
регрессии, но не на пересечение с функцией
потребления (то есть прожиточный
минимум). В соответствии с такой
теоретической формулировкой регрессионная
модель есть:
(3.19).
где переменные
определены так же. В этом случае мы
имеем:
—
война
—
мир.
Уравнение (3.19)
показывает, что эффект войны изменяет
предельную склонность к потреблению,
как показано на рисунке 10.
П
Военное время
отребление
Мирное
время
Доходы
Рис. 10
Это
значение может быть проверено при помощи
гипотезы о равенстве нулю 
.
Третья,
последняя возможность оценки различий
между потреблением в военное и мирное
время состоит в предположении, что и
свободный член и наклон линии регрессии
изменяются для военного времени.
Регрессионное уравнение примет вид:
(3.20).
Тогда имеем:
—
война
—
мир.
Эти
взаимоотношения иллюстрируются рисунком
11. Интересным в уравнении является то,
что оценка МНК регрессионных коэффициентов
совершенно та же как и те, что были бы
получены из двух отдельных регрессий
Ct
и Yt ,
одна из которых получена для данных
военного времени, а другая для данных
мирного времени. Это можно доказать
путем преобразования формул МНК, но мы
не будем это делать. Разница в двух
подходах заключается только оценке
относительно 
.
Если мы предполагаем нормальное
распределение, то вариация 
не
изменяется в течение периода, тогда их
оценка из (3.19?) основанная на всех
наблюдениях, будет эффективной. Тогда
как две оценки, полученные из двух
различных подвыборок не будут таковыми.
Это происходит вследствие того, что
оценка 
основана на любой повыборке и не
использует информацию о 
,
содержащуюся в другой подвыборке.
Военное
время
П
отребление
Мирное
время
Доходы
Тема 2: Отбор факторов, включаемых в модель множественной регрессии
Тема 1: Спецификация эконометрической модели
1. Ошибки спецификации эконометрической модели имеют место вследствие …
неправильного выбора математической функции или недоучета в уравнении регрессии какого-то существенного фактора
недостоверности или недостаточности исходной информации
неоднородности данных в исходной статистической совокупности
недостаточного количества данных
Решение:
Спецификацией модели называется отбор факторов, включаемых в модель, и выбор математической функции для 
. Поэтому к ошибкам спецификации относятся не только неправильный выбор той или иной математической функции для , но и недоучет в уравнении регрессии какого-то существенного фактора, то есть использование парной регрессии вместо множественной.
2. Для регрессионной модели вида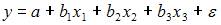 
необходим минимальный объем наблюдений, содержащий _____ объектов наблюдения.
Решение:
Считается, на каждый оцениваемый коэффициент регрессии необходимо не менее 5–7 объектов статистических наблюдений. Так как представленная модель содержит 3 независимые переменные, то на каждый из параметров регрессии при независимой переменной необходимо по 5–7 наблюдений, то есть в совокупности не менее 15–21 наблюдения. Берем нижнюю границу интервала, тогда правильный вариант ответа – «15».
3. Нелинейным по объясняющим переменным, но линейным по параметрам уравнением регрессии является …
Решение:
Из приведенных функций только в функции параметры имеют степень 1, а объясняющая переменная х имеет степень, отличную от 1.
4. В модели вида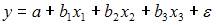 
количество объясняющих переменных равно …
Решение:
Эконометрическая модель уравнения регрессии может быть представлена линейным уравнением множественной регрессии в виде выражения 
, где y – зависимая переменная; xj – объясняющая независимая переменная (j = 1,…, k; k – количество независимых переменных); a, bj – параметры (a – свободный член уравнения, bj – коэффициент регрессии); 
– случайные факторы. Независимые переменные xj называются также факторами, объясняющими переменными. На количество объясняющих переменных в линейном уравнении указывает также количество коэффициентов регрессии bj. Поэтому количество объясняющих переменных в модели равно 3.
5. При идентификации модели множественной регрессии 
количество оцениваемых параметров равно …
Решение:
При оценке модели множественной регрессии рассчитываются следующие параметры: свободный член a и четыре параметра при независимых переменных х. Итого 5 параметров.
Тема 2: Отбор факторов, включаемых в модель множественной регрессии
1. В модели множественной регрессии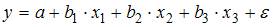 
определитель матрицы парных коэффициентов корреляции между факторами 
, 
и 
близок к единице. Это означает, что факторы , и …
Решение:
Для оценки мультиколлинеарности факторов может использоваться определитель матрицы парных коэффициентов корреляции между факторами. Если факторы не коррелированы между собой, то матрица парных коэффициентов корреляции между факторами была бы единичной. Поскольку все недиагональные элементы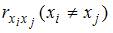 
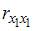
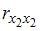
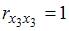
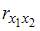
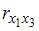
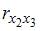
были бы равны нулю.
, поскольку 
= 
= 
и 
= 
= 
=0.
Если между факторами существует полная линейная зависимость и все коэффициенты парной корреляции равны единице, то определитель такой матрицы равен нулю.
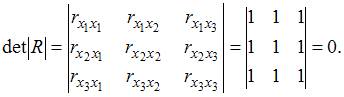
Чем ближе к нулю определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И, наоборот, чем ближе к единице определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов.
2. При моделировании линейного уравнения множественной регрессии вида 
необходимо, чтобы выполнялось требование отсутствия взаимосвязи между …
Решение:
Эконометрическая модель уравнения регрессии может быть представлена линейным уравнением множественной регрессии в виде выражения , где y – зависимая переменная; xj – независимая переменная (j = 1,…, k; k – количество независимых переменных); a, bj – параметры (a – свободный член уравнения, bj – коэффициент регрессии); – случайные факторы. При построении модели множественной регрессии необходимо исключить возможность существования тесной линейной зависимости между независимыми (объясняющими) переменными, которая ведет к проблеме мультиколлинеарности. Поэтому в данной модели необходимо, чтобы выполнялось требование отсутствия взаимосвязи между x1 и x2.
Линейная множественная регрессия
Тесты по эконометрике
Введение
1. Эконометрическая модель имеет вид
2. Установите соответствие
| а) регрессионная модель | 1) x-1=0, x=0x-1, x>0 |
| b) система одновременных уравнений | 2) R=a1+b11M+b12Y+ε1,Y=a2+b21R+ε2, |
| c) модель временного ряда | 1. 3) y=a+b1x1+b2x2+ε |
| 4) yt=Tt+St+Et |
3. Регрессия – это
a. зависимость значений результативной переменной от значений объясняющих переменных (факторов)
b. правило, согласно которому каждому значению одной переменной ставится в соответствие единственное значение другой переменной
c. правило, согласно которому каждому значению независимой переменной ставится в соответствие значение зависимой переменной
d. зависимость среднего значения результативной переменной от значений объясняющих переменных (факторов)
4. Метод наименьших квадратов …
a. Позволяет получить оценки параметров линейной регрессии, исходя из условия i=1nyi-yi2→min
b. Позволяет получить оценки параметров регрессии, исходя из условия ln(i=1nf(yi,)→max
c. Позволяет проверить статистическую значимость параметров регрессии
d. Позволяет получить оценки параметров нелинейной регрессии, исходя из условия i=1ny-yi2→min
Линейная множественная регрессия
5. Уравнение линейной множественной регрессии
6. Для линейного уравнения множественной регрессии установите соответствие
| 5. а) Факторные переменные | 6. 1) y |
| 7. b) Результативная переменная | 8. 2) a |
| 9. c) Параметры | 10. 3) a, ε |
| 11. d) Случайная компонента | 12. 4) x1, x2 |
| 13. | 14. 5) ε |
| 15. | 16. 6) a, b1, b2 |
17. Ответ: a-4, b-1, c-6, d-5
7. Проблема спецификации регрессионной модели включает в себя
a. Отбор факторов, включаемых в уравнение регрессии
b. Оценка параметров уравнения регрессии
c. Оценка надежности результатов регрессионного анализа
d. Выбор вида уравнения регрессии
19. Требования к факторам, включаемым в модель линейной множественной регрессии…
a. Число факторов должно быть в 6 раз меньше объема совокупности
b. Факторы должны представлять временные ряды
c. Факторы должны иметь одинаковую размерность
d. Между факторами не должно быть высокой корреляции
21. Верные утверждения относительно мультиколлинеарности факторов
e. В модель линейной множественной регрессии рекомендуется включать мультиколлинеарные факторы
f. Мультиколлинеарность факторов приводит к снижению надежности оценок параметров уравнения регрессии
g. Мультиколинеарность факторов проявляется в наличии парных коэффициентов межфакторной корреляции со значениями, большими 0,7
h. Мультиколинеарность факторов проявляется в наличии парных коэффициентов межфакторной корреляции со значениями, меньшими 0,3
23. Верные утверждения о включении в уравнение линейной множественной регрессии факторов
i. Включение фактора в модель приводит к заметному возрастанию коэффициента множественной детерминации
j. Коэффициент парной корреляции для фактора и результативной переменной меньше 0,3
k. Значение t-критерия Стьюдента для коэффициента регрессии при факторе меньше табличного значения
l. Фактор должен объяснять поведение изучаемого показателя согласно принятым положениям экономической теории
25. При построении модели множественной регрессии методом пошагового включения переменных на первом этапе рассматривается модель с …
m. Одной объясняющей переменной, которая имеет с зависимой переменной наименьший коэффициент корреляции
n. Одной объясняющей переменной, которая имеет с зависимой переменной наибольший коэффициент корреляции
o. Несколькими объясняющими переменными, которые имеют с зависимой переменной коэффициенты корреляции по модулю больше 0,5
p. Полным перечнем объясняющих переменных
8. Параметры при факторах в линейной множественной регрессии
y=a+b1x1+b2x2+…+bpxp характеризуют
a. Долю дисперсии результативной переменной, объясненную регрессией в его общей дисперсии
b. Тесноту связи между результативной переменной и соответствующим фактором, при устранении влияния других факторов, включенных в модель
c. Среднее изменение результативной переменной с изменением соответствующего фактора на единицу, при неизменном значении других факторов, закрепленных на среднем уровне
d. На сколько процентов в среднем изменяется результативная переменная с изменением соответствующего фактора на 1%
28. Стандартизация переменных проводится по формуле
9. Уравнение множественной регрессии в стандартизованном масштабе имеет вид ty=20+0,9tx1+0,5tx2+ε. На результативный признак оказывает большое влияние:
x. нельзя сделать вывод
10. Уравнение множественной регрессии в естественной форме имеет вид
y=20+0,7×1+0,5×2+ε. На результативный признак оказывает большое влияние:
bb. нельзя сделать вывод
30. К свойствам уравнения регрессии в стандартизированном виде относятся …
cc. Коэффициенты регрессии при объясняющих переменных равны между собой
dd. Постоянный параметр (свободный член уравнения) регрессии отсутствует
ee. Стандартизированные коэффициенты регрессии несравнимы между собой
ff. Входящие в состав уравнения переменные являются безразмерными
32. Тесноту совместного влияния факторов на результат в уравнении линейной множественной регрессии оценивает
gg. Коэффициент парной корреляции
hh. Коэффициент частной корреляции
ii. Коэффициент множественной корреляции
jj. Коэффициент множественной детерминации
34. Установите соответствие
| 35. а) общая сумма квадратов отклонений TSS | 36. 1) y-y2 |
| 37. b) регрессионная сумма квадратов отклонений RSS | 38. 2) y-x2 |
| 39. c) остаточная сумма квадратов отклонений ЕSS | 40. 3) y-y2 |
| 41. | 42. 4) y-y2 |
43. Коэффициент множественной корреляции для линейной зависимости можно рассчитать по формуле
mm. 
45. Верные утверждения относительно коэффициента множественной корреляции
oo. Чем ближе значение к единице Ryx1…xp, тем теснее связь результативного признака со всеми факторами
pp. Чем ближе значение к нулю Ryx1…xp, тем теснее связь результативного признака со всеми факторами
qq. Ryx1…xp принимает значения из промежутка [0, 1]
rr. Ryx1…xp принимает значения из промежутка [– 1, 1]
47. Коэффициент множественной детерминации характеризует
ss. Тесноту совместного влияния факторов на результат в уравнении линейной множественной регрессии
tt. Тесноту связи между результатом и соответствующим фактором, при устранении влияния других факторов, включенных в модель
uu. Долю дисперсии результативного признака, объясненную регрессией в его общей дисперсии
vv. Среднее изменение результативной переменной с изменением соответствующего фактора на единицу, при неизменном значении других факторов, закрепленных на среднем уровне
49. Для общей (TSS), регрессионной (RSS) и остаточной (ESS) суммы квадратов отклонений и коэффициента детерминации R2 выполняется равенство …
51. Отношение остаточной дисперсии к общей дисперсии равно 0,05. Это означает …
bbb. Коэффициент детерминации R2=0,95
ccc. Коэффициент детерминации R2=0,05
ddd. Разность (1-R2)=0,95, где R2 – коэффициент детерминации
eee. Разность (1-R2)=0,05, где R2 – коэффициент детерминации
53. Для устранения систематической ошибки остаточной дисперсии для оценки качества модели линейной множественной регрессии используется
fff. Коэффициент множественной детерминации
ggg. Коэффициент множественной корреляции
hhh. Скорректированный коэффициент множественной детерминации
iii. Скорректированный коэффициент частной корреляции
55. Оценка статистической значимости уравнения линейной множественной регрессии в целом осуществляется с помощью
jjj. Критерия Стьюдента
kkk. Критерия Фишера
lll. Критерия Дарбина-Уотсона
56. Оценка статистической значимости коэффициентов линейной множественной регрессии осуществляется с помощью
nnn. Критерия Стьюдента
ooo. Критерия Фишера
ppp. Критерия Дарбина-Уотсона
qqq. Критерия Фостера-Стюарта
57. Если коэффициент регрессии является существенным, то для него выполняются условия
rrr. Фактическое значение t-критерия Стьюдента меньше критического
sss. Фактическое значение t-критерия Стьюдента больше критического
ttt. Доверительный интервал проходит через ноль
uuu. Стандартная ошибка не превышает половины значения параметра
59. Если уравнение регрессии является существенным, то фактическое значение F-критерия …
vvv. больше критического
www. меньше критического
xxx. близко к единице
yyy. близко к нулю
61. Предпосылками МНК являются…
zzz. Дисперсия случайных отклонений постоянна для всех наблюдений
aaaa. Дисперсия случайных отклонений не постоянна для всех наблюдений
bbbb. Случайные отклонения коррелируют друг с другом
cccc. Случайные отклонения являются независимыми друг от друга
63. Укажите выводы, которые соответствуют графику зависимости остатков
dddd. Нарушена предпосылка МНК о независимости остатков друг от друга
eeee. Имеет место автокорреляция остатков
ffff. Отсутствует закономерность в поведении остатков
gggg. Отсутствует автокорреляция остатков
66. При выполнении предпосылок метода наименьших квадратов (МНК) остатки уравнения регрессии, как правило, характеризуются…
hhhh. Нулевой средней величиной
jjjj. Случайным характером
kkkk. Высокой степенью автокорреляции
68. К методам обнаружения гетероскедастичности остатков относятся
llll. Критерий Дарбина-Уотсона
mmmm. Тест Голдфелда-Квандта
nnnn. Графический анализ остатков
oooo. Метод наименьших квадратов
70. Фиктивными переменными в уравнении множественной регрессии являются …
pppp. Качественные переменные, преобразованные в количественные
qqqq. Переменные, представляющие простейшие функции от уже включенных в модель переменных
rrrr. Дополнительные количественные переменные, улучшающие решение
ssss. Комбинации из включенных в уравнение регрессии факторов, повышающие адекватность модели
71. Для отражения влияния качественной сопутствующей переменной, имеющей m состояний, обычно включают в модель … фиктивную переменную
Нелинейная регрессия
72. Регрессии, нелинейные по объясняющим переменным, но линейные по оцениваемым параметрам
73. Регрессии, нелинейные по оцениваемым параметрам
74. Укажите верные утверждения по поводу модели
jjjjj. Относится к типу моделей нелинейных по объясняющим переменным, но линейных по оцениваемым параметрам
kkkkk. Относится к типу моделей, нелинейных по оцениваемым параметрам
lllll. Относится к типу линейных моделей
mmmmm. Нельзя привести к линейному виду
nnnnn. Можно привести к линейному виду
76. Укажите верные утверждения по поводу модели
ooooo. Линеаризуется линейную модель множественной регрессии
ppppp. Линеаризуется линейную модель парной регрессии
qqqqq. Относится к классу нелинейных моделей по объясняющим переменным, но линейных по оцениваемым параметрам
rrrrr. Относится к классу линейных моделей
79. Модель y=a∙bx∙ε относится к классу … эконометрических моделей нелинейной регрессии
81. Модель y=a∙xb∙ε относится к классу … эконометрических моделей нелинейной регрессии
83. Модель y=a+bx+cx2+ε относится к классу … эконометрических моделей нелинейной регрессии
85. Было замечено, что при увеличении количества вносимых удобрений урожайность также возрастает, однако, по достижении определенного значения фактора моделируемый показатель начинает убывать. Для исследования данной зависимости можно использовать спецификацию уравнения регрессии…
87. Для получения оценок параметров степенной регрессионной модели y=a∙xb …
iiiiii. Метод наименьших квадратов неприменим
jjjjjj. Требуется подобрать соответствующую подстановку
kkkkkk. Необходимо выполнить логарифмическое преобразование
llllll. Необходимо выполнить тригонометрическое преобразование
89. С помощью метода наименьших квадратов нельзя оценить значения параметров уравнения регрессии …
Уравнение множественной регрессии
Назначение сервиса . С помощью онлайн-калькулятора можно найти следующие показатели:
- уравнение множественной регрессии, матрица парных коэффициентов корреляции, средние коэффициенты эластичности для линейной регрессии;
- множественный коэффициент детерминации, доверительные интервалы для индивидуального и среднего значения результативного признака;
Кроме этого проводится проверка на автокорреляцию остатков и гетероскедастичность.
- Шаг №1
- Шаг №2
- Видеоинструкция
- Оформление Word
Отбор факторов обычно осуществляется в два этапа:
- теоретический анализ взаимосвязи результата и круга факторов, которые оказывают на него существенное влияние;
- количественная оценка взаимосвязи факторов с результатом. При линейной форме связи между признаками данный этап сводится к анализу корреляционной матрицы (матрицы парных линейных коэффициентов корреляции). Научно обоснованное решение задач подобного вида также осуществляется с помощью дисперсионного анализа — однофакторного, если проверяется существенность влияния того или иного фактора на рассматриваемый признак, или многофакторного в случае изучения влияния на него комбинации факторов.
Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям:
- Они должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, не имеющий количественного измерения, то ему нужно придать количественную определенность.
- Каждый фактор должен быть достаточно тесно связан с результатом (т.е. коэффициент парной линейной корреляции между фактором и результатом должен быть существенным).
- Факторы не должны быть сильно коррелированы друг с другом, тем более находиться в строгой функциональной связи (т.е. они не должны быть интеркоррелированы). Разновидностью интеркоррелированности факторов является мультиколлинеарность — тесная линейная связь между факторами.
Пример . Постройте регрессионную модель с 2-мя объясняющими переменными (множественная регрессия). Определите теоретическое уравнение множественной регрессии. Оцените адекватность построенной модели.
Решение.
К исходной матрице X добавим единичный столбец, получив новую матрицу X
| 1 | 5 | 14.5 |
| 1 | 12 | 18 |
| 1 | 6 | 12 |
| 1 | 7 | 13 |
| 1 | 8 | 14 |
Матрица Y
Транспонируем матрицу X, получаем X T :
| 1 | 1 | 1 | 1 | 1 |
| 5 | 12 | 6 | 7 | 8 |
| 14.5 | 18 | 12 | 13 | 14 |
| Умножаем матрицы, X T X = |
|
В матрице, (X T X) число 5, лежащее на пересечении 1-й строки и 1-го столбца, получено как сумма произведений элементов 1-й строки матрицы X T и 1-го столбца матрицы X
| Умножаем матрицы, X T Y = |
Находим обратную матрицу (X T X) -1
| 13.99 | 0.64 | -1.3 |
| 0.64 | 0.1 | -0.0988 |
| -1.3 | -0.0988 | 0.14 |
Вектор оценок коэффициентов регрессии равен
| (X T X) -1 X T Y = y(x) = |
|
* | = |
Получили оценку уравнения регрессии: Y = 34.66 + 1.97X1-2.45X2
Оценка значимости уравнения множественной регрессии осуществляется путем проверки гипотезы о равенстве нулю коэффициент детерминации рассчитанного по данным генеральной совокупности. Для ее проверки используют F-критерий Фишера.
R 2 = 1 — s 2 e/∑(yi — yср) 2 = 1 — 33.18/77.2 = 0.57
F = R 2 /(1 — R 2 )*(n — m -1)/m = 0.57/(1 — 0.57)*(5-2-1)/2 = 1.33
Табличное значение при степенях свободы k1 = 2 и k2 = n-m-1 = 5 — 2 -1 = 2, Fkp(2;2) = 19
Поскольку фактическое значение F = 1.33 Пример №2 . Приведены данные за 15 лет по темпам прироста заработной платы Y (%), производительности труда X1 (%), а также по уровню инфляции X2 (%).
| Год | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| X1 | 3,5 | 2,8 | 6,3 | 4,5 | 3,1 | 1,5 | 7,6 | 6,7 | 4,2 | 2,7 | 4,5 | 3,5 | 5,0 | 2,3 | 2,8 |
| X2 | 4,5 | 3,0 | 3,1 | 3,8 | 3,8 | 1,1 | 2,3 | 3,6 | 7,5 | 8,0 | 3,9 | 4,7 | 6,1 | 6,9 | 3,5 |
| Y | 9,0 | 6,0 | 8,9 | 9,0 | 7,1 | 3,2 | 6,5 | 9,1 | 14,6 | 11,9 | 9,2 | 8,8 | 12,0 | 12,5 | 5,7 |
Решение. Подготовим данные для вставки из MS Excel (как транспонировать таблицу для сервиса см. Задание №2) .
Включаем в отчет: Проверка общего качества уравнения множественной регрессии (F-статистика. Критерий Фишера, Проверка на наличие автокорреляции),
После нажатия на кнопку Дале получаем готовое решение.
Уравнение регрессии (оценка уравнения регрессии):
Y = 0.2706 + 0.5257X1 + 1.4798X2
Скачать.
Качество построенного уравнения регрессии проверяется с помощью критерия Фишера (п. 6 отчета).
Пример №3 .
В таблице представлены данные о ВВП, объемах потребления и инвестициях некоторых стран.
| ВВП | 16331,97 | 16763,35 | 17492,22 | 18473,83 | 19187,64 | 20066,25 | 21281,78 | 22326,86 | 23125,90 |
| Потребление в текущих ценах | 771,92 | 814,28 | 735,60 | 788,54 | 853,62 | 900,39 | 999,55 | 1076,37 | 1117,51 |
| Инвестиции в текущих ценах | 176,64 | 173,15 | 151,96 | 171,62 | 192,26 | 198,71 | 227,17 | 259,07 | 259,85 |
Решение:
Для проверки полученных расчетов используем инструменты Microsoft Excel «Анализ данных» (см. пример).
Пример №4 . На основе данных, приведенных в Приложении и соответствующих Вашему варианту (таблица 2), требуется:
- Построить уравнение множественной регрессии. При этом признак-результат и один из факторов остаются теми же, что и в первом задании. Выберите дополнительно еще один фактор из приложения 1 (границы наблюдения должны совпадать с границами наблюдения признака-результата, соответствующего Вашему варианту). При выборе фактора нужно руководствоваться его экономическим содержанием или другими подходами. Пояснить смысл параметров уравнения.
- Рассчитать частные коэффициенты эластичности. Сделать вывод.
- Определить стандартизованные коэффициенты регрессии (b-коэффициенты). Сделать вывод.
- Определить парные и частные коэффициенты корреляции, а также множественный коэффициент корреляции; сделать выводы.
- Оценить значимость параметров уравнения регрессии с помощью t-критерия Стьюдента, а также значимость уравнения регрессии в целом с помощью общего F-критерия Фишера. Предложить окончательную модель (уравнение регрессии). Сделать выводы.
Решение. Определим вектор оценок коэффициентов регрессии. Согласно методу наименьших квадратов, вектор получается из выражения:
s = (X T X) -1 X T Y
Матрица X
| 1 | 3.9 | 10 |
| 1 | 3.9 | 14 |
| 1 | 3.7 | 15 |
| 1 | 4 | 16 |
| 1 | 3.8 | 17 |
| 1 | 4.8 | 19 |
| 1 | 5.4 | 19 |
| 1 | 4.4 | 20 |
| 1 | 5.3 | 20 |
| 1 | 6.8 | 20 |
| 1 | 6 | 21 |
| 1 | 6.4 | 22 |
| 1 | 6.8 | 22 |
| 1 | 7.2 | 25 |
| 1 | 8 | 28 |
| 1 | 8.2 | 29 |
| 1 | 8.1 | 30 |
| 1 | 8.5 | 31 |
| 1 | 9.6 | 32 |
| 1 | 9 | 36 |
Матрица Y
| 7 |
| 7 |
| 7 |
| 7 |
| 7 |
| 7 |
| 8 |
| 8 |
| 8 |
| 10 |
| 9 |
| 11 |
| 9 |
| 11 |
| 12 |
| 12 |
| 12 |
| 12 |
| 14 |
| 14 |
Матрица X T
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 3.9 | 3.9 | 3.7 | 4 | 3.8 | 4.8 | 5.4 | 4.4 | 5.3 | 6.8 | 6 | 6.4 | 6.8 | 7.2 | 8 | 8.2 | 8.1 | 8.5 | 9.6 | 9 |
| 10 | 14 | 15 | 16 | 17 | 19 | 19 | 20 | 20 | 20 | 21 | 22 | 22 | 25 | 28 | 29 | 30 | 31 | 32 | 36 |
Умножаем матрицы, (X T X)
Умножаем матрицы, (X T Y)
Находим определитель det(X T X) T = 139940.08
Находим обратную матрицу (X T X) -1
Уравнение регрессии
Y = 1.8353 + 0.9459X 1 + 0.0856X 2
Для несмещенной оценки дисперсии проделаем следующие вычисления:
Несмещенная ошибка e = Y — X*s
| 0.62 |
| 0.28 |
| 0.38 |
| 0.01 |
| 0.11 |
| -1 |
| -0.57 |
| 0.29 |
| -0.56 |
| 0.02 |
| -0.31 |
| 1.23 |
| -1.15 |
| 0.21 |
| 0.2 |
| -0.07 |
| -0.07 |
| -0.53 |
| 0.34 |
| 0.57 |
se 2 = (Y — X*s) T (Y — X*s)
Несмещенная оценка дисперсии равна
Оценка среднеквадратичного отклонения равна
Найдем оценку ковариационной матрицы вектора k = σ*(X T X) -1
| k(x) = 0.36 |
|
= |
|
Дисперсии параметров модели определяются соотношением S 2 i = Kii, т.е. это элементы, лежащие на главной диагонали
С целью расширения возможностей содержательного анализа модели регрессии используются частные коэффициенты эластичности, которые определяются по формуле
Тесноту совместного влияния факторов на результат оценивает индекс множественной корреляции (от 0 до 1)
Связь между признаком Y факторами X сильная
Частные коэффициенты (или индексы) корреляции, измеряющие влияние на у фактора хi при неизменном уровне других факторов определяются по стандартной формуле линейного коэффициента корреляции — последовательно берутся пары yx1,yx2. , x1x2, x1x3.. и так далее и для каждой пары находится коэффициент корреляции
Коэффициент детерминации
R 2 = 0.97 2 = 0.95, т.е. в 95% случаев изменения х приводят к изменению y. Другими словами — точность подбора уравнения регрессии — высокая
Значимость коэффициента корреляции
По таблице Стьюдента находим Tтабл: Tтабл (n-m-1;a) = (17;0.05) = 1.74
Поскольку Tнабл Fkp, то коэффициент детерминации статистически значим и уравнение регрессии статистически надежно
Построение парной регрессионной модели
Рекомендации к решению контрольной работы.
Статистические данные по экономике можно получить на странице Россия в цифрах.
После определения зависимой и объясняющих переменных можно воспользоваться сервисом Множественная регрессия. Регрессионную модель с 2-мя объясняющими переменными можно построить используя матричный метод нахождения параметров уравнения регрессии или метод Крамера для нахождения параметров уравнения регрессии.
Пример №3 . Исследуется зависимость размера дивидендов y акций группы компаний от доходности акций x1, дохода компании x2 и объема инвестиций в расширение и модернизацию производства x3. Исходные данные представлены выборкой объема n=50.
Тема I. Парная линейная регрессия
Постройте парные линейные регрессии — зависимости признака y от факторов x1, x2, x3 взятых по отдельности. Для каждой объясняющей переменной:
- Постройте диаграмму рассеяния (поле корреляции). При построении выберите тип диаграммы «Точечная» (без отрезков, соединяющих точки).
- Вычислите коэффициенты уравнения выборочной парной линейной регрессии (для вычисления коэффициентов регрессии воспользуйтесь встроенной функцией ЛИНЕЙН (функция находится в категории «Статистические») или надстройкой Пакет Анализа), коэффициент детерминации, коэффициент корреляции (функция КОРЕЛЛ), среднюю ошибку аппроксимации
. - Запишите полученное уравнение выборочной регрессии. Дайте интерпретацию найденным в предыдущем пункте значениям.
- Постройте на поле корреляции прямую линию выборочной регрессии по точкам .
- Постройте диаграмму остатков.
- Проверьте статистическую значимость коэффициентов регрессии по критерию Стьюдента (табличное значение определите с помощью функции СТЬЮДРАСПОБР) и всего уравнения в целом по критерию Фишера (табличное значение Fтабл определите с помощью функции FРАСПОБР).
- Постройте доверительные интервалы для коэффициентов регрессии. Дайте им интерпретацию.
- Постройте прогноз для значения фактора, на 50% превышающего его среднее значение.
- Постройте доверительный интервал прогноза. Дайте ему экономическую интерпретацию.
- Оцените полученные результаты — сделайте выводы о качестве построенной модели, влиянии рассматриваемого фактора на показатель.
Тема II. Множественная линейная регрессия
1. Постройте выборочную множественную линейную регрессию показателя на все указанные факторы. Запишите полученное уравнение, дайте ему экономическую интерпретацию.
2. Определите коэффициент детерминации, дайте ему интерпретацию. Вычислите среднюю абсолютную ошибку аппроксимации и дайте ей интерпретацию.
3. Проверьте статистическую значимость каждого из коэффициентов и всего уравнения в целом.
4. Постройте диаграмму остатков.
5. Постройте доверительные интервалы коэффициентов. Для статистически значимых коэффициентов дайте интерпретации доверительных интервалов.
6. Постройте точечный прогноз значения показателя y при значениях факторов, на 50% превышающих их средние значения.
7. Постройте доверительный интервал прогноза, дайте ему экономическую интерпретацию.
8. Постройте матрицу коэффициентов выборочной корреляции между показателем и факторами. Сделайте вывод о наличии проблемы мультиколлинеарности.
9. Оцените полученные результаты — сделайте выводы о качестве построенной модели, влиянии рассматриваемых факторов на показатель.
источники:
http://megaobuchalka.ru/4/7472.html
http://math.semestr.ru/regress/corel.php
4.
Использование
предварительной информации о значениях некоторых параметров. Иногда значения некоторых неизвестных параметров
модели могут быть определены по пробным выборочным наблюдениям, тогда
мультиколлинеарность может быть устранена путем установления значений параметра
у одной коррелирующих переменных. Ограниченность метода – в сложности получения
предварительных значений параметров с высокой точностью.
5.
Преобразование переменных. Для устранения мультиколлинеарности можно
преобразовать переменные, например, путем линеаризации или получения
относительных показателей, а также перехода от номинальных к реальным
показателям (особенно в макроэкономических исследованиях).
При построении модели множественной регрессии с точки
зрения обеспечения ее высокого качества возникают следующие вопросы:
1.
Каковы признаки качественной
модели?
2.
Какие ошибки спецификации могут
быть?
3.
Каковы последствия ошибок
спецификации?
4.
Какие существуют методы
обнаружения и устранения ошибок спецификации?
Рассмотрим основные признаки качественной модели
множественной регрессии:
1.
Простота. Из двух моделей примерно одинаковых статистических
свойств более качественной является та, которая содержит меньше переменных, или
же более простая по аналитической форме.
2.
Однозначность. Метод вычисления коэффициентов должен быть одинаков
для любых наборов данных.
3.
Максимальное соответствие. Этот признак говорит о том, что основным критерием
качества модели является коэффициент детерминации, отражающий объясненную
моделью вариацию зависимой переменной. Для практического использования выбирают
модель, для которой расчетное значение F-критерия для
коэффициента детерминации б четыре раза больше табличного.
4.
Согласованность с теорией. Получаемые значения коэффициентов должны быть
интерпретируемы с точки зрения экономических явлений и процессов. К примеру,
если строится линейная регрессионная модель спроса на товар, то соответствующий
коэффициент при цене товара должен быть отрицательным.
5.
Хорошие прогнозные качества.
Обязательным условием построения
качественной модели является возможность ее использования для прогнозирования.
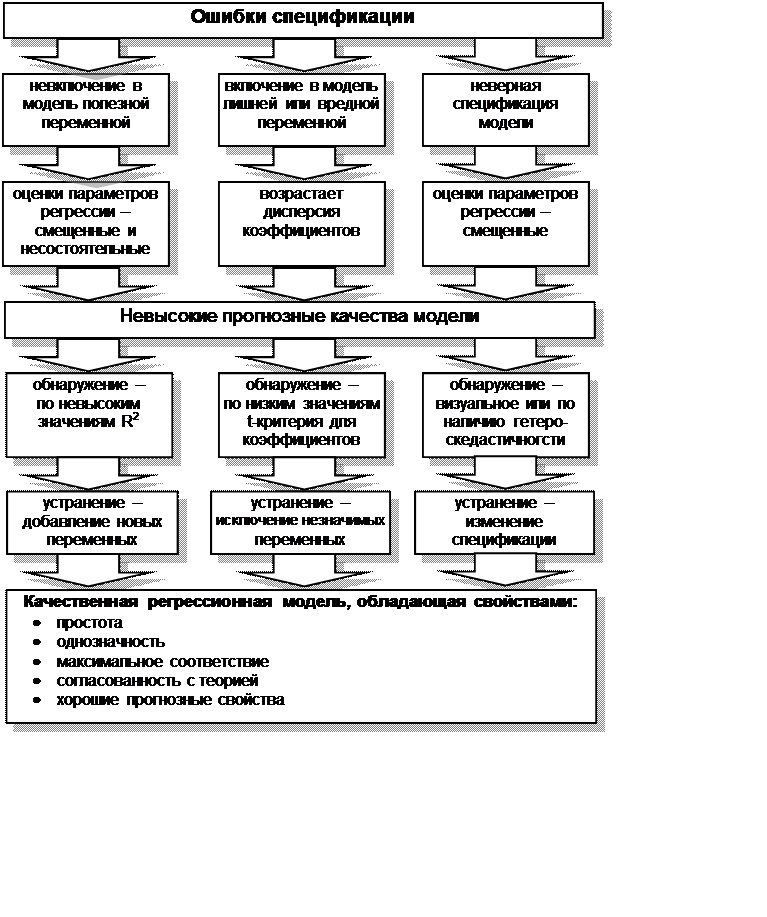
Одной из основных ошибок, допускаемых при построении
регрессионной модели, является ошибка спецификации (рис. 4.3).
Под ошибкой спецификации понимается неправильный выбор функциональной формы
модели или набора объясняющих переменных.
Различают следующие виды ошибок спецификации:
1.
Невключение в модель полезной
(значимой) переменной.
2.
Добавление в модель лишней
(незначимой) переменной
3.
Выбор неправильной функциональной
формы модели
Последствия ошибки первого вида (невключение в
модель значимой переменной) заключаются в том, что полученные по МНК оценки
параметров являются смещенными и несостоятельными, а значение коэффициента
детерминации значительно снижаются.
При добавлении в модель лишней переменной
(ошибка второго вида) ухудшаются статистические свойства оценок
коэффициентов, возрастают их дисперсии, что ухудшает прогнозные качества модели
и затрудняет содержательную интерпретацию параметров, однако по сравнению с
другими ошибками ее последствия менее серьезны.
Если же осуществлен неверный выбор
функциональной формы модели, то есть допущена ошибка третьего вида, то
получаемые оценки будут смещенными, качество модели в целом и отдельных
коэффициентов будет невысоким. Это может существенно сказаться на прогнозных
качествах модели.
Ошибки спецификации первого вида можно обнаружить только
по невысокому качеству модели, низким значениям R2.
Обнаружение ошибок спецификации второго вида, если лишней
является только одна переменная, осуществляется на основе расчета t — статистики для коэффициентов. При лишней переменной коэффициент
будет статистически незначим.
Рис. 4.3 Ошибки спецификации и свойства качественной
регрессионной модели