Ошибки статистического наблюдения это

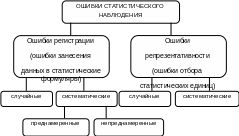
Ошибка
статистического наблюдения – это
отклонение расчетных значений показателей
от фактических. Классификация различных
видов ошибок представлена на схеме 2.1.

Ошибки
регистрации
– это просто ошибки записей при заполнении
статистических формуляров. Такие ошибки
встречаются при любых видах наблюдений.

Ошибки
репрезентативности
(то есть представительности)¹
характерны только для так называемых
выборочных
наблюдений (которые более подробно
будут изучаться в дальнейшем). Их суть
заключается в том, что статистические
единицы, отобранные для проведения
наблюдения (включенные в выборочную
совокупность или «выборку») недостаточно
полно представляют всю (генеральную)
статистическую совокупность. Например,
при проведении социологического опроса
были собраны данные о среднедушевом
доходе только у лиц в возрасте от 30 до
50 лет, и не были охвачены другие категории
населения.

Случайные
ошибки
бывают всегда,
а процент систематических
ошибок
можно уменьшить
за счет улучшения организации самого
наблюдения. Однако, если эти ошибки
являются преднамеренными
(например, скрываются данные о доходах,
чтобы снизить величину налоговых
отчислений), то снизить процент таких
ошибок можно, только выходя за рамки
компетенции статистических органов.

Схема
2.1

Классификация ошибок статистического наблюдения

3. Организационные формы, виды и способы статистического наблюдения

Существует
три основных организационных формы
статистического наблюдения:

1. Официальная
   статистическая отчетность;

2. Специально
   организованные наблюдения;

3. Регистры
   (регистрационная форма наблюдения)

Роль
официальной статистической отчетности
для статистических исследований в том,
что она позволяет в течение длительного
промежутка времени накапливать
статистические данные, представленные
в виде единообразного, официально
утвержденного перечня показателей. Эти
показатели обычно комплексно характеризуют
развитие отдельных социально-эконо­ми­ческих
процессов во времени. Однако с переходом
к рыночной экономике в нашей стране
существенно изменились многие формы
статистической отчетности. Поэтому,
как правило, статистические ряды данных,
сформированные в период до начала 1990-х
годов, фактически несопоставимы с той
статистической информацией, которая
была накоплена в течение последнего
десятилетия.

Официальная
статистическая отчетность является
обязательной,
документально обоснованной, периодической.
Все
сведения в отчетности должны быть
юридически заверены подписью руководителя
предприятия.

Официальная
статистическая отчетность делится на:

1) 
типовую (обязательную для всех
предприятий),

2)  специальную
(заполняют только предприятия одной
отрасли).

Специально
организованные наблюдения –
это те, для которых всякий раз, независимо
от их периодичности и сроков проведения,
разрабатывается специальная программа
(например, к таким наблюдениям относится
перепись, опросы общественного мнения
и т.д.)

Регистр
– это особая форма непрерывного
наблюдения за социально-экономическими
процессами, имеющими фиксированное
начало и фиксированный конец. Проще
говоря, регистр – это список, в который
заносятся статистические единицы с
определенными признаками, некоторые
из которых имеют постоянное значение,
а другие изменяются. Все эти изменения
фиксируются и также заносятся в регистр.
Примером такого наблюдения является
регистрация актов гражданского состояния
или регистрация всех предприятий,
создаваемых на территории Российской
Федерации.

Кроме
того, все статистические наблюдения
разделяют на различные виды, в зависимости
от периодичности их проведения:

1. Периодические
   (которые проводятся через равные
   промежутки времени, например, через
   год, месяц, квартал): примером такого
   наблюдения является официальная
   статистическая отчетность);

2. Непрерывные
   (или текущие),
   которые фиксируют все факты, имеющие
   отношения к данному социально-эко­номическому
   явлению, независимо от момента времени,
   когда происходят соответствующие
   события: примером такого наблюдения
   является регистрация дорожно-транспортных
   происшествий;

3. Разовые
   или единовременные,
   которые могут больше не повториться:
   например, опрос общественного мнения
   перед выборами.

В
зависимости от степени охвата
статистических единиц, статистические
наблюдения также разделяют на сплошные
и несплошные
наблюдения. В свою очередь, несплошные
наблюдения разделяют на выборочные,
обследования
основного массива
и монографические
исследования.

Нередко
всякие наблюдения, не являющиеся
сплошными, называют выборочными. Однако
выборочные
наблюдения
– это только одна
из нескольких возможных разновидностей
несплошных наблюдений. При выборочных
наблюдениях
отбор обследуемых единиц осуществляется
с помощью особых, научно обоснованных
способов формирования выборочной
совокупности единиц. Другой формой
несплошных наблюдений являются
обследования основного
массива, при которых
отбирается такая часть статистических
единиц, которая дает наибольший вклад
в итоговый показатель. (Например,
отбираются предприятия с наибольшим
объемом реализованной продукции или
магазины с наибольшим объемом
товарооборота). Наконец, при монографических
исследованиях обычно обследуется совсем
немного статистических единиц, но очень
детально, по чрезвычайно широкому
перечню признаков. Например, изучаются
только те предприятия, где внедрена
совершенно новая форма оплаты труда,
но необходимо очень тщательно изучить
влияние этой новой формы на результаты
работы предприятия (с привлечением
большого числа показателей, характеризующих
деятельность предприятия).

В
зависимости от способа проведения
статистического наблюдения выделяют:

1. непосредственное
   наблюдение (подсчет, измерение,
   взвешивание);

2. наблюдение
   на основе документальных источников
   первичной информации (например, на
   основе форм бухгалтерского учета и
   отчетности);

3. опрос
   (письменный или устный).

Таблица 2.1

Классификация форм, видов и способов

статистических наблюдений

Лекция
№3.
Сводка
и группировка статистических материалов

Введение

На
предыдущих лекциях мы изучили
содержание
трех этапов статистического исследования
и
более подробно ознакомились
с
основным
методом сбора информации на первом
этапе исследования, то есть со
статистическим наблюдением, его основными
видами и формами.
На
втором этапе статистического исследования
основную
роль играют такие методы обработки
статистической информации, как сводка
и группировка. Это давно известные в
статистике методы, исторически
сформировавшиеся еще в позапрошлом
веке.

Но
раньше эти методы использовались для
сложного и трудоемкого процесса обработки
данных вручную. В настоящее время те же
самые процессы осуществляются с
использованием современных компьютерных
программ.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

From Wikipedia, the free encyclopedia

«Systematic bias» redirects here. For the sociological and organizational phenomenon, see Systemic bias.

Observational error (or measurement error) is the difference between a measured value of a quantity and its true value.^[1] In statistics, an error is not necessarily a «mistake». Variability is an inherent part of the results of measurements and of the measurement process.

Measurement errors can be divided into two components: random and systematic.^[2]
Random errors are errors in measurement that lead to measurable values being inconsistent when repeated measurements of a constant attribute or quantity are taken. Systematic errors are errors that are not determined by chance but are introduced by repeatable processes inherent to the system.^[3] Systematic error may also refer to an error with a non-zero mean, the effect of which is not reduced when observations are averaged.^{[citation needed]}

Measurement errors can be summarized in terms of accuracy and precision.
Measurement error should not be confused with measurement uncertainty.

Science and experiments[edit]

When either randomness or uncertainty modeled by probability theory is attributed to such errors, they are «errors» in the sense in which that term is used in statistics; see errors and residuals in statistics.

Every time we repeat a measurement with a sensitive instrument, we obtain slightly different results. The common statistical model used is that the error has two additive parts:

1. Systematic error which always occurs, with the same value, when we use the instrument in the same way and in the same case.
2. Random error which may vary from observation to another.

Systematic error is sometimes called statistical bias. It may often be reduced with standardized procedures. Part of the learning process in the various sciences is learning how to use standard instruments and protocols so as to minimize systematic error.

Random error (or random variation) is due to factors that cannot or will not be controlled. One possible reason to forgo controlling for these random errors is that it may be too expensive to control them each time the experiment is conducted or the measurements are made. Other reasons may be that whatever we are trying to measure is changing in time (see dynamic models), or is fundamentally probabilistic (as is the case in quantum mechanics — see Measurement in quantum mechanics). Random error often occurs when instruments are pushed to the extremes of their operating limits. For example, it is common for digital balances to exhibit random error in their least significant digit. Three measurements of a single object might read something like 0.9111g, 0.9110g, and 0.9112g.

Characterization[edit]

Measurement errors can be divided into two components: random error and systematic error.^[2]

Random error is always present in a measurement. It is caused by inherently unpredictable fluctuations in the readings of a measurement apparatus or in the experimenter’s interpretation of the instrumental reading. Random errors show up as different results for ostensibly the same repeated measurement. They can be estimated by comparing multiple measurements and reduced by averaging multiple measurements.

Systematic error is predictable and typically constant or proportional to the true value. If the cause of the systematic error can be identified, then it usually can be eliminated. Systematic errors are caused by imperfect calibration of measurement instruments or imperfect methods of observation, or interference of the environment with the measurement process, and always affect the results of an experiment in a predictable direction. Incorrect zeroing of an instrument leading to a zero error is an example of systematic error in instrumentation.

The Performance Test Standard PTC 19.1-2005 “Test Uncertainty”, published by the American Society of Mechanical Engineers (ASME), discusses systematic and random errors in considerable detail. In fact, it conceptualizes its basic uncertainty categories in these terms.

Random error can be caused by unpredictable fluctuations in the readings of a measurement apparatus, or in the experimenter’s interpretation of the instrumental reading; these fluctuations may be in part due to interference of the environment with the measurement process. The concept of random error is closely related to the concept of precision. The higher the precision of a measurement instrument, the smaller the variability (standard deviation) of the fluctuations in its readings.

Sources[edit]

Sources of systematic error[edit]

Imperfect calibration[edit]

Sources of systematic error may be imperfect calibration of measurement instruments (zero error), changes in the environment which interfere with the measurement process and sometimes imperfect methods of observation can be either zero error or percentage error. If you consider an experimenter taking a reading of the time period of a pendulum swinging past a fiducial marker: If their stop-watch or timer starts with 1 second on the clock then all of their results will be off by 1 second (zero error). If the experimenter repeats this experiment twenty times (starting at 1 second each time), then there will be a percentage error in the calculated average of their results; the final result will be slightly larger than the true period.

Distance measured by radar will be systematically overestimated if the slight slowing down of the waves in air is not accounted for. Incorrect zeroing of an instrument leading to a zero error is an example of systematic error in instrumentation.

Systematic errors may also be present in the result of an estimate based upon a mathematical model or physical law. For instance, the estimated oscillation frequency of a pendulum will be systematically in error if slight movement of the support is not accounted for.

Quantity[edit]

Systematic errors can be either constant, or related (e.g. proportional or a percentage) to the actual value of the measured quantity, or even to the value of a different quantity (the reading of a ruler can be affected by environmental temperature). When it is constant, it is simply due to incorrect zeroing of the instrument. When it is not constant, it can change its sign. For instance, if a thermometer is affected by a proportional systematic error equal to 2% of the actual temperature, and the actual temperature is 200°, 0°, or −100°, the measured temperature will be 204° (systematic error = +4°), 0° (null systematic error) or −102° (systematic error = −2°), respectively. Thus the temperature will be overestimated when it will be above zero and underestimated when it will be below zero.

Drift[edit]

Systematic errors which change during an experiment (drift) are easier to detect. Measurements indicate trends with time rather than varying randomly about a mean. Drift is evident if a measurement of a constant quantity is repeated several times and the measurements drift one way during the experiment. If the next measurement is higher than the previous measurement as may occur if an instrument becomes warmer during the experiment then the measured quantity is variable and it is possible to detect a drift by checking the zero reading during the experiment as well as at the start of the experiment (indeed, the zero reading is a measurement of a constant quantity). If the zero reading is consistently above or below zero, a systematic error is present. If this cannot be eliminated, potentially by resetting the instrument immediately before the experiment then it needs to be allowed by subtracting its (possibly time-varying) value from the readings, and by taking it into account while assessing the accuracy of the measurement.

If no pattern in a series of repeated measurements is evident, the presence of fixed systematic errors can only be found if the measurements are checked, either by measuring a known quantity or by comparing the readings with readings made using a different apparatus, known to be more accurate. For example, if you think of the timing of a pendulum using an accurate stopwatch several times you are given readings randomly distributed about the mean. Hopings systematic error is present if the stopwatch is checked against the ‘speaking clock’ of the telephone system and found to be running slow or fast. Clearly, the pendulum timings need to be corrected according to how fast or slow the stopwatch was found to be running.

Measuring instruments such as ammeters and voltmeters need to be checked periodically against known standards.

Systematic errors can also be detected by measuring already known quantities. For example, a spectrometer fitted with a diffraction grating may be checked by using it to measure the wavelength of the D-lines of the sodium electromagnetic spectrum which are at 600 nm and 589.6 nm. The measurements may be used to determine the number of lines per millimetre of the diffraction grating, which can then be used to measure the wavelength of any other spectral line.

Constant systematic errors are very difficult to deal with as their effects are only observable if they can be removed. Such errors cannot be removed by repeating measurements or averaging large numbers of results. A common method to remove systematic error is through calibration of the measurement instrument.

Sources of random error[edit]

The random or stochastic error in a measurement is the error that is random from one measurement to the next. Stochastic errors tend to be normally distributed when the stochastic error is the sum of many independent random errors because of the central limit theorem. Stochastic errors added to a regression equation account for the variation in Y that cannot be explained by the included Xs.

Surveys[edit]

The term «observational error» is also sometimes used to refer to response errors and some other types of non-sampling error.^[1] In survey-type situations, these errors can be mistakes in the collection of data, including both the incorrect recording of a response and the correct recording of a respondent’s inaccurate response. These sources of non-sampling error are discussed in Salant and Dillman (1994) and Bland and Altman (1996).^[4][5]

These errors can be random or systematic. Random errors are caused by unintended mistakes by respondents, interviewers and/or coders. Systematic error can occur if there is a systematic reaction of the respondents to the method used to formulate the survey question. Thus, the exact formulation of a survey question is crucial, since it affects the level of measurement error.^[6] Different tools are available for the researchers to help them decide about this exact formulation of their questions, for instance estimating the quality of a question using MTMM experiments. This information about the quality can also be used in order to correct for measurement error.^[7][8]

Effect on regression analysis[edit]

If the dependent variable in a regression is measured with error, regression analysis and associated hypothesis testing are unaffected, except that the R² will be lower than it would be with perfect measurement.

However, if one or more independent variables is measured with error, then the regression coefficients and standard hypothesis tests are invalid.^{[9]: p. 187} This is known as attenuation bias.^[10]

See also[edit]

References[edit]

Further reading[edit]

• Cochran, W. G. (1968). «Errors of Measurement in Statistics». Technometrics. 10 (4): 637–666. doi:10.2307/1267450. JSTOR 1267450.

From Wikipedia, the free encyclopedia

«Systematic bias» redirects here. For the sociological and organizational phenomenon, see Systemic bias.

Observational error (or measurement error) is the difference between a measured value of a quantity and its true value.^[1] In statistics, an error is not necessarily a «mistake». Variability is an inherent part of the results of measurements and of the measurement process.

Measurement errors can be divided into two components: random and systematic.^[2]
Random errors are errors in measurement that lead to measurable values being inconsistent when repeated measurements of a constant attribute or quantity are taken. Systematic errors are errors that are not determined by chance but are introduced by repeatable processes inherent to the system.^[3] Systematic error may also refer to an error with a non-zero mean, the effect of which is not reduced when observations are averaged.^{[citation needed]}

Measurement errors can be summarized in terms of accuracy and precision.
Measurement error should not be confused with measurement uncertainty.

Science and experiments[edit]

When either randomness or uncertainty modeled by probability theory is attributed to such errors, they are «errors» in the sense in which that term is used in statistics; see errors and residuals in statistics.

Every time we repeat a measurement with a sensitive instrument, we obtain slightly different results. The common statistical model used is that the error has two additive parts:

1. Systematic error which always occurs, with the same value, when we use the instrument in the same way and in the same case.
2. Random error which may vary from observation to another.

Systematic error is sometimes called statistical bias. It may often be reduced with standardized procedures. Part of the learning process in the various sciences is learning how to use standard instruments and protocols so as to minimize systematic error.

Random error (or random variation) is due to factors that cannot or will not be controlled. One possible reason to forgo controlling for these random errors is that it may be too expensive to control them each time the experiment is conducted or the measurements are made. Other reasons may be that whatever we are trying to measure is changing in time (see dynamic models), or is fundamentally probabilistic (as is the case in quantum mechanics — see Measurement in quantum mechanics). Random error often occurs when instruments are pushed to the extremes of their operating limits. For example, it is common for digital balances to exhibit random error in their least significant digit. Three measurements of a single object might read something like 0.9111g, 0.9110g, and 0.9112g.

Characterization[edit]

Measurement errors can be divided into two components: random error and systematic error.^[2]

Random error is always present in a measurement. It is caused by inherently unpredictable fluctuations in the readings of a measurement apparatus or in the experimenter’s interpretation of the instrumental reading. Random errors show up as different results for ostensibly the same repeated measurement. They can be estimated by comparing multiple measurements and reduced by averaging multiple measurements.

Systematic error is predictable and typically constant or proportional to the true value. If the cause of the systematic error can be identified, then it usually can be eliminated. Systematic errors are caused by imperfect calibration of measurement instruments or imperfect methods of observation, or interference of the environment with the measurement process, and always affect the results of an experiment in a predictable direction. Incorrect zeroing of an instrument leading to a zero error is an example of systematic error in instrumentation.

The Performance Test Standard PTC 19.1-2005 “Test Uncertainty”, published by the American Society of Mechanical Engineers (ASME), discusses systematic and random errors in considerable detail. In fact, it conceptualizes its basic uncertainty categories in these terms.

Random error can be caused by unpredictable fluctuations in the readings of a measurement apparatus, or in the experimenter’s interpretation of the instrumental reading; these fluctuations may be in part due to interference of the environment with the measurement process. The concept of random error is closely related to the concept of precision. The higher the precision of a measurement instrument, the smaller the variability (standard deviation) of the fluctuations in its readings.

Sources[edit]

Sources of systematic error[edit]

Imperfect calibration[edit]

Sources of systematic error may be imperfect calibration of measurement instruments (zero error), changes in the environment which interfere with the measurement process and sometimes imperfect methods of observation can be either zero error or percentage error. If you consider an experimenter taking a reading of the time period of a pendulum swinging past a fiducial marker: If their stop-watch or timer starts with 1 second on the clock then all of their results will be off by 1 second (zero error). If the experimenter repeats this experiment twenty times (starting at 1 second each time), then there will be a percentage error in the calculated average of their results; the final result will be slightly larger than the true period.

Distance measured by radar will be systematically overestimated if the slight slowing down of the waves in air is not accounted for. Incorrect zeroing of an instrument leading to a zero error is an example of systematic error in instrumentation.

Systematic errors may also be present in the result of an estimate based upon a mathematical model or physical law. For instance, the estimated oscillation frequency of a pendulum will be systematically in error if slight movement of the support is not accounted for.

Quantity[edit]

Systematic errors can be either constant, or related (e.g. proportional or a percentage) to the actual value of the measured quantity, or even to the value of a different quantity (the reading of a ruler can be affected by environmental temperature). When it is constant, it is simply due to incorrect zeroing of the instrument. When it is not constant, it can change its sign. For instance, if a thermometer is affected by a proportional systematic error equal to 2% of the actual temperature, and the actual temperature is 200°, 0°, or −100°, the measured temperature will be 204° (systematic error = +4°), 0° (null systematic error) or −102° (systematic error = −2°), respectively. Thus the temperature will be overestimated when it will be above zero and underestimated when it will be below zero.

Drift[edit]

Systematic errors which change during an experiment (drift) are easier to detect. Measurements indicate trends with time rather than varying randomly about a mean. Drift is evident if a measurement of a constant quantity is repeated several times and the measurements drift one way during the experiment. If the next measurement is higher than the previous measurement as may occur if an instrument becomes warmer during the experiment then the measured quantity is variable and it is possible to detect a drift by checking the zero reading during the experiment as well as at the start of the experiment (indeed, the zero reading is a measurement of a constant quantity). If the zero reading is consistently above or below zero, a systematic error is present. If this cannot be eliminated, potentially by resetting the instrument immediately before the experiment then it needs to be allowed by subtracting its (possibly time-varying) value from the readings, and by taking it into account while assessing the accuracy of the measurement.

If no pattern in a series of repeated measurements is evident, the presence of fixed systematic errors can only be found if the measurements are checked, either by measuring a known quantity or by comparing the readings with readings made using a different apparatus, known to be more accurate. For example, if you think of the timing of a pendulum using an accurate stopwatch several times you are given readings randomly distributed about the mean. Hopings systematic error is present if the stopwatch is checked against the ‘speaking clock’ of the telephone system and found to be running slow or fast. Clearly, the pendulum timings need to be corrected according to how fast or slow the stopwatch was found to be running.

Measuring instruments such as ammeters and voltmeters need to be checked periodically against known standards.

Systematic errors can also be detected by measuring already known quantities. For example, a spectrometer fitted with a diffraction grating may be checked by using it to measure the wavelength of the D-lines of the sodium electromagnetic spectrum which are at 600 nm and 589.6 nm. The measurements may be used to determine the number of lines per millimetre of the diffraction grating, which can then be used to measure the wavelength of any other spectral line.

Constant systematic errors are very difficult to deal with as their effects are only observable if they can be removed. Such errors cannot be removed by repeating measurements or averaging large numbers of results. A common method to remove systematic error is through calibration of the measurement instrument.

Sources of random error[edit]

The random or stochastic error in a measurement is the error that is random from one measurement to the next. Stochastic errors tend to be normally distributed when the stochastic error is the sum of many independent random errors because of the central limit theorem. Stochastic errors added to a regression equation account for the variation in Y that cannot be explained by the included Xs.

Surveys[edit]

The term «observational error» is also sometimes used to refer to response errors and some other types of non-sampling error.^[1] In survey-type situations, these errors can be mistakes in the collection of data, including both the incorrect recording of a response and the correct recording of a respondent’s inaccurate response. These sources of non-sampling error are discussed in Salant and Dillman (1994) and Bland and Altman (1996).^[4][5]

These errors can be random or systematic. Random errors are caused by unintended mistakes by respondents, interviewers and/or coders. Systematic error can occur if there is a systematic reaction of the respondents to the method used to formulate the survey question. Thus, the exact formulation of a survey question is crucial, since it affects the level of measurement error.^[6] Different tools are available for the researchers to help them decide about this exact formulation of their questions, for instance estimating the quality of a question using MTMM experiments. This information about the quality can also be used in order to correct for measurement error.^[7][8]

Effect on regression analysis[edit]

If the dependent variable in a regression is measured with error, regression analysis and associated hypothesis testing are unaffected, except that the R² will be lower than it would be with perfect measurement.

However, if one or more independent variables is measured with error, then the regression coefficients and standard hypothesis tests are invalid.^{[9]: p. 187} This is known as attenuation bias.^[10]

See also[edit]

References[edit]

Further reading[edit]

• Cochran, W. G. (1968). «Errors of Measurement in Statistics». Technometrics. 10 (4): 637–666. doi:10.2307/1267450. JSTOR 1267450.

Важнейшей задачей статистического наблюдения является достоверность и точность собираемой статистической информации.

Любое статистическое наблюдение предполагает получение данных, которые будут полно и точно отражать действительность.

В процессе проведения статистического наблюдения могут возникать погрешности, которые приводят к снижению достоверности статистического наблюдения.

Основное требование, которое предъяввляется к статистическому наблюдению – это точность статистических данных.

Точность – это уровень соответствия значения какого-либо признака или показателя, который был получен вследствие статистического наблюдения, действительному его значению. В процессе подготовки и проведения статистического исследования, чтобы предупредить возможность появления отклонений или разности между исчисленными показателями, нужно предусмотреть и осуществить ряд мероприятий. Если же такие отклонения возникли, их называют ошибками статистического наблюдения.

Материалы, собранные в результате наблюдения, подвергаются всесторонней проверке и контролю. Они проверяются с точки зрения полноты охвата всех единиц совокупности наблюдения и правильности заполнения документов и в порядке логического и арифметического контроля.

Ошибки статистического наблюдения – это ошибки репрезентативности и ошибки регистрации.

Ошибки репрезентативности показывают, в какой степени выборочная совокупность представляет генеральную совокупность. Эти ошибки возникают потому, что наблюдению подвергается только часть единиц изучаемой совокупности, и сведения эти не могут абсолютно точно отобразить свойства всей массы явлений совокупности.

Возникающие в результате неправильного установления фактов ошибки регистрации можно подразделить на:

•  случайные – это ошибки, которые могут дать искажения как в одну, так и в другую сторону;
•  систематические ошибки, возникающие вследствие нарушения принципов непреднамеренного отбора единиц изучаемой совокупности. Систематические ошибки опасны, потому что они влияют на полученные итоговые показатели;
•  преднамеренные ошибки возникают вследствие умышленного искажения фактов.

Для обеспечения достоверности данных статистического наблюдения предусматривают проверку их качества с точки зрения полноты охвата изучаемого объекта статистическим наблюдением, качества и др.

Проверка данных статистического наблюдения на достоверность – это проведение логического, арифметического и синтаксического контроля.

6. Достоверность статистических данных и
ошибки статистического наблюдения

Важнейшим требованием
предъявляемым к статистическим данным является их достоверность. Под достоверностью
данных наблюдения понимается степень приближения, соответствия
данных тому, что есть на самом деле. Расхождение межу фактическим значением и
результатом наблюдения называют погрешностью (ошибкой) наблюдения.

Ошибки наблюдения
разнообразны по происхождению и своему содержанию. В зависимости от
причин возникновения различают следующие виды ошибок:

• методические ошибки;

• ошибки регистрации;

• ошибки
репрезентативности (представительности).

Методические ошибки возникают
в результате использования несовершенных методик, неправильных теоретических
концепций, лежащих в основе исследования.

Ошибки регистрации возникают при
получении данных об отдельных единицах совокупности вследствие неправильного
установления фактов в процессе наблюдения или неправильной их записи. Они
подразделяются на:

-объективные (непреднамеренные)
причиной появления которых является неправильное восприятие наблюдаемых фактов,
неисправность измерительных приборов и неправильная регистрация. Такие ошибки
являются результатом добросовестного заблуждения регистратора;

— субъективные (преднамеренные)
ошибки, возникающие по причине сознательного искажения фактов. К ним относятся
всевозможные преднамеренные ошибки и приписки, при которых опрашиваемый
преднамеренно сообщает неправильные сведения; регистратор преднамеренно
воздействует на респондента с целью получения нужного ответа; регистратор
преднамеренно искажает в формулярах результаты наблюдения.

Ошибки репрезентативности
(представительности) характерны только для несплошного наблюдения.
Они возникают в результате того, что состав отобранной для обследования части
единиц совокупности (выборки) не полностью отражает состав и свойства всей
изучаемой совокупности, несмотря на то, что регистрация сведений по каждой
отобранной единице была проведена точно.

По форме проявления (по
влиянию на результат) ошибки делятся на:

• систематически;

• случайные.

Систематические ошибки возникают
по какой-то определенной причине и вызывают одностороннее искажение значений
признака у наблюдаемых единиц (увеличение или уменьшение). Они очень опасны,
так как величина показателя, рассчитанная в целом по всей совокупности будет
включать накопленную ошибку.

Случайные ошибки являются
результатом действия различных случайных факторов. Они не имеют какой-либо
направленности. В больших совокупностях в результате действия закона больших
чисел эти ошибки взаимно погашаются и не оказывают существенного влияния на
точность наблюдения.

Оба вида ошибок в любом
исследовании выступают совместно и составляют совокупную ошибку наблюдения Δ:

Δ=σ+ε;

где σ — систематическая
ошибка наблюдения,

ε — случайная ошибка
наблюдения.

Для выявления и
исправления ошибок, данные наблюдения необходимо тщательно контролировать.
Процедура контроля сводится к следующему:

• Проверка материалов
наблюдения на полноту и правильность оформления. Проверяется полнота охвата
статистических единиц наблюдения, правильность заполнения каждого формуляра.

• Арифметический
(счетный) контроль. Этот вид контроля основан на использовании
количественных связей между показателями, которые могут быть проверены
арифметическими действиями. Такие связи обычно отражаются в заголовках граф или
строк формуляров. Например, графа x = графа y — графа z и т.д. Арифметический
контроль используется для проверки итоговых данных, с его помощью устанавливается
наличие ошибки.

• Логический контроль основан
на использовании логической взаимосвязи показателей, установлении логического
соответствия между ними. Он не выявляет ошибки наблюдения, а лишь ставит под
сомнение правильность полученных данных. Логический контроль заключается в
проверке ответов на вопросы программы наблюдения путем их логического
осмысления или сравнения полученных данных с другими источниками по данному
вопросу. Классическим примером логического контроля является соответствие данных
при переписи населения о возрасте, образовании и семейном положении. Для
проверки данных наблюдения обычно составляется схема контроля, в которую
включаются различные виды контроля. При обнаружении ошибок нельзя
самостоятельно их исправлять. Для этого необходимо получить дополнительную
информацию путем повторного наблюдения. Данные наблюдения считаются принятыми,
если они прошли контроль, и в них внесены все необходимые исправления.
Проверкой собранных данных заканчивается начальная стадия статистического
исследования. После этого можно переходить ко второй стадии исследования
обработке данных наблюдения. Обработка заключается в классификации и
систематизации полученного статистического материала, осуществляемых через
сводку и группировку.

О сводке и группировке мы
поговорим с Вами в следующей лекции.