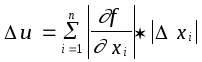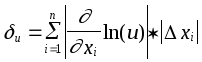Под ошибкой или погрешностью а приближенного числа а обычно понимается разность между

Данные пособия являются тестами по численным методам для подготовки к экземенам, проработки численных методов. Подойдет как для студентов ВУЗов, так и для преподователей для организации тестирования в колледжах, ВУЗах.

Тесты по численным методам с ответами вы можете как скачать бесплатно и без регистрации, так и просмотреть ниже. Внимание, правильный ответ везде А!

1)Приближенным числом а называют число, незначительно отличающиеся от
a) точного А
b) неточного А
c) среднего А
d) точного не известного
e) приблизительного А

 
2) а называется приближенным значением А по недостатку, если
a) а < A
b) a > A
c) a = A
d) a ≥ A
e) a ≤ A

 
3) а называется приближенным значением числа А по избытку, если
a) a > A
b) a < A
c) a = A
d) a ≥ A
e) a ≤ A
Под ошибкой или погрешностью ∆а приближенного числа а обычно понимается разность между соответствующим точным числом А и данным приближением, т.е.
a) ∆а = А — а
b) ∆а = А + а
c) ∆а = А/а
d) а = ∆а — А
e) А = ∆а + А

 
7) Если ошибка положительна А>, то
a) ∆a > 0
b) ∆a < 0
c) ∆a = 0
d) ∆a ≤ 0
e) a > a

 
Абсолютная погрешность приближенного числа
a) ∆ = ׀∆а׀
b) ∆а = а
c) ∆ = ׀а׀
d) А = ׀∆а׀
e) ∆а = ׀∆в׀

 
9) Абсолютная погрешность
a) ∆ = ׀А — а׀
b) ∆А = а
c) ∆ = ׀В — а׀
d) а = ׀А + а׀
e) ∆а = ׀А + в׀

 
10) Предельную абсолютную погрешность вводят если
a) число А не известно
b) число а не известно
c) ∆ не известно
d) А – а не известно
e) не известно В

 
11) Предельная абсолютная погрешность
a) ∆а
b) ∆в
c) ∆А
d) А
e) А

 
12) Определить предельную абсолютную погрешность числа а = 3,14, заменяющего число π
a) 0,002
b) 0,001
c) 3,141
d) 0,2
e) 0,003

 
13) Относительная погрешность
a) σ = ∆/׀А׀
b) σ = ∆
c) σ = ∆/в
d) σ = с/а
e) σ = а – А

 
14) Погрешность, связанная с самой постановкой математической задачи  
a) погрешность задачи
b) погрешность метода
c) остаточная погрешность
d) погрешность действия
e) начальная

 
15) Погрешности,  связанная с наличием бесконечных  процессов в   математическом анализе
a) остаточная    погрешность
b) абсолютная
c) относительная
d) погрешность условия
e) начальная погрешность

 
16) Погрешности, связанные с наличием  в математических формулах, числовых параметров
a) начальном
b) конечной
c) абсолютной
d) относительной
e) остаточной

 
17)  Погрешности, связанные с системой счисления
a) погрешность  округления
b) погрешность действий
c) погрешности задач
d) остаточная  погрешность
e) относительная погрешность

 
18)  Округлить число π = 3,1415926535… до пяти значащих цифр  
a) 3,1416
b) 3,1425
c) 3,142
d) 3,14
e) 0,1415

 
19) Абсолютная погрешность при округлении числа π до трёх значащих цифр
a) 0,5*10-2
b) 0,5*10-3
c) 0,5*10-4
d) 0,5*10-1
e) 0,5  

 
20)  Предельная абсолютная погрешность разности
a) ∆u=∆x1+∆x2  
b) ∆u=a+b
c) ∆u=A+b
d) ∆=x1+x2
e) ∆a=b+c

 
21)  Числовой ряд названия сходящимся, если  
a) существует предел последовательности его частных сумм  
b) можно найти сумму ряда
c) существует последовательность
d) частные суммы равны нулю
e) существует предел разности

 
24) Найти   ln3 c точностью до 10-5
a) 1,09861  
b) 1,01
c) 1,098132
d) 1,02
e) 1,3

 
25) Найти sin 20030I
a) 0,35
b) 0,36
c) 0,2
d) 0,47
e) 0,5

 
26) Найти tg 400
a) 0,839100  
b) 0,84  
c) 0,9
d) 1,0
e) 1,2

 
27) С помощью  этого метода число верных  цифр примерно удваивается на  каждом этапе  по сравнению с первоначальным количеством
a) процесс Герона  
b) формула Тейлора
c) формула  Маклорена
d) метод Крамера
e) процесс Даломбера
Методом половинного деления уточнить корень уравнения х4+2х3-х-1=0  
a) 0,867
b) 0,234
c) 0,2
d) 0,43
e) 0,861

 
31) Используя метод хорд найти положительный корень уравнения х4-0,2х2-0,2х-1,2=0
a) 1,198+0,0020
b) 1,16+0,02
c) 2+0,1
d) 3,98+0,001
e) 4,2+0,0001

 
32) Вычислить методом Ньютона отрицательный корень уравнения х4-3х2+75х-10000=0
a) −10,261
b) −10,31
c) −5,6
d) −3,2
e) −0,44

 
33) Используя комбинированный метод вычислить с точностью до 0,005 единственный положительный корень уравнения
a) 1,04478
b) 1,046
c) 2,04802
d) 3,45456
e) 802486

 
34) Найти действительные корни уравнения х-sinх=0,25
a) 1,17
b) 1,23
c) 2,45
d) 4,8
e) 5,63

 
35) Определить число положительных и число отрицательных корней уравнения х4-4х+1=0
a) 2 и 0
b) 3 и 2
c) 0 и 4
d) 0 и 1
e) 0 и 4

 
36) Определить нижнее число и верхнее число перемен знаков в системе 1, 0, 0, -3, 1.
a) 2 и 4
b) 3 и 1
c) 0 и 4
d) 0 и 5
e) 3 и 2

 
37) Определить состав корней уравнения х4+8х3-12х2+104х-20=0
a) один положительный и один отрицательный  
b) нет ни одного корня
c) невозможно найти число корней
d) уравнение не имеет положительных корней
e) два отрицательных корня

 
38) Две матрицы одного и того же типа, имеющие одинаковое число строк и столбцов, и соответствующие элементы их равны, называют
a) равными
b) одинаковыми
c) разными по рангу
d) схожими
e) транспонированными

 
39) Укажите свойства суммы матриц А+(В+С)=…
a) (А+В)+С
b) (В+А)*С
c) АВС
d) А+В+С*А
e) А*С+В*С

 
40) Укажите название матрицы –А=(-1)А
a) противоположная
b) обратная
c) равная
d) матрица не существует
e) транспонированная

 
41) Заменив в матрице типа m×n строки соответственно столбцами получим
a) транспонированную матрицу
b) равную матрицу
c) среднюю матрицу
d) обратную матрицу
e) квадратную матрицу

 
42) С какой матрицей совпадает дважды транспонированная матрица
a) с исходной
b) с обратной
c) с нулевой
d) с единичной
e) с квадратной

 
43) Нахождение обратной матрицы для данной называется
a) обращение данной матрицы
b) транспонированием
c) суммой матриц
d) заменой строк и столбцов
e) произведением матриц

 
44) Максимальный порядок минора матрицы, отличного от нуля, называют
a) рангом
b) пределом
c) рядом
d) сходимостью
e) определителем

 
45) Разность между наименьшим из чисел m и n и рангом матрицы называется
a) дефектом
b) пределом
c) рангом
d) определителем
e) разницей

 
46) Существующие и имеющие важное значение матричные степенные ряды
a) правые и левые
b) средние
c) верхние и нижние
d) высокие
e) дифференцируемые

 
47) Матричные ряды дают возможность определять
a) трансцендентные функции матрицы
b) миноры матричного ряда
c) сходящиеся ряды
d) геометрические прогрессии
e) каноническую форму ряда

 
48) Матрица разбитая на клетки, называется клеточной и …
a) блочной
b) равной
c) окаймленной
d) квазидиагональной
e) средней

 
49) Если элементы квадратной матрицы, стоящие выше (ниже) главной диагонали, равны нулю, то матрицу называют
a) треугольной
b) нулевой
c) диагональной
d) такая матрица не существует
e) единичной

 
50) Метод, представляющий собой конечные алгоритмы для вычисления корней системы
a) точный метод
b) метод релаксации
c) метод итерации
d) приближенный метод
e) относительный метод

 
51) Метод позволяющий получить корни системы с заданной точностью путем сходящихся бесконечных процессов
a) итерационный метод
b) точный метод
c) приближенный метод
d) относительный метод
e) метод Зейделя

 
52) Этот метод является наиболее распространенным приемом решения систем линейных уравнений, алгоритм последовательного исключения неизвестных
a) метод Гаусса
b) метод Крамера
c) метод обратный матриц
d) ведущий метод
e) аналитический метод

 
53) Целый однородный полином второй степени от n переменных называется
a) квадратичной формой
b) кубической формой
c) прямоугольной формой
d) треугольной формой
e) матричной формой

 
54) Квадратичная форма называется положительно (отрицательно) определенной, если она принимает положительные (отрицательные) значения, обращаясь в нуль лишь при
a) х1=х2=…=хn=0
b) х1+х2+…+хn=0
c) х1х2…хn=0
d) a+b+c+…=0
e) х1+х2+…+хn=5

 
55) Простейшая форма этого метода заключается в том, что на каждом шаге обращают в нуль максимальную по модулю невязку путем изменения значения соответствующей компоненты приближения
a) метод ослабления
b) итерационный метод
c) метод обратных матриц
d) ведущий метод
e) метод Гаусса

 
56) Произведением вектора х=(х1,х2,…,хn) на число k называется вектор
a) kx=(kx1,kx2,…kxn)
b) k=x1+x2+…xn
c) ab=x1+x2+…+xn
d) нельзя вектор умножать на число
e) с=a+b

 
57) Для векторов x и y естественно определяется линейная комбинация
a) αх+βy
b) αx*βy
c) αx/βy
d) x+y=о
e) (x+y)α=о

 
58) Любая совокупность n-мерных векторов, рассматриваемая с установленными в ней операциями сложения векторов и умножения вектора на число, не выводящими за пределы этой совокупности называется
a) линейным векторным пространством
b) плоскостью векторов
c) скалярным произведением векторов
d) суммой векторов
e) сходимостью векторного пространства

 
59) Максимальное число линейно независимых векторов n-мерного пространства Еn в точности равно
a) размерности этого пространства
b) соразмерности векторов
c) сумме линейных векторов
d) совокупности единичных векторов
e) сумме n векторов

 
60) Название любой совокупности n линейно независимых векторов n-мерного пространства
a) базис
b) орт
c) вектор
d) координата
e) скаляр

 
61) Как иначе называют метод бисекций?
a) Метод половинного деления
b) Метод хорд
c) Метод пропорциональных частей
d) Метод «начального отрезка»
e) Метод коллокации

 
62) Методы решения уравнений делятся на:
a) Прямые и итеративные
b) Прямые и косвенные
c) Начальные и конечные
d) Определенные и неопределенные
e) Простые и сложные

 
63) Кто опубликовал формулу для решения кубического уравнения?
a) Кардано
b) Галуа
c) Абеле
d) Дарбу
e) Фредгольм

 
64) Основная теорема алгебры:
a) Уравнение вида α0xn + α1xn-1 + …+ αn-1x + αn=0 имеет ровно n корней, вещественных или комплексных, если k-кратный корень считать за k корней
b) Если функция f(x) определена и непрерывна на отрезке [α;b] и принимает на его концах значения разных знаков, то на[α;b] содержится, по меньшей мере, один корень уравнения f(x)=0
c) Если функция f(x) монотонна на отрезке [α;b], то она интегрируема на этом отрезке    
d) Если функция f(x) монотонна на отрезке [α;b], то она дифференцируема на этом отрезке    
e) Определитель D=|αij| n-го порядка равен сумме произведений элементов какой-либо строки (столбца) на их алгебраические дополнения  

 
65) Отделение корней можно выполнить двумя способами:
a) аналитическим и графическим
b) приближением и отделением
c) аналитическим и систематическим
d) систематическим и графическим
e) приближением последовательным и параллельным

 
66) Укажите первую теорему Больцано-Коши:
a) Если функция f(x) определена и непрерывна на отрезке [α;b] и принимает на его концах значения разных знаков, то на[α;b] содержится, по меньшей мере, один корень уравнения f(x)=0
b) Уравнение вида α0xn + α1xn-1 + …+ αn-1x + αn=0 имеет ровно n корней, вещественных или комплексных, если k-кратный корень считать за k корней
c) Если функция f(x) монотонна на отрезке [α;b], то она интегрируема на этом отрезке      
d) Если функция f(x) монотонна на отрезке [α;b], то она дифференцируема на этом отрезке    
e) Определитель D=|αij| n-го порядка равен сумме произведений элементов какой-либо строки (столбца) на их алгебраические дополнения    

 
67) Отделим корни уравнения х3 – 2х – 3=0
a) Единственный корень расположен между √⅔ и ∞
b) Корней нет
c) Один из корней находится на отрезке [1,2]
d) Один из корней находится на отрезке [-1,2]
e) Единственный корень расположен между √⅛ и √⅜

 
68) При контроле решения алгебраического уравнения может быть полезна:
a) Теорема Виета
b) Теорема Ньютона
c) Теорема Перрона
d) Теорема Штурма
e) Теорема Бюдана-Фурье

 
69) Итерация iteratio в переводе с латинского:
a) повторение
b) замещение
c) возвращение
d) умножение
e) удаление

 
70) Укажите рекуррентную формулу метода простой итерации:
a) хn+1=φ(хn)
b) х=φ
c) х=C
d) хn+1=ψ(хn)+φ(хn)
e) хn-1=ψ(хn)-φ(хn)

 
71) От латинского слова recurrens:
a) возвращающийся
b) меняющийся
c) повторяющийся
d) заменяющийся
e) приближающийся

 
72) Последовательность, удовлетворяющая условию Коши, называется:
a) фундаментальной последовательностью
b) рекуррентной последовательностью
c) итеративной последовательностью
d) двусторонней последовательностью
e) односторонней последовательностью
Метод хорд-
a) Частный случай метода итераций
b) Частный случай метода коллокации
c) Частный случай метода прогонки
d) Частный случай метода квадратных корней
e) Частный случай метода Гаусса

 
75) Свойство самоисправляемости:
a) Усиливает надежность метода
b) Не влияет на конечный результат
c) Влияет на конечный результат
d) Не учитывается
e) Считается ошибочным

 
76) Как иначе называют метод Ньютона?
a) Метод касательных
b) Метод коллокации
c) Метод прогонки
d) Метод итераций
e) Метод хорд

 
77) Как иначе называют метод хорд?
a) Метод пропорциональных частей
b) Метод касательных
c) Метод коллокации
d) Метод бисекций
e) Метод квадратных корней

 
78) Метод хорд имеет еще одно имя:
a) Метод пропорциональных частей
b) Метод касательных
c) Метод бисекций
d) Метод коллокации
e) Метод прогонки

 
79) Что общего у метода хорд и метода итераций?
a) Общая скорость и свойство самоисправляемости
b) Свойство самоисправляемости
c) Общая скорость
d) Легкость при решении
e) Требуется нахождение производной

 
80) Метод Ньютона-
a) обладает свойством самоисправляемости и имеет высокую скорость сходимости
b) дает большой выигрыш во времени
c) занимает очень много времени
d) предельно прост
e) надежен

 
81) Методом хорд уточнить корень уравнения х3 – 2х – 3=0, ξ[1;2]; ε=10-3
a) ξ=1.8933±0.0001
b) ξ=0.0001±1
c) ξ=0.0033±0.0001
d) ξ=±1
e) ξ=±3.3

 
82) Если точка движется равномерно υ(t)=υ=const, то ответ готов:
a) S=υ(T2 — T1)
b) S=0  
c) υ= υ0+at  
d) υ=s/t  
e) S= υ0t+ at2/2

 
83) Предел суммы S ≈ υ(τ1)∆t1+υ(τ2)∆t2+…+υ(τn)∆tn называется:
a) Определенным интегралом
b) Неопределенным интегралом
c) Рекуррентной формулой
d) Формулой численного дифференцирования
e) Схемой Халецкого

 
84) Если сила постоянна, ответ дается формулой:
a) A=F(b-
b) A=F(a-
c) F=const
d) A=0
e) F=ma

 
85) Все методы вычисления интегралов делятся на:
a) Точные и приближенные
b) Прямые и итеративные
c) Прямые и косвенные
d) Аналитические и графические
e) Приближенные и систематические

 
86) Точный метод вычисления интегралов был предложен:
a) Ньютоном и Лейбницем
b) Ньютоном и Гауссом
c) Гауссом и Стирлингом  
d) Вольтерром  
e) Гауссом и Крамером    

 
87) Геометрически нижняя сумма Дарбу равна:
a) Площади ступенчатого многоугольника, содержащегося в криволинейной трапеции
b) Площади ступенчатого многоугольника, содержащего внутри себя криволинейную трапецию
c) Площади прямоугольного параллелепипеда      
d) Площади ступенчатого шестиугольника    
e) Площади ступенчатого прямоугольника    

 
88) Геометрически верхняя сумма Дарбу равна:
a) Площади ступенчатого многоугольника, содержащего внутри себя криволинейную трапецию
b) Площади ступенчатого многоугольника, содержащегося в криволинейной трапеции
c) Площади прямоугольного параллелепипеда      
d) Площади ступенчатого шестиугольника        
e) Площади ступенчатого прямоугольника

 
89) Приближенные методы вычисления интегралов можно разделить на 2 группы:
a) аналитические и численные
b) аналитические и графические
c) систематические и численные
d) систематические и случайные
e) приближенные и неприближенные
конец тестов по численным методам, правильный ответ везде А

1. Элементы теории погрешностей.

1.1.Определение абсолютной и относительной погрешности численного результата.

Приближенным
числом а
называется число, незначительно
отличающееся от точного А
и заменяющее последнее в вычислениях.
Под ошибкой
или
погрешностью
а
приближенного числа а
обычно понимается разность между
соответствующим точным числом А
и данным приближением, т.е.

а
= А — а .

Абсолютной
погрешностью 
приближенного числа а
называется абсолютная величина разности
между соответствующим точным числом А
и числом а,
т.е.

 =
А
— а
.

Если
число А
не
известно, то по этой формуле нельзя
определить абсолютную погрешность,
Поэтому вместо неизвестной теоретической
абсолютной погрешности вводят ее оценку
сверху, называемую предельной абсолютной
погрешностью .

Под
предельной
абсолютной погрешностью
приближенного числа понимается всякое
число, не меньшее абсолютной погрешности
этого числа. Таким образом, если а
—
предельная абсолютная погрешность, то

 =
А
— а

а
.

Относительной
погрешностью 
приближенного
числа а
называется
отношение абсолютной погрешности 
этого
числа к модулю соответствующего точного
числа А
(А0)
т.е.

.

Так
же как и для абсолютной погрешности
вводят понятие предельной относительной
погрешности. Под предельной
относительной погрешностью _а
понимают
всякое число, не меньшее относительной
погрешности этого числа. В качестве
предельной относительной погрешности
числа а
можно
принять число

.

1.2.Основные составляющие абсолютной погрешности.

1.3.Формулы для оценки абсолютной и относительной погрешности для значения функции и переменных.

При сложении или
вычитании чисел их абсолютные погрешности
складываются. Относительная погрешность
суммы заключена между наибольшим и
наименьшим значениями относительных
погрешностей слагаемых; на практике
принимается наибольшее значение.

(a

b) = a
+ b
.

При умножении или
делении чисел друг на друга их относительные
погрешности складываются.

;

При возведении в
степень приближенного числа его
относительная погрешность умножается
на показатель степени.

Погрешность
разности:
предельная
абсолютная погрешность разности (u
= x₁
— x₂)
равна
сумме предельных абсолютных погрешностей
уменьшаемого и вычитаемого:

_u
= _x1
+ _x2

Отсюда
предельная относительная погрешность
разности

где
А
—
точное значение абсолютной величины
разности чисел х₁
и
х₂
.

Погрешность
произведения:
относительная погрешность произведения
нескольких приближенных чисел, отличных
от нуля, не превышает суммы относительных
погрешностей этих чисел:

  ₁
+
₂
+ … + _n
.

Поэтому
при вычислении произведения нескольких
приближенных чисел применяют следующие
правила:

—
округляют эти числа так, чтобы каждое
из них содержало на одну (или две) значащие
цифры больше, чем число верных значащих
цифр в наименее точном из сомножителей;

—
в результате умножения сохраняют столько
значащих цифр, сколько верных цифр
имеется в наименее точном из сомножителей.

Погрешность
частного:
относительная погрешность частного не
превышает суммы относительных погрешностей
делимого и делителя.

Основная
задача теории погрешности заключается
в следующем: известны погрешности
некоторой системы величин, требуется
определить погрешность данной функции
от этих величин.

Пусть
задана дифференцируемая функция
u=(x₁,x₂,
… , x_n)
и
пусть x_i
— абсолютные
погрешности аргументов функции.

Тогда
предельная
абсолютная погрешность функции
может быть вычислена по формуле:

Предельная
относительная погрешность функции
вычисляется следующим образом:

Соседние файлы в предмете Методы оптимизации

• #
• #