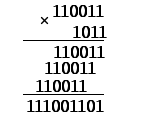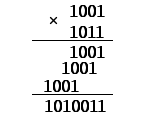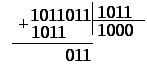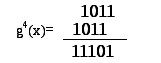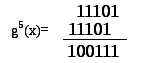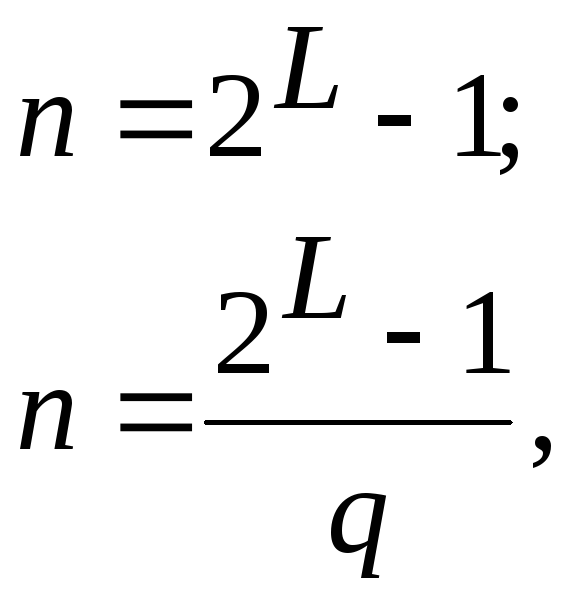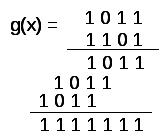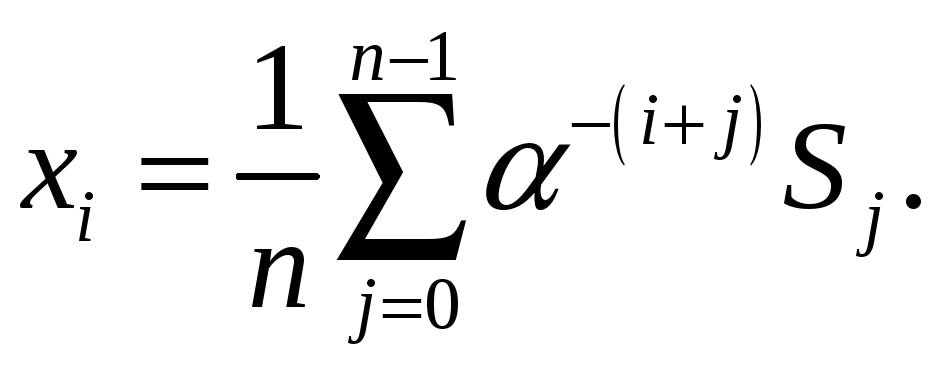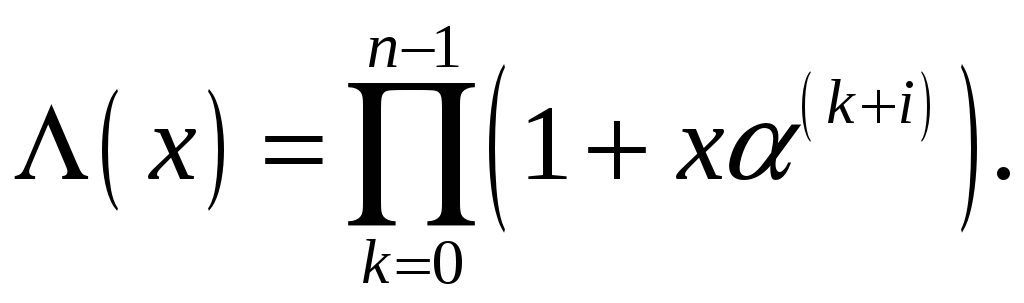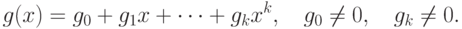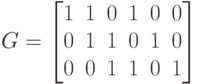Полиномиальное кодирование нахождение ошибки - Исправление ошибок и поиск оптимальных решений проблем

После
того, как мы ознакомились с правилами
образования корректирующих алгебраических
кодов, можно рассматривать наиболее
мощную группу корректирующих кодов,
предложенную в свое время тем же
Р.Хеммингом.

Для
того чтобы получить представление о
полиномиальных кодах, необходимо
предварительно получить представление
о математике в области полей Галуа.

В
области высшей алгебры существует
несколько понятий, определяемых рядом
аксиом. Среди таких образований
существуют, в частности, моноид, кольцо,
полугруппа, поле, векторное пространство.
Они различаются операциями, на которых
они заданы, а также исходным множеством
объектов. Наиболее употребимы двоичные
коды в качестве базовой конструкции, а
главной операцией представляется
сложение по модулю 2. Если к ней добавить
логическое умножение, получается поле
Галуа
.

В
пределах поля Галуа заданы две процедуры:
умножение и деление. Формально они могут
представляться цифровыми аналогами
арифметических умножения и деления.
Отличие в том, что базовая операция –
сложение по модулю 2, является
самодвойственной (сложение и вычитание
являются одной операцией). Продемонстрируем
операции в поле Галуа на конкретных
примерах.

Перемножим
два двоичных кода в поле Галуа: множимое
110011, множитель 1011. Умножение представим
в классическом арифметическом виде, т.
е. столбиком (рис. 6.40).

Рис.
6.40. Умножение в поле Галуа GF(2)

При
умножении на 1 код множимого просто
повторяется; при умножении на 0 происходит
простой сдвиг налево на один разряд.
Суммирование частичных произведений
производится по законам двоичной логики:
если количество единиц четно, результат
равен 0, если нечетно – 1. количество
разряда результата равно сумме разрядов
множимого и множителя без 1.

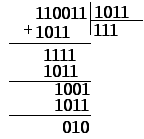
Деление
в поле Галуа осуществляется еще «веселее»,
чем умножение. Оно, как в арифметике,
производится углом, но с учетом того,
что вычитание заменяется также сложением
по модулю 2. Главный критерий деления –
первая цифра делимого должна начинаться
с 1 (в противном случае в частное заносится
0, а делитель сдвигается на один разряд
вправо).

Приведем
пример деления на тех же кодах (рис.
6.42). Пример не совсем удачный, так как
каждый остаток начинался с 1, и дальнейшее
деление оказывалось возможным. Если
это выполняется, в частном 1, в противном
случае – 0. В приведенном варианте
деление произошло с остатком 010 (остаток
всегда на разряд короче делителя).

Рис.
6.41. Деление в поле Галуа GF(2)

Гениальным
решением Р. Хемминга, предложившего
полиномиальные коды, является совершенно
новый подход к кодированию/декодированию,
не ограничивающий корректирующую
способность кода. В первоначальном
варианте полиномиальный код состоял
из двух взаимодополняющих операций,
умножения и деления. Выбирается некоторый
код из

разрядов, который называется образующим
полиномом. Название вытекает из
представления кода в виде полинома от
х, в котором степень любого члена равна
номеру разряда, а его коэффициент равен
0 или 1. Так, код 10011 эквивалентен полиному
;
полином

соответствует коду 1100011.

Простейший
принцип образования полиномиального
кода заключается в том, что информационный
полином

на передающей части умножается на
образующий
:

(6.38)

В
приемной части производится деление
принятого кода на образующий полином:

(6.39)

При
этом, если ошибок не произошло, остаток
от деления равен 0; ненулевой остаток
или воспринимается как признак ошибки
(код, обнаруживающий ошибки) или как
синдром ошибки (код, исправляющий
ошибки).

Приведем
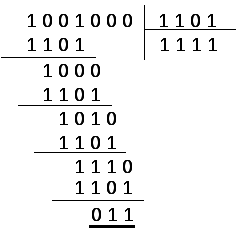
пример. Предположим, исходный код равен

(или
),
образующий полином

(или
).
При перемножении получаем код

(рис. 6.42).

Рис.
6.42. Кодирование прямым методом

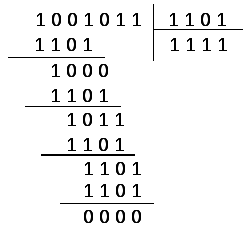
При
декодировании (т. е. при делении на
образующий полином) получим в остатке
0 (рис. 6.43).

Рис.
6.43. Декодирование прямым методом

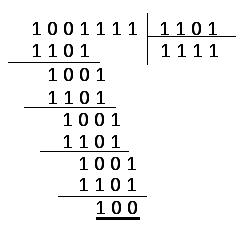
Предположим,
в коде 1011011 появилась ошибка. В результате
деления на образующий полином получаем
ненулевой остаток (рисунок 6.45).

Рис.
6.44. Декодирование при наличии ошибки

Из
приведенного примера следует интересное
правило: чем больше возможно различных
остатков, тем больше корректирующая
способность кода.

Для
того, чтобы остатков было как можно
больше, желательно, чтобы образующий
полином был неприводимым. Неприводимым
называется такой полином, который не
может представляться в виде произведения
полиномов низших степеней. Еще Л. Эйлером
была доказана теорема, согласно которой
количество различных остатков
неприводимого полинома степени

равно
.
Это значение полностью соответствует
границе Хемминга в соответствии с
(6.28).

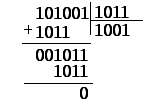
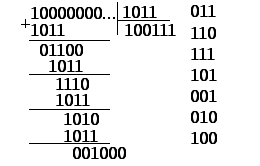
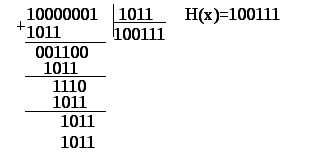
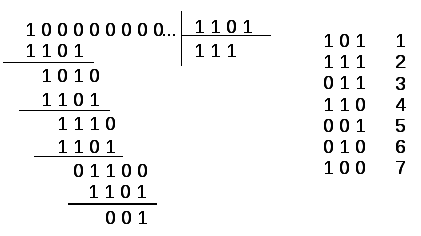
Приведем
пример. Известно, что полином вида

(или в кодах 1011) является неприводимым.
Докажем это тривиальным делением с
приведением остатков. Для этого в
качестве делимого всегда выбирается
код вида: 10000…. . Результаты деления
представлены на рис. 6.45.

а)
б)

Рис.
6.45. К определению неприводимого полинома

Здесь
поле а) представляет собственно механизм
деления, б) – запись остатков. Как видим
различных остатков ровно 7, что
соответствует критерию неприводимости.
Другой неприводимый полином этой же
степени образуется при чтении предыдущего
в обратном порядке, т. е. 1101.

К
сожалению, формальных правил для
формирования или обнаружения неприводимых
полиномов не существует, что породило
достаточно представительный класс
различных полиномиальных кодов, а также
способов их декодирования. Тем не менее,
некоторые признаки неприводимости, в
том числе установленные автором, можно
сформулировать.

1.
Неприводимый полином в его кодовом
эквиваленте начинается и заканчивается
1. Это легко интерпретируется: если код
полинома заканчивается нулем, значит,
в него входит множитель

или его степени.

2.
Неприводимый полином обязательно
соответствует несимметричному коду,
который слева направо и наоборот читается
по-разному. Кроме того, код должен иметь
свойства нерегулярного (как можно больше
«кособокого»).

3.
Практика показывает, что количество
различных неприводимых полиномов для
четных и нечетных степеней различно и
для четных степеней всегда меньше.

4.
Также из практики кодообразования
наилучшими свойствами обладают полиномы,
в которых вес (т. е. количество единиц)
близок к половине их длины.

5.
Если полином

неприводим, то неприводимым будет
полином

с инверсией его разрядов. Так, если
полином 1011 неприводим, то неприводимым
будет и полином 1101.

Что
характерно, возможностей для организации
полиномиальных кодов гораздо больше,
чем для алгебраических. Существует
множество различных полиномиальных
кодов, отличающихся способом получения
образующих полиномов. Прежде, чем об
этом говорить, рассмотрим три классических
способа кодирования/декодирования.

1.
Первый способ кодирования описан
выражениями (6.38) и (6.39). С классических
позиций, это не очень удачный вариант,
так как корректирующий код является
неразделимым: исходная комбинация не
может быть выделена из кода

и требует обязательного деления.

С
другой стороны, такое кодирование может
поддерживать режим шифрования: если
при несанкционированном перехвате
нарушителю неизвестен образующий
полином, он вынужден подбирать, на что
тратится время. Если при этом легальные
клиенты связи в ходе взаимодействия
меняют образующие полиномы, особенно
по случайному закону, условия перехвата
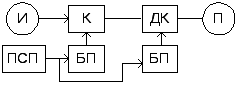
заметно усложняются. В качестве примера
представим структуру следующего
устройства (рисунок 6.46).

Рис.
6.46. Защищенный помехоустойчивый канал

Здесь
обозначено: И/П – источник/приемник;
К/Д – кодер/декодер; БП – блоки памяти,
хранящие семейство образующих полиномов;
ПСП – блок, реализующий одновременную
выборку из БП нужных образующих полиномов.
Не вдаваясь в подробности о способах
выборки, отметим, что по структуре
рисунка 3.36 возможно достаточно большое
число сценариев работы информационной
системы, обеспечивающих при этом
требуемый уровень защиты и нужную
помехоустойчивость. Собственно говоря,
это может обеспечивать новое научное
направление в области защиты информации.

2.
Второй способ кодирования/декодирования
является базовым и обеспечивает надежные
технологии, реализованные как на
аппаратном, так и на программном уровнях.
Рассмотрим вначале передающую часть.
Способ кодирования заключается трех
этапах.

а)
Исходный информационный код I(x)
умножается на
,
где

– степень образующего полинома:

(6.40)

б)
Полученный код делится на образующий
полином с получением остатка степени
:

(6.41)

в)
Остаток вписывается в смещенный код
вместо присутствовавших там нулей:

(6.42)

Несмотря
на кажущуюся сложность, алгоритм
становится понятным на примере.
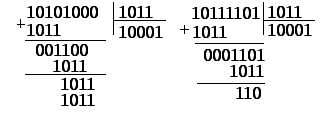
Предположим, исходный код 5-разрядный
и имеет вид 10101. Возьмем в качестве
образующего полинома код 1011. Применив
п. а), получаем код 10101000 (образующий
полином третьей степени). Далее используем
п. б) (рис. 6.47).

а)
б)

Рис.
6.47. Применение второго алгоритма
кодирования
полиномиального кода

Это
и есть необходимый корректирующий код.

Рассмотрим
теперь процедуру декодирования. При
правильном приеме кода и отсутствии
ошибок в остатке получается 0. На том же
примере приведем проверки, для чего
разделим на образующий полином коды
без ошибки и с одиночной ошибкой (рисунок
6.48)

а)
б)

Рис.
6.48. Декодирование полиномиального кода

Из
приведенного примера видно, что индикатор
ошибки – ненулевой остаток. Методы
декодирования и исправления ошибок –
предмет особого анализа, не входящего
в материал этого пособия.

4.
Кодирование на основе генераторных
многочленов. Генераторным называется
многочлен
,
образующийся при делении полинома типа

на образующий полином:

(6.43)

Предположим,
для кода (7,4) и образующего полинома

получим образующий полином вида:

а)
б)

Рис.
6.49. К образованию генераторного многочлена

Правило
кодирования состоит в получении
результирующего кода по рекуррентной
процедуре:

(6.44)

Декодирование
полиномиальных кодов относится как к
процедуре однозначного распознавания
синдромов, так и к области более
математизированных операций и алгоритмов.

Рассмотрим
некоторые процедуры формирования
образующих полиномов, от которых и
зависят свойства кодов. Простейшая
процедура – увеличение степени полинома.
Алгоритм Хемминга – элементарное
умножение на бином
:

(6.45)

Приведем
простой пример. Предположим, базовый
полином

(или в двоичном коде 1011). Для повышения
степени образующего полинома применим
правило (6.45):

(6.46)

Аналогично
дальше:

(6.47)

Дальнейшая
методика понятна, но она неэффективна.

Более
продуктивными являются коды Файра. Для
них образующие полиномы строятся по
правилу:

(6.48)

Здесь
–
неприводимый полином степени
;

– константа, не делящаяся нацело на
.

Достаточно
мощным являются коды БЧХ (по начальным
буквам создателей: Боуз, Чоудхури,
Рой-Хоквингем). В абстрактной математике
механизм формирования образующего
полинома достаточно сложен, но в практике
он записывается в форме:

(6.49)

Здесь НОК –
наименьшее общее кратное;
–
примитивные многочлены степени

(объяснение дадим позже).

Приведем методику
получения образующих полиномов для
кодов БЧХ. Главное – это то, что количество
разрядов кода n не может
быть произвольным, а удовлетворяет
одному из двух правил:

(6.50)

где

и

– целые числа. Исходя из этого ограничения,
можно составить числовые ряды из
возможных значений
.
Например, для первого уравнения

Второй
шаг – выбор корректирующей способности.
Выбирается, исходя из требований. Обычно
задаются количеством исправляемых
ошибок

(соответственно кодовое расстояние
).
Значению

соответствует количество примитивных
многочленов
.
Образующий полином вычисляется как
тривиальное произведение примитивных
многочленов.

В
качестве примера приведем достаточно
упрощенный алгоритм вычисления
образующего полинома для группы кодов
БЧХ. В таблице .1 приведены примитивные
многочлены степени L для
нескольких возможных вариантов.

Таблица
6.1. Примитивные
многочлены кодов БЧХ

	2	3	4	5	6	7	8	9
М1	111	1011	10011	100101	1000011	10001001	100011101	1000010001
М3		1101	11111	111101	1010111	10001111	101110111	1001011001
М5			111	111101	1100111	10011101	11111011	1100110001
М7			11001	110111	1001001	11110111	101101001	1010011001
М9				101111	1101	10111111	110111101	1100010011
М11				110111	1101101	11010101	111100111	1000101101
М13						10000011	100101011	1001110111

Каждый из столбцов
представляет множество примитивных
многочленов степени L.
Если вспомнить, что количество разрядов
при этом определяется как
,
то таблица перекрывает все возможные
коды БЧХ для n до

разрядов. При этом количество строк в
предполагаемом произведении равно
количеству исправляемых ошибок. Например,
первый элемент таблицы определяет
3-разрядный код, в котором существует
единственная разрешенная ненулевая
кодовая комбинация, а именно 111 (вторая
разрешенная кодовая комбинация равна
000). Код имеет расстояние, равное 3, и
исправляет одиночные ошибки.

Обратимся
ко второму столбцу. Здесь общее количество
разрядов

и возможны два варианта: код, исправляющий
одиночные ошибки и имеющий

с полиномом
,
и код, исправляющий двойные ошибки,
класса (7,1) с одним информационным
разрядом. Вычислим последний полином:

Рис.
6.50. Вычисление
полинома

В
результате образуется полином 6-й степени
с двумя разрешенными кодовыми комбинациями
и с кодовым расстоянием
.

Рассуждая
аналогично, можно получить семейство
кодов БЧХ с разной корректирующей
способностью. Рассмотрим, в частности
пример кода, исправляющего трехкратные
ошибки ()
для

().
Обнаруживается, что третий примитивный
многочлен имеет степень 2, что приводит
к тому, что результирующий полином на
2 разряда короче, т. е. получен код (15, 5),
исправляющий трехкратные ошибки, что
относит его к классу совершенных.
Пройдемся по этому столбцу возможных
кодов БЧХ:

–
код (15, 11), исправляющий
одиночные ошибки и имеет

(совпадает с совершенным кодом Хемминга);

–
код (15, 7), исправляющий
двойные ошибки,
;

–
код (15, 5), исправляющий
тройные ошибки,

и являющийся уникальным;

–
код (15, 1) с единственной
разрешенной кодовой комбинацией и
исправляющий тройные ошибки.

Если
рассмотреть таблицу полностью, то можно
обнаружить еще одни уникальный код: в
6-м столбце с многочленом М9. Это код (63,
9), исправляющий 5-кратные ошибки (т. е.
).

Используя
таблицу примитивных многочленов, можно
достаточно просто создавать корректирующие
коды заданной длины

и корректирующей способности
.

Из
других полиномиальных кодов можно
отметить коды Голея: это коды,
обладающие свойством совершенства, т.
е. обеспечивающие максимальную скорость
при заданной корректирующей способности.

Наиболее
популярны коды Голея (23, 12) или (24,12).
Базовый код Голея имеет кодовое расстояние
,
т. е. способен исправлять тройные ошибки.
Он имеет уникальные образующие полиномы:

или

(в кодовом изображении они имеют вид
101011100011 или 110001110101, что полностью
соответствует свойству 5) из перечисленных
выше признаков неприведенности).

Код
Голея (24, 12) имеет тот же образующий
полином, но лишний информационный
разряд, что дает приведение кода к
3-байтовой системе кодирования.

Одним
из наиболее перспективных, но практически
почти нереализованных корректирующих
кодов являются коды Рида-Соломона
(РС). Это недвоичные коды (т. е. коды с
системой счисления, отличающейся от
2). Для их определения введем понятие
примитивного элемента в кольце по
модулю q. Примитивный
элемент
–
это такое целое число, которое будучи
возводимым в целые степени (в модулярной
арифметике) дает последовательно все
числа от 1 до
.
Это свойство лучше рассмотреть на
конкретном примере. Предположим,
.
Докажем, что

является примитивным элементом для
.

(это очевидно),
,
,

Поясним в терминах модулярной арифметики.
Результат любой операции должен
находиться в числе разрешенных: 0, 1,2,….
Если он выходит «за габарит», из него
вычитают число, кратное
,
после чего он подходит под определение
кольца. Приведем пример для

и проверим на «примитивность» числа

и 3.

Рис.
6.51. К определению примитивного элемента

Из
рисунка 6.51 видно, что

не является примитивным элементом, а

является.

Большой
вклад в область теории чисел внес Л.
Эйлер. Он доказал, что для любого

существует хотя бы один примитивный
элемент. Более того, он ввел специальную
функцию,
,
определяющую количество таких примитивных
элементов.

Коды
РС имеют элегантный механизм вычисления
образующего полинома для ошибок кратности
:

(6.51)

Если
выбирается первый сомножитель,
исправляются одиночные ошибки, два
первых – двойные и т.д.

Сконструируем
код, исправляющий двойные ошибки для
.
Согласно (6.51),
.
Последнее означает, что все операции
производятся в кольце. В данном случае
при

образующий полином второй степени
обеспечивает исправление двойных
ошибок. Основным недостатком кодов РС
является трудная привязка к цифровым
системам, поэтому их обычно привязывают
к модулям, кратным степени двойки (7,
15,31, 63,…).

Рис.
6.52. Вычисление образующего многочлена

Большое
значение имеют алгоритмы декодирования;
для полиномиальных кодов они чрезвычайно
развиты.

Существуют
две большие группы, так называемое
жесткое (синдромное) и мягкое
декодирование. При жестком декодировании
составляется перечень возможных
синдромов, каждый из которых «отвечает»
за конкретную ошибку или их комбинацию.
Мягкое декодирование имеет много
направлений и должно рассматриваться
отдельно.

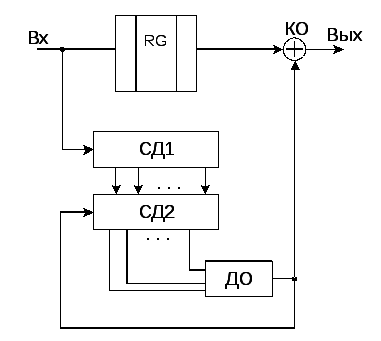
Рис.
6.53. Декодер полиномиального кода

Общая
структура декодера полиномиального
кода при жестком декодировании может
быть представлена структурной схемой,
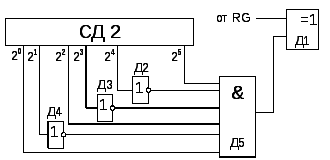
приведенной на рис.6.53. Здесь обозначено:
RG – буферный регистр на
n разрядов; СД1 и СД2 –
схемы деления на образующий полином;
ДО – детектор ошибок; КО – корректор
ошибок.

Принцип
действия кодера рассмотрим на конкретном
примере. Предположим, реализуется
полиномиальный код (7, 4) с образующим
полиномом 1101; на входе код 1001. Кодируем
по второму способу (см. рисунок 6.55).
Получили остаток, который приписываем
к «сдвинутому» коду, т. е. 1001011.

Рис.
6.54. К образованию
кода

При
декодировании производится обратная
операция, т. е. деление на образующий
полином:

Рис. 6.55.
Декодирование без ошибки

Рис. 6.56.
Декодирование с одиночной ошибкой

Предположим,
произошла одиночная ошибка в разряде
:
т. е. принят код 1001111. Тогда после деления
на образующий полином появляется остаток
110, свидетельствующий о наличии ошибки.
Для ее исправления существует
алгебраический прием, основанный на
том, что код с ошибкой может восприниматься
как алгебраическая сумма кода без ошибки
и собственно ошибки. Обозначим коды в
виде векторного
-мерного
пространства. Допустим, исходный
-разрядный
код представлен в виде вектора в
-мерном
пространстве. Обозначим его в виде
,
к вектору добавляется вектор синдрома
размерности
:

(6.52)

На
приемной части принят некоторый код

той же размерности. На основе гипотезы
независимости сигнала и ошибки можно
рассматривать принятую КК как сумму
векторов сигнала и ошибки:

(6.53)

Рассмотрим
простейший вариант декодирования, когда
принятый код делится на образующий
полином:

(6.54)

Уравнение
(6.54) можно переписать в виде:

(6.55)

Последний
член выражения (6.55) можно рассматривать
на основе гипотезы независимости как
индикатор ошибки. Первый член в (6.55) дает
в остатке 0 вследствие закона
кодообразования. Второй полностью
определяется конфигурацией вектора
ошибки. На этом основана структура
жесткого декодера, приведенная на рис.
6.53.

При
использовании методики жесткого
декодирования используется следующий
прием. Предположим, появилась некоторая
ошибка
,
не зависящая от кода
.
При ее делении на полином

появляется характерный остаток, появление
которого приводит к распознаванию
ошибки в выявленном разряде.

Предположим,
используется индикатор одиночных
ошибок. Для его настройки необходимо и
достаточно разделить вектор ошибки
100…..на образующий полином и получить
остаток на такте n.
Существуют две схемы деления, за

и

тактов.

Рассмотрим
тот же пример деления за n
тактов при образующем полиноме
.
При этом делится вектор ошибки 100….на
образующий полином

раз, и последний остаток служит декодером
ошибки (см. рисунок 6.57).

Таким
образом, детектор ошибки расстраивается
на вектор типа 100….(
разрядов), что соответствует ситуации,
когда разряд с ошибкой находится на
выходе дешифратора.

Рис.
6.57. К определению детектора ошибки

Обратимся
к структуре дешифратора на рисунке
6.53. Поступающий код подается одновременно
на регистр RG и на СД1. За
первые n тактов код делится
на образующий полином
,
после чего остаток (если он появляется
при наличии ошибок) переписывается в
СД2, после чего деление продолжается.

Независимо
от кода, при наличии ошибок вектор ошибки
не равен нулю, и остаток переписывается
в схему деления СД2. Когда код на СД2
совпадает с кодом по рис. 6.57, срабатывает
ДО, который отправляет импульс коррекции
на разряд с ошибкой, который в это время
присутствует на выходе RG.

При
необходимости исправления большего
числа ошибок схема дешифратора заметно
усложняется. Обратная связь, показанная
на рис. 6.53 от ДО к СД2 достаточно условна,
так как ДО должен срабатывать на все
конфигурации вектора ошибки (например,
вектор 11000… или 10100…).

Приведем
пример исправления двойной ошибки, взяв
за основу
.
Подберем по неравенству Хемминга
необходимое количество контрольных
разрядов. По той же методике последовательно
перебора определяем
.
В этом случае
,
,

,
а
.
Осталось подобрать образующий полином.
Следуем алгоритму Хемминга повышения
степени:

В
качестве исходного полинома выберем
.
Вычислим
:
1111. Тогда (см. рисунок 3.58)
.
Теперь определим синдромы одиночной и
двойной ошибок по предыдущей методике
(т. е. делением на образующий полином
векторов 1000… и и11000… до 10-го такта). Не
приводя собственно иллюстрацию вычисления
делением на образующий полином, приводим
результаты: в первом варианте остаток
равен 100101, во втором – 000001. Вообще, список
индикаторов (синдромов) необходимо
продолжить, т.к. существуют векторы
ошибок 1010000000, 1001000000, 1000100000 (дальнейшие
векторы циклически повторяются и их
можно не учитывать).

Рис.
6.58. Вычисление

Комбинационная
схема только одного типа синдрома и
исправления одиночной ошибки приведена
на рис. 6.59. Логическая схема включает
инверторы Д2, Д3, Д4 и схему логического
умножения Д5. Собственно исправление
происходит на вентиле Д1 (исключающее
ИЛИ). Если учесть все возможные синдромы,
аналогичные схемы подключаются
дополнительно через схему ИЛИ.

Рис.
6.59. Детектор
ошибки

Таким
образом, жесткое декодирование
полиномиальных кодов достаточно
громоздко аппаратно. Практически
ограничиваются обнаружением ошибок.

Мягкое
декодирование полиномиальных кодов
возможно в нескольких вариантах. Так
как это очень большой и очень
математизированный раздел, отметим
только два способа.

1.
Вместо конкретных значений 0 или 1
выбирается более тонкое, например,
двоичный код амплитуды сигнала в момент
отсчета. Если блочный код имеет n
разрядов, получается

отсчетов, которые впоследствии
оптимизируются по одному из алгоритмов.
В том числе возможны нечеткие решения,
когда часть разрядов однозначно не
идентифицируется. Это так называемые
стирания. Такой алгоритм называется
поэлементным приемом. После такого
решения возможен так называемый прием
в целом, когда на второй стадии
анализируется весь код. При этом
используются методы максимального
правдоподобия или аналогичные методы
оптимизации.

2.
Второй способ трансформирует код в
условную частотную область с помощью
операции, косвенно трансформирующую
код по подобию интеграла Фурье. Само
выражение имеет вид:

(6.56)

где

– примитивный элемент в кольце по модулю
(n-1),

– текущий разряд кода. Это – тоже
-разрядный
код, в котором суммирование осуществляется
по циклическому принципу, но с особыми
свойствами. Обратное преобразование
выглядит так:

(6.57)

Здесь
знак «–» означает обратный порядок
счета примитивных элементов.

Кроме
предложенных спектральных оценок S_j,
используется также локаторный
многочлен: код, определяемый
соотношением:

(6.58)

Это также код (в
частном случае двоичный) со специфическими
свойствами, которые позволяют обнаружить
как одиночные ошибки, так и их пачки
(пачкой называется несколько ошибок
подряд).

Источник

Авторы
Резюме
Файлы
Ключевые слова
Литература

Барсагаев А.А.

1

Калмыков М.И.

1 Федеральное государственное автономное образовательное учреждение высшего профессионального образования «Северо-Кавказский федеральный университет»

В работе рассмотрены вопросы, связанные с анализом корректирующих способностей модулярных полиномиальных кодов (МПК). Данные коды позволяют осуществлять обработку данных в реальном масштабе времени за счет использования малоразрядных данных. При этом обработка информации осуществляется параллельно по вычислительным трактам и независимо друг от друга. Такое свойство МПК позволяет осуществлять процедуры поиска и коррекции ошибок. Для повышения корректирующих способностей кодов в МПК вводят дополнительные контрольные основания. С целью определения местоположения и глубины ошибки используются позиционные характеристики. В статье представлен алгоритм поиска и коррекции ошибок с использованием псевдоортогональных базисов модулярных полиномиальных кодов.

модулярные полиномиальные коды

параллельные вычисления

остатки

псевдоортогональные базисы

коррекция ошибок.

1. Бережной В.В., Калмыков И.А., Червяков Н.И., Щелкунова Ю.О., Шилов А.А. Нейросетевая реализация в полиномиальной системе классов вычетов операций ЦОС повышенной разрядности // Нейрокомпьютеры: разработка и применение. – 2004. – № 5-6. – С. 94.

2. Бережной В.В., Калмыков И.А., Червяков Н.И., Щелкунова Ю.О., Шилов А.А. Архитектура отказоустойчивой нейронной сети для цифровой обработки сигналов // Нейрокомпьютеры: разработка и применение. – 2004. – № 12. – С. 51-57.

3. Емарлукова Я.В., Калмыков И.А., Зиновьев А.В. Высокоскоростные систолические отказоустойчивые процессоры цифровой обработки сигналов для инфотелекоммуникационных систем // Инфокоммуникационные технологии. Самара. – 2009. – №2. – С. 31-37.

4. Калмыков И.А., Червяков Н.И., Щелкунова Ю.О., Шилов А.А. Нейросетевая реализация в полиномиальной системе классов вычетов операций ЦОС повышенной разрядности // Нейрокомпьютеры: разработка и применение. – 2004. – № 5-6. – С. 94.

5. Калмыков И.А., Чипига А.Ф. Структура нейронной сети для реализации цифровой обработки сигналов повышенной разрядности // Вестник Ставропольского государственного университета. – 2004. – Т.38. – С. 46.

6. Калмыков И.А., Петлеванный С.В., Сагдеев А.К., Емарлукова Я.В. Устройство для преобразования числа из полиномиальной системы классов вычетов в позиционный код с коррекцией ошибки // Патент России № 2309535. 31.03.2006. Бюл. № 30 от 27.10.2007.

7. Калмыков И.А., Гахов В.Р., Емарлукова Я.В. Устройство обнаружения и коррекции ошибок в кодах полиномиальной системы классов вычетов // Патент России № 2300801. 30.06.2005. Бюл. № 16 от 10.06.2007.

8. Хайватов А.Б., Калмыков И.А. Математическая модель отказоустойчивых вычислительных средств, функционирующих в полиномиальной системе классов вычетов // Инфокоммуникационные технологии. – 2007. – Т.5. – №3. – С.39-42.

9. Червяков Н.И., Калмыков И.А., Щелкунова Ю.О., Бережной В.В. Математическая модель нейронной сети для коррекции ошибок в непозиционном коде расширенного поля Галуа // Нейрокомпьютеры: разработка и применение. – 2003. – № 8-9. – С. 10-17.

10. Чипига А.А., Калмыков И.А., Лободин М.В. Устройство спектрального обнаружения и коррекции в кодах полиномиальной системы классов вычетов // Патент России № 2301441. Бюл. № 17 от 20.06.2007.

Введение

В последние годы цифровая обработка сигналов (ЦОС) занимает доминирующее положение в системах и средствах передачи и обработки информации в связи с неоспоримыми достоинствами – точность, гибкость и высокая скорость обработки. Кроме того, с развитием средств вычислительной техники системы ЦОС становятся все дешевле и компактнее. Эффективность ЦОС полностью определяется объемом вычислений, которые получаются при реализации математической модели процесса цифровой обработки сигнала с помощью специализированного процессора (СП). Снижение объема вычислений приводит к уменьшению аппаратурных затрат при реализации систем ЦОС или к повышению производительности вычислительного устройства. Таким образом, выбор алгебраической системы оптимальной с точки зрения минимума объема вычислений при реализации методов ЦОС является актуальной и важной.

Постановка задачи исследований. Как правило, в подавляющем большинстве приложений задачи ЦОС сводится к нахождению значений ортогонального преобразования конечной реализации сигнала для большого числа точек, что предопределяет повышенные требования к скорости обработки и разрядности вычислительного устройства. Решить данную проблему можно за счет перехода от одномерных вычислений к многомерным. В основу данного преобразования положена китайская теорема об остатках (КТО) [1-5].

Особое место среди таких систем занимает модулярная полиномиальная система класса вычетов, с помощью которых возможна организация ортогональных преобразований сигналов в расширенных полях Галуа . Если исходное число А представить в полиномиальной форме, а в качестве оснований выбрать минимальные многочлены поля Галуа, то справедливо

A (z) = (α1 (z), α2 (z).., αn (z)), (1)

где αi (z) ≡ A (z mod pi(z); pi (z) – минимальный многочлен.

Применение модулярных полиномиальных кодов позволяет свести операции в кольце полиномов к соответствующим операциям над остатками [1-6]. В этом случае

, (1)

где и — модулярный код в кольце полиномов; ; ; — операции сложения, вычитания и умножения в GF(p); l = 1, …,n.

Таким образом, основным достоинством непозиционных кодов является, то, что данные представляются в виде малоразрядных остатков, которые обрабатываются по параллельным вычислительным трактам. Это позволяет повысить скорость вычислений, что и предопределяет интерес к полиномиальным непозиционным кодам в различных областях применения [1-6].

В работах [1-5] предлагается для эффективной реализации ортогональных преобразований с высокой точностью и скоростью вычислений реализация дискретного преобразования Фурье (ДПФ) в кольце полиномов. В этом случае, если имеется кольцо полиномов P(z), с коэффициентами в виде элементов поля GF(p), то данное кольцо разлагается в сумму

, (2)

где Pl(z) – локальное кольцо полиномов, образованное неприводимым полиномом pl(z) над полем GF(p); l=1, …, n.

При этом в кольце полиномов можно организовать ортогональное преобразование, представляющее собой полиномиальное ДПФ, вида

, (3)

где , l=1,2,…,m; k=0,1,…d-1.

При этом должны выполняться следующие условия:

1. — первообразный элемент порядка d для локального кольца Pl(z).

2. d имеет мультипликативный обратный элемент d*.

Если отмеченные условия выполняются, то получается циклическая группа, которая имеет порядок d. В этом случае ортогональное преобразование является полиномиальным ДПФ для кольца вычетов P(z) если существуют преобразования над конечным кольцом Pl(z)

Поэтому ДПФ над Pl(z) можно обобщить над кольцом P(z), если конечное кольцо Pl(z) содержит корень d-ой степени из единицы и d имеет мультипликативный обратный элемент d*, такой что справедливо

. (4)

Основным достоинством системы класса вычетов является сравнительная простота выполнения модульных операций (сложения, вычитания, умножения). Формальные правила выполнения таких операций в МПК позволяют существенно повысить скорость вычислительных устройств ЦОС [5].

Кроме модульных операций, позволяющих повысить скорость обработки информации, модулярные коды позволяют обнаруживать и исправлять ошибки, возникающие в процессе функционирования СП. Если в качестве рабочих оснований выбрать k минимальных многочленов МПК (k<n), то данные основания определяют рабочий диапазон

. (5)

Если , то такой полином считается разрешенным и не содержит ошибок. В противном случае, полином, представленный в модулярном полиномиальном коде, содержит ошибки [6-10].

Для определения местоположения и глубины ошибки в полиномиальной системе классов вычетов используются позиционные характеристики. В работе [9] представлен алгоритм вычисления такой характеристики как интервальный номер. Синдром ошибки для полиномиального кода вычисляется в работе [8]. В работе [7] показана математическая модель поиска ошибочного основания с использованием алгоритма нулевизации. Структура устройства спектрального обнаружения и коррекции в кодах полиномиальной системы классов вычетов приведена в работе [10].

Одной из характеристик, использующемой при выполнении процедур поиска и коррекции ошибок в модулярных кодах, является след полинома. Для получения данной характеристики используются псевдоортогональные полиномы. Они представляют собой ортогональные полиномы, у которых нарушена ортогональность по нескольким основаниям. Известно, что если в псевдоортогональных полиномах нарушена ортогональность по контрольным основаниям, то данные полиномы являются ортогональными полиномами безизбыточной системы оснований полиномиальной системы классов вычетов.

Для получения псевдоортогональных полиномов проведем расширение системы оснований p1(z), …, pk(z) на r контрольных оснований pk+1(z), …, pk+r(z) и представим ортогональные полиномы в виде:

(6)

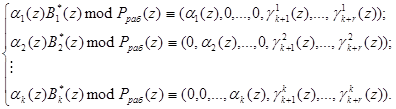
Выражение (6) определяет значения псевдоортогональных полиномов, у которых нарушена ортогональность по контрольным основаниям.

Согласно китайской теореме об остатках

, (7)

полином можно представить в виде:

. (8)

Тогда каждое слагаемое выражения (4) представляет собой

, (9)

где Bi*(z) – ортогональный базис безизбыточной системы оснований МПК.

Подставив выражение (6) в равенство (8), и учитывая, что в процессе выполнения операции не бывает выход за пределы Pраб(z), получаем

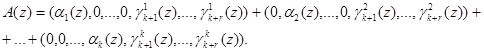
Следовательно, справедливо

(9)

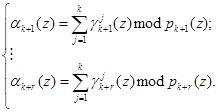
Таким образом, на основании (9) и воспользовавшись значениями псевдоортогональных полиномов, определяемых равенством (6), можно вычислить значения остатков по контрольным основаниям согласно

. (10)

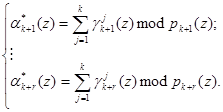
Затем на основании полученных значений и значений, поступающих на вход устройства коррекции ошибок, можно определить синдром ошибки согласно выражения

(11)

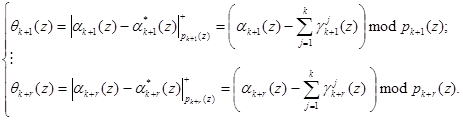
Если разность равна нулю, т.е. , то исходный полином является разрешенным и не содержит ошибки. В противном случае модулярная комбинация является запрещенной. Тогда в зависимости от величины синдрома ошибки осуществляется коррекция ошибки, т.е.

(12)

где— вектор ошибки модулярного кода; — глубина ошибки по i-му модулю МПК.

В работе [6] представлена структура устройства для преобразования числа из полиномиальной системы классов вычетов в позиционный код с коррекцией ошибки, в процессе функционирования которого используется данный алгоритм. Следует отметить, что этот алгоритм поиска и коррекции ошибок позволяет осуществить поиск и коррекцию всех однократных ошибок с использованием двух контрольных оснований и 90 процентов двоичных ошибок.

Вывод. В работе показана возможность осуществления цифровой обработки сигналов с использованием математической модели ЦОС, обладающей свойством кольца и поля. Применение полиномиальных кодов позволяет повысить скорость обработки данных за счет применения малоразрядных остатков и их параллельной архитектуре вычислений. Кроме того, МПК могут использоваться для повышения отказоустойчивости вычислительных систем. В работе рассмотрен алгоритм вычислений позиционной характеристики на основе ортогональных базисов, у которых нарушена ортогональность по контрольным основаниям.

Патент России № 2301441. Бюл. № 17 от 20.06.2007.

Библиографическая ссылка

Барсагаев А.А., Калмыков М.И. АЛГОРИТМЫ ОБНАРУЖЕНИЯ И КОРРЕКЦИИ ОШИБОК В МОДУЛЯРНЫХ ПОЛИНОМИАЛЬНЫХ КОДАХ // Международный журнал экспериментального образования. – 2014. – № 3-1.
– С. 103-106;

URL: https://expeducation.ru/ru/article/view?id=4672 (дата обращения: 12.02.2023).

Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»

(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)

Источник

Полиномиальные коды

При полиномиальном
кодировании
каждое сообщение отождествляется с многочленом, а само кодирование
состоит в умножении на фиксированный
многочлен. Полиномиальные коды — блочные и отличаются от рассмотренных
ранее только алгоритмами кодирования и декодирования.

Пусть $a=a_0ldots a_{m-1}$ — двоичное сообщение. Тогда
сопоставим ему многочлен $a(x)=a_0+a_1x+cdots+a_{m-1}x^{m-1}$ . Все вычисления
происходят в поле классов вычетов по модулю 2, т. е. от результата любой
арифметической операции берется остаток от его деления на 2.

Например, последовательности 10011 при m=5 соответствует
многочлен .

Зафиксируем некоторый многочлен степени ,

Полиномиальный код с кодирующим многочленом g(x) кодирует слово сообщения a(x) многочленом $b(x)=a(x)g(x)=b_0+b_1x+cdots+b_{n-1}x^{n-1}$ или кодовым словом
из коэффициентов этого многочлена $b=b_0ldots b_{n-1}$ . Условия g_0ne0 и g_kne0 необходимы, потому что в противном случае b_0 и $b_{n-1}$ не будут
нести никакой информации, т.к. они всегда будут нулями.

Пример. Рассмотрим кодирующий многочлен .
Сообщение 01011, отвечающее многочлену , будет закодировано
коэффициентами многочлена 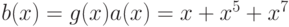, т.е. .

Полиномиальный код с кодирующим многочленом g(x) степени является матричным кодом с кодирующей матрицей размерности :

$G=leftlbrackmatrix{ g_0 & g_1 & g_2 & cdots & g_k & 0 & 0 & cdots & 0cr 0 & g_0 & g_1 & cdots & g_{k-1} & g_k & 0 & cdots & 0cr 0 & 0 & g_0 & cdots & g_{k-2} & g_{k-1} & g_k & cdots & 0cr cdots&cdots&cdots& cdots &cdots & cdots &cdots& cdots &cdotscr 0 &0 &0 & cdots &cdots & cdots &cdots& cdots &g_kcr} rightrbrack.$

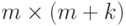
Т е. ненулевые элементы в 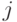-й строке — это
последовательность коэффициентов кодирующего многочлена, расположенных с 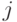-го по (j+k) -й
столбцах.

Например, (3,6) -код с кодирующим многочленом 1+x+x^3 отвечает матрице

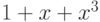
или отображению: ; ; ; ; ; ; ; .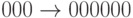

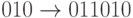
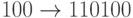
Полиномиальные коды являются групповыми.

Это следует из того, что коды,
получаемые матричным кодированием, — групповые.

Рассмотрим (m,n) -код с кодирующим многочленом g(x) . Строка ошибок $e=e_0ldots e_{n-1}$ останется необнаруженной в том и только в том
случае, если соответствующий ей многочлен $e(x)=e_0+e_1x+cdots+e_{n-1}x^{n-1}$ делится на g(x) .

Действительно, 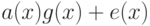делится на g(x) тогда и только
тогда, когда e(x) делится на g(x) . Поэтому любая
ошибка, многочлен которой не делится на g(x) , будет обнаружена и, соответственно,
любая ошибка, многочлен которой делится на g(x) , не может быть
обнаружена.

Таким образом, обнаружение ошибки при использовании полиномиального кода с
кодирующим многочленом g(x) может быть реализовано при помощи
алгоритма деления многочленов с остатком: если остаток ненулевой, то при передаче
произошло искажение данных.

Коды Хэмминга можно строить как полиномиальные, например, кодирующий
многочлен определяет совершенный (4,7) -код, отличный от
рассмотренного ранее.

Вообще же, если кодирующий многочлен g(x) , порождающий
соответствующий (m,n) -код, не является делителем ни одного из многочленов вида x^j+1 при j<n , то минимальное расстояние между кодовыми словами
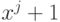
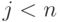
порожденного им кода не меньше 3.

Пусть 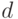— минимальное расстояние между кодовыми
словами, оно равно минимуму среди весов ненулевых кодовых слов. Предположим 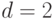d=2 .
Тогда существует a(x) такой, что и
степень b(x) не больше . Вес равен 2, поэтому
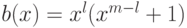
и l<m<n . Следовательно, $b(x)=x^l(x^{m-l}+1)$ , что означает, что $x^{m-l}+1$
должен делиться на g(x) , а это невозможно по условию. Если предположить, что d=1 , то это
приведет к утверждению о том, что x^m должен делиться на g(x) , что тоже
противоречит условию. Итак, dge3 .

Кодирующий многочлен $x^{11}+x^9+x^7+x^6+x^5+x+1$ определяет
совершенный (12,23) -код Голея (Golay) с минимальным расстоянием
между кодовыми словами 7.

В 1971 году финскими и советскими математиками было доказано³²⁰, что
кроме кодов Хэмминга и Голея других совершенных кодов нет.

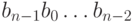
Наиболее интересными среди полиномиальных кодов являются циклические коды, в которых вместе с любым кодовым словом вида $b_0ldots b_{n-2}b_{n-1}$ есть кодовое слово $b_{n-1}b_0ldots b_{n-2}$ .

Упражнение 43
По кодирующему многочлену 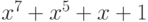построить полиномиальные
коды для двоичных сообщений 0100, 10001101, 11110.

Упражнение 44
Принадлежат ли коду Голея кодовые слова 10000101011111010011111
и 11000111011110010011111?

Источник

From Wikipedia, the free encyclopedia

In coding theory, a polynomial code is a type of linear code whose set of valid code words consists of those polynomials (usually of some fixed length) that are divisible by a given fixed polynomial (of shorter length, called the generator polynomial).

Definition[edit]

Fix a finite field GF(q) , whose elements we call symbols. For the purposes of constructing polynomial codes, we identify a string of symbols $a_{{n-1}}ldots a_{0}$ with the polynomial

$a_{{n-1}}x^{{n-1}}+cdots +a_{1}x+a_{0}.,$

Fix integers mleq n and let g(x) be some fixed polynomial of degree , called the generator polynomial. The polynomial code generated by is the code whose code words are precisely the polynomials of degree less than that are divisible (without remainder) by g(x) .

Example[edit]

Consider the polynomial code over with n=5 , m=2 , and generator polynomial $g(x)=x^{2}+x+1$ . This code consists of the following code words:

0cdot g(x),quad 1cdot g(x),quad xcdot g(x),quad (x+1)cdot g(x),

$x^{2}cdot g(x),quad (x^{2}+1)cdot g(x),quad (x^{2}+x)cdot g(x),quad (x^{2}+x+1)cdot g(x).$

Or written explicitly:

$0,quad x^{2}+x+1,quad x^{3}+x^{2}+x,quad x^{3}+2x^{2}+2x+1,$

$x^{4}+x^{3}+x^{2},quad x^{4}+x^{3}+2x^{2}+x+1,quad x^{4}+2x^{3}+2x^{2}+x,quad x^{4}+2x^{3}+3x^{2}+2x+1.$

Since the polynomial code is defined over the Binary Galois Field , polynomial elements are represented as a modulo-2 sum and the final polynomials are:

$0,quad x^{2}+x+1,quad x^{3}+x^{2}+x,quad x^{3}+1,$

$x^{4}+x^{3}+x^{2},quad x^{4}+x^{3}+x+1,quad x^{4}+x,quad x^{4}+x^{2}+1.$

Equivalently, expressed as strings of binary digits, the codewords are:

This, as every polynomial code, is indeed a linear code, i.e., linear combinations of code words are again code words. In a case like this where the field is GF(2), linear combinations are found by taking the XOR of the codewords expressed in binary form (e.g. 00111 XOR 10010 = 10101).

Encoding[edit]

In a polynomial code over GF(q) with code length and generator polynomial g(x) of degree ,
there will be exactly $q^{{n-m}}$ code words. Indeed, by definition, p(x) is a code word if and only if it is of the form , where q(x) (the quotient) is of degree less than n-m . Since there are $q^{{n-m}}$ such quotients available, there are the same number of possible code words.
Plain (unencoded) data words should therefore be of length n-m

Some authors, such as (Lidl & Pilz, 1999), only discuss the mapping as the assignment from data words to code words. However, this has the disadvantage that the data word does not appear as part of the code word.

Instead, the following method is often used to create a systematic code: given a data word d(x) of length n-m , first multiply d(x) by $x^{m}$ , which has the effect of shifting d(x) by places to the left. In general, $x^{m}d(x)$ will not be divisible by g(x) , i.e., it will not be a valid code word. However, there is a unique code word that can be obtained by adjusting the rightmost symbols of $x^{m}d(x)$ .
To calculate it, compute the remainder of dividing $x^{m}d(x)$ by g(x) :

$x^{m}d(x)=g(x)cdot q(x)+r(x),,$

where r(x) is of degree less than . The code word corresponding to the data word d(x) is then defined to be

$p(x):=x^{m}d(x)-r(x),,$

Note the following properties:

, which is divisible by . In particular, is a valid code word.
Since is of degree less than , the leftmost symbols of agree with the corresponding symbols of $x^{m}d(x)$ . In other words, the first symbols of the code word are the same as the original data word. The remaining symbols are called checksum digits or check bits.

Example[edit]

For the above code with n=5 , m=2 , and generator polynomial $g(x)=x^{2}+x+1$ , we obtain the following assignment from data words to codewords:

000 ↦ 00000
001 ↦ 00111
010 ↦ 01001
011 ↦ 01110
100 ↦ 10010
101 ↦ 10101
110 ↦ 11011
111 ↦ 11100

Decoding[edit]

An erroneous message can be detected in a straightforward way through polynomial division by the generator polynomial resulting in a non-zero remainder.

Assuming that the code word is free of errors, a systematic code can be decoded simply by stripping away the checksum digits.

If there are errors, then error correction should be performed before decoding. Efficient decoding algorithms exist for specific polynomial codes, such as BCH codes.

Properties of polynomial codes[edit]

As for all digital codes, the error detection and correction abilities of polynomial codes are determined by the minimum Hamming distance of the code. Since polynomial codes are linear codes, the minimum Hamming distance is equal to the minimum weight of any non-zero codeword. In the example above, the minimum Hamming distance is 2, since 01001 is a codeword, and there is no nonzero codeword with only one bit set.

More specific properties of a polynomial code often depend on particular algebraic properties of its generator polynomial. Here are some examples of such properties:

The algebraic nature of polynomial codes, with cleverly chosen generator polynomials, can also often be exploited to find efficient error correction algorithms. This is the case for BCH codes.

Specific families of polynomial codes[edit]

Cyclic codes – every cyclic code is also a polynomial code; a popular example is the CRC code.
BCH codes – a family of cyclic codes with high Hamming distance and efficient algebraic error correction algorithms.
Reed–Solomon codes – an important subset of BCH codes with particularly efficient structure.

References[edit]

W.J. Gilbert and W.K. Nicholson: Modern Algebra with Applications, 2nd edition, Wiley, 2004.
R. Lidl and G. Pilz. Applied Abstract Algebra, 2nd edition. Wiley, 1999.

Источник

From Wikipedia, the free encyclopedia

Definition[edit]

Fix a finite field GF(q) , whose elements we call symbols. For the purposes of constructing polynomial codes, we identify a string of symbols $a_{{n-1}}ldots a_{0}$ with the polynomial

$a_{{n-1}}x^{{n-1}}+cdots +a_{1}x+a_{0}.,$

Example[edit]

Consider the polynomial code over with n=5 , m=2 , and generator polynomial $g(x)=x^{2}+x+1$ . This code consists of the following code words:

$x^{2}cdot g(x),quad (x^{2}+1)cdot g(x),quad (x^{2}+x)cdot g(x),quad (x^{2}+x+1)cdot g(x).$

Or written explicitly:

$0,quad x^{2}+x+1,quad x^{3}+x^{2}+x,quad x^{3}+2x^{2}+2x+1,$

$x^{4}+x^{3}+x^{2},quad x^{4}+x^{3}+2x^{2}+x+1,quad x^{4}+2x^{3}+2x^{2}+x,quad x^{4}+2x^{3}+3x^{2}+2x+1.$

Since the polynomial code is defined over the Binary Galois Field , polynomial elements are represented as a modulo-2 sum and the final polynomials are:

$0,quad x^{2}+x+1,quad x^{3}+x^{2}+x,quad x^{3}+1,$

$x^{4}+x^{3}+x^{2},quad x^{4}+x^{3}+x+1,quad x^{4}+x,quad x^{4}+x^{2}+1.$

Equivalently, expressed as strings of binary digits, the codewords are:

Encoding[edit]

$x^{m}d(x)=g(x)cdot q(x)+r(x),,$

where r(x) is of degree less than . The code word corresponding to the data word d(x) is then defined to be

$p(x):=x^{m}d(x)-r(x),,$

Note the following properties:

, which is divisible by . In particular, is a valid code word.
Since is of degree less than , the leftmost symbols of agree with the corresponding symbols of $x^{m}d(x)$ . In other words, the first symbols of the code word are the same as the original data word. The remaining symbols are called checksum digits or check bits.

Example[edit]

For the above code with n=5 , m=2 , and generator polynomial $g(x)=x^{2}+x+1$ , we obtain the following assignment from data words to codewords:

000 ↦ 00000
001 ↦ 00111
010 ↦ 01001
011 ↦ 01110
100 ↦ 10010
101 ↦ 10101
110 ↦ 11011
111 ↦ 11100

Decoding[edit]

An erroneous message can be detected in a straightforward way through polynomial division by the generator polynomial resulting in a non-zero remainder.

Assuming that the code word is free of errors, a systematic code can be decoded simply by stripping away the checksum digits.

If there are errors, then error correction should be performed before decoding. Efficient decoding algorithms exist for specific polynomial codes, such as BCH codes.

Properties of polynomial codes[edit]

More specific properties of a polynomial code often depend on particular algebraic properties of its generator polynomial. Here are some examples of such properties:

The algebraic nature of polynomial codes, with cleverly chosen generator polynomials, can also often be exploited to find efficient error correction algorithms. This is the case for BCH codes.

Specific families of polynomial codes[edit]

Cyclic codes – every cyclic code is also a polynomial code; a popular example is the CRC code.
BCH codes – a family of cyclic codes with high Hamming distance and efficient algebraic error correction algorithms.
Reed–Solomon codes – an important subset of BCH codes with particularly efficient structure.

References[edit]

W.J. Gilbert and W.K. Nicholson: Modern Algebra with Applications, 2nd edition, Wiley, 2004.
R. Lidl and G. Pilz. Applied Abstract Algebra, 2nd edition. Wiley, 1999.

Источник

В теории кодирования, полиномиальный код — это тип линейного кода, чей набор допустимых кодовых слов состоит из этих полиномов (обычно некоторой фиксированной длины) которые делятся на заданный фиксированный полином (меньшей длины, называемый порождающим полиномом).

Содержание

1 Определение
2 Пример
3 Кодирование
- 3.1 Пример
4 Декодирование
5 Свойства полиномиальных кодов
6 Конкретные семейства полиномиальных кодов
7 Ссылки

Определение

Зафиксируйте конечное поле GF (q) { displaystyle GF (q)} GF (q) , элементы которого мы называем символами. Для построения полиномиальных кодов мы идентифицируем строку из n { displaystyle n}символов an — 1… a 0 { displaystyle a_ {n-1} ldots a_ {0}} $a _ {{n-1}} ldots a_ {0}$ с многочленом

an — 1 xn — 1 + ⋯ + a 1 x + a 0. { displaystyle a_ {n-1} x ^ {n-1} + cdots + a_ {1} x + a_ {0}. ,} $a _ {{n- 1}} x ^ {{n-1}} + cdots + a_ {1} x + a_ {0}. ,$

Исправить целые числа m ≤ n { displaystyle m leq n} m leq n и пусть g (x) { displaystyle g (x)} g (x) будет некоторым фиксированным многочленом степени m { displaystyle m}, называемый образующим полиномом. Код полинома, сгенерированный функцией g (x) { displaystyle g (x)} g (x) , представляет собой код, кодовые слова которого являются в точности полиномами степени меньше n { displaystyle n}, которые делятся (без остатка) на g (x) { displaystyle g (x)} g (x) .

Пример

Рассмотрим код полинома над GF (2) = {0, 1} { displaystyle GF (2) = {0,1 }}с n = 5 { displaystyle n = 5} n = 5 , m = 2 { displaystyle m = 2} m = 2 и порождающий многочлен g (x) = x 2 + x + 1 { displaystyle g (x) = x ^ {2} + x +1} $g (x) = x ^ {2} + x + 1$ . Этот код состоит из следующих кодовых слов:

0 ⋅ g (x), 1 ⋅ g (x), x ⋅ g (x), (x + 1) ⋅ g (x), { displaystyle 0 cdot g (x), quad 1 cdot g (x), quad x cdot g (x), quad (x + 1) cdot g (x),}

x 2 ⋅ g (x), (х 2 + 1) ⋅ g (x), (x 2 + x) ⋅ g (x), (x 2 + x + 1) ⋅ g (x). { Displaystyle х ^ {2} cdot g (x), quad (x ^ {2} +1) cdot g (x), quad (x ^ {2} + x) cdot g (x), quad (x ^ {2} + x + 1) cdot g (x).} $x ^ {2} cdot g (x), quad (x ^ {2} +1) cdot g (x), quad (x ^ {2} + x) cdot g (x), quad (x ^ {2} + x +1) cdot g (x).$

Или явно написано:

0, x 2 + x + 1, x 3 + x 2 + x, x 3 + 2 Икс 2 + 2 Икс + 1, { Displaystyle 0, quad x ^ {2} + x + 1, quad x ^ {3} + x ^ {2} + x, quad x ^ {3 } + 2x ^ {2} + 2x + 1,} $0, quad x ^ {2} + x + 1, quad x ^ {3} + x ^ {2} + x, quad x ^ {3} + 2x ^ {2} + 2x + 1,$

x 4 + x 3 + x 2, x 4 + x 3 + 2 x 2 + x + 1, x 4 + 2 x 3 + 2 x 2 + x, x 4 + 2 x 3 + 3 x 2 + 2 x + 1. { displaystyle x ^ {4} + x ^ {3} + x ^ {2}, quad x ^ {4} + x ^ { 3} + 2x ^ {2} + x + 1, quad x ^ {4} + 2x ^ {3} + 2x ^ {2} + x, quad x ^ {4} + 2x ^ {3} + 3x ^ {2} + 2x + 1.} $x ^ {4 } + x ^ {3} + x ^ {2}, quad x ^ {4} + x ^ {3} + 2x ^ {2} + x + 1, quad x ^ {4} + 2x ^ {3 } + 2x ^ {2} + x, quad x ^ {4} + 2x ^ {3} + 3x ^ {2} + 2x + 1.$

Поскольку полиномиальный код определен над двоичным полем Галуа GF (2) = {0, 1} { displaystyle GF (2) = {0,1 }}, полиномиальные элементы представлены в виде суммы по модулю -2, а окончательные многочлены:

0, x 2 + x + 1, x 3 + x 2 + Икс, Икс 3 + 1, { Displaystyle 0, quad x ^ {2} + x + 1, quad x ^ {3} + x ^ {2} + x, quad x ^ {3} +1, } $0, quad x ^ {2} + x + 1, quad x ^ {3} + x ^ {2} + x, quad x ^ {3} +1,$

x 4 + x 3 + x 2, x 4 + x 3 + x + 1, x 4 + x, x 4 + x 2 + 1. { displaystyle x ^ {4} + x ^ {3} + x ^ {2}, quad x ^ {4} + x ^ {3} + x + 1, quad x ^ {4} + x, quad x ^ {4} + x ^ {2} +1.} $x ^ {4} + x ^ {3} + x ^ {2}, quad x ^ {4} + x ^ {3} + x + 1, quad x ^ {4} + x, quad x ^ {4} + x ^ {2} +1.$

Эквивалентно, выраженные как строки двоичных цифр, кодовые слова:

00000, 00111, 01110, 01001, { displaystyle 00000, quad 00111, quad 01110, quad 01001,}

11100, 11011, 10010, 10101. { displaystyle 11100, quad 11011, quad 10010, quad 10101.}

Это, как и любой полиномиальный код, действительно является линейным кодом, то есть линейные комбинации кодовых слов снова являются кодовыми словами. В случае, подобном этому, когда поле — GF (2), линейные комбинации находятся путем выполнения XOR кодовых слов, выраженных в двоичной форме (например, 00111 XOR 10010 = 10101).

Кодирование

В полиномиальном коде над GF (q) { displaystyle GF (q)} GF (q) с длиной кода n { displaystyle n }и порождающий полином g (x) { displaystyle g (x)} g (x) степени m { displaystyle m}, там будет точно qn — m { displaystyle q ^ {nm}} $q ^ {{nm}}$ кодовых слов. Действительно, по определению p (x) { displaystyle p (x)} p (x) является кодовым словом тогда и только тогда, когда оно имеет форму p (x) = g (x) ⋅ Q (Икс) { Displaystyle р (х) = г (х) cdot q (х)}, где q (х) { Displaystyle q (х)} q (x) (частное) имеет степень меньше n — m { displaystyle nm}. Поскольку существует q n — m { displaystyle q ^ {n-m}} $q ^ {{nm}}$ таких частных, существует такое же количество возможных кодовых слов. Поэтому простые (незакодированные) слова данных должны иметь длину n — m { displaystyle nm}

Некоторые авторы, такие как (Lidl Pilz, 1999), обсуждают только отображение q (x) ↦ g (x) ⋅ q (x) { displaystyle q (x) mapsto g (x) cdot q (x)}как присвоение слов данных кодовым словам. Однако это имеет тот недостаток, что слово данных не появляется как часть кодового слова.

Вместо этого для создания систематического кода часто используется следующий метод: задано слово данных d (x) { displaystyle d (x)} d (x) длины n — m { displaystyle nm}, сначала умножьте d (x) { displaystyle d (x)} d (x) на xm { displaystyle x ^ {m}} $x ^ {m}$ , что приводит к сдвигу d (x) { displaystyle d (x)} d (x) на m { displaystyle m}слева. Как правило, xmd (x) { displaystyle x ^ {m} d (x)} $x ^ {m} d (x)$ не делится на g (x) { displaystyle g (x)} g (x) , т. Е. Это не будет допустимое кодовое слово. Однако существует уникальное кодовое слово, которое можно получить, настроив крайние правые символы m { displaystyle m}в xmd (x) { displaystyle x ^ {m} d ( x)} $x ^ {m} d (x)$ . Чтобы вычислить его, вычислите остаток от деления xmd (x) { displaystyle x ^ {m} d (x)} $x ^ {m} d (x)$ на g (x) { displaystyle g (x) } g (x) :

xmd (x) = g (x) ⋅ q (x) + r (x), { displaystyle x ^ {m} d (x) = g (x) cdot q (x) + r ( x), ,} $x ^ {m} d (x) = g (x) cdot q (x) + r (x), ,$

где r (x) { displaystyle r (x)} r (x) имеет степень меньше m { displaystyle m}. Кодовое слово, соответствующее слову данных d (x) { displaystyle d (x)} d (x) , затем определяется как

p (x): = xmd (x) — r ( x), { displaystyle p (x): = x ^ {m} d (x) -r (x), ,} $p (x): = x ^ {m} d (x) -r (x), ,$

Обратите внимание на следующие свойства:

p (x) = g (x) ⋅ q (x) { displaystyle p (x) = g (x) cdot q (x)}, который делится на g (x) { displaystyle g (x)}. В частности, p (x) { displaystyle p (x)}является допустимым кодовым словом.
Поскольку r (x) { displaystyle r (x)}имеет степень меньше m { displaystyle m}, крайний левый n — m { displaystyle nm}символов p (x) { displaystyle p (x)}согласен с соответствующими символами xmd (x) { displaystyle x ^ {m} d (x)} $x ^ {m} d (x)$ . Другими словами, первые символы n — m { displaystyle n-m}кодового слова совпадают с исходным словом данных. Оставшиеся символы m { displaystyle m}называются цифрами контрольной суммы или контрольными битами.

Пример

Для приведенного выше кода с n = 5 { displaystyle n = 5} n = 5 , m = 2 { displaystyle m = 2} m = 2 и порождающий многочлен g (x) = x 2 + x + 1 { displaystyle g (x) = x ^ {2} + x + 1} $g (x) = x ^ {2} + x + 1$ , мы получаем следующее присвоение слов данных кодовым словам:

000 ↦ 000 00
001 ↦ 001 11
010 ↦ 010 01
011 ↦ 011 10
100 ↦ 100 10
101 ↦ 101 01
110 ↦ 110 11
111 ↦ 111 00

Декодирование

Ошибочное сообщение может быть обнаружено прямым способом с помощью полиномиального деления на порождающий полином, что приводит к ненулевому остатку.

Предполагая, что кодовое слово не содержит ошибок, систематический код может быть декодирован простым удалением m { displaystyle m}цифр контрольной суммы.

Если есть ошибки, то перед декодированием следует выполнить исправление ошибок. Эффективные алгоритмы декодирования существуют для конкретных полиномиальных кодов, таких как коды BCH.

Свойства полиномиальных кодов

Как и для всех цифровых кодов, возможности обнаружения и исправления ошибок полиномиальных кодов определяются минимальным расстоянием Хэмминга кода. Поскольку полиномиальные коды являются линейными кодами, минимальное расстояние Хэмминга равно минимальному весу любого ненулевого кодового слова. В приведенном выше примере минимальное расстояние Хэмминга равно 2, поскольку 01001 — это кодовое слово, и нет ненулевого кодового слова с только одним набором битов.

Более конкретные свойства полиномиального кода часто зависят от конкретных алгебраических свойств его порождающего полинома. Вот несколько примеров таких свойств:

Алгебраическая природа полиномиальных кодов с умно выбранными порождающими полиномами, также часто можно использовать для поиска эффективных алгоритмов исправления ошибок. Это имеет место для кодов BCH.

Конкретные семейства полиномиальных кодов

Циклические коды — каждый циклический код также является полиномиальным кодом; популярным примером является код CRC.
коды BCH — семейство циклических кодов с большим расстоянием Хэмминга и эффективными алгоритмами исправления алгебраических ошибок.
Коды Рида – Соломона — важное подмножество кодов BCH с особенно эффективной структурой.

Ссылки

WJ Гилберт и В.К. Николсон: Современная алгебра с приложениями, 2-е издание, Wiley, 2004.
R. Lidl и G. Pilz. Прикладная абстрактная алгебра, 2-е издание. Wiley, 1999.

Источник

Библиографическая ссылка

Полиномиальные коды

Definition[edit]

Example[edit]

Encoding[edit]

Example[edit]

Decoding[edit]

Properties of polynomial codes[edit]

Specific families of polynomial codes[edit]

References[edit]

Definition[edit]

Example[edit]

Encoding[edit]

Example[edit]

Decoding[edit]

Properties of polynomial codes[edit]

Specific families of polynomial codes[edit]

References[edit]

Содержание

Определение

Пример

Кодирование

Пример

Декодирование

Свойства полиномиальных кодов

Конкретные семейства полиномиальных кодов

Ссылки

Читайте также: